Abstract
The extension of 2D ferromagnetic structures into 3D curved geometry enables to tune its magnetic properties such as uniaxial magnetic anisotropy. Tuning the anisotropy with strain and curvature has become a promising ingredient in modern electronics, such as flexible and stretchable magnetoelectronic devices, impedance-based field sensors, and strain gauges, however, has been limited to extended thin films and to only moderate bending. By applying a self-assembly rolling technique using a polymeric platform, we provide a template that allows homogeneous and controlled bending of a functional layer adhered to it, irrespective of its shape and size. This is an intriguing possibility to tailor the sign and magnitude of the surface strain of integrated, micron-sized devices. In this article, the impact of strain and curvature on the magnetic ground state and anisotropy is quantified for thin-film Permalloy micro-scale structures, fabricated on the surface of the tubular architectures, using solely electrical measurements.
Similar content being viewed by others
Introduction
Flexible, stretchable, and modern 3D microscale electronic devices based on magnetic materials such as impedance-based magnetic field sensors1,2,3, strain gauges4, and magnetoelectronics5 require an understanding of the magneto-electric behavior with respect to the experienced bending and reassembling into a modified geometry. Bending a 2D ferromagnetic membrane into a tubular geometry alters the curvature and induces strain, which influences the size, and orientation of magnetic domains, and the domain wall dynamics6,7,8,9. Hence, bending a magnetic membrane significantly affects the performance of electronic devices7,10. On one hand, efforts have been made to reduce these effects to achieve stable magnetic properties under moderate deformation for flexible and stretchable magnetoelectronic applications11,12,13. On the other hand, equally promising findings on deformation-induced magnetic properties14,15 have already provided highly sensitive microscale magnetoelectronic devices1,16. Additionally, reassembling 2D magnetic structures into 3D geometries allows tapping into the unexplored rich physics emerging from the curvature gradient17,18,19,20,21,22,23. These studies and theoretical investigations have proven that strain and shape-induced magnetostatic interactions are influential across multiple scales, while the curvature and shape-driven exchange interactions are regulated by the gradient of curvature, which for tubular geometry becomes relevant at small radii (hundreds of nanometers and below)10,19,20,21,23,24. Strain-induced changes in magnetic properties have been studied with different mechanisms, mainly by applying in-plane tensile strain25,26,27, and bending a 2D extended magnetic thin film28. Bending has been performed by either bonding a magnetic film (deposited on a flexible polymeric substrate) onto cylindrical support of known radius ranging from millimeter to centimeter or by bending it through a mechanical set-up29.
Recent reports30,31,32,33 have presented reliable methods to induce curvature and strain in magnetic films via a self-assembled geometrical transformation. One approach consists of preparing strained mono or bilayer metallic thin-films30,31,32, e.g. by heteroepitaxy, which self-assembled into a tubular “Swiss-roll” architecture, once the layers are released from the substrate. This can create multi-winding tubes with diameters ranging from a few to tens of micrometers. With the functional layer being part of the strain architecture, one is however restricted in the choice of magnetic film thickness and size. It is not possible to homogeneously strain structured micron-sized magnetic elements. A remedy to that is the use of a polymeric platform33—a structured polymer layer architecture consisting of a sacrificial layer, hydrogel as a swellable layer, and a stiff polyimide layer—that self-assembles into a multi-winding tube and provides the curved and strained template for an arbitrary magnetic structure on top of it. In a first work, on a 100 nm-thick extended Permalloy membrane, the giant magnetoimpedance (GMI) signal was found to increase by about 80 times1, which was attributed to azimuthal magnetic domains forming upon rolling. Possible origins are magnetostatic coupling between the side edges of the rolled membrane and strain-induced magnetic anisotropy32,34,35, but a clear recipe for acquiring azimuthal magnetic domains in rolled-up soft ferromagnetic materials is not available. Advantages of azimuthal domains have also been observed in the form of a 2 times increased domain wall velocity9,36 in comparison with transverse domains in flat stripes. This is very attractive for potential applications in future magnetic devices such as race-track memory37,38 and magnetic logical devices39.
Thus, it is crucial to understand the favorable conditions for achieving a specific magnetic anisotropy in soft magnetic materials. For that, the behavior of rolled magnetoelectronic micron-sized structures needs to be extensively studied with respect to the magnitude and sign of the external strain. Furthermore, this also requires the development of characterization methods suitable for quantifying anisotropies in tubular geometries.
In this work, we address the influence of curvature on magnetization due to applied strain. We assess the magnetization reversal of rolled structures grown on polymeric bilayers with two conventional methods, namely by imaging with optical Kerr microscopy and by electrical measurements based on the anisotropic magnetoresistance (AMR) effect to qualify and quantify the strain-induced magnetic anisotropy. These measurements are supported by micromagnetic simulations to correctly evaluate the effect of a strain-induced uniaxial magnetic anisotropy (UMA) on the AMR response. The specifically designed self-assembled “Swiss-roll” architectures allow to tune the geometry of the rolled membrane (rolling direction, radius of curvature, number of windings, and spacing between the winding layers) and hence the strain (sign and magnitude) and anisotropy (orientation and magnitude) of arbitrary magnetic micron-sized geometries prepared on their surface. By designing micron-sized Permalloy (Ni78Fe22) structures with dimensions in the azimuthal direction small compared to the circumference of the polymeric tube, curvature-induced changes in shape anisotropy1,34 (magnetostatic interaction between side edges) can be neglected. This allows us to probe the effect of strain on planar micro-scale Permalloy stripes by rolling them down- and up-wards of different diameters to achieve curvature and strains with different signs and magnitudes as illustrated in Fig. 1a, b. For this work, we choose soft ferromagnetic NiFe alloy with 78% nickel, as it possesses large enough positive magnetostriction such that the strain-induced changes in magnetic anisotropy can be seen with small strain values, at the same time the composition stays close to the maximum permeability region40, which is suitable for later experiments on domain wall dynamics in rolled structures and giant magnetoimpedance (GMI) based field sensors. With the chosen film thickness of 100 nm, the AMR coefficient of Permalloy reaches its maximum value41, providing sufficient sensitivity to probe magnetization reversal. Thus, self-assembly based on the polymeric platform12 provides the possibility to pattern and transform planar micro-scale structures into 3D architectures with tailored strain irrespective of their initial 2D shape and size.
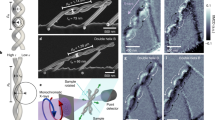
Schematic illustration of self-assembly a-i roll-down and b-i roll-up approach for adjusting sign and size of curvature and strain in a functional layer on top of the polymeric platform (PP). a-ii, b-ii Magnified view of the rolled structures, indicating tensile (yellow arrows) and compressive (black arrows) strain in the magnetic layer and illustrating the corresponding azimuthal and axial domain states. a-iii, b-iii Optical image of rolled-down and rolled-up polymer structure with contacted Ni78Fe22 stripe (scale bar, 200 µm) and a-iv, b-iv corresponding Kerr microscopical image of the domain state. Scale bar, 15 µm. c Schematic set-up of simultaneous magneto-optical and AMR measurement of a strained magnetic stripe lying on the dome of the polymeric tube. d Magnetic hysteresis and e AMR hysteresis were measured simultaneously on the Permalloy (Ni78Fe22) stripe with field along the stripe’s long axis (x-axis) before and after rolling.
Results
Controlled self-assembly rolling of microscale structures
Self-assembled rolling of the functional magnetic structures is achieved by depositing the functional structures on a transformable polymeric platform composed of a bilayer of hydrogel (HG) and polyimide (PI)33. Due to the large stiffness (Young’s modulus, YPI = 3.2 GPa42) and thickness of the PI layer, the strain state is hardly influenced by the functional magnetic layer, and the complete layer stack can be rolled down (Fig. 1a–i) or rolled-up (Fig. 1b–i) into tightly rolled tubes with diameters adjustable by the thickness of the PI and HG layers and the pH of solution used for rolling. Hence, the curvature and strain state in the functional layer is adjustable both in sign and size via the rolling direction (down or up) and rolling diameter, respectively. Schematics are seen in Fig. 1a-ii for negative curvature and tensile strain in rolled-down structures and in Fig. 1b-ii for positive curvature and compressive strain in rolled-up structures. The actual self-assembled devices are shown in Fig. 1a-iii, b-iii for roll-down and roll-up approaches, respectively. As the strain is induced in a post-growth step, no surface or curvature-related modifications can occur during the growth of the functional layer and the influence of strain is isolated. This provides a macroscopic strain stage on the scale of the self-assembled tubular structure with diameters down to 20 µm1. The effect of strain on the domain configuration in the long Permalloy stripe is right away visible by magneto-optical Kerr microscopy. Tensile strain in patterned Permalloy structures induces azimuthal anisotropy, which consequently aligns the magnetization transverse to the stripe (i.e. in the azimuthal direction, Fig. 1a–iv), whereas compressive strain leads to an induced axial anisotropy, which favors a monodomain state with magnetization along the stripe length (Fig. 1b–iv).
Although quantification of strain-induced anisotropy would be possible from MOKE hysteresis measurements (Fig. 1d), such an analysis is only feasible when the functional layer or structure is completely within the field of view, i.e. on the dome of the self-assembled tube (Fig. 1c). A much more elegant approach is to retrieve the anisotropy from the AMR response of the Permalloy stripe in a sweeping magnetic field (Fig. 1e). The application of a magnetic field rearranges the magnetic domain state and thus the local orientation of magnetic moments with respect to the current direction, leading to a configuration dependent resistance according to the following equation43:
where \(\theta\) = \(({{{\mathbf{m}}}},\hat J)\) is the angle between the magnetization m(H) and the electric current flowing along the stripe’s long axis. To guarantee a well-controlled field orientation irrespective of the position of the AMR stripe within the self-assembled tube, a field parallels the tube axis, and thus the stripe length has been chosen. All strain-related changes in the anisotropy are detectable in the AMR signal, either through an increased nucleation field for the rolled-up structures with increased axial anisotropy (see spike features in the low-field region for planar and rolled-up structures in Supplementary Fig. 1 and Supplementary Note 1), or through the domain reorientation into the azimuthal multidomain zero-field state for \(\left| {{{\boldsymbol{H}}}} \right| \,<\, H_{{{{\mathrm{sat}}}}}\) in the rolled-down structures being responsible for the gradual decrease in R in the same field range. The details of these processes will be discussed further below.
Qualitative characterization of strained Permalloy structures
To realize a bending with positive and negative curvature, the order of the HG and PI layers in the PP has to be adapted. The order SL/PI/HG (Fig. 2a), where the hydrogel swell in an alkaline solution against the retaining force of the PI, will lead to a rolling down of the structure, once it is released from the substrate by etching the SL (Fig. 2e). The reversed order, SL/HG/PI (Fig. 2b), leads to a self-assembled rolling up (Fig. 2f). Furthermore, the HG is structured to provide a non-covered window of pure PI, which is used as a template for the functional layer(s). The full material architecture, design, and self-assembly process are detailed in the “Methods” section.
Polymeric platform (PP) before rolling for a rolled-down and b rolled-up fabrication. c Schematic images of magnetic domains in c-i disc, c-ii square, c-iii rectangle, and c-iv stripe structures in the planar state. d Kerr images of these four planar structures. Schematic image of the polymeric platform (with magnetic stripe and contact wires) after etching the sacrificial layer (SL) and e rolling down, and f rolling up. Kerr images of g rolled-down, and h rolled-up magnetic structures after ac-demagnetization in a field transverse to the induced anisotropy axis. Scale bars in d, g, h are 15 µm. The black and white arrows in the domains indicate the magnetization direction. The yellow and black arrows next to the Kerr images show the tensile and compressive strain (ε) direction.
Micron-sized patterns of 100 nm-thick Permalloy prepared on the PI window (Fig. 2c-i–iv) qualitatively reveal the anisotropy in the as-prepared (Fig. 2d) and rolled states (Fig. 2g, h). In the unrolled state, the patterns with an aspect ratio 1:1 (discs, squares) adopt a point symmetric flux closure configuration following the van den Berg’s principle seen in the Kerr images43 (Fig. 2d-i, ii), with no magnetization direction favored. Elongated structures (rectangles, long stripes) reduce their magnetostatic energy conforming to the shape of the patterned element, i.e. favoring domains along the long axis of the patterns44 (Fig. 2d-iii, iv). After self-assembled roll-down, Kerr images with sensitivity along the vertical axis in the image show a clear preference for magnetization orientation transverse to the stripe’s long axis, specifically, in the azimuthal direction (Fig. 2g–i–iv). This is understood from the following equation45:
Ku is a positive magnetoelastic energy constant in the orientation of the uniaxial strain, resulting from the positive magnetostriction (λ) of the Ni78Fe22 layer and the positive (tensile) stress (σ > 0) upon rolling down. In the case of self-assembled roll-up (Fig. 2h), uniaxial compressive stress (σ < 0) causes an inversion of the sign of the magnetoelastic energy constant. Therefore a magnetization transverse to the uniaxial stress is preferred, resulting in basic domains that are now axially magnetized (Fig. 2h–i–iv).
The magnetization reversal and its consequence for the AMR signal due to the strain-induced changes in anisotropy are partly discussed in Fig. 1d, e. The shape-dominated anisotropy along the long axis of the unstrained stripe leads to a square-shaped easy axis hysteresis with sharp magnetization reversal at a field which we term nucleation field, Hn.
As the magnetization is mostly along the same axis as the electric current direction Ix, the AMR signal is constant except at Hn, where the nucleation process leads to an intermediate deviation of magnetization from the electric current axis. This behavior remains qualitatively unchanged when compressive strain in the rolled-up state supports the shape anisotropy with an additional induced uniaxial anisotropy along the tube axis. The increased effective anisotropy value merely leads to the increased nucleation field being visible in the magnetization hysteresis (Fig. 1d) and the AMR signal (shown in Supplementary Fig. 1). For an induced azimuthal anisotropy, the dense arrangement of azimuthal domains at zero field leads to a vanishing zero-field magnetization along the tube axis and consequently to a minimum in the AMR signal.
Quantitative analysis of strain-induced anisotropy
One of the central challenges in magnetism is the understanding of the magnetization reversal of functional material. In the case of 3D curved geometries, this task is complicated by the difficulties in accessing the whole structure with direct imaging techniques. Magnetization reversal of a magnetic structure depends on the structure’s shape, size, and magnetic properties of the material. Magnetization reversal in Permalloy films takes place mainly by magnetization rotation or domain wall motion when a low-frequency magnetic field is applied perpendicular and parallel to the easy axis, respectively. Despite the availability of advanced techniques such as X-ray spectroscopic imaging32,46,47, magnetoresistance48,49,50,51, and dynamic cantilever magnetometry52 for measuring the global magnetization of micro-and nanosized curved 3D structures, it remains difficult to draw a complete picture of the magnetic microstructure evolution upon analyzing a global hysteresis. A microscopic look at the domain configuration of structures curved in 3D, however, is likewise difficult. A promising possibility has been discussed recently for magnetization processes in rolled-up ferromagnetic membranes, where the domain configuration was observed in detail after transforming the tubular structure back into a flat membrane53. In the present experiments, we do not rely on unrolling a buried magnetization structure. Instead, we arrive at a complete characterization of the curvature-induced modification in the rolled-down structures using three factors: (i) due to the even curvature of the rolled-down membrane, the resulting homogeneously induced anisotropy is independent of position and can thus be observed locally at any region on the dome of the rolled-structure accessible to magnetic microscopy; (ii) domain observation is linked to a global electronic signal by simultaneously measuring magnetoresistance; (iii) micromagnetic simulations confirm the observed correlation between local (microscopic) and global (AMR) behavior as a general feature of an elongated AMR structure and connect the AMR signal quantitatively with the induced anisotropy.
Figure 3a displays the magnetic domain evolution of an AMR stripe in the rolled-down state as a function of an axial field together with the simultaneously measured AMR signal (the detailed magnetization reversal as a function of field transverse to the stripe for the rolled-down stripe and as a function of field along the stripe for a rolled-up stripe is reported in Supplementary Figs. 2, 3, Supplementary Note 2, and Supplementary Fig. 4 and Supplementary Note 3, respectively). The micromagnetically calculated counterpart is seen in Fig. 3b. The dimensions in the simulations are smaller than those of the experimentally investigated stripes due to limitations in computing power. However, the chosen dimensions of hundreds of nanometers are sufficiently large to replicate the experimentally observed magnetization patterns of the domains and domain walls (the reason for choosing larger UMA in simulated stripes is explained in Supplementary Note 4). All the features generally discussed in Fig. 1e are now detailed by direct Kerr observations. Above a saturating field, (|H | > Hsat) the magnetization is fully aligned along the strip leading to a constant resistance Rmax. Owing to the induced azimuthal anisotropy, at |H | = Hsat, first azimuthal domains with alternating my-components are nucleated and the magnetostatic energy is reduced by the formation of flux closure domains with m = mx. The non-collinear magnetic arrangement (m non-parallel to Ix) leads to the observed decrease in the AMR, with the absolute value depending on the remaining mx-component in the azimuthal domains and the fraction of closure domains. At zero field, the magnetic moments in the azimuthal domains are fully aligned in the y-direction and the closure domain size is reduced to a minimum, coinciding with the minimum in the AMR signal. Except for an unavoidable small hysteresis (visible in a small shift along the μ0Hx axis), the behavior is symmetric with respect to |H|.
a Top panel: AMR measurement on rolled-down stripe (length = 550 µm, width = 15 µm, thickness = 100 nm) with field sweep from negative to positive values along the stripe’s long axis. The black arrow inside the plot shows the field sweep direction and the red arrow points at the saturation field. Middle panel: the optical image of the self-assembled rolled-down stripe with four contacted wires, the area surrounded by a light blue dashed line is the area imaged in Kerr microscopy. Scale bar, 100 µm. Bottom panel: Magnetic domain states imaged at different stages of field sweep. Scale bar, 15 µm. b Top panel: AMR signal calculated for magnetization reversal of a simulated Permalloy planar stripe (length = 8 µm, width = 0.8 µm, thickness = 100 nm) with uniaxial magnetic anisotropy [(Ku)y = 40 kJ m−3] transverse to stripe’s axis (y-axis). Middle panel: schematic view of the simulated stripe with transverse magnetic anisotropy. Bottom panel: Magnetic domain states of the simulated stripe at different stages of the field sweep. Scale bar, 0.8 µm.
The field µ0Hsat, at which the magnetic and AMR hysteresis saturate nearly corresponds to the anisotropy field54. This suggests that the anisotropy field value can be extracted from the AMR hysteresis. The UMA energy Ku can be determined using the relation25:
where Ms is the saturation magnetization of Permalloy. This correlation of Hsat with the induced azimuthal anisotropy is anticipated, but nevertheless is non-trivial for a magnetization process involving domain processes and competing anisotropies and thus needs further proof. In a series of micromagnetic simulations, the domain evolution and corresponding AMR signal were calculated for Permalloy stripes of two different lengths and varying uniaxial anisotropies transverse to the stripes. In all cases, the saturation field Hsat, identified as a 1% reduction of AMR signal from Rmax (normalized to the maximum AMR signal ΔRmax), corresponds to the introduced anisotropy field Hani of the simulation to within 12% (see Supplementary Fig. 5). Hence, we can reliably quantify the strain-induced uniaxial anisotropy constant Ku for all rolled-down membranes by simple analysis of the measured AMR response and do not further need to rely on, e.g. optical access to the sensor stripe.
By increasing the diameter of the rolled-down membrane from 64 to 105 and 130 µm (Fig. 4a-i–iv), the saturation field Hsat as deduced for the AMR measurement (Fig. 4b) increases monotonously and can be converted into the uniaxial anisotropy energy Ku with the experimentally determined saturation polarization Ms = 0.69 MA m−1. Figure 4c summarizes Ku as a function of strain (ε) for three rolled-down Permalloy stripes. The strain in the magnetic stripe is estimated quantitatively by ε = ±h/R55, where h is the distance between the center of the magnetic stripe and the neutral axis of the PI/Ni78Fe22 bilayer and R is the radius of curvature. The calculation of h is exemplified in Supplementary Fig. 6 and Supplementary Note 5. The linear relation is the expected magnetoelastic behavior from the following equation43:
with Young’s modulus Y = 96.4 GPa for Permalloy56. The estimated value of the magnetostriction constant (λ) resulting from the slope of the linear fit is (1.42 ± 0.01) × 10–6 in close agreement with the direct measurement of the magnetostriction constant of the alloy Ni78Fe2240. As it is apparent from Eq. (4), relating induced anisotropy and strain, and from the linear fitting in Fig. 4c, the value of intercept is zero. That means, that any non-zero strain should contribute to the induced anisotropy45. However, to quantify the induced anisotropy with the presented method, the saturation field detected by AMR should be at least of the order of the field range of the switching event in the unstrained magnetic element.
a-i Optical image of the planar magnetic stripe with contact wires fabricated on top of the polymeric platform. a-ii,iii,iv Optical images of magnetic stripe after rolling down the polymeric platform with different diameters. Scale bar, 100 µm. Depending on the diameter of the tube, the magnetic stripe may be displaced from the tube’s dome as indicated by the blue arrows. The stripe in the case of a-ii is hidden under the polymeric tube. The red dashed lines in the images show the position from the bottom where the sacrificial layer starts in the planar polymeric platform. b AMR hysteresis measured for rolled stripes of different curvatures. c Estimated azimuthal uniaxial magnetic anisotropy, derived from the measured AMR signal vs. strain in the magnetic stripes. The error bars along the x- and y-axis represent the least count errors resulting from the measurement of bilayer (PI/Ni78Fe22) thicknesses, the radius of curvature, and AMR hysteresis measurements, respectively.
Discussion
We employed a self-assembly rolling technology based on a polymeric bilayer platform to controllably bend or roll a functional thin film microstructure. By means of this platform, the applied strain could be tailored both in sign and magnitude. This approach offers numerous possibilities for modifying the properties of functional materials for micron-sized devices. In the present case, bending/curving a Permalloy film with positive magnetostriction creates a strain-induced uniaxial anisotropy in the either azimuthal or axial direction. This is immediately visible in the equilibrium domain state of small structured elements and will, e.g. promote azimuthal domains in tubular GMI sensors.
Owing to the measurable anisotropic magnetoresistance of Permalloy, the modified magnetic configuration and reversal behavior in applied fields have a significant impact on the resistance signal and allow quantifying the induced uniaxial anisotropy. The developed electrical characterization method is easy to perform and capable of providing properties of magnetic structures hidden under the 3D polymer architecture as well as of tubular magnetic membranes1,32.
In summary, this work represents a fundamental study of the relationship between strain and magnetic microstructure and contributes to the understanding of the rich physics in the rapidly emerging field of 3-dimensional nanomagnetism57,58,59. The advanced creation and control of strain-induced anisotropy will favorably impact the area of field sensorics for magnetoencephalography1, magnetofluidic applications60, spin-wave filters61, and energy-efficient memory devices9,38 based on self-assembled rolled geometries. In addition, with the AMR ratio being sensitive to small strains as low as 0.17% and with the potential of further increasing the sensitivity, a simple Permalloy AMR structure has the potential to be used as a strain gauge in “Swiss-roll” architecture-based devices62,63.
Methods
Sample fabrication
We apply strain engineering to prepare rolled Permalloy structures after designing planar Permalloy elements on top of a polymeric shapeable platform33 relying on photo-patternable, thermally and chemically stable imide- and acrylic-based polymers. The polymeric shapeable platform contains three polymer layers; a sacrificial layer (SL) and a strained bilayer [Hydrogel (HG) and Polyimide (PI)]. The used polymer layers are stable at high temperatures up to 270 °C and are inert in common organic nonpolar, polar, protic, and aprotic solvents, as well as in moderate bases and acids allowing for lithography processing. Differential strain in the polymeric bilayers is introduced by swelling the HG films in an aqueous media while the stiffer PI keeps its shape and size. We use two different polymer stacks (SL/PI/HG and SL/HG/PI) to roll the polymer platform down- and upwards, respectively. A rolled-down tubular geometry avoids burying the Permalloy structure under the micron-size thick polymer, which makes Kerr microscopy measurements easier. In this geometry, the polymeric layers might experience slight friction when during rolling they touch the substrate, however, due to the large stiffness of Polyimide and its thickness of thousands of nanometers, small friction is unable to bring significant distortion into the polymeric platform and it still rolls into a tubular geometry with several windings. Regarding the effect of friction on the Permalloy structure, no effects other than tensile strain are observed in the AMR hysteresis, regardless of the position of the stripe (for stripe position see Fig. 4a-ii–iv). This might be supported by the 50 nm-thick gold contacts, which avoid the direct contact of the Permalloy with the substrate. Different rolling directions (roll-down and roll-up) allow to create different strain states (tensile and compressive) in the magnetic elements. The polymer layer stack is spin-coated onto a 50 × 50 mm2 glass substrate. Using optical lithography, we design arrays polymer rectangles with a typical size of 3.5 × 3.2 mm2. Our technology allows us to process up to 126 functional polymer layer stacks over the entire 50 × 50 mm2 substrates in a single fabrication run with a 90–95% yield. On top of the predetermined areas in the polymer layer stack, we prepare a liftoff photoresist mask to define the Permalloy elements of thickness 100 nm by magnetron sputter deposition at room temperature. Permalloy deposited on the polymeric platform thus does not meet high temperatures during the deposition process. Nevertheless, the effect of increased temperature (if there is any) will be in the form of a reduction in coercivity.
The patterned polymeric platform is self-assembled into 3D tubular structures by selectively etching the sacrificial layer in an aqueous solution containing ethylenediaminetetraacetic acid [EDTA, 7.0 pH]. Furthermore, in the humid environment, the hydrogel-based polymer swells, generating mechanical stress in the plane parallel to the reinforcing polyimide layer. This leads to a downward or upward bending (Fig. 2e, f) of the polymer layer stack (depending on the position of the HG layer in the stack and initiates the rolling process. After etching and rolling, the sample is washed in deionization (DI) water and dried under ambient conditions. Different rolling diameters and with it the curvature of the ferromagnetic structure were achieved by varying the thickness of the HG layer and by changing the pH of the rolling solution. With the given experimental conditions, the tube diameters ranged between 64 and 130 µm, with the Permalloy elements placed on top of the tubes having the same curvature as the tube.
Kerr microscopy
A digitally enhanced wide-field Kerr microscope set-up64, making use of the magneto-optical Kerr effect (MOKE) and equipped with an electromagnet, was applied to measure magnetic hysteresis loops (MOKE magnetometry) and to image the magnetic domains. Throughout the paper, the longitudinal Kerr effect was applied at orthogonal planes of incidence with the magnetic field and magneto-optical sensitivity being aligned along or transverse to the AMR stripe axis. Hysteresis loops were generated by plotting the image intensity of a selected image spot as a function of the applied magnetic field. To reduce the noise, the MOKE intensity of 16 image frames was averaged for each measurement point. Before observing the domain configuration, the ground state of the ferromagnetic element was set by an ac-field demagnetizing procedure (frequency = 35 Hz, maximal amplitude = 20 mT, decay time to zero field = 5 s) with field orientation transverse to the strain-induced anisotropy for rolled structures.
Micromagnetic simulations
To mimic the experimentally observed domain patterns of the rolled Permalloy stripes and to calculate the AMR hysteresis in OOMMF micromagnetic simulations, uniaxial magnetic anisotropy energy was added to the planar Permalloy stripes (Fig. 3b, middle panel). The added anisotropy was implemented transverse to the stripe axis to achieve the same azimuthal domain state as in the rolled-down tubes. Simulations were performed for two stripe geometries: (1) length 8 µm, width 0.8 µm, and thickness 100 nm, (2) length 4 µm, width 0.4 µm, and thickness 100 nm, with a cell size of 5 × 5 × 5 nm3 and with the following material parameters: saturation magnetization Ms = 800 kA m−1 and exchange coefficient A = 13 pJ m−1.
AMR calculations
The anisotropic magnetoresistance signal of the simulated, field-dependent magnetization patterns has been calculated by considering the magnetic moment orientation in each elementary cell with respect to the current direction and applying a resistor network model to the simulated geometry. The details are given in Supplementary Fig. 7 and Supplementary Note 6.
Statistical analysis
All the magnetic and AMR hysteresis presented are results of single scan measurements, but each measurement point in the hysteresis plots is an average over integration time of 0.8 s to improve the signal-to-noise ratio in M(H) and AMR(H) plots.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Code availability
Software codes that support the finding of this study are available from the corresponding author upon reasonable request.
References
Karnaushenko, D. et al. Self‐assembled on‐chip‐integrated giant magneto‐impedance sensorics. Adv. Mater. 27, 6582–6589 (2015).
Becker, C. et al. Self-assembly of highly sensitive 3D magnetic field vector angular encoders. Sci. Adv. 5, eaay7459 (2019).
Becker, C. et al. A new dimension for magnetosensitive e-skins: active matrix integrated micro-origami sensor arrays. Nat. Commun. 13, 2121 (2022).
Ota, S., Ando, A. & Chiba, D. A flexible giant magnetoresistive device for sensing strain direction. Nat. Electron. 1, 124–129 (2018).
Melzer, M., Makarov, D. & Schmidt, O. G. A review on stretchable magnetic field sensorics. J. Phys. D Appl. Phys. 53, 083002 (2020).
Hertel, R. Ultrafast domain wall dynamics in magnetic nanotubes and nanowires. J. Phys. Condens. Matter 28, 483002 (2016).
Staňo, M. & Fruchart, O. Magnetic nanowires and nanotubes. Handb. Magn. Mater. 27, 155–267 (2018).
Hertel, R. Curvature-induced magnetochirality. SPIN 3, 1340009–1 (2013).
Yan, M., Andreas, C., Kákay, A., García-Sánchez, F. & Hertel, R. Fast domain wall dynamics in magnetic nanotubes: suppression of Walker breakdown and Cherenkov-like spin wave emission. Appl. Phys. Lett. 99, 2011–2014 (2011).
Bran, C. et al. Magnetization Ratchet in cylindrical nanowires. ACS Nano 12, 5932–5939 (2018).
Sheng, P., Wang, B. & Li, R. Flexible magnetic thin films and devices. J. Semicond. 39, 011006 (2018).
Karnaushenko, D., Kang, T., Bandari, V. K., Zhu, F. & Schmidt, O. G. 3D Self-assembled microelectronic devices: concepts, materials, applications. Adv. Mater. 32, 1902994 (2020).
Rivkin, B. et al. Electronically integrated microcatheters based on self-assembling polymer films. Sci. Adv. 7, eabl5408 (2021).
Streubel, R. et al. Magnetism in curved geometries. J. Phys. D Appl. Phys. 49, 363001 (2016).
Kwon, J. H., Kwak, W. Y. & Cho, B. K. Magnetization manipulation of a flexible magnetic sensor by controlled stress application. Sci. Rep. 8, 1–9 (2018).
Karnaushenko, D. D. et al. Rolled-up self-assembly of compact magnetic inductors, transformers and resonators. Adv. Electron. Mater. 4, 1800298 (2018).
Tretiakov, O. A., Morini, M., Vasylkevych, S. & Slastikov, V. Engineering curvature-induced anisotropy in thin ferromagnetic films. Phys. Rev. Lett. 119, 1–5 (2017).
Volkov, O. M. et al. Experimental and theoretical study of curvature effects in parabolic nanostripes. Phys. Status Solidi - Rapid Res. Lett. 13, 1–5 (2019).
Sheka, D. D. et al. Fundamentals of curvilinear ferromagnetism: statics and dynamics of geometrically curved wires and narrow ribbons. Small 2105219, 2105219 (2022).
Volkov, O. M. et al. Experimental observation of exchange-driven chiral effects in curvilinear magnetism. Phys. Rev. Lett. 123, 077201 (2019).
Kechrakos, D., Tzannetou, L. & Patsopoulos, A. Magnetic skyrmions in cylindrical ferromagnetic nanostructures with chiral interactions. Phys. Rev. B 102, 1–10 (2020).
Yan, M., Andreas, C., Kákay, A., García-Sánchez, F. & Hertel, R. Chiral symmetry breaking and pair-creation mediated Walker breakdown in magnetic nanotubes. Appl. Phys. Lett. 100, 252401 (2012).
Otálora, J. A., Yan, M., Schultheiss, H., Hertel, R. & Kákay, A. Curvature-induced asymmetric spin-wave dispersion. Phys. Rev. Lett. 117, 1–6 (2016).
Kravchuk, V. P. et al. Multiplet of skyrmion states on a curvilinear defect: reconfigurable skyrmion lattices. Phys. Rev. Lett. 120, 67201 (2018).
Asai, R. et al. Stress-induced large anisotropy field modulation in Ni films deposited on a flexible substrate. J. Appl. Phys. 120, 083906 (2016).
Matsumoto, H., Ota, S., Koyama, T. & Chiba, D. Control of magnetic anisotropy in a Co thin film on a flexible substrate by applying biaxial tensile strain. Appl. Phys. Lett. 118, 022406 (2021).
González, M. T., García, K. L. & Valenzuela, R. Circumferential magnetization curves of Co-rich amorphous wires under tensile stress. J. Appl. Phys. 85, 319–324 (1999).
Zighem, F. & Faurie, D. A review on nanostructured thin films on flexible substrates: links between strains and magnetic properties. J. Phys. Condens. Matter 33, 233002 (2021).
Soldatov, I. V. et al. Advanced, Kerr-microscopy-based MOKE magnetometry for the anisotropy characterisation of magnetic films. J. Magn. Magn. Mater. 529, 167889 (2021).
Bermúdez Ureña, E. et al. Fabrication of ferromagnetic rolled-up microtubes for magnetic sensors on fluids. J. Phys. D Appl. Phys. 42, 055001 (2009).
Müller, C. et al. Tuning magnetic properties by roll-up of Au/Co/Au films into microtubes. Appl. Phys. Lett. 94, 2–5 (2009).
Streubel, R. et al. Magnetic microstructure of rolled‐up single‐layer ferromagnetic nanomembranes. Adv. Mater. 26, 316–323 (2014).
Karnaushenko, D. D., Karnaushenko, D., Makarov, D. & Schmidt, O. G. Compact helical antenna for smart implant applications. NPG Asia Mater. 7, 1–10 (2015).
Streubel, R. et al. Rolled-up permalloy nanomembranes with multiple windings. SPIN 03, 1340001 (2013).
Staňo, M. et al. Flux-closure domains in high aspect ratio electroless-deposited CoNiB nanotubes. SciPost Phys. 5, 038 (2018).
Hurst, J. et al. Theoretical study of current-induced domain wall motion in magnetic nanotubes with azimuthal domains. Phys. Rev. B 103, 1–13 (2021).
Sáez, G., Díaz, P., Cisternas, E., Vogel, E. E. & Escrig, J. Information storage in permalloy modulated magnetic nanowires. Sci. Rep. 11, 1–9 (2021).
Parkin, S. S. P., Hayashi, M. & Thomas, L. Magnetic domain-wall Racetrack memory. Science (80-.)320, 190–194 (2008).
Logic, M. D. Magnetic domain-wall logic. Science 309, 1688–1693 (2005).
Bozorth, R. M. The permalloy problem. Rev. Mod. Phys. 25, 42–48 (1953).
Mitchell, E. N., Haukaas, H. B., Bale, H. D. & Streeper, J. B. Compositional and thickness dependence of the ferromagnetic anisotropy in resistance of iron–nickel films. J. Appl. Phys. 35, 2604–2608 (1964).
Karnaushenko, D. et al. Biomimetic microelectronics for regenerative neuronal cuff implants. Adv. Mater. 27, 6797–6805 (2015).
Hubert, A. Schäfer, R. Magnetic Domains: The Analysis of Magnetic Microstructures (Springer, Berlin, 1998).
Schäfer, R. “Magnetic domains” in Handbook of Magnetism and Magnetic Materials (Springer International Publishing, Cham, 2021).
Cullity, B. D. & Graham, C. D. Introduction to Magnetic Materials, 2nd edn (John Wiley & Sons, Inc., 2008).
Streubel, R. et al. Retrieving spin textures on curved magnetic thin films with full-field soft X-ray microscopies. Nat. Commun. 6, 1–11 (2015).
Wyss, M. et al. Imaging magnetic vortex configurations in ferromagnetic nanotubes. Phys. Rev. B 96, 1–7 (2017).
Singh, A., Mukhopadhyay, S. & Ghosh, A. Tracking random walk of individual domain walls in cylindrical nanomagnets with resistance noise. Phys. Rev. Lett. 105, 1–4 (2010).
Rüffer, D. et al. Magnetic states of an individual Ni nanotube probed by anisotropic magnetoresistance. Nanoscale 4, 4989–4995 (2012).
Zimmermann, M. et al. Origin and manipulation of stable vortex ground states in permalloy nanotubes. Nano Lett. 18, 2828–2834 (2018).
Wegrowe, J. E., Gilbert, S. E., Kelly, D., Doudin, B. & Ansermet, J. P. Anisotropic magnetoresistance as a probe of magnetization reversal in individual nano-sized nickel wires. IEEE Trans. Magn. 34, 903–905 (1998).
Weber, D. P. et al. Cantilever magnetometry of individual Ni nanotubes. Nano Lett. 12, 6139–6144 (2012).
Neu, V. et al. Creating ferroic micropatterns through geometrical transformation. Nano Lett. 21, 9889–9895 (2021).
Sander, D. The magnetic anisotropy and spin reorientation of nanostructures and nanoscale films. J. Phys. Condens. Matter 16, R603–R636 (2004).
Amjadi, M. & Sitti, M. Self-sensing paper actuators based on graphite–carbon nanotube hybrid films. Adv. Sci. 5, 1800239 (2018).
Li, X., Ding, G., Ando, T., Shikida, M. & Sato, K. Micromechanical characterization of electroplated permalloy films for MEMS. Microsyst. Technol. 14, 131–134 (2007).
Schöbitz, M. et al. Fast domain wall motion governed by topology and Œrsted fields in cylindrical magnetic nanowires. Phys. Rev. Lett. 123, 217201 (2019).
Donnelly, C. et al. Three-dimensional magnetization structures revealed with X-ray vector nanotomography. Nature 547, 328–331 (2017).
Fernández-Pacheco, A. et al. Three-dimensional nanomagnetism. Nat. Commun. 8, 15756 (2017).
Mönch, I. et al. Rolled-up magnetic sensor: nanomembrane architecture for in-flow detection of magnetic objects. ACS Nano 5, 7436–7442 (2011).
Balhorn, F. et al. Spin-wave interference in three-dimensional rolled-up ferromagnetic microtubes. Phys. Rev. Lett. 104, 1–4 (2010).
Rivkin, B. et al. Shape‐controlled flexible microelectronics facilitated by integrated sensors and conductive polymer actuators. Adv. Intell. Syst. 3, 2000238 (2021).
Lin, S. et al. An ultralight, flexible, and biocompatible all-fiber motion sensor for artificial intelligence wearable electronics. npj Flex. Electron. 6, 27 (2022).
Soldatov, I. V. & Schäfer, R. Selective sensitivity in Kerr microscopy. Rev. Sci. Instrum. 88, 073701 (2017).
Acknowledgements
We would like to thank C. Krien and I. Fiering (Leibniz IFW Dresden) for the deposition of metallic thin films and K. Leger for polymer synthesis (Leibniz IFW Dresden). We acknowledge Martin Hantusch (Leibniz IFW Dresden) for the characterization of the Permalloy composition and Andy Thomas (Leibniz IFW Dresden) for providing access to the workstation for performing micromagnetic simulations. We thank S. Pofahl (Leibniz IFW Dresden) for providing technical help in the Kerr microscopy setup. We acknowledge B. Rivkin and R. Ravishankar (Leibniz IFW Dresden) for helping with wire bonding the electrical contacts and R. Doineau (Leibniz IFW Dresden) for performing high-resolution images of tubular geometries. B. Singh thanks A. Mirhajivarzaneh (Leibniz IFW Dresden) for providing an introduction to the polymeric platform and appreciates helpful discussions with B. Rivkin and R. Huber (Leibniz IFW Dresden). J.A. Otálora acknowledges funding by Fondecyt Iniciacion Grant No. 11190184. This work is part of projects that have received funding from the German Research Foundation DFG (Gottfried Wilhelm Leibniz Prize granted in 2018, SCHM 1298/22-1 and KA5051/1-1 and KA5051/3-1), the Leibniz Association (Leibniz Transfer Program T62/2019).
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
D.K., V.N., and O.G.S. conceived the idea, V.K. and D.K. designed the research, B.S. performed the experiments and simulations and interpreted the data with the help of sample preparation by T.H.K., in Kerr measurements by I.S. and in data analysis by J.A.O., V.N., and R.S. supervised the experiments and data interpretation, D.D.K. and C.B. organized the polymeric self-assembly technology, B.S., V.N., D.K., and R.S. wrote the manuscript with the input from all other authors, and all authors contributed to the discussion of the results.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Singh, B., Otálora, J.A., Kang, T.H. et al. Self-assembly as a tool to study microscale curvature and strain-dependent magnetic properties. npj Flex Electron 6, 76 (2022). https://doi.org/10.1038/s41528-022-00210-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41528-022-00210-7