Introduction

New photodetectors based on flexible thin films are pushing the boundaries of sensitivity, mechanical flexibility, spatial resolution, and low-cost scalability1,2,3,4,5. In particular, there is significant interest in developing thin-film devices that extend photodetection to the near-infrared (NIR, wavelength λ = 0.7–1 μm) and shortwave infrared (SWIR, λ = 1–3 μm), since conventional devices based on crystalline III–V semiconductors require complex and costly fabrication processes6. In comparison to detectors operating at visible wavelengths, infrared detection poses a significant challenge resulting from the increased thermal generation of dark current because of the reduced semiconductor bandgap. The dark-current noise limits the signal-to-noise ratio, i.e., detectivity. It has been notoriously difficult to determine the origins of noise in thin film devices7, and sometimes erroneous assumptions cause a significant under-estimation of noise current and, in turn, unrealistic value for the detectivity7,8,9,10. A critical analysis of noise is presented in ref. 7, which provides proper measurement protocols and cautions on characterization pitfalls. While ref. 7 provides practical experimental guidelines, a conceptual framework is critically needed to understand and predict thermal noise current in disordered materials.

Among flexible thin-film materials, organic semiconductors offer versatile tunability, mechanical flexibility, and broadband high performance9,11,12,13,14,15,16. Therefore, organic bulk heterojunction (BHJ) photodiodes are used in our experimental studies. This paper presents a dramatic reduction of noise and significant improvement of detectivity in organic photodiodes using low disorder semiconductors. We present a physical model to explain the dependence of thermal noise on the bandgap and the feature of tail states in disordered semiconductors. These physical insights reveal the theoretical limits of thermal noise and detection range for infrared photodiodes with disorder inherent to non-crystalline thin-film systems. While our experimental studies use organic semiconductors, the physical model may be generalized to other disordered systems used in flexible photodiodes.

As a basis for the model, measurement data are taken on 10 BHJ combinations covering λ = 800–1600 nm and with two categories of acceptors, either fullerene or non-fullerene derivatives. Non-fullerene acceptors (NFAs) have recently demonstrated reduced recombination losses in organic solar cells17,18,19,20. However, it is unclear how NFAs affect photodetector metrics such as noise current density and detectivity. We compare photodiodes with NFAs to those with fullerenes and discover that NFA blends display a trend of lower noise density and offer a new path to noise reduction, a critical requirement to raise detectivity.

To pinpoint the attributes that suppress noise, we correlate dark current characteristics to the density of states measured at multiple temperatures, which leads to the observation that the degree of disorder is one of the fundamental factors influencing thermal noise. This disorder creates localized states with energy levels near the edge of the transport band. Based on the experimental findings, we derive the relationship of thermally generated carrier concentration as a function of two key parameters—the effective bandgap and the degree of disorder in BHJ devices. While it is a basic given in semiconductor physics to relate bandgap to intrinsic carrier concentration, the energetic disorder is an additional parameter not included in crystalline semiconductor models. We show that by accounting for the energetic disorder, the predicted thermal noise current closely matches measurements on a variety of BHJ blends.

The model here gives important criteria for screening and selecting materials, but it applies only to thermal noise and does not include other noise components, such as shot noise and flicker noise. As such, the experimental verifications are restricted to devices at zero bias, operating in conditions where thermal noise dominates21. Nonetheless, this scenario is often met when an infrared photodetector is used in photovoltaic mode near room temperature. In this work, the experimental and modeling studies infer the noise floor in the presence of disorder, provide a comparison to the ultimate background-limited performance, and give the theoretical upper limit for organic infrared photodiodes.

Results

Energy level alignment and degree of disorder in BHJs with different acceptors

Acceptor choices

The BHJ photodiodes consist of a blend of donor and acceptor semiconductors. The donor and acceptor are chosen such that their energy levels have an offset to facilitate exciton dissociation. The effective bandgap ECT is the difference between the highest occupied molecular orbital (HOMO) of the donor and the lowest unoccupied molecular orbital (LUMO) of the acceptor. The ECT is also known as the charge-transfer state and is defined here for BHJ blends, not to be confused with the bandgap of an individual pristine material.

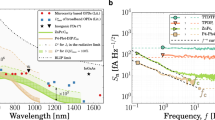
While this work will examine photodiodes with a wide range of ECT from 1.55 to 0.6 eV, the majority of the discussions focus on three exemplar donor–acceptor pairs shown in Fig. 1. The same infrared donor polymer P1 is matched with either a fullerene derivative or non-fullerene small molecules to adjust the ECT. The IUPAC name for P1 is poly(4-(5-(4-(3,5-bis(dodecyloxy)benzylidene)-4H-cyclopenta[2,1-b:3,4-b′]dithiophen-2-yl)thiophen-2-yl)-6,7-dioctyl-9-(thiophen-2-yl)-[1,2,5]thiadiazolo[3,4-g]quinoxaline). The fullerene derivative is [6,6]-Phenyl-C71-butyric acid methyl ester ([70]PCBM), one of the most commonly used acceptors in organic BHJ photodiodes. The non-fullerene small molecules are derivatives of 3,9-bis(2-methylene-(3-(1,1-dicyanomethylene)-indanone))-5,5,11,11-tetrakis(4-hexylphenyl)-dithieno[2,3-d:2′,3′-d′]-s-indaceno[1,2-b:5,6-b′]dithiophene, with methyl (ITIC-M) or fluoro (ITIC-F) end groups. The energy levels of all the materials used in this work are shown in Fig. 1b and in Supplementary Fig. 1.

Fig. 1: Materials characteristics.
figure 1

a Chemical structures and b energy levels of an infrared donor polymer P1 with respect to different acceptors. c Normalized absorption spectra for pristine organic semiconductor films.

Full size image

Figure 1c shows the absorption spectra of the pristine films. The broad absorption of [70]PCBM makes it hard to define a clear-cut edge and is a reason that its reported LUMO values are not precise, varying between −3.9 and −4.2 eV22. It is noteworthy that absorption drops off more abruptly in the NFAs and in the infrared polymer; that is, the [70]PCBM bandtail is the least sharp among the semiconductors. Below we examine for trends in device noise as ECT and the bandtail are tuned in the BHJs.

Device characteristics in the dark and under illumination

The device characteristics measured in the dark for noise analysis are shown in Fig. 2a–c. The dark current density Jd versus applied voltage in Fig. 2a is related to the root mean square of the shot noise10 by 〈ishot2〉 = 2qJdΔf, where q is the elementary charge and Δf is the measurement bandwidth. The shunt resistance RSH measured in Fig. 2b is often linked to the thermal noise by 〈ithermal2〉 = (4kBT/RSH)Δf, where kB is the Boltzmann constant and T is the temperature; however, this relationship may not apply if the impedance characteristics are convoluted with interfacial barrier resistance23. When the infrared devices are biased at 0 V, the dominant contribution to the noise current is the thermal noise, as the ithermal calculated from RSH in Fig. 2b is an order of magnitude higher than the ishot estimated from Fig. 2a. On the other hand, when the devices are under non-zero bias, the shot noise value overtakes the thermal noise.

Fig. 2: Characteristics of the organic infrared photodiodes.
figure 2

a Dark current density versus applied voltage. b Imaginary versus real impedance. c Noise current density measured by a power spectrum analyzer. The equipment background noise is included as the gray line. d Photocurrent density versus voltage measured under a 1.2 mW/cm2 continuous light with λ = 1100 nm. e External quantum efficiency and f specific detectivity measured under a monochromatic light modulated at 400 Hz. The devices in b, c, e, and f are biased at 0 V.

Full size image

While Fig. 2a, b give rough extrapolations of different noise components, it is critical to directly measure the total noise current with a power spectrum analyzer, as seen in Fig. 2c. This measurement includes all the noise components inoise = [ishot2 + ithermal2 + i1/f2 + …]1/2, where i1/f is the flicker noise, and the ellipsis indicates that there can be other mechanisms, such as trapping and detrapping, that add to the total noise current. For instance, if we extrapolate the noise current relying only on RSH in Fig. 2b, the ITIC-F and [70]PCBM blends show nearly the same RSH values, suggesting that the noise levels are similar. However, this extrapolation does not account for all the noise components, and the total noise current is higher in the device with [70]PCBM than the one with ITIC-F. Comparing the BHJ acceptors in Fig. 2c, the noise current decreases in the order of [70]PCBM > ITIC-F > ITIC-M.

In addition to noise analysis, we briefly discuss the photoresponse characteristics and the associated signal-to-noise metrics for the BHJs in Fig. 2d–f. The expressions for external quantum efficiency (EQE) and detectivity (D*) are provided in the “Methods” section. In Fig. 2d, the photocurrent in the ITIC-F blend does not saturate under reverse bias, and this characteristic suggests a photoconductive gain effect due to the high density of deep traps, which we will revisit in the next section. We also note that, for the BHJs with [70]PCBM or with ITIC-M, the devices show similar built-in potential Vbi, suggesting that the effective bandgaps are comparable in these photodiodes under the same illumination conditions.

In Fig. 2e, the EQE of the devices with NFAs is two times less than the one with [70]PCBM. On the other hand, the NFA blends display lower noise current than the [70]PCBM blend; for example, the noise in the device with ITIC-M is five times lower than the device with [70]PCBM. As a result, in Fig. 2f, the best detectivity is observed in the device using ITIC-M. Suppressing noise is critical for improving the detectivity. Next we will determine the origins of the noise suppression observed in the NFA blends by comparing the density of states in our device series.

Localized states with energy levels near the transport band edge, as revealed by density-of-state (DOS) measurements

As already seen in Fig. 1c, the NFA films show sharper absorption bandtails than the [70]PCBM film, and the bandtail variations indicate different levels of energetic disorder inherent in non-crystalline materials. To further investigate the extent of disorder in operational devices, we carry out capacitance C versus frequency ω measurements24,25 in Fig. 3a–c to infer the corresponding sub-bandgap DOSs in Fig. 3d–f. The measurements are done across the temperature range of −6 to 40 °C. The equations for extracting the DOS are explained in the “Methods” section. In short, a rapid change in the slope ∂C(ω)/∂ln(ω) reflects an increase of the sub-bandgap DOS. The DOS measured at the energy Eω is expressed as an exponential distribution of bandtail shallow traps26,27, and it may include a Gaussian distribution of deep traps25,28, if they are present:

$${\mathrm {DOS}}\left( {E_\omega } \right) = N_{\mathrm {T}}\,\exp \left( {\frac{{ - E_\omega }}{{\Delta E}}} \right) + \frac{{N_{\mathrm {G}}}}{{\sigma \sqrt {2\pi } }}\exp \left( { - \frac{{\left( {E_\omega - E_{\mathrm {{G0}}}} \right)^2}}{{2\sigma ^2}}} \right)$$
(1)
Fig. 3: Analysis of sub-bandgap density of states (DOS) via capacitance vs. frequency measurements.
figure 3

a–c Variable-temperature measurements of capacitance versus frequency on the organic photodiodes. Each plot has six shadings to represent data taken at different temperatures, i.e., 40, 30, 20, 10, 0, and −6 °C. The solid lines are fits to determine the density of states (DOS). d–f DOS near the band edge. For the solid lines, the shading indicates the measurement temperature: dark = 40 °C; medium = 20 °C; light = −6 °C. The dashed lines are fits to the exponential bandtails, and the ΔE slope is the bandtail disorder spread.

Full size image

In the first term denoting the exponential bandtail, NT is the DOS near the mobility edge, and ΔE is the bandtail disorder spread. In the second Gaussian term, the NG is the DOS for deep traps, and σ is the Gaussian disorder spread, and EG0 is the mean energy of the deep traps.

By fitting the DOS data to Eq. (1), we determine the exponential bandtail spread ΔE to be 50 meV for the [70]PCBM blend, whereas the NFAs are less disordered at 35 meV for the ITIC-M blend and 29 meV for the ITIC-F blend. On the other hand, the ITIC-F blend shows a high density of deep traps, evident from the prominent Gaussian peak next to the bandtail.

Upon changing temperature, the carrier concentration changes and in turn shifts the measurement edge in the DOS as shown in Fig. 3d–f (the intrinsic DOS does not change with temperature, but the apparent/effective DOS shifts with temperature, as discussed in Supplementary Fig. 2). As carrier transport in organic semiconductors is thermally activated29,30, the carriers located deep in the bandgap are not mobile at low temperature. With increasing temperature, the deep carriers can be promoted into the transport level, resulting in the DOS shifted to the right. In addition, an increase in ΔE correlates to a dark current that is more sensitive to temperature change (Supplementary Fig. 3). Nonetheless, albeit the edge shifts, there is no significant change in the bandtail spread ΔE within the temperature range of −6 to 40 °C, as the bandtail slopes for each BHJ combination are the same regardless of the temperature. Thus the parameter ΔE is treated as independent of temperature to simplify our model.

Relating noise current and photo-response to DOS

In addition to the above three BHJ combinations, we compile in Fig. 4a the shunt resistance characteristics of seven other donor–acceptor pairs from refs. 9,31,32. The chemical structures and energy levels of all the BHJs are listed in the Supplementary Information. For each ECT we have measured multiple devices with different BHJ film thicknesses between 100 and 700 nm, to account for their thickness dependence. Since the devices in this dataset did not show significant contact problems, we infer that the measurements are probing the intrinsic resistance due to BHJ material choices.

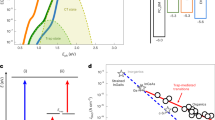
Fig. 4: Thermal noise for different effective bandgap.
figure 4

a Shunt resistance of organic BHJ photodiodes as a function of the effective bandgap. The orange series are devices with the same polymer donor P1 matched with different non-fullerene acceptors. The gray series are devices using different polymer donors with the acceptor [70]PCBM. The dashed lines are linear fits to the boundary of each series. Schematics of the electronic structures and carrier distributions for devices b in the dark and c under illumination. The shaded areas represent states filled up to the quasi-fermi levels EFp/n by photogenerated charges.

Full size image

In Fig. 4a, the devices span a large range of effective bandgap ECT and show an expected trend that shunt resistance is reduced with decreasing ECT. More interestingly, the data also indicate that devices with NFAs consistently display better shunt resistance, up to 10 times higher RSH values, in comparison to those with [70]PCBM acceptors. As the shunt resistance is inversely proportional to ithermal, Fig. 4a confirms that the thermal noise can be mitigated by using NFAs for a wide range of BHJ combinations. Moreover, we can correlate the low noise in NFA blends to their reduced disorder in DOS bandtails.

Based on the DOS characteristics in Fig. 3d–f, the two schematics in Fig. 4b, c provide an intuitive physical understanding on the dark current noise and photocurrent characteristics of the three BHJ photodiodes. The schematics illustrate the materials’ DOS based on the measured ΔE in Fig. 3 and the LUMO values in Fig. 1b. For disordered films, the LUMO is defined as the energy level at which the DOS starts to drop exponentially, at the start of the transport/mobility band edge. The donor semiconductors display sharper bandtails than [70]PCBM and NFAs, and currently, the acceptors are the limiting factor. Here we assign the LUMO of [70]PCBM to be −3.9 eV, the upper bound for the transport edge as reported in literature from solar cells22. The LUMO levels start out deeper into the bandgap for NFAs, but their ΔE slopes are sharp and their exponential bandtail DOS are less stretched out than in [70]PCBM. In Fig. 3e, the exponential bandtail of [70]PCBM is stretched 0.5 eV into the bandgap, while the NFAs are ~0.4 eV into the bandgap. There are Gaussian deep states in the ITIC-F blend around 0.5 eV, but its DOS magnitude of 1016 cm−3 eV−1 is lower than 1017 cm−3 eV−1 in the [70]PCBM blend. Because of the broad ΔE in [70]PCBM, the bandtail states reach farther into the bandgap in [70]PCBM than in NFAs.

In the dark in Fig. 4b, the low concentration of thermally generated carriers mainly occupies the lowest energy states far away from the band edges. In [70]PCBM, the disorder is high and the bandtail states extend deep into the bandgap. Thus, the effective barrier to thermal generation of dark current is the lowest for the BHJ with [70]PCBM, and the barrier increases in the devices with ITIC-F and further with ITIC-M, following the trend as highlighted in Fig. 2c.

On the other hand, under illumination in Fig. 4c, a large number of carriers are photogenerated and the energy states in the bandtails are filled up to the mobility band edges. The difference between the quasi-Fermi levels constitutes the built-in potential Vbi. This band diagram explains the Vbi results in Fig. 2d, in which Vbi is smallest for the BHJ with ITIC-F, whereas for the two BHJs with[70]PCBM and ITIC-M, the Vbi values are similar. As photocarriers populate the sub-bandgap states, the mobility band edges of [70]PCBM and ITIC-M are filled up to similar quasi-Fermi energy levels EFn, and hence the Vbi of these two devices are comparable. This diagram also explains why in solar cells, the [70]PCBM LUMO is often found to be −3.9 eV, because photovoltaic characterization is usually carried out using strong illumination that probes the mobility edge rather than the bandtail states.

Physical model of thermal noise as a function of effective bandgap and disorder

Modeling intrinsic carrier concentrations with respect to experimental values

Based on the experimental data above on organic infrared photodiodes, the key factors that influence the thermal noise are the effective bandgap ECT and the bandtail disorder spread ΔE. Thus we derive a physical model to predict the thermal noise as a function of ECT and ΔE. The thermal noise is proportional to the device conductivity. In turn, the device conductivity (σ = qμNi) is proportional to thermally generated intrinsic carrier concentration Ni, assuming that mobility μ is similar within the same class of materials. Hence, the first step in our derivation is to state the dependence of Ni on ECT and ΔE.

As recalled from semiconductor physics textbooks, the thermally generated intrinsic carrier concentration is found by

$$N_{\mathrm {i}} = \mathop {\smallint }\limits_0^\infty {\mathrm{DOS}}\left( E \right) \cdot {F}\left( E \right){\mathrm{d}}E = \mathop {\smallint }\limits_0^\infty {\mathrm{DOS}}\left( E \right) \cdot \frac{1}{{{\mathrm{exp}}\left[ {\left( {E - E_{\mathrm {F}}} \right){\mathrm{/}}k_{\mathrm {B}}T} \right] + 1}}{\mathrm{d}}E$$
(2)

where EF is the Fermi level, E is the energy level, and F(E) is the Fermi–Dirac distribution. For crystalline materials, the DOS is proportional to \(\sqrt E\). For disordered thin films, we need to modify the DOS33 and express it as two parts:

$${\mathrm{DOS}}\left( E \right) = N_{\mathrm {C}} \cdot \exp \left( { - \frac{{\frac{{E_{{\mathrm {CT}}}}}{2} - E}}{{\Delta E}}} \right)\,, {\mathrm{for}}\,E \, < \, \frac{{E_{{\mathrm {CT}}}}}{2}$$
(3a)
$${\mathrm{DOS}}\left( E \right) = \frac{{N_C}}{{\sqrt {\frac{{E_{{\mathrm {CT}}}}}{2}} }} \cdot \sqrt E \,,{\mathrm{for}}\,E \ge \frac{{E_{{\mathrm {CT}}}}}{2}$$
(3b)

where Nc is the effective DOS at the band edge. We define the band edge to be the level at half of the effective bandgap, as illustrated in Fig. 5a inset. Equation (3a) accounts for the exponential distribution of bandtail states below the band edge. Equation (3b) includes the factor of \(1/\sqrt {E_{\mathrm {{CT}}}/2}\) to avoid discontinuity at the band edge, and it follows the conventional \(\sqrt E\) dependence for energies above the band edge. Equations (2) and (3a) quantify that a large ECT and low ΔE, i.e., sharp bandtail, would reduce the DOS overlap with F(E) and consequently decrease the number of thermal carriers.

Fig. 5: Physical model of thermal noise.
figure 5

a Normalized thermally generated carrier concentration as a function of the effective bandgap or the bandtail disorder in organic photodiodes. The inset shows the parameters for calculating the carrier concentration indicated by the shaded area. To offer different perspectives, b and c display the data in a as contour plots. d The predicted thermal noise from our model. The dots indicate the measured noise in photodiodes with different acceptors. The horizontal bars on the dots represent ±1 meV uncertainties in the measured ΔE values. The color bands show the predicted noise with ECT held at the indicated values within ±0.01 eV. e The upper bound for detectivity and noise-equivalent power for organic infrared photodiodes with disorder. The red dotted line shows the detectivity of a background-limited infrared photodiode with the background at 300 K and the field of view of 180°.

Full size image

We impose a boundary condition in our physical model to restrict the extent of bandtail states spreading into the bandgap, such that at the middle of the bandgap, the DOS(E = 0) < 10−3 Nc. The 10−3 ratio is extrapolated from the DOS measurements in Fig. 3. The reason for this condition is that, if the density of bandtail states is very high at similar levels as the band edges, the device would not have a thermal barrier and the above equations would no longer apply. The boundary condition can be written as

$$N_{\mathrm {C}} \cdot \exp \left( { - \frac{{\frac{{E_{{\mathrm {CT}}}}}{2}}}{{\Delta E}}} \right) > 10^{ - 3}N_{\mathrm {C}},{\mathrm{and}}\,{\mathrm{simplifying}}\,{\mathrm{it}},\Delta E < \frac{{E_{{\mathrm {CT}}}}}{{13.8}}$$
(4)

Based on Eqs. (2) and (3a), along with the restriction set by Eq. (4), the thermal carrier concentration Ni(ECT, ΔE) is obtained for ECT from 1.2 to 0.4 eV (λ = 1–3 μm) and for ΔE from 80 to 20 meV, at room temperature as shown in Fig. 5a. The calculations are normalized by the Nc value in Eq. (3a). Figure 5b shows the trend that Ni decreases with widening ECT, same as in crystalline semiconductors. More surprisingly, the Ni is very sensitive to the disorder spread ΔE in thin-film semiconductors; with a merely 10 meV decrease in ΔE, the Ni drops by more than an order of magnitude in Fig. 5c. In other words, in order to decrease Ni by a factor of 10, ECT needs to be raised by 100 meV, or disorder should be reduced by lowering ΔE by just 10 meV. This comparison demonstrates the dramatic effect of ΔE on thermal carrier concentration, highlighting that lower bandtail disorder is crucial to mitigate the noise current.

Predicting the minimum noise current and boundaries for detectivities

After setting up Ni(ECT, ΔE), the next step is to relate this calculated term to the measured noise current. The photodiodes in Fig. 2c are at zero applied bias, and the dominant source of noise in those devices is from the thermal noise component. Thus we assume that the measured noise is proportional to the thermal carrier concentration by a scaling factor C, that is, inoise = C*Ni. We find the scaling factor by using the photodiode with the ITIC-M acceptor as the reference. For this device the measured noise is 9 × 10−14 A/Hz0.5, at ECT = 0.77 eV and ΔE = 35 meV. Based on this data point, we scale the z-axis in Fig. 5a to the one in Fig. 5d. Subsequently, we verify that the resulting inoise(ECT, ΔE) plot accurately predicts other experimental data. For example, for the BHJs with ITIC-F or with [70]PCBM, the estimated noise matches very well with the actual noise current measured in those devices with their specific (ECT, ΔE) dependence.

With the inoise(ECT, ΔE) model in Fig. 5d, we ask what is theoretical limit for the detectivity D* of infrared photodiodes using disordered organic semiconductors. We calculate the maximum achievable D* and its inverse (noise-equivalent power (NEP)), by assuming that the photocurrent EQE is at 90%, using equations shown in the “Methods” section. This EQE assumption is idealistic, since organic infrared photodiodes currently show low EQE < 30% at 0 V bias, and their photoresponse is hampered by increasing recombination with narrow bandgaps34. Nonetheless, in assuming a constant EQE for all bandgaps, we determine an upper bound for D* with respect to detection wavelengths, as shown in Fig. 5e.

Because D* is inversely proportional to inoise(ECT, ΔE), the decrease in D* at longer wavelengths is due to the noise increase with the lower bandgap. The maximum D* also drops when the device noise rises with bandtail disorder. A ΔE of 25 meV (~kBT at room temperature) is very low for disordered semiconductors35, and the black line in Fig. 5e is the theoretical limit for organic photodiodes at room temperature. For comparison, the red dotted line is the D* of an ideal background-limited infrared photodiode (BLIP), in which the detection limit is determined only by the noise from background fluctuations from the ground at 300 K21. The background fluctuations become significant for λ > 1.5 μm. In photodiodes with disordered semiconductors, the D* will be at least one order of magnitude lower than BLIP. A realistic disorder spread of ΔE = 35 meV, as observed in NFAs, would reduce D* by at least two orders of magnitude.

Our physical model reveals an implication of bandtail disorder on limiting the detection wavelength in photodiodes. In crystalline systems, the longest detectable wavelength corresponds to the material’s bandgap. Whereas in disordered BHJs, in addition to the effective bandgap, the wavelength limit is affected by the bandtail. If the HOMO and LUMO tail states merge, the device would not be a diode anymore. With larger bandtail spread, the tail states merge sooner at a given ECT. Hence, to retain diode characteristics with a bandgap set by the condition in Eq. (4), the detection range is cut to a shorter wavelength when ΔE increases in Fig. 5e. The model here provides insights into the fundamental limitations imposed by ECT and ΔE.

Discussions

This work analyzed a series of 10 infrared BHJ photodiodes and found significant noise reduction and higher detectivity in devices using NFAs compared to those with fullerene derivatives. The reason for the substantial improvement in noise characteristics is revealed through variable-temperature sub-bandgap DOS measurements, which show that the distribution of bandtail states drops off more sharply in NFAs than in fullerene derivative blends. With low bandtail disorder in NFAs, there is a low concentration of sub-bandgap states that can be occupied; thus, the thermal generation of carriers is suppressed, resulting in low thermal noise current.

The experimental data demonstrate that minimizing bandtail disorder spread ΔE is key to reduce noise inherent in the materials. This approach complements prior strategies, such as injection blocking layers36,37 and links to the efforts in controlling disorder through molecular designs and structure–processing relationships38,39. As such, the absorption spectra bandtail and the sub-bandgap DOS can serve as critical screening criteria to select materials with low disorder for future devices.

To further conceptualize our understanding of thermal noise in a general framework, we examine the dependence of thermal noise on the effective bandgap and bandtail disorder through a physical model, in which the DOS is modified to include sub-bandgap states. The calculations predict the photodiode noise level at zero bias for a range of ECT and ΔE, and the predictions match very well with the measured values for three BHJs with different acceptors. This model quantifies the dramatic change in thermal carrier concentration due to the ΔE spread; in order to decrease Ni by a factor of 10, it requires raising ECT by 100 meV, or reducing the disorder ΔE by just 10 meV.

Taking disorder into account, the model enables prediction of the maximum achievable D* and the longest detectable wavelength in organic infrared photodiodes. For disordered devices, the upper bound of D* is reduced by at least one order of magnitude compared to BLIPs. The theoretical limits offer targets for future work on improving D* and extending the range of detection wavelength of thin-film infrared photodiodes.

Methods

Materials and device fabrication

The synthesis of the donor polymer P1 in Fig. 1a is described in ref. 40. The acceptors were purchased from Ossila Ltd. Glass substrates with indium tin oxide (ITO, resistivity ~15 Ω/sq) were cleaned by ultrasonication in detergent, deionized water, and isopropanol for 15 min each. A zinc oxide solgel41 was spincoated onto the ITO to form a 50 nm film for electron transport. A donor:acceptor ratio of 1:1.5 was used for the BHJ with [70]PCBM, dissolved in dichlorobenzene with 3% 1,8-diiodooctane. The BHJs with ITIC derivatives were at a 1:1 donor:acceptor ratio and were dissolved in dichlorobenzene. The BHJ solutions were spincoated to form layers with thicknesses around 150–200 nm, as measured using a stylus profilometer (Dektak). For the hole transport layer and top electrode, 15 nm MoO3 and Ag were deposited by thermal evaporation to complete the photodiode. The devices were encapsulated with cover-glass slides bonded onto the substrates with epoxy.

Device characterization

For measuring device EQE, the monochromatic light source was modulated with an optical chopper at 400 Hz. Optical filters with a cut-off wavelength at 455, 645, or 1025 nm were used to reduce light from higher-order diffraction. A Si photodiode (Thorlabs DET36A2) and a Ge photodiode (Newport 818-IR/DB) were references for the light intensity in the spectral regions of 480–780 and 780–1600 nm, respectively. The devices are all measured at 0 V external bias. The photocurrent was amplified through a low-noise amplifier connected to a lock-in amplifier (SRS 510). The EQE is calculated using the expression EQE = (Jph/Pillumin)(hc/λq), where h is Planck’s constant, c is the speed of light, λ is the wavelength of the incident light, q is the electron charge, Jph is the photocurrent density, Pillumin is the intensity of the incident light.

The photodiode noise spectral density was recorded by a power spectrum analyzer (HP 89410A) connected to the device through a preamplifier (SRS 570). The device noise is calculated by subtracting the background equipment noise in Fig. 2c, as \(i_{\mathrm {{noise}}}=\sqrt {i_{\mathrm {{measure}}}^2-i_{\mathrm {{equip}}}^2},\) where inoise is the device noise, imeasure is the as-measured noise as shown in Fig. 2c, and iequip is the background noise. The device detectivity is D* = (A Δf)0.5R/inoise = (AΔf)0.5NEP, where R = EQE(λq/hc) is the responsivity, A is the effective photodetector area = 0.0.9 cm2 for the devices in this report, Δf is the detection bandwidth, and inoise is the noise current measured in the dark. The NEP = inoise/R is inversely proportional to D*.

Electrochemical impedance spectroscopy was measured with a potentiostat (Bio-Logic SP200) in the dark in the frequency range of 2 Hz–2 MHz. The ac voltage was 20 mV, low enough to ensure the linearity of the response and sufficiently high to get good signal-to-noise. A Peltier cooler/heater was used to control the device temperature in the range of −10 to 40 °C. For the sub-bandgap DOS measurements, the measurement frequency ω is related to the energy of sub-gap states (traps) by Eω = kBT ln(ω0/ω), where ω0 is the rate of trap release and around 1012 s−1 for typical organic photodiodes24. The DOS distribution is DOS(Eω) = −(Vbi/qAkBTd) (∂C(ω)/∂ln(ω)), where d is the thickness of the BHJ layer and C(ω) is the capacitance at a specific frequency. Due to the uncertainty in the thermal escape factor ω0, the estimated magnitudes of DOS are accurate to within an order of magnitude among different devices. Nonetheless, the shape of the DOS is very repeatable, and in particular, the fit to ΔE is precise to within 5% (<2 meV uncertainty).