Introduction

With the ongoing digitization of manufacturing (often referred to as Industry 4.0), companies are aiming towards energy-efficient production processes. This transition requires billions of sensor nodes, which need to be powered. A similar trend is observed with the growing Internet of Things (IoT)1. Again, billions of small electronic units need to be powered, many of them not connected to a grid. To avoid adverse effects on global energy consumption, these autonomous devices need to be powered by green energy2,3. It is therefore crucial to develop sustainable energy technologies alongside the innovations of digitization to power its hardware by harvesting renewable energies.

Thermoelectric generators (TEG) present a versatile and maintenance-free solution for low-temperature energy-harvesting applications ranging from wearable electronics over energy self-sufficient sensors for IoT and Industry 4.0 to large-scale waste heat recovery4,5,6,7,8. The unique ability of TEGs to utilize small temperature differences in industrial settings or clothes or wearables to convert thermal energy into electricity makes them a key technology in this field. Bulk Bi2Te3-based thermoelectric devices are already commercially available, however, their use is limited to niche applications9. The wide use in energy-harvesting and waste heat recovery applications suffers from high costs and the limited availability of tellurium10. Printed TEGs7,11,12,13,14,15,16,17,18 using earth-abundant elements are a possible low-cost and promising alternative to conventional devices. Large-scale printing technologies such as roll-to-roll screen printing, ink-jet printing, or other additive manufacturing such as 3D printing have several advantages. They allow for complex and highly customizable device geometries19 needed for an easy adaptation of the devices to the large range of heat sources in applications to optimize their output power via thermal impedance matching. Furthermore, with these manufacturing techniques, a reduction of processing steps comes along and therefore an easier and more speedy production, while the production process of conventional thermoelectric devices is far more complex and requires a large number of steps20,21. This can potentially reduce the manufacturing costs and thereby enable market competitiveness.

Thermoelectric (TE) materials directly convert thermal energy into electrical energy without any moving parts using the Seebeck effect. When a TE material experiences a temperature difference ΔΤ at its ends, a thermoelectric voltage Vth = S·ΔT is induced with S being the Seebeck coefficient of the material. Together with the electrical conductivity σ and the thermal conductivity κ, we can obtain the TE figure of merit zT22:

$$zT = \frac{{S^2\sigma }}{\kappa }T,$$
(1)

with T as the absolute temperature of the material. Furthermore, S2σ is defined as the material’s power factor. The zT-value directly factors in the maximum efficiency ηmax of power conversion of a TEG by23:

$$\eta _{{\mathrm{max}}} = \frac{{T_{\mathrm{H}} - T_{\mathrm{C}}}}{{T_{\mathrm{H}}}} \cdot \frac{{\sqrt {1 + zT} - 1}}{{\sqrt {1 + zT} + \frac{{T_{\mathrm{C}}}}{{T_{\mathrm{H}}}}}},$$
(2)

where TH and TC are the temperatures of the hot and the cold side of the TE material. Seebeck coefficients in conventional TE materials have a magnitude of several hundred µVK−1 resulting in a voltage for a single TE element which is generally too low, to be used in most electronic applications.

Therefore, a typical TEG comprises numerous TE elements connected thermally in parallel and electrically in series. The elements alternate between n-type (S < 0) and p-type (S > 0) in such a way that the current in the n-type elements flows from the cold to the hot side of the device and vice versa in the p-type elements (Fig. 1a). Hence, the induced Seebeck voltages add up to higher voltages and thus become usable for electronic applications. Analogously to Eq. (1), we can calculate the effective ZT-value for a TEG with N pairs of p- and n-elements to24:

$$ZT = \frac{{N^2 \cdot \left( {S_{\mathrm{p}} - S_{\mathrm{n}}} \right)^2}}{{K \cdot R}}T_{\mathrm{m}}.$$
(3)
Fig. 1: Classical vs. corrugated TEG architecture.
figure 1

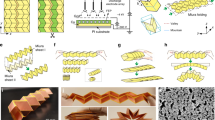
Yellow: n-type material, blue: p-type material, gray: substrate material. Arrows indicate the current flow through the device resulting from an applied temperature difference (hot side: red, cold side: cyan). a Schematic of the typical architecture of a TEG with four thermocouples in a row. b Left: A folded substrate with four thermally parallel aligned thermocouples. Right: printed thermocouples on a substrate with a periodic temperature profile.

Full size image

Here, Tm is the average temperature of the hot and the cold side, Sp and Sn are the Seebeck coefficients of the p-type and n-type materials, K is the total thermal conductance, and R is the total electrical resistance of the device when no electrical current runs through it.

Operating a TEG at its maximum output power requires simultaneously a thermal impedance matching of the device to the heat source and heat sink as well as an electrical impedance matching to the load25. Previously reported designs of printed TE devices fail to meet this condition which severely limits the amount of converted energy. For devices with an effective figure of merit ZT, this results in the thermal impedance matching condition25,26:

$$\frac{{K_{{\mathrm{contac}}t}}}{K} = \sqrt {ZT + 1}$$
(4)

with

$$K_{{\mathrm{contact}}}^{\qquad\, - 1} = K_{{\mathrm{source}}}^{\quad\;\;\; - 1} + K_{{\mathrm{sink}}}^{\quad\; - 1}.$$
(5)

Ksource and Ksink being the thermal conductance between the TEG and the hot and cold reservoir, respectively. The electrical impedance matching condition corresponds to25,26:

$$\frac{{R_{{\mathrm{load}}}}}{R} = \sqrt {ZT + 1} ,$$
(6)

where Rload is the electrical resistance of the load. Thin layers can be printed in a very effective manner in large areas using printable thermoelectric materials15,17,27,28,29,30. However, the resulting cross-plane thermal conductance is usually far too large for realistic applications, since the printed layers are only a few micrometers thick31.

Applying the temperature difference in-plane of the printed TE legs is a possible solution to this limitation. This way, the device thickness is not determined by the printed layer thickness but by the length of the printed two-dimensional thermoelectric legs. This enables us to adjust the device thickness and thus meet both impedance matching conditions via the print layout. A detailed elaboration of achieving simultaneous impedance matching via device thickness optimization is shown in Supplementary Note 1. To achieve this, the TE legs are printed on a thin and flexible substrate and subsequently folded into a three-dimensional cuboid close to the classical TEG device architecture. One approach is a corrugated architecture11,15,31,32,33 as depicted in Fig. 1b. The TE elements are printed in rows on a thin and flexible substrate and then folded to a meandering band to form the characteristic TEG structure. At the joints of the n-type and p-type legs, the two materials overlap to ensure good electrical contact between the elements of the series connection. The height and therefore the thermal conductance of the device is then determined by the length of the printed elements. However, due to the flexibility of the substrate, the structure of the device is not rigid, which can result in direct contact of the active materials between two folds under mechanical stress, thus shorting the TE legs electrically and causing a failure of the device. In contrast to classical TEG where the TE elements are separated by air, flexible devices require a layer of insulation between them. This drawback can be overcome by a two-step ‘origami’ folding technique. This folding provides electrical insulation between the TE elements by introducing an intermediate folding step and using the substrate itself as the insulating material. Hence, no extra non-thermoelectric material is introduced into the system reducing parasitic heat flux and therefore reducing the device’s parasitic thermal conductance. This origami design combines the advantages of mass producibility via large-scale printing and impedance matching via simple print layout design changes. Here we report a fully printed and robust origami TEG with a compact structure resulting in a high thermocouple density of 190 per cm² leading to a high-power output of up to 47.8 µWcm−2 at a ΔΤ of 30 K. The electrical output allows to power a Bluetooth data transmitter in an industrial application. The device is thus suitable as a green energy supply for autonomous sensor nodes for Industry 4.0 and IoT applications.

Results and discussion

Origami TEG device architecture

The underlying design principle of the TEG layout is shown in Fig. 2a. The figure displays one corner comprising four thermocouples of a scalable TEG. The TE elements are printed in a two-dimensional checkerboard type pattern arranged in m rows and n columns. Within a column, the TE legs connect electrically through a small overlap between the n-type and the p-type printed materials. The columns are connected by an extra horizontal strip of the TE material with higher conductivity. Alternatively, a highly conducting metallic strip can be printed. The blue and the red lines indicate those areas which will touch the cold and the hot side after folding. The thermoelectrically induced voltages in the element add up in the desired manner. This layout allows for the realization of a 3D cuboid with the following folding approach comprising two different folding operations: first, all columns are folded on top of each other in n folding operations including one column of empty substrate between the first and the second column to ensure electrical insulation. In the second series of m-1 folding operations, the resulting ribbon is folded into a corrugated pattern making the fold lines alternate between cold and hot sides. The working principles are seen in Fig. 2b, which displays the side-view of a folded TEG which comprises for the sake of clarity just four thermocouples. Like the corrugated structure in Fig. 1b, the thermocouples are all aligned vertically allowing an in-plane heat flow; however here the TE legs are all insulated by a layer of the substrate material. The result is a compact multi-layered cuboidal TEG.

Fig. 2: Origami folding technique.
figure 2

Yellow: n-type material, blue: p-type material, gray: substrate material. Arrows indicate the current flow through the device resulting from an applied temperature difference (hot side: red, cold side: cyan). Dashed arrows indicate folding procedures. a 2D layout of four thermocouples on a substrate with an extra strip of unprinted substrate. b Origami folded TEG with four thermocouples with inlaid substrate material for electrical insulation of the thermocouples.

Full size image

Fabrication of origami folded devices

We fabricated and characterized a total of 24 printed TEGs. It is essential for the output power of the devices that their internal resistance is as low as possible, which requires large layer thicknesses. Screen printing allows the deposition of large layer thicknesses in one printing step by using wide meshed screens while still providing a good printing resolution. Inkjet or aerosol jet printing would need to print numerous layers on top of each other to reach the same layer thicknesses. Furthermore, screen printing can easily be scaled up using a roll-to-roll process with cylindrical screens. The used thermoelectric inks, the design of the used print layout (Fig. 3a), and the used printing process are described in the Methods section below.

Fig. 3: Production of an origami TEG.
figure 3

a 2D print layout for an origami TEG with 254 p-legs (blue) and 253 n-legs (yellow) (green: overlapping area) arranged in a checkerboard pattern of 13 columns by 39 rows. b Screen printed TEGs with TiS2 as n-type material and PEDOT as p-type material with extended contact fields of PEDOT deposited by calligraphy. c First folding step stacking all columns plus one extra strip of substrate. d Fully folded thermoelectric ribbon. e Thermoelectric ribbon creased at the fold lines. f Fully folded thermoelectric generator fixed with a Kapton ribbon.

Full size image

To fold the 2D printed layout as seen in Fig. 3b into a functioning device we first remove the excess substrate material leaving only the printed area plus an additional strip of substrate material at the right edge of the layout with the exact width of one column of elements (here 10.62 mm). The additional strip is then folded on top of the first column covering it up, therefore, functioning as an insulator between the first and the second column (Fig. 3c). Afterward, we folded the stack on top of the following column and repeat the process until only one strip (generator ribbon) with the width of one column was left (Fig. 3d). The ribbon consists of 13 layers of thermoelectric elements insulated from each other and the exterior by a total of 14 layers of the substrate material. As a result, the TE elements in the flat ribbon and the fold lines are aligned on top of each other. For the 2nd series of folding operations, we crease the ribbon at the precise location of the fold lines with a hot blade to a corrugated ribbon to facilitate the subsequent folding (Fig. 3e). Finally, we join the folds to form a cuboid with dimensions of 12.5 × 10.6 × 4.1 mm. A Kapton tape glued to the sides fixes the cuboid to a mechanically stable device (Fig. 3f). The origami folding allows the printed thermocouples to be aligned vertically, decreasing the device’s thermal conductance significantly compared to planarly printed generators. Due to the insulation layer between the TE elements realized by the ultrathin folded substrate foil itself, the spacing between the TE legs is given by the substrate thickness (6 µm in our case) with no additional air gap between the TE legs needed. This favorable design results in an extremely high density of thermocouples per cross-section area of roughly 190 per cm2 and subsequentially in a high open-circuit voltage and a high-power density.

The inlaid insulation however leads to a parasitic heat flow bypassing the thermoelectric material and an overall reduction of the power conversion efficiency. For the devices fabricated in this work a quick estimation with the dimension given in the layout, the thermal conductivities from Table 1, and the thermal conductivity of PEN34 of 0.22 Wm−1K−1 yields that the thermal resistance of the origami TEGs is 24.53% lower than if the TE elements were separated by 6 µm of air35 with the thermal conductivity of 0.0264 Wm−1K−1. This effect is thereby rather significant.

Table 1 Material properties at room temperature of the materials used in the generator.
Full size table

To minimize the parasitic heat flow, the substrate should, therefore, be as thin as possible while still providing the necessary mechanical stability and protection against punctuations. Additionally, the thickness of the printed layers should be as high as possible to reduce the internal resistance and maximize the percentage of TE material in the device. Screen printing with a large theoretical ink volume is therefore a suitable method to print large areas with a high layer thickness of thermoelectric material. We can adjust the printing layout to control the geometrical dimensions of the TEG therefore allowing precise setting of its thermal and electrical impedances. The expected performance for a specific print layout and geometry is calculated using a software tool considering all material properties as input parameters. This allows us to optimize the layout for a given application. Specifically, the thermal conductance is tunable within several orders of magnitude, since the height of the elements directly determines the distance of the folds and therefore the height and thermal conductance of the generator. The height of the elements however has a negligible influence on the electrical resistance of the device, since the total length of the series connection remains unaltered. We can adjust the electrical resistance by increasing the element width, however only to the extent, that the minimum number of columns therefore the number of thermocouples to provide the necessary output voltage and the minimum distance between columns to avoid electrical short circuits to is not undercut. This allows the design of a customized device which satisfies thermal and electrical impedance matching condition for a given application.

Electrical characterization of origami TEGs

We have carried out a systematic study of the series of 24 TEGs. All of them were first characterized regarding the electrical properties. Subsequently, the thermoelectric performance was measured. Figure 4a shows a histogram of the internal resistances of all 24 TEGs before and after the folding process.

Fig. 4: Characterization of the origami TEGs.
figure 4

a Histogram of the internal electrical resistance of the devices unfolded after printing (light) and after the origami folding (dark). b TEG characterization setup with two copper blocks as thermal contacts. c Open circuit voltage vs. applied temperature difference for TEG #6. d I–V characteristics and output power vs. voltage for different applied temperature differences at TEG #6. e Output power vs. electrical load for different applied temperature differences at TEG #6. f Histogram of the maximal output power and the open circuit voltages of all produced TEGs at ∆T = 30 K.

Full size image

On average, the devices before the folding process exhibited a resistance of 840Ω ± 7.46% while the finished folded devices had an internal resistance of 1007Ω ± 27.5%. We attribute this increase mostly to the formation of microcracks in the printed layers induced at the edges during the folding process while the increased variance was introduced by the manual folding. Four devices showed a lower internal resistance after folding, which is likely the result of larger particles in the TiS2 ink piercing the substrate and causing a shortcut between the TE elements.

We characterized the TE performance of the devices using an in-house measurement setup consisting of two temperature-controlled copper blocks working as a heat source and a heat sink. The TEGs were placed between the two blocks to apply a precise temperature difference between the top and bottom sides of the TEG (Fig. 4b). For improved thermal contact between the copper blocks and the upper and lower surface of the TEG, we applied a thermally conductive paste at the interfaces. The displayed ΔT values have an uncertainty of ±0.5 K. The electrical measurements were made with an uncertainty of 0.33 %. A comprehensive error analysis for this setup can be found in Supplementary Note 2.

Figure 4c shows the linear dependence of the open-circuit voltage of the TEG with the best performance (#6) as a function of the applied temperature difference. The open-circuit voltage is proportional to the applied temperature difference with a slope of 19.7 mVK−1. Figure 4d shows the detailed I–V characteristics of TEG #6 for different temperature differences. The electrical behavior of the printed device corresponded to a typical real linear voltage source. Due to the high number of TE legs, our design enables macroscopic voltages of several 100 mV for a moderate temperature difference. Furthermore, the output power at the maximum power point (MPP) is high enough to supply low power electronic circuits. The output power increased with ΔΤ² reaching 243 µW for ΔT = 60 K. Even for ΔT = 30 K this device generated PMPP = 63.4 µW and an open circuit voltage Voc = 534 mV corresponding to a power density of 47.8 µWcm−2 while the internal resistance is 1124 Ω. Figure 4e shows the output power of TEG #6 vs. the connected electrical load. The device had its MPP at roughly Rload = R regardless of the applied temperature difference. This was due to the low current and the small effective ZT of the device which result in a negligible Peltier effect.

The device variations were studied by characterizing all 24 TEGs. The produced output powers at the MPP, as well as the open-circuit voltages for all devices for ΔT = 30 K (Cold side: 25 °C; Hot side: 55 °C), are displayed in Fig. 4f. We chose these temperatures to simulate a possible application scenario in an industrial environment where the heat source would be a pipe carrying a warm fluid and the heat sink would be the ambient air. The average PMPP amounted to 40.5 µW ± 28.9% with an average Voc of 394 mV ± 16.5%. We mention that the TiS2 used as an n-type material oxidizes within several hours under normal atmospheric conditions. To protect the device from degradation, it can be sealed in a pouch encapsulation despite further decreasing the effective ΔΤ applied to the TE legs.

Energy self-sufficient wireless weather sensor

To demonstrate an energy-harvesting sensor application, we used a TEG to power a customized sensor board. The board comprises a weather sensor (Bosch BME280) which measures ambient temperature, humidity, and pressure. The values are periodically sent to a receiver (e.g., a smartphone) using the Bluetooth Low Energy (BLE) standard. The energy supplied by the TEG was continuously collected via a power management system, which allowed the operation of the TEG close to its MPP. Furthermore, the power management system uses a capacitor with 57.5 µF at a working voltage of 6.3 V as energy storage to allow the release of the collected energy as short current pulses, enough to operate the sensor board. The BLE module requires 1.8 V which is provided at the output of the power management by an on-chip step-up converter. A schematic of the system is displayed in Fig. 5a and detailed information is provided in Supplementary Note 3. The BLE module was programmed to read-out the sensor and transmit the data at an interval of 4 s encoded in its advertising signal to minimize average power consumption. Figure 5b shows the transient current used by the sensor board over 2 min.

Fig. 5: Bluetooth beacon.
figure 5

a Schematic of an energy-harvesting wireless sensor application powered by a TEG. b Current used by the wireless sensor application operated at 1.8 V and transmitting every 4 s for a duration of 12 ms resulting in an average current of 8.3 µA and an average power consumption of 14.9 µW. c Current at the input of the power with an average current of 194.3 µA drawn from the TEG resulting in average total power consumption of 61.3 µW.

Full size image

After an initiation process, the BLE module starts to transmit periodically with a total active time in each interval of only 12 ms. The long downtime of the signal results in a low average current of only 8.3 µA and average power consumption of 14.9 µW. To characterize the power management, the whole system was connected to a voltage source at 0.534 V in series to a resistance of 1124 Ω, simulating TEG #6 at a temperature difference of 30 K. The total current at the input of the power management is shown in Fig. 5c. After drawing a high current from the TEG at initiation to charge the energy storage for the first time, the MPP tracking stabilizes the input voltage at 0.267 V and an input current of 238 µA. When the energy storage is fully charged the power management stops drawing power from the TEG resulting in an average input current of 194.3 µA and an average input voltage of 0.316 V. Even though the efficiency of the power management at this low input voltage is rather low, it is enough to power the BLE module with the TEG. The total average power needed by the complete system is 61.3 µW and thus smaller than the maximum output power of the TEG.

In conclusion, we report a device architecture for a fully printed thermoelectric generator by screen printing an n-type and a p-type thermoelectric material in a checkerboard layout followed by a two-step origami folding process. It produces a mechanically stable cuboid in which the heat flow occurs in-plane with respect to the printed TE elements by arranging them vertically. This self-aligned process ensures insulation between the neighboring thermocouples by the substrate foil itself. Our design allows us to tune the height and therefore maximizing the power output of the generator via impedance matching to the heat source and heat sink by simply altering the print layout allowing to set its correct thermal conductance. The high density of thermocouples resulted in an output power of 63.4 µW at a 30 K temperature difference, enough to power an energy self-sufficient wireless weather sensor in an IoT application harvesting heat energy from e.g., a hot pipe. We demonstrated the operation of a customized sensor board comprising a weather sensor and a BLE module as an energy self-sufficient wireless sensor node with a TEG at a temperature difference of 30 K or higher. Our TEG design can be realized with any screen printable TE material and paves the way for potentially low-cost and customizable energy harvesting TEGs for powering autonomous sensor nodes. Using environmental thermal energy as a decentralized energy source marks a significant milestone towards large-scale energy-harvesting of waste heat.

Methods

Materials

We synthesized PEDOT nanowires and formulated ink for printing the p-type thermoelectric material with ethylene glycol as the solvent. The synthetic route for the nanowires followed Han and Foulger36 and the ink was formulated using a recipe published in a patent application by Aslan et al.37. The selected route enables higher conductivities paired with a screen printability of the PEDOT nanowires. As the n-type TE material, we used a TiS2:Hexylamine-complex previously reported by Wan et al.38,39. The ink was formulated using N-Methylformamide as the solvent, following a process published in a patent application by Aslan et al.40. This route gives easy access to a screen printable TiS2 ink. The synthesis details and process steps for the ink formulations are further explained in Supplementary Note 4.

We determined the Seebeck coefficient of the materials by measuring doctor-bladed thin films in an in-house-built setup of which we provided a complete description in Supplementary Note 5. The electrical conductivity was characterized using a 4-point measurement method of a well-defined material strip. The strip is fabricated by doctor-blading the ink through a mask on top of a glass substrate with four gold contacts. We measured the thickness of the sample with a Bruker contour GT-K 3D Optical Microscope.

A comprehensive error analysis of the measured values can be found in Supplementary Note 2. Measuring in-plane thermal conductivities is however very challenging, therefore we refer here to reported values in literature38,41. Table 1 lists the material properties of the printed films at room temperature. The thermal conductivities and the ZT-values in Table 1 merely serve as orientation and are not used to conclude or estimate the thermal conductance or the efficiency of the printed devices.

Layout design

We designed the layout shown in Fig. 3a with a total height of 154 mm and a total width of 156 mm using the maximum area printable by the used screen printer. The layout consists of 254 p-legs (shown in blue) and 253 n-legs (shown in yellow) arranged in a checkerboard type pattern of 13 columns and 39 rows. The individual elements are 10.62 mm wide and have a height of 4.17 mm including the overlapping area (shown in cyan) between two legs with a width of 0.3 mm. The columns are separated by 1.5 mm and are connected by strips of the p-type material with a width of 2 mm.

Printing process

We printed the generators (Fig. 3b) on a 6 µm thin substrate foil of PEN using the semi-automatic screen printing machine Kammann K15 Q-SL. To achieve a large layer thickness, we deposited two layers of each material on top of each other and dried the layers on a hotplate at 140 °C for 2 min after each printing step. One exemplary printing step is visible in Supplementary Movie 1. The resulting thickness for the PEDOT nanowire layer and the TiS2 layer was approximately 7 µm, which we measured with a Bruker contour GT-K 3D Optical Microscope. The first and the last element in the series connection were extended with the p-type ink using calligraphy and dried with a heat gun. These contact fields provided better accessibility to the circuit.