Abstract
The global carbon and water cycles are governed by the coupling of CO2 and water vapour exchanges through the leaves of terrestrial plants, controlled by plant adaptations to balance carbon gains and hydraulic risks. We introduce a trait-based optimality theory that unifies the treatment of stomatal responses and biochemical acclimation of plants to environments changing on multiple timescales. Tested with experimental data from 18 species, our model successfully predicts the simultaneous decline in carbon assimilation rate, stomatal conductance and photosynthetic capacity during progressive soil drought. It also correctly predicts the dependencies of gas exchange on atmospheric vapour pressure deficit, temperature and CO2. Model predictions are also consistent with widely observed empirical patterns, such as the distribution of hydraulic strategies. Our unified theory opens new avenues for reliably modelling the interactive effects of drying soil and rising atmospheric CO2 on global photosynthesis and transpiration.
Similar content being viewed by others
Main
The fundamental dilemma of plants following the C3 photosynthetic pathway is that when stomata, that is, the tiny ‘valves’ on the surface of leaves, are opened to take in carbon dioxide (CO2) for carbon assimilation, water is lost through them via transpiration1. The plant’s transpiration stream is maintained by negative water potentials (suction pressures) in roots, transport vessels and leaves. Withstanding negative water potentials requires adapted stem, leaf and root tissues or energy-intensive repair efforts, and extreme water potentials in the xylem can lead to hydraulic failure2,3,4. The risks of hydraulic failure increase when water availability declines across the plants’ rooting zone or when vapour pressure deficit increases at their leaf surfaces. Plants can avoid hydraulic failure by closing their stomatal openings in response to dry soil and atmospheric conditions. However, closing the stomata also leads to a decline in carbon assimilation, creating a tight coupling between carbon uptake and water loss. At the ecosystem level, this coupling of the carbon and water cycles governs the rates of gross primary production (GPP) and evapotranspiration in response to water stress. On one hand, rising atmospheric CO2 and increased precipitation are enhancing water use efficiency5,6, potentially increasing tree growth rates. On the other hand, rising atmospheric vapour pressure deficits are leading to decreases in stomatal conductance7, and rising frequency and intensity of droughts are leading to increased mortality rates8. It has been argued that a persistent increase in tree mortality rates, together with a saturating increase in growth rates, is negatively affecting the carbon sink of tropical forests9. Accurate predictions of carbon and water fluxes under water stress thus require vegetation models that explicitly account for plant hydraulic processes10 to resolve the limiting effect of atmospheric water demand and soil moisture stress on plant photosynthesis11.
A plant’s hydraulic machinery places key constraints on how much water it can transpire and, consequently, on its stomatal conductance. Considerable effort has gone into the development of stomatal control models with an explicit treatment of plant hydraulics (see reviews12,13). Hydraulically explicit stomatal models have shown success in simulating short-term stomatal responses to drying soil and air on sub-daily and daily timescales14,15,16,17 and are now being implemented in Earth System Models18,19,20,21. However, we still lack understanding of how plant physiology acclimates to the development of soil-moisture drought on daily to weekly timescales and how such longer-term acclimation in turn affects stomatal sensitivity to short-term water stress. Such understanding is especially crucial for predicting stomatal and biochemical responses to novel environments and for explaining widely observed patterns related to plant hydraulic strategies (Box 1) in a parsimonious way.
The classic stomatal optimization model22 states that plants adjust their stomatal conductance to maximize total carbon assimilation for a fixed amount of water loss, by assuming a constant unit cost for transpired water. This model implies that plants can save water for future use. However, recent stomatal models recognize that plants competitively consume available water23. Therefore, an alternative approach conceives the costs of transpiration as arising from the risks of hydraulic failure and the structural and energetic expenditures for withstanding high suction pressures. Thus, many extensions of this classic model explicitly represent plant hydraulics and the associated costs23,24,25. These models require an a priori specification of photosynthetic capacity, which then becomes an additional parameter to be fitted to enable accurate predictions of assimilation rates. By contrast, the least-costs optimization framework26 includes the costs of maintaining carboxylation capacity, reflecting a trade-off between investing in photosynthetic and hydraulic capacities27. Building upon this approach, a recent model predicts acclimated carboxylation capacity28 using the photosynthetic-coordination hypothesis28,29. It also explicitly optimizes electron-transport capacity (albeit using a separate optimization criterion)28, and has been successful in predicting CO2 assimilation rates and leaf-internal CO2 concentrations across climatic gradients. However, this model requires an empirical factor to account for the effects of soil moisture30,31,32.
Here we develop a unified first-principles theory combining the photosynthetic-coordination hypothesis with the principles of plant hydraulics within a single optimality framework. Our framework simultaneously predicts the stomatal responses and biochemical acclimation of leaves to environments changing on multiple timescales. We test the resulting model predictions with published data obtained from soil drought experiments conducted with 18 plant species spanning diverse plant functional types. We show that, with just three hydraulic traits and two parameters, our model correctly predicts key observations related to plant photosynthetic responses and hydraulic strategies, as described in Box 1.
Model summary
We now list the principles and hypotheses underlying our model in general terms, followed by a summary of the optimality framework, plant traits used in our model, the interpretation of model parameters and our strategy for testing the model with experimental data. A detailed model description is presented in Methods, and a full derivation of the model is presented in Supplementary Information section 1.
Model principles and hypotheses
Our model is based on three principles and hypotheses as follows.
-
(1)
Water-balance principle. Any plant must maintain a continuous stream of water across its entire hydraulic pathway (through roots, stems and leaves) to ensure that the atmospheric demand for transpiration is met by the supply of water from the soil33. If supply does not equal demand, xylem may embolize or leaves and roots may get damaged, causing catastrophic failure of the hydraulic system. Demand through transpiration depends on the stomatal conductance gs and the atmospheric vapour pressure deficit D, whereas supply depends on the soil-to-leaf water-potential difference Δψ and the hydraulic properties of the transpiration pathway. Therefore, this principle predicts gs as a function of Δψ and is widely used in stomatal models that explicitly represent water transport. We use the term ‘principle’ rather than ‘hypothesis’ for this assumption to indicate its rooting in basic physical laws.
-
(2)
Photosynthetic-coordination hypothesis. Photosynthetic carbon assimilation is limited by a plant’s capacity for carboxylation Vcmax and by light availability Iabs, which, together with the electron-transport capacity Jmax, determine the rates of biochemical and photochemical reactions governing CO2 fixation34. In general, the rate of photosynthesis is the minimum of the carboxylation-limited rate Ac and the light-limited rate Aj. The light-limited rate is further modulated by Jmax. Since the carboxylation and electron-transport capacities are costly to maintain, they are hypothesized to acclimate to typical daytime conditions on a weekly timescale, such that the two photosynthetic rates are coordinated, that is, Ac = Aj 29,35.
-
(3)
Profit-maximization hypothesis. We posit that, on a weekly timescale (medium-term responses), plants simultaneously optimize their photosynthetic capacity and stomatal conductance to maximize net assimilation (profit, F), after accounting for the costs of maintaining photosynthetic capacity and the hydraulic pathway, including the risks of hydraulic failure. On a daily timescale (short-term responses), the acclimated photosynthetic capacities are fixed, and plants can optimize only their stomatal conductance. The parameters scaling the photosynthetic and hydraulic costs, α and γ, respectively, are the only two latent (that is, not directly observable) parameters in our model and are henceforth called ‘unit costs’.
Hydraulic pathway and hydraulic traits
Water from the soil first enters the roots, where it flows through the root cortex, the endodermis and the stele. It then flows through the xylem in roots, the stem and leaf veins. After exiting the xylem, it flows through the bundle sheath and spongy mesophyll cells in the leaf, until it evaporates from the stomatal cell walls and diffuses out to the ambient air36 (Fig. 1a). Under moderate water stress, which is the focus of the present work, the outside-xylem segments of the pathway may experience reversible losses in conductivity. For example, the soil-root interface may lose conductivity as roots shrink and disconnect from the soil, while leaves and roots may lose conductivity due to reductions in aquaporin activity or cell membrane permeability37,38. Extremely high suction pressures may lead to irreversible loss of xylem conductivity due to cavitation, although some species can reverse it by refilling xylem conduits or growing new xylem39. The flow of water through the plant can be described as depending on three effective hydraulic traits, which characterize the combined effect of the individual segments of the pathway: (1) the maximum plant conductance per unit leaf area, that is, the maximum leaf-specific whole-plant conductance Kp, (2) the water potential ψ50 that causes a 50% loss of whole-plant conductance, and (3) a shape parameter b that determines the sensitivity of conductance loss to water potential during progressive drought. There is increasing evidence that roots are the most resistive parts of the hydraulic pathway40 and leaves are the most vulnerable37,41. This is primarily due to the properties of the outside-xylem segments in roots and leaves, which thus form the hydraulic bottleneck of a plant. Further, there are lags in the recovery of root and stem conductivity upon rehydration, causing hysteresis in the response of the conductivity of these tissues to water potential42. While an explicit treatment of such hysteresis may be important for predicting root recovery on short timescales and xylem recovery from extreme drought, we focus on one-way drying in this study, reflecting data limitations and maintaining simplicity and analytical tractability.
a, Water-transport pathway. Purple labels indicate the three hydraulic traits that determine the conductance to water flow of each of the three segments of the water-transport pathway. Water potentials are shown at various points along the pathway: ψs in soil, ψr in roots at the beginning of the xylem segment, ψx at the end of the xylem segment and ψl in leaves near the stomata. The soil-to-leaf water potential difference Δψ = ψs − ψl thus comprises the successive pressure drops along the three segments, that is, Δψr = ψs − ψr along the radial outside-xylem segment within the roots, \({\Delta}\psi _\mathrm{x} = \psi _\mathrm{r} - \psi _\mathrm{x}\) along the xylem and \({\Delta}\psi _\mathrm{l} = \psi _\mathrm{x} - \psi _\mathrm{l}\) along the outside-xylem segment within the leaves. b, Model-calibration pathway. The model takes as inputs three effective whole-plant hydraulic traits (Kp, ψ50 and b) together with two cost parameters (the unit costs of photosynthetic and hydraulic capacities, α and γ, respectively). It predicts as outputs the optimal values (denoted by asterisks) of stomatal conductance \(g_\mathrm{s}^ \ast\), assimilation rate A*, transpiration E*, acclimated photosynthetic capacities \(V_{{{{\mathrm{cmax}}}}}^ \ast\) and \(J_{{{{\mathrm{max}}}}}^ \ast\), soil-to-leaf water-potential difference Δψ* and leaf internal-to-external CO2 ratio χ*. Each variable is first calculated as a function of Δψ and χ, as shown by the four light-green arrows, from which the optimal combination (Δψ*, χ*) is then calculated by maximizing profit F according to equation (1). Blue arrows and boxes indicate the process through which the best-fit traits and unit costs for each species are calculated by minimizing the model error. Orange labels indicate the three principles and hypotheses underlying the model, displayed next to the processes they affect.
Medium-term responses
To predict the acclimation of photosynthetic capacity on a weekly timescale, we assume that plants independently control their weekly-average stomatal conductance gs and their electron-transport capacity Jmax to maximize their net profit F, as defined below. After expressing all quantities in Fig. 1b in dependence on gs and Jmax, or equivalently, in a mathematically more convenient form, in terms of the leaf internal-to-external CO2 ratio χ and the soil-leaf water-potential difference Δψ (Methods and Supplementary Information section 1.3), F can be written as
where A is the assimilation rate calculated by combining the standard biochemical model of photosynthesis34 with the photosynthetic-coordination hypothesis (equation 6 in Methods). We find the optimal solution (χ*, Δψ*) semi-analytically by first calculating the derivatives of F with respect to χ and Δψ analytically (Supplementary equation 16) and then determining their roots numerically.
Short-term responses
To predict stomatal responses on hourly and daily timescales, we follow a two-step procedure. First, we find the acclimated photosynthetic capacities using the multivariate optimization described above, driven by a 7 d rolling mean of the soil water potential. Once the acclimated Jmax and Vcmax are known, A, gs and χ can all be expressed in terms of Δψ alone. We again use the net profit in equation (1) to optimize Δψ. In this case, we determine A as the minimum of the carboxylation-limited rate Ac and the light-limited rate Aj. Also, since Jmax is fixed, the term αJmax becomes constant and can thus be ignored during optimization.
Interpretation of costs
The photosynthetic costs consist of the costs incurred by maintaining photosynthetic capacities, including the regeneration of RuBP. Since the two photosynthetic capacities are coordinated, these costs are assumed to be proportional to Jmax. The hydraulic costs include (1) the construction and respiration costs of stem and leaf tissues, (2) the costs of maintaining osmotic potential and (3) the prospective costs of hydraulic failure. Since these costs are difficult to quantify through mechanistic arguments, we have taken a phenomenological approach and used the expression Δψ2 after assessing various alternative cost expressions (Supplementary Fig. 6). A cost expression that is quadratic in Δψ has also been adopted previously23. Sensitivity of our model predictions to the two cost parameters α and γ is shown in Supplementary Fig. 5.
Testing the model with data
We use published data from experiments conducted with 18 species, in which plants were grown in greenhouses under controlled conditions and subjected to progressive soil drought; values of A and gs (and sometimes also of Δψ) are reported for different values of predawn leaf water potentials, which are indicative of the soil water potential in the plant’s rooting zone. The dataset has been previously assembled using tables and digitized figures from published literature as detailed in ref. 43, which we expanded to include Δψ measurements. Table 1 lists the sources and the data can be found in Supplementary Datasets 1 and 2. In some experiments, each value of soil water potential was maintained for a long duration, so that photosynthetic capacity could acclimate (species with drought duration =∞ in Table 1). For such species, we use the multivariate optimization model as described above (equation 1). In other experiments, the progression of drought occurred at a natural rate, ranging 12–60 d (Table 1). For such species, we use the two-step procedure outlined above to obtain the instantaneous values of the assimilation rate and stomatal conductance.
Results
We show that across 18 species, our model correctly predicts photosynthetic responses to the environment. We also show that model-predicted hydraulic strategies for the species in our dataset are consistent with widely observed empirical patterns.
Photosynthetic responses to soil moisture
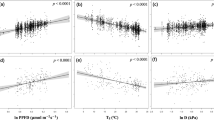
Our model correctly predicts the variation in assimilation rate (A), stomatal conductance (gs), leaf-internal-to-external CO2 ratio (ci:ca, or χ) and soil-to-leaf water-potential difference (Δψ) in response to soil-moisture availability (ψs; Fig. 2). Specifically, the shapes of these dependencies closely resemble those observed during experimental drought: Fig. 3 shows predicted and observed responses for two Eucalyptus species from contrasting habitats, and Supplementary Fig. 1 shows the corresponding responses for all 18 species. Moreover, cross-validation analysis shows that our model generalizes to out-of-sample soil-moisture conditions (Supplementary Table 1).
a–c, Pooled data from all 18 species comparing assimilation rate A (a), stomatal conductance gs (b) and leaf-internal-to-external CO2 ratio χ (c) for different values of soil (predawn leaf) water potential ψs. d, Predicted values of soil-to-leaf water-potential difference Δψ compared to observations for (1) six species for which midday leaf water potentials were reported in the corresponding experiments, and thus measured under the same environmental conditions as the gas-exchange rates (circles), and (2) two species (Pseudotzuga menziesii and Olea europea var. Meski) for which values were obtained from literature 67 (triangles). Colours indicate soil water potential relative to the stomatal closure point (ψg88) of the species; thus, yellow points represent soil water potentials at or beyond stomatal closure. Black lines show linear regressions, while grey lines are the 1:1 lines that represent perfect predictions. In c, we ignore points with ψs < ψg88 (yellow points) while calculating the regression line, since there is a known bias in predictions of χ beyond stomatal closure (see Discussion).
Matches are shown here for two Eucalyptus species from contrasting climates, and corresponding matches for all 18 species are shown in Supplementary Fig. 1. a–f, Predicted responses (lines) and observed responses (points) to decreasing soil water potential (ψs, measured as predawn leaf water potential): assimilation rate A (a), stomatal conductance gs (b), leaf-internal-to-external CO2 ratio χ (c), soil-to-leaf water-potential difference Δψ (d), carboxylation capacity Vcmax (e) and electron-transport capacity Jmax (f). Eucalyptus pilularis (blue lines and squares) typically occupies warm and humid coastal areas in eastern Australia, whereas Eucalyptus populnea (green lines and triangles) typically occupies semi-arid interior regions of eastern Australia. Since both species were grown in the same greenhouse during the experiment, their contrasting responses reveal genetic adaptations to their native environments. For both species, progressive drought was experimentally induced over 12 d, resulting in a fast instantaneous response of stomatal conductance in combination with a slow acclimating response of photosynthetic capacity. Our model predictions readily account for both responses.
Empirical studies report that photosynthetic capacity (Vcmx and Jmax) declines in response to developing soil drought44,45. A unique feature of our model is its ability to predict these responses correctly, qualitatively in accordance with these studies (Fig. 3e,f). Since χ depends on both Jmax and gs, correct predictions of χ require predicting both quantities correctly. Therefore, a close match between predicted and observed values of χ (Fig. 2c) provides further quantitative validation of the photosynthetic capacity predicted by our model.
Photosynthetic responses to vapour pressure deficit
Our work builds on the principles introduced by ref. 28, and thus inherits the capacity to accurately predict32 photosynthetic responses to temperature, atmospheric CO2 and light intensity (Supplementary Fig. 2c–e). Furthermore, by explicitly accounting for plant hydraulics, our model delivers improved predictions of photosynthetic responses to soil moisture and vapour pressure deficit (Supplementary Fig. 2a,b).
The functional relationship between logit(χ) and log(D) predicted by our model shows a close match with observations (Box 1, point 3). In particular, our model predicts this relationship to be linear, with a median slope value of −0.697 and 5%–95% quantile range of (−0.75, −0.67) (Fig. 4a). These predicted slope values are well within the confidence interval reported in the literature46. Also, we find that this slope is negatively correlated with ψ50 (Fig. 4b), such that species with highly negative ψ50 have less negative slope values. Since earlier datasets were dominated by temperate evergreen species, this could explain why a slope value of −0.5 predicted by previous models was supported by such datasets. We offer our predicted correlation between the slope and ψ50 as an empirically testable prediction for future studies.
a, The model-predicted distribution of the slope of the relationship between logit(χ) and log(D) for the analysed species (grey bars) is well within the range reported in ref. 46 (their reported mean and confidence interval is shown by the green line and green region, respectively). It is significantly different from −0.5 (orange line; a one-sample t-test shows a predicted mean slope of −0.7 and a 95% confidence interval of (−0.72, −0.68)). For each species, we calculate the predicted slope by varying vapour pressure deficit in the range 5–5,000 Pa while keeping other environmental parameters constant (at values reported in the respective experiments, with ψs = 0) and using fitted trait values (Table 1). b, This slope is correlated with the ψ50 (black points are species-specific values and the blue line is a linear regression line), with more negative slopes observed for species with less negative ψ50 (drought avoiders). This could be a reason why earlier datasets supported a slope value of −0.5, as such datasets were often dominated by temperate evergreen species, which are typically characterized by highly negative values of ψ50.
Predicted hydraulic strategies match observations
In this section, we compare several widely observed empirical patterns among plant hydraulic traits with the corresponding model-predicted patterns. This qualitative comparison allows us to validate our model at an even deeper level.
First, we compare the distribution of the model-predicted degree of anisohydricity for the 18 analysed species (Box 1) to an empirically observed distribution obtained from a recently compiled database on 102 species across the globe47. For each species, the degree of anisohydricity is determined by the slope of the relationship between the water potential in the leaf (ψl) and in the soil (ψs), measured at low ψs (slope <1 for isohydric, =1 for isohydrodynamic and >1 for anisohydric species). The observed global distribution of these slopes peaks at approximately 1, suggesting that the global majority of species follow the isohydrodynamic strategy47. The corresponding distribution predicted by our model lies within the observed distribution (Fig. 5a). Similarly, the predicted distribution of typical operating water potentials (ψl at ψs = 0) also closely matches the corresponding empirically observed distribution (Supplementary Fig. 3).
a, The predicted distribution of the degree of anisohydricity among the 18 analysed species (grey bars) lies within the observed global distribution (green bars; as reported in ref. 47). b, Consistent with empirical observations, the observed turgor loss point (thick green line) lies between the model-predicted water potential at 50% loss of plant conductivity (ψ50; black line) and the model-predicted water potential at 88% stomatal closure (ψg88; brown line). c, Plant hydraulic conductance (Kp) is weakly negatively correlated with ψ50, with no species having high values of both traits, implying a weak safety-efficiency trade-off in line with empirical observations. d, When leaf water potential is at ψg88, the observed loss of xylem conductivity is typically less than 50% (implied by observed xylem hydraulic vulnerability \(\tilde \psi _{50\mathrm{x}}\) being less than model-predicted ψg88), which means that plants close their stomata before the onset of substantial xylem embolism. Furthermore, the difference between the regression line (black) and the 1:1 line (grey) is low, implying that the hydraulic safety margin \(\tilde \psi _{50\mathrm{x}} - \psi _{\mathrm{g}88}\) is small on average. Sources for values of \(\tilde \psi _{50\mathrm{x}}\) are given in Supplementary Table 2. Closed circles indicate species for which γ was estimated using data on Δψ, whereas open circles refer to species for which such data were not available and for which we therefore used an average value of γ estimated for the respective plant types.
Second, we compare the relationship between model-predicted plant hydraulic vulnerability and empirically observed turgor loss point for a subset comprising 7 of the 18 analysed species for which these empirical data were available. Empirical observations show that the turgor loss point lies between the point where the leaf loses 50% conductivity (ψ50) and the point of stomatal closure (ψg88)48. Our model predictions are consistent with this observation for most of those 7 species (Fig. 5b).
Third, we compare how model-estimated plant hydraulic vulnerability (ψ50), a measure of hydraulic safety, covaries with model-estimated plant hydraulic conductance (Kp), a measure of hydraulic efficiency. Global data reveal a trade-off between safety and efficiency, that is, no plants score high on both, but only a weak correlation between them, that is, many plants score low on both. Consistent with these observations, we find only a weak correlation between model-estimated values of ψ50 and Kp, with a few species having low values of both traits, but no species having high values of both (Fig. 5c).
Fourth, we compare how the model-estimated stomatal closure point (ψg88) relates to empirically observed xylem hydraulic vulnerability (\(\tilde \psi _{50\mathrm{x}}\)) for the 18 analysed species. Empirical observations show that stomatal closure occurs before the onset of substantial xylem embolism37,49,50,51, which is probably an adaptation to prevent plant mortality during drought4. At the same time, the minimum water potential experienced by the leaves (ψmin) is close to the water potential at which the xylem loses 50% conductivity (\(\tilde \psi _{50\mathrm{x}}\)), leading to extremely low hydraulic safety margins52. Both of these observations are matched by our model, confirmed by a close correlation between ψg88 (which is a proxy of ψmin) and \(\tilde \psi _{50\mathrm{x}}\) (Fig. 5d).
Discussion
We have presented an analytical trait-based optimality model, unifying plant photosynthesis and hydraulics to predict the stomatal responses and biochemical acclimation of plants to changing hydroclimates. Consistent with widely observed empirical patterns and benchmarked with experimental data available for 18 different plant species, our model correctly predicts the stomatal and photosynthetic responses to soil drought and the dependencies of photosynthesis on vapour pressure deficit, temperature, light intensity and CO2.
Comparison with other stomatal optimization models
To our knowledge, our model is probably the first to combine semi-analytical simplicity with physiological realism to predict the simultaneous stomatal and biochemical responses of plants to the environment, including water stress. Our approach has four key strengths: (1) the multivariate optimization used in our model allows for predicting the observed s-shaped decline of Vcmax in response to drying soil from first principles, in contrast to most other models that require specification of Vcmax as a species-specific trait; (2) explicit inclusion of plant hydraulics in our model enables separating the stomatal responses to atmospheric drought and soil-moisture availability, which could be used for improving remote-sensing estimates of GPP; (3) being based on optimality principles and specified with just two latent parameters, our model can be expected to perform well even under out-of-sample environmental conditions, that is, those outside the domain of environmental factors used for calibration, such as elevated CO2 levels; and (4) enabling a semi-analytical solution, our model is computationally efficient and can thus be readily incorporated into existing vegetation modelling frameworks. A quantitative model intercomparison between stomatal models including ours would provide valuable insights into the relative accuracy and strengths of different stomatal optimization frameworks and would thus be an interesting direction for future research.
Leaf photosynthesis is known to be jointly constrained by stomatal and non-stomatal limitations. A vast majority of photosynthesis models account only for stomatal limitations, where stomatal conductance is optimized to maximize photosynthetic gain. Non-stomatal limitations, such as the constraints imposed by leaf mesophyll, photosynthetic capacity and sugar transport, have received attention only in the most recent stomatal models. Even such models account for them using a pre-determined functional response, in which mesophyll conductance53 or photosynthetic capacity24,53,54 is scaled in a prescribed way with stomatal conductance. By contrast, our model can account for non-stomatal limitations without the need to specify photosynthetic capacity a priori. This is especially important when applying it to out-of-sample environmental conditions and to species for which empirical estimates of photosynthetic capacity are not available.
Almost all current models of stomatal optimization focus on water transport through the xylem. By contrast and in line with growing evidence37,40,41,42, we hypothesized that the outside-xylem segments of the hydraulic pathway (in the leaves and roots) together form the hydraulic bottleneck of the plant. The hydraulic-segmentation hypothesis55 states that expendable organs such as leaves and fine roots act as a ‘safety valve’ by losing conductivity and driving stomatal closure before the onset of fatal xylem cavitation. Therefore, we hypothesized that our model-based estimates of ψ50 would arise from leaves and roots and thus be less negative than the corresponding empirically observed values for xylem (\(\tilde \psi _{50\mathrm{x}}\)). Our findings are consistent with these hypotheses. We offer the fitted values of these traits (ψ50 and Kp) as testable predictions that can be validated by explicitly measuring these traits for the leaves and roots of the corresponding species.
Model assumptions and extensions
Under extreme hydroclimatic conditions, such as extremely dry or flooded soils, or extremely low atmospheric CO2 levels, our model predictions may deviate slightly from observations. For example, most species in our dataset show an increase in the leaf-internal-to-external CO2 ratio (χ) after stomatal closure (Fig. 3). The model-predicted χ does not increase, asymptotically approaching a constant value instead (Fig. 3 and Supplementary equation 18). The increase in χ is due to a build-up of CO2 in the leaf, which can happen via two mechanisms: (1) if dark respiration continues even after assimilation has ceased, or (2) if assimilation and respiration decline together due to reduced photosynthetic activity while CO2 continues to ‘leak in’ through the leaf cuticle56. Future research could identify which of these processes is observed in leaves: since the source of CO2 is different in the two mechanisms (plant metabolism or ambient air), they can be distinguished on the basis of whether the build-up is detected also in δ13C measurements. Our model could be extended to include these mechanisms, but this would not affect the predicted assimilation rates because these mechanisms are relevant only after stomatal closure.
For simplicity, we have assumed a single effective hydraulic pathway characterized by effective traits summarily describing water flow through the different segments (leaves, xylem and roots) of the pathway. However, a more realistic extension of our model could readily be developed by explicitly modelling water transport through each segment. In Supplementary Information section 2, we present a derivation of an extended model accounting for a multi-segment pathway. Such an extension would be particularly useful for resolving the roles of roots and leaves in stomatal control and drought survival.
To avoid making the model too complex and parameter-heavy and to enable a semi-analytical solution, we have neglected two physiological details, inclusion of which offers promising directions for further research: (1) the leaf’s energy balance and (2) hysteresis in the conductivity-soil-moisture relationship. First, when soil dries, reduced transpiration raises the leaf temperature, which in turn affects the temperature-dependent photosynthetic parameters and the dark-respiration rate. Second, the recovery of root and stem conductivity after rehydration is typically slower than the corresponding loss of conductivity during dehydration42. This leads to hysteresis in the relationship between conductivity and soil water potential. The speed of recovery is especially hampered under extreme drought when xylem becomes cavitated because recovery from cavitation requires embolism refilling or growth of new xylem. In our model, the relationship between soil water potential and conductivity is described by a vulnerability curve P(ψ) that does not include hysteresis. To account for hysteresis, one may use a separate vulnerability curve during recovery or use a hysteretic submodel for conductivity39. Further research focusing on drought and rewetting experiments can help generate data for robustly parameterizing and validating such a model.
Plants respond to increasing water stress on multiple timescales and at multiple scales of organization (leaves, whole plants and even stands). Our model accounts for leaf-level responses on daily and weekly timescales, capturing the role of stomatal closure in preventing damagingly negative stem water potentials. Scaling responses from the leaf level to the whole-plant level requires considering the distribution of leaves within the plant canopy as well as the total canopy area: this could be achieved by embedding our model within a model of plant canopies. Such a model could then be extended further to yield optimality-based first-principles models for the plant level57, accounting for responses beyond the point of stomatal closure, such as the shedding of leaves on a monthly timescale, which occurs either in full to prevent loss of water through cuticular tissue4 or in part to reduce transpiration demand and continue photosynthesis58. Similarly, changes to the characteristics and architecture of the transpiration pathway, as reflected in stem traits59, could be modelled on yearly to decadal timescales. Trait adaptation on centennial or millennial timescales could be modelled by embedding our leaf-level optimality theory into evolutionary models60,61,62.
In our model, on the shortest timescale (minutes to days), plants may optimize leaf water potential for a fixed (acclimated) photosynthetic capacity. On the timescale of weeks, plants additionally adjust their photosynthetic capacities. In principle, the weekly timescale can be modelled either with nested optimization (that is, optimizing daily, or sub-daily, stomatal conductance for a given photosynthetic capacity, and optimizing weekly photosynthetic capacity by maximizing the total profit over a week), or with simultaneous optimization (that is, optimizing both variables together by assuming a constant environment during the week, representative for mean daytime conditions). In this work, we have taken the latter approach for theoretical and computational simplicity, but the alternative nested approach is worth exploring in future work.
Implications for global vegetation modelling
Taking advantage of the increasing availability of global data on plant traits, our model can be applied at the global scale by making a few additional assumptions. For the species in our dataset, we find that the photosynthetic unit cost α lies within a narrow range of values (0.08–0.12), which could therefore be treated as a constant. Furthermore, variations in the hydraulic unit cost γ are primarily driven by differences between plant types, with relatively lesser variability within plant types, suggesting that γ could also be treated as a constant within plant types (Supplementary Fig. 4). To infer the global distribution of α and γ, our model can be used in a Bayesian framework on global data on gas-exchange measurements. When plant-level hydraulic traits ψ50 and Kp are not available, these could be derived from other widely measured traits on the basis of observed patterns of functional coordination among plant organs. As a starting point, we have shown that Kp is weakly correlated with ψ50 (Fig. 5c) and specific leaf area (Supplementary Fig. 4b). Further studies could test for similar correlations with leaf vein density and root mass fraction, which are respectively expected to affect leaf and root conductivities.
Accurate models of plant photosynthesis are crucial for improving projections of the global carbon and water cycles, because photosynthesis and transpiration by terrestrial plants account for 56% and 30% of the global fluxes of carbon dioxide and water, respectively63,64. It is especially important to develop models that can generalize to new climatic conditions, because the projected increase in the frequency and intensity of droughts may lead to unprecedented climatic conditions in future. The inclusion of plant hydraulics into vegetation models has been shown to improve predictions of global productivity and evapotranspiration17,18,19,20,21, as well as predictions of the spatiotemporal diversity of vegetation65. Spearheading the development initiated by these studies, our model is ideally suited for being embedded into global vegetation models: by accounting for biochemical acclimation, plant hydraulics and photosynthetic trade-offs through optimality principles, our model can extend to new species and new environmental conditions with a raised degree of confidence. Furthermore, accounting for photosynthetic and hydraulic costs is bound to yield more accurate estimates of the energy spent on resource acquisition and, consequently, of the resources available for growth and reproduction. Therefore, embedding our model of photosynthesis and hydraulics into a demographic model of plant communities can help improve the scaling of assimilation and transpiration from the leaf level to the whole-plant level, and even from plants to communities, thus paving the way for more accurate and robust land-surface models.
Methods
Our model consists of three key components or modules, corresponding to the three principles and hypotheses: a water-transport module to account for plant hydraulics and water balance, a photosynthesis module to account for photosynthesis and the photosynthetic-coordination hypothesis, and a profit-maximization module to implement the optimization. Here we describe the equations used for each module, as well as our strategy for model calibration. Full derivations of the equations can be found in Supplementary Information section 1.
Water-transport module
We model water transport using Darcy’s law applied to small cross-sections of the hydraulic pathway (Supplementary Information section 1.1.4). In principle, our model of water transport can explicitly represent multiple segments (Supplementary Information section 2), but for simplicity, we represent the entire pathway by a single ‘effective segment’ with traits Kp, ψ50 and b. Thus, our hydraulic model is mathematically similar to the model for xylem water transport described in ref. 24, but the effective hydraulic traits in our model correspond not necessarily to the xylem but to the whole plant. As the outside-xylem segments (in leaves and roots) are the hydraulic bottlenecks of the plant for many species37,40,41,42, the traits modelled here probably correspond to these segments.
The conductivity κ of any cross-section of the pathway declines as the water potential becomes increasingly negative. This decline in conductivity is phenomenologically described by a so-called vulnerability curve P(ψ), such that κ(ψ) = κ(0)P(ψ). The vulnerability curve is typically described by a Weibull function with two parameters: the water potential ψ50 at which 50% conductivity is lost and a shape parameter b that determines the sensitivity of conductivity loss to water potential,
Water potential drops continuously along the hydraulic pathway, from ψs in the soil to ψl at the leaf surface, with a continuous decline in conductivity along the pathway. The volumetric flow of water per unit leaf area in the pathway, Q, is therefore described by a differential equation (see Supplementary Information section 1.1.4 for derivation), which can be solved for Q as follows,
where κp is the effective conductivity of the whole plant per unit leaf area, L is the effective length of the hydraulic pathway and η is the dynamic viscosity of water. The composite term κp/L = Kp is the whole-plant conductance per unit leaf area (Supplementary Information section 1.1). To keep the number of parameters low to prevent overfitting of the model to data, we use equation (3) to model water flow. In Supplementary Information section 2, we propose an extension of this model, deriving an expression for Q by explicitly accounting for segments of the hydraulic pathway in the roots, stem and leaves.
The water-balance principle states that the atmospheric demand for water imposed by vapour pressure deficit at the leaf surface matches the supply of water from the soil via the stem and leaf segments of the hydraulic pathway. The transpiration rate at which water vapour diffuses out of the leaf into the atmosphere is given by (see Supplementary Information section 1.1.6 for derivation)
where gs is the stomatal conductance and D is the atmospheric vapour pressure deficit divided by the atmospheric pressure. This rate E equals the rate Q at which water enters the leaf according to equation (3), which allows us to calculate gs by solving
Photosynthesis module
The assimilation rate A is calculated from the Farquhar-von Caemmerer-Berry biochemical model34 (Supplementary Information section 1.2.1), with the photosynthetic capacities Jmax and Vcmax linked through the photosynthetic-coordination hypothesis (Fig. 1b and Supplementary Information section 1.2.4). Temperature responses of photosynthesis parameters, such as the Michaelis-Menten coefficient and the light-compensation point, are modelled with Arrhenius functions for enzymatic rates as previously described31.
The photosynthetic-coordination hypothesis states that under typical daytime conditions, assimilation operates at the point of co-limitation, such that the carboxylation-limited and light-limited assimilation rates are equal. With this assumption, the co-limited assimilation rate can be written as (Supplementary Information section 1.2)
where J is the effective electron-transport capacity, which increases with light availability Iabs but saturates due to limitation by the leaf’s intrinsic maximum electron-transport capacity Jmax,
Here, ca is the atmospheric CO2 concentration, χ is the ratio of the leaf-internal and external CO2 concentrations (ci:ca), \({\Gamma}^ \ast\) is the light-compensation point, KM is the Michaelis-Menten coefficient for C3 photosynthesis, ϕ0 is the quantum yield efficiency, Iabs is the absorbed photosynthetically active radiation and br is the ratio of dark respiration to carboxylation capacity (dark respiration is assumed to be proportional to carboxylation capacity, that is, Rd = brVcmax). Temperature dependencies of \({\Gamma}^ \ast\) and KM are modelled according to ref. 31. The ratio br also has a weak dependence on temperature66, which we have ignored in this work. Variation in Jmax in response to light and water availability (by optimization) implies a coordinated variation in both carboxylation and electron-transport capacities.
Profit-maximization module
We assume that plants maximize net assimilation (or profit, F) defined in equation (1). Without loss of generality, we also assume that the unit benefit of assimilation is one, that is, α and γ represent the ratios of the unit costs to unit benefits of assimilation. To optimize equation (1), we express all quantities in terms of the two independent variables χ and Δψ and set the gradient of the profit function to 0. This can be done analytically (Supplementary equation 16). However, except in the special case of strong Jmax limitation, the roots of the gradient must be found semi-analytically (Supplementary Information section 1.3.2). Solving for optimal χ* and Δψ* in turn allows us to predict the optimal photosynthetic capacities (\(V_{{{{\mathrm{cmax}}}}}^ \ast\) and \(J_{{{{\mathrm{max}}}}}^ \ast\)), stomatal conductance (\(g_{{{\mathrm{s}}}}^ \ast\)) and CO2 assimilation rate (A*).
Parameter estimation and model testing
We drive the model with environmental variables (temperature, vapour pressure deficit, light intensity and CO2) as specified in the experimental studies. Other parameters used in the model are as follows: ϕ0 = 0.087, br = 0.002. In the case of instantaneous responses, we use the daily maximum light intensity under growth conditions to calculate the acclimated response, and saturating light intensity (as specified in the studies) to calculate the instantaneous response, so as to mimic the conditions present during LiCor measurements.
Since measurements of effective whole-plant hydraulic traits are not readily available, we treat them as model parameters and estimate them along with the two cost parameters. Values of Δψ were reported for 6 of the 18 species from the same drought experiments. We supplement Δψ observations with typical values reported in the literature67 for two additional species (Pseudotsuga menziesii and Olea europea var. Meski). For such species (for which measurements of Δψ are available), we calibrate five parameters (α, γ, ψ50, b, Kp) by minimizing the sum of squared errors (Er) between predicted and observed values of A, gs, χ and Δψ, defined as
where i represents different values of ψs, E[] denotes the mean value, and variables with tilde (for example, \(\tilde \chi\)) represent observations.
From this calibration, we obtain the mean estimated value of γ for each plant type. For all other species (for which measurements of Δψ are not available), we use this mean value of γ and estimate the remaining four parameters. To further reduce the degrees of freedom in model parameterization, we fix the value of b = 1 for all species, except for H. annuus for which b also had to be estimated. For each species for which data on Δψ are available, we evaluate model performance using fivefold cross-validation (or leave-one-out cross-validation when data points are limited).
P-hydro R and C++ packages
R code to run our model (P-hydro) is provided as an extension of the ‘rpmodel’ package (the version used in this paper is archived at https://github.com/jaideep777/rpmodel/releases/tag/v1.0.0h), with options to use the acclimating and instantaneous responses. A C++/Rcpp version is also provided for potential integration with vegetation models (https://github.com/jaideep777/phydro). These packages provide the option to either use the semi-analytical solution derived in this work, or to directly optimize the profit function numerically. The numerical implementation also allows for quick extension of the model with different profit and cost functions. The C++ version also allows the use of an approximate calculation of gs, which substantially improves computational speed with only a minor loss of accuracy.
Reporting summary
Further information on research design is available in the Nature Research Reporting Summary linked to this article.
Data availability
All data used in this manuscript are compiled from the literature. We have provided citations to publications and databases at appropriate locations in the manuscript. The compiled database can be found in the Supplementary Information.
Code availability
R code to run our model (P-hydro) is provided as an extension of the ‘rpmodel’ package (the version used in this paper is archived at https://github.com/jaideep777/rpmodel/releases/tag/v1.0.0h), with options to use the acclimating and instantaneous responses. A C++ version is also provided for potential integration with existing vegetation models (https://github.com/jaideep777/phydro). The vignettes folder of this package also contains R code to reproduce key results.
References
Raschke, K., Monteith, J. L. & Weatherley, P. E. How stomata resolve the dilemma of opposing priorities. Phil. Trans. R. Soc. Lond. B 273, 551–560 (1976).
Brodribb, T. J. & Cochard, H. Hydraulic failure defines the recovery and point of death in water-stressed conifers. Plant Physiol. 149, 575–584 (2009).
Brodribb, T. J., Bowman, D. J. M. S., Nichols, S., Delzon, S. & Burlett, R. Xylem function and growth rate interact to determine recovery rates after exposure to extreme water deficit. New Phytol. 188, 533–542 (2010).
Choat, B. et al. Triggers of tree mortality under drought. Nature 558, 531–539 (2018).
Keeling, R. F. et al. Atmospheric evidence for a global secular increase in carbon isotopic discrimination of land photosynthesis. Proc. Natl Acad. Sci. USA https://doi.org/10.1073/pnas.1619240114 (2017).
Guerrieri, R. et al. Disentangling the role of photosynthesis and stomatal conductance on rising forest water-use efficiency. Proc. Natl Acad. Sci. USA 116, 16909–16914 (2019).
Grossiord, C. et al. Plant responses to rising vapor pressure deficit. New Phytol. 226, 1550–1566 (2020).
McDowell, N. G. & Allen, C. D. Darcy’s law predicts widespread forest mortality under climate warming. Nat. Clim. Change 5, 669–672 (2015).
Brienen, R. J. W. et al. Long-term decline of the Amazon carbon sink. Nature 519, 344–348 (2015).
McDowell, N. G. et al. Pervasive shifts in forest dynamics in a changing world. Science 368, eaaz9463 (2020).
Novick, K. A. et al. The increasing importance of atmospheric demand for ecosystem water and carbon fluxes. Nat. Clim. Change 6, 1023–1027 (2016).
Damour, G., Simonneau, T., Cochard, H. & Urban, L. An overview of models of stomatal conductance at the leaf level. Plant Cell Environ. 33, 1419–1438 (2010).
Wang, Y., Sperry, J. S., Anderegg, W. R. L., Venturas, M. D. & Trugman, A. T. A theoretical and empirical assessment of stomatal optimization modeling. New Phytol. 227, 311–325 (2020).
Anderegg, W. R. L. et al. Woody plants optimise stomatal behaviour relative to hydraulic risk. Ecol. Lett. 21, 968–977 (2018).
Venturas, M. D. et al. A stomatal control model based on optimization of carbon gain versus hydraulic risk predicts aspen sapling responses to drought. New Phytol. 220, 836–850 (2018).
Sabot, M. E. B. et al. Plant profit maximization improves predictions of European forest responses to drought. New Phytol. 226, 1638–1655 (2020).
Eller, C. B. et al. Stomatal optimization based on xylem hydraulics (SOX) improves land surface model simulation of vegetation responses to climate. New Phytol. 226, 1622–1637 (2020).
Hickler, T., Prentice, I. C., Smith, B., Sykes, M. T. & Zaehle, S. Implementing plant hydraulic architecture within the LPJ Dynamic Global Vegetation Model. Glob. Ecol. Biogeogr. 15, 567–577 (2006).
Bonan, G. B., Williams, M., Fisher, R. A. & Oleson, K. W. Modeling stomatal conductance in the earth system: linking leaf water-use efficiency and water transport along the soil–plant–atmosphere continuum. Geosci. Model Dev. 7, 2193–2222 (2014).
Christoffersen, B. O. et al. Linking hydraulic traits to tropical forest function in a size-structured and trait-driven model (TFS v.1-Hydro). Geosci. Model Dev. 9, 4227–4255 (2016).
Kennedy, D. et al. Implementing plant hydraulics in the Community Land Model, Version 5. J. Adv. Model. Earth Syst. 11, 485–513 (2019).
Cowan, I. R. & Farquhar, G. D. Stomatal function in relation to leaf metabolism and environment. Symp. Soc. Exp. Biol. 31, 471–505 (1977).
Wolf, A., Anderegg, W. R. L. & Pacala, S. W. Optimal stomatal behavior with competition for water and risk of hydraulic impairment. Proc. Natl Acad. Sci. USA 113, E7222–E7230 (2016).
Sperry, J. S. et al. Predicting stomatal responses to the environment from the optimization of photosynthetic gain and hydraulic cost. Plant Cell Environ. 40, 816–830 (2017).
Bartlett, M. K., Detto, M. & Pacala, S. W. Predicting shifts in the functional composition of tropical forests under increased drought and CO2 from trade-offs among plant hydraulic traits. Ecol. Lett. 22, 67–77 (2019).
Prentice, I. C., Dong, N., Gleason, S. M., Maire, V. & Wright, I. J. Balancing the costs of carbon gain and water transport: testing a new theoretical framework for plant functional ecology. Ecol. Lett. 17, 82–91 (2014).
Wright, I. J., Reich, P. B. & Westoby, M. Least‐cost input mixtures of water and nitrogen for photosynthesis. Am. Nat.161, 98–111 (2003).
Wang, H. et al. Towards a universal model for carbon dioxide uptake by plants. Nat. Plants 3, 734–741 (2017).
Maire, V. et al. The coordination of leaf photosynthesis links C and N fluxes in C3 plant species. PLoS ONE 7, e38345 (2012).
Stocker, B. D. et al. Quantifying soil moisture impacts on light use efficiency across biomes. New Phytol. 218, 1430–1449 (2018).
Stocker, B. D. et al. P-model v1.0: an optimality-based light use efficiency model for simulating ecosystem gross primary production. Geosci. Model Dev. 13, 1545–1581 (2020).
Lavergne, A. et al. Historical changes in the stomatal limitation of photosynthesis: empirical support for an optimality principle. New Phytol. 225, 2484–2497 (2020).
Sperry, J. S. & Love, D. M. What plant hydraulics can tell us about responses to climate-change droughts. New Phytol. 207, 14–27 (2015).
Farquhar, G. D., von Caemmerer, S. & Berry, J. A. A biochemical model of photosynthetic CO2 assimilation in leaves of C3 species. Planta 149, 78–90 (1980).
Chen, J.-L., Reynolds, J. F., Harley, P. C. & Tenhunen, J. D. Coordination theory of leaf nitrogen distribution in a canopy. Oecologia 93, 63–69 (1993).
Buckley, T. N., John, G. P., Scoffoni, C. & Sack, L. How does leaf anatomy influence water transport outside the xylem? Plant Physiol. 168, 1616–1635 (2015).
Scoffoni, C. et al. Outside-xylem vulnerability, not xylem embolism, controls leaf hydraulic decline during dehydration. Plant Physiol. 173, 1197–1210 (2017).
Carminati, A. & Javaux, M. Soil rather than xylem vulnerability controls stomatal response to drought. Trends Plant Sci. 25, 868–880 (2020).
Klein, T. et al. Xylem embolism refilling and resilience against drought-induced mortality in woody plants: processes and trade-offs. Ecol. Res. 33, 839–855 (2018).
Rodriguez-Dominguez, C. M. & Brodribb, T. J. Declining root water transport drives stomatal closure in olive under moderate water stress. New Phytol. 225, 126–134 (2020).
Sack, L. & Holbrook, N. M. Leaf hydraulics. Annu. Rev. Plant Biol. 57, 361–381 (2006).
Bourbia, I., Pritzkow, C. & Brodribb, T. J. Herb and conifer roots show similar high sensitivity to water deficit. Plant Physiol. 186, 1908–1918 (2021).
Zhou, S., Duursma, R. A., Medlyn, B. E., Kelly, J. W. G. & Prentice, I. C. How should we model plant responses to drought? An analysis of stomatal and non-stomatal responses to water stress. Agric. Meteorol. 182–183, 204–214 (2013).
Kanechi, M., Uchida, N., Yasuda, T. & Yamaguchi, T. Non-stomatal inhibition associated with inactivation of rubisco in dehydrated coffee leaves under unshaded and shaded conditions. Plant Cell Physiol. 37, 455–460 (1996).
Salmon, Y. et al. Leaf carbon and water status control stomatal and nonstomatal limitations of photosynthesis in trees. New Phytol. 226, 690–703 (2020).
Dong, N. et al. Components of leaf-trait variation along environmental gradients. New Phytol. 228, 82–94 (2020).
Martínez‐Vilalta, J., Poyatos, R., Aguadé, D., Retana, J. & Mencuccini, M. A new look at water transport regulation in plants. New Phytol. 204, 105–115 (2014).
Bartlett, M. K., Klein, T., Jansen, S., Choat, B. & Sack, L. The correlations and sequence of plant stomatal, hydraulic, and wilting responses to drought. Proc. Natl Acad. Sci. USA 113, 13098–13103 (2016).
Brodribb, T. J., Holbrook, N. M., Edwards, E. J. & Gutiérrez, M. V. Relations between stomatal closure, leaf turgor and xylem vulnerability in eight tropical dry forest trees. Plant Cell Environ. 26, 443–450 (2003).
Martin‐StPaul, N., Delzon, S. & Cochard, H. Plant resistance to drought depends on timely stomatal closure. Ecol. Lett. 20, 1437–1447 (2017).
Skelton, R. P. et al. Low vulnerability to xylem embolism in leaves and stems of North American oaks. Plant Physiol. 177, 1066–1077 (2018).
Choat, B. et al. Global convergence in the vulnerability of forests to drought. Nature 491, 752–755 (2012).
Dewar, R. et al. New insights into the covariation of stomatal, mesophyll and hydraulic conductances from optimization models incorporating nonstomatal limitations to photosynthesis. New Phytol. 217, 571–585 (2018).
Hölttä, T., Lintunen, A., Chan, T., Mäkelä, A. & Nikinmaa, E. A steady-state stomatal model of balanced leaf gas exchange, hydraulics and maximal source–sink flux. Tree Physiol. 37, 851–868 (2017).
Pivovaroff, A. L., Sack, L. & Santiago, L. S. Coordination of stem and leaf hydraulic conductance in southern California shrubs: a test of the hydraulic segmentation hypothesis. New Phytol. 203, 842–850 (2014).
Boyer, J. S., Wong, S. C. & Farquhar, G. D. CO2 and water vapor exchange across leaf cuticle (epidermis) at various water potentials. Plant Physiol. 114, 185–191 (1997).
Deans, R. M., Brodribb, T. J., Busch, F. A. & Farquhar, G. D. Optimization can provide the fundamental link between leaf photosynthesis, gas exchange and water relations. Nat. Plants 6, 1116–1125 (2020).
Zhou, S.-X., Medlyn, B. E. & Prentice, I. C. Long-term water stress leads to acclimation of drought sensitivity of photosynthetic capacity in xeric but not riparian Eucalyptus species. Ann. Bot. 117, 133–144 (2016).
Rungwattana, K. et al. Trait evolution in tropical rubber (Hevea brasiliensis) trees is related to dry season intensity. Funct. Ecol. 32, 2638–2651 (2018).
Dybzinski, R., Farrior, C., Wolf, A., Reich, P. B. & Pacala, S. W. Evolutionarily stable strategy carbon allocation to foliage, wood, and fine roots in trees competing for light and nitrogen: an analytically tractable, individual-based model and quantitative comparisons to data. Am. Nat. 177, 153–166 (2011).
Hikosaka, K. & Anten, N. P. R. An evolutionary game of leaf dynamics and its consequences for canopy structure. Funct. Ecol. 26, 1024–1032 (2012).
Franklin, O. et al. Organizing principles for vegetation dynamics. Nat. Plants 6, 444–453 (2020).
Le Quéré, C. et al. Global carbon budget 2017. Earth Syst. Sci. Data 10, 405–448 (2018).
Jasechko, S. et al. Terrestrial water fluxes dominated by transpiration. Nature 496, 347–350 (2013).
Xu, X., Medvigy, D., Powers, J. S., Becknell, J. M. & Guan, K. Diversity in plant hydraulic traits explains seasonal and inter-annual variations of vegetation dynamics in seasonally dry tropical forests. New Phytol. 212, 80–95 (2016).
Wang, H. et al. Acclimation of leaf respiration consistent with optimal photosynthetic capacity. Glob. Change Biol. 26, 2573–2583 (2020).
Papastefanou, P. et al. A dynamic model for strategies and dynamics of plant water-potential regulation under drought conditions. Front. Plant Sci. 11, 373 (2020).
Grieu, P., Guehl, J. M. & Aussenac, G. The effects of soil and atmospheric drought on photosynthesis and stomatal control of gas exchange in three coniferous species. Physiol. Plant. 73, 97–104 (1988).
Liu, F., Andersen, M. N., Jacobsen, S.-E. & Jensen, C. R. Stomatal control and water use efficiency of soybean (Glycine max L. Merr.) during progressive soil drying. Environ. Exp. Bot. 54, 33–40 (2005).
Tezara, W., Driscoll, S. & Lawlor, D. W. Partitioning of photosynthetic electron flow between CO2 assimilation and O2 reduction in sunflower plants under water deficit. Photosynthetica 46, 127–134 (2008).
Liu, C.-C. et al. Influence of drought intensity on the response of six woody karst species subjected to successive cycles of drought and rewatering. Physiol. Plant. 139, 39–54 (2010).
Posch, S. & Bennett, L. T. Photosynthesis, photochemistry and antioxidative defence in response to two drought severities and with re-watering in Allocasuarina luehmannii. Plant Biol. 11, 83–93 (2009).
Jiang, M., Kelly, J. W. G., Atwell, B. J., Tissue, D. T. & Medlyn, B. E. Drought by CO2 interactions in trees: a test of the water savings mechanism. New Phytol. 230, 1421–1434 (2021).
Ennajeh, M., Tounekti, T., Vadel, A. M., Khemira, H. & Cochard, H. Water relations and drought-induced embolism in olive (Olea europaea) varieties ‘Meski’ and ‘Chemlali’ during severe drought. Tree Physiol. 28, 971–976 (2008).
Peguero-Pina, J. J., Sancho-Knapik, D., Morales, F., Flexas, J. & Gil-Pelegrín, E. Differential photosynthetic performance and photoprotection mechanisms of three Mediterranean evergreen oaks under severe drought stress. Funct. Plant Biol. 36, 453–462 (2009).
Liu, C.-C. et al. Exploitation of patchy soil water resources by the clonal vine Ficus tikoua in karst habitats of southwestern China. Acta Physiol. Plant. 33, 93–102 (2011).
Leuning, R. A critical appraisal of a combined stomatal-photosynthesis model for C3 plants. Plant Cell Environ. 18, 339–355 (1995).
Medlyn, B. E. et al. Reconciling the optimal and empirical approaches to modelling stomatal conductance. Glob. Change Biol. 17, 2134–2144 (2011).
Brodribb, T. et al. Linking xylem network failure with leaf tissue death. New Phytol. 232, 68–79 (2021).
Klein, T. The variability of stomatal sensitivity to leaf water potential across tree species indicates a continuum between isohydric and anisohydric behaviours. Funct. Ecol. 28, 1313–1320 (2014).
Acknowledgements
We thank B. Medlyn and O. Franklin for discussions and feedback on the manuscript. J.J. and U.D. acknowledge funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie Actions fellowship (grant agreement No. 841283 – Plant-FATE). J.J., F.H. and U.D. gratefully acknowledge funding from the International Institute for Applied Systems Analysis (IIASA) and the National Member Organizations that support the institute. J.J. also gratefully acknowledges support from the Divecha Centre for Climate Change, Indian Institute of Science in the form of initial funding. This work is a contribution to the Imperial College initiative on Grand Challenges in Ecosystems and the Environment, and has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement no: 787203 REALM). B.D.S. was funded by the Swiss National Science Foundation grant no. PCEFP2_181115. All authors thank the Okinawa Institute of Science and Technology Graduate University and the European Research Council for equally sharing the cost for enabling the open-access publication of this article.
Author information
Authors and Affiliations
Contributions
J.J., B.D.S., I.C.P. and U.D. designed the study. J.J. developed the model and performed the analysis. S.Z., U.D. and F.H. contributed data and/or complementary analysis tools. J.J. wrote the first draft of the paper, and all authors contributed to revised versions of the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Plants thanks Florian Busch and Tim Brodribb for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary text, Figs. 1–6, and Tables 1 and 2.
Supplementary Data 1
Dataset containing meta-analysis of soil drought experiments used for model calibration and validation.
Supplementary Data 2
Dataset containing Δψ measurements from the soil drought experiments in Dataset 1.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Joshi, J., Stocker, B.D., Hofhansl, F. et al. Towards a unified theory of plant photosynthesis and hydraulics. Nat. Plants 8, 1304–1316 (2022). https://doi.org/10.1038/s41477-022-01244-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41477-022-01244-5