Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

Maintenance of carbohydrate transport in tall trees

Nature Plants volume 3, pages 965–972 (2017)Cite this article

Subjects

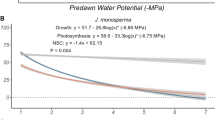
Abstract

Trees present a critical challenge to long-distance transport because as a tree grows in height and the transport pathway increases in length, the hydraulic resistance of the vascular tissue should increase. This has led many to question whether trees can rely on a passive transport mechanism to move carbohydrates from their leaves to their roots. Although species that actively load sugars into their phloem, such as vines and herbs, can increase the driving force for transport as they elongate, it is possible that many trees cannot generate high turgor pressures because they do not use transporters to load sugar into the phloem. Here, we examine how trees can maintain efficient carbohydrate transport as they grow taller by analysing sieve tube anatomy, including sieve plate geometry, using recently developed preparation and imaging techniques, and by measuring the turgor pressures in the leaves of a tall tree in situ. Across nine deciduous species, we find that hydraulic resistance in the phloem scales inversely with plant height because of a shift in sieve element structure along the length of individual trees. This scaling relationship seems robust across multiple species despite large differences in plate anatomy. The importance of this scaling becomes clear when phloem transport is modelled using turgor pressures measured in the leaves of a mature red oak tree. These pressures are of sufficient magnitude to drive phloem transport only in concert with structural changes in the phloem that reduce transport resistance. As a result, the key to the long-standing mystery of how trees maintain phloem transport as they increase in size lies in the structure of the phloem and its ability to change hydraulic properties with plant height.

This is a preview of subscription content, access via your institution

Relevant articles

Open Access articles citing this article.

Access options

Rent or buy this article

Get just this article for as long as you need it

$39.95

Learn more

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Diagram of sieve tube anatomy and structural parameters that contribute to hydraulic resistance in angiosperms.
Fig. 2: Relationship between phloem anatomical parameters and height.
Fig. 3: Model of pressure differential required to drive phloem transport with increasing tree height under three different scenarios.
Fig. 4: Parameterization of carbohydrate transport in a 120-year-old red oak tree.
Fig. 5: Structural changes in sieve plate anatomy that affect sieve tube resistance.
Fig. 6: Comparison of xylem and phloem anatomy.

References

  1. Knoblauch, M. & Oparka, K. The structure of the phloem—still more questions than answers. Plant J. 70, 147–156 (2012).

    Article  CAS  PubMed  Google Scholar 

  2. De Schepper, V., De Swaef, T., Bauweraerts, I. & Steppe, K. Phloem transport: a review of mechanisms and controls. J. Exp. Bot. 64, 4839–4850 (2013).

    Article  PubMed  Google Scholar 

  3. Münch, E. Material Flow in Plants (trans. Milburn, J. A. & Kreeb, K. H., Univ. Bremen, 2003) (Gustav Fischer, Jena, 1930).

  4. Thompson, M. V. & Holbrook, N. M. Scaling phloem transport: water potential equilibrium and osmoregulatory flow. Plant Cell Environ. 26, 1561–1577 (2003).

    Article  Google Scholar 

  5. Jensen, K. H., Rio, E., Hansen, R., Clanet, C. & Bohr, T. Osmotically driven pipe flows and their relation to sugar transport in plants. J. Fluid Mech. 636, 371–396 (2009).

    Article  CAS  Google Scholar 

  6. LaBarbera, M. Principles of design of fluid transport systems in zoology. Science 249, 992–1000 (1990).

    Article  CAS  PubMed  Google Scholar 

  7. Knoblauch, M. et al. Testing the Münch hypothesis of long distance phloem transport in plants. eLife 5, e15341 (2016).

    Article  PubMed  PubMed Central  Google Scholar 

  8. Lalonde, S., Wipf, D. & Frommer, W. B. Transport mechanisms for organic forms of carbon and nitrogen between source and sink. Annu. Rev. Plant Biol. 55, 341–372 (2004).

    Article  CAS  PubMed  Google Scholar 

  9. Rennie, E. A. & Turgeon, R. A comprehensive picture of phloem loading strategies. Proc. Natl Acad. Sci. USA 106, 14162–14167 (2009).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  10. Turgeon, R. The puzzle of phloem pressure. Plant Physiol. 154, 578–581 (2010).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  11. West, G. B., Brown, J. H. & Enquist, B. J. A general model for the structure and allometry of plant vascular systems. Nature 400, 664–667 (1999).

    Article  CAS  Google Scholar 

  12. McCulloh, K. A., Sperry, J. S. & Adler, F. R. Water transport in plants obeys Murray’s law. Nature 421, 939–942 (2003).

    Article  CAS  PubMed  Google Scholar 

  13. Murray, C. D. The physiological principle of minimum work: I. The vascular system and the cost of blood volume. Proc. Natl Acad. Sci. USA 12, 207–214 (1926).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  14. Anfodillo, T., Carraro, V., Carrer, M., Fior, C. & Rossi, S. Convergent tapering of xylem conduits in different woody species. New Phytol. 169, 279–290 (2006).

    Article  PubMed  Google Scholar 

  15. Mencuccini, M. Hydraulic constraints in the functional scaling of trees. Tree Physiol. 22, 553–565 (2002).

    Article  PubMed  Google Scholar 

  16. Enquist, B. J. Cope’s rule and the evolution of long-distance transport in vascular plants: allometric scaling, biomass partitioning and optimization. Plant Cell Environ. 26, 151–161 (2003).

    Article  Google Scholar 

  17. Savage, V. M. et al. Hydraulic trade-offs and space filling enable better predictions of vascular structure and function in plants. Proc. Natl Acad. Sci. USA 107, 22722–22727 (2010).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  18. Turgeon, R. & Wolf, S. Phloem transport: cellular pathways and molecular trafficking. Annu. Rev. Plant Biol. 60, 207–221 (2009).

    Article  CAS  PubMed  Google Scholar 

  19. van Bel, A. J. E., Ehlers, K. & Knoblauch, M. Sieve elements caught in the act. Trends Plant Sci. 7, 126–132 (2002).

    Article  PubMed  Google Scholar 

  20. Eschrich, W. in Transport in Plants I: Phloem Transport (Encyclopedia of Plant Physiology) Vol. 1 (eds Zimmermann, M. H. & Milburn, J. A.) 39–56 (Springer, Berlin, 1975).

  21. Jensen, K. H. et al. Optimality of the Münch mechanism for translocation of sugars in plants. J. R. Soc. Interface 8, 1155–1165 (2011).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  22. Pickard, W. F. Münch without tears: a steady-state Münch-like model of phloem so simplified that it requires only algebra to predict the speed of translocation. Funt. Plant Biol. 39, 531–537 (2012).

    Article  Google Scholar 

  23. Hölttä, T., Mencuccini, M. & Nikinmaa, E. Linking phloem function to structure: analysis with a coupled xylem–phloem transport model. J. Theor. Biol. 259, 325–337 (2009).

    Article  PubMed  Google Scholar 

  24. Petit, G. & Crivellaro, A. Comparative axial widening of phloem and xylem conduits in small woody plants. Trees 28, 915–921 (2014).

    Article  Google Scholar 

  25. Jyske, T. & Hölttä, T. Comparison of phloem and xylem hydraulic architecture in Picea abies stems. New Phytol. 205, 102–115 (2015).

    Article  CAS  PubMed  Google Scholar 

  26. Rosner, S., Baier, P. & Kikuta, S. B. Osmotic potential of Norway spruce Picea abies (L.) Karst. secondary phloem in relation to anatomy. Trees 15, 472–482 (2001).

    Article  Google Scholar 

  27. Woodruff, D. R. The impacts of water stress on phloem transport in Douglas-fir trees. Tree Physiol. 34, 5–14 (2014).

    Article  CAS  PubMed  Google Scholar 

  28. Jensen, K. H. et al. Modeling the hydrodynamics of phloem sieve plates. Front. Plant Sci. 3, 151 (2012).

    Article  PubMed  PubMed Central  Google Scholar 

  29. Liesche, J., Pace, M. R., Xu, Q., Li, Y. & Chen, S. Height‐related scaling of phloem anatomy and the evolution of sieve element end wall types in woody plants. New Phytol. 214, 245–256 (2017).

    Article  CAS  PubMed  Google Scholar 

  30. Knoblauch, M. & Peters, W. S. What actually is the Münch hypothesis? A short history of assimilate transport by mass flow. J. Integr. Plant Biol. 59, 292–310 (2017).

    Article  PubMed  Google Scholar 

  31. Ryan, M. G. & Asao, S. Phloem transport in trees. Tree Physiol. 34, 1–4 (2014).

    Article  PubMed  Google Scholar 

  32. Mullendore, D. L., Windt, C. W., Van As, H. & Knoblauch, M. Sieve tube geometry in relation to phloem flow. Plant Cell 22, 579–593 (2010).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  33. Knoblauch, J., Mullendore, D. L., Jensen, K. H. & Knoblauch, M. Pico gauges for minimally invasive intracellular hydrostatic pressure measurements. Plant Physiol. 166, 1271–1279 (2014).

    Article  PubMed  PubMed Central  Google Scholar 

  34. Jensen, K. H., Savage, J. A. & Holbrook, N. M. Optimal concentration for sugar transport in plants. J. R. Soc. Interface 10, 20130055 (2013).

    Article  PubMed  PubMed Central  Google Scholar 

  35. Liesche, J., Windt, C., Bohr, T., Schulz, A. & Jensen, K. H. Slower phloem transport in gymnosperm trees can be attributed to higher sieve element resistance. Tree Physiol. 35, 376–386 (2015).

    Article  CAS  PubMed  Google Scholar 

  36. De Schepper, V. et al. 11C-PET imaging reveals transport dynamics and sectorial plasticity of oak phloem after girdling. Front. Plant Sci. 4, 200 (2013).

    Article  PubMed  PubMed Central  Google Scholar 

  37. Canny, M. J. Phloem Translocation 205–207 (Cambridge Univ. Press, Cambridge, 1973).

    Google Scholar 

  38. Windt, C. W., Vergeldt, F. J., De Jager, P. A. & Van As, H. MRI of long-distance water transport: a comparison of the phloem and xylem flow characteristics and dynamics in poplar, castor bean, tomato and tobacco. Plant Cell Environ. 29, 1715–1729 (2006).

    Article  CAS  PubMed  Google Scholar 

  39. Gould, N., Thorpe, M. R., Koroleva, O. & Minchin, P. E. H. Phloem hydrostatic pressure relates to solute loading rate: a direct test of the Münch hypothesis. Funt. Plant Biol. 32, 1019–1026 (2005).

    Article  Google Scholar 

  40. Oner-Sieben, S. & Lohaus, G. Apoplastic and symplastic phloem loading in Quercus robur and Fraxinus excelsior. J. Exp. Bot. 65, 1905–1916 (2014).

    Article  PubMed  PubMed Central  Google Scholar 

  41. Liesche, J., Martens, H. J. & Schulz, A. Symplasmic transport and phloem loading in gymnosperm leaves. Protoplasma 248, 181–190 (2011).

    Article  CAS  PubMed  Google Scholar 

  42. Croser, C., Bengough, A. G. & Pritchard, J. The effect of mechanical impedance on root growth in pea (Pisum sativum). II. Cell expansion and wall rheology during recovery. Physiol. Plant. 109, 150–159 (2000).

    Article  CAS  Google Scholar 

  43. Pritchard, J. Aphid stylectomy reveals an osmotic step between sieve tube and cortical cells in barley roots. J. Exp. Bot. 47, 1519–1524 (1996).

    Article  CAS  Google Scholar 

  44. Rygol, J., Pritchard, J., Zhu, J. J., Tomos, A. D. & Zimmermann, U. Transpiration induces radial turgor pressure gradients in wheat and maize roots. Plant Physiol. 103, 493–500 (1993).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  45. Sperry, J. S., Hacke, U. G. & Wheeler, J. K. Comparative analysis of end wall resistivity in xylem conduits. Plant Cell Environ. 28, 456–465 (2005).

    Article  Google Scholar 

  46. van Bel, A. J. E. The phloem, a miracle of ingenuity. Plant Cell Environ. 26, 125–149 (2003).

    Article  Google Scholar 

  47. Fensom, D. S. The bio-electric potentials of plants and their functional signficance: I. An electrokinetic theory of transport. Can. J. Bot. 35, 573–582 (1957).

    Article  Google Scholar 

  48. Spanner, D. C. The translocation of sugar in sieve tubes. J. Exp. Bot. 9, 332–342 (1958).

    Article  CAS  Google Scholar 

  49. Lang, A. Relay mechanism for phloem translocation. Ann. Bot. 44, 141–145 (1979).

    Article  Google Scholar 

  50. Aikman, D. P. Contractile proteins and hypotheses concerning their role in phloem transport. Can. J. Bot. 58, 826–832 (1980).

    Article  CAS  Google Scholar 

  51. Comtet, J., Jensen, K. H., Turgeon, R., Stroock, A. D. & Hosoi, A. E. Passive phloem loading and long-distance transport in a synthetic tree-on-a-chip. Nat. Plants 3, 17032 (2017).

    Article  CAS  PubMed  Google Scholar 

  52. Turgeon, R., Medville, R. & Nixon, K. C. The evolution of minor vein phloem and phloem loading. Am. J. Bot. 88, 1331–1339 (2001).

    Article  CAS  PubMed  Google Scholar 

  53. Gamalei, Y. Phloem loading and its development related to plant evolution from trees to herbs. Trees 5, 50–64 (1991).

    Article  Google Scholar 

  54. Carvalho, M. R., Turgeon, R., Owens, T. & Niklas, K. J. The scaling of the hydraulic architecture in poplar leaves. New Phytol. 214, 145–157 (2017).

    Article  CAS  PubMed  Google Scholar 

  55. Woodruff, D. R., Bond, B. J. & Meinzer, F. C. Does turgor limit growth in tall trees? Plant Cell Environ. 27, 229–236 (2004).

    Article  Google Scholar 

  56. Ryan, M. G. & Yoder, B. J. Hydraulic limits to tree height and tree growth. Bioscience 47, 235–242 (1997).

    Article  Google Scholar 

  57. Koch, G. W., Sillett, S. C., Jennings, G. M. & Davis, S. D. The limits to tree height. Nature 428, 851–854 (2004).

    Article  CAS  PubMed  Google Scholar 

  58. Mencuccini, M., Hölttä, T. & Martínez-Vilalta, J. in Size- and Age-Related Changes in Tree Structure and Function (eds Meinzer, F. C. et al.) 309–339 (Springer, New York, NY, 2011).

  59. Aloni, R. Control of xylogenesis within the whole tree. Ann. For. Sci. 46, 267s–272s (1989).

    Article  Google Scholar 

  60. Anfodillo, T. et al. Widening of xylem conduits in a conifer tree depends on the longer time of cell expansion downwards along the stem. J. Exp. Bot. 63, 837–845 (2012).

    Article  CAS  PubMed  Google Scholar 

  61. Savage, J. A., Haines, D. F. & Holbrook, N. M. The making of giant pumpkins: how selective breeding changed the phloem of Cucurbita maxima from source to sink. Plant Cell Environ. 38, 1543–1554 (2015).

    Article  CAS  PubMed  Google Scholar 

  62. Savage, J. A. et al. Allocation, stress tolerance and carbon transport in plants: how does phloem physiology affect plant ecology? Plant Cell Environ. 39, 709–725 (2016).

    Article  CAS  PubMed  Google Scholar 

  63. Scholz, A., Klepsch, M., Karimi, Z. & Jansen, S. How to quantify conduits in wood? Front. Plant Sci. 4, 56 (2013).

    Article  PubMed  PubMed Central  Google Scholar 

  64. Ruzin, S. E. Plant Microtechnique and Microscopy 132 (Oxford Univ. Press, Oxford, 1999).

    Google Scholar 

  65. Phillips, R. J. & Dungan, S. R. Asymptotic analysis of flow in sieve tubes with semi-permeable walls. J. Theor. Biol. 162, 465–485 (1993).

    Article  Google Scholar 

  66. Thompson, M. V. & Holbrook, N. M. Application of a single-solute non-steady-state phloem model to the study of long-distance assimilate transport. J. Theor. Biol. 220, 419–455 (2003).

    Article  PubMed  Google Scholar 

  67. Jensen, K. H. et al. Sap flow and sugar transport in plants. Rev. Mod. Phys. 88, 035007 (2016).

    Article  Google Scholar 

Download references

Acknowledgements

Funding was provided by the National Science Foundation (IOS 1021779 and 1456682 to N.M.H. and M.K.), a Katharine H. Putnam Fellowship in Plant Science (J.A.S.), a Harvard Bullard Fellowship (M.K.), and the University of Minnesota Duluth (J.A.S.). Samples were collected at the Arnold Arboretum of Harvard University (permit no. 22-2013), the Harvard Forest and the main campus of Harvard University. Imaging was completed at the Harvard Center for Biological Imaging, Franceschi Microscopy and Imaging Center at WSU, the Center for Nanoscale Systems (Harvard University) and the Weld Hill Microscopy Lab at the Arnold Arboretum.

Author information

Authors and Affiliations

  1. Department of Biology, University of Minnesota, Duluth, MN, USA

    Jessica A. Savage

  2. Department of Organismic and Evolutionary Biology, Harvard University, Cambridge, MA, USA

    Jessica A. Savage, Laura Clerx, Jessica T. Gersony, Juan M. Losada & N. Michele Holbrook

  3. School of Biological Sciences, Washington State University, Pullman, WA, USA

    Sierra D. Beecher, Jan Knoblauch & Michael Knoblauch

  4. Department of Physics, Technical University of Denmark, Lyngby, Denmark

    Kaare H. Jensen

Authors
  1. Jessica A. Savage
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Sierra D. Beecher
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Laura Clerx
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Jessica T. Gersony
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Jan Knoblauch
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Juan M. Losada
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Kaare H. Jensen
    View author publications

    You can also search for this author in PubMed Google Scholar

  8. Michael Knoblauch
    View author publications

    You can also search for this author in PubMed Google Scholar

  9. N. Michele Holbrook
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

J.A.S., K.H.J., M.K. and N.M.H. designed the research. J.A.S., S.D.B., L.C., J.T.G., J.K., M.K. and J.M.L. collected the data and standardized protocols. J.A.S. and K.H.J. analysed the data. J.A.S., N.M.H., K.H.J. and M.K. wrote the paper.

Corresponding author

Correspondence to Jessica A. Savage.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Additional information

Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Electronic supplementary material

Supplementary Information

Supplementary Tables 1–6, Supplementary Figures 1–3, Supplementary Information 2.

Life Sciences Reporting Summary

Rights and permissions

Reprints and Permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Savage, J.A., Beecher, S.D., Clerx, L. et al. Maintenance of carbohydrate transport in tall trees. Nature Plants 3, 965–972 (2017). https://doi.org/10.1038/s41477-017-0064-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41477-017-0064-y

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing