Abstract
Purpose
Breast cancer (BC) risk prediction allows systematic identification of individuals at highest and lowest risk. We extend the Breast and Ovarian Analysis of Disease Incidence and Carrier Estimation Algorithm (BOADICEA) risk model to incorporate the effects of polygenic risk scores (PRS) and other risk factors (RFs).
Methods
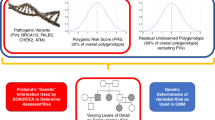
BOADICEA incorporates the effects of truncating variants in BRCA1, BRCA2, PALB2, CHEK2, and ATM; a PRS based on 313 single-nucleotide polymorphisms (SNPs) explaining 20% of BC polygenic variance; a residual polygenic component accounting for other genetic/familial effects; known lifestyle/hormonal/reproductive RFs; and mammographic density, while allowing for missing information.
Results
Among all factors considered, the predicted UK BC risk distribution is widest for the PRS, followed by mammographic density. The highest BC risk stratification is achieved when all genetic and lifestyle/hormonal/reproductive/anthropomorphic factors are considered jointly. With all factors, the predicted lifetime risks for women in the UK population vary from 2.8% for the 1st percentile to 30.6% for the 99th percentile, with 14.7% of women predicted to have a lifetime risk of ≥17–<30% (moderate risk according to National Institute for Health and Care Excellence [NICE] guidelines) and 1.1% a lifetime risk of ≥30% (high risk).
Conclusion
This comprehensive model should enable high levels of BC risk stratification in the general population and women with family history, and facilitate individualized, informed decision-making on prevention therapies and screening.
Similar content being viewed by others
INTRODUCTION
Breast cancer (BC) is the most common cancer among females in the Western world. However, a large proportion of BCs occur in a minority of the population who are at increased risk.1,2 Screening and prevention options are available to reduce morbidity and mortality, including more frequent mammograms and other screening modalities (e.g., magnetic resonance imaging [MRI]) and the use of chemoprevention (e.g., tamoxifen). In the United Kingdom3 such strategies are only recommended for women at increased BC risk, who are currently identified through family history (FH) of cancer or through screening for pathogenic variants in high-risk genes, such as BRCA1 and BRCA2. Susceptibility to BC is, however, multifactorial and many genetic variants and reproductive, hormonal, anthropomorphic, lifestyle, and imaging factors are known to be associated with the risk of developing the disease. Comprehensive risk models that incorporate all known factors would improve the ability to identify those at increased risk, and thus those most likely to benefit.4
Genetic susceptibility to BC is conferred by rare, high-penetrance variants in BRCA1 and BRCA2;5 rare, intermediate-risk variants (e.g., in PALB2, ATM, and CHEK2);6 and by commoner variants (mostly single-nucleotide polymorphisms [SNPs]) conferring lower risks.7,8 It has been shown that the BC risks associated with SNPs combine multiplicatively and hence that their joint effect can be conveniently represented as a polygenic risk score (PRS).7,9 PRSs have been shown to result in substantial levels of BC risk stratification in the population.2,7,10,11 However, the known genetic factors explain only about 45% of the observed familial aggregation.
Several other risk factors are also associated with increased BC risk, including mammographic density12 (MD), reproductive factors (e.g., age at menarche,13 age at menopause,13 parity,14 and age at first live birth14), exogenous hormonal factors (e.g., use of oral contraceptive [OC]15 and use of postmenopausal hormone replacement therapy [HRT]16), anthropometric factors (e.g., height17 and body mass index [BMI]12,16), and lifestyle factors (e.g., alcohol intake18) (collectively referred to as risk factors [RFs]; we refer to the set of RFs excluding MD as questionnaire-based risk factors [QRFs]). Each of these RFs has only a modest effect on cancer risk, but in combination and with FH and known genetic factors, they can improve risk stratification.2,10,19 Moreover, as some of these factors can be modified, they can be used in the counseling process to guide at-risk women on possible risk-reducing options through changes in behavior or lifestyle (e.g., reduction in BMI, alcohol intake, or HRT use).
Genetic data and data on other RFs are now becoming easily available in clinical practice through electronic health records, cost-effective sequencing technologies, and efforts such as the 100,000 Genomes Project. Therefore, there is a growing need for BC risk prediction to be made available more widely than specialist cancer family clinics. Risk prediction models that incorporate all known genetic and other RFs allow for the objective and systematic identification of those at increased risk in front-line health care and enable their referral to the most appropriate health-care pathway.3 They can also transform the current genetic testing and counseling processes at the clinical genetics level.
The Breast and Ovarian Analysis of Disease Incidence and Carrier Estimation Algorithm (BOADICEA)20,21,22,23 is a risk prediction model that is used to compute the probabilities of carrying rare loss-of-function variants in the breast or ovarian cancer susceptibility genes BRCA1, BRCA2, PALB2, CHEK2, and ATM (referred to as the “major genes”), and to estimate the future risks of developing breast or ovarian cancer. BOADICEA uses information on cancer FH, screening for variants in the high-risk genes, tumor pathology, and basic demographic factors (such as year of birth and country). BOADICEA accounts for the residual familial aggregation of BC through a polygenic component that models the multiplicative effects of a large number of variants, each having a small contribution to the familial risk.22
In this work, we have extended the BOADICEA BC risk prediction model to incorporate the explicit effects of common BC susceptibility loci, MD, and other QRFs. This is the first comprehensive model of its kind that allows for consistent prediction of personal BC for unaffected women on the basis of their rare (high risk and moderate risk) BC genetic susceptibility variants, common genetic variants, explicit FH and other known RFs.
MATERIALS AND METHODS
Breast cancer incidence in BOADICEA
BOADICEA models cancer incidence explicitly as a function of genotypes for rare susceptibility variants together with a polygenic component.20,21,22,23,24 By using an explicit genetic model, BOADICEA can account for both measured genotypes and FH. Specifically, BOADICEA assumes that the BC incidence, λ(i)(t), for individual i at age t, depends on their underlying genotype through:
λ0(t) is the baseline incidence (applicable to a nonpathogenic variant carrier with a zero polygenotype, \(x_P^{(i)} = 0\)); \(G_\mu ^{(i)}\)are indicator variables for the presence/absence of a pathogenic variant in a major gene, taking values 1 if a pathogenic variant is present and 0 otherwise with μ = 1,…,5 representing BRCA1, BRCA2, PALB2, CHEK2, and ATM respectively; and βMGμ(t) represents the age-specific log-relative risks (log-RRs) associated with the major genes, relative to the baseline incidence (for a person with more than one rare pathogenic variant, the risks are determined by the lowest μ). These parameter estimates are identical to those previously published,20 with the exception of CHEK2 for which the estimates have been updated based on a recent large-scale association analysis25 (Supplementary Material). \(x_P^{(i)}\) is the polygenotype for individual i, assumed normally distributed in the general population with mean 0 and variance 1, and βPG(t) is the age-specific log-RR associated with the polygene, relative to the baseline incidence. The baseline incidence is chosen such that the overall incidence agrees with the population incidence.22 The population incidence is birth cohort and country specific, but for simplicity this is ignored here. We have previously adapted the model based on incidence for a number of geographic regions23 and have extended it to utilize Spanish cancer incidences (Supplementary Material). The absolute risks presented here are based on UK incidences.
BOADICEA also models the incidence of ovarian cancer, assumed independent of the BC incidence given the major genotype, and not dependent on the polygenotype. The ovarian cancer component of the model is identical to that published previously22 and not considered further here.
Including the effects of risk factors and mammographic density
To incorporate the effects of RFs into the BOADICEA model we extended Eq. 1 such that the BC incidence is:
where \(\mu = 6\) corresponds to a noncarrier of pathogenic variants in the major genes, with \(\beta _{MG6}\left( t \right) = 0\), and \(G_6^{\left( i \right)} = 1\) for noncarriers of pathogenic variants, and 0 otherwise.
Here ρ indexes the RFs that are present in the model, which are modeled as categorical factors and hence define a (potentially very large) set of possible RF combinations; \({\beta}_{RF_{\rho \mu}}(t)\) is the vector (length κρ − 1 where κρ is the number of categories for RF ρ, with one category being the baseline) of the log-RRs associated with RF ρ at age t, which may depend on the major genotype, μ; and \({\boldsymbol{z}}_{RF\rho }^{(i)}\) is the corresponding vector of indicator variables (0 or 1) that indicate the category of RF ρ for individual i (1 for the observed category, 0 otherwise, with all elements 0 for the baseline).
As above, the baseline incidence λ0(t) is determined so that the total age-specific incidences, summed over all possible RFs and genotypes, agree with the population incidence (given the assumed population distributions and RRs for each RF).26 To allow appropriately for missing RF information, only those RFs measured on a given individual are considered (thus, the baseline incidence, λ0(t), is determined for each individual dependent on their measured RFs).
Note that the RF categories for an individual are assumed not to change with age, because otherwise the model would involve the joint distributions of RFs over ages and become intractable. However, the log-RRs can be age-dependent. In cases where there are nonmultiplicative interactions between RFs, the RFs are considered as a single factor in Eq. 2, using estimates of their joint effect.
The RR estimates and population distributions for each RF were obtained from large-scale external studies and from national surveillance data sources or large-scale population-based studies, using a synthetic approach as previously described.2 Where possible we used RR estimates that were adjusted for the other RFs included in the model, and distributions from the UK. We incorporated the RFs included in the synthetic empirical model of Garcia-Closas2 with updated estimates derived by Pal Choudhury (unpublished data). For the current implementation we assumed that the RF distributions do not vary by birth cohort. We assumed that the effects of the RFs on BC risk were independent (i.e., log additive, as in Eq. 2). The RFs incorporated in the model were MD, age at menarche, age at menopause, parity, age at first live birth, OC use, HRT use, height, BMI, and alcohol intake. Details of their categories, RRs, and population distributions are given in the Supplementary Tables s2.1–s2.10.
The time required to calculate the age-specific baseline incidence in Eq. 2 is proportional to the product of the number of categories for each RF. For the full set of RFs described above, this leads to lengthy runtimes, which would compromise real-time calculations in clinical practice. To reduce the runtime of the code we combined a number of factors (age at menarche, parity, height, and alcohol intake) into a single factor with fewer categories (Supplementary Material). This approximation resulted in almost no change in the predicted risks (differences in the fourth significant figure), and achieved a significant (160-fold) speed up.
Including the effects of common breast cancer susceptibility variants
BOADICEA accounts for the residual familial aggregation of BC not due to rare variants in the major genes via a polygenic component, xP (Eqs. 1 and 2). In previous versions, the polygenic component was treated as unmeasured. To incorporate the effects of known common variants, the polygenic component is decomposed into a measured and an unmeasured component:
xPRS is the (observed) PRS, summarizing the effects of multiple SNPs, which is assumed normally distributed with mean 0 and variance α2 in the general population, with 0 ≤ α ≤ 1. The parameter α2 is interpreted as the proportion of the overall polygene explained by the PRS. The residual component, xR, representing other unmeasured genetic and familial effects, is then normally distributed with mean 0 and variance 1−α2.
BOADICEA defines the absolute BC risks and the probabilities of being a carrier of a rare pathogenic variant as ratios of pedigree likelihoods.21,22,27 Calculating pedigree likelihoods involves taking the joint sum/integration over all possible genotypic values for each person in the pedigree, of the probability that they exhibit their observed phenotypes given their genotype (penetrance27). In principle, the PRS could be incorporated using separate polygenes as described in Eq. 3, however this can lead to very large numbers of possible genotypes and hence runtimes that are impractically long. Instead, under the assumption that α is age-independent, it was incorporated by expressing the penetrance as a function of the conditional probability of observing the PRS given the total polygenotype:
which follows a normal distribution (Supplementary Material, Eq. s1.12).
BOADICEA evaluates likelihoods using the MENDEL software.28 Because MENDEL considers only finite discrete genotypes, the polygenotype is approximated via the hypergeometric polygenic model (HPM).26,27 Under the HPM, the continuous polygenotype is discretized according to:
where R can take values 0,…,2N and has a binomial distribution, \(B\left( {2N,\frac{1}{2}} \right)\), in the general population. For BOADICEA26 N was taken to be 3. The conditional probability in Eq. 4 needs to account for the discrete distribution of xP assumed in Eq. 5 (Supplementary Material).
Implementation of the PRS
For the current implementation, we used the BC PRS based on 313 SNPs.9 The overall polygenic log-RR in BOADICEA varies with age22 (Eqs. 1 and 2), but the proportion of the variance explained by the PRS (denoted as α2 above) is assumed to be constant with age. This assumption induces a specific form to the age-specific RRs conferred by the PRS. The proportion α2 was estimated by Mavaddat et al.9 using logistic regression applied to data from the Breast Cancer Association Consortium, in which the age-specific log-relative risk was constrained to be a function of the age-dependent polygenic relative risk in BOADICEA. The latter had been estimated previously using complex segregation analysis.22 Using this approach α was estimated to be 0.45 (95% confidence interval [CI]: 0.43–0.46). The PRS implemented here is therefore assumed to explain 20% of the total polygenic variance (α2 = 0.20).
RESULTS
Breast cancer risk distributions defined by combinations of risk factors
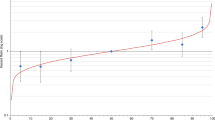
Figs. 1–3, Table 1, and Supplementary Figures s6.1–4 show the BC risk distributions predicted by BOADICEA as defined by different RFs. Due to BOADICEA using explicit FH configurations, risks are shown conditional on FH. The distributions of 10-year risk at age 40 and lifetime (defined here as risk from age 20 to 80 years) BC risks in the population (i.e., a woman with unknown FH) are shown in Fig. 1 and Table 1. The backgrounds of the graphs are shaded indicating National Institute for Health and Care Excellence (NICE) risk categories for women with a FH of BC:3 (1) near-population risk (pink: 10-year risk of <3%, lifetime risks of <17%), (2) moderate risk (yellow: 10-year risk of ≥3% but <8%, lifetime risks of ≥17% but <30%), and (3) high risk (blue: 10-year risk of ≥8%, lifetime risks of ≥30%). We also consider a low risk category, corresponding to a risk of less than 30% of the population risk (i.e. a 10-year risk <0.5%, lifetime risk <3.6%). For simplicity we discuss these results in terms of the 10-year risks, but results based on lifetime risks are similar.
Breast and Ovarian Analysis of Disease Incidence and Carrier Estimation Algorithm (BOADICEA)-predicted breast cancer risk for a female with unknown family history (equivalent to the distribution of risk in the population) and untested for rare pathogenic variants on the basis of the different predictors of risk (questionnaire-based risk factors [QRFs], mammographic density [MD], and polygenic risk scores [PRS]). Variability due to residual family history of cancer is not taken into account. (a, c) Ten-year risk from age 40 to age 50 years; (b, d) lifetime risk (from age 20 to 80 years). (a, b) Probability density function against absolute risk for 10-year and lifetime risks respectively; (c, d) absolute risk against cumulative distribution. The backgrounds of the graphs are shaded to indicate the familial breast cancer risk categories based on the National Institute for Health and Care Excellence (NICE) guidelines:3 (1) near-population risk shaded in pink (<17% for lifetime risk and <3% for 10-year risk), (2) moderate risk shaded in yellow (≥17% and <30% for lifetime risk and ≥3% and <8% for 10-year risk), and (3) high risk, shaded in blue (≥30% for lifetime risk and ≥8% for 10-year risk). Specific values are given in Table 1. The vertical lines in (a, b) and horizontal lines in (c, d) (labeled “No QRFs, MD or PRS”) correspond to the population risk of breast cancer. Predictions based on UK breast cancer incidence.
Predicted Breast and Ovarian Analysis of Disease Incidence and Carrier Estimation Algorithm (BOADICEA) breast cancer risk for a female with a mother affected at age 50 and untested for rare pathogenic variants on the basis of the different predictors of risk (questionnaire-based risk factors (QRFs), mammographic density (MD), and polygenic risk scores [PRS]). (a, c) Ten-year risk from age 40 to age 50 years; (b, d) lifetime risk (age 20 to 80 years). The backgrounds of the graphs are shaded to indicate the familial breast cancer risk categories based on the National Institute for Health and Care Excellence (NICE) guidelines:3 (1) near-population risk, shaded in pink (<17% for lifetime risk and <3% for 10-year risk); (2) moderate risk, shaded in yellow (≥17% and <30% for lifetime risk and ≥3% and <8% for 10-year risk); and (3) high risk, shaded in blue (≥30% for lifetime risk and ≥8% for 10-year risk). Predictions based on UK breast cancer incidence.
Predicted Breast and Ovarian Analysis of Disease Incidence and Carrier Estimation Algorithm (BOADICEA) breast cancer risk for a female intermediate-risk rare pathogenic variant carrier, on the basis of the different predictors of risk (questionnaire-based risk factors [QRFs], mammographic density [MD], and polygenic risk scores [PRS]). (a, c) Lifetime risk (age 20 to 80 years) for a CHEK2 1100delC carrier with unknown family history; (b, d) lifetime risk for a CHEK2 1100delC carrier with her mother affected at age 50. (e, f) Risk for a PALB2 and an ATM rare pathogenic variant carrier respectively, both with unknown family history. The backgrounds of the graphs are shaded to indicate the familial breast cancer risk categories based on the National Institute for Health and Care Excellence (NICE) guidelines:3 (1) near-population risk shaded in pink (<17%), (2) moderate risk shaded in yellow (≥17% and <30%), and (3) high risk shaded in blue (≥30%). Predictions based on UK breast cancer incidence.
As expected, the variation in risk is greatest when including all RFs in the model (light blue line labeled “QRFs, MD and PRS,” Fig. 1a). When considered separately, the distribution is widest for the PRS, followed by MD, and narrowest for the QRFs only. Using the full set of RFs (i.e., combined effects of the PRS, MD, and QRFs), the predicted 10-year risks at age 40 vary from 0.2% for the women in the 1st percentile to 7.0% for the 99th. Approximately 86.4% of women in the population are predicted to be at near-population risk of developing BC, including 12.1% who are at low risk, with 13.6% at moderate or high risk (Table 1). Supplementary Figures s6.1 and s6.2 show the reclassification of women with unknown FH between risk categories, as the different factors are considered in the risk prediction.
Figure 2, Table 1, and Supplementary Figures s6.3 and s6.4 show the corresponding distributions of risk for a woman whose mother has been diagnosed with BC at age 50 years and the reclassification into different risk categories. On the basis of FH alone these women would be in the NICE moderate risk category. Using the full set of RFs (light blue line labeled “QRFs, MD and PRS,” Fig. 2a), the predicted 10-year risks at age 40 vary from 0.5% for women in the 1st percentile to 11.0% for those in the 99th. Of women with this FH, 60.1% will be at near-population risk, 36.2% at moderate risk, and 3.7% at high risk. As in Fig. 1, the variation in risk is largest for the PRS and smallest for the QRFs only. However, the overall variation in log-risk by PRS is somewhat smaller, because some of the effect of the PRS is accounted for by knowledge of the explicit FH. The joint effect of FH and PRS on predicted BC risks is further demonstrated in Figure s5.1 and Table s5.1. With unmeasured PRS (green circles) a woman’s risk increases with increasing FH. Although the variance of the log-risk decreases with the number of affected relatives, the difference in absolute risk between women in the top (brown squares) and bottom (red crosses) percentiles increases with the number of affected relatives. Further, the difference between the risks with unmeasured PRS and a woman on the 50th percentile (orange triangles) increases with FH, showing that an increased FH implies a higher PRS.
Figure 3 shows the distribution of risks for a woman who carries a moderate risk CHEK2 1100delC, ATM pathogenic variant, or a rare moderate- to high-risk pathogenic variant in PALB2. In the absence of other data, a CHEK2 pathogenic variant carrier with unknown FH (Fig. 3a, c) would fall in the moderate risk category (lifetime risk of 22.1%). However, on the basis of the full set of RFs (light blue line labeled “QRFs, MD and PRS,” Fig. 3a), 35.2% of CHEK2 1100delC carriers would be reclassified as at near-population risk and 20.1% as at high risk. On the other hand, a CHEK2 1100delc carrier with a mother affected with BC at age 50 would be categorized as high risk (lifetime risk of 32.2%) on the basis of FH alone (Fig. 3b, d), whereas on the basis of the full set of RFs (light blue line labeled “QRFs, MD and PRS,” Fig. 3b), 54.2% of such women would be reclassified as moderate or near-population risk. Similar patterns are seen for ATM and PALB2 pathogenic variant carriers (Fig. 3e, f).
DISCUSSION
Over the past decade, there have been significant advances in our understanding of susceptibility to BC. Reliable estimates of the effects of deleterious variants in susceptibility genes, and of multiple common low-risk variants, on cancer risk have become available. These estimates can be used to counsel women and inform targeted screening and prevention, but an important challenge is to combine these effects with other RFs. Incorporating the effects of all known factors together in a single model should provide a more consistent approach to risk prediction and improve risk stratification. We have presented a methodological framework for incorporating the effects of lifestyle, hormonal and reproductive RFs, of MD, and of the common BC susceptibility genetic variants into the BOADICEA BC risk prediction model. This is the first comprehensive BC risk model of its kind to incorporate the effects of these RFs together with complete information on the FH of cancer (Table 2).
The results demonstrate that by incorporating the effects of all known RFs into the model, much greater levels of BC risk stratification can be achieved both in the general population and in women with a FH of BC. Ignoring FH, the combined QRFs, MD, and PRS effects can identify ~13% of the women in the population who would be classified at moderate or high risk of developing BC (Table 1). On the other hand, ~12% will be at low risk. Similarly, on the basis of the BOADICEA-predicted risk, given FH alone, women with an affected first-degree relative at age 50 would classified as being at moderate risk of developing BC (Table 1). However, the addition of the RFs and PRS can identify 60.7% of those women who would be recategorized as near-population risk and 3.5% who would be recategorized as high risk of developing BC (Table 1). The PRS gives the biggest contribution to risk stratification, followed by MD. The results also show that significant levels of risk recategorization can occur for carriers of rare pathogenic variants in the moderate- and high-risk genes included in BOADICEA; Fig. 3. The results are in line with the expected risk stratification levels suggested by other theoretical studies.2,29
Several assumptions were made in the development of this model. In incorporating the effects of the common SNPs, we assumed that the polygenic component in BOADICEA,22 which models the residual familial aggregation not due to the effects of rare pathogenic variants in the major genes, could be decomposed into the sum of a known component, measured by the PRS, and an unknown component. While the RRs associated with the overall polygene can vary with age, the age-specific RR conferred by the PRS is constrained to decline with age according to the same pattern as the overall polygenic component. This assumption allows computations in pedigrees to be tractable, ensures compatibility with the existing validated model,22 and ensures that the same algorithm can be used whether or not PRS data are available. The analyses of Mavaddat et al.9 indicate an age-specific effect of the PRS, but it may be that some modification will be required to allow the age-specific components of the PRS and residual polygenic component to be modeled separately. Note that the model implies that the effect of the residual FH (or residual familial RR) is attenuated by the PRS, as expected on theoretical grounds and as has been observed empirically in case–control studies.7,9 This is a unique aspect of the model that ensures that the overall predicted familial relative risk (over all known and unknown genetic effects) remains constant and there is no “double counting” of the effect of the SNPs.
We also assumed that the joint effects of the PRS with the RFs incorporated in the model are multiplicative. Although no studies have yet evaluated the joint effects of the 313-SNP PRS used here and other RFs, analyses of large case–control studies that have assessed the joint effects of an earlier 77-SNP PRS indicate that the joint effects are well described by a multiplicative model.10,30,31 The modeling framework is, however, sufficiently flexible to incorporate interactions, if they are identified.
Our implementation also assumes that the effect of the PRS is multiplicative with the effects of rare pathogenic variants in the major genes. Published data on the effect of SNPs as risk modifiers for rare pathogenic variant carriers suggest that this is a reasonable assumption in the case of BRCA2 and CHEK2 (refs. 32,33). The fit is less good for BRCA1 rare pathogenic variant carriers;32 however, better discrimination can be obtained by using a PRS that is optimized for estrogen receptor (ER)-negative BC (consistent with the observation that the majority of breast tumors in BRCA1 carriers are ER-negative).34 To allow for this in the model, it would be necessary to extend BOADICEA such that it models ER-positive and ER-negative disease simultaneously and allows for a separate PRS for each disease. This is computationally more complex but would allow prediction of subtype-specific risks, and would be of potential relevance to prevention programs based on risk-reducing medication. Data on the joint effects of the PRS with PALB2 or ATM rare pathogenic variants are currently sparse, but given that risks for carriers of such variants are modified by FH,35,36,37 the multiplicative assumption seems a reasonable approximation.
We have developed a flexible modeling framework that allows for the RRs of the lifestyle/hormonal/reproductive RFs and MD to be different for rare pathogenic variant carriers in each of the major genes and nonpathogenic variant carriers. Although some evidence from studies in BRCA1 and BRCA2 suggests that effects may be different, their precise effects in rare pathogenic variant carriers are not well estimated.38 Therefore, for the current implementation we have assumed the same effect sizes in rare pathogenic variant carriers and noncarriers. As future studies, in particular prospective studies, report on these associations, the model can be easily adjusted to allow for potential differences.
This is the first BC risk model to include the effects of most well-known BC RFs, including the effects of both common and rare genetic variants and FH. However, a key limitation arises from the fact that no single study that includes information on all the factors is currently available. Therefore, a synthetic approach was used to develop the model by using RR estimates from large well-designed studies and RF distributions from national surveillance data sources, or large-scale population-based studies in the case of genetic factors. Although we have included estimates based on analyses adjusted for the other RFs included in the model, we cannot rule out that some biases may affect the RR estimates and their joint effects. Our modeling assumptions and any other possible biases will therefore need to be assessed through validations using prospective cohort data. One of the most important tests will be the accuracy of the risk predictions in the tails of the distribution, where the predictions are most likely to affect clinical decisions. The current model is based on UK RF distributions, several of the other model parameters were estimated using UK data,22 and the PRS is based on samples of European ancestry. A key question in validation studies will be how well the model performs in other populations. It may be necessary to use population-specific RF parameters and PRS, and refit the model parameters for use in other populations, particularly for women of non-European ancestry.
A number of other risk factors that are not included in the model have been reported to be associated with breast cancer risk: these include duration of oral contraceptive and duration of hormone replacement therapy use.15,16 Considering the reported effect sizes and the results from the current study, the effect on risk stratification by adding these factors in the model is likely to be small. The model also does not incorporate the known increased risk in the immediate period after birth and, while this is unlikely to change the model discrimination, the absolute risks are expected to be underestimated in this period.39 Our implementation also assumed that the RF distributions are independent of birth cohort. Some risk factor distributions (e.g., reproductive factors) do change, and our modeling framework allows for cohort-specific effects, but cohort-specific distributions are not readily available for all RFs. For the current implementation we have therefore used the RF distributions from recent birth cohorts, which are most relevant for the majority of women undergoing breast cancer risk prediction.
A major strength of our model is that it incorporates known genetic and other RFs, and full FH, into a single coherent model. As such, once validated, the model should be suitable for counseling women consistently across different levels of clinical care, even though information available to populate the model may vary. To facilitate this, a new user-friendly interface (CanRisk.org) is being developed, including graphical pedigree construction.40 The model should enable more individualized informed decision-making around prevention options, screening, or RF modification. It can also be used to inform population-based approaches by identifying groups in the population for targeted screening or prevention approaches.
Change history
21 February 2019
The original version of this article contained a typographical error in Eq. 2. This has now been corrected in both the PDF and HTML versions of the Article. The authors regret this error.
References
Pharoah PD, Antoniou A, Bobrow M, Zimmern RL, Easton DF, Ponder BA. Polygenic susceptibility to breast cancer and implications for prevention. Nat Genet. 2002;31:33–36.
Garcia-Closas M, Gunsoy NB, Chatterjee N. Combined associations of genetic and environmental risk factors: implications for prevention of breast cancer. J Natl Cancer Inst. 2014;106:dju305.
National Institute for Health and Care Excellence. Familial breast cancer: classification and care of people at risk of familial breast cancer and management of breast cancer and related risks in people with a family history of breast cancer (CG164). 2013. http://www.nice.org.uk/CG164.
Pashayan N, Morris S, Gilbert FJ, Pharoah PP. Cost-effectiveness and benefit-to-harm ratio of risk-stratified screening for breast cancer: a life-table model. JAMA Oncol. 2018;4:1504–1510.
Kuchenbaecker KB, Hopper JL, Barnes DR, et al. Risks of breast, ovarian, and contralateral breast cancer for BRCA1 and BRCA2 mutation carriers. JAMA. 2017;317:2402–2416.
Easton DF, Pharoah PD, Antoniou AC, et al. Gene-panel sequencing and the prediction of breast-cancer risk. N Engl J Med. 2015;372:2243–2257.
Mavaddat N, Pharoah PD, Michailidou K, et al. Prediction of breast cancer risk based on profiling with common genetic variants. J Natl Cancer Inst. 2015;107:djv036.
Garcia-Closas M, Couch FJ, Lindstrom S, et al. Genome-wide association studies identify four ER negative-specific breast cancer risk loci. Nat Genet. 2013;45:392–398.
Mavaddat N, Michailidou K, Dennis J, et al. Polygenic risk scores for prediction of breast cancer and breast cancer subtypes. Am J Hum Genet. 2019;104:1–14.
Maas P, Barrdahl M, Joshi AD, et al. Breast cancer risk from modifiable and nonmodifiable risk factors among white women in the United States. JAMA Oncol. 2016;2:1295–1302.
Chatterjee N, Shi J, Garcia-Closas M. Developing and evaluating polygenic risk prediction models for stratified disease prevention. Nat Rev Genet. 2016;17:392–406.
Nelson HD, Zakher B, Cantor A, et al. Risk factors for breast cancer for women aged 40 to 49 years: a systematic review and meta-analysis. Ann Intern Med. 2012;156:635–648.
Collaborative Group on Hormonal Factors in Breast Cancer. Menarche, menopause, and breast cancer risk: individual participant meta-analysis, including 118 964 women with breast cancer from 117 epidemiological studies. Lancet Oncol. 2012;13:1141–1151.
Reeves GK, Pirie K, Green J, Bull D, Beral V, Million Women Study Collaborators. Comparison of the effects of genetic and environmental risk factors on in situ and invasive ductal breast cancer. Int J Cancer. 2012;131:930–937.
Hunter DJ, Colditz GA, Hankinson SE, et al. Oral contraceptive use and breast cancer: a prospective study of young women. Cancer Epidemiol Biomarkers Prev. 2010;19:2496–2502.
Beral V, Reeves G, Bull D, Green J, Million Women Study Collaborators. Breast cancer risk in relation to the interval between menopause and starting hormone therapy. J Natl Cancer Inst. 2011;103:296–305.
Zhang B, Shu XO, Delahanty RJ, et al. Height and breast cancer risk: evidence from prospective studies and Mendelian randomization. J Natl Cancer Inst. 2015;107:djv219.
Hamajima N, Hirose K, Tajima K, et al. Alcohol, tobacco and breast cancer—collaborative reanalysis of individual data from 53 epidemiological studies, including 58,515 women with breast cancer and 95,067 women without the disease. Br J Cancer. 2002;87:1234–1245.
Quante AS, Whittemore AS, Shriver T, Hopper JL, Strauch K, Terry MB. Practical problems with clinical guidelines for breast cancer prevention based on remaining lifetime risk. J Natl Cancer Inst. 2015;107.
Lee AJ, Cunningham AP, Tischkowitz M. et al. Incorporating truncating variants in PALB2, CHEK2, and ATM into the BOADICEA breast cancer risk model. Genet Med. 2016;18:1190–1198.
Antoniou AC, Pharoah PP, Smith P, Easton DF. The BOADICEA model of genetic susceptibility to breast and ovarian cancer. Br J Cancer. 2004;91:1580–1590.
Antoniou AC, Cunningham AP, Peto J, et al. The BOADICEA model of genetic susceptibility to breast and ovarian cancers: updates and extensions. Br J Cancer. 2008;98:1457–1466.
Lee AJ, Cunningham AP, Kuchenbaecker KB, Mavaddat N, Easton DF, Antoniou AC. BOADICEA breast cancer risk prediction model: updates to cancer incidences, tumour pathology and web interface. Br J Cancer. 2014;110:535–545.
Mavaddat N, Rebbeck TR, Lakhani SR, Easton DF, Antoniou AC. Incorporating tumour pathology information into breast cancer risk prediction algorithms. Breast Cancer Res. 2010;12:R28.
Schmidt MK, Hogervorst F, van Hien R, et al. Age- and tumor subtype-specific breast cancer risk estimates for CHEK2*1100delC carriers. J Clin Oncol. 2016;34:2750–2760.
Antoniou AC, Pharoah PD, McMullan G, Day NE, Ponder BA, Easton D. Evidence for further breast cancer susceptibility genes in addition to BRCA1 and BRCA2 in a population-based study. Genet Epidemiol. 2001;21:1–18.
Lange K. Mathematical and statistical methods for genetic analysis. New York: Springer; 1997.
Lange K, Weeks D, Boehnke M. Programs for pedigree analysis: MENDEL, FISHER, and dGENE. Genet Epidemiol. 1988;5:471–472.
Milne RL, Antoniou AC. Modifiers of breast and ovarian cancer risks for BRCA1 and BRCA2 mutation carriers. Endocr Relat Cancer. 2016;23:T69–84.
Rudolph A, Song M, Brook MN, et al. Joint associations of a polygenic risk score and environmental risk factors for breast cancer in the Breast Cancer Association Consortium. Int J Epidemiol. 2018;47:526–536.
Vachon CM, Pankratz VS, Scott CG, et al. The contributions of breast density and common genetic variation to breast cancer risk. J Natl Cancer Inst. 2015;107:dju397.
Kuchenbaecker KB, McGuffog L, Barrowdale D, et al. Evaluation of polygenic risk scores for breast and ovarian cancer risk prediction in BRCA1 and BRCA2 mutation carriers. J Natl Cancer Inst. 2017;109:djv315.
Muranen TA, Greco D, Blomqvist C, et al. Genetic modifiers of CHEK2*1100delC-associated breast cancer risk. Genet Med. 2017;19:599–603.
Milne RL, Kuchenbaecker KB, Michailidou K, et al. Identification of ten variants associated with risk of estrogen-receptor-negative breast cancer. Nat Genet. 2017;49:1767–1778.
Antoniou AC, Casadei S, Heikkinen T, et al. Breast-cancer risk in families with mutations in PALB2. N Engl J Med. 2014;371:497–506.
Cybulski C, Kluzniak W, Huzarski T, et al. Clinical outcomes in women with breast cancer and a PALB2 mutation: a prospective cohort analysis. Lancet Oncol. 2015;16:638–644.
Decker B, Allen J, Luccarini C, et al. Rare, protein-truncating variants in ATM, CHEK2 and PALB2, but not XRCC2, are associated with increased breast cancer risks. J Med Genet. 2017;54:732–741.
Friebel TM, Domchek SM, Rebbeck TR. Modifiers of cancer risk in BRCA1 and BRCA2 mutation carriers: systematic review and meta-analysis. J Natl Cancer Inst. 2014;106:dju091.
Albrektsen G, Heuch I, Hansen S, Kvale G. Breast cancer risk by age at birth, time since birth and time intervals between births: exploring interaction effects. Br J Cancer. 2005;92:167–175.
Carver T, Cunningham AP, Babb de Villiers C, et al. pedigreejs: a web-based graphical pedigree editor. Bioinformatics. 2018;34:1069–1071.
Acknowledgements
This work was supported by Cancer Research UK grants C12292/A20861 and C1287/A16563; the European Union’s Horizon 2020 research and innovation programme under grant agreement numbers 633784 (B-CAST) and 634935 (BRIDGES); a Wellcome Trust Collaborative Award (203477/B/16/Z); and the PERSPECTIVE programme: The Government of Canada through Genome Canada and the Canadian Institutes of Health Research (grant GPH-129344), the Ministère de l’Économie, de la Science et de l’Innovation du Québec through Genome Québec, and the Québec Breast Cancer Foundation. F.M.W. was supported by a National Institute for Health Research (NIHR) Clinician Scientist award (NIHR-CS-012-03). M.T. is funded by the European Union Seventh Framework Programme (2007–2013)/European Research Council (310018). We thank Adria López Fernández and the Spanish Network of Cancer Registries (REDECAN) for their support with the Spanish incidence data analysis that was possible thanks to a fellowship from Roses Foundation Against Cancer.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Disclosure
The BOADICEA model has been licensed to Cambridge Enterprise for commercialization, with the authors D.F.E., A.C.A., A.P.C., A.L. and T.C. listed as its inventors. These authors may receive royalties in the future if commercialization is realized. The other authors declare no conflicts of interest.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, and provide a link to the Creative Commons license. You do not have permission under this license to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Lee, A., Mavaddat, N., Wilcox, A.N. et al. BOADICEA: a comprehensive breast cancer risk prediction model incorporating genetic and nongenetic risk factors. Genet Med 21, 1708–1718 (2019). https://doi.org/10.1038/s41436-018-0406-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41436-018-0406-9
Keywords
This article is cited by
-
Weighted metrics are required when evaluating the performance of prediction models in nested case–control studies
BMC Medical Research Methodology (2024)
-
A cost-effectiveness analysis of lung cancer screening with low-dose computed tomography and a polygenic risk score
BMC Cancer (2024)
-
Recent advances in polygenic scores: translation, equitability, methods and FAIR tools
Genome Medicine (2024)
-
Attitudes towards risk-stratified breast cancer screening: a population-based survey among 5,001 Danish women
BMC Cancer (2024)
-
EMQN best practice guidelines for genetic testing in hereditary breast and ovarian cancer
European Journal of Human Genetics (2024)