Abstract
In this study, using the Pt/Cr2O3/Pt epitaxial trilayer, we demonstrate the giant voltage modulation of the antiferromagnetic spin reversal and the voltage-induced 180° switching of the Néel vector in maintaining a permanent magnetic field. We obtained a significant modulation efficiency of the switching field, Δμ0HSW/ΔV (Δμ0HSW/ΔE), reaching a maximum of −500 mT/V (−4.80 T nm/V); this value was more than 50 times greater than that of the ferromagnetic-based counterparts. From the temperature dependence of the modulation efficiency, X-ray magnetic circular dichroism measurements and first-principles calculations, we showed that the origin of the giant modulation efficiency relied on the electric field modulation of the net magnetization due to the magnetoelectric effect. From the first-principles calculation and the thickness effect on the offset electric field, we found that the interfacial magnetoelectric effect emerged. Our demonstration reveals the energy-efficient and widely applicable operation of an antiferromagnetic spin based on a mechanism distinct from magnetic anisotropy control.
Similar content being viewed by others
Introduction
There is a growing demand for voltage-based control of the magnetization/spin direction because of various advantages, such as low power and fast operation, accessibility to single elements in integrated devices, and good matching with the CMOS architecture1,2. Since the magnetic moment is not conjugated with a voltage or an electric field, an intermediate path between them is needed. The voltage-controlled magnetic anisotropy (VCMA) effect3,4 is one possible mechanism. The VCMA effect occurs at the metal/insulator interface due to charge doping and/or charge redistribution causing changes in the orbital magnetic moment and quadrupolar magnetic moment, respectively5,6,7,8. Since the discovery of the VCMA effect in FePt in an electrolyte3 and its later development in the Fe/MgO thin film system4, controlling the spin reversal field by the voltage (the electric field) has been an area of active pursuit. The VCMA effect has been demonstrated in various systems, such as Fe80Co20/MgO9, Co-Fe-B/MgO10, FePt/MgO11, and Co/CoO/TiOx12. The magnitude of the effect is quantified by the modulation efficiency of the spin switching field, μ0HSW/ΔV (Δμ0HSW/ΔE), which can be inferred from the slope of the μ0HSW–V(E) curve. While a high modulation efficiency of the switching field is clearly desired, Δμ0HSW/ΔV (Δμ0HSW/ΔE) reaches a maximum of only ~10 mT/V (63 mT nm/V)12. Since most previous studies have employed ferromagnetic (FM) metal layers, the region where the sizable VCMA effect occurs is in the vicinity of the metal/oxide interface due to Thomas-Fermi screening13. Therefore, reducing the FM layer thickness to the ultrathin regime, typically below 1 nm, is essential, and this causes the degradation of the thermal stability of magnetization orientation.
Antiferromagnetic (AFM) insulators are another platform for voltage-driven spintronics. Magnetoelectricity is a coupling between magnetism and electricity and can compensate for the absence of the net magnetization of antiferromagnets; additionally, it provides an advanced pathway for controlling AFM spins by the voltage (the electric field). The magnetoelectric (ME) effect is referred to as the induction of the net magnetization (the dielectric polarization) by an electric field (a magnetic field)14,15,16. Since the conventional ME effect is a bulk effect, in principle, the magnetic layer thickness is not limited for the attainment of a large effect. Although the ME effect was discovered in the early 1960s14,15, much earlier than the VCMA effect, ME effect has been overlooked as a modulation scheme of the switching field because ME materials typically exhibit AFM ordering17, which has caused difficulty for the detection of the ME-controlled magnetic order parameter. Controlling the surface/interface magnetism facilitates overcoming this problem. The broken inversion symmetry at the surface/interface of ME materials induce a robust spin-polarized state on the surface of magnetoelectric materials; this is referred to as the boundary magnetization (the surface magnetization)18,19, due to the presence of a built-in electric field in conjunction with magnetoelectricity. Since the boundary magnetization strongly couples with the bulk AFM order parameter, switching the boundary magnetization is concomitant with the switching of the Nèel vector. Although the boundary magnetization results in a Zeeman energy gain by coupling with an external magnetic field20, this contribution is very minimal compared to the total magnetic energy in bulk and thick films due to the low surface-to-volume ratio. Historically, the exchange bias in the FM/AFM stacked system, which is a shift of the magnetization curve along a magnetic field direction21,22, has been used as a fingerprint of the boundary magnetization to complement its small magnitude23,24,25. However, the FM/AFM interfacial exchange coupling to induce the exchange bias became an additional source of the switching energy barrier of the AFM spin and boundary magnetization25,26,27. Alternatively, the FM-free structure, such as the nonmagnetic heavy metal (HM)/AFM system, is expected to be an active target28,29,30,31,32,33,34. Very recently, using Cr2O3, a prototypical ME AFM material, we reported the isothermal and low-field (<1 T) reversal of the boundary magnetization, e.g., the Néel vector, by reducing the Cr2O3 thickness down to 15 nm35; here, the contribution of the boundary magnetization became sizable due to the reduced ME film thickness20. In this study, we advance this finding and explore the voltage-induced modulation of the switching field, which corresponds to the voltage-induced coercivity change in FM systems. We demonstrate the giant modulation of the switching field; this modulation is typically a few 100 mT/V (a few T nm/V) to a maximum of 500 mT/V (4.8 T nm/V), by the combination of the bulk ME effect and the magnetoelectricity of the boundary magnetization, e.g., the interfacial ME effect. The demonstrated value is more than 50 times larger than the voltage-induced coercivity change originating from the VCMA effect in the FM system. We also demonstrate the voltage-induced deterministic 180° switching of the Néel vector in maintaining a permanent magnetic field using this simple structure.
Results
Giant modulation of the switching field
For this purpose, we fabricated Pt(2 nm)/Cr2O3(tCr2O3 = 8, 10 nm)/Pt(20 nm) epitaxial trilayers on α-Al2O3(0001) substrates. Structural analysis revealed the formation of a Cr2O3(0001) layer in which the Cr3+ spins lie perpendicular to the film according to the bulk spin configuration36. The actual tCr2O3 values were determined by X-ray reflectivity measurements (see the Supplementary Information). Hereafter, we use the designed tCr2O3 value to describe the film for simplicity. The detailed fabrication methods and structural information are described in the “Methods” section and the Supplementary Information, respectively. For the detection of the boundary magnetization, we employed the anomalous Hall effect (AHE) emerging at the HM/Cr2O3 interface28,29,31. Kosub et al. reported that the AHE resistance at the Pt/Cr2O3 interface showed a sizable remanent value below the Néel temperature (TN)28. Although some mechanisms for the AHE at the heavy-metal/Cr2O3 interface have been proposed28,37,38,39, they remain debatable. Nonetheless, the AHE is considered to be relevant to the boundary magnetization of Cr2O3. This finite remanent AHE resistance is initially regarded as “field invariant” due to the high Cr2O3 thickness (~200 nm), in which the Zeeman energy of the boundary magnetization is subtle and barely contributes to the total free energy20.
Figure 1b shows the representative μ0H-dependence of the transverse resistance Rxy for the Pt (2 nm)/Cr2O3 (8 nm)/Pt (20 nm) trilayer. Rxy shows rectangular hysteresis as a function of H applied perpendicular to the film, resembling the magnetization curve along the magnetic easy direction for an FM film with perpendicular magnetic anisotropy (PMA). According to the magnetocrystalline anisotropy (MCA) of the bulk Cr2O340,41 and the abovementioned Cr3+ spin orientation, it is reasonable for the film to exhibit PMA. The emergence of hysteresis is a consequence of the reduction in the Cr2O3 thickness and agrees with our previous report35. The remanence ratio is unity, and the remanent Rxy value is fully switched. The full switching of Rxy was confirmed by the zero-offset Hall measurements (see Supplementary Information), indicating the 180° switching of the boundary magnetization and, consequently, the Néel vector. While the rectangular shape is maintained under the gate voltage application, the switching field μ0HSW is modulated. The μ0HSW value at a gate voltage VG of 0 V was ~0.6 T, and this value increases (decreases) for the negative (positive) VG. Figure 1c plots the μ0HSW as a function of VG (the electric field E). μ0HSW monotonically decreases with increasing VG (E). μ0HSW changes over 100 mT when ±0.3 V (±38.9 mV/nm) is applied. Based on the rough hypothesis of a linear relationship between μ0HSW and VG(E), the modulation efficiency Δμ0HSW/ΔVG (Δμ0HSW/ΔE) is deduced to be −180 mT/V (−1400 mT nm/V). These values are significantly large and are more than 10 times (20 times) greater than those of the FM counterparts based on the VCMA mechanism, at most 12 mT/V (63 mT nm/V)12. Similar behavior is observed in the different devices, as shown by the open and closed symbols in Fig. 1c. We further investigated the voltage-induced switching under constant H to reinforce the voltage-induced change in the switching field. Figure 1d, e shows Rxy as a function of VG (E) under a constant magnetic field of −0.58 T and the simultaneously obtained I–V curve, respectively. Starting from the negative Rxy state formed by the proper magnetic field cycle, VG was swept from −0.3 V to +0.3 V and then to −0.3 V. Rxy was switched from negative to positive at VG = 55 mV (7.1 mV/nm). The positive state was stable after VG was set to −0.3 V. We observed VG-induced switching of Rxy at different temperatures and under an inverted constant magnetic field (see the Supplementary Information). This behavior is basically reversible, as discussed below, although Fig. 1c shows one-directional switching. The leakage current at the switching voltage was only 1.2 nA, corresponding to a quite low current density J of ~1.5 A/m2, which indicates good crystallinity of the film with fewer defects (see the Supplementary Information).
a Schematic of a device structure of magnetoelectric Cr2O3 equipped with Pt gate electrodes. At the interface between the top Pt heavy metal layer and the Cr2O3 antiferromagnetic layer, boundary magnetization is present due to the built-in electric field in conjunction with magnetoelectricity. The voltage (electric field) impacts the bulk spin state via the magnetoelectric effect. In the figure, the equivalent electrical circuit for the transport measurements is also depicted. b Anomalous Hall resistance Rxy as a function of magnetic field μ0H under an applied gate voltage VG. The measurement temperature was 240 K. The black, blue and red lines represent the curves for VG = 0, −0.3 and +0.3 V, respectively. c μ0HSW as a function of VG and the electric field E (refer to the top axis). The open and closed circles represent the curves for the different devices fabricated from identical films. The red and blue symbols represent the μ0HSW in the ascending and descending branches of the Rxy–H curve in (b), respectively. d, e Rxy and leakage current |I| as a function of VG at a constant magnetic field of μ0H = −0.58 T. The results are shown for the film with tCr2O3 = 8 nm. The arrows in (d) represent the sweep direction of VG (E). f Modulation efficiency of the switching field, Δμ0HSW/ΔE (closed symbol) and −2μ0Keff·α−1·Ε0−2 (open symbol) derived in Eq. (4).
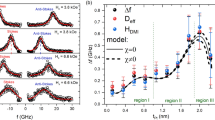
In the case of FM materials, the impact of the gate voltage on the switching field can be quantified by the VCMA efficiency, the change in the interfacial magnetic anisotropy energy density Ki per electric field, and ΔKi/ΔE8. However, a similar treatment is difficult for AFM materials because of the lack of net magnetization. Therefore, we first investigated the mechanism of the large gate-induced modulation of the switching field based on the temperature dependence of Δμ0HSW/ΔE, as sometimes employed in FM materials42,43. Figure 1f shows plots of the Δμ0HSW/ΔE values as a function of temperature by closed circles. Δμ0HSW/ΔE shows a complex temperature dependence, which is significant for the Pt (2 nm)/Cr2O3 (10 nm)/Pt (20 nm) trilayer. The TN value of this film is 260 K for tCr2O3 of 8 nm and 265 K for tCr2O3 of 10 nm (see Supplementary Materials); below this temperature, the above effects occur. With decreasing temperature, Δμ0HSW/ΔE first increases, reaches a maximum, and then decreases. The highest value is −4.80 T nm/V, corresponding to −500 mT/V at 245 K. This value is significantly large, more than 50 times larger in magnitude compared with the FM counterparts based on the VCMA effect12. To interpret the complex temperature dependence of Δμ0HSW/ΔE, we consider the switching energy condition driven by the ME effect expressed as follows44:
where Mbulk is the net magnetization at the bulk site. Although the Mbulk value at 0 V is basically zero in a pure antiferromagnet, this value can be nonzero due to the un-compensation of the magnetic moment for several reasons, such as defects29 and impurities45. The E-dependence of Mbulk is attributed to the bulk linear ME effect. Mb is the net boundary magnetization, and t is the Cr2O3 thickness. When the top and bottom interfaces are exactly the same, the net boundary magnetization can be canceled out at 0 V. However, Mb can also be nonzero when the magnitude of Mb is imbalanced at the top and bottom, for example, by defects29 and/or inhomogeneous strain46. Keff represents the energy equivalent to the spin reversal. Although Keff is related to the magnetic anisotropy energy, the Keff value should not be equal to the MCA energy of Cr2O3 because domain wall motion is involved in the switching process in the film35. Equation (1) assumes that Mbulk and Mb behave in the same way due to their strong coupling20. The ME effect is incorporated in Eq. (1) by the following:
where Mbk_0 and Mb_0 are the abovementioned uncompensated magnetic moments at the bulk and interface at 0 V. The first equation is based on the bulk linear ME effect with the ME susceptibility α. α in Eq. (2) is α33 (αzz) in the ME tensor since both magnetic and electric fields are applied along the c-axis of Cr2O3. Because the ME tensor for the boundary magnetization is nonanalytic, unlike the bulk ME coefficient19, we phenomenologically associate the ME coefficient β for the boundary magnetization. The effective ME coefficient αeff and the offset electric field E0 relevant to the boundary magnetization are defined as follows:
The Δμ0HSW/ΔE value evaluated above can be directly compared with a first-order derivative of Eq. (1) with respect to E. The first-order derivative of Eq. (1) at E = 0 is derived as follows:
The μ0HSW-VG (μ0HSW-E) relationship (Fig. 1c) was analyzed using Eq. (1), and a factor of −2μ0Keff·αeff−1·E0−2 was deduced. The deduced parameter is plotted as a function of temperature in Fig. 1f, and it effectively reproduces the temperature dependence of Δμ0HSW/ΔE, indicating that the ME effect is the main mechanism of the HSW modulation.
Bipolar switching attainable by the ME-driven mechanism
Bipolar switching is of particular importance for deterministic switching. This is a significant advantage of the ME mechanism because it cannot be obtained by the VCMA mechanism. For these observations, there is a risk of dielectric breakdown by high voltage application, and we used a Pt(2 nm)/Cr2O3(40, 90 nm)/Pt(20) epitaxial trilayer. As previously reported28, the boundary magnetization and the Néel vector were “magnetic-field invariant” for the thick Cr2O3 within the field range of ±9 T. (Detailed AHE loops are presented in the Supplementary Information.) However, under finite voltage (the electric field), the Zeeman energy of the E-induced magnetization overcomes the switching energy barrier, and consequently, hysteresis can emerge. Figure 2a, b show the AHE loops at VG = ±4.0 V (E = ±0.1 V/nm). A clear hysteresis was indeed observed. Notably, the switching direction was reversed for the positive and negative VG (E), as indicated by the blue and red arrows in the loops; thus, the direction of the E-induced magnetization is reversed with the polarity of VG (E), which is in agreement with the ME mechanism. Figure 2c shows μ0HSW as a function of E for both tCr2O3 = 40 and 90 nm. The hyperbolas with a finite offset electric field of E0 ~ 0.01 V/nm are observed and agree with the switching conditions shown in Eq. (1). The red- and blue-painted areas outside of each hyperbola show the monostable states. The monostable states in any of the four quadrants indicate that deterministic access to any of the four regions is possible by the suitable combination of E and H. The bistable region shown by the green-painted area can be interpreted as analogous to ordinal ferromagnets with uniaxial magnetic anisotropy; there are two energy minima in the energy landscape47. When the map is horizontally intercepted, e.g., the E-sweep under constant H, it is possible that the E-induced reversible switching of the AFM state occurs at a constant magnetic field; down-to-up switching is demonstrated in Fig. 1d. These observations reinforce the ME mechanism as the origin of the observed change in the switching field.
a, b Rxy as a function of magnetic field at VG = +4.0 V (E = +0.1 V/nm) and −4.0 V (−0.1 V/nm), respectively, for the Pt(2 nm)/Cr2O3(40 nm)/Pt(20 nm) trilayer. Red and blue arrows represent the sweep direction of the field and show the switching direction: up to down (blue) and down to up (down). c E-dependence of the switching field for tCr2O3 = 40 nm (closed) and 90 nm (open). The blue and red symbols represent the switching fields for up-to-down and down-to-up, respectively. The blue and red regions in (c) denote deterministic (or monostable) states, with the magnetization directing downward and upward, respectively. The green region in (c) represents the bistable state corresponding to the inside of the hysteresis loops in (a) and (b), where the magnetization direction can be either upward or downward, depending on the applied magnetic field and voltage history. “Up” and “down” are defined by the state of the AHE hysteresis loop.
Discussion on the mechanism of giant modulation of the switching field X-ray spectroscopy
In general, the switching field is relevant to the effective anisotropy field, HK: HK = 2Keff/MS, where Keff is the effective uniaxial magnetic anisotropy energy density and MS is the saturation magnetization. In the case of FM materials, HK is modulated via the modulation of Keff by VG (E), e.g., the VCMA effect. The VCMA efficiency should show a monotonic increase with decreasing temperature42,43, which contradicts our observation (Fig. 1f). The VCMA is mainly caused by the change in the orbital angular momentum for the 3d elements, and the charge redistribution is associated with the 5d elements5,8. To address whether a similar effect occurred in our film, we measured soft and hard X-ray magnetic circular dichroism (XMCD). For this purpose, we used a Pt(2 nm)/Cr2O3(8 nm) epitaxial bilayer for the XMCD measurements of the top Pt layer. If we used the Pt(2 nm)/Cr2O3/Pt(20 nm) trilayer, the absorption signal of the top Pt(2 nm) would be masked by the strong signal from the bottom Pt(20 nm). Although the stacking structure is different, the film quality of the Pt/Cr2O3 bilayer is comparable to that of the film used for the AHE measurements. We also confirmed that the Rxy of the Pt/Cr2O3 bilayer exhibited rectangular hysteresis as a function of magnetic field (see Supplementary Information). Figure 3a shows the soft X-ray absorption spectra (XAS) and the XMCD spectra at the Cr L2,3 edges. The shape of the XAS peak is similar to that of the reported spectrum for Cr2O348, confirming the presence of trivalent Cr and eliminating other phases such as CrO2. An XMCD signal is also observed, indicating the presence of spin-polarized interfacial Cr3+ attributed to boundary magnetization35. Figure 3b shows the magnetic field dependence of the XMCD intensity at hν = 577.5 eV, which yields the largest XMCD signal. The XMCD curve shows a rectangular hysteresis similar to that of the AHE loop, indicating that the AHE loop is attributed to the reversal of the interfacial spin-polarized Cr3+. The difference in the loop shapes of Figs. 3b and 1b should be due to the detection area; the XMCD method detects a large area (~400 × 400 μm2) compared with the AHE measurements (5 × 5 μm2), and the spatial distribution of the switching field manifests in the XMCD measurements. Recently, emerging imaging techniques for AFM domains, such as nitrogen-vacancy (NV) magnetometry49,50,51 and scanning XMCD microscopy35, will aid in obtaining a deep understanding of the switching process. We note that the contribution of E-induced magnetization to XMCD should be zero since XMCD was measured at zero VG. In addition, the XMCD signal was not detected by the bulk-sensitive transmission mode in the Pt/Co/Cr2O3/Pt thin film, where the boundary magnetization was enhanced by exchange coupling with FM Co52. Therefore, the bulk contribution to the XMCD intensity was negligible, and the magnetic moment responsible for the observed XMCD signal should exist at the interface.
a, c XAS and XMCD spectra at the Cr L2,3 and Pt L3 edges, respectively. b, d XMCD intensity as a function of magnetic field measured at the Cr L3 and Pt L3 edges, respectively. The magnetic field direction was perpendicular to the film. The measurement temperature was 230 K. The film used for these measurements was a Pt(2 nm)/Cr2O3(10 nm) bilayer prepared on α-Al2O3(0001) (Refer to the text).
The sum rule analysis with the spin correction factor53,54,55 provides the effective spin moment and the orbital moment per Cr3+ as ms_eff = 0.016 ± 0.007 μB and morb = 0.006 ± 0.004 μB, respectively. The ms_eff and morb values are comparable to those in previous reports for Pt/Cr2O3(10 nm)/Pt trilayers35; however, they are lower than the magnetic moment of Cr3+ in Cr2O3, 2.48 μB determined by neutron diffraction56 and 1.51 μB deduced from XMCD/PEEM57. The low magnetic moment values obtained from our XMCD measurements can be attributed to the effective probing depth of the total electron yield (TEY) technique and the alternating spin alignment along <0001>36. The probing depth is ~0.9 nm at the Cr L2,3 edge58, and the XMCD signal from the topmost Cr layer is partially canceled by the opposite spin of the underlying Cr layers. According to the VCMA mechanism associated with the orbital moment of the 3d element, morb/mspin_eff is correlated with the modulation efficiency59. The morb/mspin_eff value derived from the XMCD measurements is 0.3 ± 0.3. This value is comparable to that of the Pt/Co/Co/TiOx system, which shows a Δμ0HSW/ΔV value of ~6.6 mT/V, two orders of magnitude lower than our observation59.
We further measured the XAS and XMCD spectra at the Pt L3 edge to address the possible existence of spin-polarized Pt, which was initially assumed in ref. 28. Figure 3c shows the XAS and XMCD spectra at the Pt L3 edge measured at 230 K. We applied a constant magnetic field of 2.0 T, which was sufficiently high to saturate the Cr magnetic moment. The peak position and the white line intensity are similar to those for metallic Pt60. As shown in Fig. 3c, the XMCD signal is virtually zero, indicating that the Pt-induced moment should be below the detection limit. Since the XMCD intensity is almost independent of the magnetic field strength (Fig. 3d), no appreciable XMCD signal is observed from Pt. Therefore, the alternative mechanism of the VCMA effect, e.g., charge redistribution in nonmagnetic heavy metals8, does not support our observations.
First-principles calculations
To evaluate the contribution of the VCMA effect to the observed switching field modulation, we performed a first-principles calculation. Figure 4b shows the MCA energy density as a function of E calculated for the system shown in Fig. 4a. As a reference system, we also plotted the calculated results for the Cu/Cr2O3 system. The calculated values depend on the metal species on the Cr2O3 layer, indicating that the magnetic anisotropy is mainly attributed to the interfacial magnetic anisotropy Ki. The calculated value for Pt/Cr2O3 is negative, indicating in-plane magnetic anisotropy, which does not support the experimental observation. This probably occurs because the values obtained by the first-principles calculation originate from the spin-orbit coupling (SOC) alone, and the contribution from the dipolar-dipolar interaction favoring the PMA41,61 is not considered. In the case of bulk Cr2O3, the SOC and dipolar-dipolar interactions have comparable contributions to the total MCA energy61. In the case of Pt/Cr2O3, the calculated MCA energy density monotonically decreases with increasing E, as in the case of the VCMA effect. The modulation ratio of the MCA energy density is approximately −99 fJ/(V m), comparable to the FM cases8 showing a much smaller Δμ0HSW/ΔV. In addition, the monotonic E-dependence of the MCA energy density is inappropriate for the bipolar switching shown in Fig. 2. Both XMCD measurements and first-principles calculations support that the modulation of the net magnetization via the ME effect is a plausible mechanism of the giant Δμ0HSW/ΔV, rather than the VCMA effect.
a Top and side views of the calculated interface structure of Pt/Cr2O3. The green, light blue and gray circles are Cr3+, O2− and nonmagnetic atoms, respectively. b Magnetocrystalline anisotropy (MCA) energy density as a function of the electric field, where red and black circles represent the values for Pt/Cr2O3 and Cu/Cr2O3, respectively. The Cu/Cr2O3 system was used as a reference. c Spin magnetic moment of Cr located at the interface as a function of the electric field. Filled and open symbols represent the values for Cr located at the topmost and second layers from the interface, respectively. d–f Density of states of Cr at 0 V located on the topmost (Cr1, down spin), second (Cr2, up spin) and third (Cr3, down spin) layers from the top interface.
To obtain a deep understanding of the mechanism, we investigated the impact of E on the interfacial Cr spin, e.g., the emergence of the interfacial ME effect. Figure 4c plots the spin magnetic moment ms of Cr as a function of E, obtained by first-principles calculations. The ms value of Cr located at the topmost and third layers with downward spin orientations decreases with increasing E, whereas the ms value of Cr on the second layer with an upward spin orientation is almost constant. The modulation of ms by the electric field is 16 times greater for the topmost Cr than for the interior Cr. Figure 4d–f show the density of states (DOS) of Cr located at the topmost (Cr1, down spin), second (Cr2, up spin) and third (Cr3, down spin) layers from the interface. The DOS under an electric field are shown in the Supplementary Information. The topmost Cr has a finite DOS at the Fermi level EF due to orbital hybridization with Pt. For a positive electric field, the electron accumulates at the top interface, and the energy of the d orbital shifts to a lower level with respect to EF (Supplementary Fig. S6b). The electric field significantly modulates the ms of the topmost Cr because it induces a substantial change in the number of electrons analogous to the surface ME effect associated with the spin-dependent Thomas-Fermi screening in FM metals62,63; additionally, the modulation of the ms of the interior Cr, e.g., Cr2 and Cr3, is insignificant because there is no state in the vicinity of the Fermi energy. The slight change in ms for the interior Cr is attributed to the DOS below EF associated with the dielectricity (Supplementary Fig. S6c, d), which is related to the bulk ME effect. At the bottom interface, the opposite effects occur because the electron is depleted by the positive electric field. Since the ME effect occurs due to the imbalance of magnetic moments for two sublattices, the large change in ms of the topmost Cr indicates the emergence of the interfacial ME effect, and its magnitude is larger than that of the bulk ME effect.
Thickness effect on the offset electric field
The interfacial ME effect manifests in the Cr2O3 thickness dependence of E0, as shown in Eq. (3). Figure 5 shows a plot of the E0 values as a function of Cr2O3 thickness measured at the same reduced temperature, T/TN = 0.94 ± 0.01. If the interfacial contribution to the net magnetization and the ME effect are both negligible, E0 is anticipated to be independent of t, corresponding to the linear increase in VG with t. E0 monotonically increases as t decreases, indicating a significant interface effect. Considering the details of the E0–t relationship, neither E0–1/t nor 1/E0–t is linear (see the insets). These results indicate that Mbk_0 and β are both nonzero (see also Eq. (3)). The values of Mbk_0/α and β/α are determined to be 0.048 V/nm and −5.9 nm, respectively, using Eq. (3). With the assumption of the bulk α value64, the bulk uncompensated moment, Mbk_0, is very small, 1.5 × 10−4 Wb/m2 (3.1 × 10−4 μB/Cr) and would be undetectable in the thin film by magnetization measurements. The nonzero β supports the emergence of the interfacial ME effect predicted by the first-principles calculation. A negative β/α indicates that the sign of the interfacial ME susceptibility is opposite to that of the bulk term. In bulk Cr2O3, the sign of α depends on the temperature due to the combination of the distinct mechanisms16,65: the electronic origin, such as changes in the g value and the single-ion anisotropy, and the imbalanced thermal average of the magnetic moments for the two sublattices. In the low-temperature regime below ~75 K, the former mechanism causes a negative ME susceptibility; however, in the high-temperature regime, the latter mechanism causes a positive ME susceptibility. Specifically, the negative β value obtained in this study indicates that the former mechanism exists at a rather high temperature of T/TN = 0.94. Since our first-principles calculations address the former mechanism, the persistence of the negative β supports the emergence of large interfacial ME effects.
In conclusion, we demonstrated that the giant modulation of the switching field reached −500 mT/V (−4800 mT nm/V); this value is more than 50 times larger than the reported modulation based on the VCMA effect. The voltage-induced deterministic 180° switching of the Nèel vector in maintaining a magnetic field was also demonstrated and enabled the investigation of the switching dynamics using the pulse voltage. Although we did not investigate the switching dynamics, conventional films with an FM layer showed the switching within 10 ns66. The pure AFM component without the FM elements used in this work is expected to exhibit faster switching because of the inherent AFM spin dynamics. Comprehensive investigations, including the temperature dependence of the modulation efficiency, bipolar switching and DFT calculations, revealed that the observed giant modulation relied on the ME effect in the AFM insulator Cr2O3 in conjunction with the boundary magnetization. The thickness dependence of the offset electric field together with the first-principles calculation showed the emergence of the interfacial ME effect. This result is important for enhancing the effective ME susceptibility, which is desirable for improving the modulation efficiency. The maximum ME susceptibility due to the imbalanced thermal average mechanism is limited by magnetic and dielectric susceptibility tensors65, and the bulk ME susceptibility of reported compounds was low, at 75 ps/m at 1.5 K in the highest case67. The interfacial ME effect relies on the energy band structure at EF and can be used to enhance the effective ME susceptibility via proper interface design.
In addition to the advances in voltage-based spintronics, our study is also highly important for AFM spintronics. The current-driven switching of interfacial AFM spins via spin torque has been explored30,32,33,34 and requires a large current density exceeding 1011 A/m230,32. Although voltage-driven switching of the AFM order parameter, e.g., the Néel vector, has also been attempted, elaborate materials such as B−-doped Cr2O368 are essential, and the strain effect is involved. The switching angle remains at 90° for both cases. Our study provides a scheme for the energy-efficient, nonvolatile, deterministic 180° switching of the magnetic state in the pure AFM component. This study represents a great advancement in the AFM-based ME random access memory with ultralow writing power, an inherently fast switching speed and superior robustness to the magnetic state.
Methods
Film fabrication
Pt(2 nm)/Cr2O3(tCr2O3 = 8, 10, 15, 40, 90 nm)/Pt(20 nm) trilayers were fabricated on an α-Al2O3(0001) substrate by the DC magnetron sputtering method (base pressure below 1 × 10−6 Pa). Before introducing the substrate to the vacuum chamber, the substrate was ultrasonically cleaned using acetone, isopropanol, distilled water and ethanol. In the vacuum chamber, the substrate was heated for >5 h at 873 K. A 20-nm thick Pt buffer layer was deposited on the substrate at 873 K. Cr2O3 was subsequently formed at 773 K by sputtering a pure Cr target in an Ar and O2 gas mixture. A 2-nm-thick Pt layer was formed at room temperature. The gas pressures during sputtering were 0.35 Pa for the Cr2O3 layer and 0.5 Pa for the Pt layers. A Pt/Cr2O3 bilayer was also prepared for XMCD measurements using an identical deposition system. This type of film was fabricated under the same deposition conditions, with the exception of the Pt buffer layer.
Structural characterizations
The epitaxial growth of each layer was confirmed by in situ reflection high-energy electron diffraction (RHEED) and X-ray diffraction (XRD). RHEED observations were carried out in situ on the surface of every layer. The acceleration voltage of the electrons was 25 kV, and the emission current was typically 20 μA. XRD measurements were performed ex situ with monochromatic Cu Kα irradiation. The acceleration voltage and emission current for the XRD measurements were 45 kV and 200 mA, respectively. The X-ray reflectivity (XRR) was measured to determine the actual thickness, density of each layer and interface roughness. The experimentally obtained XRR profile was fitted by the conventional theoretical model69. High-angle XRD profiles were measured to determine the crystallographic orientation along the growth direction.
AHE measurements
For the AHE measurements, the films were patterned into a Hall cross with 5 μm width and 25 μm length by conventional photolithography and Ar ion milling. The Hall device was equipped with a bottom electrode for application of a gate voltage VG to the Cr2O3 layer, as shown in Fig. 1a. In the device, the bottom Pt layer functioned as the bottom electrode. The electric field E was calculated as VG/tCr2O3. The transverse resistance (Rxy) was measured as a function of the external magnetic field H applied perpendicular to the film plane. The positive directions of E and H were defined as the bottom-to-top direction, as indicated in Fig. 1a. The AHE measurements were performed with the lock-in technique using AC current. The equivalent electric circuit is shown in Fig. 1a. The measurement temperature was varied from 150 to 270 K. The leakage current I across the Cr2O3 layer was also evaluated using the same device. The current density J was calculated as I/A, where A is the total area including the Hall cross and the electrode pad, 791 μm2, which was measured using an optical microscope image from the device used.
XMCD measurements
X-ray absorption spectroscopy (XAS) and X-ray magnetic circular dichroism (XMCD) spectroscopy were performed at soft and hard X-ray beamlines BL25SU and BL39XU of the SPring-8 synchrotron radiation facility, respectively. The XMCD data, \(\Delta \mu ={\mu }^{+}-{\mu }^{-}\), were collected as the difference between the XAS for left- and right-circularly polarized X-rays, denoted as μ+ and μ−, respectively. The XAS signals were detected via the total electron yield (TEY) method at a bias voltage of −18 V for Cr and in florescence mode using a silicon drift detector for Pt. The incident angle of the X-ray beam was 10° from the film normal. During the XMCD measurements, a magnetic field was applied in a direction perpendicular to the film. The measurement temperature was 230 K. In the measurement at the Pt L3 edge using hard X-rays with a large probing depth of a few µm, a Pt (2 nm)/Cr2O3 (8 nm) bilayer was used to detect the XAS and XMCD signals from the top Pt (2 nm) layer, which was responsible for the AHE signal. On the other hand, both the Pt (2 nm)/Cr2O3 (8, 10 nm)/Pt (20 nm) trilayer and Pt (2 nm)/Cr2O3 (8 nm) bilayers were measured at the Cr L2,3 edges using soft X-rays with a short probing depth of a few nm.
DFT calculations
Calculations were carried out using the full-potential linearized augmented plane-wave method70 in local density approximation with correlation correction +U in Cr (U = 4.0 eV and J = 0.58 eV)71, where spin-orbit coupling was introduced by the second variational method. The magnetocrystalline anisotropy (MCA) energy was determined by the force theorem70, which is defined by the energy difference for the magnetization oriented along the in-plane (x-axis) and perpendicular (z-axis) directions to the film plane. A homogenous external electric field was applied perpendicular to the film plane. The polarity of the electric field is defined as the direction in which an electron accumulates in the top layer for a positive electric field. Pt/Cr2O3 was modeled by twelve atomic layers of Cr2O3(0001) and two atomic layers of Pt(111), as shown in Fig. 4a; here, the in-plane lattice constant matches the experimental value of bulk Cr2O3, while the atomic positions along the z-axis were relaxed by atomic force calculations. At the interface, a Cr-terminated surface structure71 was assumed.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Dieny, B. & Chshiev, M. Perpendicular magnetic anisotropy at transition metal/oxide interfaces and applications. Rev. Mod. Phys. 89, 025008 (2017).
Nozaki, T. et al. Recent progress in the voltage-controlled magnetic anisotropy effect and the challenges faced in developing voltage-torque MRAM. Micromachines 10, 327 (2019).
Weisheit, M. et al. Electric field–induced modification of magnetism in thin-film ferromagnets. Science 315, 349–351 (2007).
Maruyama, T. et al. Large voltage-induced magnetic anisotropy change in a few atomic layers of iron. Nat. Nanotechnol. 4, 158–161 (2009).
Bruno, P. Tight-binding approach to the orbital magnetic moment and magnetocrystalline anisotropy of transition-metal monolayers. Phys. Rev. B 39, 865–868 (1989).
van der Laan, G. Microscopic origin of magnetocrystalline anisotropy in transition metal thin films. J. Phys. Condens. Matter 10, 3239–3253 (1998).
Suzuki, Y. & Miwa, S. Magnetic anisotropy of ferromagnetic metals in low-symmetry systems. Phys. Lett. A 383, 1203–1206 (2019).
Miwa, S. et al. Perpendicular magnetic anisotropy and its electric-field-induced change at metal-dielectric interfaces. J. Phys. D Appl. Phys. 52, 063001 (2019).
Nozaki, T., Shiota, Y., Shiraishi, M., Shinjo, T. & Suzuki, Y. Voltage-induced perpendicular magnetic anisotropy change in magnetic tunnel junctions. Appl. Phys. Lett. 96, 022506 (2010).
Endo, M., Kanai, S., Ikeda, S., Matsukura, F. & Ohno, H. Electric-field effects on thickness dependent magnetic anisotropy of sputtered MgO/Co40Fe40B20/Ta structures. Appl. Phys. Lett. 96, 212503 (2010).
Seki, T., Kohda, M., Nitta, J. & Takanashi, K. Coercivity change in an FePt thin layer in a Hall device by voltage application. Appl. Phys. Lett. 98, 212505 (2011).
Nozaki, T. et al. Large voltage‑induced coercivity change in Pt/Co/CoO/amorphous TiOx structure and heavy metal insertion effect. Sci. Rep. 11, 21448 (2021).
Ashcroft, N. W. & Mermin, N. D. in Solid State Physics revised edn, 265–268 (Cengage Learning Asia Pte Ltd., 2016).
Astrov, D. N. The magnetoelectric effect in antiferromagnets. Zh. Exp. Teor. Fiz. 38, 984–985 (1960). [Sov. Phys. JETP 11, 708–709 (1960).]
Folen, V. J., Rado, G. T. & Stalder, E. W. Anisotropy of the magnetoelectric effect in Cr2O3. Phys. Rev. Lett. 6, 607–608 (1961).
Fiebig, M. Revival of the magnetoelectric effect. J. Phys. D Appl. Phys. 38, R123–R152 (2005).
Arima, T. Spin-driven ferroelectricity and magneto-electric effects in frustrated magnetic systems. J. Phys. Soc. Jpn. 80, 052001 (2011).
Andreev, A. F. Macroscopic magnetic fields of antiferromagnets. JETP Lett. 63, 758–762 (1996).
Belashchenko, K. D. Equilibrium magnetization at the boundary of a magnetoelectric antiferromagnet. Phys. Rev. Lett. 105, 147204 (2010).
Fallarino, L., Berger, A. & Binek, C. Magnetic field induced switching of the antiferromagnetic order parameter in thin films of magnetoelectric chromia. Phys. Rev. B 91, 054414 (2015).
Nogués, J. & Schuller, I. K. Exchange bias. J. Magn. Magn. Mater. 192, 203–232 (1999).
Berkowitz, A. E. & Takano, K. Exchange anisotropy. J. Magn. Magn. Mater. 200, 552–570 (1999).
Borisov, P., Hochstrat, A., Chen, X., Kleemann, W. & Binek, C. Magnetoelectric switching of exchange bias. Phys. Rev. Lett. 94, 117203 (2005).
He, X. et al. Robust isothermal electric control of exchange bias at room temperature. Nat. Mater. 9, 579–585 (2010).
Shiratsuchi, Y., Toyoki, K. & Nakatani, R. Magnetoelectric control of antiferromagnetic domain state in Cr2O3 thin film. J. Phys. Condens. Matter 33, 243001 (2021).
Toyoki, K. et al. Switching of perpendicular exchange bias in Pt/Co/Pt/α-Cr2O3/Pt layered structure using magneto-electric effect. J. Appl. Phys. 117, 17D902 (2015).
Nguyen, T. V. A., Shiratsuchi, Y., Kobane, A., Yoshida, S. & Nakatani, R. Magnetic field dependence of threshold electric field for magnetoelectric switching of exchange-bias polarity. J. Appl. Phys. 122, 073905 (2017).
Kosub, T., Kopte, M., Radu, F., Schmidt, O. G. & Makarov, D. All-electric access to the magnetic-field-invariant magnetization of antiferromagnets. Phys. Rev. Lett. 115, 097201 (2015).
Kosub, T. et al. Purely antiferromagnetic magnetoelectric random access memory. Nat. Commun. 8, 13985 (2017).
Moriyama, T., Oda, K., Ohkochi, T., Kimata, M. & Ono, T. Spin torque control of antiferromagnetic moments in NiO. Sci. Rep. 8, 14167 (2018).
Wang, X., Ujimoto, K., Toyoki, K., Nakatani, R. & Shiratsuchi, Y. Increase of Néel temperature of magnetoelectric Cr2O3 thin film by epitaxial lattice matching. Appl. Phys. Lett. 121, 182402 (2022).
Grzybowski, M. J. et al. Electrical switching of antiferromagnetic CoO | Pt across the Néel temperature. Appl. Phys. Lett. 120, 122405 (2022).
Meer, H., Gomonay, O., Wittmann, A. & Kläui, M. Antiferromagnetic insulatronics: spintronics in insulating 3d metal oxides with antiferromagnetic coupling. Appl. Phys. Lett. 122, 080502 (2023).
Wang, M. et al. Field-free spin-orbit torque switching via out-of-plane spin-polarization induced by an antiferromagnetic insulator/heavy metal interface. Nat. Commun. 14, 2871 (2023).
Ujimoto, K. et al. Direct observation of antiferromagnetic domains and field-induced reversal in Pt/Cr2O3/Pt epitaxial trilayers. Appl. Phys. Lett. 123, 022407 (2023).
Corliss, L. M., Hastings, J. M., Nathans, R. & Shirane, G. Magnetic structure of Cr2O3. J. Appl. Phys. 36, 1099–1100 (1965).
Moriyama, T. et al. Giant anomalous Hall conductivity at the Pt/Cr2O3 interface. Phys. Rev. Appl. 13, 034052 (2020).
Wang, J.-L., Echtenkamp, W., Mahmood, A. & Binek, C. Voltage controlled magnetism in Cr2O3 based all-thin-film systems. J. Magn. Magn. Mater. 486, 165262 (2019).
Iino, I., Tada, T., Toyoki, K., Nakatani, R. & Shiratsuchi, Y. Anomalous Hall effect in Pt/Al-doped Cr2O3 epitaxial film. AIP Adv. 13, 015035 (2023).
Foner, S. High-field antiferromagnetic resonance in Cr2O3. Phys. Rev. 130, 183–197 (1963).
Tachiki, M. & Nagamiya, T. Origin of the magnetic anisotropy energy of antiferromagnetic Cr2O3. J. Phys. Soc. Jpn. 13, 452–455 (1958).
Alzate, J. G. et al. Temperature dependence of the voltage-controlled perpendicular anisotropy in nanoscale MgO|CoFeB|Ta magnetic tunnel junctions. Appl. Phys. Lett. 104, 112410 (2014).
Sugihara, A. et al. Temperature dependence of higher-order magnetic anisotropy constants and voltage-controlled magnetic anisotropy effect in a Cr/Fe/MgO junction. Jpn. J. Appl. Phys. 59, 010901 (2020).
Nguyen, T. V. A., Shiratsuchi, Y., Yonemura, S., Shibata, T. & Nakatani, R. Energy condition of isothermal magnetoelectric switching of perpendicular exchange bias in Pt/Co/Au/Cr2O3/Pt stacked film. J. Appl. Phys. 124, 233902 (2018).
Nozaki, T. et al. Manipulation of antiferromagnetic spin using tunable parasitic magnetization in magnetoelectric antiferromagnet. Phys. Status Solidi RPL 12, 1800366 (2018).
Makushko, P. et al. Flexomagnetism and vertically graded Néel temperature of antiferromagnetic Cr2O3 thin films. Nat. Commun. 13, 6745 (2022).
Bertotti, G. in Hysteresis in Magnetism, Ch. 13 (Academic Press, Inc., 1998)
Theil, C., van Elp, J. & Folkmann, F. Ligand field parameters obtained from and chemical shifts observed at the Cr L2,3 edges. Phys. Rev. B 59, 7931–7936 (1999).
Appel, P. et al. Nanomagnetism of magnetoelectric granular thin-film antiferromagnets. Nano Lett. 19, 1682 (2019).
Wörnle, M. S. et al. Coexistence of Bloch and Néel walls in a collinear antiferromagnet. Phys. Rev. B 103, 094426 (2021).
Erickson, A. et al. Nanoscale imaging of antiferromagnetic domains in epitaxial films of Cr2O3 via scanning diamond magnetic probe microscopy. RSC Adv. 13, 178–185 (2023).
Toyoki, K. et al. Equilibrium surface magnetization of α-Cr2O3 studied through interfacial chromium magnetization in Co/α-Cr2O3 layered structures. Appl. Phys. Express 7, 114201 (2014).
Thole, B. T., Carra, P., Sette, F. & van der Laan, G. X-ray circular dichroism as a probe of orbital magnetization. Phys. Rev. Lett. 68, 1943–1946 (1992).
Carra, P., Thole, B. T., Altarelli, M. & Wang, X. X-ray circular dichroism and local magnetic fields. Phys. Rev. Lett. 70, 694 (1993).
Goering, E. X-ray magnetic circular dichroism sum rule correction for the light transition metals. Philos. Mag. 85, 2895–2911 (2005).
Brown, P. J., Forsyth, J. B., Leliévre-Berna, E. & Tasset, F. Determination of the magnetization distribution in Cr2O3 using spherical neutron polarimetry. J. Phys. Condens. Matter 14, 1957 (2002).
Wu, N. et al. Imaging and control of surface magnetization domains in a magnetoelectric antiferromagnet. Phys. Rev. Lett. 106, 087202 (2011).
Frazer, B. H., Gilbert, B., Sonderegger, B. R. & De Stasio, G. The probing depth of total electron yield in the sub-keV range: TEY-XAS and X-PEEM. Surf. Sci. 537, 161–167 (2003).
Nozaki, T. et al. Understanding voltage-controlled magnetic anisotropy effect at Co/oxide interface. Sci. Rep. 13, 10640 (2023).
Kolobov, A. V., Wilhelm, F., Rogalev, A., Shima, T. & Tominaga, J. Thermal decomposition of sputtered thin PtOx layers used in super-resolution optical disks. Appl. Phys. Lett. 86, 121909 (2005).
Artman, J. O., Murphy, J. C. & Foner, S. Magnetic anisotropy in antiferromagnetic corundum-type sesquioxides. Phys. Rev. 138, A912–A917 (1965).
Zhang, S. Spin-dependent surface screening in ferromagnets and magnetic tunnel junctions. Phys. Rev. Lett. 83, 640–643 (1999).
Duan, C.-G. et al. Surface magnetoelectric effect in ferromagnetic metal films. Phys. Rev. Lett. 101, 137201 (2008).
Borisov, P., Hochstrat, A., Shvartsman, V. V. & Kleemann, W. Superconducting quantum interference device setup for magnetoelectric measurements. Rev. Sci. Instrum. 78, 106105 (2007).
Brown, W. F. Jr., Hornreich, R. M. & Shtrikman, S. Upper bound on the magnetoelectric susceptibility. Phys. Rev. 168, 574–577 (1968).
Nguyen, T. V. A., Shiratsuchi, Y. & Nakatani, R. Pulse-voltage-driven dynamical switching of perpendicular exchange bias in Pt/Co/Au/Cr2O3/Pt thin film. Appl. Phys. Express 10, 083002 (2017).
Rado, G. T., Ferrari, J. M. & Maisch, W. G. Magnetoelectric susceptibility and magnetic symmetry of magnetoelectrically annealed TbPO4. Phys. Rev. B 29, 4041–4048 (1984).
Mahmood, A. et al. Voltage controlled Néel vector rotation in zero magnetic field. Nat. Commun. 12, 1674 (2021).
Underwood, J. H. & Barbee, T. W. Jr. Layered synthetic microstructures as Bragg diffractors for X rays and extreme ultraviolet: theory and predicted performance. Appl. Opt. 20, 3027–3034 (1981).
Nakamura, K., Akiyama, T., Ito, T., Weinert, M. & Freeman, A. J. Role of an interfacial FeO layer in the electric-field-driven switching of magnetocrystalline anisotropy at the Fe/MgO interface. Phys. Rev. B 81, 220409 (2010).
Rohrbach, A., Hafner, J. & Kresse, G. Ab initio study of the (0001) surfaces of hematite and chromia: influence of strong electronic correlations. Phys. Rev. B 70, 125426 (2004).
Acknowledgements
XMCD measurements were performed at BL25SU and BL39XU of the SPring-8 synchrotron facility with the approval of the Japan Synchrotron Radiation Research Institute (JASRI) (Proposal Nos. 2015A1215, 2017A1212, 2018B1338, 2022A1205, 2021B1206, 2022B1247, and 2022B1245). This work is partly supported by JSPS KAKENHI (Grant Nos. 22H01757, 22K18903 and JP21H04592) and the Iketani Science and Technology Foundation (Project No. 0341023-A). The first-principles calculations were partially performed using computational facilities at the Research Institute for Information Technology, Kyushu University.
Author information
Authors and Affiliations
Contributions
Y.S. conducted the study; K.U. and H.S. prepared the samples, performed the structural characterizations, and conducted the AHE measurements with the help of K.T. and R.N.; K.U., H.S., K.T., Y.K., M.S., I.I., N.K. and Y.S. carried out the XAS and XMCD measurements; K.U., H.S. and Y.S. analyzed the data with the help of T.M. and K.N.; K.N. performed the DFT calculations. Y.S. prepared the manuscript using the input from all coauthors. All authors discussed the results and wrote the manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no nonfinancial interests but declare competing financial interests. A patent application related to this research has been filed.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ujimoto, K., Sameshima, H., Toyoki, K. et al. Giant gate modulation of antiferromagnetic spin reversal by the magnetoelectric effect. NPG Asia Mater 16, 20 (2024). https://doi.org/10.1038/s41427-024-00541-z
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41427-024-00541-z