Abstract
Fast oxygen-ion conductors for use as electrolyte materials have been sought for energy conversion and storage. Bi2O3-based ionic conductors that exhibit the highest known oxygen-ion conductivities have received attention for use in next-generation solid electrolytes. However, at intermediate temperatures below ~600 °C, their conductivities degrade rapidly owing to a cubic-to-rhombohedral phase transformation. Here, we demonstrate that physical manipulation of the grain structure can be used to preserve the superior ionic conductivity of Bi2O3. To investigate the effects of microstructural control on stability, epitaxial and nanopolycrystalline model films of Er0.25Bi0.75O1.5 were fabricated by pulsed laser deposition. Interestingly, in situ impedance and ex situ XRD analyses showed that the grain boundary-free epitaxial film significantly improved the stability of the cubic phase, while severe degradation was observed in the conductivity of its polycrystalline counterpart. Consistently, the cation interdiffusion coefficient measured by the Boltzmann–Matano method was much lower for the epitaxial thin film compared to the polycrystalline thin film. Furthermore, first-principles calculations revealed that the presence of grain boundaries triggered the structural resemblance between cubic and rhombohedral phases, as evidenced by radial distribution functions. Additionally, phase transition energetics predicted that the thermodynamic stability of the cubic phase with respect to the rhombohedral counterpart is reduced near grain boundaries. Thus, these findings provide novel insights into the development of highly durable superionic conductors via microstructural engineering.
Similar content being viewed by others
Introduction
Extensive research has been conducted on the potential of oxygen-ion conductors for use as solid electrolytes in electrochemical devices such as oxygen sensors1,2, solid oxide fuel cells3,4,5, and oxygen pumps6. To date, most studies of oxygen-ion electrolytes have been focused on oxide materials with cubic fluorite structures, such as doped ZrO27, CeO28,9,10, and Bi2O311,12,13. Among these, the δ-Bi2O3 polymorph, stands out as a promising electrolyte because of its high oxygen ionic conductivity (≈1 S·cm−1 at 800 °C); this stems from the high concentration of disordered oxygen vacancies, which account for 25% of the anion sublattice14.
Despite the superior ionic conductivity of δ-Bi2O3, the thermodynamic stability of the δ phase is confined within a narrow temperature range (729–824 °C); outside of this temperature range, the structure undergoes phase transitions to structures with reduced symmetries, such as the tetragonal β or monoclinic α phases, which exhibit insufficient ionic conductivities at lower temperatures15. Such phase transitions severely limit the application of δ-Bi2O3 and have inspired multiple attempts to stabilize the cubic phase across a broader temperature range by doping with rare earth oxides16,17,18,19,20. In particular, Er2O3 is frequently selected because it allows fast ionic conduction (≈0.35 S·cm−1 at 700 °C). Notably, an Er2O3 concentration of ~15% is sufficient to stabilize the cubic phase, while associations among the dopant and oxygen vacancies are lower than those of alternative dopants21.
However, it has been reported that when erbia-stabilized Bi2O3 (ESB) is exposed to reduced temperatures (below ~600 °C), the conductivity deteriorates dramatically due to a phase transformation to a rhombohedral structure that involves breaking the high symmetry of the cubic phase22. Therefore, studies have been conducted to sustain the cubic structure and fast ionic conductivity of stabilized Bi2O322,23,24. A recent study reported that the cubic phase was maintained by doping aliovalent cations and may enhance the long-term behavior25. Specifically, it was demonstrated that the phase transition kinetics were highly associated with diffusion of cations by investigating the time-dependent ionic conductivities of acceptor- and donor-doped systems. Consequently, it was suggested that the control of cation diffusion enhanced the stability of Bi2O3.
In parallel, for many ionic-conducting polycrystalline oxides, grain boundaries (GBs) often interfere with rapid ionic diffusion, particularly during the transfer of ionic carriers26. This is the case for fluorite-based electrolytes such as doped zirconia and ceria, which has led to many attempts to improve the conductivity by increasing the grain size and thereby reducing the GB density27,28. However, unlike other fluorites, the GBs of stabilized Bi2O3 are remarkably conductive and, therefore, have little effect on the overall ionic conductivity29. Partly due to these unique interfacial properties of Bi2O3, there have not been many attempts to control the microstructure of the Bi2O3 electrolyte and manipulate the density of the GBs. Considering the influence of GBs on phenomena involving atomic movement and recrystallization30,31,32, such as grain growth, precipitation, and phase transitions, a systematic study elucidating the correlations between GBs and the phase stability of stabilized Bi2O3 would suggest new insights.
In this study, we used pulsed laser deposition (PLD) techniques to investigate how the long-term phase stabilities of ESBs change depending on rigorously controlled grain boundary conditions. Both epitaxial and polycrystalline thin films of Er0.25Bi0.75O1.5 (25ESB) were prepared on two different single crystal substrates (SiO2 (001) and C-plane Al2O3 (0001)). These polycrystalline films with nanosized columnar grains are expected to clarify the contribution of GBs to cubic phase stability when compared to the GB-free epitaxial counterpart. The surface morphologies and crystallographic structures of the fabricated model samples were characterized through atomic force microscopy (AFM) and X-ray diffraction (XRD), respectively. Next, the time-dependent behavior of the ionic conductivity was analyzed in situ using electrochemical spectroscopy (EIS). To elucidate the effects of GBs on the phase transition kinetics, the cation interdiffusion coefficient was measured by the Boltzmann–Matano method. An atomic-level understanding of the stabilities of ESBs arising from the presence of GBs was obtained by density functional theory (DFT) calculations with a focus on local atomic geometries, electronic structures of the GB region, and phase transition energetics. To the best of our knowledge, the current work provides the first indication of how the grain boundary condition affects the long-term behaviors of ESBs with a thin-film model study.
Materials and methods
Sample preparation
The ESB thin films and CeO2 interlayer were prepared using PLD from oxide targets of the respective materials. The ESB target was prepared via a conventional solid-state reaction in which a mixture containing stoichiometric amounts of Bi2O3 (99.99% pure, YeeYoung Cerachem) and Er2O3 (99.99% pure, Alfa Aesar) was ball-milled for 24 h with zirconia media in a HDPE bottle. The powder mixture was calcined at 800 °C for 16 h before the calcined powder was crushed finely with a mortar and pestle and sieved with a 45 μm mesh. The CeO2 target was prepared using micron powder (99.9%, Alfa Aesar). Finally, the ESB and CeO2 powders were uniaxially pressed under a pressure of 50 MPa to obtain the disk-shaped PLD target with a diameter of 2.54 cm (1 in.) and a thickness of 1 cm. The final ESB and CeO2 targets were obtained after sintering at 890 °C for 16 h and 1400 °C for 6 h, respectively.
Polycrystalline thin films were grown on a single-crystal SiO2 (001) substrate with a CeO2 interlayer to prevent diffusion of Si. The effect of the interlayer is described in the Supporting Information and Fig. S1. Epitaxial thin films were grown on C-plane Al2O3 (0001) substrates. The PLD system was operated using a KrF excimer laser with an emission wavelength of 248 nm (Coherent COMPex 205) at a pulsed laser energy of 270 mJ and a laser repetition rate of 5 Hz for a selected duration. During the laser ablation process, the substrate temperature and O2 working pressure were kept at 700 °C and 10 mTorr, respectively. After the deposition process was completed, the chamber was kept at 700 °C under an O2 working pressure of 1 Torr for 30 min to facilitate oxidation of the films. It was confirmed in Fig. S2, which shows XRD results obtained before and after heat treatment, that the ESB films were prepared well and without any oxygen deficiency.
Characterization
To investigate the crystal structures of the deposited ESB films, XRD measurements were conducted using a Bragg–Brentano diffractometer (Rigaku Ultima IV, Tokyo, Japan, Cu Kα wavelength of 1.541 Å). The in-plane reflections recorded in the high-resolution XRD measurements were utilized to perform a precise analysis of the growth structures and crystallinities of the deposited films using a diffractometer (X’Pert-PRO MRD, PANalytical) operated at 45 kV and 40 mA with a fixed Cu anode. An AFM (Park Systems XE-150) was used to study the surface morphologies of the specimens.
The electrical conductivities of the ESB thin films were evaluated using two-probe electrochemical impedance spectroscopy (EIS, Biologic VMP-300). The details of the experimental setup and analytical method for the in-plane conductivity measurements are given in the Supporting Information and Fig. S3. The impedance of each specimen was measured under ambient air conditions (balanced by mixing O2 and Ar gas flows) over a frequency range of 5 MHz to 0.05 Hz and an amplitude range of 100–400 mV. In addition, the measurements were carried out based on a carefully controlled heating schedule, considering the degradation occurring at elevated temperatures. The details are included in the Supporting Information and Fig. S4.
A focused ion beam (FIB, Hitachi NB 5000) was used to prepare trenches for the thin films, and a composition analysis was performed at each location using transmission electron microscopy combined with energy-dispersive X-ray spectroscopy (TEM EDS, Hitachi HF-3300). The impurity diffusion profiles of the polycrystalline ESB thin film samples were analyzed by time-of-flight secondary ion mass spectrometry (ToF-SIMS; TOF-SIMS5, Germany) after the annealing process. Here, 30 keV Bi+ clusters with a raster of 256 × 256 measured points scanned over an area of 100 × 100 μm2 were used to generate negatively charged secondary ions, and the secondary ion intensity levels of all relevant isotopes and clusters were analyzed simultaneously. For depth profiling, 1 keV Cs+ ions (300 × 300 μm2) were used in noninterlaced mode (analyze 1 frame, sputter 3 s, pause 4 s) for sequential ablation of the surface between measurements of the mass spectra.
Computational details
DFT calculations were performed using VASP33,34. The generalized gradient approximation (GGA-PBE) was chosen for the exchange-correlation functionals. Projector-augmented-wave (PAW) potentials with valence configurations of 4f25d106s26p3 and 2s22p4 were applied to describe Bi and O, respectively. Plane waves with an energy cutoff of 450 eV based on the convergence test within 0.02 eV/f.u. were used to expand the electronic wave functions. We used 1 × 1 × 1 and 2 × 2 × 2 k-meshes35 within the Monkhorst–Pack scheme for the GB and bulk models, respectively. The k-point settings were optimized by energy convergence tests based on a 1 × 1 × 1 Bi2O3 unit cell. The convergence threshold for the electronic self-consistent iterations was set to 10–4 eV/cell. The atomic positions and cell parameters were relaxed until the residual force reached 10–3 eV/Å. We obtained a lattice constant of x = y = z = 5.7 Å for the 1 × 1 × 1 unit cell after fitting the calculated total energy as a function of the unit cell volume to the Birch–Murnaghan equation of state36. This yielded good agreement (~3%) with the experimental result37 extrapolated to 0 K (5.553 Å), which was within the typical overestimation calculated by GGA functionals. Based on the lattice constant of the grain condition, a tilt ∑3[11̅0]/(111) GB model was generated because it was reported based on previous calculations to have a lower GB formation energy compared to other models for fluorite systems38,39,40. A slab model with a vacuum region was developed to depict the atomic structure of the GB region with a sufficient bulk region. The GB model was constructed by mirroring and shifting the (111) plane, which featured 240 atoms and had dimensions of 8.06 × 8.06 × 98.98 Å3. We used slabs sandwiched by a vacuum region of approximately 20 Å along the z-direction to simulate the GBs. To minimize the effects of surface electronic redistribution on the GB area and to describe the bulk region adequately, three terminal atomic layers were fixed (one stoichiometric Bi2O3 (111) trilayer). In addition, two oxygen layers were fixed at the center of the GB model to prevent the structure from being fully relaxed along the GB region because the GB blurs and dissipates owing to facile relaxation of oxygen ions originating from the disordered nature of the anion sublattice in Bi2O3. To approximate the disorder of oxygen vacancies, the special quasi-random structure (SQS) method from the Alloy Theoretical Automated Toolkit (ATAT) was used. In the SQS approach, oxygen ions are arranged on the anion sublattice so that their most relevant radial correlation functions imitate those of the reference structure, which is perfectly random41. Doublet and triplet clusters are considered as proposed from previous studies42,43, and the generated structures showed energy convergence to within 0.1 eV/f.u. However, additional consideration of quadruplets did not lead to improvements. Furthermore, the maximum cutoff radius within the supercell was used to ensure that all possible ranges of clusters were covered. The effective coordination number (ECN) was calculated by weighting the individual bond lengths between the central ion and the nearby ions in comparison to the minimum bond length of the central ion44. The ECN was calculated by summing the weights as follows:
where li denotes the bond lengths between the central and nearby i ions, while lmin denotes the minimum bond lengths from the central ion.
Results and discussion
Grain boundary manipulation via thin-film deposition
Two types of thin films with different microstructures were used as model samples to confirm the effect of GBs on phase stability and ion conductivity. Figure 1a shows a schematic drawing of the epitaxial and columnar growth of the ESB thin films. Figure 1b, c present AFM images of the as-deposited surface morphologies of the epitaxial ESB thin film (Epi-ESB) and polycrystalline ESB thin film (Poly-ESB), respectively. Epi-ESB had a smooth surface (Rq = 0.686 nm) without GBs, whereas Poly-ESB exhibited widespread surface irregularities (Rq = 2.737 nm) corresponding to GBs over an area of 1 μm × 1 μm. Figure 2a shows the out-of-plane XRD patterns (ω-2θ) for Epi-ESB and Poly-ESB. The crystalline cubic fluorite structure (\(\delta\)-phase) was observed for both films without any secondary phase formation. Indeed, Epi-ESB showed only the (111) peak, which, as reported elsewhere, was indicative of coherent film growth. The in-plane diffraction patterns shown in Fig. 2b provided further evidence for epitaxial growth of Epi-ESB. In contrast to Poly-ESB, for which no peaks were observed in the in-plane ϕ-scan results, Epi-ESB showed sharp in-plane peaks with a six-fold rotational symmetry of 60°, thus confirming the strong alignment registry between the film and the substrate. These crystallographic features of epitaxially grown ESB films on C-Al2O3 (0001) substrates were repeatedly confirmed in previous studies45,46. Alternatively, several orientations, namely, (111), (200), (220), and (331), were observed for Poly-ESB, indicating the polycrystalline growth of ESB. The possibility of a phase change for SiO2 at high temperature was reported in a previous study47. However, as seen from the high-temperature real-time XRD results of the z-cut SiO2 substrate in Fig. S5, the phase change of SiO2 was negligible and certainly had no effect on the growth of Poly-ESB films.
a Out-of-plane X-ray diffraction patterns for ESB thin films. The asterisks indicate artifacts attributed to the aged X-ray tube. b In-plane X-ray diffraction patterns of the ESB thin films. c Arrhenius plots for the total conductivities of the ESB thin films and the ESB bulk sample measured in air.
Furthermore, additional characterization of the Epi-ESB film was performed by means of high-resolution TEM (HR-TEM), as shown in Figs. S6, 7. First, the cross-sectional HR-TEM image (Fig. S6d, e) of the ESB film region and ESB|Substrate interface region revealed that the dense ESB thin film was well grown and without any grain boundaries. Figure S6b, c shows the selected area electron diffraction (SAED) patterns for the film area and interface region, respectively, as marked in Fig. S6a. The heteroepitaxial relationship between the ESB thin film and the C-Al2O3 substrate is clearly shown, and the highly oriented and crystalline growth feature of Epi-ESB was confirmed. The strong spots are the Bragg reflections of fluorite-like structures, while the other spots are satellite reflections, as reported elsewhere26,48.
Figure 2c presents the ionic conductivities of Epi-ESB and Poly-ESB alongside that of bulk ESB in the Arrhenius plots. The conductivity values were derived by investigating the origin of the resulting impedance spectra, and the detailed process is included in the Supporting Information and Figs. S3 and S8–S10. Initially, measured ionic conductivities and calculated activation energies of bulk (1.1 eV), Epi- (1.1 eV), Poly-ESB (1.0 eV) matched each other well and agreed with the results of our previous work, which demonstrated that GBs in ESB serve neither as preferential paths for oxygen diffusion nor as obstacles to oxygen conduction29,49. In summary, these results emphasize that the thin films fabricated herein were well defined, thereby maintaining the inherent transport properties of ESB.
Time-dependent conductivity behavior
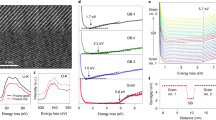
Figure 3 shows how the ionic conductivity and crystal structure of ESB change over time at 600 °C. Specifically, Fig. 3a shows the Nyquist plots for Epi-ESB and Poly-ESB annealed for 20 h. Surprisingly, the ohmic resistance was maintained in Epi-ESB, whereas a dramatic increase in the resistance was observed for Poly-ESB. Figure 3b presents the time-dependent conductivity behaviors of ESB thin films heated at 600 °C for 100 h: the conductivity of Poly-ESB decreased by 94.6% from 9 × 10–2 to 1 × 10–3 S/cm after approximately 20 h of operation, while the initial conductivity (~7 × 10−2 S/cm) of Epi-ESB remained almost constant during annealing for up to 100 h (~6 × 10–2 S/cm). Furthermore, additional experiments were performed to investigate the effect of lattice strain on conduction characteristics and long-term phase stability. Under identical PLD process conditions with different durations of deposition, films with three different thicknesses (140, 500, and 780 nm) were grown on identical Al2O3 substrates. As seen from Fig. S11, all of the films showed epitaxial growth features with highly preferred orientations in the (111) direction. In Fig. S11b, the thinner the film was, the greater the influence received from the substrate, and a larger peak shift was observed compared to that of the fully relaxed ESB25 bulk. Based on the (111) peak shift value, the respective strain level was evaluated as shown in Table S1 by referring to the previous method50,51. Next, conductivity measurements and long-term stability tests at 600 °C were performed on the thin films, as shown in Fig. S12. The conductivity values of the strained films were slightly lower than that of the bulk, but the conductivity value of the 500 nm film was similar to that of the bulk. Furthermore, the results of the long-term stability tests shown in Fig. S12b indicated that all three epitaxial thin films underwent sluggish degradation with rates several orders of magnitude slower than that of the polycrystalline thin film. In this regard, enhancement of the long-term durabilities of epitaxial films did not show a significant correlation with the thicknesses (and lattice strain) of the epitaxial films. Thus, it was demonstrated that, regardless of their thickness, epitaxial ESB films exhibited long-term phase stability much superior to that of polycrystalline ESB film. Figure S13 shows the ToF-SIMS analysis of possible Ce diffusion due to the CeO2 interlayer in Poly-ESB after the conductivity measurement. However, the level of Ce content in the interior of the ESB thin film was only at the noise level, indicating the absence of chemical reactions or intermixing of chemical species.
a Nyquist plots of epitaxial and polycrystalline ESB thin films. b Time-dependent conductivities of epitaxial and polycrystalline ESB thin films. XRD spectra of c epitaxial and d polycrystalline ESB thin films after long-term operation. The asterisks indicate artifacts attributed to the aged X-ray tube.
After the long-term stability tests, XRD analyses of both samples revealed that the long-term heat treatment led to a clear difference between the films, as shown in Fig. 3c, d. Overall, the cubic phase was maintained for Epi-ESB, except for growth of a negligible rhombohedral peak (Fig. 3c); however, for Poly-ESB, several rhombohedral peaks were formed after 30 h of heat treatment, while minor peaks for the cubic structure vanished, and only the (111) oriented peak remained (Fig. 3d). This result suggested that the degraded conductivities of the films following long-term annealing were mainly due to a transition from the conductive cubic phase to the resistive rhombohedral phase, as reported in our previous work25. In the XRD spectra of Poly-ESB, it appeared that cubic and rhombohedral phases coexisted. Specifically, as a substantial transition occurred, the (111) peak of the cubic phase dropped in intensity and widened, whereas the (211) peak, which is the main peak of the rhombohedral phase, became relatively larger. In the XRD spectra of Epi-ESB, cubic peaks remained, and only a minor rhombohedral peak was observed, indicating significant suppression of the phase transition. Effects related to nanoscale structural evolution, such as amorphous phases and local dislocations, were not considered in this study, and further studies may be necessary.
Cation interdiffusion coefficient
An association between cation diffusion and phase transition kinetics has been suggested in previous studies22,23,24,25, and we used microstructural control to determine whether there exists a corresponding correlation in this study. The interdiffusion coefficients of Bi cations were measured via the Boltzmann–Matano method. To this end, films with different compositions were deposited sequentially to establish bilayered diffusion couple specimens (40ESB|15ESB) for each of Epi-ESB and Poly-ESB. After subjecting each diffusion couple specimen to heat treatment at 700 °C for 10 h, specimens for transmission electron microscopy (TEM) analysis were fabricated by using an in situ lift-out technique with a FIB. Figure 4a shows the detailed steps of sample preparation. The layer at the diffusion couple interface was obtained by FIB etching and attached to the grid. The Bi concentration as a function of distance was then quantified using the energy-dispersive X-ray spectroscopy (EDS) capability of the TEM system. The concentration profile was drawn with x = 0 representing the Matano interface, that is, the interface where the mass is balanced and the diffusion-induced loss on one side equals the corresponding gain on the other side. The concentration profiles after heat treatment of Epi-ESB and Poly-ESB are shown in Fig. 4b. Upon inspecting the changes in slopes near the Matano interface, the change in the Bi concentration gradient was found to be significantly lower in Epi-ESB than in Poly-ESB. This implied that the diffusion coefficient of Bi in the epitaxial specimen was smaller than that in the polycrystalline specimen. The diffusion coefficient of Bi was quantitatively determined via the Boltzmann–Matano method, as follows:
where t denotes a specific time, C0 is the Bi concentration at the end of the diffusion couple, and C* represents the Bi content at a specific position. The composition-dependent Bi interdiffusion coefficients were measured for Epi-ESB and Poly-ESB with this method, and they were plotted in Fig. 4c. The measured interdiffusion coefficient of Epi-ESB observed for the 25ESB composition (0.02 nm2/s) was 71% lower than that of Poly-ESB (0.07 nm2/s). This result indicated that cation diffusion can be controlled by microstructural manipulation. Thus, slower diffusion of Bi cations would result in effective suppression of a phase transition for stabilized bismuth oxide.
Role of grain boundaries in phase transitions
To further understand the stability of the cubic phase in the presence of GBs, the atomic-level behavior was simulated using DFT calculations. The GB model was envisaged as alternating O and Bi planes, as shown in Fig. 5a. To explore how the atomic structure of the grain condition changed due to the presence of GBs, a structural model containing slab layers representing the bulk and GB conditions was developed (Fig. S14). Then, a gradual change due to the presence of GB was observed. The local geometry of the GB model was analyzed from the perspective of Bi cations, and the ECNs44 of the Bi ions (ECNBi) were averaged for each layer of the GB model. The ECNBi gradually decreased as the Bi ions approached the GB, as shown in Table S2, implying that interactions of Bi with O were weakened near the GB. This might free Bi cations to move from the initial sublattice and thereby speed diffusion of Bi ions, as observed in Poly-ESB, which contained numerous GBs. To understand the changes in stability resulting from reduced interactions between Bi and O upon moving from the bulk condition toward the GB condition, two sets of cubic and rhombohedral structures are prepared with varying degrees of oxygen occupation. One set represented the bulk condition with minimal GB influence (Epi condition), and the other represented the GB condition with maximal GB influence (Poly condition). Cubic and rhombohedral phases for each condition were denoted XY (X = Cubic, or Rhom; Y = Epi, or Poly) for consistency with the experiments. The reproducibilities of the two sets for each condition were verified from the atomic and electronic perspectives, and details are described in the Supporting Information. The schematic processes used for calculations are depicted in Fig. S15.
a Side view along the [\(1\bar 10\)] axis of a tilt Bi2O3 Σ3[\(1\bar 10\)]/(111) grain boundary model. The blue and red balls represent Bi and O atoms, respectively. The yellow region in the middle of the model indicates the Σ3 grain boundary of Bi2O3. Radial distribution functions of the cubic and rhombohedral phases under the b Epi and c Poly conditions. d Atom-projected density of states and partial charge density maps for the CubicPoly model. e Energetics for the cubic-to-rhombohedral phase transition under Epi (red) and Poly (blue) conditions.
Figure 5b, c shows the bonding characteristics of the cubic and rhombohedral phases for each condition, as analyzed using radial distribution functions. The frequencies of the Bi–O bonds were described as a function of distance within the first coordination shell. The most dominant bond lengths were marked with red and blue circles for the cubic and rhombohedral phases, respectively. While there were significant bonding differences between the cubic and rhombohedral phases in the Epi condition, the bonding distributions of the two phases in the Poly condition were more closely aligned, as evidenced by the overlapping red and blue circles. From this structural resemblance between the cubic and rhombohedral phases in the Poly condition, it can be inferred that transformation from the cubic to the rhombohedral phase became easier with less structural deformation near the GBs. Figure 5d shows the density of states and corresponding charge density maps for CubicPoly. While the states in the lower energy range (Fig. 5d, green data below −1 eV) showed results similar to those for CubicEpi (Fig. S17a), the states below the Fermi energy (purple data from −1 to 0 eV) showed antibonding characteristics, which implied instability of the cubic phase under Poly conditions. This behavior can be attributed to the distinctive tendencies observed for atomic relaxation (represented by ECNBi). As shown in Table S3, the ECNBi of the rhombohedral phase underwent a greater change on going from Epi to Poly than the ECNBi of the cubic phase. Specifically, while the ECNBi of the rhombohedral phase (4.13) was higher than that of the cubic phase (3.99) under the Epi condition, the reverse was true for the Poly condition, where the ECNBi of the rhombohedral phase (2.87) was lower than that of the cubic phase (3.04). This indicated that rhombohedral Bi2O3 responded more readily to changes in the local atomic environment than its cubic counterpart.
In Fig. 5e, the calculated DFT energy, ΔEDFT (= \(E_{{{{\mathrm{DFT}}}}}^{{{{\mathrm{Rhom}}}}} - E_{{{{\mathrm{DFT}}}}}^{{{{\mathrm{Cubic}}}}}\)), predicts the energy cost for transformation from the cubic to the rhombohedral phase under each condition. Under the Epi condition, represented by the red bar, ΔEDFT is positive, signifying that the cubic phase is likely to be maintained. However, under the Poly condition (blue bar), ΔEDFT becomes negative, which indicates that the transformation from the cubic to rhombohedral phase is energetically favorable. In other words, it is predicted that the cubic structure is more stable than the rhombohedral structure in the absence of GB effects; the rhombohedral structure becomes energetically favorable with respect to the cubic structure when there is a grain boundary effect. Even taking the finite-temperature error (~meV/f.u.) into account52,53, the difference in energy of ~3 eV (0.25 eV/f.u.) for the two conditions is distinguishable, indicating that the phase stability is highly sensitive to the grain boundary condition. These predictions indicate that the presence of GBs induces a phase transition for Bi2O3, and these results strongly support our experimental data.
Conclusion
In this study, the long-term stability of the Bi2O3-based superionic conductor was enhanced significantly via precise manipulation of GBs. While the conductivity of the poly-ESB thin film declined rapidly from 9 × 10–2 to 1 × 10–3 S/cm at 600 °C due to the cubic-to-rhombohedral phase transformation, the Epi-ESB thin film maintained its initial conductivity for 100 h without a phase transition. Successful modification of cation diffusion was investigated with the interdiffusion coefficient of Bi, and a proportional relationship was observed between cation diffusion and phase transition kinetics. Furthermore, DFT calculations revealed that under the influence of GBs, a strong structural resemblance was observed between the cubic and rhombohedral phases; antibonding characteristics were observed for the cubic phase, implying high feasibility of transformation from the cubic to rhombohedral phase in ESB. These observations suggest that the superionic conductivity of stabilized Bi2O3 can be effectively secured by physically manipulating GB conditions in the bulk, such as by elongating heat treatment conditions, applying a thermomechanical treatment, or adding sintering agents. Thus, our findings provide novel insights for the development of highly conductive and durable solid electrolytes for next-generation energy applications.
References
Gao, X. A., Liu, T., Zhang, X. F., He, B. G. & Yu, J. K. Properties of limiting current oxygen sensor with La0.8Sr0.2Ga0.8Mg0.2O3-delta solid electrolyte and La0.8Sr0.2(Ga0.8Mg0.2)(1-) xCrxO3-delta dense diffusion barrier. Solid State Ion. 304, 135–144 (2017).
Park, J. Y., Jung, N. H., Jung, D. W., Ahn, S.-J. & Park, H. J. Electrochemical properties of a zirconia membrane with a lanthanum manganate-zirconia composite electrode and its oxygen permeation characteristics by applied currents. J. Korean Ceram. Soc. 56, 197–204 (2019).
Wachsman, E. D. & Lee, K. T. Lowering the temperature of solid oxide fuel cells. Science 334, 935–939 (2011).
Park, J. W., Joh, D. W., Yun, B.-H., Samdani, K. J. & Lee, K. T. Development of nanostructured La0.8Sr0.2MnO3−δ-Er0.4Bi1.6O3 cathodes via an infiltration process with different polymeric agents for intermediate temperature solid oxide fuel cells. Int. J. Hydrog. Energy 42, 6332–6337 (2017).
Park, J. W. & Lee, K. T. Enhancing performance of La0. 8Sr0.2MnO3−δ-infiltrated Er0.4Bi1.6O3 cathodes via controlling wettability and catalyst loading of the precursor solution for IT-SOFCs. J. Ind. Eng. Chem. 60, 505–512 (2018).
Li, M. et al. A family of oxide ion conductors based on the ferroelectric perovskite Na0.5Bi0.5TiO3. Nat. Mater. 13, 31–35 (2014).
Joh, D. W., Park, J. H., Kim, D. Y., Yun, B.-H. & Lee, K. T. High performance zirconia-bismuth oxide nanocomposite electrolytes for lower temperature solid oxide fuel cells. J. Power Sources 320, 267–273 (2016).
Andersson, D. A., Simak, S. I., Skorodumova, N. V., Abrikosov, I. A. & Johansson, B. Optimization of ionic conductivity in doped ceria. Proc. Natl Acad. Sci. USA 103, 3518–3521 (2006).
Joh, D. W. et al. Sintering behavior and electrochemical performances of nano-sized gadolinium-doped ceria via ammonium carbonate assisted co-precipitation for solid oxide fuel cells. J. Alloy. Compd. 682, 188–195 (2016).
Lee, K. T., Vito, N. J., Yoon, H. S. & Wachsman, E. D. Effect of Ni-Gd0.1Ce0.9O1.95 anode functional layer composition on performance of lower temperature SOFCs. J. Electrochem. Soc. 159, F187 (2012).
Jung, D. W., Lee, K. T. & Wachsman, E. D. Dysprosium and gadolinium double doped bismuth oxide electrolytes for low temperature solid oxide fuel cells. J. Electrochem. Soc. 163, F411 (2016).
Jung, D. W., Duncan, K. L. & Wachsman, E. D. Effect of total dopant concentration and dopant ratio on conductivity of (DyO1.5)x–(WO3)y–(BiO1.5)1−x−y. Acta Mater. 58, 355–363 (2010).
Yun, B.-H. et al. Highly active and durable double-doped bismuth oxide-based oxygen electrodes for reversible solid oxide cells at reduced temperatures. J. Mater. Chem. A 7, 20558–20566 (2019).
Azad, A., Larose, S. & Akbar, S. Bismuth oxide-based solid electrolytes for fuel cells. J. Mater. Sci. 29, 4135–4151 (1994).
Harwig, H. & Gerards, A. Electrical properties of the α, β, γ, and δ phases of bismuth sesquioxide. J. Solid State Chem. 26, 265–274 (1978).
Verkerk, M. & Burggraaf, A. High oxygen ion conduction in sintered oxides of the Bi2O3‐Dy2O3 system. J. Electrochem. Soc. 128, 75 (1981).
Takahashi, T., Esaka, T. & Iwahara, H. High oxide ion conduction in the sintered oxides of the system Bi2O3-Gd2O3. J. Appl. Electrochem. 5, 197–202 (1975).
Takahashi, T., Iwahara, H. & Arao, T. High oxide ion conduction in sintered oxides of the system Bi2O3-Y2O3. J. Appl. Electrochem. 5, 187–195 (1975).
Takahashi, T., Iwahara, H. & Nagai, Y. High oxide ion conduction in sintered Bi2O3 containing SrO, CaO or La2O3. J. Appl. Electrochem. 2, 97–104 (1972).
Keizer, K., Verkerk, M. & Burggraaf, A. Preparation and properties of new oxygen ion conductors for use at low temperatures. Ceramurg. Int. 5, 143–147 (1979).
Verkerk, M., Keizer, K. & Burggraaf, A. High oxygen ion conduction in sintered oxides of the Bi2O3-Er2O3 system. J. Appl. Electrochem. 10, 81–90 (1980).
Fung, K. Z., Chen, J. & Virkar, A. V. Effect of aliovalent dopants on the kinetics of phase transformation and ordering in RE2O3‐Bi2O3 (RE = Yb, Er, Y, or Dy) solid solutions. J. Am. Ceram. Soc. 76, 2403–2418 (1993).
Fung, K. Z. & Virkar, A. V. Phase stability, phase transformation kinetics, and conductivity of Y2O3—Bi2O3 solid electrolytes containing aliovalent dopants. J. Am. Ceram. Soc. 74, 1970–1980 (1991).
Fung, K. Z., Virkar, A. V. & Drobeck, D. L. Massive transformation in the Y2O3‐Bi2O3 system. J. Am. Ceram. Soc. 77, 1638–1648 (1994).
Yun, B.-H., Lee, C.-W., Jeong, I. & Lee, K. T. Dramatic enhancement of long-term stability of erbia-stabilized bismuth oxides via quadrivalent Hf doping. Chem. Mater. 29, 10289–10293 (2017).
Kwak, N. W. & Jung, W. Analysis of the grain boundary conductivity of singly and doubly doped CeO2 thin films at elevated temperature. Acta Mater. 108, 271–278 (2016).
Martin, M. C. & Mecartney, M. L. Grain boundary ionic conductivity of yttrium stabilized zirconia as a function of silica content and grain size. Solid State Ion. 161, 67–79 (2003).
Lee, K.-R., Lee, J.-H. & Yoo, H.-I. Grain size effect on the electrical properties of nanocrystalline ceria. J. Eur. Ceram. Soc. 34, 2363–2370 (2014).
Jeong, S. J., Kwak, N. W., Byeon, P., Chung, S.-Y. & Jung, W. Conductive nature of grain boundaries in nanocrystalline stabilized Bi2O3 thin-film electrolyte. ACS Appl. Mater. Interfaces 10, 6269–6275 (2018).
Woo, J.-Y., Oh, K.-S., Chung, T.-J., Lee, H.-J. & Paek, Y.-K. Low-temperature sintering behaviors in a titanium oxide–copper oxide system through two-step heat treatment. J. Korean Ceram. Soc. 58, 219–224 (2021).
Kim, T. et al. Confined growth of high-quality single-crystal MAPbBr3 by inverse temperature crystallization for photovoltaic applications. Electron. Mater. Lett. 17, 347–354 (2021).
Liu, Y., Zhu, X., Li, M., O’Hayre, R. P. & Yang, W. Nanoparticles at grain boundaries inhibit the phase transformation of perovskite membrane. Nano Lett. 15, 7678–7683 (2015).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169 (1996).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758 (1999).
Monkhorst, H. J. & Pack, J. D. Special points for Brillouin-zone integrations. Phys. Rev. B 13, 5188 (1976).
Birch, F. Finite elastic strain of cubic crystals. Phys. Rev. 71, 809 (1947).
Yashima, M., Ishimura, D. & Ohoyama, K. Temperature dependence of lattice parameters and anisotropic thermal expansion of bismuth oxide. J. Am. Ceram. Soc. 88, 2332–2335 (2005).
Yuan, F., Liu, B., Zhang, Y. & Weber, W. J. Segregation and migration of the oxygen vacancies in the Σ3 (111) tilt grain boundaries of ceria. J. Phys. Chem. C 120, 6625–6632 (2016).
Zhou, G., Li, P., Ma, Q., Tian, Z. & Liu, Y. Density functional theory plus Hubbard U study of the segregation of Pt to the CeO2–x grain boundary. Nano Lett. 18, 1668–1677 (2018).
Shibata, N., Ikuhara, Y., Oba, F., Yamamoto, T. & Sakuma, T. Atomic structure and solute segregation of a Σ= 3,[110]/{111} grain boundary in an yttria-stabilized cubic zirconia bicrystal. Philos. Mag. Lett. 82, 393–400 (2002).
Van de Walle, A. et al. Efficient stochastic generation of special quasirandom structures. Calphad 42, 13–18 (2013).
Shitara, K. et al. First-principles selection of solute elements for Er-stabilized Bi2O3 oxide-ion conductor with improved long-term stability at moderate temperatures. Chem. Mater. 29, 3763–3768 (2017).
Music, D., Konstantinidis, S. & Schneider, J. M. Equilibrium structure of δ-Bi2O3 from first principles. J. Phys.: Condens. Matter 21, 175403 (2009).
Hoppe, R. Effective coordination numbers (ECoN) and mean fictive ionic radii (MEFIR). Z. Kristallogr. Cryst. Mater. 150, 23–52 (1979).
Sanna, S. et al. Structural instability and electrical properties in epitaxial Er2O3-stabilized Bi2O3 thin films. Solid State Ion. 266, 13–18 (2014).
Takeyama, T., Takahashi, N., Nakamura, T. & Itoh, S. Microstructure characterization of δ-Bi2O3 thin film under atmospheric pressure by means of halide CVD on c-sapphire. J. Cryst. Growth 275, 460–466 (2005).
Ringdalen, E. Changes in quartz during heating and the possible effects on Si production. JOM 67, 484–492 (2015).
Sanna, S. et al. Enhancement of the chemical stability in confined delta-Bi2O3. Nat. Mater. 14, 500–504 (2015).
Jung, H. J. & Chung, S.-Y. Absence of distinctively high grain-boundary impedance in polycrystalline cubic bismuth oxide. J. Korean Ceram. Soc. 54, 413–421 (2017).
Koo, B. et al. Enhanced oxygen exchange of perovskite oxide surfaces through strain-driven chemical stabilization. Energy Environ. Sci. 11, 71–77 (2018).
Kim, K. et al. Control of transition metal–oxygen bond strength boosts the redox ex-solution in a perovskite oxide surface. Energy Environ. Sci. 13, 3404–3411 (2020).
Friedrich, R. et al. Coordination corrected ab initio formation enthalpies, npj Computational. Materials 5, 1–12 (2019).
Bartel, C. J. et al. Physical descriptor for the Gibbs energy of inorganic crystalline solids and temperature-dependent materials chemistry. Nat. Commun. 9, 1–10. (2018).
Acknowledgements
This work was supported by a National Research Foundation of Korea (NRF) grant funded by the Korean government (MSIT) (2019M3E6A1103944, 2020R1A2C2010690, 2021M3H4A1A01002695, 2017M3A7B4049547, 2021M3H4A1A01079300 and 2018M3A7B4065596). The computational resources used in this work were provided by the National Supercomputing Center, including technical support (KSC-2021-CRE-0140).
Author information
Authors and Affiliations
Contributions
I.J., S.J.J., B.-H.Y. performed the experiments, analyzed and interpreted the data, and drafted and modified the article. J.-W.L. contributed to conception of the paper. C.-W.L., W.J., K.T.L., initiated and supervised the work and modified the manuscript. All authors discussed the results and commented on the manuscript.
Corresponding authors
Ethics declarations
Conflict of interest
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Jeong, I., Jeong, S.J., Yun, BH. et al. Physically driven enhancement of the stability of Bi2O3-based ionic conductors via grain boundary engineering. NPG Asia Mater 14, 53 (2022). https://doi.org/10.1038/s41427-022-00402-7
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41427-022-00402-7
This article is cited by
-
Recent progress in oxygen electrodes for protonic ceramic electrochemical cells
Journal of the Korean Ceramic Society (2024)