Abstract
The size effects of mechanical properties influence the microdeformation behaviors and failure mechanisms of hierarchical lamellar bones. Investigations of the continuous deformation behaviors and structure–behavior–property relationships of nanoscale lamellar bones provide essential data for reducing the risk of fracture. Here, five pillars with diameters ranging from 640 to 4971 nm inside a single lamella were fabricated. In situ pillar compressive tests inside a scanning electron microscope directly revealed the diameter-dependent enhanced strength, ductility, and stress fluctuation amplitude. Real-time observations also revealed the segmented deformation and morphological anisotropy of pillars with smaller diameters and the slight elastic recovery of pillars with larger diameters. The critical diameter leading to the brittle-to-ductile transition was confirmed. The “analogous to serrated flow” stress fluctuation behaviors at the nanoscale exhibited a significant size effect, with coincident fluctuation cycles independent of diameter, and each cycle of the fluctuation manifested as a slow stress increase and a rapid stress release. The discontinuous fracture of collagen fibrils, embedded enhancement of hydroxyapatite crystals, and layered dislocation movement on the basis of strain gradient plasticity theory were expected to induce cyclical stress fluctuations with different amplitudes.
Similar content being viewed by others
Introduction
As important carriers of the mechanical support and mineral metabolism of vertebrates, including humans, cortical bones utilize hierarchical and ordered mineralized collagen fibrils and embedded hydroxyapatite (HA) crystals to create resistance to fracture at both macroscopic and microscopic scales1,2. The rigid–flexible coupling performance of collagen and HA owing to the complex anisotropic and heterogeneous microstructure3,4 causes significant differences in mechanical responses correlated with various loading types5,6, sampling orientations7, loading rates8, ages9,10, diseases11, in vivo environments12, degrees of dehydration13 and geometrical effects14. Although great progress has been made in understanding the mechanical properties and failure mechanisms of cortical bones at the microscale, an accurate understanding of the micromechanical behaviors of lamellar bones at the nanoscale could provide support for the development of bone biomechanics and biomimetic artificial bone materials15,16. For instance, at the microscale, the depth-sensing nanoindentation measurement technique allows not only obtaining the hardness and Young’s modulus distributions of microregions but also determining the nanomechanical heterogeneity17,18,19,20,21. In particular, combined with atomic force microscopy (AFM)-based nanoindentation with an indenter tip radius less than 15 nm, high-resolution mechanical tests based on nanoscale indentation depth and micronewton scale indentation load were performed and facilitated to obtain nanomechanical property maps and energy dissipation mechanisms22. Although the biomechanical testing of lamellar bones with hierarchical microstructures has revealed their superior performance in overcoming the strength–ductility trade-off, the establishment of the structure–behavior–property relationships of lamellar bones at the micro/nanoscale remains a challenge23 due to nanoscale heterogeneity24, energy dissipation22, data scatters of strength9,12 and toughness25,26. Considering the diversity of the orientation and distribution of collagen fibrils and HA crystals27, a change in the volume fraction of collagen fibrils and HA crystals inside a bone lamella would intensify the variability and complexity of the deformation behaviors at the nanoscale. In particular, the lack of in situ observation of microstructural evolution has restricted real-time measurements of the anisotropic, heterogeneous, and post-yield deformation behaviors of lamellar bones.
In situ mechanical testing is frequently used for the real-time investigation of the structural evolution of lamellar bones combined with the stress−strain relationship28 and can quantitatively discover the morphological anisotropy29, crack nucleation and propagation30, discontinuous splitting31, interfacial shearing behaviors13 and cooperative deformation of mineralized composition and collagen fibrils32. For instance, Gupta et al. carried out tensile testing of hydrated bovine parallel-fibered bone combined with in situ high-brilliance synchrotron radiation to establish the relationship between fibril strain and tissue strain33 and investigated the inhomogeneous deformation of collagen fibrils at the nanoscale34. Among the diversified in situ biomechanical testing technologies, in situ scanning electron microscopy (SEM) micropillar compression exhibits unique advantages, including controllable and accurate preparation of pillars and continuous loading with high resolution and observation of the entire pillar surface with a wide field of view. It is available for the investigation of significant variations in the mechanical properties of pillars with various diameters or length–diameter ratios. In particular, when carrying out AFM-based in situ nanoindentation, the structural interference between the indenter tip and surface can cause a blind zone underneath the indenter. Schwiedrzik et al. carried out in situ micropillar monotonic and cyclic compressive tests on micrometer-sized pillars (with a diameter of 5.21 µm) to investigate the evolution of the mechanical response of a single osteon lamella, and the enhanced strength, ductility, and transition from a quasi-brittle response at the macroscale to a ductile response at the microscale were experimentally revealed34. The in situ SEM compression and transmission electron microscopic characterization of a 4.73 µm micropillar from a hydrated bone extracellular matrix also revealed anisotropic nanoscale deformation behavior owing to localized shearing and axial splitting13. Tertuliano et al. fabricated a series of pillars with diameters ranging from 250 to 3000 nm, and a brittle-to-ductile transition and enhanced compressive strength with decreasing diameter were also experimentally revealed 35.
Nevertheless, considering the significant effect of collagen fibril orientation on the fracture energy (by two orders of magnitude)36 and the inherent orientation differences between the collagen fibril and pillar axes, the continuous microstructural evolution under stress needs to be further investigated through in situ experiments. The critical pillar diameter corresponding to the brittle-to-ductile transition and elastic–inelastic recovery after post-yield failure is still unclear. In addition, similar to the serrated flow phenomenon of bulk metallic glass, which exhibits regular and periodic load fluctuations caused by the consumed elastic energy and shear band movement37,38,39, previous studies have revealed the stress-induced discontinuous fracture, shearing, and bending of collagen fibrils13,32,40 and dislocation movement inside HA crystals41, which might also result in severe stress fluctuations during the post-yield stage. Considering the volume fraction change in collagen fibrils and HA crystals in pillars with various diameters, the anisotropic deformation behaviors and stress fluctuations similar to the serrated flow phenomenon need to be further revealed for larger-sized pillars. Through in situ SEM compression of pillars with diameters ranging from 640 to 4971 nm, this paper focuses on the mechanical size effects of nanoscale lamellar bones, including the enhanced strength, ductility, and stress fluctuation amplitude of micro/nanoscale lamellar bones. Real-time observation of the compressive deformation behaviors directly reveals the morphological anisotropy and critical diameter to induce the brittle-to-ductile transition. Combined with a proposed hypothesis on the discontinuous fracture of collagen fibrils and layered dislocation movement on the basis of strain gradient plasticity theory, the “analogous to serrated flow” stress fluctuation of nanoscale pillars is reasonably explained.
Materials and methods
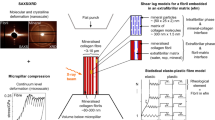
Fresh bovine femoral bones were selected to prepare the pillars. The cortical bones were sliced from the middle femur, wrapped with medical cotton, and soaked in −20 °C normal saline42. Thin plate-like lamellar bones with a thickness of 2 mm along the radial direction were cut, and transverse sections perpendicular to the long axis26 were mechanically polished to facilitate the selection of osteons. The focused ion beam (FIB) technique (Helios Nanolab 600, Dual Beam FIB, FEI system, Hillsboro, OR, USA) was used to fabricate five pillars with diameters ranging from 640 to 4971 nm inside a single lamella. The sampling locations of five pillars around the Haversian canal inside a single lamella were confirmed by differentiating the interfaces between different concentric lamellae in a distinctly visible SEM micrograph of a single osteon43, as illustrated in Fig. 1a. To weaken the effect of the collagen fibril orientation on the size effect of pillars, through the FIB technique, five pillars inside a single lamella with diameters of 640, 878, 1091, 3066, and 4971 nm and approximately uniform collagen fibril orientations were fabricated. To reduce the measurement error of the mechanical parameters, three pillars for each diameter were fabricated inside the same lamella. As seen from Fig. 1b, the minimum spacing between the parallel axes of pillars was larger than 20 μm, which prevented the structural interference of the flat indenter. The safety distances in a range from 34 to 56 μm between the center of the Haversian canal and the pillars’ axes prevented the oblique movement of the pillars toward the flexible Haversian hollow structure, as obvious cracks with radial features and width at a submicron scale were observed around the Haversian canal. To prevent the potential buckling of pillars and considering the visualization requirement of microstructural evolution during the real-time in situ monitoring process, a uniform length–diameter (l–d) ratio of 2:1 was designed for pillars with diameters in a range from 640 to 4971 nm according to ASTM E9-89a44. It should be noted that on the basis of an l–d ratio of 2:1, previous literature has revealed that a 5 μm diameter pillar exhibited axial bulk splitting13 and induced a significantly irregular fluctuation in compressive stress45. Attributed to the potential risks of brittle fracture and the transient splitting of a micropillar with a relatively larger diameter, an l–d ratio of 1:1 was designed for the 4971 nm diameter pillar, which also met the requirements of the l–d ratio range for the compressive testing of short cylindrical specimens in ASTM E9-89a44. Thus, the potential discontinuity of stress-strain curves and corresponding measurement errors of mechanical parameters induced by the transient splitting effect could be effectively avoided.
a Sampling locations of five pillars around the Haversian canals; b specific parameters of pillars fabricated through the focused ion beam technique with diameters in a range from 640 to 4971 nm; and c illustration of the relative position between a flat diamond indenter and the 4971 nm diameter pillar.
Furthermore, as shown in Fig. 1c, the in situ compressive tests were carried out by using a Hysitron PI 85L PicoIndenter inside a SEM (Helios Nanolab 600, FEI system, Hillsboro, OR, USA). The pillars were located inside the corresponding circular grooves with a uniform diameter of 25 μm and heights equal to the pillar heights. Although an inherent crack with a width at the submicron scale was observed on the fabricated surface, the smooth cylindrical surfaces of all five pillars indicated the structural integrity inside the pillars. During the uniaxial compressive process, a flat diamond indenter with a bottom diameter of 10 μm was immediately above the pillars. The testing processes can be divided into three steps, including a loading step with a constant displacement rate of 5 nm/s, a constant displacement step lasting for 15 s when the displacement reached the compressive-failure displacement, and an unloading step after keeping the displacement constant with the same displacement rate compared with the loading step. The engineering stresses were calculated by dividing the compressive loads by the cross-sectional areas of the top surfaces of the pillars. Furthermore, the engineering strains were directly calculated as the ratios of the axial compressive displacements to the initial heights of the pillars46. High-resolution transmission electron microscopy (HRTEM) characterization was carried out to reveal the stress fluctuation mechanism and discover the distributions and movements of collagen fibrils and HA crystals in a compressive-failed pillar. TEM micrographs (using a JEOL JJEM-2100F, field emission electron microscope) were captured to distinguish the attributes of the collagen fibrils and HA crystals. The FIB technique (using FEI Helios Nanolab 600) was used to fabricate a thinned rectangular specimen. The symmetry plane of the rectangular region coincided with the pillar axis to observe the interior rather than surface microstructures. In addition, two theories were proposed to reasonably explain the stress fluctuation mechanisms in the stress−strain curves. The discontinuous fracture of collagen fibrils and the oblique effect of HA crystals were used to describe the macroscopic stress fluctuation behavior. A layered dislocation movement theory on the basis of strain gradient plasticity theory was also proposed to elaborate the microscopic stress fluctuation behaviors.
Results
The mechanical properties of pillars with different diameters were directly revealed through compressive stress−strain (σ–ε) relationships, as shown in Fig. 2. The experimental evidence indicated the enhanced strength, ductility, and stress fluctuation amplitude of pillars with decreasing diameter. When subjected to uniaxial compressive stresses, all σ–ε curves exhibited initial elastic deformation behaviors owing to the linearly increasing stress in terms of strain and distinct yield stages47. In particular, significant stress fluctuations accompanied by slow stress increases and rapid stress release phenomena were visible in the post-yield deformation stages. During the constant displacement steps after the last stress fluctuation cycles, the engineering strains reached the compressive failure strains, and the slowly decreasing stresses on the basis of constant strains were mainly attributed to the stress relaxations of the pillars, which induced the nonmonotonicity of the engineering σ–ε curves. With regard to the unloading processes, all the pillars exhibited consistent elastic recovery behaviors with the same slopes compared with the corresponding linear elastic loading processes, as the top surface of the pillars kept contact with the indenter during the entire unloading process. The total elastic recovery strains also indicated a significant size effect. As seen from Fig. 2a, four notable aspects of the mechanical behaviors dependent on the pillar diameter were determined from the σ–ε curves. First, an extremely significant strength enhancement trend was verified (Fig. 2b). The compressive strength σb gradually increased from 0.952 ± 0.123 GPa for the 4971 nm diameter micropillar to 1.771 ± 0.217 GPa for the 878 nm diameter pillar. A previous study revealed a similar compressive strength of 0.75 ± 0.07 GPa along the axial direction of a 5 μm micropillar extracted from a dehydrated cortical bone34. In particular, σb of the 640 nm diameter pillar reached 2.004 ± 0.233 GPa, which is approximately 15 times greater than the macroscopic values according to the report of Zhang et al. on a strength statistical analysis of bovine femoral cortical bone tissues41. The extremely enhanced strength at the micro/nanoscale indicated a significant difference from previous simulation studies on the strength differences between the macroscopic and microscopic values described by Lucchini et al.2. Second, to equivalently represent the compressive ductility and failure strain, the variation tendency of the residual compressive ratio δ, which denoted the critical failure strain excluding elastic recovery and was defined as the difference between the maximum compressive strain δmax and the elastic recovery strain δe, could be described by dividing the difference between the maximum compressive displacement Δlmax and elastic recovery displacement Δls by the initial pillar’s height lo, as described in Eq. 1. As shown in Fig. 2c, δ also indicated significantly enhanced ductility. Even the 4791 nm diameter micropillar exhibited a compressive ratio δ of 0.062, which is larger than the macroscopic value (approximately 0.024)32. As the diameter gradually decreased from 3066 to 640 nm, δ rapidly increased from 0.093 to 0.299. This phenomenon directly illustrated the transition from a quasi-brittle mechanical response at the microscale to a ductile response at the nanoscale. The post-yield plastic behavior with high ductility compared with macroscopic cortical bones was also consistent with the statement of Schwiedrzik et al.34. Third, similar to the variation tendency of the compressive strength, the total yield strain range Δεs, which was calculated by subtracting the strain corresponding to the initial upper yield point in yield stage εσus from the strain corresponding to the last lower yield point in yield stage εσls, as described in Eq. 2, increased with decreasing pillar diameter. In particular, the increasing trend was approximately linear for pillars with diameters in the range from 4791 (Δεs of 0.69 × 10−3) to 878 nm (Δεs of 3.89 × 10−3). However, Δεs of the 640 nm diameter pillar sharply increased to 10.71 × 10−3, which indicated that at the nanoscale, a small decrease in pillar diameter would lead to a sharp increase in the total yield strain range (Fig. 2d). Although a previous study revealed axial strain-softening behavior with obvious yield stages through monotonic micropillar compressive tests13, diameter-dependent continuous yield stages were not visible in the axial stress−strain curves. Considering the simultaneously increased volume fraction of single collagen fibrils and HA crystals inside a pillar at the nanoscale with decreasing diameter, the size-dependent enhancement of δ and Δεs was definitely related to the distribution and movement of collagen fibrils and HA crystals. Finally, different from typical smooth σ–ε curves with regular strain-hardening stages, the compressive σ–ε curve exhibited a stress fluctuation to varying degrees dependent on the pillar diameter. This phenomenon is different from previous studies, as no obvious stress fluctuation was observed on 250 and 500 nm diameter lamella pillars35. During each cycle of stress fluctuation, as shown in Fig. 2e, a slow stress increase with the same increasing slope as the linearly elastic stage indicated a strong resistance to deformation owing to the distribution and movement of collagen fibrils and HA crystals. Then, a sharp stress-release stage with a gradually increasing derivative was visible. The stress fluctuation amplitude Δσ was closely related to the diameter. Specifically, Δσ for the 4791 nm diameter micropillar was only 3 MPa, but at a submicron scale, Δσ significantly increased to 342 and 635 MPa for the pillars with diameters of 878 and 640 nm, respectively. According to previous studies, the mechanical responses of cortical bones at a millimeter-scale (as stated by Zhang et al.42) and a microscale34 both exhibited smooth σ–ε curves with strain-hardening stages and without visible stress fluctuation behaviors. Although a very small deformation fluctuation with an amplitude of hundreds of microns was observed from the macroscopic creep strain as a function of time48, the enhanced stress fluctuation amplitude at the nanoscale was revealed for the first time. In addition, regarding the pillars with diameters smaller than 1091 nm, the numbers of stress fluctuation cycles were all coincidentally counted as nine independent of the diameter. With regard to the 3066 nm diameter micropillar, the number of cycles was larger than 10. This phenomenon demonstrated that the total number of stress fluctuation cycles was closely related to the volume fraction of collagen fibrils and HA crystals inside a pillar. Nevertheless, at the nanoscale, the minimum number of stress fluctuation cycles until compressive failure inside a single lamella was consistent.
a engineering stress-strain (σ–ε) curves of pillars with diameters ranging from 640 to 4971 nm subjected to uniaxial compressive stresses; corresponding variations in mechanical parameters to directly reveal the size effects: b compressive strength σb; c compressive ratio δ; d total yield strain range ∆εs; and e stress fluctuation amplitude ∆σ.
To further describe the size effects on the mechanical properties of lamellar bones, the quasistatic microdeformation behaviors and continuous morphological evolution of five pillars were investigated in real-time via SEM (using an FEI Helios Nanolab 600i Microscope). During the post-yield plastic deformation stages, the corresponding morphologies on the basis of four strain values are shown in Fig. 3. The strain values involved 25% maximum plastic strain 25% δb (δb denotes the maximum plastic strain without considering the elastic recovery), 50% δb, 75% δb, and 100% δb before critical compressive collapse failure. The morphologies after complete unloading were also captured to investigate the elastic or inelastic recovery behaviors. The profiles of the pillars were highlighted in the compressive morphologies to facilitate the in situ observation. Corresponding to the strain stages with 25% δb, 50% δb, 75% δb and δb, the 640 nm diameter pillar successively exhibited plastic deformation responses, including local unilateral shrinking at 25% δb, downward movement of shrinkage at 50% δb, the disappearance of shrinkage and longitudinal expansion owing to Poisson’s effect at 75% δb, and reappearance of shrinkage combined with minimal plastic collapse at δb. After completely unloading the flat diamond indenter, clear elastic recovery was visible. As seen from the profiles, significant morphological anisotropy was confirmed. The gradually aggravated shrinkage behavior when subjected to compressive stress and local plastic collapse was also visible for the 878 nm diameter pillar. A tendency toward a mushroom structure with increased curvature adjacent to the flat indenter indicated a local plastic flow near the contact surface. The mushroom-shaped deformation located at the top surface of the pillars did not extend downward and completely disappeared after elastic recovery. Similarly, the unilateral shrinkage movement also indicated significant morphological anisotropy. With a pillar diameter of 1091 nm, except for similar phenomena, including unilateral shrinkage deformation in the middle part of the micropillar, elastic recovery, and morphological anisotropy, mushroom-shaped deformation also maintained its previous appearance after unloading the indenter. The segmented deformation behaviors for pillars with diameters smaller than 1091 nm were confirmed due to the appearance, disappearance, and reappearance of shrinkage in the upper part of the micropillars. Furthermore, the 3066 nm diameter micropillar exhibited completely different deformation characteristics, as the micropillar was evenly and steadily compressed without obvious plastic flow or shrinkage, which indicated an isotropic morphological change. However, an obvious elastic recovery was also visible. The obvious layered and segmented deformation behaviors observed from the continuous uniaxial compressive processes agreed with the segmented deformation characteristics stated by Kochetkova et al.45 and Wang et al.46 although no obvious stress fluctuation behaviors were confirmed in the post-yield plastic deformation stages in their studies. When the diameter reached 4971 nm, a quasi-brittle response including visible cracks adjacent to the contact surface accompanied by slight recovery after the unloading and recovery of local depression was confirmed. In particular, at δb, an obvious depression on the top surface of the micropillar immediately above the tip of a crack indicated a partially plastic mechanical response. Therefore, the in situ observation of morphologies illustrates a mechanical response transition from ductility to quasi-brittleness, which also agrees with a statement by Schwiedrzik et al.34 on a comparison between macroscopic and microscale deformation behaviors. Through in situ SEM compressive tests, the segmented and anisotropic deformation behaviors with the obvious elastic recovery of pillars at the nanoscale and the isotropic deformation behaviors with slight elastic recovery at the microscale were revealed. Although Koester et al.25 revealed the anisotropic behavior of crack propagation along both transverse (breaking) and longitudinal (splitting) directions, and the anisotropy of post-yield plastic deformation behaviors and morphological differences at the nanoscale were directly observed. As the diameter gradually decreased, the volume fraction of single collagen fibrils inside a pillar increased, and the flexible effect of collagen fibrils on the enhanced ductility was gradually intensified at the nanoscale.
Through in situ SEM compressive tests, the segmented and anisotropic deformation behaviors of pillars with diameters ranging from 640 to 1091 nm and the isotropic deformation behaviors of pillars with diameters ranging from 3066 to 4971 nm were revealed. Elastic recovery, local plastic flow, shrinkage, and even collapse were visible in pillars with relatively smaller diameters. Slight elastic recovery for pillars with relatively larger diameters was also observed.
Evidence of the transition from ductility to quasi-brittleness49 related to diameter was directly revealed by analyzing the fracture morphologies of compressive-failure pillars. As seen from the global fracture morphologies shown in Fig. 4a, the heads of mushroom-shaped structures with larger and smaller curvatures were observed from the morphologies of the 640 and 878 nm diameter pillars, which indicated that an obvious plastic flow induced local collapse adjacent to the contact surfaces. This phenomenon also illustrated the segmented deformation behaviors of the lamellar bone pillars at the nanoscale, as no obvious plastic deformation was observed away from the contact surfaces. The curvatures of the bottom edges of the mushroom-shaped structures gradually decreased as the diameters increased from 640 to 1091 nm, accompanied by gradually weakened ductility. The 1091 nm diameter pillar exhibited a quasi-ductile morphology with partially brittle characteristics, as microcracking and splitting structures appeared at the edges of the mushroom-shaped structures. A quasi-brittle fracture morphology without plastic mushrooms mixed with a strip-shaped depression adjacent to a critical splitting structure and an already formed splitting structure was also confirmed. In addition, different from the monotonic compressive morphologies of a 4.73 μm diameter micropillar (l–d ratio: 2.35) with localized shear deformation and axial splitting13, the diameter-dependent brittleness was fully embodied in the 4971 nm diameter micropillar. Obvious longitudinal and transverse cracks running through the micropillar were also visible, and a separate boundary at the bottom also illustrated a brittle splitting trend. As seen from the top of the pillars (Fig. 4b), as the quantity and area fractions of edge cracks gradually increased as the diameter increased, especially considering the scattered fragments of the 4971 nm diameter pillar, the mechanical response transition from a ductile feature at the nanoscale to a mixed ductile-brittle feature at the scale of one micron and then to a brittle feature at the scale of several microns was further verified. Although the effect of dehydration has been verified to cause a transition from quasi-brittle (wet bone) to brittle material (dry bone)35, the size effect-induced brittle-to-ductile transition at the nanoscale was directly confirmed through the failure morphologies.
Discussion
HRTEM characterization was carried out to distinguish the attributes of collagen fibrils and HA crystals and obtain the distributions of collagen fibrils and HA crystals in a compressive-failed pillar. As seen from Fig. 5, a thinned TEM specimen with a thickness of 100 nm parallel to the long bone axis24 inside the 1091 nm diameter pillar was fabricated. As seen from the HRTEM micrograph, obvious local shrinkage with a curvature radius over 1 μm revealed the abovementioned anisotropic deformation behavior50. Adjacent to the shrinkage microregion, the orientations of collagen fibrils were approximately parallel to the edge profile of the shrinkage, which indicated that the stress concentration effects induced by the local shrinkage have caused a directional bending effect on the collagen fibrils51. A local bright-field image and selected area electron diffraction (SAED) pattern of isolated bright zones in the HRTEM micrograph revealed the microstructure of the HA crystals due to the obvious crystalline spots, rather than halo rings without spot distribution. The interspersed strip-shaped microstructures also indicated the features of collagen fibrils13. Furthermore, the bending and fracture of the collagen fibrils and the oblique effect of the HA crystals were also directly observed from the magnified micrographs in two randomly selected microregions (A and B). A previous study indicated that homogeneous bone deformation consisted of deformed fibrils and shearing movement in the interfibrillar matrix between fibrils33,52. The initial orientation difference between the vast majority of collagen fibrils and the axis of the pillars was calculated to be approximately 30°. A number of collagen fibrils with lengths over 100 nm were clearly visible. The HRTEM micrographs exhibited periodically arranged collagen fibrils, which was consistent with previous studies regarding the structure of lamellar bones40. In particular, quite a few bent and fractured short fibrils with multiple orientations were also observed. Regarding the HA crystals, with a similar initial orientation compared with the collagen fibrils, local oblique behaviors with approximately consistent oblique angles indicated that the HA crystals maintained a stable embedded state. In particular, adjacent to the HA crystals, the collagen fibrils exhibited a tendency to accumulate and converge. This result indicated that the brittle HA crystals restricted the directional movement of flexible fibrils. The bent and fractured short fibrils with multiple orientations improved the resistance to deformation of the pillars.
Bent and fractured collagen fibrils were directly observed in two randomly selected microregions (A and B). SAED patterns with obvious diffraction spots indicated the features of HA crystals, bent and fractured short fibrils with multiple orientations, and the oblique phenomenon of HA crystals was visible.
Since the in situ SEM compressive tests revealed the diameter-dependent stress fluctuation phenomenon of the pillars and the HRTEM micrographs of a compressive-failure pillar also revealed bent and fractured short fibrils with multiple orientations and the oblique phenomenon of HA crystals, the distribution, and orientation of the collagen fibrils and HA crystals might affect the stress fluctuation behaviors. A strength-enhancement theory was proposed to explain the macroscopic slow stress increase and rapid stress decrease behaviors during a stress fluctuation cycle. The distribution of collagen fibrils and HA crystals is illustrated in Fig. 6a. The orientations of collagen fibrils inside different pillars were considered approximately uniform and independent of the pillar diameter, as the five pillars were fabricated around a Haversian canal inside a single lamella. HA crystals with a uniform distribution exhibited an array layout and were embedded between the gaps of collagen fibrils. Combined with the brittleness of the HA crystals50 and the toughness effect of the collagen fibrils27, the ductility of the collagen fibrils may play a dominant role in the compressive deformation behavior of pillars at the nanoscale. Considering the difference β between the axis of the pillars and the initial orientation of the collagen fibrils, when subjected to a uniaxial external compressive load, the collagen fibrils will suffer from compressive-bending combined stress.
a Diagram of the distribution of HA crystals and collagen fibrils—the orientations of collagen fibrils were considered approximately uniform inside a single lamella and independent of pillar diameter—a discontinuous fracture theory of collagen fibrils was also illustrated involving a slow stress increase process owing to the bending of collagen fibrils and a rapid stress release owing to the instantaneous fracture of collagen fibrils with relatively large length–diameter ratios; b calculation of oblique angle θha and movement distance fha of a single HA crystal by analyzing the superposition behavior induced by the bending and compressive stress components.
Moreover, a discontinuous fracture theory for collagen fibrils under compressive-bending combined stress conditions was proposed. Considering that bone strength and stiffness are closely related to the arrangement of collagen fibrils at the nanoscale53, collagen fibrils with different axial lengths and length–diameter ratios inside a single pillar will exhibit various stress responses on the basis of identical combined stress conditions. During a cyclic period of stress fluctuation, collagen fibrils exhibited a considerable ability to take stress due to their ductility33. Therefore, with an increase in compressive-bending combined stress, the pillar will produce a gradually enhanced resistance to deformation54. It would also exhibit a relatively slower stress increase rate, accompanied by shrinkage in axial length Δcyc-i. The bending component Fb (described as:\(\frac{{F\sin \beta }}{{n_c}}\)) of collagen fibrils will induce the corresponding functions of deflection curve fb(x), maximum angle θha-b and deflection fb, as shown in Eq. 3, where Ec, nc, dc, and lo denote Young’s modulus, the quantity of collagen fibrils, initial diameter, and length of pillars, respectively. Therefore, the length of a bent collagen fibril lb can be calculated via the definite integration of the derived form of fb(x), as shown in Eq. 4. Specifically, the angle θha-x denoted the first-order derivative of fb(x), and lb was considered the integration of the reciprocal value of cos θha-x55. The simultaneous compressive component Fc (described as:\(\frac{{F\cos \beta }}{{n_c}}\)) would also induce a displacement fc parallel to the bent collagen fibril derived from lb. Therefore, the movement distance fha and oblique angle θha of a single HA crystal were calculated as\(\sqrt {f_b^2 + f_c^2}\)and the sum of θha-b and θha-c, respectively, where θha-c denoted the additional angle increase induced by fc, as shown in Eq. 5.
According to Eq. 3, a collagen fibril with a large length–diameter ratio will produce a relatively large bending angle θha-b and deflection fb, and the fracture will first occur under low stress. Owing to the potentially instantaneous fracture of collagen fibrils, the stress will rapidly decrease accompanied by axial length shrinkage Δcyc-d. During the subsequent cyclic period, collagen fibrils with relatively large length–diameter ratios would transform into relatively short fibrils, which regained the ability to resist continuous deformation and combined stress. As seen from the stress fluctuation stages of the σ–ε curves, Δcyc-d was significantly larger than Δcyc-i. It also indicated that the fracture of collagen fibrils with relatively large length–diameter ratios caused a rapid reduction in the resistance to deformation56. To quantitatively evaluate the oblique effect of HA crystals on strength enhancement57, the oblique angle θha, and movement distance fha when subjected to compressive load F were calculated. Figure 6b illustrates the movement of a single HA crystal by analyzing the superposition behavior induced by the bending and compressive stress components55. Combined with the stress fluctuation behavior of σ–ε curves, as shown in Fig. 2, the quantitative relationship between the known amplitude of stress increment ∆σ during the fluctuation stages and the calculated oblique parameters of HA crystals (described as the angle θha and distance fha of a single HA crystal) were established according to Eqs. 3−5. Therefore, the initial collagen fibril orientation β was a crucial factor in determining the stress response of the pillars, which agreed with the statement of Peterlik et al.36 on the fracture energy and toughening mechanisms depending on the collagen orientation. The proposed macroscopic deformation theory involving discontinuous fracture of collagen fibrils and oblique effect of HA crystals also agreed with the HRTEM characterization of the distributions of collagen fibrils and HA crystals in a compressive-failed pillar in Fig. 5.
Moreover, at the micro/nanoscale, on the basis of strain gradient plasticity theory58, under quasi-static compressive stress, the heterogeneous deformation of pillars gradually propagates from the top to the bottom surfaces along the axis59. With regard to the pillars with relatively smaller diameters, due to the boundary effect and interfacial shearing between the collagen fibrils and extrafibrillar matrix, as illustrated in Fig. 7a, the layered heterogeneous deformation behaviors were more significant. Previous studies have revealed that stress induces a large number of dislocation defects inside HA crystals, accompanied by the rotational and translational motion of HA crystals41. On the basis of a compressive stress σ, the first and second deformation layers would produce corresponding compressive deformations (∆lc-1, ∆lc-2) and rotational angles (θc-1, θc-2). Evidently, the stress fluctuation behaviors of the stress−strain curves of the pillars were closely related to the dislocation movement inside the HA crystals and the dislocation pile-up and pinning effect at the interfaces between the HA crystals and fibrillar matrix. Regarding the pillars with heterogeneous plastic deformations, the regions nearby or far away from the indenter exhibited diverse dislocation movement behaviors on the basis of different degrees of plastic deformations. As shown in Fig. 7b, a layered dislocation movement theory on the basis of strain gradient plasticity theory was used to elaborate the microscopic stress fluctuation behaviors. The essence lies in the dislocation movements inside the HA crystals and at the interfaces. Specifically, during the post-yield deformation stage, with regard to the upper layer, as the compressive stress gradually increased, a large number of dislocations nucleated inside the HA crystals, and the rapid growth of dislocations was accompanied by an increase in the dislocation density. When the dislocations moved to the interfaces between the HA crystals and fibrillar matrix, the interface hindered the further movement of dislocations. The dislocation pile-up resulted in the increment of stress, and the rate of stress increase was determined by the rate of dislocation growth and pile-up60. Furthermore, when a large number of dislocations penetrated the interface and the dislocations overflowed from the free surface of the pillar, the resistance to plastic deformation of the pillars decreased sharply, which caused a rapid decrease in stress.
a Layered deformation behaviors of pillars from the top to the bottom surface on the basis of strain gradient plasticity theory; b slow stress increment induced by the dislocation movement inside the HA crystal and dislocation pile-up at the fibrillar matrix interface and rapid stress decrease induced by the dislocation penetration at the interface or dislocation loops inside the HA crystal.
With the further increase in compressive stress, the plastic deformation propagated to the next deformation layer. The layered gradient deformation behaviors can be confirmed by the segmented deformation characteristics in Fig. 3 and the mushroom-shaped residual morphologies in Fig. 4. Similarly, the dislocation movement inside the HA crystal and the dislocation accumulation at the interface also induced a slow stress increment in the second deformation layer. The penetration of dislocations through the interface and the overflow of dislocations at the free surface also led to a rapid decrease in stress; thus, a new stress fluctuation period was formed. When the plastic deformation further propagated to the bottom layer of the pillar, the resistance to deformation of the pillar was exhausted. The above processes ultimately induced stress fluctuations in different deformation layers. Moreover, as shown in Fig. 5, the orientations of mineralized collagen fibrils in the randomly selected pillar morphologies were almost identical. Therefore, the constitutive relations of the deformed layers in the pillar were considered to be approximately consistent. Each deformation layer exhibited the same stiffness under compressive loading, and during the fluctuation process of the stress−strain curve, the stress-increasing stages showed approximately consistent stiffness. In addition, as shown in Fig. 2, the pillars with relatively smaller diameters exhibited larger amplitudes of stress fluctuation. With regard to the pillars with relatively larger diameters, the volume fraction of a single HA crystal was relatively smaller. Considering the differences in the initial orientations of HA crystals, the orientations and synchronization of the nucleation and movement of the internal dislocations were different. Correspondingly, the resistance to dislocation motion and pinning effect of each interface exhibited differences in synchronization, which resulted in a decrease in the stress fluctuation amplitude. Therefore, the stress fluctuation amplitudes were dependent on the statistical law of the effects of multiple HA crystals and interfaces on dislocation motion. Furthermore, the distances between the dislocations and free surfaces in the pillars with relatively larger diameters were longer, which enhanced the possibilities of interaction between dislocations and the accumulation of dislocation loops. Accordingly, the probabilities of dislocations penetrating the interfaces or overflowing the free surface were reduced, which would also lead to a decrease in the stress fluctuation amplitude.
Conclusion
In situ SEM compression directly revealed the size-dependent mechanical properties, segmented and anisotropic deformation behaviors, and brittle-to-ductile transition of lamellar bone pillars from the micro to nanoscale. The principal conclusions are summarized below:
-
(1)
The diameter-dependent mechanical properties of pillars, including strength, residual compressive ratio, total yield strain range, and stress fluctuation amplitude, were investigated in detail. A 640 nm diameter pillar exhibited a superior compressive strength of 2.004 ± 0.233 GPa, the residual compressive ratio of 0.299, total yield strain range of 10.71 × 10−3, and stress fluctuation amplitude of 635 MPa, which manifested as approximately 2.1, 4.8, 15.5, and 211.7 times greater than the corresponding mechanical parameters of a 4971 nm diameter pillar, respectively.
-
(2)
Continuous observation of microstructures during in situ SEM compression revealed segmented and anisotropic deformation behaviors, including elastic recovery and local plastic flow, shrinkage and even collapse failure at the nanoscale, and isotropic behaviors with slight elastic recovery at the microscale. A size effect-induced brittle-to-ductile transition was also visible, seen from the gradually increased ductility and fracture morphological change from a plastic feature with mushroom-shaped structures to a brittle feature with splitting cracks with decreasing diameter. Critical diameters in the range from 1 to 3 μm corresponded to the brittle-to-ductile transition of deformation behavior.
-
(3)
A discontinuous fracture theory of collagen fibrils was proposed to describe the macroscopic stress fluctuation behavior. The slow bending and instantaneous fracture of collagen fibrils with relatively larger length–diameter ratios facilitated the stress increment and decrement, respectively. The microscopic stress fluctuation behaviors were elaborated through a layered dislocation movement theory on the basis of strain gradient plasticity theory. The dislocation movement inside the HA crystal and dislocation pile-up at the fibrillar matrix interface induced a slow stress increase, and the penetration of dislocations through the interface and the overflow of dislocations at the free surface induced a rapid stress decrease.
Data availability
The data that support the findings of this study are available from the corresponding authors on reasonable request.
References
Taylor, D., Hazenberg, J. & Lee, T. C. Living with cracks: damage and repair in human bone. Nat. Mater. 6, 263–268 (2007).
Lucchini, R. et al. Role of damage mechanics in nanoindentation of lamellar bone at multiple sizes: experiments and numerical modelling. J. Mech. Behav. Biomed. 4, 1852–1863 (2011).
Currey, J. D. Hierarchies in biomineral structures. Science 309, 253–254 (2005).
Fratzl, P. & Weinkamer, R. Nature’s hierarchical materials. Prog. Mater. Sci. 52, 1263–1334 (2007).
Zimmermann, E. A., Launey, M. E., Barth, H. D. & Ritchie, R. O. Mixed-mode fracture of human cortical bone. Biomaterials 30, 5877–5884 (2009).
Silva, F. G. A., Moura, M. F. S. F. & Dourado, N. Mixed-mode I-II fracture characterization of human cortical bone using the single leg bending test. J. Mech. Behav. Biom. 54, 72–81 (2016).
Ma, Z. C., Qiang, Z. F., Zhao, H. W., Piao, H. L. & Ren, L. Q. Mechanical properties of cortical bones related to temperature and orientation of Haversian canals. Mater. Res. Express 7, 015408 (2020).
Michael, J. K., Devon, L. A., Amanda, M. A. & Kemper, A. R. Effects of sex, age, and two loading rates on the tensile material properties of human rib cortical bone. J. Mech. Behav. Biomed. 102, 10341 (2020).
Zioupos, P. & Currey, J. D. Changes in the stiffness, strength, and toughness of human cortical bone with age. Bone 22, 57–66 (1998).
Rho, J. Y., Zioupos, P., Currey, J. D. & Pharr, G. M. Microstructural elasticity and regional heterogeneity in human femoral bone of various ages examined by nano-indentation. J. Biomech. 35, 189–198 (2002).
Giannoudis, P., Tzioupis, C., Almalki, T. & Buckley, R. Fracture healing in osteoporotic fractures: is it really different? A basic science perspective. Injury 38, S90–S99 (2007).
Wachter, N. J. et al. Correlation of bone mineral density with strength and microstructural parameters of cortical bone in vitro. Bone 31, 90–95 (2002).
Schwiedrzik, J. et al. Nanoscale deformation mechanisms and yield properties of hydrated bone extracellular matrix. Acta Biomater. 60, 302–314 (2017).
Gustafsson, A. et al. Linking multiscale deformation to microstructure in cortical bone using in situ loading, digital image correlation, and synchrotron X-ray scattering. Acta Biomater. 69, 323–331 (2018).
Nalla, R. K., Kinney, J. H. & Ritchie, R. O. Mechanistic fracture criteria for the failure of human cortical bone. Nat. Mater. 2, 164–168 (2003).
Wang, Y. Y., Naleway, S. E. & Wang, B. Biological and bioinspired materials: structure leading to functional and mechanical performance. Bioact. Mater. 5, 745–757 (2020).
Grünewald, T. A. et al. Mapping the 3D orientation of nanocrystals and nanostructures in human bone: Indications of novel structural features. Sci. Adv. 6, eaba4171 (2020).
Rho, J. Y., Zioupos, P., Currey, J. D. & Pharr, G. M. Variations in the individual thick lamellar properties within osteons by nanoindentation. Bone 25, 295–300 (1999).
Oliver, W. C. & Pharr, G. M. An improved technique for determining hardness and Young’s modulus using load and displacement sensing indentation experiments. J. Mater. Res. 7, 1564–1583 (1992).
Ma, Z. C. et al. Deformation behavior of micro-indentation defects under uniaxial and biaxial loads. Rev. Sci. Instrum. 86, 095112 (2015).
Zhang, A. R., Zhang, S. & Bian, C. R. Mechanical properties of bovine cortical bone based on the automated ball indentation technique and graphics processing method. J. Mech. Behav. Biomed. Mater. 78, 321–328 (2018).
Tai, K., Dao, M., Suresh, S., Palazoglu, A. & Ortiz, C. Nanoscale heterogeneity promotes energy dissipation in bone. Nat. Mater. 6, 454–462 (2007).
Weiner, S., Traub, W. & Wagner, H. D. Lamellar bone: structure-function relations. J. Struct. Biol. 126, 241–255 (1999).
Yao, H. M., Dao, M., Carnelli, D., Tai, K. S. & Ortiz, C. Size-dependent heterogeneity benefits the mechanical performance of bone. J. Mech. Phys. Solids 59, 64–74 (2011).
Koester, K. J., Ager, J. W. & Rtchie, R. O. The true toughness of human cortical bone measured with realistically short cracks. Nat. Mater. 7, 672–677 (2008).
Nalla, R. K., Kruzic, J. J., Kinney, J. H. & Ritchie, R. O. Effect of aging on the toughness of human cortical bone: evaluation by R-curves. Bone 35, 1240–1246 (2004).
Rho, J. Y., Kuhn-Spearing, L. & Zioupos, P. Mechanical properties and the hierarchical structure of bone. Med. Eng. Phys. 20, 92–102 (1998).
Ma, Z. C. et al. A novel tensile device for in situ scanning electron microscope mechanical testing. Exp. Tech. 39, 3–11 (2015).
Alderete, N., Zaheri, A. & Espinosa, H. D. A novel in situ experiment to investigate wear mechanisms in biomaterials. Exp. Mech. 59, 659–667 (2019).
Hazenberg, J. G., Taylor, D. & Lee, T. C. Mechanisms of short crack growth at constant stress in bone. Biomaterials 27, 2114–2122 (2006).
Nalla, R. K., Kruzic, J. J., Kinney, J. H. & Ritchie, R. O. Aspects of in vitro fatigue in human cortical bone: time and cycle dependent crack growth. Biomaterials 26, 2183–2195 (2005).
Gupta, H. S. et al. Cooperative deformation of mineral and collagen in bone at the nanoscale. Proc. Natl Acad. Sci. USA 103, 17741–17746 (2006).
Gupta, H. S. et al. Nanoscale deformation mechanisms in bone. Nano. Lett. 5, 2108–2011 (2005).
Schwiedrzik, J. et al. In situ micropillar compression reveals superior strength and ductility but an absence of damage in lamellar bone. Nat. Mater. 13, 740–747 (2014).
Tertuliano, O. A. & Greer, J. R. The nanocomposite nature of bone drives its strength and damage resistance. Nat. Mater. 15, 1195–1202 (2016).
Peterlik, H., Roschger, P., Klaushoffer, K. & Fratzl, P. From brittle to ductile fracture of bone. Nat. Mater. 5, 52–55 (2006).
Qiao, J. W., Zhang, Y. P. & Liaw, K. Serrated flow kinetics in a Zr-based bulk metallic glass. Intermetallics 18, 2057–2064 (2010).
Leamy, H. J., Wang, T. T. & Chen, H. S. Plastic flow and fracture of metallic glass. Metall. Trans. 3, 699–708 (1972).
Ma, Z. C. et al. Cyclic stress induced surface nanocrystallization adjacent to indentation edge of Zr-based bulk metallic glass at room temperature. Appl. Surf. Sci. 506, 145044 (2020).
Reznikov, N., Almany-Magal, R., Shahar, R. & Weiner, S. Three-dimensional imaging of collagen fibril organization in rat circumferential lamellar bone using a dual beam electron microscope reveals ordered and disordered sub-lamellar structures. Bone 52, 676–683 (2013).
Huang, W. et al. A natural impact-resistant bicontinuous composite nanoparticle coating. Nat. Mater. 19, 1236–1243 (2020).
Zhang, G. J. et al. The effect of formalin preservation time and temperature on the material properties of bovine gemoral cortical bone tissue. Ann. Biomed. Eng. 47, 937–952 (2019).
Lim, Y. C., Altman, K. J., Farson, D. F. & Flores, K. M. Micropillar fabrication on bovine cortical bone by direct-write femtosecond laser ablation. J. Biomed. Opt. 14, 064021 (2009).
ASTM: E9-89a. Standard Test Methods of Compression Testing of Metallic Materials at Room Temperature (ASTM, 2020).
Kochetkova, T. et al. Combining polarized Raman spectroscopy and micropillar compression to study microscale structure-property relationships in mineralized tissues. Acta Biomater. 119, 390–404 (2021).
Wang, Y. C. et al. In situ TEM study of deformation-induced crystalline-to-amorphous transition in silicon. NPG Asia Mater. 8, e291 (2016).
Burstein, A. H., Currey, J. D., Frankel, V. H. & Reilly, D. T. The ultimate properties of bone tissue: the effects of yielding. J. Biomech. 5, 35–44 (1972).
Deymier-Black, A. C. et al. Evolution of load transfer between hydroxyapatite and collagen during creep deformation of bone. Acta Biomater. 8, 253–261 (2012).
Dorothee-Marx, M. F. et al. Dehydration of individual bovine trabeculae causes transition from ductile to quasi-brittle failure mode. J. Mech. Behav. Biomed. Mater. 87, 296–305 (2018).
Giri, B., Tadano, S., Fujisaki, K. & Sasaki, N. Deformation of mineral crystals in cortical bone depending on structural anisotropy. Bone 44, 1111–1120 (2009).
Ascenzi, M. G. & Lomovtsev, A. Collagen orientation patterns in human secondary osteons, quantified in the radial direction by confocal microscopy. J. Struct. Biol. 53, 14–30 (2006).
Li, Z. W., Du, T. M., Ruan, C. S. & Niu, X. F. Bioinspired mineralized collagen scaffolds for bone tissue engineering. Bioact. Mater. 6, 1491–1511 (2021).
Zimmermann, E. A. & Ritchie, R. O. Bone as a structural material. Adv. Healthc. Mater. 4, 1287–1304 (2015).
Taylor, D. Microcrack growth parameters for compact bone deduced from stiffness variations. J. Biomech. 31, 587–592 (1998).
Ma, Z. C. et al. Evaluation of nanoindentation load-depth curve of MEMS bridge structures by calculating the critical elastic-plastic bending deflections. Appl. Surf. Sci. 434, 1–10 (2018).
Zimmermann, E. A., Launey, M. E. & Ritchie, R. O. The significance of crack-resistance curves to the mixed-mode fracture toughness of human cortical bone. Biomaterials 31, 5297–5305 (2010).
Sasaki, N. & Odajima, S. Elongation mechanism of collagen fibrils and force–strain relations of tendon at each level of structural hierarchy. J. Biomech. 29, 1131–1136 (1996).
Aifantis, K. E., Soer, W. A., De Hosson, J. T. M. & Willis, J. R. Interfaces within strain gradient plasticity: theory and experiments. Acta Mater. 54, 5077–5085 (2006).
Akarapu, S., Zbib, H. M. & Bahr, D. F. Analysis of heterogeneous deformation and dislocation dynamics in single crystal micropillars under compression. Int. J. Plasticity 26, 239–257 (2010).
Jennings, A. T., Burek, M. J. & Greer, J. R. Microstructure versus size: mechanical properties of electroplated single crystalline Cu nanopillars. Phys. Rev. Lett. 104, 135503 (2010).
Acknowledgements
This work is funded by the National Natural Science Foundation of China (51875241), National Key R&D Program of China (2018YFF010124), and Jilin Province Science and Technology Development Plan (20190302078GX, YDZJ202101ZYTS129).
Author information
Authors and Affiliations
Contributions
The initial research concept was proposed by Z.C.M., Y.J., H.W.Z., and C.W.; the fabrication of pillars was conducted by C.W.G.; the in situ micropillar compressive tests were performed by Z.F.Q. and C.W.G.; SEM and TEM analysis was carried out by Z.C.M. and Y.J.; H.W.Z. and L.Q.R. reviewed the paper. Data analysis and stress fluctuation theory were performed by Z.C.M., and the paper was written by Z.C.M. with the assistance of Z.F.Q. All authors read and approved the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ma, Z., Qiang, Z., Guo, C. et al. Aggravated stress fluctuation and mechanical size effects of nanoscale lamellar bone pillars. NPG Asia Mater 13, 61 (2021). https://doi.org/10.1038/s41427-021-00328-6
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41427-021-00328-6