Abstract
The broken inversion symmetry and time-reversal symmetry along with the large spin–orbit interactions in monolayer MoS2 make it an ideal candidate for novel valleytronic applications. However, the realization of efficient spin-valley-controlled devices demands the integration of perpendicular magnetic anisotropy (PMA) electrodes with negligible Schottky barriers. Here, as the first demonstration, we fabricated a monolayer MoS2 field-effect transistor with PMA electrodes: Pt/[Co/Pt]3 and [Co/Pt]2. The I–V curves of PMA/MoS2 contacts show symmetric and linear behavior reflecting Ohmic nature. The flat-band Schottky barrier heights (SBHs) extracted using the temperature and gate voltage dependence of the I–V curves were found to be 10.2 and 9.6 meV. The observed SBHs are record low values reported thus far for any metal/monolayer MoS2 contact. High-quality PMA electrodes with almost zero SBH play a paramount role in the future development of novel spintronic/valleytronic devices; hence, our results can open a new route toward the realization of novel technological devices employing two-dimensional materials.
Similar content being viewed by others
Introduction
While electronic devices exploit the charge degree of freedom (DoF) of an electron for information propagation and storage, spintronic devices add a spin DoF to them. Conventional spintronic devices exploit charge and spin DoFs, i.e., a spin-polarized electric current, because up- and down-spins allow propagation and storage of “1” and “0” information. Furthermore, motion of only the spin DoF, i.e., a pure spin current, has also been gaining significant attention in spintronics because a pure spin current is in principle a dissipationless current, which may overcome Joule heating-based problems in charge-based devices1,2,3. In addition to the charge and spin DoFs, an electron can also have a valley (extrema in the electronic band structure) DoF. In semiconductors with multiple valleys in their electronic band structures, it is possible to confine charge carriers in one of these valleys (K or -K). Depending on the confinement of the charge carriers in these valleys, information can be encoded in 0s and 1s, which could lead to the realization of valleytronic devices4,5,6. Two-dimensional (2D) transition metal dichalcogenides (TMDs), owing to their interesting properties, have great potential in the development of future low-power spin and valley-based electronics. Monolayer TMDs, such as molybdenum disulfide (MoS2), naturally lack inversion symmetry (Fig. 1a); therefore, it is easy to dynamically control the valley DoF in these materials. In addition, the presence of large spin–orbit coupling in monolayer MoS2 results in spin-valley locking and breaking of the spin degeneracy of the valence and conduction bands with a quantization axis perpendicular to the sample7. Most experiments performed on monolayer TMDs show dynamic control of spin-valley polarization under optical excitation8,9. As the valley DoF is locked to the perpendicular spin in monolayer MoS2, spin-valley polarization can also be realized electrically by injecting and detecting spin-polarized carriers using ferromagnets with perpendicular magnetic anisotropy (PMA). Hence, for electrically detecting spin-valley polarization in monolayer TMDs, integration of PMA electrodes is a prerequisite. Despite having much potential, there are two major challenges, among others, that hinder the exploitation and integration of monolayer MoS2 in spintronic/valleytronic devices. These challenges are the realization and integration of PMA electrodes and the prevention of large Schottky barriers at the metal–semiconductor interface. It can be noted that the development of PMA using a [Co/Ni] structure has been reported on bilayer MoS2; however, the purpose of this study was to strengthen the PMA using underlayer MoS210.
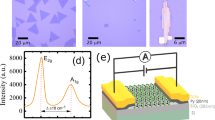
a Hexagonal crystal structure (top view) of monolayer MoS2, composed of transition metal atom Mo (blue) and chalcogen atom S (green). b Schematic of the two-terminal monolayer MoS2 field-effect transistor (FET) device employing perpendicular magnetic anisotropy (PMA) electrodes. Spins (yellow arrows) shown on the PMA electrodes represent the magnetization easy axis in the out-of-plane direction. The letters S and D on the electrodes represent the source and drain, respectively.
In this paper, we focus on the challenges of integrating PMA electrodes into monolayer MoS2 devices and obtaining low-barrier PMA/monolayer MoS2 interfaces, which are missing aspects in MoS2-based valleytronics and can provide new possibilities to integrate 2D materials into spintronic/valleytronic applications. We, for the first time, fabricate a monolayer MoS2-based field-effect transistor with PMA electrodes. Various multilayer structures were tested to realize PMA, and later, the PMA was confirmed by the observation of the anomalous Hall effect and magnetization measurements. To check the suitability of these electrodes in monolayer MoS2-based FET devices, we studied the I–V characteristics of FETs (Fig. 1b) as a function of temperature and back gate voltage (Vg) and estimated the Schottky barrier height (SBH). The extracted SBH for PMA/monolayer MoS2 (Fig. S1) contacts was found to be very small and approaches zero at smaller Vg values. Realization of good-quality PMA electrodes with negligible SBH can take researchers one step closer toward integration and exploitation of 2D materials in spintronic/valleytronic devices for future low-power technology.
Results and discussion
Various materials, such as ordered intermetallic compounds (CoPt, FePt, etc.), and multilayer structures, such as (NM/FM)n (where NM is a nonmagnetic layer, FM is a ferromagnet, and n is the number of layers), were found to show PMA. The origin of PMA in ordered intermetallic compounds is mainly magnetocrystalline anisotropy, while in multilayers, it is interface anisotropy11. Multilayer structures have two advantages over intermetallic compounds: (1) they are easy to grow via conventional techniques, such as sputtering, due to the closed-packed growth plane, and (2) we can change the magnetic properties by varying the thickness and number of layers, allowing a variety of material systems11. Among other multilayer structures, [Co/Pt] is one of the systems most suited for PMA applications due to its large effective magnetic anisotropy constant, Keff (~107 erg/cm3), or strong PMA12.
We deposited four samples, #1: Pt(3.8)/[Co(0.7)/Pt(3.8)]3, #2: Pt(3.8)/[Co(0.5)/Pt(3.8)]3, #3: [Co(0.5)/Pt(3.8)]3, and #4: [Co(0.5)/Pt(3.8)]2], on Si/SiO2 substrates and Si/SiO2/MoS2 via the magnetron sputtering technique at room temperature (please see “Experimental section” for more information). The number in parentheses is the layer thickness in nm. These structures differ in (i) Co layer thickness, (ii) Pt buffer layer, and (iii) number of repeated layers. Figure S2a shows the perpendicular field (H⊥) dependence of the Hall resistance (Rxy) at 5 K for all multilayer structures. The observation of the anomalous Hall effect (AHE) confirms that all prepared films exhibit PMA. Although structure #2 exhibits PMA with sharp switching (please see Supplementary information for more details), the Pt buffer layer (which forms an interface with MoS2 in FET devices) in this structure might hamper the detection of spin-valley polarization. As Pt is a heavy metal, it might absorb spins at the interface when used as a bottom layer in PMA electrodes. Taking this into account, we deposited structures #3 and #4 without a Pt buffer layer. Now, in these samples, Co is the bottom layer. It can be noted from Fig. S2a that PMA strongly depends on the buffer layer (or choice of bottom layer). As we confirmed PMA in all four structures (please see Supplementary information, Figs. S3 and S4), we sputtered structure #2: Pt(3.8)/[Co(0.5)/Pt(3.8)]3 and structure #4: [Co(0.5)/Pt(3.8)]2 on Si/SiO2/MoS2 and patterned Hall bar devices to verify the survival of PMA on MoS2. Figure 2a, b shows the AHE measured at 5 K in structures #2 and #4 sputtered on Si/SiO2/MoS2, respectively. A clear signature of PMA is observed in these samples. One can note that when structure #4 is sputtered on Si/SiO2/MoS2, it shows single-step switching rather than two-step switching, as observed when sputtered on Si/SiO2. The reason behind this can be the underlayer MoS2, which might act as a Pt buffer layer strengthening interlayer coupling.
To fabricate FETs, structure #2: Pt(3.8)/[Co(0.5)/Pt(3.8)]3 and structure #4: [Co(0.5)/Pt(3.8)]2 were integrated into our monolayer MoS2 FET devices as PMA electrodes. Hereafter, devices with electrode structure #2 (with a Pt buffer/bottom layer) and structure #4 (with a Co bottom layer) are referred to as devices A and B, respectively. We employed high-quality monolayer MoS2 channels directly grown on Si/SiO2 substrates by the salt-assisted chemical vapor deposition (CVD) technique13. Direct growth of monolayer MoS2 avoids unwanted contamination, structural distortion, and other effects that would otherwise affect its physical properties. Monolayer TMDs grown using this method were found to show excellent optical14 and electrical properties with values among the largest mobilities15,16 and smallest SBHs17 those of exfoliated/transferred and CVD-grown samples. The thickness of monolayer MoS2 was confirmed by performing Raman experiments with laser light of a wavelength of 488 nm (Fig. S1, Supplementary information).
In the next step, we recorded IDS − VDS (where IDS is the measured source-drain current and VDS is the applied source-drain voltage) curves in a two-probe geometry, as shown in Fig. 1b. The results for room temperature IDS − VDS curves as a function of Vg on a semilogarithmic scale for FET devices A and B are shown in Fig. 3a, b, respectively. Symmetric and linear IDS − VDS curves, as seen in the insets in the main figures, suggest a better quality of FET devices with an ohmic nature of the contacts. The current on/off ratio estimated from transfer curves (IDS vs. Vg) is found to be ~105 at VDS = 1 V for device A, as shown in Fig. S5 (Supplementary information). The application of Vg can affect the carrier transport efficiency at the junction either by band bending and/or electrical doping in the semiconductor. The increase in IDS with Vg exhibits the gate tunability of our devices.
Bias dependence (VDS) of the source-drain current (IDS) on a semilogarithmic scale as a function of the back gate voltage (Vg) at room temperature for a device A and b device B. The insets show IDS − VDS curves on a linear scale in a small range of VDS. c, d The Arrhenius plots at Vg = 0 V as a function of VDS for devices A and B, respectively. Solid lines are the fit of Eq. (2) in the main text.
To understand the behavior of PMA/MoS2 contacts, we recorded IDS − VDS curves as a function of Vg and temperature and estimated the SBH. The following 2D thermionic emission model was used to extract the SBH18.
where A is the contact surface area, A* is the effective Richardson constant, kB is the Boltzmann constant, \(e\phi _B\) is the SBH in eV, and n is the ideality factor. The activation energy in the above equation can be described as \(E_A = e\left( {\phi _B - \frac{{V_{DS}}}{n}} \right)\).
Upon taking the logarithm of both sides, the above equation can be written as
Figure 3c, d shows the Arrhenius plot, \(ln\left( {I_{DS}/T^{\frac{3}{2}}} \right)\) vs. 1/T, for various VDS at Vg = 0 V for FET devices A and B, respectively. The slope is extracted from the fit using Eq. (2), as shown by solid lines. It can be noted that both devices show negative slopes, indicating a positive SBH. The slope is steeper in device A than in device B. This suggests that the SBH is larger in device A than in device B; therefore, device B can show better performance.
To extract the SBH, we plotted the slopes (−EA/1000kB) from the Arrhenius plots as a function of VDS at Vg = 0 V, which show a linear dependence (solid lines), as shown in Fig. 4a, b. The extrapolated value of slopes at VDS = 0 gives the SBH, which is found to be 49.6 and 10.5 meV at Vg = 0 V for devices A and B, respectively.
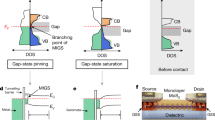
Bias voltage (VDS) dependence of the slope (−EA/1000kB) obtained from the Arrhenius plots at Vg = 0 V for a device A and b device B. c, d The Vg dependence of the SBH and extraction of the flat-band SBH (e\(\phi\)FB) for FET devices A and B, respectively. The point of deviation from a linear dependence gives the flat-band SBH. The shaded region is where thermionic emission predominantly contributes to the current, whereas the nonshaded region represents an increasing contribution from tunneling carriers.
The current through the SB is mainly contributed by two types of carriers: (i) thermionic emission carriers and (ii) tunneling carriers. To extract the true SB, it is very important to evaluate the flat-band gate voltage (VFB), which separates the dominance of the thermionic emission current and tunneling current. For Vg < VFB, the current is predominantly contributed by thermionic emission carriers, while for Vg > VFB, the tunneling current starts contributing increasingly. It is expected that the SBH shows a linear dependence on Vg when Vg < VFB and starts deviating from the linear response when Vg > VFB19. The SBH at the point where it starts deviating from the linearity is the true SBH and is called the flat-band SBH (e\(\phi\)FB). The Vg dependence of the SBH is plotted in Fig. 4c, d for devices A and B, respectively. The SBH shows a linear dependence at lower values of Vg and starts deviating at higher Vg. The flat-band SBHs extracted from Fig. 4c, d are 10.2 and 9.6 meV for devices A and B, respectively. The observed values are the smallest SBHs reported thus far using any metal contacts in monolayer MoS2 FETs. It can be noted that the SBH for device A (electrodes with a Pt bottom layer) is larger than that for device B (electrodes with a Co bottom layer). To the best of our knowledge, this is the first report on employing PMA electrodes in monolayer MoS2 FETs. One can note that the values of SBHs reported in Co/monolayer-MoS220 and Pt/few layer-MoS219 are 38 and 230 meV, respectively. The possible reason for the low SBH in our multilayer electrodes can be explained as follows. As we know, a single layer of Co is ferromagnetic with an in-plane magnetic easy axis. In a [Co/Pt] multilayer, the strong spin–orbit interaction (SOI) in Pt helps to develop PMA in Pt/Co multilayer structures. Pt possesses magnetism due to the proximity effect, and its magnetism also exhibits PMA. Here, Pt is famous for being a low-carrier-density metal (whereas Co is not), and in fact, the carrier density of Pt was reported to be 6 × 1021 cm−3 in experiments (please see, for example, Fan et al.21 and Dushenko et al.22; as a representative theoretical work, please see Fischer et al.23). Hence, for the combination of Co and Pt under equilibrium, carrier diffusion between Pt and Co layers occurs (the carrier diffusion is most likely from Co to Pt), which results in realignment of the Fermi levels of Pt and Co. Therefore, the effective work function of the [Pt/Co] multilayer structure can be different from their individual work functions (depending on the difference in the Fermi levels of Co and Pt before equilibrium). It has also been reported that various multilayer and bilayer stacks are sufficient to shift the work function of the interface metal24. Furthermore, as an example of modulation of the physical properties of Pt by carrier density modulation, we note the SOI modulation of Pt by carrier doping (increase of the carrier density by ionic gating), resulting in suppression of the inverse spin Hall effect in Pt22. Because even the SOI can be controlled by modulation of the electronic states due to charge transfer, the work function, which is more strongly related to the electronic states of condensed matter, can be modulated. Hence, given that carrier flow from the Co to the Pt in the [Co/Pt] multilayer occurs for equilibrium and the electronic states of the Pt are largely modulated by it, the work function of [Co/Pt] can be largely modulated in the formation of the multilayer, which can be the physics behind the formation of the low SBH. Moreover, it is worth mentioning that the MoS2 channels in previous reports were obtained by exfoliation from bulk single crystals. CVD-grown MoS2 channels directly grown on the substrate with better interface quality with metal electrodes can also result in a change in the SBH compared to exfoliated channels. Exfoliation/transfer of MoS2 can induce contamination and surface distortion, which may result in a change in the electrical properties of monolayer MoS2 due to chemical disorder and defect-induced gap states resulting in Fermi level pinning25. A comparison of SBHs at various ferromagnetic/nonmagnetic metal contacts with monolayer MoS2 is shown in Table 1. By examining the nature of the PMA/MoS2 contacts of both types of electrodes, we observe that Co bottom layer electrodes are a better choice for the integration of PMA electrodes into next-generation valleytronic/spintronic devices. These electrodes show smaller zero-gate and flat-band SBHs than Pt bottom layer electrodes. Furthermore, the Pt layer at the interface might work as a spin absorber, which limits the detection of spin-valley polarization. In device B, the SBH approaches zero with very small gate voltage application, which is remarkable and makes Co bottom layer PMA electrodes the best choice for the contacts in monolayer MoS2 devices. The results are reproduced in other devices, as shown in Figs. S6 and S7 in the Supplementary information. We anticipate that the development of PMA electrodes with a negligible SB would open a way to exploit valley properties in 2D TMDs and will have a significant impact on the improvement of spintronic/valleytronic technologies.
Conclusions
In summary, as the first demonstration, we examined the quality of perpendicular PMA in monolayer MoS2 FETs. The PMA in these electrodes is confirmed by the observation of the anomalous Hall effect and magnetization measurements. The I–V characteristics show a linear and symmetric response, reflecting the ohmic nature of the PMA/MoS2 contacts. The SBH estimated for FET devices is the smallest reported thus far for any metal/monolayer MoS2 contact. The SBH approaches zero with further application of a gate voltage. Gate-tunable PMA contacts with an ohmic nature may prove to be instrumental in the future design of 2D-material-based spintronic/valleytronic devices.
Experimental section
[Co/Pt] multilayer structures were deposited at room temperature using the magnetron sputtering technique. The base pressure of the chamber was ~1 × 10−5 Pa, and the Ar pressure was 0.5 Pa. Co and Pt were sputtered at rates of 0.7 and 3.8 nm/min with sputtering powers of 20 and 50 W, respectively. Hall measurements were carried out using a Physical Property Measurement System (Quantum Design) equipped with the transport option, and magnetization measurements were performed with in-plane and out-of-plane configurations using a SQUID, Quantum Design. Monolayer MoS2 was grown by the salt-assisted CVD technique on Si/SiO2 (SiO2 thickness of 285 nm). To verify PMA on Si/SiO2/MoS2, Hall bar devices (Fig. S3, Supplementary information) of length 40 µm and channel size 6 µm were fabricated on MoS2. Multilayer structures were sputtered under similar conditions as in the case of the Si/SiO2 substrate. Monolayer MoS2 channels of size 6 × 8 µm were patterned by electron beam (EB) lithography using TGMR resist, followed by oxygen plasma and wet etching. PMA electrodes were deposited on the top of MoS2 channels using magnetron sputtering. The center-to-center distance between adjacent electrodes was 0.65 µm. Ti(3)/Au(100) pads were deposited by the EB deposition technique. Two-terminal IDS − VDS curve measurements were carried out in a helium-free cryostat in the temperature range of 10–300 K.
References
Wunderlich, J. et al. Spin Hall effect transistor. Science 330, 1801 (2010).
Roche, S. et al. Graphene spintronics: the European Flagship perspective. 2D Mater. 2, 030202 (2015).
Parkin, S. S. P., Hayashi, M. & Thomas, L. Magnetic domain-wall racetrack memory. Science 320, 190 (2008).
Rycerz, A., Tworzydło, J. & Beenakker, C. W. J. Valley filter and valley valve in graphene. Nat. Phys. 3, 172 (2007).
Xu, X., Yao, W., Xiao, D. & Heinz, T. F. Spin and pseudospins in layered transition metal dichalcogenides. Nat. Phys. 10, 343 (2014).
Schaibley, J. R. et al. Valleytronics in 2D materials. Nat. Rev. Mater. 1, 16055 (2016).
Zhu, Z. Y., Cheng, Y. C. & Schwingenschlögl, U. Giant spin-orbit-induced spin splitting in two-dimensional transition-metal dichalcogenide semiconductors. Phys. Rev. B 84, 153402 (2011).
Mak, K. F., He, K., Shan, J. & Heinz, T. F. Control of valley polarization in monolayer MoS2 by optical helicity. Nat. Nanotechnol. 7, 449 (2012).
Mak, K. F., McGill, K. L., Park, J. & McEuen, P. L. The valley hall effect in MoS2 transistors. Science 344, 1489 (2014).
Xie, Q. et al. Giant enhancements of perpendicular magnetic anisotropy and spin-orbit torque by a MoS2 layer. Adv. Mater. 31, 1900776 (2019).
Lee, T. Y., Won, Y. C., Son, D. S., Lim, S. H. & Lee, S. R. Effects of Co layer thickness and annealing temperature on the magnetic properties of inverted [Pt / Co] multilayers. J. Appl. Phys. 114, 173909 (2013).
Kulkarni, P. D., Bhattacharyya, S., & Chowdhury, P. Advances in magnetic materials: processing, properties, and performance. (CRC Press Taylor & Francis Group, 2017).
Kojima, K. et al. Restoring the intrinsic optical properties of CVD-grown MoS2 monolayers and their heterostructures. Nanoscale 11, 12798 (2019).
Cunningham, P. D. et al. Charge trapping and exciton dynamics in large-area CVD grown MoS2. J. Phys. Chem. C. 120, 5819 (2016).
Li, S. et al. Halide-assisted atmospheric pressure growth of large WSe2 and WS2 monolayer crystals. Appl. Mater. Today 1, 60 (2015).
Li, Shisheng et al. Wafer-scale and deterministic patterned growth of monolayer MoS2 via vapor-liquid-solid method. Nanoscale 11, 16122 (2019).
Gupta, S. et al. Monolayer MoS2 field effect transistor with low Schottky barrier height with ferromagnetic metal contacts. Sci. Rep. 9, 17032 (2019).
Anwar, A., Nabet, B., Culp, J. & Castro, F. Effects of electron confinement on thermionic emission current in a modulation doped heterostructure. J. Appl. Phys. 85, 2663 (1999).
Das, S., Chen, H. Y., Penumatcha, A. V. & Appenzeller, J. High performance multilayer MoS2 transistors with scandium contacts. Nano Lett. 13, 100 (2013).
Cui, X. et al. Low-temperature ohmic contact to monolayer MoS2 by van der Waals bonded Co/h-BN electrodes. Nano Lett. 17, 4781 (2017).
Fan, P., Yi, K., Shao, J. D. & Fan, Z. X. Electrical transport in metallic films. J. Appl. Phys. 95, 2527 (2004).
Dushenko, S. et al. Tunable inverse spin Hall effect in nanometer-thick platinum films by ionic gating. Nat. Commn. 9, 1–7 (2018).
Fischer, G., Hoffmann, H. & Vancea, J. Mean free path and density of conductance electrons in platinum determined by the size effect in extremely thin films. Phys. Rev. B 22, 6065–6073 (1980).
Park, S., Colombo, L., Nishi, Y. & Cho, K. Ab initio study of metal gate electrode work function. Appl. Phys. Lett. 86, 073118 (2005).
Liu, Y. et al. Approaching the Schottky–Mott limit in van der Waals metal–semiconductor junctions. Nature 557, 696 (2018).
Pan, Y. et al. Reexamination of the Schottky barrier heights in monolayer MoS2 field-effect transistors. Appl. Nano Mater. 2, 4717 (2019).
Kim, C. et al. Fermi level pinning at electrical metal contacts of monolayer molybdenum dichalcogenides. ACS Nano 11, 1588 (2017).
Acknowledgements
The authors thank Prof. Kakeya Itsuhiro and Prof. H. Kageyama for their kind support in magnetization measurements and Prof. T. Kimoto and K. Kanegae for their kind support in the Raman spectroscopy experiments. This work was supported by Grant-in-Aid for Scientific Research (S) No. 16H06330, “Semiconductor spincurrentronics,” and MEXT (Innovative Area “Nano Spin Conversion Science” KAKENHI No. 26103003 and JST, PRESTO Grant Number JPMJPR20B2). Y.M. acknowledges the financial support from JST CREST (Grant No. JPMJCR16F3).
Author information
Authors and Affiliations
Contributions
S.G. and M.S. planned the research. S.G. fabricated the FET devices, performed experiments, and analyzed the results. F.R., R.O., and Y.A. provided help in the experiments. T.E. and Y.M. grew the monolayer MoS2. S.G. wrote the manuscript and discussed it with all the coauthors.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gupta, S., Rortais, F., Ohshima, R. et al. Approaching barrier-free contacts to monolayer MoS2 employing [Co/Pt] multilayer electrodes. NPG Asia Mater 13, 13 (2021). https://doi.org/10.1038/s41427-021-00284-1
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41427-021-00284-1