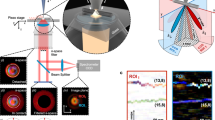
Abstract
Narrow-bandwidth luminescent materials are already used in optoelectronic devices, superresolution, lasers, imaging, and sensing. The new-generation carbon fluorescence nanomaterials—carbon dots—have attracted considerable attention due to their advantages, such as simple operation, environmental friendliness, and good photoelectric performance. In this work, two narrower-bandwidth (21 and 30 nm) emission graphene quantum dots with long-wavelength fluorescence were successfully prepared by a one-step method, and their photoluminescence (PL) peaks were at 683 and 667 nm, respectively. These red-emitting graphene quantum dots were characterized by excitation wavelength dependence of the fluorescence lifetimes, and they were successfully applied to spectral and spatial superresolved sensing. Here, we proposed to develop an infrared spectroscopic sensing configuration based on two narrow-bandwidth-emission graphene quantum dots. The advantage of the method used is that spectroscopic information was extracted without using a spectrometer, and two narrow-bandwidth-emission graphene quantum dots were simultaneously excited to achieve spatial separation through the unique temporal “signatures” of the two types of graphene quantum dots. The spatial separation localization errors of the graphene quantum dots (GQDs-Sn and GQDs-OH) were 1 pixel (10 nm) and 3 pixels (30 nm), respectively. The method could also be adjusted for nanoscope-related applications in which spatial superresolved sensing was achieved.
Similar content being viewed by others
Introduction
Luminescent materials (LMs) are an important component of many optoelectronic devices1, such as light-emitting diodes (LEDs)2, solar cells3, laser devices4, photocatalysts5, optical multiplexing devices6, imaging devices7, and sensors8. However, LMs must have a narrow bandwidth, a full-color spectral range, and high quantum yields (QYs). Narrow-bandwidth-emission LMs have been successfully applied in various fields due to their superior photoelectric properties9, narrow-bandwidth emission, etc. For instance, narrow-bandwidth-emission LMs have been used to improve the color rendering index and color purity of LEDs10. In addition, these LMs for biological sensing can exclude tissue autofluorescence and have the advantage of deep penetration11. For superresolution, narrow-bandwidth-emission LMs can increase the spatial and spectral resolution. In lasers, these LMs can be used as gain media to reduce the pumping threshold of the lasers. In addition, these LMs can also be applied for optical multiplexing, which uses different types of LMs simultaneously (using the ultranarrow bandwidth of the LMs) without interfering with each other6.
Optical microscopy is a commonly used imaging technique. However, its resolution is limited by the diffraction of light12. According to the Abbe/Rayleigh criteria of light (d = λ/(2n sinθ, where λ is the wavelength of light, n is the refractive index, and θ is the half aperture angle of the objective), it is estimated that the minimum resolution of an optical lens is 200 nm. To improve the resolution, superresolution technology has emerged. Some LMs, such as fluorescent proteins and organic dyes, are commonly used as imaging probes due to their small size and good biocompatibility13. However, the fluorescence brightness of these LMs is low, and their optical conversion and rapid photobleaching are limited. At the same time, wide-bandwidth-emission LMs have considerable limitations in terms of the resolution of superresolution technology and multichannel multiplexing. Therefore, for long-term and real-time superresolution sensing on the nanometer scale, brighter, narrower-bandwidth-emission, and more stable fluorescent probes are still needed.
Compared with traditional semiconductor quantum dots and organic dyes, carbon dots, as new carbon nanomaterials, not only have good photoelectric performance, high light resistance, low toxicity, good biocompatibility, light blinking, and no light bleaching but also involve abundant and inexpensive raw materials, simple synthesis methods, and low cost. In recent years, some results regarding narrow-bandwidth-emission carbon dots have been achieved. Graphene quantum dots (GQDs), a type of carbon dots, have achieved certain results in narrow-bandwidth emission. The bandwidth of currently reported GQDs has reached 20–40 nm (Table S1, Electronic Support Information, ESI). Common methods of reducing the emission bandwidth of GQDs include doping with heteroatoms, expanding the conjugate system, and enhancing or adopting new preparation methods. Therefore, we used a planar, highly conjugated compound as a carbon source to prepare narrow-bandwidth-emission GQDs. GQDs-Sn with an FWHM (full-width at half-maximum) of 21 nm were obtained by doping with tin(II) phthalocyanine (SnPc) as a carbon source, and it exhibited the narrow-bandwidth emission (20–40 nm) of fluorescent nanomaterials. At the same time, GQDs-OH were prepared in an alkaline environment using phthalocyanine (Pc) as the carbon source. We demonstrated the unique and novel schemes of GQDs for spectral and spatial superresolved sensing for the first time by using GQDs as fluorescent probes.
In summary, the novelty of this work is as follows: (1) novel nanoparticles (GQDs) with unique properties were developed, characterized, and used for novel imaging applications; (2) a unique spectral sensing configuration based on the unique nanoparticles allowed spectral information to be obtained without using a spectrometer; and (3) a novel spatial superresolved imaging concept based on the nanoparticles was proposed in contrast to existing nanoscopy concepts (e.g., photoactivation localization microscopy, PALM). Here, the superresolved process was achieved simultaneously (either based upon spectral scrambling or on temporal scrambling) rather than sequentially. Thus, this process is much less time consuming than previous methods (the different spectra or the different temporal arrival windows of the photons allow simultaneous excitation and sensing of several nearby nanoparticles).
This work achieved the spatial separation of GQDs in two ways: different emission spectra and different temporal arrival windows of the photons. The localization errors were approximately 1 pixel (which equals 10 nm) for GQDs-Sn and 3 pixels (30 nm) for GQDs-OH.
Results and discussion
Characterization of the GQDs-Sn and GQDs-OH
Scheme 1 shows the preparation of GQDs and their application in superresolved spectral and spatial sensing. By adjusting the precursors and additives, two types of narrow-bandwidth-emission GQDs were prepared and named GQDs-Sn (with tin(II) phthalocyanine as the carbon source) and GQDs-OH (with Pc as the carbon source and NaOH as auxiliary). It was feasible with the solvothermal method to prepare ultranarrow-bandwidth-emission GQDs with a planar, highly conjugated compound.
The morphologies of the GQDs-Sn and GQDs-OH were characterized by high-resolution transmission electron microscopy and atomic force microscopy (AFM), as seen in Fig. 1a–f. As seen in Fig. 1a, d, the GQDs-Sn and GQDs-OH were evenly distributed. The average diameter of the GQDs-Sn was 3.3 nm (Fig. 1a), and the lattice fringe spacing was 0.22 nm, which corresponded to the (001) plane of graphite14. Similarly, the average diameter of the GQDs-OH was approximately 2.3 nm (Fig. 1d), and the lattice fringe spacing was 0.25 nm, which corresponded to the (100) plane lattice of graphene15. The AFM images showed that the topographic heights of the GQDs-Sn and GQDs-OH were all approximately 1 nm, indicating (Fig. 1b, e) that the GQDs-Sn and GQDs-OH primarily consisted of 2–3 graphene layers16,17,18,19,20.
Note that the Supplementary Material includes numerical simulations of spectral sensing in Figs. S1–S4, numerical simulations of spatial superresolution in Fig. S5, and experimental results related to temporal-scrambled sensing in Figs. S6–S19.
The surface structures and composition of the GQDs-Sn and GQDs-OH were obtained by Fourier transform infrared (FT-IR) spectroscopy and X-ray photoelectron spectroscopy (XPS). In Fig. S7 (ESI), the FT-IR spectra show that the GQDs-Sn and GQDs-OH possess polar functional groups. For instance, the large broad peak at 3580–3200 cm−1 corresponded to −NH2 and −OH groups on the surface of the GQDs-Sn and GQDs-OH. The peaks at 2924 and 2850 cm−1 were attributed to the vibration of C–H. Two characteristic peaks at 1735.6 and 1655.3 cm−1 were attributed to stretching vibrations of O=C–NH20. The peaks at 1467 and 1383 cm−1 were attributed to the C=C absorption vibration of the benzene ring and the C–N–C vibration in the heteroaromatic ring, respectively. In Fig. 1c, the survey XPS spectrum of GQDs-Sn displays four typical peaks at 285, 399, 487, and 532 eV for C 1s, N 1s, Sn 3d, and O 1s, respectively. The atomic ratios were 48.09% (C), 7.14% (N), 6.72% (Sn), and 38.05% (O) (Table S2, ESI). The high-resolution C 1s XPS spectrum (Fig. S8b, ESI) exhibited peaks at 284.6, 285.4, and 288.6 eV, corresponding to C–C/C=C, C–N, and N–C=O/C=N, respectively. The high-resolution XPS spectrum of Sn 3d (Fig. S8a, ESI) was deconvolved into peaks at 487.0 and 495.4 eV, corresponding to Sn 3d5/2 and Sn 3d3/2, respectively, with a splitting energy of 8.4 eV. This result indicated that the tin in the GQDs-Sn was positive tetravalent21,22. Figures S8–10 (ESI) show the survey XPS spectra and high-resolution XPS spectra of GQDs-H, GQDs-OH, and GQDs-Sn. To verify that the alkaline environment and tin doping can increase the fluorescence intensity and reduce the emission bandwidth of GQDs, GQDs-H were prepared with Pc as the carbon source. Figure S7 (ESI) shows that the morphology of the GQDs-H was similar to those of GQDs-OH and GQDs-Sn. However, alkaline conditions increased the PL intensity of the GQDs (the absolute QYs of GQDs-OH and GQDs-H were 40.7% and 30.1%, respectively). Tin doping reduced the bandgap and emission bandwidth of the GQDs. At the same time, the FWHM of the GQDs-Sn was 21 nm, while that of the GQDs-H was 30 nm (Fig. 2a, b and Fig. S12, ESI). In Fig. S13 (ESI), the XRD spectrum showed that the 2θ peaks of the GQDs-H, GQDs-OH, and GQDs-Sn were 25.78°, 22.80°, and 23.64°, respectively, which correspond to the (002), (001), and (002) planes of graphene23. Compared with the standard card of SnO2 and the Sn 3d XPS spectrum of the GQDs-Sn, SnO2 existed on the surface of the GQDs-Sn. Based on the above data and analysis (Table S3, ESI), it was preliminarily proven that the surfaces of the GQDs-H, GQDs-OH, and GQDs-Sn were covered with N- and O-containing heterocyclic species and abundant amino functional groups.
a UV–Vis absorption spectrum of the GQDs-Sn. b Fluorescence spectrum of the GQDs-Sn (inset images: photographs of the GQDs-Sn under sunlight (left image) and a 365 nm UV lamp (right image)). c Upconversion fluorescence spectrum of the GQDs-Sn (top). d–f were the same as a–c but for GQDs-OH (bottom).
The optical performance of the GQDs-Sn and GQDs-OH
UV–vis absorption (UV–vis) spectra of the GQDs-H, GQDs-OH, and GQDs-Sn (Fig. 2 and Fig. S12, ESI) exhibited significant absorption in the visible region (550–730 nm). In the UV–vis spectra, their absorption peaks were similar to that of Pc/SnPc, indicating that the GQDs contained a planar, highly conjugated structure. The maximum absorption peak of the GQDs-Sn slightly redshifted compared with those of the GQDs-H and GQDs-OH, indicating an increase in the degree of conjugation. The emission peaks of the GQDs-Sn and GQDs-OH were 683 and 667 nm, respectively (Fig. 2b, e). The GQDs-Sn had an ultranarrow FWHM of 21 nm. It is worth noting that the GQDs-Sn were unique with ultranarrow-bandwidth emission, which was much narrower (20–40 nm) than that reported for fluorescent nanomaterials to date. Additionally, the GQDs-H, GQDs-OH, and GQDs-Sn exhibited upconversion photoluminescence (UCPL) properties, and the UCPL peaks of these GQDs were the same as the PL peaks. The UV–vis absorption spectra and PL excitation spectra of the GQDs-H, GQDs-OH, and GQDs-Sn had good overlap, indicating that the GQDs followed a surface luminescence mechanism; that is, the surface structure and functional groups of the GQDs were the main luminescence mechanism24 (Fig. S14, ESI). As seen by comparing the UV–vis absorption and PL spectra of SnPc/Pc, the GQDs-Sn and GQDs-OH retained a large amount of the planar, highly conjugated structure when SnPc/Pc was subjected to high temperature and high pressure. At the same time, compared to those of SnPc, the absorption and PL peak of the GQDs-Sn were blueshifted by 11 and 14 nm, respectively. When the absorbance was the same, the PL intensity of the GQDs-Sn was greatly increased compared to that of SnPc. Similarly, the shape of the absorption peaks of the GQDs-OH changed substantially in contrast to that of Pc. The emission peak of the GQDs-OH was blueshifted by 21 nm compared with that of Pc. Therefore, GQDs were successfully prepared via SnPc/Pc under high-temperature and high-pressure reactions, which greatly improved the fluorescence performance25.
Cyclic voltammetry was performed to calculate the HOMO and LUMO positions of the GQDs-Sn and GQDs-OH to determine the effect of alkali and tin doping on the GQDs (Fig. S16, ESI). By calculation, the HOMO and LUMO of the GQDs-Sn were −5.22 and −3.62 eV, respectively. On the other hand, the HOMO and LUMO of the GQDs-OH were −6.16 and −4.43 eV, respectively (Fig. S16 and Table S4, ESI). The bandgaps of the GQDs-Sn and GQDs-OH were 1.60 and 1.73 eV, respectively, with a difference of 0.13 eV. The reason for these results might be that the bandgap of the GQDs was mainly affected by the degree of conjugation and the surface functional groups, which mainly affected the band levels of the HOMO and LUMO. Due to the Sn oxidation state on the surface of the GQDs-Sn, the energy level of the GQDs-Sn was approximately 0.8 eV higher than that of the GQDs-OH. Because the Sn oxidation state did not correspond to a planar structure, the transfer of electrons from the LUMO to the HOMO was more difficult, leading to a decrease in the QYs of the GQDs-Sn26. It could be seen from the PL spectra that the FWHM of the GQDs-Sn was narrower than that of the GQDs-OH because the degree of discrete energy levels of the GQDs-Sn was greater than that of the GQDs-OH27,28.
The fluorescence lifetime decay curves for the GQDs-H, GQDs-OH, and GQDs-Sn are shown in Fig. S17 (ESI), which are consistent with double exponential decay. The average lifetimes of the GQDs-H, GQDs-OH, and GQDs-Sn were 6.09, 6.18, and 6.13 ns under a 635 nm laser (Table S5, ESI), respectively. τ1 was attributed to the state of the carbon core, and τ2 was attributed to the surface defect state28. In Table S5 (ESI), the τ2 ratios of the GQDs-H, GQDs-OH, and GQDs-Sn gradually decreased. This indicated that the PL of the GQDs was mainly surface-state luminescence. In addition, the proportion of carbon nuclei in the GQDs-Sn increased with tin doping, which was caused by the defect energy levels introduced by the introduction of heteroatoms. Correspondingly, the absolute QYs of the three GQDs were 30.1, 40.7, and 7.5%. The increase in the proportion of carbon nuclei would reduce the PL intensity and cause a redshift in the PL emission wavelength of the GQDs. In addition, the PL emission peak and intensity of the GQDs-Sn and GQDs-OH were slightly different in different polar solvents (Fig. S18, ESI), which also confirmed that the PL mechanism of the GQDs was mainly due to surface states29.
Therefore, considering the carbon source, surface functional groups, particle size, etc., we concluded that the reasons for the narrower-bandwidth emission of GQDs-Sn were as follows: (1) The carbon source was a planar, highly conjugated structure. Therefore, the prepared GQDs had a large π-conjugated system. (2) Tin doping adjusted the energy bandgap and the positions of the HOMO and LUMO of the GQDs. (3) Single surface functional groups were generally present. (4) The purification process was optimized to make the prepared GQDs uniform in particle size.
To further explain the luminescence properties of the red GQDs, the transient absorption (TA) spectrum showed the luminescence properties with nanosecond broadband (330–750 nm) TA spectroscopy under 400 nm excitation. Usually, the signals in the TA spectrum are affected by ground-state bleaching (GBS), excited-state absorption (ESA), and stimulated emission (SE). The TA spectra and kinetic curves at different probe wavelengths are shown in Fig. 3a–d. As seen from the TA spectrum of the GQDs-Sn (Fig. 3a, b) and the UV–vis absorption spectrum and PL spectrum of the GQDs-Sn (Fig. 2a, b), the GBS at 330–400 and 580–620 nm corresponded to the energy band structure in the steady-state absorption spectrum. The ESA range was 400–580 nm, and the SE signal was approximately 630–700 nm. The kinetic decay curves of the GQDs-Sn were single exponential decays at two excitation wavelengths (420 and 500 nm). Similarly, in the TA spectrum of the GQDs-OH, the range of 350–430 nm corresponded to GBS, 590–630 nm corresponded to the energy band structure, 430–590 nm corresponded to the ESA, 630–680 nm corresponded to the SE signal, and the kinetic decay curve belonged to a single index. By comparing the kinetic fitting data at 500 nm, Sn increased the excited-state lifetime of the GQDs and decreased the decay constant, indicating that Sn reduced the QYs of the GQDs and that the emission peak was redshifted30.
To explore the formation process of GQDs, various GQDs were synthesized with different reaction times at 180 °C and were named GQDs-Sn6, GQDs-Sn12, GQDs-Sn18, GQDs-Sn24, GQDs-Sn36, GQDs-OH6, GQDs-OH12, GQDs-OH18, GQDs-OH24, and GQDs-OH36. The GQDs mainly underwent dehydration, condensation, and carbonization processes under high temperature and high pressure. SnPc/Pc mainly underwent dehydration condensation and carbonization processes under high temperature and high pressure to form GQDs. The planar, highly conjugated structure of SnPc/Pc promoted the formation of the π-conjugated system of the GQDs. In Fig. S19 (ESI), the crude product had two main types of GQDs (blue and red GQDs). At a solvothermal reaction time of 6 h, SnPc/Pc was mainly dehydrated and condensed to form blue GQDs (mainly). The carbonization degree of SnPc/Pc increased as the reaction time was prolonged to 24 h, and the PL proportion and synthetic yields of the red GQDs increased in the crude product. When the reaction time was increased to 36 h, the GQDs were excessively carbonized, so the PL intensity of the GQDs was dominated by carbon cores, and the PL of the GQDs dropped sharply31.
Superresolved spectral and spatial sensing
To observe finer structures or images, superresolution technology is used to overcome the optical diffraction limits for imaging applications, such as the high resolution of cell structures in biological sensing. In this work, the emission peak shapes of the GQDs-Sn and GQDs-OH changed slightly (shoulder peak) under different excitation wavelengths. The PL lifetimes of the GQDs-Sn and GQDs-OH were distinguished at different excitation wavelengths, and the infrared spectrum sensing configuration depended on the special nanomaterials. This concept could also be adapted for nanomicroscopy-related applications, enabling spatial superresolution imaging in nanoapplications. In general, in superresolution, it has been proven that a proper encoding–decoding process can enhance spectral31 as well as spatial32,33 resolution.
Our aim is to realize high-spectral-resolution sensing without using a spectrometer, i.e., to decode the spectral information just from intensity readouts, while the spectrum is reconstructed when applying the a priori known spectral “signature” of the nanoparticles. Figure 4a shows a schematic sketch of the spectral distributions, and Fig. 4b shows the microscopy-based sensing configuration. It was assumed in the experiment that a large number of photoluminescent nanomaterials (LNMs) were positioned below the spectrally inspected specimen. Simultaneously, the LNMs were placed in a solution between two microscope coverslips, and the samples were positioned on top of the upper coverslips. The microscope coverslips had a uniform or previously known spectral transmission in the near-infrared region. This transmission is needed for calibration of the sample’s spectral reconstruction process. It was postulated that each group n of LNMs was excited with a different excitation wavelength λn and that the emission of this group was denoted by Ln (λ). It was also assumed that these were spectrally randomized and noncorrelated emission distributions. From the mathematical derivation presented in the theory-application section, one might see that the reconstructed spectrum indeed included a term corresponding to the original high-resolution NIR spectrum S(λ) of the inspected samples. The decoding process was as follows: \(S_{\mathrm R}\left( \lambda \right) = \mathop {\sum}\nolimits_{n = 1}^N {I\left( {n\Delta t} \right)L_n\left( \lambda \right)}\), where SR(λ) was out of the reconstructed high-resolution spectrum. On the other hand, it was assumed that the spectral emission functions of the different LNM groups were not correlated with each other, and the following equation was obtained: \(\mathop {\sum}\nolimits_{n = 1}^N {L_n\left( {\lambda^{\prime}} \right)L_n\left( \lambda \right) \approx 0.25\left( {1 + \delta \left( {\lambda ^{\prime} - \lambda } \right)} \right)}\) (the specific derivation process is described in the ESI). In this work, we realized the reconstructed spectrum and spatial separation with two types of LNMs based on the above equation.
Importantly, in the proposed approach, a discrete set of excitation wavelengths resulted in a continuous spectral reconstruction of the inspected samples. Additionally, excitation in the visible region allowed spectral reconstruction in the NIR region with high spectral resolution. Since the above-proposed sensing could be applied for each pixel of the detector, the proposed concept could be used for hyperspectral imaging, while the high spectral resolution could be extracted for each pixel of the camera while mapping a different spatial footprint in the inspected sample. Since the various spectral signatures of the different LNM types were spectrally noncorrelated to each other, the more types we had (larger N), the higher the hyperspectral mapping capability became.
If each LNM type targeted another region in space, then the proposed concept could be used to perform spatial superresolved imaging, i.e., LNM-based nanoscopy instead of using time multiplexing to enhance the signal-to-noise ratio and spatial resolution, as described in refs. 34,35; here, a method of wavelength multiplexing was proposed for wavelength multiplexing nanoscopy. In addition, the detailed theoretical verifications of the spectral reconstruction method are provided in the Supporting Material sections.
Thus, we presented an approach allowing us to extract spectral information without using a spectrometer.
Preliminary experimental validation
For the experimental validation, the aim was to perform spectral mapping with a small number of LNM groups while also providing a small number of spectrally resolved points. Instead of using different LNM groups, the GQDs-Sn and GQDs-OH were used with different fluorescence spectra under different excitation wavelengths.
In this experiment (the scheme of Fig. 4b), a microscope spectral transmission filter with a spectral transmission band of 650–680 nm was placed in front of the charge-coupled device (CCD), and the GQDs were excited by different excitation wavelengths (which changed their spectral emission). The readouts obtained for each excitation wavelength were collected, and reconstruction was performed based on Eq. (2). After performing the reconstruction of spectral transmission through the filter, the results were compared with the datasheet of the filter. For this experiment, additional types of GQDs were fabricated.
Figure 5a includes the emission spectra of the GQDs-Sn without any filter and the same measurement with a red filter having a transmission band within the range of 650–680 nm (Fig. 5b). Figure 5c shows two spectral measurements of the GQDs-Sn with and without the red filter under 360 nm excitation. In Fig. 5d, the same measurement was performed under 620 nm excitation. In Fig. 5e–h, the same operation as in Fig. 5a–d was performed but for the GQDs-OH.
a Emission spectrum of the GQDs-Sn without any filter. b Emission spectrum of the GQDs-Sn with the red filter. c Emission spectrum of the GQDs-Sn with and without the filter under excitation at 360 nm. d Emission spectrum of the GQDs-Sn with and without the filter under excitation at 620 nm. e–h as in a–d but for GQDs-OH.
Spectral reconstruction
The experimental spectral reconstruction is presented in Fig. 6, where two types of LNMs were used for the spectral measurements. Various spectral measurements were performed through the red filter, as shown in Fig. 5b (for GQDs-Sn) and Fig. 5f (for GQDs-OH). Spectral integration was performed such that the spectral information was lost, and a single readout of intensity was obtained for each excitation wavelength. Similarly, Fig. 5a (for GQDs-Sn) and Fig. 5e (for GQDs-OH) show the same data as a reference without the effect of the red filter. Spectral reconstruction was performed as shown in Eq. (2), and we normalized the reconstruction of the spectrum with and without the effect of the filter (the Wiener filter calculation36 was performed for noise insensitive inverse filtering). The obtained experimental results appear in Fig. 6 for the GQDs-Sn (solid line). For comparison, the GQDs-OH results (dashed line) are also included in Fig. 6 to show the spectral reference measurements made only on the filter alone without the involvement of any LNMs.
Since there were only 14 different spectra (using 14 different excitation wavelengths), the obtained spectral reconstruction was not perfect. Additionally, the spectral distributions of the GQDs-Sn and GQDs-OH did not match perfectly to the spectral transmission band of the red filter. The GQDs-OH were better matched to the filter and produced better reconstruction results than the GQDs-Sn. Nevertheless, with both types of LNMs, qualitative reconstruction was achieved. The reconstruction of the transmission spectrum indicated a spectral band within the region of approximately 655–690 nm, while the real filter transmitted energy in the spectral range of approximately 645–680 nm.
Thus, the obtained error for spectral reconstruction was approximately 10 nm, which was quite satisfactory given that the spectra of the LNMs had matched poorly with the spectral transmission region of the filter and that only 14 spectral functions were used for the reconstruction. Additionally, note that this spectral error was obtained in the spectral region of approximately 600–750 nm (spectra of the LNMs used); thus, an error in the spectral allocation of approximately 10 nm was less than 7% from the spectral region.
As previously indicated, instead of using spectral distributions to reconstruct spectral information, temporal-scrambled measurements could also be made and applied for spatial superresolution.
Spatial separation
Reconstruction based on spectral measurements
To reduce the problem of the time required to reconstruct superresolved images, the proposed configuration in the work allowed, as in PALM nanoscopy, conversion of localization precision into spatial resolution by localizing two GQDs positioned closer to each other than the optically identical point spread function of the microscope. However, unlike in the case of PALM, the different LNMs were separated spatially by time sequencing, i.e., being excited sequentially in time. In our case, the different GQDs were spatially separated via different temporal “signatures” by being excited simultaneously.
To preliminarily prove the ability to use the experimentally recorded spectra for spatial separation, the spectra of the GQDs-Sn under 360 nm excitation and the spectra of the GQDs-OH under 620 nm excitation were used to perform spatial separation, as shown in the simulation in Fig. S5 (ESI). The obtained results are shown in Fig. 7. Unlike in the simulation in Fig. S5 (ESI) that assumes random spectra, experimentally measured spectra were used here, yet superresolved spatial separation was feasible. Thus, the mathematical condition of Eq. (4) was fulfilled in reality.
Unlike in the theoretical case of Fig. S5, in practice, the reconstruction provided limited precision for the superresolution. As seen in Fig. 7, the localization positions of the spatial peaks were shifted by 2 pixels = 20 nm (right peak) and by 3 pixels = 30 nm (left peak) from the right position of the center of the two types of LNMs. Thus, the experimentally obtainable average precision of the reconstruction was approximately 25 nm.
Similar results were obtained when the experimentally measured spectra were used with the two LNM groups and when the excitation wavelengths for each were spectrally close. The spectra of the GQDs-Sn under 360 nm excitation and the spectra of the GQDs-OH under 380 nm excitation were used. The obtained spatial separation results were similar, with errors of 3 pixels = 30 nm (right peak) and 4 pixels = 40 nm (left peak), which corresponded to an average spatial error of 35 nm.
Reconstruction based on temporal-scrambled measurements
To test the spatial reconstruction/superresolving capabilities, we performed temporally resolved FLIM (fluorescence lifetime imaging microscopy) measurements for the GQDs-Sn and GQDs-OH. The images obtained at the different excitation wavelengths are shown in Fig. 8a; the upper row shows the results for the GQDs-Sn, and the second row shows the results for the GQDs-OH.
a FLIM experimentally collected measurements for GQDs-Sn (top) and GQDs-OH (bottom). b Time-dependent counts of GQDs-Sn and GQDs-OH at two excitation wavelengths of 405 nm and 640 nm. c Spatial superresolution allowing the separation of two spatially unresolved GQDs in space. We used the fluorescence lifetime information of different excitation wavelengths collected on the FLIMs of two GQDs to achieve spatial separation through the temporal window.
For the spatial resolution experiment, we used GQDs-Sn and GQDs-OH excited at wavelengths of 405 and 640 nm, respectively. As previously mentioned, since the photon count did not coincide in time, adjacent GQDs-Sn and GQDs-OH excited together with the same excitation wavelength emit photon counts in noncoincincing temporal windows. Thus, by taking the readouts from different temporal windows and comparing them to the previously known “temporal signatures”, the two types of LNMs could be spatially resolved and separated.
The obtained results are shown in Fig. 8b, c. Figure 8b shows the time counts for the two adjacent LNMs. The first 2.2 ns was used for the GQDs-Sn, and another temporal window of 2.2 ns starting from 2.9 ns was used since the GQDs-OH had a significant “temporal signature” of photon counts, while the GQDs-Sn had almost no counts. The inset in Fig. 8b shows the full window of the photon counts, where not only the temporal window of interest that was magnified in the figure itself.
The obtained spatial separation results are shown in Fig. 8c. The obtained results showed that spatial separation between the LNMs was feasible based on their temporal signature. The localization error was approximately 1 pixel (which equals 10 nm) for the left spatially allocated peak (for GQDs-Sn) and 3 pixels (30 nm) for the right spatial peak (for GQDs-OH).
In both approaches for spatial superresolution (the one based on spectral scrambling and the one based upon temporal scrambling), the proposed concept was much less time consuming since it allowed simultaneous (rather than sequential) spatial superresolution of nearby LNMs.
Please note that there are many papers, e.g., in ref. 37, that discuss studies regarding single SiO2 nanoparticles having photophysical properties of the luminescent centers that strongly resemble those of single dye molecules. The photoluminescence exhibits interesting properties, such as spectral broadening. Although these previous studies are very interesting and indeed present the capability of changing the spectral distribution of the nanoparticles, they do not present the capability of using a large variety of possible spectral distributions as encoding “signatures” capable of producing spectral and spatial superresolved imaging. In our paper, we present, for the first time, to the best of our knowledge, the capability of extracting the spectral information of an inspected object by decomposing it into a large number of known spectral “signatures” produced by special quantum dots that we synthesize; the same approach can also be used to perform spatial superresolved imaging of the inspected object. Thus, in our approach, we obtain the spectrum of an inspected object without using a spectrometer (our nanoparticles are used as a spectrometer), and then we apply a localization-based approach to perform spatial superresolved mapping of the inspected object.
Conclusions and discussions
In conclusion, GQDs with ultranarrow-bandwidth red emission were effectively prepared via a one-step synthesis method by using planar, highly conjugated compounds as a carbon source. At present, GQDs-Sn have an FWHM of 21 nm, which is the narrowest bandwidth of fluorescent nanomaterials reported to date. To achieve superresolved spectral and spatial sensing, we took advantage of the narrower FWHM of the GQDs-Sn and GQDs-OH, the red emission of the GQDs-Sn and GQDs-OH, the very similar emission peak positions of the GQDs-Sn and GQDs-OH (Δλem = 16 nm), and the different fluorescence lifetimes of the GQDs-Sn and GQDs-OH by changing the excitation wavelength. Superresolved spectral and spatial sensing could be achieved by obtaining spectral information without using a spectrometer and simultaneously performing superresolution processing according to the temporal “signature” characteristics of different types of GQDs.
Here, it has been shown how spectral or temporal scrambling achieved by using many groups/types of different LNMs or the same group excited at different wavelengths produces uncorrelated emission spectra or uncorrelated temporal photon counts, emitted either at the same time in different spatial locations or at different temporal sites (sequences), could be used for achieved spatial and spectral superresolved sensing, respectively. The proposed novel concept was demonstrated theoretically and validated numerically as well as tested in preliminary experiments.
For the application in which the proposed novel concept of spectrometric reconstruction was used for spatial superresolution, one does not need to use a large number of excitation wavelengths or LNM groups, unlike in the case of spectral reconstruction. Actually, the overall number of LNM types and excitation wavelengths will improve the obtainable resolution, and a factor of even 10 can be very significant in the case of spatial resolution enhancement.
Materials and methods
Materials
Tin(II) phthalocyanine (SnPc) and Pc were of analytical grade and were purchased from J&K Scientific Ltd. Petroleum ether and N,N-dimethylformamide (DMF) were purchased from Sinopharm Chemical Reagent Co., Ltd. All chemicals were used without further purification.
Preparation of GQDs
Synthesis of GQDs-H
GQDs-H were prepared from Pc by the solvothermal method. Briefly, 10 mg of Pc was dispersed in 20 mL of DMF with ultrasonic dispersion for 30 min. Subsequently, the solution was transferred into a poly(tetrafluoroethylene) (Teflon)-lined autoclave for the solvothermal reaction and heated at 180 °C for 24 h. After the reaction, the reactor was cooled to room temperature to obtain a dark green mixed solution. The mixed solution was centrifuged at 10,000 r.p.m. for 20 min to remove the flocculent precipitate. The supernatant was collected by centrifugation and filtered through a 0.22-μm microfiltration membrane to further remove flocculent particles. By using rotary evaporation (70 °C), the DMF was removed from the solution, and the GQDs were redispersed in ethanol for use. A large amount of deionized water was added to the ethanol solution to produce a precipitate, and the precipitate was collected by centrifugation and washing. This step was repeated seven to eight times until the PL intensity was very low and the PL intensity at 440 nm was less than 5% of the PL intensity at 670 nm. The precipitate was dried in a vacuum oven to obtain GQDs-H.
Synthesis of GQDs-OH
Similarly, other red GQDs (GQDs-OH) were prepared according to the same method used for GQDs-H. Pc (10 mg, carbon source) and NaOH (150 mg, sodium hydroxide) were codispersed in 20 mL of DMF in a flask. The reaction conditions and purification processes were consistent with those used for GQDs-H.
Synthesis of GQDs-Sn
The preparation and purification process of GQDs-Sn were consistent with those used for the GQDs-H, except that the carbon source was changed to tin(II) Pc.
Reconstruction spectrum algorithm
By assuming a series of constraints, a method for reconstructing spectra and space separation was derived. S(λ) denotes the spectral transmission of the mapped sample. It was assumed that there were N types of LNMs, with a large number of them located below the spectral lens. The emission of the LNMs was in the near-infrared (NIR) region with excitation in the visible region. On the other hand, it was supposed that each group n of LNMs was excited with different excitation wavelengths λn, and the emission of this group was denoted by Ln(λ), which were spectrally randomized and noncorrelated emission distributions. Thus, the LNM types were excited with different excitation wavelengths λ1, …, λn, … λN sequentially. The emission time was denoted by Δt, and for each emission, the intensity was collected in the detector. This readout intensity was denoted by I(nΔt) with n = 1, …, N.
Our intensity readout, therefore, could be denoted as
From those N intensity readouts, the original NIR spectrum S(λ) could be reconstructed. The decoding process was as follows, where SR(λ) is our reconstructed high-resolution spectrum:
Let us prove this. We substitute Eq. (1) into Eq. (2) and obtain
Since N was a large number and since we assumed that the spectral emission functions coming from the different LNM groups were not correlated with each other:
The 0.25 constant was because it was assumed that the emission intensity Ln was normalized to be between 0 and 1 and was uniformly distributed between 0 and 1, while it had no spectral correlation (white random process distribution). For other statistical distributions, the distribution was considered.
Thus, by substituting Eq. 4 into Eq. 3, one can obtain
References
Xu, J. & Shalom, M. Conjugated carbon nitride as an emerging luminescent material: quantum dots, thin films and their applications in imaging, sensing, optoelectronic devices and photoelectrochemistry. ChemPhotoChem 3, 170–179 (2019).
Qian, K. et al. Modulation effect of carbon quantum dots in organic electroluminescent devices. Org. Electron. 51, 314–321 (2017).
Choi, Y. et al. Simple microwave-assisted synthesis of amphiphilic carbon quantum dots from A3/B2 polyamidation monomer set. ACS Appl. Mater. Interfaces 9, 27883–27893 (2017).
Han, Z. et al. Highly efficient and ultra-narrow bandwidth orange emissive carbon dots for microcavity lasers. Nanoscale 11, 11577–11583 (2019).
Zhuo, S., Shao, M. & Lee, S. T. Upconversion and downconversion fluorescent graphene quantum dots: ultrasonic preparation and photocatalysis. ACS Nano 6, 1059–1064 (2012).
Fan, Y. et al. Lifetime-engineered NIR-II nanoparticles unlock multiplexed in vivo imaging. Nat. Nanotechnol. 13, 941–946 (2018).
Lin, J. et al. Novel near-infrared II aggregation-induced emission dots for in vivo bioimaging. Chem. Sci. 10, 1219–1226 (2019).
Del Rosal, B., Ximendes, E., Rocha, U. & Jaque, D. In vivo luminescence nanothermometry: from materials to applications. Adv. Opt. Mater. 5, 1600508 (2017).
Semeniuk, M. et al. Future perspectives and review on organic carbon dots in electronic applications. ACS Nano 13, 6224–6255 (2019).
Lin, H. et al. Non-rare-earth K2XF7: Mn4+(X = Ta, Nb): a highly-efficient narrow-band red phosphor enabling the application in wide-color-gamut LCD. Laser Photonics Rev. 11, 1700148 (2017).
Shi, X. et al. Far‐red to near‐infrared carbon dots: preparation and applications in biotechnology. Small 15, 1901507 (2019).
Chizhik, A. M. et al. Super-resolution optical fluctuation bio-imaging with dual-color carbon nanodots. Nano Lett. 16, 237–242 (2016).
Jin, D. et al. Nanoparticles for super-resolution microscopy and single-molecule tracking. Nat. Methods 15, 415–423 (2018).
Miao, X. et al. Synthesis of carbon dots with multiple color emission by controlled graphitization and surface functionalization. Adv. Mater. 30, 1704740 (2018).
Tan, D. et al. Photoinduced luminescent carbon nanostructures with ultra-broadly tailored size ranges. Nanoscale 5, 12092–12097 (2013).
Liu, F. et al. Facile synthetic method for pristine graphene quantum dots and graphene oxide quantum dots: origin of blue and green luminescence. Adv. Mater. 25, 3657–3662 (2013).
Song, L., Shi, J., Lu, J. & Lu, C. Structure observation of graphene quantum dots by single-layered formation in layered confinement space. Chem. Sci. 6, 4846–4850 (2015).
Zhu, S. et al. Graphene quantum dots with controllable surface oxidation, tunable fluorescence and up-conversion emission. RSC Adv. 2, 161904 (2016).
Zhu, S. et al. Strongly green-photoluminescent graphene quantum dots for bioimaging applications. Chem. Commun. (Camb.). 47, 6858–6860 (2011).
Madrakian, T., Maleki, S., Gilak, S. & Afkhami, A. Turn-off fluorescence of amino-functionalized carbon quantum dots as effective fluorescent probes for determination of isotretinoin. Sens. Actuators B Chem. 247, 428–435 (2017).
Song, H., Li, N., Cui, H. & Wang, C. Enhanced capability and cyclability of SnO2–graphene oxide hybrid anode by firmly anchored SnO2 quantum dots. J. Mater. Chem. A1, 7558–7562 (2013).
Jia, Q. et al. A magnetofluorescent carbon dot assembly as an acidic H2O2-Driven oxygenerator to regulate tumor hypoxia for simultaneous bimodal imaging and enhanced photodynamic therapy. Adv. Mater. 30, 1706090 (2018).
Wang, Z. et al. 53% efficient red emissive carbon quantum dots for high color rendering and stable warm white‐light‐emitting diodes. Adv. Mater. 29, 1702910 (2017).
Pan, L., Sun, S., Zhang, L., Jiang, K. & Lin, H. Near-infrared emissive carbon dots for two-photon fluorescence bioimaging. Nanoscale 8, 17350–17356 (2016).
Xu, Q. et al. Highly fluorescent Zn-doped carbon dots as Fenton reaction-based bio-sensors: an integrative experimental-theoretical consideration. Nanoscale 8, 17919–17927 (2016).
Xu, Q. et al. Metal charge transfer doped carbon dots with reversibly switchable, ultra-high quantum yield photoluminescence. ACS Appl. Nano Mater. 1, 1886–1893 (2018).
Goicoechea, J. et al. in Sensors Based on Nanostructured Materials (ed. Arregui, F. J.) 131–181 (Springer US, 2009).
Khan, S. et al. Time-resolved emission reveals ensemble of emissive states as the origin of multicolor fluorescence in carbon dots. Nano Lett. 15, 8300–8305 (2015).
Stepanidenko, E. A. et al. Influence of the solvent environment on luminescent centers within carbon dots. Nanoscale 12, 602–609 (2020).
Liu, Q. et al. Strong two-photon-induced fluorescence from photostable, biocompatible nitrogen-doped graphene quantum dots for cellular and deep-tissue imaging. Nano Lett. 13, 2436–2441 (2013).
Malka, D. et al. Super-resolved Raman spectroscopy. Spectrosc. Lett. 46, 307–313 (2013).
Ilovitsh, T. et al. Cellular imaging using temporally flickering nanoparticles. Sci. Rep. 5, 8244 (2015).
Ilovitsh, T. et al. Cellular superresolved imaging of multiple markers using temporally flickering nanoparticles. Sci. Rep. 5, 10965 (2015).
Yuan, B. et al. C96H30 tailored single-layer and single-crystalline graphene quantum dots. Phys. Chem. Chem. Phys. 18, 25002–25009 (2016).
Yuan, B. et al. Highly efficient carbon dots with reversibly switchable green–red emissions for trichromatic white light-emitting diodes. ACS Appl. Mater. Interfaces 10, 16005–16014 (2018).
Zalevsky, Z. & Mendlovic, D. Fractional Wiener filter. Appl Opt. 35, 3930–3936 (1996).
Anna, M. et al. Photoluminescence of a single quantum emitter in a strongly inhomogeneous chemical environment. Phys. Chem. Chem. Phys. 17, 14994–15000 (2015).
Acknowledgements
This work was supported by the National Natural Science Foundation of China (NSFC, No. 21875267, 51561145004) and the President’s International Fellowship Initiative, the Chinese Academy of Sciences (PIFI2019VMA0053).
Author information
Authors and Affiliations
Contributions
Z.W. and Z.X. conceived and designed the experiments and analyzed the data. Z.W. performed the nanomaterial preparation and characterization. X.D. assisted with the characterizations of GQDs-OH. Z.Z. performed simulations and analyzed the results for superresolution and spatial sensing. Z.W. and Z.Z. wrote the paper. Z.X., S.Z., and Z.Z. directed the project and revised the manuscript. All authors have contributed to the improvement of this article.
Corresponding authors
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wang, Z., Dong, X., Zhou, S. et al. Ultra-narrow-bandwidth graphene quantum dots for superresolved spectral and spatial sensing. NPG Asia Mater 13, 5 (2021). https://doi.org/10.1038/s41427-020-00269-6
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41427-020-00269-6
This article is cited by
-
Fluorescent carbon dots with excellent moisture retention capability for moisturizing lipstick
Journal of Nanobiotechnology (2021)