Abstract
Quantum dot light-emitting devices have emerged as an important technology for display applications. Their emission is a result of recombination between positive and negative charge carriers that are transported through the hole and electron conductive layers, respectively. The selection of electron or hole transport materials in these devices not only demands the alignment of energy levels between the layers but also balances the flow of electrons and holes toward the recombination sites. In this work, we examine a method for device optimization through control of the charge carrier kinetics. We employ impedance spectroscopy to examine the mobility of charge carriers through each of the layers. The derived mobility values provide a path to estimate the transition time of each charge carrier toward the emitting layer. We suggest that an optimal device structure can be obtained when the transition times of both charge carriers toward the active layer are similar. Finally, we examine our hypothesis by focusing on thickness optimization of the electron transport layer.
Similar content being viewed by others
Introduction
Semiconducting quantum dots (QDs) carry tunable optical properties and good stability and can be synthesized following scalable colloidal synthesis routes. They have attracted much interest in the development of quantum dot light-emitting devices (QLEDs)1,2,3,4,5,6. In a typical QLED, the nanoparticles emit light as a result of radiative recombination between positive and negative charge carriers. The emitting layer of the nanoparticles is termed the active layer. The charges are injected from the anode and cathode to the active layer with adjacent electron and hole transport layers (ETL and HTL, respectively). The device performance is directly related to the light-emission efficiency of the materials selected for the active layer of the device architecture. Among different types of light-emitting nanoparticles, CdSe and CdS QDs (II–VI elements) exhibit high efficiency and stability. Their high photoluminescence (90%) implies the high efficiency of radiative electron-hole recombination in these materials. This recombination has a significant role in electroluminescent devices. Recently, published works exhibit an external quantum efficiency of ~20% for CdSe\CdS QLED devices7,8,9. However, the heavy metal ion cadmium (Cd) raises health concerns and requires corresponding environmental regulations9,10. For example, the EU directive specifies a maximum limit of 100 ppm for the Cd concentration in electronic devices. Hence, it is of high interest to unveil alternative materials and explore the effect of the device architecture on QLED performance. Multinary compounds composed of Cu-In-S, Ag-In-S, and their alloys with ZnS are promising candidates for these applications. These materials offer structural and compositional flexibility, which can be utilized to control their optical properties. Moreover, some works exhibit 60–90% photoluminescence efficiency of these nanoparticles11,12,13. The efficiency of charge transport between layers depends on the alignment of energy levels within a device. It is generally accepted that material selection for the optimal device should give precedence to charge movement toward the active layer, where the charges then recombine14,15,16,17.
Recent works have suggested that not only does energy alignment (i.e., thermodynamics) have a role but also the rates of charge carrier transfer toward the active layer (i.e., kinetics)18. The time that is required for charge transfer from the anode or cathode toward the active layer depends on the charge mobility, concentration of the charge carriers, and thickness of the HTL or ETL. If the hole transport time through the HTL differs from the transport time of electrons through the ETL, accumulation of one type of charge carrier at the interfaces can result in a loss of emission efficiency and can induce degradation. Thus, the optimization of QLEDs requires the development of experimental approaches that will esteem to the abovementioned thermodynamic and kinetic parameters.
Impedance spectroscopy is a well-established experimental method for elucidating the charge transfer kinetics in materials. During impedance analysis, the resistance and capacitance response to alternating voltage as a function of frequency is recorded. Subsequently, the data are fitted to the analytical models, representing equivalent electrical circuits composed of elemental components, such as resistors, capacitors, and inductors. The fitting parameters shed light on the kinetics of charge transfer phenomena in electronic materials or devices.
In this work, we employ impedance spectroscopy to evaluate the apparent charge mobility of electrons and holes in the ETL and HTL, respectively. Based on these values, we estimate the optimal thickness of the ETL for a given thickness of the HTL. Finally, we show the agreement between our model and the efficiency trend of experimentally examined devices.
Results and discussion
QD characterization
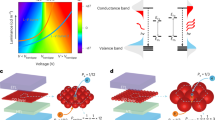
The emission properties of QLEDs are controlled by the optical properties of the nanoparticles. The absorbance combined with the electron affinity determines the alignment of energy levels within a device and the corresponding electroluminescence activation conditions. The photoluminescence spectra complete the picture by revealing radiative electron-hole recombination paths19,20,21,22. Figure 1a shows the absorbance and emission spectra of Cu-In-Zn-S (CIZS) nanoparticles in toluene solution. The broad excitonic transition and large Stokes shift are typical for multinary nanoparticles. They originate from donor–acceptor interactions as a result of crystalline and surface defects21,22,23,24,25,26. In spin-coated nanoparticle films (Fig. 1b, curve b), the distance between the nanoparticles is reduced. Thus, the probability for energy transfer from high-energy transitions to narrower transitions increases, and the corresponding emission spectrum is redshifted (Fig. 1b, the emission is redshifted from curve (a) toward curve (b))27,28,29,30. The application of an external voltage further redshifts the emission (from 685 to 715 nm), implying an enhancement of the interparticle interactions (Figure S1(A)). However, as the voltage is increased, opposite blueshifting (Figure S1(B)) can be observed, as the nanoparticles with wider donor–acceptor energy transitions (a consequence of the shape and size of the composition distribution) are activated (curves c–h).
Layer characterization
An appropriate alignment of energy levels between different layers of QLEDs is often set as one of the criteria in QLED design engineering. Figure 2a exhibits the energy levels of different materials in our devices. The characteristic values of the valence and conduction edges were reported by others16,18,30,31,32,33,34,35,36. In nanoparticles, the valence and conduction edges are size- and composition-dependent. However, the variations remain within tenths of electron volts (eV)37. Hence, these values represent the typical range for reference purposes only. The materials are selected in a manner that prioritizes electron-hole recombination in the QD layer38. Fig. 2b shows the cross section of a typical device that was fabricated in this work.
Although the energy diagram (Fig. 2a) provides an important guideline for the selection of materials, it does not offer sufficient information on the controlled thickness of each individual layer. Optimization of the device structure requires balancing the charge carrier concentrations and their mobility in both the ETL and HTL. In other words, the concentration of the holes in the active layer needs to be similar to the concentration of the electrons to maximize charge carrier recombination18. Thus, we need to achieve the transition time of the electrons from the aluminum contact to the CIZS active layer, which is the same as the transition time of the holes from the ITO to the CIZS layer. By controlling the thicknesses of the ETL and HTL, it should be possible to maximize the availability of electrons and holes at the CIZS interface. This parameter of modulating the flow of charge carriers becomes important in the design and optimization of QLEDs.
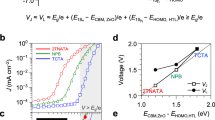
Impedance spectroscopy monitors the system response to alternating current modulation. These data can be used to shed light on the charge transfer and recombination processes39,40,41,42. We employed impedance spectroscopy to probe the apparent charge mobility in each of the layers, viz., ZnO, TPD, and CIZS QDs. A film of the examined material with varying thickness was deposited between gold electrodes (cross-section is shown in Fig. 3a). The response of the system under different frequencies of alternating perturbation can be presented using a Nyquist plot (Fig. 3b). The maximal value of the imaginary component of the impedance is obtained at a frequency corresponding to the characteristic response time of the sample (τ). The value of τ is calculated as a product of the resistivity (R1) and capacity (C1) of the represented electrical circuit (Fig. 3c)25. This characteristic time (τ) is related to the bias voltage (Vb), charge drift mobility (μ), and thickness (d) of the sample through Eq. (1):42,43,44,45,46
Finally, the mobility of the charge carriers can be calculated from the slope of the curve, which describes the dependence of τ on the reciprocal voltage (1/Vb) (Fig. 3d).
a FIB-SEM cross-section of a typical sample for charge mobility measurement, employing impedance spectroscopy analysis. b Nyquist plots for TPD at different bias voltages. c Equivalent circuit for the calculation of the characteristic transfer time. d Transfer time as a function of the reciprocal bias voltage (Vb).
The linear dependence of τ on the bias voltage confirms the validity of Eq. (1). From the slopes of the linear plots (Fig. 3d), we can obtain a ratio of \(\frac{{d^2}}{\mu }\). We further determine the thickness of each layer by scanning electron microscopy and focused ion beam cross-sectional analysis (Figure S2). This allows us to calculate the charge mobility of each of the layers that are part of the light-emitting device. It is difficult to compare the charge mobility in CIZS QDs owing to the dependence on the exact composition, crystalline structure, size, and type of ligands47,48. However, for other layers, we find good agreement with previous reports (Table 1). The mobilities of different layers vary between 1.7 × 10−4 and 1.2 × 10−2 cm2/(V*s). This varying degree of mobility indirectly prescribes the optimal thickness of each layer. To optimize the device thickness, we employ an HTL(PEDOT + TPD) thickness of 45 ± 5 nm and vary the thickness of the ETL (ZnO) layer.
Device optimization
The power conversion efficiency (PCE) of light-emitting devices is calculated as the ratio of the optical power generated from an LED to the electrical input power. The input power is a product of the operating voltage and current. The emission power can be calculated from the photocurrent of a calibrated photodiode placed close to the QD LED assuming Lambertian emission \(\left( {\eta = \frac{{P_{out}}}{{P_{in}}} = \frac{{P_{out}}}{{IV}}} \right)\)30,49. Figure 4 shows the power conversion efficiency as a function of the ZnO layer thickness. We calculate the thickness of the ZnO layer such that it promises equal transition times for electrons (through ZnO) and holes (through PEDOT/TPD) \(\left( {\tau _e(ZnO) = \tau _h} \right)\). For the calculation, we use the mobility values from Table 1 and the measured thickness of the HTL (30–40 nm). Owing to the thickness variation of the HTL, the optimal thickness range is marked by a shadowed zone (rather than by a line) in Fig. 4. Subsequently, we measure the efficiency of the devices as a function of the ZnO layer thickness, between 15 and 460 nm. Initially, increasing the thickness of the ZnO layer from 15 to 60 nm improves the balance between the positive and negative charge carriers by increasing the transition time of electrons. Accordingly, the PCE of the devices increases six times from 0.1% to ~0.6%. The characteristic PCE for multinary nanoparticle light-emitting devices reported by others is ~1%30,31,50. A further increase in ZnO thickness increases the transition length and time of the electrons. This deteriorates the balance of charge carriers with the active layer, and the PCE is reduced. This observation leads to an estimation where the optimal thickness of the ZnO layer in this device is ~80 nm. Obviously, there is an agreement between the estimated optimal range and the experimental results. A more-accurate approximation requires estimating the dependence of the emission efficiency on the depth of the radiative recombination in the active layer.
Power conversion efficiency as a function of the thickness of the electron conductive layer (ZnO) for a device with the architecture exhibited in Fig. 2b.
In this work, we showed how impedance spectroscopy analysis can be employed for the measurement of the charge transport time through hole or electron transport layers. While keeping the thicknesses of the hole and active layers constant, we could estimate the optimal thickness of the electron transport layer. Our experimental results show that the maximal emission efficiency is obtained when the negative and positive charge carrier transition times are equal. Further work is required to estimate the contribution of the active layer thickness and emissions from different depths of this layer.
Conclusions
The outstanding optical properties of colloidal QDs make them good candidates for light-emitting devices. A typical QD LED is composed of a light-emitting layer between the electron and hole conductors. The efficiency of the devices is a result of the nanoparticle emission efficiency and the device architecture. Commonly used interlayer energy alignment (a thermodynamic consideration) provides a guideline for efficient charge transfer. However, it does not provide any information regarding the film thickness, which affects the transition time of the charge carriers. Unequal transition times of positive and negative charge carriers lead to charging phenomena and subsequently nonradiative decay processes. Hence, an unequal transition time deteriorates the device efficiency. Impedance spectroscopy can be employed to obtain essential information on the charge mobility in each of the layers. Based on these data, the optimal thickness of each of the layers can be evaluated.
Supporting information
The supporting information contains experimental details, the synthesis of QDs, device fabrication, and optical and material characterizations.
Change history
26 February 2021
A Correction to this paper has been published: https://doi.org/10.1038/s41427-020-00263-y
References
Zaiats, G., Ikeda, S., Kinge, S. & Kamat, P. V. Quantum dot light-emitting devices: beyond alignment of energy levels. ACS Appl. Mater. Interfaces 9, 30741–30745 (2017).
Kim, H. et al. Characteristics of CuInS2/ZnS quantum dots and its application on LED. J. Cryst. Growth 326, 90–93 (2011).
Kim, J.-H. & Yang, H. All-solution-processed, multilayered CuInS2/ZnS colloidal quantum-dot-based electroluminescent device. Opt. Lett. 39, 5002–5005 (2014).
Qian, L., Zheng, Y., Xue, J. & Holloway, P. H. Stable and efficient quantum-dot light-emitting diodes based on solution-processed multilayer structures. Nat. Photonics 5, 543–548 (2011).
Coe, S., Woo, W. K., Bawendi, M. & Bulovic, V. Electroluminescence from single monolayers of nanocrystals in molecular organic devices. Nature 420, 800–803 (2002).
Chuang, C.-H. M., Brown, P. R., Bulović, V. & Bawendi, M. G. Improved performance and stability in quantum dot solar cells through band alignment engineering. Nat. Mater. 13, 796–801 (2014).
Mashford, B. S. et al. High-efficiency quantum-dot light-emitting devices with enhanced charge injection. Nat. Photonics 7, 407–412 (2013).
Chen, H. et al. All-solution-processed quantum dot light emitting diodes based on double hole transport layers by hot spin-coating with highly efficient and low turn-on voltage. ACS Appl. Mater. Interfaces 10, 29076–29082 (2018).
Shirasaki, Y., Supran, G. J., Bawendi, M. G., Bulovic, V. & Bulović, V. Emergence of colloidal quantum-dot light-emitting technologies. Nat. Photonics 7, 13–23 (2013).
Zhang, Y. et al. Employing heavy metal-free colloidal quantum dots in solution-processed white light-emitting diodes. Nano Lett. 11, 329–332 (2011).
Marin, R. et al. Mercaptosilane-passivated CuInS2 quantum dots for luminescence thermometry and luminescent labels. ACS Appl. Nano Mater. 2, 2426–2436 (2019).
Li, L. et al. Highly luminescent CuInS2/ZnS core/shell nanocrystals: cadmium-free quantum dots for in vivo imaging. Chem. Mater. 21, 2422–2429 (2009).
Yoon, S.-Y. et al. Systematic and extensive emission tuning of highly efficient Cu–In–S-based quantum dots from visible to near infrared. Chem. Mater. 31, 2627–2634 (2019).
Steckel, J. S. et al. Color-saturated green-emitting QD-LEDs. Angew. Chem. Int. Ed. Engl. 45, 5796–5799 (2006).
Anikeeva, P. O., Halpert, J. E., Bawendi, M. G. & Bulović, V. Quantum dot light-emitting devices with electroluminescence tunable over the entire visible spectrum. Nano Lett. 9, 2532–2536 (2009).
Lee, K.-H. et al. Highly efficient, color-pure, color-stable blue quantum dot light-emitting devices. ACS Nano 7, 7295–7302 (2013).
Park, J.-S. et al. Alternative patterning process for realization of large-area, full-color, active quantum dot display. Nano Lett. 16, 6946–6953 (2016).
Dai, X. et al. Solution-processed, high-performance light-emitting diodes based on quantum dots. Nature 515, 96–99 (2014).
Zaiats, G., Kinge, S., Kamat, P. V. Origin of dual photoluminescence states in ZnS-CuInS2 alloy nanostructures. J. Phys. Chem. 120 19461–19469 (2016).
Jara, D. H., Yoon, S. J., Stamplecoskie, K. G. & Kamat, P. V. Size-dependent photovoltaic performance of CuInS2 quantum dot-sensitized solar cells. Chem. Mater. 26, 7221–7228 (2014).
Aldakov, D., Lefrancois, A. & Reiss, P. Ternary and quaternary metal chalcogenide nanocrystals: synthesis, properties and applications. J. Mater. Chem. C. 1, 3756–3776 (2013).
Li, J. et al. Alloyed CuInS2 –ZnS nanorods: synthesis, structure and optical properties. CrystEngComm 17, 5634–5643 (2015).
Zaiats, G., Kinge, S. & Kamat, P. V. Origin of dual photoluminescence states in ZnS-CuInS2 alloy nanostructures. J. Phys. Chem. C. 120, 10641–10646 (2016).
Torimoto, T. et al. Facile synthesis of ZnS−AgInS2 solid solution nanoparticles for a color-adjustable luminophore. J. Am. Chem. Soc. 129, 12388–12389 (2007).
Dai, M. et al. Tunable photoluminescence from the visible to near-infrared wavelength region of non-stoichiometric AgInS2 nanoparticles. J. Mater. Chem. 22, 12851 (2012).
Stroyuk, O. et al., A. Origin and dynamics of highly efficient broadband photoluminescence of aqueous glutathione-capped size-selected Ag–In–S quantum dots. J. Phys. Chem. C 25, 13648–13658 (2018).
Hoffman, J. B., Choi, H. & Kamat, P. V. Size-dependent energy transfer pathways in cdse quantum dot–squaraine light-harvesting assemblies: förster versus dexter. J. Phys. Chem. C. 118, 18453–18461 (2014).
Luther, J. M. et al. Structural, optical, and electrical properties of self-assembled films of pbse nanocrystals treated with 1,2-ethanedithiol. ACS Nano 2, 271–280 (2008).
Hughes, B. K. et al. Control of PbSe quantum dot surface chemistry and photophysics using an alkylselenide ligand. ACS Nano 6, 5498–5506 (2012).
Bai, Z. et al. Hydroxyl-terminated CuInS2-based quantum dots: toward efficient and bright light emitting diodes. Chem. Mater. 28, 1085–1091 (2016).
Lee, K. H. et al. Highly efficient, color-reproducible full-color electroluminescent devices based on red/green/blue quantum dot-mixed multilayer. ACS Nano 9, 10941–10949 (2015).
Trizio, L. D. E. et al. Strongly fluorescent quaternary Cu–In–Zn–S nanocrystals prepared from Cu1-x InS2 nanocrystals by partial cation exchange. Chem. Mater. 24, 2400–2406 (2012).
Akkerman, Q. A. et al. From binary Cu2S to ternary Cu–In–S and quaternary Cu–In–Zn–S nanocrystals with tunable composition via partial cation exchange. ACS Nano 9, 521–531 (2015).
Nelson, H. D. & Gamelin, D. R. Valence-band electronic structures of Cu + -doped ZnS, alloyed Cu–In–Zn–S, and ternary CuInS2 nanocrystals: a unified description of photoluminescence across compositions. J. Phys. Chem. C. 122, 18124–18133 (2018).
Pan, J. et al. Size tunable ZnO nanoparticles to enhance electron injection in solution processed QLEDs. ACS Photonics 3, 215–222 (2016).
Fong, H. H., Lun, K. C. & So, S. K. Hole transports in molecularly doped triphenylamine derivative. Chem. Phys. Lett. 353, 407–413 (2002).
Chen, B. et al. Template synthesis of CuInS2 nanocrystals from In2S3 nanoplates and their application as counter electrodes in dye-sensitized solar cells. Chem. Mater. 27, 5949–5956 (2015).
Coe-Sullivan, S., Woo, W.-K., Steckel, J. S., Bawendi, M. & Bulović, V. Tuning the performance of hybrid organic/inorganic quantum dot light-emitting devices. Org. Electron. 4, 123–130 (2003).
Kern, R., Sastrawan, R., Ferber, J., Stangl, R. & Luther, J. Modeling and interpretation of electrical impedance spectra of dye solar cells operated under open-circuit conditions. Electrochim. Acta 47, 4213–4225 (2002).
Mora-Seró, I. et al. Recombination rates in heterojunction silicon solar cells analyzed by impedance spectroscopy at forward bias and under illumination. Sol. Energy Mater. Sol. Cells 92, 505–509 (2008).
Mora-Seró, I. et al. Implications of the negative capacitance observed at forward bias in nanocomposite and polycrystalline solar cells. Nano Lett. 6, 640–650 (2006).
Rath, A. K., Lasanta, T., Bernechea, M., Diedenhofen, S. L. & Konstantatos, G. Determination of carrier lifetime and mobility in colloidal quantum dot films via impedance spectroscopy. Appl. Phys. Lett. 104, 63504 (2014).
Das, M. et al. Equivalent circuit analysis of Al/rGO-TiO2 metal-semiconductor interface via impedance spectroscopy: graphene induced improvement in carrier mobility and lifetime. Mater. Sci. Semicond. Process. 82, 104–111 (2018).
Scher, H. Time scale invariance in transport and relaxation. AIP Conf. Proc. 256, 485–494 (1992).
Long, Q., Dinca, S. A., Schiff, E. A., Yu, M. & Theil, J. Electron and hole drift mobility measurements on thin film CdTe solar cells. Appl. Phys. Lett. 105, 42106 (2014).
Maynard, B. et al. Electron and hole drift mobility measurements on methylammonium lead iodide perovskite solar cells. Appl. Phys. Lett. 108, 173505 (2016).
Yun, H. J. et al. Charge-transport mechanisms in CuInSexS2–x quantum-dot films. ACS Nano 12, 12587–12596 (2018).
Draguta, S., McDaniel, H. & Klimov, V. I. Tuning carrier mobilities and polarity of charge transport in films of CuInSexS2-x quantum dots. Adv. Mater. 27, 1701–1705 (2015).
Gong, X. et al. Highly efficient quantum dot near-infrared light-emitting diodes. Nat. Photonics 10, 253 (2016).
Kim, J.-H. et al. White electroluminescent lighting device based on a single quantum dot emitter. Adv. Mater. 28, 5093–5098 (2016).
Heun, S. & Borsenberger, P. M. A comparative study of hole transport in vapor-deposited molecular glasses of N,N′,N″,N‴-tetrakis(4-methylphenyl)-(1,1′-biphenyl)-4,4′-diamine and N,N′-diphenyl-N,N′-bis(3-methylphenyl)-(1,1′-biphenyl)-4,4′-diamine. Chem. Phys. 200, 245–255 (1995).
Rutledge, S. A. & Helmy, A. S. Carrier mobility enhancement in poly(3,4-ethylenedioxythiophene)-poly(styrenesulfonate) having undergone rapid thermal annealing. J. Appl. Phys. 114, 133708 (2013).
Acknowledgements
We thank the ND Energy Materials Characterization Facility (MCF) for the use of their XPS and thermal evaporator. We also thank Sachin Kinge for helpful discussions and Toyota Motors Europe for their support during the preliminary work. GZ acknowledges the postdoctoral support received from ND Energy, University of Notre Dame. SI thanks Osaka Municipal Technical Research Institute for supporting his stay at the Notre Dame Radiation Laboratory. PVK acknowledges the support by the Division of Chemical Sciences, Geosciences, and Biosciences, Office of Basic Energy Sciences of the US Department of Energy through award DE-FC02-04ER15533. This is NDRL no. 5262 from the Notre Dame Radiation Laboratory.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zaiats, G., Ikeda, S. & Kamat, P.V. Optimization of the electron transport layer in quantum dot light-emitting devices. NPG Asia Mater 12, 57 (2020). https://doi.org/10.1038/s41427-020-00237-0
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41427-020-00237-0
This article is cited by
-
Recent progress in organic waste recycling materials for solar cell applications
Environmental Science and Pollution Research (2023)