Abstract
Magnetostriction is the emergence of a mechanical deformation induced by an external magnetic field. The conversion of magnetic energy into mechanical energy via magnetostriction at the nanoscale is the basis of many electromechanical systems such as sensors, transducers, actuators, and energy harvesters. However, cryogenic temperatures and large magnetic fields are often required to drive the magnetostriction in such systems, rendering this approach energetically inefficient and impractical for room-temperature device applications. Here, we report the experimental observation of giant magnetostriction in single-crystal nickel nanowires at room temperature. We determined the average values of the magnetostrictive constants of a Ni nanowire from the shifts of the measured diffraction patterns using the 002 and 111 Bragg reflections. At an applied magnetic field of 600 Oe, the magnetostrictive constants have values of λ100 = −0.161% and λ111 = −0.067%, two orders of magnitude larger than those in bulk nickel. Using Bragg coherent diffraction imaging (BCDI), we obtained the three-dimensional strain distribution inside the Ni nanowire, revealing nucleation of local strain fields at two different values of the external magnetic field. Our analysis indicates that the enhancement of the magnetostriction coefficients is mainly due to the increases in the shape, surface-induced, and stress-induced anisotropies, which facilitate magnetization along the nanowire axis and increase the total magnetoelastic energy of the system.
Similar content being viewed by others
Introduction
Significant interest in magnetostrictive nanostructures dates back to the mid-1970s1, with many reports on thin films, multilayers, and superlattices exhibiting large magnetostriction2,3,4. In these planar systems, a large magnetostrictive strain on the order of 0.1% was observed for textured Co0.75Fe0.25 thin films5, while Tb0.3Dy0.7Fe2 bulk crystals showed magnetostriction λ111 values of ~0.16%6,7. Giant magnetostriction is often achieved by alloying transition metals, such as nickel or iron, with rare-earth elements, such as dysprosium or terbium. At room temperature, TbFe2 and SmFe2 demonstrate values above 0.2% at high magnetic fields up to 25 kOe7. The magnetostriction of rare-earth HoFe2 is relatively small at room temperature but reaches −0.075% at 4.2 K8. The dependence of the magnetostriction value on the stoichiometry of Fe-Ga alloys has been extensively studied, and in Fe83Ga17, the λ100 magnetostriction coefficient can reach 0.02% at room temperature9. In Fe81Ga19 alloys, an enhanced magnetostriction coefficient of λ100 = 0.039% was measured by differential X-ray absorption spectroscopy (XAS)10.
Observation of giant magnetostriction often requires high magnetic fields (H > 0.2 T) or low temperatures, restricting its use in practical applications. Transition-metal-based alloys have been extensively used in actuator and sensor applications. At room temperature, the magnetostriction values of bulk single-crystal nickel (Ni) along the [100] and [111] crystallographic directions are λ100 = −46 × 10−6 and λ111 = −24 × 10−6, respectively6,11,12. Although the magnetostrictive coefficients of bulk nickel are not very large compared to other systems, pure nickel is resistant to corrosion, has high electrical and thermal conductivity, and has a high Curie temperature, properties that make it good for protective coatings, heat exchangers, sensors, battery components, and energy harvesting applications5,13,14,15.
In contrast to the need for recharging, the limited lifetime, and the often unrecyclable toxic remnants of electrochemical batteries, harvesting energy from magnetostrictive materials is environmentally friendly and provides continuous energy flows generated from ambient structural vibrations13. Central to the success of such applications is the need to tailor the size, shape, and nanoscale lattice strain, which originates from the growth conditions and influences the stability and functionality. To engineer magnetostrictive devices with high sensitivity and reliability, it is vital to understand the fundamental interactions between the lattice strain, dimensionality, and magnetic moment under the influence of external magnetic fields. To date, little is understood about the strain distribution or magnetostriction at the nanoscale due to the experimental challenges faced during characterization.
Traditional nondestructive methods, such as scanning electron microscopy (SEM) and atomic force microscopy (AFM), provide detailed information about the surface structure but cannot probe the volume16. Transmission electron microscopy (TEM) can provide information on the crystal structure within a material but requires an electron-transparent lamella cross-section for imaging17. Such invasive sample preparation can alter the properties of the material, prohibiting further detailed in operando studies in the presence of external stimuli.
Until recently, only measurements of magnetostriction for deformations of macroscopic objects or averaged over a large number of nanoscale objects have been possible because of the limited sensitivity and resolution in probing structural distributions at the nanoscale. Third-generation synchrotron-based, Bragg coherent X-ray diffraction imaging is a nondestructive tool for the three-dimensional (3D) visualization of strain fields18, phonon modes19, and defect dynamics20,21,22 in crystals smaller than the coherence length23, typically on the order of a few micrometers. Here, we exploit the sensitivity of Bragg coherent diffraction imaging (BCDI) to visualize the strain fields within the illuminated volume of a single-crystal (001) grown Ni nanowire (NW) induced by an external magnetic field.
Materials and methods
A Ni NW was grown by thermal chemical vapor deposition24. We employed BCDI to compare 3D images of the shape and local nanoscale strain of an individual Ni NW during the application of an external magnetic field. BCDI allows retrieval of projections of the crystal lattice displacements on the diffraction vector of a given Bragg reflection25. To measure the magnetostrictive coefficients λ100 and λ111 of the NW, we collected diffraction patterns as a function of the externally applied magnetic field H for the 002 and 111 Bragg peaks. We quantitatively determined the volume-averaged values of the λ100 and λ111 magnetostriction coefficients by tracking the angular shifts of the measured diffraction patterns with respect to the state at zero magnetic field. In this way, we measured the magnetostrictive strain induced along the [001] and [111] crystallographic directions for external magnetic fields of 200 and 600 Oe.
We collected a series of coherent diffraction patterns from a single NW at the Bragg condition for the Ni 002 reflection with the experimental setup shown in Fig. 1a. Coherent X-rays were produced by an undulator, monochromatized by a Si (111) monochromator, and focused using a set of Kirkpatrick-Baez (KB) mirrors down to a 2 × 2 μm2 coherent X-ray wavefront. For precise calculation of the magnetostriction coefficients, it is important to know the magnitudes and angles of the magnetization vector with respect to the crystallographic axes of the NW. For the measurement of the λ001 magnetostrictive coefficient, the sample was rotated at the Bragg condition for the nickel 002 reflection. By rotating the sample along θ, we tracked the maximum of the diffracted intensity for a given external magnetic field. After increasing the magnetic field, we repeated the process of rotating the sample and recorded the diffraction patterns as a function of the angle of incidence. The change in the average lattice constant inside the illuminated volume of the nanowire was calculated using Bragg’s law, \(2d\sin \theta = \lambda\). A detailed description of the X-ray data analysis used for the calculation of the magnetostriction coefficients can be found in the Supplemental Information.
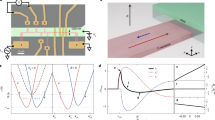
a Experimental setup of coherent X-ray diffraction measurements. A monochromatic X-ray beam with an energy of 8.9 keV focused by Kirkpatrick-Baez mirrors illuminates the Ni nanowire. Coherent X-ray diffraction patterns were collected by rocking the nanowire through the 111 and 002 Bragg peaks in increments of 0.005°, with a two-dimensional pixel array detector placed 0.5 m from the sample. The applied magnetic field H is normal to the [001] direction of the nanowire and at an arbitrary angle δ with the [100] crystal axis. b Plot of the magnetostriction coefficients λ100 and λ111 of the Ni NW as a function of the applied magnetic field. Due to the uncertainty in the exact angles of the saturation magnetization with respect to the crystal axes, we provide a range of values for the λ111 coefficient, located between the top red and bottom blue curves
Due to the presence of different structures on the substrate surface, such as nanowires, cubes, and deposited film, we were unable to determine the saturation magnetization of a single nanowire using superconducting quantum interference device (SQUID) magnetometry measurements11. In ref. 26, the saturation magnetic field of a single 200 × 200 × 8000 nm3 Ni NW was determined by magnetoresistance measurements to be ~10 kOe at room temperature26. In our experiment, we were able to apply magnetic fields parallel to the (001) crystallographic planes (roughly normal to the [001] direction of the NW long axis) up to 600 Oe, far below the saturation magnetic field. Increasing the strength of the applied magnetic field led to a reorientation of domains in the direction of the field. We also observed that the variation in the magnetostriction effect as a function of the applied magnetic field direction was negligible, consistent with previous observations in nickel27,28.
Results
Figure 1b shows the average values of the λ100 and λ111 magnetostrictive coefficients obtained by measuring the induced strain along the [001] and [111] crystallographic directions. The average values of the magnetostrictive strain were obtained by tracking the relative shifts of the 002 and 111 Bragg peaks as a function of the applied magnetic field. The measured diffraction patterns, shown in Fig. 2, show clear magnetic field-induced changes in the strain field in the Ni NW. The strain is defined with respect to the strain state of the NW in the absence of an applied magnetic field (H = 0). The measured diffraction patterns are shown in Fig. 2. As a reference for the calculation of the volume-averaged strain, the centroid of the intensity distribution of the diffraction pattern measured at zero magnetic field was used. For applied magnetic fields of 200 and 600 Oe, the 111 reflection broadens, and the centroid of the diffraction pattern shifts to a higher 2θ angle. Repeated measurements show that the transformation is reproducible and reversible. The values are summarized along with the magnetostrictive coefficients in Table 1.
For crystals with easy axes along the [100] or [111] crystallographic directions, when the magnetostrictive strain is measured along the [001] direction, \(\lambda _{{\mathrm{si}}}^{{\mathrm{002}}}\), and the saturation magnetostriction vector is normal to the [001] direction, the λ100 magnetostrictive coefficient is given by \(\lambda _{100} = - 2\lambda _{si}^{002}\). In nickel, the magnetostriction is independent of the growth direction; thus, this formula is valid for every arbitrary angle between the magnetization direction and the [100] crystallographic direction (see the Supplemental Information)11,29.
The determination of the λ111 magnetostrictive coefficient is more complicated since this coefficient depends on the directional cosines of the saturation magnetization with respect to the crystal axes of the NW. Nevertheless, by carefully considering the experimental geometry and the cases where the magnetization vector angles attain their extreme values, we bracket the value of this coefficient by \(\lambda _{111}^{{\mathrm{min}}} \le \lambda _{111} \le \lambda _{111}^{{\mathrm{max}}}\), where:
as analytically derived in the Supplemental Information.
Table 1 shows that at 600 Oe, a maximum average tensile strain of 0.081% is measured along the [001] direction. In accordance with the conservation of volume, the in-plane strain is a compressive −0.16%, equivalent to the λ100 magnetostrictive coefficient. The average in-plane strain corresponds to the direction of magnetization of the NW and has an arbitrary angle with the [100] direction. Along the [111] direction, the strain is also compressive and takes values up to 0.067%. The compressive strain along the [100] and [111] crystallographic directions within the NW leads to negative magnetostriction values, as in bulk nickel.
In addition to calculating the volume-averaged magnetostrictive coefficients directly from the Bragg coherent X-ray diffraction patterns, we inverted the coherent X-ray diffraction data to obtain 3D maps of the magnetic field-induced strain. The reconstructed u111 displacement of the NW at zero magnetic field is shown in Fig. 3. The image shows a 200 nm-wide NW with a length of ~2 μm. Even at zero magnetic field, the displacement projected on an isosurface of the nanowire shows two regions with important strain fields at the left and right edges of the nanowire. The retrieved map of the displacement field inside the illuminated volume of the Ni NW does not show significant strain induced by the Si substrate and transferred through the Si/Ni interface. In previous work on ferromagnetic Ni nanocubes, it was shown that although the substrate induced strain on the order of 0.05% at the interface of the nanocubes, the change in the magnetic anisotropy was negligible30. Thus, we believe that the effect of the interface-induced strain is not the dominant effect explaining the large magnetostriction values experimentally observed.
In addition to the effect of the interface-induced strain, the Ni NWs are likely oxidized, forming a very thin NiO shell around their Ni core. In the work of Pratt et al., TEM measurements revealed that in Fe nanoparticles, oxidization led to the formation of a 2 nm-thick FeO shell, and large strains up to 15% were experimentally measured31. In Fig. 3, we observe two important strain fields, which start at the NW interfaces and may be due to oxidation. This result suggests that there might be a local contribution of oxidation to the total strain of the Ni NW observed at zero magnetic field. Nevertheless, the reported values of magnetostriction were defined with respect to the strain state of the NW at zero magnetic field and are thus not compromised by the presence of the observed strain fields at zero magnetic field.
When the value of the applied magnetic field is increased to 200 Oe, the surface of the local strain fields is extended around the initial nucleation sites. Figure 4 shows maps of the lattice displacements directly depicting the changes in the crystal strain due to the presence of an external magnetic field. The contours are colored based on the local values of the lattice displacement components u001 and u111 for magnetic fields of 200 Oe and 600 Oe. Both the top and bottom figures indicate the presence of magnetostrictive strain intrinsic to the nanowire.
Recent studies using X-ray magnetic circular dichroism (XMCD) and X-ray photoemission electron microscopy (PEEM) showed that the magnetization inside Ni NWs has periodic patterns26. More specifically, at an applied magnetic field of 5 kOe, alternating magnetic domains with a periodicity of 240 nm were observed26. Using BCDI, we observed important strain fields at much smaller magnetic field values within the 2-μm-long region of the 200-nm-diameter single nanowire illuminated by the X-ray beam. A comparison of Fig. 4 with the results of ref. 26 shows that the strain fields at the two sites of the nanowire correspond to the presence of different magnetic domains inside the nanowire. The fact that the two regions expand as the magnetic field increases suggests that the lattice strain depends on the magnetization of the domains.
Usually, the dominant mechanism of the magnetostrictive strain is domain rotation. Rod-shaped crystals are easier to magnetize along the rod axis, as in the case of the Ni NW11. Thus, we expect that the easy axis of the NW is almost parallel to the [001] direction. During our experiment, the external magnetic field was normal to the [001] long axis of the NW; thus, the magnetic moments are expected to gradually switch by ~90° from along the [001] axis to the magnetic field direction.
The large length/diameter ratio of the Ni NW (r >10) leads to an important change in its dimensions since the NW expands along the [001] direction and contracts along the [100], consistent with the observed lattice contraction along the [111] direction and with the assumption that the total volume remains unchanged (ΔV/V = 0). This tetragonal distortion likely originates from the unsaturated bonds at the NW surface, driving the structure of the Ni unit cell from face-centered cubic (fcc) to tetragonal with ratio c/a = 1.0012. The presence of this tetragonal distortion, with a tensile axial strain along the long [001] axis of the nanowire and a compressive in-plane strain, is consistent with the charge density shifting closer to the NW axis to compensate for unsaturated bonds at the surface.
Magnetoelastic energy density calculation
In magnetoelastic vibration energy harvesters, the inverse magnetostrictive effect is used to transform the magnetoelastic energy to an electric current by coupling the generated magnetic field with coils in electric circuits13. The magnetoelastic energy produced via the inverse magnetostrictive effect is proportional to the λ100 and λ111 magnetostriction coefficients as described by the below equation:
where K1 = −5 mJ/cm3 is the magnetocrystalline anisotropy constant for nickel, σ = εE is the applied stress, ε is the induced strain, E = 190 GPa is the Young’s modulus of nickel, α1, α2, and α3 are the directional cosines of the magnetization vector, and γ1, γ2, and γ3 are the directional cosines of the applied stress with respect to the crystallographic axes32,33. For an axial stress applied along the [001] direction of the nanowire, using the magnetostriction coefficients measured at 600 Oe and assuming an elastic strain of 0.1%, the magnetoelastic energy density of a single nanowire is approximately 0.5 mJ/cm3.
Mechanism of giant magnetostriction
There are several physical mechanisms responsible for giant magnetostriction. In Fe2TiO4, the giant magnetostriction values of λ100 = 0.47% and λ111 = 0.13% for the magnetostrictive coefficients measured at a temperature of 77 K and an externally applied magnetic field of 30 kOe are explained by softening of the crystal lattice34. More specifically, the magnetostrictive coefficients are related to the elastic constants by λ100 = −3/2 B1/(c11 − c12) and λ111 = −1/3 B2/c44, where B1 and B2 are the magnetoelastic constants. The decrease in the values of the elastic constants c11−c12 and c44 with decreasing temperature is associated with Jahn-Teller distortions35. Recently, the giant magnetostriction observed in rare-earth-doped Fe–Ga alloys was attributed to nanoheterogeneities induced by the dopants2.
However, extended X-ray absorption fine-structure (XAFS) analysis of the second coordination shell around Ga provides clear evidence for the presence of one highly strained (+4%) Ga–Ga pair and five Ga–Fe pairs among six crystallographically equivalent <100> atomic pairs2. This result supports recent total energy calculations, in which the large magnetostriction in these alloys is attributed to the strain caused by the rotation of the magnetization in the vicinity of such defects. Strain is expected to increase the strain-induced anisotropy and enhance pre-existing strain heterogeneities. Total energy calculations have shown that the magnetocrystalline anisotropy will increase by orders of magnitude in the case of tetragonal distortions36, and our DFT calculations show that compressive strains on the order of 0.1% can significantly enhance the magnetization.
Another effect is the contribution of the shape anisotropy to the total magnetoelastic energy and, as a result, to the induced magnetostriction. More specifically, for single-crystal thin films, the total uniaxial anisotropy energy can be written as a sum of various contributions:
where the term \(- 2\pi M_s^2\) corresponds to the shape anisotropy, Euσ to the stress-induced anisotropy, Eui to the intrinsic magnetocrystalline anisotropy, and Es/t to the surface-induced anisotropy, with t being the thickness37. We can see that the contribution of the last term to the total anisotropy is inversely proportional to the thickness, suggesting that the total magnetic anisotropy energy will be increased by a dimension reduction. The stored magnetoelastic energy also depends on the presence of other types of anisotropy in the system11,33; thus, the contributions of all types of anisotropy to the total magnetoelastic energy should be considered. Solving Eq. (2) with respect to the magnetostrictive coefficients, we obtain the following expression:
which shows that by increasing the total magnetoelastic energy of a ferromagnetic system by increasing the magnetic anisotropies, one can enhance the magnetostrictive coefficients. Finally, since magnetic anisotropy in a crystal is mainly due to spin-orbit coupling and the orbitals are strongly coupled to the crystal lattice, we hypothesize that the orbitals will be influenced by the tetragonal distortion of the Ni unit cell. However, to verify this experimentally, XAS measurements are needed38.
Discussion
The λ100 and λ111 magnetostrictive coefficients were measured for a single-crystal nickel nanowire using coherent X-ray diffraction at the 34-ID-C end station of the Advanced Photon Source. We experimentally observed two orders of magnitude larger magnetostriction coefficients with respect to bulk nickel. The large length/diameter ratio makes the magnetization of the nanowire align along its long axis due to the increased shape anisotropy11, the surface-induced anisotropy increases due to the decrease in the diameter37, and the stress-induced anisotropy increases due to the generation of a tetragonal lattice distortion36. All these separate factors contribute to the total magnetoelastic energy of the nanowire and are responsible for enhancing the magnetostriction coefficients.
Sample growth
Ni nanostructures were grown on Si (100) substrates via a one-step catalyst-free thermal chemical vapor deposition method. A powdered NiCl2.6H2O precursor was first dried at 200 °C in a nickel boat in a quartz tube along with 5 Si (100) substrates lined up next to the boat. The temperature of the system was then raised to 650 °C, and the growth was allowed to occur for 30 min. Argon flow was maintained throughout the process. Afterwards, the entire system was cooled to room temperature while maintaining the Ar flow in the closed system. Scanning electron microscopy revealed that the nickel NWs have a wide range of lengths between 2 and 10 μm, with widths of approximately 200 nm on average23,26. While there are several NWs on the substrate, they are separated by 3–5 μm, allowing illumination of a single NW by the incident X-ray beam.
Coherent X-ray diffraction measurements
Coherent X-rays of E = 8.9 keV with a 1 eV bandwidth, resulting in a longitudinal coherence length of approximately 0.7 μm, from the 34-ID-C beamline of the Advanced Photon Source (APS) were focused onto the sample using Kirkpatrick-Baez (KB) mirrors that achieved a focus of ~2 × 2 μm2. The diffraction patterns in the vicinity of the 002 and 111 Bragg reflections were measured using a direct-detection charge-coupled device (CCD) with 20.5 × 20.5 μm2 pixels located 1.05 m from the sample. In the presence of an external magnetic field, the 3D X-ray diffraction data were acquired by rotating θ in increments of 0.005°, with a total of 81 steps.
Phase retrieval
The 3D coherent X-ray diffraction data were inverted using a support-based phasing procedure, in which the error reduction (ER) and hybrid input-output (HIO) algorithms were cycled39,40,41. The phasing process for a given initialization of the algorithm was determined to be complete when the square of the error metric was reduced to 10−8. The maximum number of iterations was typically ~4000. To confirm the reproducibility and uniqueness of the obtained solutions, we performed a series of inversions with different random initial guesses of the shape and phase of the NW for zero applied magnetic field. The differences between the many equivalent solutions obtained from random initial phases provide a measure of the resolution of the resulting NW reconstruction in the form of a phase retrieval transfer function (PRTF)42,43. The real-space resolution attained in this work was ~20 nm.
References
Chikazumi, S. Physics of Ferromagnetism. (Oxford University Press, Oxford, UK, 2005).
He, Y. et al. Interaction of trace rare-Earth dopants and nanoheterogeneities induces giant magnetostriction in Fe-Ga alloys. Adv. Funct. Mater. 28, 1800858–1800859 (2018).
Lim, S. H., Kim, H. J., Na, S. M. & Suh, S. J. Application-related properties of giant magnetostrictive thin films. J. Magn. Magn. Mater. 239, 546–550 (2002).
Szymczak, H. From almost zero magnetostriction to giant magnetostrictive effects: recent results. J. Magn. Magn. Mater. 200, 425–438 (1999).
Hunter, D. et al. Giant magnetostriction in annealed Co1-xFex thin-films. Nat. Commun. 2, 518 (2011).
Grössinger, R., Turtelli, R. S. & Mehmood, N. Materials with high magnetostriction. IOP Conf. Ser. Mater. Sci. Eng. 60, 012002 (2014).
Clark, A. E. Magnetic and magnetoelastic properties of highly magnetostrictive rare Earth-iron laves phase compounds. AIP Conf. Proc. 18, 1015–1029 (1974).
Abbundi, R., Clark, A. E. & Koon, N. C. Temperature dependence of the magnetostriction and magnetization in single crystal HoFe2. J. Appl. Phys. 50, 1671–1673 (1979).
Clark, A. E., Restorff, J. B., Wun-Fogle, M., Lograsso, T. A. & Schlagel, D. L. Magnetostrictive properties of body-centered cubic Fe-Ga and Fe-Ga-Al alloys. IEEE Trans. Magn. 36, 3238–3240 (2000).
Ruffoni, M. P. et al. Direct measurement of intrinsic atomic scale magnetostriction. Phys. Rev. Lett. 101, 147202–147204 (2008).
Cullity, B. D. & Graham, C. D. Introduction to magnetic materials. (John Wiley & Sons, Inc, Hoboken, 2009).
Lee, E. W. Magnetostriction and magnetomechanical effects. Rep. Progr. Phys. 18, 184–229 (1955).
Deng, Z. & Dapino, M. J. Review of magnetostrictive vibration energy harvesters. Smart Mater. Struct. 26, 103001–103019 (2017).
Lee, H.-S., Cho, C. & Cho, M.-W. Magnetostrictive micro mirrors for an optical switch matrix. Sensors 7, 2174 (2007).
Li, P. et al. Design and numerical simulation of novel giant magnetostrictive ultrasonic transducer. Results Phys. 7, 3946 (2017).
Bell, D. C. et al. Imaging and analysis of nanowires. Microsc. Res. Tech. 64, 373–389 (2004).
Liu, X. H. et al. Reversible nanopore formation in ge nanowires during lithiation delithiation cycling: an in situ transmission electron microscopy study. Nano Lett. 11, 3993–3997 (2011).
Robinson, I. & Harder, R. Coherent X-ray diffraction imaging of strain at the nanoscale. Nat. Mater. 8, 291–298 (2009).
Clark, J. N., Williams, G. J., Abbey, B., Harder, R. J. & Robinson, I. K. Ultrafast three-dimensional imaging of lattice dynamics in individual gold nanocrystals. Science 318, 777 (2013).
Singer, A. et al. Nucleation of dislocations and their dynamics in layered oxide cathode materials during battery charging. Nat. Energy 3, 641–647 (2018).
Ulvestad, A. et al. Topological defect dynamics in operando battery nanoparticles. Science 348, 1344–1347 (2015).
Clark, J. N. et al. Three-dimensional imaging of dislocation propagation during crystal growth and dissolution. Nat. Mater. 14, 780–784 (2015).
Fohtung, E. et al. Probing the three-dimensional strain inhomogeneity and equilibrium elastic properties of single crystal Ni nanowires. Appl. Phys. Lett. 101, 033107 (2012).
Chan, K. T. et al. Oriented growth of single-crystal Ni nanowires onto amorphous SiO2. Nano Lett. 10, 5070–5075 (2010).
Pfeifer, M. A., Williams, G. J., Vartanyants, I. A., Harder, R. & Robinson, I. K. Three-dimensional mapping of a deformation field inside a nanocrystal. Nature 442, 63–66 (2006).
Kan, J. J. et al. Periodic chiral magnetic domains in single-crystal nickel nanowires. Phys. Rev. Mater. 2, 064406–064408 (2018).
Masiyama, Y. On the magnetostriction of a single crystal of nickel. Sci. Rep. Tohoku Imp. Univ. 17, 945–961 (1928).
Heaps, C. W. The effect of strain on magnetostriction and magnetization in nickel. Phys. Rev. 42, 108–118 (1932).
Kadowaki, S. & Takahashi, M. Magnetostriction constants of nickel-cobalt alloys. J. Phys. Soc. Jpn 50, 1154–1161 (1981).
Manna, S. et al. Characterization of strain and its effects on ferromagnetic nickel nanocubes. AIP Adv. 7, 125025 (2017).
Pratt, A. et al. Enhanced oxidation of nanoparticles through strain-mediated ionic transport. Nature 13, 26–30 (2013).
Cullity, B. D. & Graham, C. D. Introduction to magnetic materials. (John Wiley & Sons, Inc, Hoboken, 2009).
Kittel, C. Introduction to Solid State Physics. 18th edn. (John Wiley & Sons, Inc, USA, 2005).
Ishikawa, Y. & Syono, Y. Giant magnetostriction due to Jahn-Teller distortion in Fe2TiO4. Phys. Rev. Lett. 26, 1335–1338 (1971).
Goodenough, J. B. Jahn-Teller distortions induced by tetrahedral-site Fe2+ ions. J. Phys. Chem. Solids 25, 151–160 (1964).
Brooks, M. S. S., Richter, M. & Sandratskii, L. M. Encyclopedia of Materials: Science and Technology pp. 2059–2070. Elsevier, Amsterdam, 2001).
Hellman, F. Encyclopedia of Materials: Science and Technology pp. 4761–4767. (Elsevier, Amsterdam, 2001).
Pettifer, R. F., Mathon, O., Pascarelli, S., Cooke, M. D. & Gibbs, M. R. J. Measurement of femtometre-scale atomic displacements by X-ray absorption spectroscopy. Nature 435, 78–81 (2005).
Marchesini, S. A unified evaluation of iterative projection algorithms for phase retrieval. Rev. Sci. Instrum. 78, 011301–011310 (2007).
Chen, C. C., Miao, J., Wang, C. W. & Lee, T. K. Application of optimization technique to noncrystalline x-ray diffraction microscopy: Guided hybrid input-output method. Phys. Rev. B 76, 064113 (2007).
Clark, J. N., Huang, X., Harder, R. & Robinson, I. K. High-resolution three-dimensional partially coherent diffraction imaging. Nat. Commun. 3, 993–996 (2012).
Chapman, H. N. et al. High-resolution ab initio three-dimensional x-ray diffraction microscopy. J. Opt. Soc. Am. A 23, 1179–1200 (2006).
Marchesini, S. et al. A unified evaluation of iterative projection algorithms for phase retrieval. Rev. Sci. Instrum. 78, 011301, https://doi.org/10.1063/1.2403783 (2007).
Acknowledgements
This research was supported by the DoD Air Force Office of Scientific Research (AFOSR) under award No FA9550-18-1-0196. Use of the Advanced Photon Source is supported by the US Department of Energy, Office of Science, and Office of Basic Energy Sciences under Contract DE-AC02-06CH11357. The work was in part supported by the Center for Integrated Nanotechnologies, a U.S. DOE BES user facility. Work at UCSD was supported by the US Department of Energy, Office of Science, Office of Basic Energy Sciences under Contract DE-SC0001805. K.T.C. and E.E.F. were supported by NSF Award DMR-0906957.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Pateras, A., Harder, R., Manna, S. et al. Room temperature giant magnetostriction in single-crystal nickel nanowires. NPG Asia Mater 11, 59 (2019). https://doi.org/10.1038/s41427-019-0160-8
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41427-019-0160-8
This article is cited by
-
Direct observation of tensile-strain-induced nanoscale magnetic hardening
Nature Communications (2023)
-
The angle-dependent in-plane magnetostriction of polycrystalline CoFe2O4 film
Applied Physics A (2023)
-
Polarized phonons carry angular momentum in ultrafast demagnetization
Nature (2022)
-
The critical role of spin rotation in the giant magnetostriction of La(Fe,Al)13
Science China Materials (2021)