Abstract
We report systematic studies of a new quasi-one-dimensional (quasi-1D) compound, Ba3TiTe5, and the high-pressure induced superconductivity therein. Ba3TiTe5 was synthesized at high pressure and high temperature. It crystallizes into a hexagonal structure (P63/mcm), which consists of infinite face-sharing octahedral TiTe6 chains and Te chains along the c axis, exhibiting a strong 1D characteristic structure. The first-principles calculations demonstrate that Ba3TiTe5 is a well-defined 1D conductor; thus, it can be considered a starting point to explore the exotic physics induced by pressure by enhancing the interchain hopping to move the 1D conductor to a high-dimensional metal. For Ba3TiTe5, high-pressure techniques were employed to study the emerging physics dependent on interchain hopping, such as the Umklapp scattering effect, spin/charge density wave (SDW/CDW), superconductivity and non-Fermi liquid behavior. Finally, a complete phase diagram was plotted. The superconductivity emerges at 8.8 GPa, near which the Umklapp gap is mostly suppressed. Tc is enhanced and reaches a maximum of ~6 K at ~36.7 GPa, where the SDW/CDW is completely suppressed, and a non-Fermi liquid behavior appears. Our results suggest that the appearance of superconductivity is associated with the fluctuation due to the suppression of the Umklapp gap and that the enhancement of the Tc is related to the fluctuation of the SDW/CDW.
Similar content being viewed by others
Introduction
The one-demensional (1D) system has attracted much attention due to its novel physics and unique phenomena, which are dramatically different from those of two-dimensional (2D) or three-dimensional (3D) systems1,2. When the motion of electrons is confined within one dimension, the electrons cannot move without pushing all the others, which leads to a collective motion and thus spin-charge separation. In this case, the concept of “quasi-particles” with charge and spin degrees of freedoms is replaced with the collective modes, and the electronic state in the 1D system is predicted by Tomonaga-Luttinger liquid (TLL) theory. Pressure is a unique tool for tuning the interchain hopping to gradually transform the 1D conductor into high-dimensional metal (HDM), during which many interesting physical phenomena emerge, such as superconductivity. The properties of quasi-1D conductors dependent on the strength of interchain coupling have been extensively explored in organic compounds, such as (TMTTF)2X and (TMTSF)2X salts, which exhibit a 1D conducting characteristic with an overlapping integral ratio of different axes ta:tb:tc ~ 200:20:13,4,5,6,7. However, the pressure-temperature phase diagrams were plotted only in a narrow range of pressure (generally <2 GPa) for each quasi-1D organic compound. For (TMTTF)2X salts, the conducting chains along the a axis are less coupled. When the temperature decreases, these (TMTTF)2X salts successively undergo a metal-insulator transition induced by Umklapp scattering (U-MIT) and an ordered phase transition, such as charge order, both of which can be gradually suppressed by pressure. While for (TMTSF)2X salts, the enhancement of interchain coupling tb completely suppresses the U-MIT. From this perspective, (TMTSF)2X can be considered the high-pressure phase of (TMTTF)2X. At low temperature, (TMTSF)2X salts exhibit HDM behavior due to single-particle interchain hopping. For (TMTSF)2PF6, a spin density wave (SDW) state forms in the HDM region8. With the application of pressure, the SDW transition is gradually suppressed, and superconductivity is induced9,10,11. When the interchain coupling further increases, such as in (TMTSF)2ClO4, superconductivity appears, with the complete suppression of the SDW12.
In addition to an organic system, inorganic quasi-1D conductors have received considerable attention. For example, in the compound Li0.9Mo6O17, the ratio of conductivity along the b, c, and a axes is ~250:10:113. It has been shown to exhibit a TLL state in the high-temperature region14,15,16. Li0.9Mo6O17 undergoes a dimensional crossover from a 1D conductor to 3D metal at ~24 K. The dimensional crossover destabilizes the TLL fixed point, induces an electronic spin/charge density wave (SDW/CDW) and thus leads to a crossover from metal to semiconductor17. As the temperature decreases further, Li0.9Mo6O17 exhibits a superconducting transition at 1.9 K13,17,18,19,20. M2Mo6Se6 (M = Rb, Na, In, and Tl) is another interesting quasi-1D system with a 4d transition metal, which consists of conducting (Mo6Se6) chains along the c axis that are separated by M cations in the ab-plane21,22,23,24. The interchain coupling is controlled by the size of the M cations and increases with the sequence of Rb, Na, In, and Tl. Rb2Mo6Se6 undergoes a CDW transition at approximately 170 K, while for Na2-δMo6Se6, In2Mo6Se6, and Tl2Mo6Se6, superconductivity appears with Tc of ~1.5, 2.8, and 4.2 K, respectively21,24. Recently, the remarkable quasi-1D superconductor of K2Cr3As3 with Tc ~ 6.1 K and its related superconductors of Cr-233-type (Na/Rb)2Cr3As3 and Cr-133-type (Rb/K)Cr3As3 have been reported25,26,27,28,29. Their conducting chains are double-walled subnanotubes [(Cr3As3)2−]∞ along the c axis that are separated by alkali metal. It is interesting that the superconducting Tc decreases monotonously with the increase in distance between the adjacent conducting chains of [(Cr3As3)2−]∞ in Cr-233-type materials, which is tuned by the radius of the cations of the alkali metal27. Regardless, for inorganic quasi-1D conductors, the dependence of the superconductivity on interchain coupling has been less studied.
Another important series are R3TiSb5 (R = La, Ce) due to their strong 1D structure characteristics, which consist of face-sharing octahedral TiSb6 chains and Sb-chains separated by R atoms30,31,32. If ignoring the contribution of the La atoms, the band structure calculation of the [TiSb5]9− substructure of the La3TiSb5 compound suggests a well-defined 1D conductor30. However, the complementary calculation proves that there are nonnegligible contributions of La to the density of state (DOS) at the Fermi level. The La3+ ions in La3TiSb5 are not perfectly ionic, which leads to a 3D band structure32. It is strongly indicated that La atoms do not play the role of interchain separation but serve as a bridge for electron hopping among the chains.
It is important to find an ideal 1D conductor with a simple structure to systematically explore the interchain-hopping-modulated Umklapp gap, the emerging SDW/CDW and the superconductivity. Here, we used the metastable compound Ba3TiTe5 via the substitution of the rare-earth metal La in La3TiSb5 with the alkali earth metal Ba, and for the charging compensation, we replaced the group VA element of Sb with the group VIA element of Te, which was synthesized under high-pressure and high-temperature (HPHT) conditions. The structure of Ba3TiTe5 consists of infinite octahedral TiTe6 chains and Te chains along the c axis, and our calculation proved that its band structure has a well-defined 1D conducting characteristic. On this basis, to explore the emergent phenomena of the sequence, we further employed high pressure, which is clean without impurity and can effectively and continuously tune the interchain hopping. Finally, we plotted a complete phase diagram with the single material of Ba3TiTe5 and within a wide pressure range to present the evolution from 1D conductor to HDM and the emergent physics, during which the pressure-induced superconductivity was observed. Our results indicate that the fluctuation due to the suppression of the Umklapp gap and SDW/CDW responds to the appearance of superconductivity and the enhancement of Tc, respectively.
Materials and methods
Materials and synthesis
The lumps of Ba (Alfa, immersed in oil, >99.2% pure), Te powder (Alfa, >99.99% pure) and Ti powder (Alfa, >99.99% pure) were purchased from Alfa Aesar. The precursor BaTe was prepared by reacting the lumps of Ba and Te powder in an evacuated quartz tube at 700 °C. Ba3TiTe5 was synthesized under HPHT conditions. The obtained BaTe powder, Te, and Ti powder were mixed according to the elemental ratio of stoichiometric Ba3TiTe5 and ground and pressed into a pellet. The prepressed pellet was treated using a cubic anvil high-pressure apparatus at 5 GPa and 1300 °C for 40 min. After the HPHT process, a black polycrystalline sample of Ba3TiTe5 was obtained.
Measurements
The ambient X-ray diffraction was conducted on a Rigaku Ultima VI (3KW) diffractometer using Cu Kα radiation generated at 40 kV and 40 mA. In situ high-pressure angle-dispersive X-ray diffraction was collected at the Beijing Synchrotron Radiation Facility at room temperature with a wavelength of 0.6199 Å. Diamond anvil cells with a 300 μm cullet were used to produce the high pressure, and silicone oil was used as the pressure medium. The Rietveld refinements on the diffraction patterns were performed using GSAS software packages33. The crystal structure was plotted with the VESTA software34.
The dc magnetic susceptibility measurement was carried out using a superconducting quantum interference device (SQUID). The resistance was measured by four-probe electrical conductivity method in a diamond anvil cell made of CuBe alloy using a Mag lab system. The diamond culet was 300 μm in diameter. A plate of T301 stainless steel covered with c-BN powder was used as a gasket, and a hole of 150 μm in diameter was drilled in the preindented gasket. Fine c-BN powders were pressed into the holes and further drilled to 100 μm, serving as the sample chamber. Then, NaCl powder was put into the chamber as a pressure-transmitting medium, on which the Ba3TiTe5 sample with dimensions of 60 × 60 × 15 μm3 and a tiny ruby were placed. The pressure was calibrated using the ruby florescent method. At each pressure point, the anvil cell was loaded into the Mag lab system to conduct the transporting measurement, which has an automatically controlled temperature and magnetic field.
Calculations
The first-principles calculations based on density functional theory implemented in VASP were carried out within a primitive cell with an 8 × 8 × 16 k-point grid35. The projector augmented wave pseudopotentials with Perdew, Burke, and Ernzerhof (PBE) exchange-correlation and a 450 eV energy cutoff were used in our calculation36,37. The experimental lattice parameters obtained from XRD were adopted.
Results and discussion
The X-ray diffraction of Ba3TiTe5 under ambient conditions is shown in Fig. 1a. All the peaks can be indexed by a hexagonal structure with lattice constants a = 10.1529 Å and c = 6.7217 Å, respectively. The space group of P63/mcm (193) was used according to the systematic absence of hkl. Finally, Rietveld refinement was performed by adopting the crystal structure of R3TiSb5 (R = La, Ce) as the initial model30,31, which smoothly converged to χ2 = 2.0, Rp = 3.1% and Rwp = 4.4%. The summary of the crystallographic data is listed in Table I.
a The X-ray diffraction pattern and the refinement of Ba3TiTe5. (b) and (c) are schematic plots of the crystal structure, with a view of the projection along the c axis and perpendicular to the c axis, respectively. The atoms in the red dashed circles are Te chains at the Te(2) site. d–f The calculated band structure, PDOS and Fermi surfaces for Ba3TiTe5 under ambient pressure, respectively. g The resistivity as a function of temperature at ambient pressure. The inset is the curve of ln(ρ) versus 1/T
A schematic plot of the crystal structure is shown in Fig. 1b, c. Figure 1b is the top view, with the projection along the c axis, displaying the triangular lattice form, while Fig. 1c is the side view, showing the chain geometry. From Fig. 1b, c, we can see that the crystal structure of Ba3TiTe5 consists of infinite face-sharing octahedral TiTe6 chains and Te chains along the c axis, which are separated by Ba cations. The distance between the adjacent TiTe6 chains is given by the lattice constant a = 10.1529 Å, which is significantly large and responsible for exhibiting a quasi-1D structure characteristic. To explore the 1D characteristics of Ba3TiTe5 from a band structure perspective, we calculated the band structure, partial density of state (PDOS) and Fermi surface via first-principles calculations for Ba3TiTe5 under ambient pressure, as shown in Fig. 1d–f. The hallmark of the band structure is that the bands with the k-point path parallel to the kz-direction intercept the Fermi level, while for the k-point path perpendicular to the kz-direction, the band dispersion is always gapped. Thus, Ba3TiTe5 is a well-defined 1D conductor with a conducting path along the z-direction. Additionally, from the PDOS, it can be seen that the DOS near the Fermi level is dominated by the 3d-orbitals of Ti. The 5p-orbitals of both Te(1) and Te(2) from the TiTe6 chains and Te chains, respectively, contribute to the DOS near the Fermi level as well, which implies that both the TiTe6 chains and Te chains are conducting chains. The DOS from the Ba 6s-orbital, presented in Fig. 1e, is close to zero at the Fermi level and can be ignored, which suggests that the conducting chains are well separated by Ba2+ ions. Figure 1f displays the calculated Fermi surfaces. There are four sheet-like Fermi surfaces perpendicular to the kz-direction, and the bottom sheet can be shifted by the wave vectors k1 and k2 to nest with the above two sheets, respectively. Therefore, the Fermi surfaces are unstable, and the transport property of the 1D conductor should be described by TLL theory. The resistivity measurement at ambient pressure for Ba3TiTe5 was carried out, as shown in Fig. 1g. The resistivity increases as the temperature decreases, exhibiting semiconducting behavior. The inset shows ln(ρ) versus the reverse temperature. By fitting the ln(ρ)-1/T curve according to the formula ρ ∝ exp(Δg/2kBT), where kB is the Boltzmann constant, the band gap of Δg can be estimated to be 232 meV. For a 1D conducting system, Umklapp scattering has an important influence on the electron transfer, which usually results in a correlation gap and insulating state38,39,40,41. In addition to the Umklapp scattering effect, the nonzero disorder in the 1D conducting system tends to localize the electrons. If the disorder dominates the localization, the electron transport should be described by the model of various range hopping. Here, the resistivity following the Arrhenius law within the measured temperature range proves that the Umklapp scattering effect should play a role in the metal-insulating transition, as the Umklapp process produces a real correlation gap. Therefore, the inconsistency between the measured resistivity and the calculated results should arise from the Umklapp scattering effect. In addition, the magnetic susceptibility measurement shows that Ba3TiTe5 is nonmagnetic in the measured temperature range from 2 K to room temperature, as shown in Fig. S1.
High pressure is an effective way to tune the lattice of a crystal structure. In the 1D system, it can significantly decrease the distance between adjacent conducting chains, thus enhancing the interchain hopping and moving the 1D conductor to a HDM, during which rich interesting physics are induced, such as the SDW/CDW and superconductivity. Therefore, continually compressing a 1D conductor can provide a potential pathway to understanding the rich phase diagram and the fundamental underlying mechanism. Here, high-pressure X-ray diffraction experiments for Ba3TiTe5 were performed first to study the structural stability and the pressure dependence of the lattice parameters, as shown in Figs. S2–S8. Within the highest measured pressure of 50.6 GPa, the hexagonal structure of Ba3TiTe5 is stable, and the distance between the adjacent conducting chains decreases gradually by 12.1%, which is ideal to explore the exotic emergent physics dependent on the interchain hopping tuned by the pressure. Therefore, we carried out the resistance measurements under high pressure, as shown in Fig. 2a, b. Although the resistance decreases with increasing pressure when the pressure is lower than 7 GPa, it is still very high (~106 Ω at 6.7 GPa and 2 K). At a pressure of 8.8 GPa, the resistance drops dramatically by four orders of magnitude down to ~10–100 Ω, which suggests that the Umklapp scattering-induced gap should be mostly suppressed. A closer view at this pressure shows that there is a downward trend in the low-temperature region of the resistance curve (seen in Fig. S9a, b). The downward transition temperature increases from ~5 K to ~7.5 K as the initial pressure increases and then decreases to ~5.4 K at 15.9 GPa. When the pressure increases further, the downward transition temperature begins to increase again, and the downward behavior gradually develops into a superconducting transition, which persists to the highest measured pressure of 58.5 GPa. Therefore, we suggest that the superconductivity appearance is associated with the fluctuation due to the suppression of the Umklapp gap. In addition, there is an unknown hump independent of pressure at approximately 150 K, as shown in Fig. 2b, which has nothing to do with the superconducting transition and therefore is not discussed in this work. Figure 2c displays the superconducting transition dependent on the magnetic field at 17.3 GPa. At zero field, the onset transition temperature is approximately 3.8 K, and the resistance drops to zero at ~2.8 K. Upon application of the magnetic field, the transition is gradually suppressed. With the criterion of the onset transition as the superconducting transition temperature, the curve of Hc2 versus Tc is plotted in the inset of Fig. 2c, where the slope of –dHc2/dT|Tc is ~3.07 T/K. Using the Werthamer-Helfand-Hohenberg formula μ0Hc2Orb (0) = −0.69 (dHc2/dT) Tc and taking Tc = 3.8 K 42, the upper critical field limited by the orbital mechanism is estimated to be μ0Hc2Orb(0) ~ 8 T. Another mechanism determining the upper critical field is the Pauli paramagnetic effect. The upper critical field is estimated with the formula μ0Hc2P(0) = 1.84 Tc ≈ 7 T43, which is comparable with μ0Hc2Orb(0).
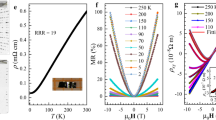
The enlarged view of the resistance curves is plotted in Fig. 3a, b and Fig. 3d, e to display more detailed information. The resistances below 36.7 GPa are normalized by R(150 K). Above 18.9 GPa, in addition to the superconducting transition, a metallic state starts to develop at relatively high temperature and is then followed by a resistance upturn while the temperature decreases, forming a resistance minimum at Tm marked by the arrow shown in Fig. 3a. Tm shifts to low temperature with increasing pressure. At 28.7 GPa, the metal-semiconductor crossover (MSC) Tm was determined by the minimum value of the temperature derivative of the resistance dR/dT (shown in Fig. S10). Although the crossover temperature cannot be unambiguously determined when the pressure exceeds 28.7 GPa, it is clear that the upturn is completely suppressed at 36.7 GPa. Figure 3b shows the superconducting transition below 36.7 GPa. Tc increases from 4.3 K to 6.4 K when the pressure increases from 18.9 GPa to 36.7 GPa. Tc and Tm as a function of pressure are plotted in Fig. 3c; when pressure increases, Tm decreases, while Tc increases. Tc reaches its maximum at the critical pressure of 36.7 GPa, where the MSC is completely suppressed.
The resistance curve for Ba3TiTe5, with an enlarged view of the pressure region from 18.9 to 36.7 GPa shown in (a, b) and from 36.7 to 58.8 GPa in (d, e). c The pressure dependence of the superconducting temperature Tc and the MSC temperature Tm in the range of 18.9–36.7 GPa. f The pressure dependence of the superconducting temperature Tc and the exponent n in the range of 36.7–58.8 GPa
The MSC phenomenon has been reported in the quasi-1D compounds of Li0.9Mo6O17 and Na2-δMo6Se615,17,18,19,21,44. Several mechanisms can cause MSC or MIT, such as Mott instability, SDW/CDW formation, and disorder-induced localization. For Li0.9Mo6O17, the MSC can be gradually suppressed and tuned to be metallic by the magnetic field, suggesting that the MSC is the consequence of the SDW/CDW gap (<1 meV) formation19. Above Tm, Li0.9Mo6O17 exhibits TLL behavior15,16. A dimensional crossover occurs at Tm and causes the destabilization of the TLL fixed point, leading to the formation of an electronic SDW/CDW, which is suggested to be the origin of MSC in Li0.9Mo6O1717. For Na2-δMo6Se6, the MSC temperature Tm is sample dependent and ranges from 70 to 150 K due to a small variation in the Na stoichiometry. It is speculated that the MSC arises from the localization induced by disorder21. For an ideal 1D conducting system, the Fermi surface is unstable, and the system is in the TLL state. When increasing the interchain hopping to move the 1D system towards a HDM, the Fermi surface nesting established in the quasi-1D conducting system can usually give a SDW/CDW transition and open a gap. In the case of Ba3TiTe5 under high pressure, for example, at 19.5 GPa, Fermi surface nesting can be observed, as will be discussed in the following. Therefore, the MSC found in Ba3TiTe5 under high pressure is suggested to arise from the SDW/CDW transition, and the MSC Tm in Fig. 3a, c should correspond to the SDW/CDW transition temperature. Tc increases with SDW/CDW suppression and reaches a maximum when the SDW/CDW transition is suppressed to zero. It is speculated that the superconductivity is enhanced by the fluctuation of the SDW/CDW.
Figure 3d, e shows the temperature dependence of the resistance at pressures exceeding 36.7 GPa. There is an obvious hump below the onset Tc. The resistance curve demonstrates a two-step superconducting transition. In fact, the two-step superconducting transition has been reported in other quasi-1D superconductors, where the onset transition is ascribed to the superconducting fluctuation along individual chains, and the hump signifies the onset of transverse phase coherence due to the interchain coupling21,45,46,47. Here, the lower temperature transition should be attributed to the transverse phase coherence since the two-step transition feature becomes more pronounced when the interchain coupling is enhanced by pressure. The Tc versus pressure in this pressure region is plotted in Fig. 3f. The Tc monotonously decreases with increasing pressure. The normal state of resistance between 10 and 60 K is fitted by the formula R = R0 + ATn, as shown in Fig. 3d, where R0 is the residual resistance, A is the coefficient of the power law, and n is the exponent. The R0 value ranges from 0.07 to 0.11 Ω. The size of our sample for high-pressure measurements is approximately 60 μm × 60 μm with a height of ~15 μm. Thus, the residual resistivity can be estimated to be 1.0–1.6 × 10−4 Ω-cm, which is comparable with that reported for (TMTTF)2AsF67. The obtained exponent n dependent on pressure is plotted in Fig. 3f, which shows that n increases from 0.9 to 1.8 as the pressure increases, i.e., the system develops from a non-FL to an FL state. To further demonstrate the crossover from a non-FL to an FL state, the temperature- and pressure-dependent exponent in the metallic region is plotted in Fig. 5, where the color shading represents the value of the exponent n. The fact that the n value approaches 2 near 26.2 GPa should be due to the effect of the MSC. When the pressure exceeds 36.7 GPa, the Fermi surface nesting should be broken, as will be discussed in the following, and the FL state develops gradually as the pressure increases. It is interesting that the non-FL behavior appears at the critical pressure where the SDW/CDW is wholly suppressed. Therefore, the non-FL behavior may be caused by the SDW/CDW fluctuation. When the system is turned away from the instability of the SDW/CDW, the FL state gradually develops. Although the non-Fermi liquid behavior is generally observed in a 2D system, it was also reported in organic TMTSF salts, an archetypal quasi-1D system7,48,49. In fact, the superconductivity of TMTSF salts shares a common border with the SDW, and the magnetic fluctuation gives rise to the linear temperature dependence of resistivity at low temperature49.
To help understand the above emergent phenomena, we carried out calculations of the band structure, PDOS and Fermi surface for Ba3TiTe5 under different high pressures, which are presented in Fig. 4a–c for 19.5 GPa and Fig. 4d–f for 42.2 GPa. For a pressure of 19.5 GPa, the main difference from ambient pressure is that the conduction band bottom around the Γ and M points sinks down and just touches the Fermi level, thus producing small electronic Fermi pockets, which means that the electrons have coherent interchain hopping. These conduction bands are very flat, suggesting that the interchain electron mobility is small. In addition to the newly formed Fermi pockets, the four Fermi sheets warp slightly such that the bottom sheet can only roughly nest with the second sheet from the top with the vector k2. According to the electron response function,
where χ(q) is the generalized susceptibility, fk is the occupation function of the single-particle states and Ek is the single-particle energy. If part of the Fermi surfaces nest, the susceptibility χ(q) should significantly increase, and thus, the Fermi surfaces lose stability, which generally induces the formation of the SDW/CDW. Therefore, the MSC observed experimentally in the pressure range of 15–30 GPa should arise from the formation of the SDW/CDW induced by Fermi surface nesting. For a higher pressure of 42.2 GPa, the band near the Γ point further sinks down and crosses the Fermi level, which displays a more 3D-like metal character. The Fermi surfaces become more complex. The Fermi surface around the Γ point is more quasi-1D-like, while the Fermi surfaces around the A point are between 2D and 3D. Thus, the Fermi surfaces lose the nesting, and the SDW/CDW are completely suppressed under this pressure, which agrees well with the experimental results. Overall, the ambient 1D electronic state is gradually changed to high dimensions but still with the anisotropic band structure as the pressure increases.
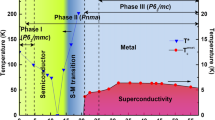
The above emergent phenomena induced by pressure are intrinsic to Ba3TiTe5. First, the possibility of superconductivity from other impurities can be ruled out. Within the X-ray resolution limit, no discernable impurity phase was found in the specimen even in the X-ray diffraction pattern replotted with the intensity on the logarithmic scale, as shown in Fig. S11. Moreover, if there is any impurity containing Ba, Ti, or Te, only the Te is superconducting under high pressure, and the pressure dependence of Tc for Te is completely different from that for Ba3TiTe550,51. Second, the pressure dependence of the superconductivity, the MSC associated with the SDW/CDW and the non-Fermi liquid behavior can be reproduced, as shown in Fig. S12a, b, which confirms the intrinsic properties of Ba3TiTe5. Based on the above experiments and discussions, the final temperature-pressure phase diagram of Ba3TiTe5 is plotted in Fig. 5. At ambient pressure, the quasi-1D conductor Ba3TiTe5 exhibits semiconducting behavior with a gap of approximately 232 meV due to the U-MIT. After the suppression of the U-MIT, the SDW/CDW emerges due to Fermi surface nesting, which leads to an MSC. Subsequently, the SDW/CDW is gradually suppressed by pressure. Superconductivity appears at 8.8 GPa, where the Umklapp gap has been completely suppressed, and Tc increases with the suppression of the SDW/CDW. It reaches a maximum of ~6 K at 36.7 GPa, where the normal state of resistance presents a non-FL behavior due to the SDW/CDW fluctuation. As the pressure increases further, the system develops from a non-FL to an FL state since it is away from the SDW/CDW instability. Our results suggest that the pressure-induced superconductivity in quasi-1D conductor Ba3TiTe5 is initiated by the fluctuation due to the suppression of the Umklapp gap and enhanced by the fluctuation of the SDW/CDW.
The red circle denotes the superconducting temperature Tc, and the purple star is the MSC temperature Tm. In the metallic region, the color shading represents the value of the exponent \({n} = {\mathrm{d}}\left( {{\mathrm{ln}}\left( {{R} - {R}_0} \right)} \right)/{\mathrm{d}}\left( {{\mathrm{ln}}\left( {T} \right)} \right)\)
Conclusions
The novel quasi-1D Ba3TiTe5 conductor was synthesized and extensively studied at high pressure. The conducting paths are the TiTe6 and Te chains, which are separated by Ba cations and thus present a quasi-1D conducting characteristic. For Ba3TiTe5, a complete temperature-pressure phase diagram was obtained within a wide pressure range, which presents the evolution from 1D conductor to HDM and the emergent physics. During the increase in pressure, the increased interchain coupling transformed the ambient 1D conductor to a HDM, during which the pressure-induced SDW/CDW, superconductivity, and non-FL behavior appeared. The superconducting transition temperature Tc reaches its maximum, accompanied by non-FL behavior, when the SDW/CDW gap is suppressed to zero. The superconductivity emergence is closely associated with the suppression of the Umklapp gap and is enhanced by the fluctuation of the SDW/CDW.
References
Voit, J. One-dimensional fermi liquids. Rep. Prog. Phys. 58, 977 (1995).
Giamarchi, T. Quantum physics in one dimension. (Oxford University Press, Oxford, England, 2004).
Jerome, D. Organic conductors: from charge density wave TTF-TCNQ to superconducting (TMTSF)2PF6. Chem. Rev. 104, 5565 (2004).
Kohler, B. et al. Comprehensive transport study of anisotropy and ordering phenomena in quasi-one-dimensional (TMTTF)2X salts (X = PF6,AsF6,SbF6,BF4,ClO4, ReO4). Phys. Rev. B 84, 035124 (2011).
Rose, E. et al. Pressure-dependent structural and electronic properties of quasi-one-dimensional (TMTTF)2PF6. J. Phys.: Condens. Matter 25, 014006 (2013).
Moser, J. et al. Transverse transport in (TM)2X organic conductors: possible evidence for a Luttinger liquid. Eur. Phys. J. B 1, 39 (1998).
Itoi, M. et al. Pressure-induced superconductivity in the quasi-one-dimensional organic conductor (TMTTF)2AsF6. J. Phys. Soc. Jpn. 76, 053703 (2007).
Degiorgi, L. et al. Direct observation of the spin-density-wave gap in (TMTSF)2PF6. Phys. Rev. Lett. 76, 3838 (1996).
Narayanan, A. et al. Coexistence of spin density waves and superconductivity in (TMTSF)2PF6. Phys. Rev. Lett. 112, 146402 (2014).
Vuletic, T. et al. Coexistence of superconductivity and spin density wave orderings in the organic superconductor (TMTSF)2PF6. Eur. Phys. J. B 25, 319 (2002).
Machida, K. & Matsubara, T. Possibility of coexistence of spin-density wave and superconductivity in organic conductor (TMTSF)2PF6. Mol. Cryst. Liq. Cryst. 79, 289 (1982).
Bechgaard, K. et al. Superconductivity in an organic-solid - synthesis, structure, and conductivity of Bis(Tetramethyltetraselenafulvalenium) Perchlorate, (TMTSF)2ClO4. J. Am. Chem. Soc. 103, 2440 (1981).
Greenblatt, M. et al. Quasi two-dimensional electronic-properties of the lithium molybdenum bronze, Li0.9Mo6O17. Solid State Commun. 51, 671 (1984).
Denlinger, J. D. et al. Non-Fermi-liquid single particle line shape of the quasi-one-dimensional non-CDW metal Li0.9Mo6O17: comparison to the Luttinger liquid. Phys. Rev. Lett. 82, 2540 (1999).
Hager, J. et al. Non-fermi-liquid behavior in quasi-one-dimensional Li0.9Mo6O17. Phys. Rev. Lett. 95, 186402 (2005).
Wang, F. et al. New Luttinger-liquid physics from photoemission on Li0.9Mo6O17. Phys. Rev. Lett. 96, 196403 (2006).
Dos Santos, C. A. M. et al. Dimensional crossover in the purple bronze Li0.9Mo6O17. Phys. Rev. Lett. 98, 266405 (2007).
Filippini, C. E. et al. Pressure effect on the transport-properties of superconducting Li0.9 Mo6O17 bronze. Phys. C 162, 427 (1989).
Xu, X. F. et al. Directional field-induced metallization of quasi-one-dimensional Li0.9Mo6O17. Phys. Rev. Lett. 102, 206602 (2009).
Mercure, J. F. et al. Upper critical magnetic field far above the paramagnetic pair-breaking limit of superconducting one-dimensional Li0.9Mo6O17 single crystals. Phys. Rev. Lett. 108, 187003 (2012).
Petrovic, A. P. et al. A disorder-enhanced quasi-one-dimensional superconductor. Nat. Commun. 7, 12262 (2016).
Potel, M., Chevrel, R. & Sergent, M. New pseudo-one-dimensional metals - M2Mo6Se6 (M = Na, in, K, Tl), M2Mo6S6 (M = K, Rb, Cs), M2Mo6Te6 (M = in, Tl). J. Solid State Chem. 35, 286 (1980).
Tarascon, J. M., Disalvo, F. J. & Waszczak, J. V. Physical properties of several M2Mo6X6 compounds (M = group IA metal - X=Se,Te). Solid State Commun. 52, 227 (1984).
Petrovic, A. P. et al. Phonon mode spectroscopy, electron-phonon coupling, and the metal-insulator transition in quasi-one-dimensional M2Mo6Se6. Phys. Rev. B 82, 235128 (2010).
Bao, J. K. et al. Superconductivity in quasi-one-dimensional K2Cr3As3 with significant electron correlations. Phys. Rev. X 5, 011013 (2015).
Tang, Z. T. et al. Unconventional superconductivity in quasi-one-dimensional Rb2Cr3As3. Phys. Rev. B 91, 020506 (2015).
Mu, Q. G. et al. Ion-exchange synthesis and superconductivity at 8.6 K of Na2Cr3As3 with quasi-one-dimensional crystal structure. Phys. Rev. Mater. 2, 034803 (2018).
Liu, T. et al. Superconductivity at 7.3 K in the 133-type Cr-based RbCr3As3 single crystals. Epl 120, 27006 (2017).
Mu, Q. G. et al. Superconductivity at 5 K in quasi-one-dimensional Cr-based KCr3As3 single crystals. Phys. Rev. B 96, 140504 (2017).
Moore, S. H. D., Deakin, L., Ferguson, M. J. & Mar, A. Physical properties and bonding in RE3TiSb5 (RE = La, Ce, Pr, Nd, Sm). Chem. Mater. 14, 4867 (2002).
Bollore, G., Ferguson, M. J., Hushagen, R. W. & Mar, A. New ternary rare-earth transition-metal antimonides RE3MSb5 (RE=La,Ce,Pr,Nd,Sm; M=Ti,Zr,Hf,Nb). Chem. Mater. 7, 2229 (1995).
Murakami, T. et al. Hypervalent bismuthides La3MBi5 (M = Ti, Zr, Hf) and related antimonides: absence of superconductivity. Inorg. Chem. 56, 5041 (2017).
Larson, A. C. & Dreele, R. B. V. General structure analysis system (GSAS). Los Alamos Natl. Lab. Rep. 86, 748 (1994).
Momma, K. & Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 44, 1272 (2011).
Kresse, G. & Hafner, J. Abinitio molecular dynamics for liquid-metals. Phys. Rev. B 47, 558 (1993).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758 (1999).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).
Giamarchi, T. Umklapp process and resistivity in one-dimensional fermion systems. Phys. Rev. B 44, 2905 (1991).
Vescoli, V. et al. Dimensionality-driven insulator-to-metal transition in the Bechgaard salts. Science 281, 1181 (1998).
Pashkin, A., Dressel, M. & Kuntscher, C. A. Pressure-induced deconfinement of the charge transport in the quasi-one-dimensional Mott insulator (TMTTF)2AsF6. Phys. Rev. B 74, 165118 (2006).
Raczkowski, M. & Assaad, F. F. Dimensional-crossover-driven Mott transition in the frustrated hubbard model. Phys. Rev. Lett. 109, 126404 (2012).
Werthamer, N. R., Helfand, K. & Hqhenberg, P. C. Temperature and purity dependence of the superconducting critical field, Hc2. III. electron spin and spin-orbit effects. Phys. Rev. 147, 295 (1966).
Clogston, A. M. Upper limit for critical field in hard superconductors. Phys. Rev. Lett. 9, 266 (1962).
Wu, G. Q. et al. Direct observation of charge state in the quasi-one-dimensional conductor Li0.9Mo6O17. Sci. Rep. 6, 20721 (2016).
Bergk, B. et al. Superconducting transitions of intrinsic arrays of weakly coupled one-dimensional superconducting chains: the case of the extreme quasi-1D superconductor Tl2Mo6Se6. New J. Phys. 13, 103018 (2011).
He, M. Q. et al. 1D to 3D dimensional crossover in the superconducting transition of the quasi-one-dimensional carbide superconductor Sc3CoC4. J. Phys.: Condens. Matter 27, 075702 (2015).
Ansermet, D. et al. Reentrant phase coherence in superconducting nanowire composites. Acs Nano 10, 515 (2016).
Doiron-Leyraud, N. et al. Correlation between linear resistivity and Tc in the Bechgaard salts and the pnictide superconductor Ba(Fe1-xCox)2As2. Phys. Rev. B 80, 214531 (2009).
Jerome, D. & Yonezawa, S. Novel superconducting phenomena in quasi-one-dimensional Bechgaard salts. Comptes Rendus Phys. 17, 357 (2016).
Akahama, Y., Kobayashi, M. & Kawamura, H. Pressure-induced superconductivity and phase-transition in selenium and tellurium. Solid State Commun. 84, 803 (1992).
Gregoryanz, E. et al. Superconductivity in the chalcogens up to multimegabar pressures. Phys. Rev. B 65, 064504 (2002).
Acknowledgements
The present work was supported by the National Key R&D Program of China under grant no. 2018YFA0305700, 2017YFA0302900, and 2015CB921300 and the NSFC under grant no. 11474344. The work from HPSTAR was mainly supported by the National Natural Science Foundation of China (Grant no. U1530402). Jinlong Zhu was supported by the National Thousand-Young-Talents Program.
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhang, J., Jia, Y., Wang, X. et al. A new quasi-one-dimensional compound Ba3TiTe5 and superconductivity induced by pressure. NPG Asia Mater 11, 60 (2019). https://doi.org/10.1038/s41427-019-0158-2
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41427-019-0158-2
This article is cited by
-
Quasi-one-dimensional hydrogen bonding in nanoconfined ice
Nature Communications (2024)
-
Pressured-induced superconducting phase with large upper critical field and concomitant enhancement of antiferromagnetic transition in EuTe2
Nature Communications (2022)
-
A combinatory ferroelectric compound bridging simple ABO3 and A-site-ordered quadruple perovskite
Nature Communications (2021)