Abstract
Harvesting waste heat for useful purposes is an essential component of improving the efficiency of primary energy utilization. Today, approaches such as pyroelectric energy conversion are receiving renewed interest for their ability to turn wasted energy back into useful energy. From this perspective, the need for these approaches, the basic mechanisms and processes underlying their operation, and the material and device requirements behind pyroelectric energy conversion are reviewed, and the potential for advances in this area is also discussed.
Similar content being viewed by others
Power generation processes are plagued by inefficiencies and reject approximately two-thirds of the primary energy produced as waste heat1. A significant portion of this waste is low-grade heat (generally below 100–230 °C), which is both ubiquitous and underutilized. The recovery of this waste heat for energy generation, however, is limited due to the poor efficiency of energy harvesting systems working with small temperature differentials that are well below the fundamental Carnot limit. Solid-state approaches to harvest this energy, like thermoelectrics2, are generally limited by their relatively low figures of merit (FoM) for energy conversion below 100 °C. Vapor-based organic Rankine cycles (ORC) have been demonstrated to be cost effective at a large scale but become cost prohibitive at low powers due to turbine inefficiency3. In turn, research is driven by a need to develop techniques that convert low-grade waste heat with high fractions of Carnot efficiency4,5. Here, we discuss an approach to do just that—pyroelectric energy conversion (PEC).
Pyroelectrics constitute a class of noncentrosymmetric polar crystals that exhibit an inherent coupling between electrical polarization \(P\) and temperature \(T\), such that a change in temperature results in a change in the electric dipole moment or a pyroelectric effect (PE) (Fig. 1a), which is quantitatively described by the pyroelectric coefficient, \(\pi = \left( {\frac{{\partial P}}{{\partial T}}} \right)\). Since the PE manifests as a temperature-dependent change in the surface-charge density, PEs can also be generated via the temperature-dependence of the dielectric permittivity, thermally induced strain in piezoelectric materials6, and flexoelectric effects7 from thermal gradients in all materials. Ferroelectrics are a subset of pyroelectrics that can switch polarization under an applied electric-field and exhibit some of the largest PEs near their phase-transition temperatures, thus often forming the basis of modern PEC devices.
Unlike thermoelectrics that utilize a spatial-temperature gradient, PEC requires a temporal variation in temperature (\(\frac{{\partial T}}{{\partial t}}\)), making PEC highly desirable in instances where temperature gradients are either difficult to establish or the temperature of the heat source is fluctuating. These temperature changes result in a pyroelectric current \(i_p = \pi A\frac{{dT}}{{dt}}\), where A is the area of the device, which means performance scales with the area, not the volume, of a material. This fact leads to a number of potential advantages for thin-film-based devices and thus motivates our focus on materials at such geometries here. To actually harvest waste heat, a PEC device mimics a thermodynamic heat engine. The polarization is analogous to the volume, and the electric-field is analogous to the pressure of the working fluid. A variety of thermodynamic cycles8 have been proposed for PEC and are distinguished by their polarization vs. electric-field (P–E) pathways. While it is possible to envision a Carnot cycle (i.e., two adiabatic (\(2 \to 3\), \(4 \to 1\)) and two isothermal (\(1 \to 2\), \(3 \to 4\)) processes, Fig. 1b), realization of adiabatic processing in a ferroelectric is difficult, making these cycles impractical. Stirling (i.e., two isodisplacement (\(2 \to 3\), \(4 \to 1\)) and two isothermal (\(1 \to 2\), \(3 \to 4\)) processes, Fig. 1c), Brayton (i.e., two isoelectric (\(2 \to 3\), \(4 \to 1\)) and two adiabatic (\(1 \to 2\), \(3 \to 4\)) processes, Fig. 1d), and Ericsson (or Olsen) cycles (i.e., two isothermal and isoelectric processes, Fig. 1e), are used in various situations depending on the sample geometry and heat source8,9. The Olsen cycle has been most widely employed and has been demonstrated to produce some of the highest PEC efficiencies, defined as:10
where \(C\)(T) is the heat capacity, \(T_H\) (\(T_L\)) is the temperature for the heat source (heat sink), \(\oint E\mathrm{d}P\) is the net electrical work done (\(W_E\)), and \(Q_{{\mathrm{ECE}}}\) is the electrocaloric work. Since the vibrational entropy change (associated with the heat capacity) is typically much larger than the dipolar entropy change, the electrocaloric work can be ignored in the denominator of Eq. (1), which represents the heat input. The FoM for PEC11 is thus \(FoM_{\mathrm{PEC}} = \frac{\pi ^{2}T}{C\varepsilon _{0}\varepsilon _{r}}\) ; therefore, a large PEC efficiency requires independently enhancing \(\pi\) and reducing dielectric permittivity \(\varepsilon _r\).
The second-order derivatives of the free energy typically diverge in the vicinity of phase transitions; thus, positioning the material at the brink of a ferroelectric-to-paraelectric phase-transition (Curie temperature, TC) serves as a route to enhance the intrinsic \(\pi\). Consequently, considerable effort has focused on tuning TC via the chemistry12, hydrostatic pressure13, or epitaxial strain14 in the case of thin films. In addition, transitions between various ferroelectric phases can result in polarization rotation (e.g., in proximity to a morphotropic phase boundary) that can result in divergence of the surface-charge density. The order of these phase transitions is important. First-order transitions, despite having a steep change in the polarization with respect to temperature (large \(\pi\)), are associated with a wasteful temperature hysteresis that limits the operating temperature regime. Second-order transitions (usually the case under a large electric-field and for clamped thin films) circumvent thermal hysteresis but are associated with a relatively smaller magnitude of \(\pi\), leaving the ultimate choice of material (first- vs. second-order) to be jointly optimized with the operating temperature range. The increase in the dielectric constant and specific heat around the phase-transition can reduce the overall benefit of any increase in intrinsic \(\pi\), as seen in the equation for the FoMPEC. Increasing the power density of the device often necessitates the application of high electric fields that also tend to dampen first-order transitions. Direct measurements of the PE have also shown a reduction in the PEC at low electric fields for polydomain thin films and that nonintrinsic effects can have the same order of magnitude as intrinsic effects15,16.
Temperature perturbations change the polar structure/order not only at a unit-cell level (i.e., the intrinsic response) but also at a mesoscopic level (e.g., domain structures). Prior work on polydomain ferroelectric thin films has shown that the temperature-dependent motion of ferroelastic domains can result in enhancements to the PE via so-called extrinsic contributions17. In turn, research is focused on identifying systems with large structural phase instabilities and engineering novel domain structures that respond dramatically to temperature. For example, temperature-induced competition between various classical ferroelectric and toroidal polar-vortex phases in PbTiO3/SrTiO3 superlattices18 and mixed-phase hierarchical domain structures in tetragonal PbZr1–xTixO319 offer exciting opportunities to enhance extrinsic contributions. Thin films are also mechanically clamped to their substrate, and the thermal expansion mismatch between the film and the substrate results in secondary contributions to the PE, which are mediated by piezoelectricity. Unlike the intrinsic contribution, the secondary contribution may be either negative or positive, enhancing the PE in the former and suppressing it in the latter case17. Accordingly, the use of “unclamped” microfabricated or free-standing architectures could offer new possibilities for a large \(\pi\) and PEC.
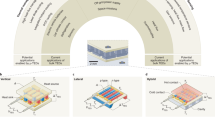
As noted, PEC requires the implementation of thermodynamic cycles using a solid-state device. These devices are generally structured around a pyroelectric capacitor with auxiliary structures dedicated to thermal/electrical management. The active material in a PEC device is coupled to electrical and thermal waveforms, resulting in charge → heat → discharge → cool cycles that produce electric work. For any cycle (Fig. 1b–e), electric-field cycling with a large magnitude is readily achieved in thin-film devices and is mainly limited by the charge-discharge electrical losses, which scale with the cycle frequency, loss tangent, dielectric constant, and DC electrical losses20. Producing temperature oscillations, however, presents a more interesting challenge. This results in PEC devices falling broadly into two categories based on the nature of the thermal resources available: those that induce periodic heating from two static temperature reservoirs (Fig. 2a, b) and those that couple to a single, time-varying heat source (Fig. 2c). In both cases, the PEC device can be optimized for maximal efficiency, energy density, or power density. Application of large electric fields leads to high-energy densities and efficiencies21 that are always limited by \(\eta _{{\mathrm{Carnot}}}\). The power density, however, is governed by the combined electrical and thermal-time constant, \(\tau\), of the PEC device, where the maximum power \(P_{{\mathrm{max}}} = W_Ef_{{\mathrm{max}}} = W_E/\tau\) and \(f_{{\mathrm{max}}}\) is the maximum cycling frequency. The thermal-time constant can be much larger than the electrical-time constant and is, therefore, the limiting factor in achieving a large power density. Neglecting contact resistance between the heat source and the PEC device, \(\tau _{{\mathrm{thermal}}} = L^2/\alpha\), where \(L\) and \(\alpha\) are the thickness and thermal diffusivity of the device, respectively. It follows that \(P_{{\mathrm{max}}} = W_E{\mathrm{/}}\tau _{{\mathrm{thermal}}} \propto 1{\mathrm{/}}L^2\) and thus thin-film devices21 inherently have a better power density than bulk devices22. This was demonstrated recently, where thin-film relaxor ferroelectrics21 achieved a power density that is 3 orders of magnitude larger than that of bulk versions22 despite having an energy density that is only one order of magnitude larger. Looking forward, it appears that thin-film geometries are promising for future PEC device design.
a A PEC device mechanically cycled between the heat source and sink to implement an Ericsson cycle. b The same thermodynamic cycle can be achieved using heat switches to pump/discharge heat to the PEC device. c A PEC device coupled with a single-sided heat source with a periodically varying temperature
Despite advances in the energy and power densities, much needs to be done to enhance the efficiency of the PEC process. The high specific heat of pyroelectric materials results in more heat energy absorbed than electrical dipolar energy gained. Although the lattice always dominates PEC conversion physics, regenerative schemes employing multi-staged heat reservoirs have been proposed to reduce the total heat input and thus increase efficiency10. This device, however, must operate quasistatically; thus, the power density (and utility) suffers. Instead of seeking reversible devices, investigators have, therefore, focused on different energy harvesting cycles (e.g., Ericsson and Brayton) to maximize performance. Recent efforts have, however, moved even further by considering, for example, hybrid cycles. In this spirit, combined piezo/pyroelectric devices have demonstrated larger maximum output voltages23,24,25, and others have even fabricated thin films capable of harvesting solar, thermal, and mechanical energies26. Combined ferro-/antiferroelectric cycles have been realized in a single device, taking advantage of the bidirectional nature of the pyroelectric coefficient in these materials20. These hybrid generators aim to increase device performance by integrating systems to maximize the extractable energy between two temperature extrema. Within the conventional PEC approach, there are several opportunities for improving performance. At a bare minimum, there is a need for a targeted design of materials tailored to a specific waste-heat source. Beyond this, it is possible to minimize heat losses to auxiliary structures (e.g., through the use of free-standing films) or to combine corresponding effects arising from pyromagnetism (via multiferroic and magnetoelectric materials) to enhance overall performance.
Ultimately, the development of modern PEC materials and devices is poised for a renaissance. Advances in our ability to accurately measure materials27, focus on the design of high-performance pyroelectrics, and production of nanoscale device structures offer unprecedented access to innovation. These developments enable further investment in a burgeoning field, the formation of a robust research community, and a sustained research effort like that seen in thermoelectrics. Today marks the beginning of a time of great development for pyroelectric materials and their application in the field of PEC.
References
Livermore Lawrence National Laboratory and Department of Energy. Estimated U.S. Energy Consumption in 2016. (2017). at https://flowcharts.llnl.gov/content/assets/images/energy/us/Energy_US_2016.png.
Vining, C. B. An inconvenient truth about thermoelectrics. Nat. Mater. 8, 83–85 (2009).
Tchanche, B. F., Lambrinos, G., Frangoudakis, A. & Papadakis, G. Low-grade heat conversion into power using organic Rankine cycles - A review of various applications. Renew. Sustain. Energy Rev. 15, 3963–3979 (2011).
Lee, S. W. et al. An electrochemical system for efficiently harvesting low-grade heat energy. Nat. Commun. 5, 3942 (2014).
Straub, A. P., Yip, N. Y., Lin, S., Lee, J. & Elimelech, M. Harvesting low-grade heat energy using thermo-osmotic vapour transport through nanoporous membranes. Nat. Energy 1, 16090 (2016).
Zook, J. D. & Liu, S. T. Pyroelectric effects in thin film. J. Appl. Phys. 49, 4604–4606 (1978).
Zubko, P., Catalan, G. & Tagantsev, A. K. Flexoelectric effect in solids. Annu. Rev. Mater. Res. 43, 387–421 (2013).
Olsen, R. B., Bruno, D. A. & Briscoe, J. M. Pyroelectric conversion cycles. J. Appl. Phys. 58, 4709–4716 (1985).
Hanrahan, B. M., Sze, F., Smith, A. N. & Jankowski, N. R. Thermodynamic cycle optimization for pyroelectric energy conversion in the thin film regime. Int. J. Energy Res. 41, 1880–1890 (2017).
Olsen, R. B. & Brown, D. D. High efficiency direct conversion of pyroelectric measurements heat to electrical energy-related. Ferroelectrics 40, 17–27 (1982).
Sebald, G., Lefeuvre, E. & Guyomar, D. Pyroelectric energy conversion: Optimization principles. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 55, 538–551 (2008).
Zhang, N. et al. The missing boundary in the phase diagram of PbZr1-xTixO3. Nat. Commun. 5, 5231 (2014).
Merz, W. J. The effect of hydrostatic pressure on the curie point of barium titanate single. Cryst. Phys. Rev. 77, 52–54 (1950).
Martin, L. W. & Rappe, A. M. Thin-film ferroelectric materials and their applications. Nat. Rev. Mater. 2, 16087 (2016).
Hanrahan, B. et al. Accounting for the various contributions to pyroelectricity in lead zirconate titanate thin films. J. Appl. Phys. 123, 124104 (2018).
Pandya, S. et al. Understanding the role of ferroelastic domains on the pyroelectric and electrocaloric effects in ferroelectric thin films. Adv. Mater. 31, 1803312 (2019).
Karthik, J., Agar, J. C., Damodaran, A. R. & Martin, L. W. Effect of 90° domain walls and thermal expansion mismatch on the pyroelectric properties of epitaxial PbZr0.2Ti0.8O3 thin films. Phys. Rev. Lett. 109, 257602 (2012).
Damodaran, A. R. et al. Phase coexistence and electric-field control of toroidal order in oxide superlattices. Nat. Mater. 16, 1003–1009 (2017).
Damodaran, A. R. et al. Three-state ferroelastic switching and large electromechanical responses in PbTiO3thin films. Adv. Mater. 29, 1–9 (2017).
Hanrahan, B. M. et al. Combining inverse and conventional pyroelectricity in antiferroelectric thin films for energy conversion. J. Mater. Chem. C. 6, 9828–9834 (2018).
Pandya, S. et al. Pyroelectric energy conversion with large energy and power density in relaxor ferroelectric thin films. Nat. Mater. 17, 432–438 (2018).
Sebald, G., Pruvost, S. & Guyomar, D. Energy harvesting based on Ericsson pyroelectric cycles in a relaxor ferroelectric ceramic. Smart Mater. Struct. 17, 015012 (2007).
Zakharov, D. et al. Combined pyroelectric, piezoelectric and shape memory effects for thermal energy harvesting. J. Phys. Conf. Ser. 476, 012021 (2013).
McKinley, I. M., Lee, F. Y. & Pilon, L. A novel thermomechanical energy conversion cycle. Appl. Energy 126, 78–89 (2014).
Khassaf, H., Patel, T. & Alpay, S. P. Combined intrinsic elastocaloric and electrocaloric properties of ferroelectrics. J. Appl. Phys. 121, 144102 (2017).
Yang, Y. et al. Flexible hybrid cell for simultaneously harvesting thermal and mechanical energies. ACS Nano 7, 785–790 (2013).
Pandya, S. et al. Direct measurement of pyroelectric and electrocaloric effects in. Thin Films. Phys. Rev. Appl. 7, 034025 (2017).
Acknowledgements
We acknowledge the support of the Army Research Office under grant W911NF-14–1–0104; the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under Award Number DE-SC-0012375 and the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, Materials Sciences and Engineering Division under Contract No. DE-AC02–05-CH11231 (Materials Project program KC23MP); and the National Science Foundation under grants CMMI-1434147, DMR-1451219, OISE-1545907, DMR-1608938, DMR-1708615, and DGE-1752814.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Pandya, S., Velarde, G., Zhang, L. et al. New approach to waste-heat energy harvesting: pyroelectric energy conversion. NPG Asia Mater 11, 26 (2019). https://doi.org/10.1038/s41427-019-0125-y
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41427-019-0125-y
This article is cited by
-
Transparent integrated pyroelectric-photovoltaic structure for photo-thermo hybrid power generation
Nature Communications (2024)
-
Vehicle Classification Using Deep Learning-Assisted Triboelectric Sensor
Arabian Journal for Science and Engineering (2024)
-
Harvesting waste heat based on thermoelectric generation to drive LED car lamps
Journal of Thermal Analysis and Calorimetry (2024)
-
Energy conversion and storage via photoinduced polarization change in non-ferroelectric molecular [CoGa] crystals
Nature Communications (2023)
-
Effect of bulk porosity on the pyroelectric properties of Na0.5Bi0.5TiO3–0.06BaTiO3 ceramics
Journal of Materials Science (2023)