Introduction

Two-dimensional (2D) semiconductor materials have recently received extensive attention because of their large bandgap1,2,3,4,5,6,7,8,9,10. Among 2D semiconductors, transition-metal dichalcogenides (TMDs), specifically MoS2, are considered as promising materials for advanced electronic devices based on their stable electronic properties and high feasibility for large-scale mass production11,12,13,14,15,16,17,18,19,20,21,22,23,24. Furthermore, their electrical properties depend on their atomic-structure deformation13 and surface defect concentration14, and they can be tuned over a wide range by changing their thickness12. For example, MoS2 transistors generally exhibit n-type conduction in a standard transistor structure. However, ambipolar behavior can be engineered via dielectric and substrate effects, and even p-type characteristics were obtained by applying specific metal-oxide contacts15,16,25. In addition, an anomalous band-structure transition from indirect to direct was observed while thinning MoS2 to a single atomic layer26,27.

To utilize 2D TMDs as a homojunction device, a difference in thickness is necessary. However, homojunctions using 2D TMDs have a perfectly aligned stepwise junction, which is distinct from a randomly stacked homojunction. Thus far, there have not been systematic studies on the electronic properties of these two types of junctions. We fabricated field effect transistor (FET) devices with a single MoS2 flake that consisted of different numbers of layers ranging from thin (less than three layers) to thick (more than four layers). Such devices are termed “naturally stepwise junction” (NSJ) devices. Subsequently, we compared the performance of the NSJ devices with that of a lattice-mismatched junction (LMJ) device. Although both type-I and type-II junctions have been reported recently for the NSJ structure28,29, our experimental and calculational results are consistent with a type-I junction. In this study, surface-potential measurements using the scanning Kelvin probe microscopy (SKPM) technique allowed us to determine the work function of MoS2 for different layer thicknesses. In addition, we could deduce the junction type from the conduction-band minimum (CBM) and valence band maximum (VBM) obtained from density functional theory (DFT). For the LMJ structure, the potential barrier was very small, and layer decoupling at the interface was observed. Furthermore, the band structures of LMJ and NSJ as well as temperature-dependent current values were investigated.

Materials and methods

Device fabrication

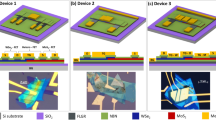
Figure 1a shows a schematic of the fabricated device. The MoS2 devices had a thickness step in the middle, which was formed via two different approaches. For the ohmic contact, graphene electrodes were adopted and deposited Pd/Cr/Au (30 nm/5 nm/20 nm) as metal pads (Fig. S2). Metal electrodes were patterned by e-beam lithography (TESCAN VEGA3). For the NSJ, we used a MoS2 flake including naturally adjacent atomic steps with a perfectly aligned atomic lattice (Fig. 1b). The LMJ-MoS2 devices were produced by transferring a thicker MoS2 flake onto a thinner one using a transferring device (MSTech Probe Station Series MST 5500B, Fig. S1).

Fig. 1
figure 1

Images of a FET device with thickness-dependent MoS2 isotype heterojunction with graphene electrodes and Pd metal pads. Our surface-potential measurement suggests that work-function value increases with thickness of MoS2 layer. Schematics for b NSJ device and c LMJ device indicating the presence of junction resistance in addition to each contact resistance for layers 1 and 2. Current–voltage relationship at various back gate voltages for d NSJ and e LMJ

Full size image

Characterization of junction devices

To compare transport characteristics between NSJ and LMJ, both types of devices were experimentally measured and theoretically analyzed via surface potential measurement, I–V measurement with temperature variation, Y-function analysis, and DFT analysis. The surface potential value was obtained using SKPM, and the work function translated from the value was obtained through Eq. (1) in chapter 2 of the supporting information. CBM and VBM were obtained by applying DFT, which is the theoretical calculation method (see chapter 4 of the supporting information). For the geometry optimization calculations, the Brillouin zone (BZ) was sampled in the Monkhorst-Pack scheme where the convergence of energy as a function of the number of k-points was tested. The Y-function method was used to obtain the contact resistance. The data obtained from the I–V results were calculated using Eqs. (2–5) from the supporting information for strong inversion cases. Additionally, using Eq. (6) from the supporting information to plot Arrhenius, we deduced the junction barrier height. In this work, each I–V data was measured in a low-temperature chamber and controller (LakeShore 336 Temperature controller) since we had to know the change in temperature.

Results and discussion

Layer dependent homojunction of MoS2

Figure 1d shows the output curves of a representative NSJ-MoS2 device consisting of two and five layers clearly indicating the quasi-current-rectifying effect and the n-type response to the back-gate voltage. Such asymmetrical current–voltage behavior implies a built-in electric field at the junction, which can arise from the thickness-dependent electron affinity and bandgap of MoS212,26,27,30,31,32,33. The LMJ-MoS2 device, fabricated by transferring a six-layer (6L) MoS2 onto a 2L flake yielding a large-area 2D interface, as shown in Fig. 1c, and the corresponding output curves are presented in Fig. 1e. Contrary to the NSJ-MoS2 device, these output curves are linear and symmetric indicating that the misorientationally stacked device had ohmic-like contacts at the vdW interface (rectification ratio for both types can be seen in Fig. S3).

Naturally stepwise junction (NSJ)

To understand the band alignment of the layer-dependent MoS2 junction, we evaluated the layer-dependent work function using SKPM (Fig. S4). Figure 2a shows the evolution of the work function, CBM, and VBM of MoS2 with layer number. The work function is obtained via SKPM, while CBM and VBM values are from the DFT calculation. The surface potential of the MoS2 layer decreases with layer number indicating an increase in the work function (Figs. S5–6). The work function of MoS2 linearly increases for up to five layers and asymptotically approaches 4.68 eV. The work function of monolayer MoS2 was 4.43 eV, which is similar to the previously reported value34. The CBM decreases as the number of layers increases, while the VBM decreases. The CBM of thin MoS2 is higher than that of thick MoS2 and the VBM is lower. Therefore, when two MoS2 that have different thicknesses meet, a type-I junction is formed.

Fig. 2
figure 2

a Summary of energy band structure of MoS2 with its layer number. Work function values were obtained via SKPM. CBM and VBM values were calculated. The results indicate a consistent increase in work function with layer thickness. b Energy-band alignment of layer-dependent MoS2-NSJ. c Side view of NSJ comprising 6L and 2L MoS2 structures (inset). LDOS of atoms is indicated in atomic structure. Vertical dashed lines show CBM and VBM energies of uniform 2L and 6L structures

Full size image

The distinctive difference between the NSJ and LMJ is the lattice alignment. For the LMJ, the lattice structures of the two layers are misoriented with respect to each other. Conversely, in the NSJ, each layer of MoS2 is well-stacked to form smoothly oriented lattice structures. We performed DFT calculations to elucidate the different electronic properties of these two cases (Figs. S10–11). For the NSJ, the interface is considered 1D and the effect of the imperfectly terminated edge of the thicker side can be very significant. Figure 2c shows the calculated local density of states (LDOS) for the 2L–6L NSJ. Here, the LDOS away from the interface recovers the expected bulk band edges for 2L and 6L MoS2. However, at the interface, we observed a reduced LDOS at the band edges. This reduced LDOS, albeit only occurring across a few atomic layers, can be a significant source of carrier scattering. By considering the CBM and the work function of each side of the MoS2, the band alignment is determined for the NSJ, as shown in Fig. 2b. The current rectifying behavior is mainly due to the existence of band bending and a potential barrier at the interface. We observed a higher current amplitude under negative voltage bias on the thicker layer. Although MoS2 homojunction certainly forms a type I junction, the CBM difference between layers can be much smaller than that of the work function, especially in the case that a mono-layer MoS2 is not involved. Therefore, as described in Fig. 2b, the potential barrier for electrons can be minimized when it comes from a thicker layer to a thinner layer.

Lattice-mismatched junction (LMJ)

Figure 3a, b show the distribution of the wave function in real space along the layers of a perfectly aligned, uniform 6L MoS2 structure and a misaligned 2L/4L structure, respectively. The results show that the wave functions are well separated between the misaligned 2L and 4L MoS2 in the latter structure, while the perfectly aligned 6L MoS2 has a strongly mixed wave function. Thus, when the lattice structures of randomly stacked MoS2 layers are mismatched, each stacked layer is electronically decoupled and should be regarded as two separate materials. Consequently, the lattice-mismatched homojunction interface is 2D.

Fig. 3
figure 3

a Distribution of wave functions in real space along layers of perfectly aligned uniform 6L MoS2. The wave functions for each conduction band at point K are represented by different colors, as indicated in the inset, where n = 1 corresponds to CBM. b Same as a but for misaligned 6L MoS2. Here, 2L MoS2 (indicated by black and red spheres) is shifted and misaligned with respect to the remaining four layers (4L) to create the 2L–4L interface. Conduction-band wave functions are mixed along layers in a, whereas in b they are separated from each other at the 2L–4L interface. Surface-potential image of c single MoS2 flake comprising two to 10 layers and d MoS2 flake comprising two and three layers covered by transferred four-layer MoS2. Measured thickness and potential values corresponding to e single flake and f covered flake. Covered region (six layer) exhibited identical values to original flake (four layer). g Schematic of rotated LMJ and energy-band alignment of layer-dependent MoS2 LMJ. h Misalignment of misorientationally stacked MoS2 layers in reciprocal space. i Transmission coefficient as a function of energy computed for the various interlayer conditions

Full size image

Figure 3c presents a surface-potential image of a MoS2 flake obtained by SKPM. The MoS2 flake contains various regions with different thicknesses. In Fig. 3c, we observe a clear transition in the surface-potential values as the number of layers is increased from two to seven. As the thickness is increased, the MoS2 nanosheet tends to have a lower surface potential and higher work function. Figure 3d shows a surface-potential image of artificially stacked MoS2 flakes, which were fabricated by transferring a 4L MoS2 (red dotted line) onto a 2L MoS2 (yellow dotted line). There are four separate regions: 2L, 3L of the bottom MoS2, 4L of the transferred MoS2, and 6L of the misorientationlly stacked MoS2. It was confirmed that the 2L, 3L of the bottom MoS2, and 4L of the top MoS2 had distinct surface-potential differences. However, the overlapped region of 6L exhibited no surface-potential change compared with the 4L of the top MoS2. Figure 3e, f show the results for each sample. While the surface potential of each MoS2 layer exhibits a consistent decrease with layer number, the overlapped layer shows only identical values. This result strongly supports the physical picture of interlayer decoupling owing to lattice-mismatches between the overlapped MoS2 flakes. To systematically analyze these layer-dependent work-function differences and the layer decoupling effect, we extracted the junction resistance of each NSJ and LMJ device.

For an LMJ, the thickness of the device is far smaller than the relevant carrier screening length. Figure 3g shows a rotated schematic of an LMJ device and an energy band diagram for the LMJ case. Since the actual band structure is restricted in atomic thickness, the potential barrier between the two layers can be identified by the CBM difference, and it is much smaller than that of the NSJ case in most cases. Additionally, the LDOS for each atomic region at the interface of LMJ indicated CBM alignment and no significant band shift (Figs. S10–11). In addition, for an LMJ, the relative misorientation of each layer implies a mismatch in reciprocal space, as illustrated in Fig. 3h. Hence, the carrier transport across this 2D interface would require the assistance of a large-momenta supplied by optical phonons. To understand the effect of the lattice misorientation, explicit conductance simulations were performed35. The corresponding transmission coefficients are plotted in Fig. 3i. The result of this calculation is that the misoriented junction exhibits similar interlayer conductance with respect to bulk MoS2 and even higher conductance in the valence band region and around CBM. The reasons for such unexpected behavior lie in a “charge compression” effect. In the bulk system, black curve in Fig. 3i, the repulsion of the electronic clouds of the S atoms pushes the valence band to higher energy, especially at the Γ point, producing a decrease in the indirect band gap29,36,37. Additionally, the rotational angle in the LMJ case may be another issue, but studies regarding twisted, misaligned TMD heterojunctions and graphene layers suggest an insensitivity to angle38,39. Basically, the twist angle controls the effective interlayer coupling and induces a van Hove singularity at some energy39.

Junction resistance analysis by using Y-function method

To quantitatively evaluate the junction resistances at the interfaces, we employed the Y-function method. Figure 4a shows a representative transfer curve of a MoS2 homojunction device. We choose the samples showing gate independent attenuation as “strong inversion” (Fig. S7). Because of the interfaces in both junction devices, the junction resistances should be considered as both effective mobility attenuation factors and the contact resistances. Figure 4b shows the extracted sum of the contact resistance and junction resistance as a function of the work function and CBM difference for both homojunction devices. Because the contact resistances are expected to have small values (less than a few kΩ) and do not differ regardless of the device structure and thickness, the difference in the resistance originates entirely from the junction resistance at the interface. The resistance of the NSJ increases exponentially with the surface-potential difference between the two MoS2 layers. It is evident that the barrier resulting from the band bending in the NSJ case can be determined by the Fermi-level difference. This indicates that the junction resistance dominates the total resistance. It also justifies our assumption in the modification of the Y-function method. In the LMJ case, the barrier at the interface can be determined by the alignment of the CBM in equilibrium. The suggested values in Fig. 4b are given by the work function and CBM transition shown in Fig. 2a. The LMJ devices exhibit significantly smaller resistances than the NSJ devices in most cases and show a rough dependence on the energy difference, although the LMJ cases have many uncontrolled variables at the interface (Figs. S8–9). We measured the entire devices at room temperature, and the phonon-assist effect may have been significant. Cases with an energy difference smaller than 50 meV exhibit particularly small resistance values. Furthermore, at energies higher than 50 meV, the resistance is drastically increased to values comparable to the NSJ cases. The phonon-assisted charge-transfer mechanism may explain this behavior given the reported optical phonon energy of MoS240.

Fig. 4
figure 4

a The transfer curve of MoS2 homojunction transistor (inset). The mobility attenuation factor, θ, with back gate bias. b Sum of contact resistance and junction resistance for various homojunction devices extracted using Y-function analysis. c Device image designed to separate junction resistance from contact resistance. Contact resistance was determined by measuring a pair of electrodes on the same MoS2 layer (1a–1b, 2a–2b, and 3a–3b). d Extracted junction resistance for NSJ and LMJ cases

Full size image

To further verify this conclusion, we fabricated both types of MoS2 homojunction devices on the same MoS2 flake, as shown in Fig. 4c. We used MoS2 flakes with 2L (blue dotted line) and 10L (yellow dotted line) regions for the NSJ. Another MoS2 flake of 10L was transferred onto the 2L region for forming the LMJ. The MoS2 devices were measured by using 1a–1b, 2a–2b, and 3a–3b contacts where the contact resistances for the three devices were extracted via the Y-function method. The contact resistances for the three devices were significantly smaller than the total device resistance (<5 kΩ) (Fig. 4d). Both devices were measured by using 1a–2a and 2a–3a contact cases. By substituting the measured contact resistance from the total resistance, we separated the junction resistance for each device. The junction resistance of the LMJ device was significantly smaller than that of the NSJ device. For all NSJ cases and most LMJ cases, it is reasonable to assume that the contact resistance has a negligible contribution to the total device resistance. Thus, we conclude that the carrier transport mechanisms in the both MoS2 homojunction cases differ significantly. While the NSJ case exhibits a strong potential-barrier dependence based on the work-function difference, the decoupled LMJ emphasizes the importance of phonons in the charge transfer across the misaligned lattices.

Junction barrier height characterization of homojunctions by temperature modulation

In intrinsic MoS2 devices, the temperature affects the I–V characteristics in two dominant ways. The first is the thermionic effect where the number of charge carriers increases as the temperature rises from low to high. In contrast, phonon scattering, which interferes with the movement of electrons, increases as the temperature rises. In junction devices, there is another way for temperature to affect the I–V characteristics. After the temperature rises and the phonon scattering energy becomes higher than the barrier height of the junction, the charge carrier can overcome the junction barrier easily by the phonon-assist effect. Therefore, temperature-dependent electrical measurements were carried out to characterize the specific junction barrier height according to the lattice matching of the junction.

In LMJ, decoupling between two different MoS2 occur causing band bending by Fermi level pinning at the junction to be drastically reduced compared to NSJ (Fig. 5a, b). To observe a reduced barrier height by decreasing Fermi level pinning, two probe based I–V were measured from 77.4 to 300 K. In the case of the NSJ device, drain current shows a monotonous tendency without large temperature dependent change below 250 K and shows rectifying behavior like a Schottky junction due to the barrier at the junction (Fig. 5d). However, above 250 K, the current level increases sharply and the rectifying ratio decreases. This is because the charge carrier was impeded by the junction barrier and the thermionic effect cannot appear under 250 K. However, above 250 K, the phonon-assist effect allows the charge carriers to sufficiently overcome the junction’s barrier in NSJ. Conversely, in the LMJ, as the temperature increases, the drain current level initially increases before approximately 150 K and then decreases after approximately 200 K, which is similar to an intrinsic MoS2 device (Fig. 5e). Since the barrier height of LMJ is relatively lower than that of NSJ, and the phonon-assist carrier appears before 77.4 K, the level of drain current of the LMJ device is higher even at low temperature, and it shows more ohmic I-V characteristics than the NSJ device (Fig. 5c). These results are related to the phonon-assisted carrier and show good agreement with Fig. 4b. When the temperature is further increased, the drain current of LMJ decreases since the mobility decreases due to phonon scattering. Since the junction barrier height of LMJ is relatively small, the tendency of the drain current shows similar results as an intrinsic MoS2 device. Since an intrinsic MoS2 device does not have a junction other than the graphene contact, the overall trend is similar to LMJ devices (Fig. 5f). However, LMJ have small junction barriers such that the drain current decreases more when the temperature decreases.

Fig. 5: Energy-band diagrams for MoS2
figure 5

a NSJ, and b LMJ. c The junction barrier height for NSJ, LMJ, and intrinsic MoS2. The junction barrier height at the NSJ interface is higher than the junction barrier height at the LMJ interface. The drain current–voltage curves with various temperatures from 77.4 to 300 K for d NSJ device, e LMJ device, and f intrinsic MoS2 device, (inset) drain current versus temperature at various drain-source biases

Full size image

As a result of the Arrhenius plot (Fig. S12), we calculated the barrier height. According to a previous study, and because multilayered graphene/MoS2 heterostructure has negative Schottky barriers41, the results indicate that the junction barrier height at LMJ is much lower than the junction barrier height at NSJ, and this is enough for electrons to overcome the barrier by phonon-assist. Moreover, the barrier height difference between both MoS2 homojunctions is strong evidence that perfectly aligned band structure causes a stronger Fermi level pinning effect than a lattice-mismatched band structure.

Contact resistance enhancement by lattice-mismatched homojunction effect

A thicker MoS2 exhibits smaller contact resistance for high-work function metals owing to the lower Schottky barriers within them42. By utilizing the small junction resistance of the LMJ, we demonstrated high-performance MoS2 transistors with a reduced contact resistance leading to an enhanced two-terminal mobility. We fabricated two devices with different contact structures for comparison, as illustrated in Fig. 6a, b. When a drain bias was applied, thin MoS2 generally had a high Schottky barrier for high-work function metals leading to a large contact resistance and a reduced two-terminal field-effect mobility (Fig. 6c). However, thicker MoS2 had smaller Schottky-barrier heights owing to the lowered position of the conduction band. When thick MoS2 was inserted, charge carriers could be more easily transported into the metal (Fig. 6d). The output curves in Fig. 6e, f indicate that the 2 L MoS2 device with Pd contacts had a high Schottky barrier. However, the 2L MoS2 device with the stacked contacts of 6L MoS2 exhibited a dramatic improvement in the charge-carrier injection from the electrode to the channel.

Fig. 6
figure 6

a Schematic of FET devices with and without a thick MoS2 contact between thin MoS2 channel and Pd electrodes. b Optical image of FET device comprising two-layer (green dotted line) and six-layer (orange dotted line) MoS2. Energy-band diagrams for c thin MoS2/metal junction and d thin MoS2/thick MoS2/metal junction. One high Schottky barrier can be split into two low barriers via application of thick MoS2 contacts. ID–VG transfer curves for e device 1 and f device 2 (insets show corresponding ID–VD output curves)

Full size image

In this study, we evaluated the junction decoupling effects of MoS2 layers for a lattice mismatched junction structure. SKPM and a junction-resistance evaluation suggested that the work function of MoS2 changed according to the number of layers and indicated the formation of a finite potential barrier at the layer-dependent MoS2 junction. Subsequent analysis revealed that the junction resistance for a lattice-mismatched state was far smaller than that for a perfectly aligned state. The small junction resistance of the LMJ structure was utilized for contact resistance reduction. The junction effects revealed may be useful in the development of new strategies that can be widely employed to engineer the energy-band structure in the heterostructure on the basis of the combination of various TMDs.