Abstract
Thermal stability, precision, and large output are desired for applications of electromechanical materials. However, this combination has been hardly attained because both the commercially used materials and currently promising candidates are confronted with a critical challenge: the intrinsic incompatibility among the broad temperature window, low hysteresis, and high strain. Here we report a re-entrant relaxor–ferroelectric composite that solves this long-standing challenge: a combination of low hysteresis and large electrostrain over a broad temperature range (i.e., a 168-K temperature window for hysteresis <20% and strain >0.1%) in sufficiently disordered (Ba0.925Bi0.05)(Ti1−x/100Snx/100)O3 ceramics. In situ transmission electron microscopic observations and permittivity measurements reveal the existence of a re-entrant anomaly that guarantees the relaxor–ferroelectric microstructure over a broad temperature range and the resulting combination of exceptional properties. Our finding of a re-entrant relaxor–ferroelectric composite not only solves the incompatibility of the electromechanical properties but may also open a way to develop thermally stable high-performance materials.
Similar content being viewed by others
Introduction
Electromechanical materials, which convert electrical energy to mechanical work, have been widely used in actuators, ultrasonic imagers, and telecommunications1. Among them, ferroelectrics and relaxors are mainstays, as represented by two commercially used materials: ferroelectric Pb(Zr,Ti)O3 (hard PZT) and relaxor Pb(Mg1/3Nb2/3)O3 (PMN)2,3. For most applications, a combination of large strain and small hysteresis over a wide temperature range is always desired3,4. Yet, these two properties do not go hand in hand since a large strain originates from a large lattice deformation, which usually makes it difficult to transform from one state to another (i.e., more energy dissipation), thereby leading to a large hysteresis2,3,4,5,6,7,8,9,10,11,12,13,14,15. For example, the actively reported bismuth-alkali titanate-based (Bi1/2Na1/2TiO3-based) materials generate a large strain as high as 0.3–0.7% but accompanied by a very large hysteresis (>50%)5,6,7,8,9,10,11,12,13. To overcome the incompatibility between large strain and small hysteresis, an effective approach has been reported by introducing a relaxor into ferroelectrics15,16, e.g., the K1/2Na1/2NbO3 (KNN)-doped 0.94Bi1/2Na1/2TiO3-0.06BaTiO3 (BNT-6BT) relaxor–ferroelectric composite16 exhibiting a strain of 0.12–0.15% with a hysteresis of 20–35%.
However, the relaxor–ferroelectric composites and even relaxors face a vital problem—the increased hysteresis with cooling, which yields a possible overheating failure due to energy dissipation. The origin of the hysteresis increase is that, at low temperatures, the thermodynamically favored state is the ferroelectric state instead of the relaxor state, and the ferroelectric state generates a large hysteresis, which explains the remarkable temperature instable hysteresis of the BNT-based materials7,8,9,10,17 and PMN18 (increasing to >70% upon cooling), as shown in Fig. 1c. The current ways to avoid a large hysteresis are limiting the usage temperature range (e.g., in PMN) or limiting the applied field below the saturated field (e.g., in hard PZT). In short, to date, no mechanism has been found to overcome the intrinsically cooling-driven ferroelectric stabilization and the associated hysteresis increase, thus causing current materials not meeting the requirement of a thermal stability–hysteresis–strain combination (i.e., a broad temperature window, low hysteresis, and large electrostrain).
a Comparison of the hysteresis and the maximum electrostrain (Smax) under 4 kV/mm at room temperature among the RRFC (both 4 and 6 kV/mm), hard PZT4, 17, PMN18 (2 kV/mm due to the low breakdown field), and several typical lead-free electrostrictive systems, including BNT-based7,8,9,10,11,12,13, SrTiO3-based (ST-based)15, and BT-based ceramics. Contrasting with the conventional tendency of a larger electrostrain with a larger hysteresis and vice versa, the RRFC exhibits the long-sought result of small hysteresis and large strain. b Temperature range of a small hysteresis (<20%) with a large strain (>0.1%) for the RRFC, PMN, and two representative BNT-based ceramics: (Bi1/2(Na0.84K0.16)1/2)0.96Sr0.04Ti0.975Nb0.025O3 (BNT-2.5Nb)9 and Bi1/2Na1/2TiO3–Bi1/2K1/2TiO3-K1/2Na1/2NbO3 (BNT-BKT-KNN)10. c Temperature-dependent hysteresis of the RRFC, PMN, BNT-2.5Nb, and BNT-BKT-KNN, where Tf represents the freezing temperature (see Fig. 3 for details). Upon cooling, the small hysteresis (<20%) of RRFC can persist to temperatures below Tf (red line), whereas both PMN- and BNT-based ceramics exhibit drastic hysteresis increases
To overcome the initial issue of cooling-driven ferroelectric stabilization, in this work, we introduce a sufficiently disordered ceramic, viz., the system (Ba0.925Bi0.05)(Ti1−x/100Snx/100)O3 (BT-5Bi-xSn), which allows a re-entrant relaxor transition of a coexisting low-temperature re-entrant relaxor phase19,20,21,22 with additional electromechanical degrees of freedom due to its clustered glass nature of frozen polar nanoregions (PNRs)23. Here the disorder induced by heterovalent Bi3+ and Sn4+ doping plays a crucial role in creating a re-entrant relaxor phase out of the percolating ferroelectric phase. It should be noted that the re-entrant phenomenon due to the disorder has been reported in many magnetic systems, e.g., Fe-xAu, where cluster spin glass grows out of the percolating ferromagnetic phase upon cooling, i.e., a transition from the ferromagnetic state to the cluster spin glass24,25.
Our established phase diagram of BT-5Bi-xSn shows that the re-entrant transition from the ferroelectric to the relaxor state indeed exists in the middle composition regime (3 < x < 7), which resembles the above-mentioned typical re-entrant spin glass phase diagram of Fe-xAu. More importantly, an extraordinary combination of low hysteresis (<20%) and large electrostrain (>0.1%) over a broad temperature range (168 K) is achieved at a critical composition (x = 7), where the ferroelectric transition, relaxor transition, and re-entrant relaxor transition meet and produce a re-entrant relaxor–ferroelectric composite (RRFC). In situ transmission electron microscopy (TEM) shows that a heterogeneous microstructure of ferroelectric domains embedded into the relaxor matrix at room temperature persists down to lower temperatures without significant ferroelectric domain coarsening. The good temperature stability of the properties and microstructures confirms the vital role of the re-entrant relaxor transition. Our work indicates that introducing the re-entrant relaxor transition through creating enough disorder in ferroelectric systems may become an integral step toward developing applicable high-performance electromechanical materials.
Materials and methods
BT-5Bi-xSn ceramics were fabricated via a conventional solid-state reaction method with starting materials of BaCO3 (99.8%+), Bi2O3 (99.9%+), TiO2 (99.8%+), and SnO2 (99.9%+). The calcining was performed at 1473 K for 2 h and the sintering at 1673 K for 2 h. Dielectric permittivity curves were measured by a HIOKI LCR meter from 423 to 123 K with a cooling rate of 2 K/min. The structural evolution through varying the temperature was detected by an X-ray diffractometer (Shimadzu XRD-7000). The electrostrain was measured by a photonic sensor during the polarization electric field (P-E) hysteresis loop measurement (Radiant workstation). The microstructure characterization was performed by a JEM-2100F TEM with a double tilt liquid nitrogen cooling holder.
Results and discussion
Thermal stability–hysteresis–strain combination achieved by the RRFC
Figure 1 shows the property comparison of hysteresis, strain, and temperature stability among the previously reported lead-based and lead-free ceramics4,5,6,7,8,9,10,11,12,13,14,15,16,17,18 and our results. First, the RRFC stands out for the best combination of low hysteresis and large strain (most desired) at room temperature in the hysteresis versus strain plot (Fig. 1a). The strain of RRFC is larger than that of the practically used PMN4, and its hysteresis is much smaller than that of hard PZT4,17, with a similar strain level. Second, the RRFC exhibits the best temperature stability compared with that of the PMN-18 and BNT-based materials9,10 (Fig. 1b, c). Here we plot the temperature range of a small hysteresis (<20%) with a large strain (>0.1%) in Fig. 1b and the hysteresis over temperature curve in Fig. 1c. It is clear that the RRFC possesses a much better temperature stability of the hysteresis (a slight increase from ~9.4% at 293 K to ~17% at 183 K, where the freezing temperature Tf is ~200 K) compared with the dramatic increase of PMN (from 7% at 333 K to 73% at 213 K, where Tf is ~210 K)18 and BNT-based materials (from 10% at 423 K to 49% at 298 K for BNT-BKT-KNN; from 44% at 373 K to 75% at 298 K for BNT-2.5Nb)9,10.
Re-entrant phase diagram and the re-entrant transition
To explain the exceptional thermal stability–hysteresis–strain combination achieved by the RRFC, we will next show the unusual composition–temperature phase diagram of BT-5Bi-xSn (0 < x < 12). Figure 2a shows the phase diagram determined by the dielectric permittivity upon cooling (Fig. 3 and Supplementary Fig. S1). Different from the common phase diagrams such as PMN-PbTiO3(PT) and BNT-BT, it has an additional transition, the re-entrant transition, which gives rise to the coexistence regime of the re-entrant relaxor and the ferroelectric. We can find that our phase diagram resembles the typical re-entrant ferromagnetic spin glass phase diagram of Fe-xAu (Fig. 2b)24,25. With the increasing Sn or Au concentration, the ferroelectric/ferromagnetic transition gradually vanishes, and a glass transition appears above the critical composition. Abnormally, at an intermediate concentration, the system first undergoes a ferroelectric/ferromagnetic transition and then a re-entrant transition from the ferroelectric/ferromagnetic state to the glass state (forming a coexistence of the glass and ferroelectric/ferromagnetic states). Specially, at a critical concentration (BT-5Bi-7Sn and Fe-84Au, indicated by the dashed red arrow), the ferroelectric/ferromagnetic, glass, and re-entrant transitions merge and form a direct transition from the para-state to the re-entrant composite state. Later, we will show why this unique transition is the origin of a broad temperature window of superior properties.
a-b At a low concentration of Sn/Au, the ferroelectric/ferromagnetic transition occurs, whereas the corresponding relaxor/cluster spin glass transition appears at a high concentration. The coexistence of the glass and ferroelectric/ferromagnetic states at the intermediate concentration stems from the re-entrant transition. A unique state (see below) forms at the critical composition (indicated by the dashed red arrow)
a–c Dielectric permittivities of x = 2, x = 7, and x = 9, respectively. The insets show the in situ XRD profiles at different temperatures of x = 2 and x = 9 and the determination of Tf by Vogel–Fulcher fitting43 for x = 7 using \({\mathrm{\omega }} = \omega _0e^{ - E_{{\rm a}}/\left( {T_{\mathrm{m}} - T_{{\rm f}}} \right)}\). d–f Evidence of the ferroelectric and re-entrant relaxor coexistence state of x = 4. The permittivity and loss curves exhibit a frequency-independent ferroelectric transition peak at TC and a frequency-dependent re-entrant transition peak at Trg. The insets in d show the corresponding structure changes upon varying the temperature. The temperature dependence of the remanent polarization (f) and P-E loops [insets in f] further confirms the above transition sequence. Note that the transition behavior of x = 7 (b), different from that of x = 4 (d), shows a weak frequency-dependent RRFC transition at Tm and a sluggish re-entrant-like transition at a lower temperature
Next, we will show the detailed determination of the phase diagram and especially the re-entrant transition. First, the transition in the ferroelectrics (e.g., x = 2, Fig. 3a) is featured by a sharp frequency-independent permittivity peak at TC and a structural change manifested by the splitting of the (220) peak in the X-ray diffraction patterns. Second, the transition in the relaxors (e.g., x = 9, Fig. 3c) is featured by a frequency-dependent permittivity peak at Tm and the invariance of the average structure. Third, at an intermediate Sn composition (e.g., x = 4, Fig. 3d, e), upon cooling, it shows the signatures of a ferroelectric transition and then a relaxor transition. This subsequent abnormal relaxor transition at Trg is the so-called re-entrant relaxor transition19,20,21,22. The temperature dependence of the electrical hysteresis (P-E) loop and saturated remanent polarization (Pr) in Fig. 3f shows the same transition sequence of a ferroelectric transition, indicated by an increase in the remanent polarization, and then a re-entrant relaxor transition, indicated by a decrease in the remanent polarization (see Supplementary Fig. S2 for more details and examples).
The in situ microscopic TEM observation (Fig. 4) further reveals that, after the re-entrant relaxor transition, the contrast of the coarse ferroelectric domains becomes blurred, which is due to the formation of PNRs within these large ferroelectric domains. Being different from the normal relaxor, after the re-entrant transition, the ferroelectric domains still remain, and the average structure remains tetragonal instead of cubic. To determine the local symmetry of the re-entrant relaxor and its difference from the ferroelectric matrix, convergent beam electron diffraction was performed along the [001], [011], and [111] beam incidence directions at room temperature and at a lower temperature (103 K). The local symmetry of the ferroelectric domain (RT-FE) is determined to be 4 mm (i.e., T phase), while the diffraction symmetry of the re-entrant relaxor (LT-RE) is m (i.e., O phase), less symmetric than 4 mm. In short, an unusual re-entrant relaxor transition occurs from the ferroelectric state to the re-entrant relaxor state upon cooling (i.e., the re-entrant transition weakens the ferroelectric stabilization by a decay into a local random electric-field-stabilized PNR of variant orientation as approved for standard relaxor ferroelectrics such as PMN26), which apparently explains the enigma of the low hysteresis and high electrostrain.
Combination of small hysteresis and large strain of the RRFC at room temperature
Next, we will present the superior electrostrain properties of the RRFC over the ferroelectric and relaxor in BT-5Bi-xSn systems at room temperature. The well-known hysteresis–strain trade-off in the ferroelectric and relaxor is vividly demonstrated by the electrostrain behavior, as shown in Fig. 5a: the ferroelectric (e.g., x = 4) exhibits large hysteresis (bad) and large strain (good), while the relaxor (e.g., x = 9) exhibits small hysteresis (good) and small strain (bad). However, the RRFC (x = 7) overcomes the trade-off and generates the highest electrostrain (~0.1% at 3 kV/mm, good) together with a slim hysteresis (~9.4%, good); the strain value is even higher than that of the typical Pb-based piezoelectric and electrostrictive ceramics (hard PZT and PMN)3,4. Figure 5b, c reveal the composition dependences of the electrostrain and hysteresis. The maximum electrostrain (Smax) first increases and then decreases, i.e., forming a peak at the RRFC (x = 7) composition. The same composition dependence of the electrostrain also appears along the transition temperature TC/Tm (see Supplementary Fig. S3), ruling out the effect of measuring the temperature of the RRFC close to TC/Tm. The hysteresis, calculated by (△S)max/Smax in which (△S)max is the largest width of the loop3, continuously decreases with the increasing Sn concentration. The Smax of the RRFC increases with the electric field and can reach ~0.165% at 6.5 kV/mm, while the slim hysteresis remains even in such a high field (see Supplementary Fig. S4). In short, at room temperature, the RRFC exhibits a superior combination of low hysteresis and large electrostrain over both the ferroelectric and the relaxor.
a Electrostrain of ferroelectric (x = 4), RRFC (x = 7), and relaxor (x = 9), together with the typical Pb-based piezoelectric and electrostrictive ceramics of hard PZT and PMN [refs. 2,3,4]. b, c Composition dependences of Smax and hysteresis under an electric field of 3 kV/mm. d TEM images showing the microstructures of a typical ferroelectric (x = 4), RRFC (x = 7), and relaxor (x = 9). The inset shows the fast Fourier transform spectrum with the spot splitting of (121) and (220)
To understand this combination of slim hysteresis and large strain achieved at the RRFC, microscopic observations were performed at room temperature on x = 7 (RRFC) as well as the x = 4 (ferroelectric) and x = 9 (relaxor) compositions for comparison. Figure 5d shows that micron-size ferroelectric domains are observed in the ferroelectric (x = 4), whereas PNRs appear in the relaxor (x = 9), as indicated by the splitting of the (121) and (220) reflections in the fast Fourier transform spectrum. Uniquely, the RRFC (x = 7) has ferroelectric domains of size ~350 nm embedded in the relaxor matrix. It should be mentioned that the conventional mechanism for the ferroelectric and relaxor coexistence owing to chemical inhomogeneity27 is ruled out by the element distribution mapping (see Supplementary Fig. S5).
The slim-hysteretic large strain of the RRFC can be understood based on this ferroelectric and relaxor coexisting microstructure: under the electric field, the rotation of isolated ferroelectric domains (especially non-180° domains) contributes to a large strain, and its reversible rotation with few domain wall motions leads to a small hysteresis (see more details in Supplementary Fig. S6). In short, designing a material with a ferroelectric and relaxor coexisting microstructure is indeed an effective approach to achieve a superior combination of small hysteresis and large electrostrain, as reported before28.
Thermal-stable electrostrain properties originating from the re-entrant transition
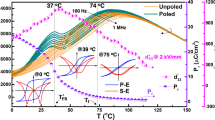
Next, we present the temperature stability of the hysteresis and electrostrain of the RRFC. Figure 6a shows that, upon cooling, the bipolar electrostrain curves under 3 and 6 kV/mm have two temperature-dependent regions, as indicated by the blue and red lines, which correspond to the temperature windows of the ergodic relaxor and the RRFC (see below for evidence). The temperature dependence of Smax in the RRFC region is obviously weaker than that in the ergodic relaxor region. The weaker temperature dependence of the hysteresis in the RRFC is also different from that in the conventional relaxor (e.g., PMN, see Fig. 1b)18. The RRFC only exhibits a slight hysteresis increase from ~9.4% at 293 K to ~17% at 183 K, which may be useful for potential low-temperature precise actuation applications, as in airborne platforms (~220–330 K) as adaptive structure drives for shape/position/force control29.
a Bipolar Smax at 3 and 6 kV/mm shows two temperature dependences (blue and red lines), corresponding to the temperature windows of the ergodic relaxor and RRFC (x = 7). The insets show the bipolar strain–field curves at 233, 253, and 293 K. b–d In situ TEM observations of the RRFC at 250, 293, and 360 K
The origin of the above abnormal temperature dependence of the electrostrain and hysteresis is revealed through in situ temperature-changing TEM observations. Figure 6b–d show that, upon cooling, the ergodic relaxor transforms into a relaxor–ferroelectric coexisting state. This coexisting microstructure seems to be “frozen” over a broad temperature range, and no obvious ferroelectric domain coarsening is observed. This explains the temperature insensitivity of the macroscopic property changes of the hysteresis and electrostrain.
Interestingly, a similar relaxor–ferroelectric coexisting microstructure has also been found around the spontaneous/crystallization transition temperature of the relaxor30,31,32, but upon cooling, a very large hysteresis comparable to that of the ferroelectric is inevitable (e.g., PMN, BNT-based materials in Fig. 1b)9,10,18 since the volume fraction of the ferroelectric domains becomes larger and larger. These temperature-dependent differences in both the macroscopic properties and microstructures clearly reveal the integral role of the re-entrant transition, which is absent in all the current electromechanical systems.
Conclusion
In summary, for the first time, we experimentally demonstrate that the RRFC generates an exceptional thermal stability–hysteresis–strain combination (i.e., slim hysteresis and large electrostrain in a broad temperature range) in a (Ba0.925Bi0.05)(Ti1−x/100Snx/100)O3 system. This exceptional combination is achieved by the RRFC design strategy, i.e., introducing sufficient disorder to enable a re-entrant transition, thereby creating a relaxor–ferroelectric coexisting microstructure over a broad temperature range. Because the re-entrant glass transition prefers the relaxor state instead of the ferroelectric state upon cooling, it can solve the long-standing cooling-driven ferroelectric stabilization problem (i.e., guaranteeing the thermal stability). This observation is significantly different from the previously reported conventional design methods based on the conventional ferroelectric, relaxor, and ferroelectric–relaxor composite, e.g., morphotropic phase boundaries with the lowest free energy anisotropy in ferroelectrics (see Supplementary Fig. S7) or PNRs in relaxor PbTiO333,34,35,36,37,38,39,40. Our work suggests that the re-entrant transition may serve as a general approach not only to explore more high-performance electrostrain properties, especially with high operating temperatures, but also to find high-performance re-entrant magnetostrictive materials (e.g., which may be superior to expensive rare-earth alloys41,42 such as Tb1–xDyxFe2).
References
Gandhi, M. V. & Thompson, B. S. Smart Materials and Structures (Chapman & Hall, London, 1992).
Newnham, R. E. Properties of Materials: Anisotropy, Symmetry, Structure (Oxford University Press, UK, 2004).
Uchino, K. Ferroelectric Devices (Marcel Dekker, New York, NY, 2000).
Park, S. & Shrout, T. R. Ultrahigh strain and piezoelectric behavior in relaxor based ferroelectric single crystals. J. Appl. Phys. 82, 1804–1811 (1997).
Jo, W. et al. Giant electric-field-induced strains in lead-free ceramics for actuator applications -status and perspective. J. Electroceram. 29, 71–93 (2012).
Hiruma, Y., Imai, Y., Watanabe, Y., Nagata, H. & Takenaka, T. Large electrostrain near the phase transition temperature of (Bi0.5Na0.5)TiO3-SrTiO3 ferroelectric ceramics. Appl. Phys. Lett. 92, 262904 (2008).
Chen, P.-Y., Chen, C.-S., Tu, C.-S. & Chang, T.-L. Large E-field induced strain and polar evolution in lead-free Zr-doped 92.5%(Bi0.5Na0.5)TiO3-7.5%BaTiO3 ceramics. J. Eur. Ceram. Soc. 34, 4223–4233 (2014).
Chen, P.-Y., Chen, C.-S., Tu, C.-S., Cheng, C.-D. & Cherng, J.-S. Relaxor effect on electric field induced large strain in (1-x)(Bi0.5Na0.5)TiO3-xBaTiO3 lead-free piezoceramics. Ceram. Int. 40, 6137–6142 (2014).
Liu, X. & Tan, X. Giant strains in non‐textured (Bi1/2Na1/2)TiO3‐based lead‐free ceramics. Adv. Mater. 28, 574–578 (2016).
Seifert, K. T. P. & Rödel, J. Temperature-insensitive large strain of (Bi1/2Na1/2)TiO3-(Bi1/2K1/2)TiO3-(K0.5Na0.5)NbO3 lead-free piezoceramics. J. Am. Ceram. Soc. 93, 1392–1396 (2010).
Groh, C. et al. Relaxor/ferroelectric composites: a solution in the quest for practically viable lead-free incipient piezoceramics. Adv. Funct. Mater. 24, 356–362 (2014).
Zhang, H. et al. Large strain in relaxor/ferroelectric composite lead-free piezoceramics. Adv. Electron. Mater. 1, 1500018 (2015).
Jo, W. et al. Giant electric-field-induced strains in lead-free ceramics for actuator applications-status and perspective. J. Electroceram. 29, 71–93 (2012).
Ren, X. Large electric-field-induced strain in ferroelectric crystals by poing-defect-mediated reversible domain switching. Nat. Mater. 3, 91–94 (2004).
Ang, C. & Yu, Z. Highly, purely electrostrictive strain in lead-free dielectrics. Adv. Mater. 18, 103–106 (2006).
Zhang, S. et al. High-strain lead-free antiferroelectric electrostrictors. Adv. Mater. 21, 4716–4720 (2009).
Shrout, T. R. & Zhang, S. J. Lead-free piezoelectric ceramics: alternatives for PZT? J. Electroceram. 19, 113–126 (2007).
Tsurumi, T., Soejima, K., Kamiya, T. & Daimon, M. Mechanism of diffuse phase transition in relaxor ferroelectrics. Jpn. J. Appl. Phys. 33, 1959–1964 (1994).
Guo, H. Y., Lei, C. & Ye, Z. G. Re-entrant type relaxor behavior in (1-x)BaTiO3-xBiScO3 solid solution. Appl. Phys. Lett. 92, 172901 (2008).
Kleemann, W. Random fields in relaxor ferroelectrics-a jubilee review. J. Adv. Dielect. 2, 124001 (2012).
Shvartsman, V. V. & Lupascu, D. C. Lead-free relaxor ferroelectrics. J. Am. Ceram. Soc. 95, 1–26 (2012).
Simon, A., Ravez, J. & Maglione, M. Relaxor properties of Ba0.9Bi0.067(Ti1-xZrx)O3 ceramics. Solid State Sci. 7, 925–930 (2005).
Kleemann, W. Relaxor ferroelectrics: cluster glass ground state via random fields and random bonds. Phys. Status Solidi B 251, 1993–2002 (2014).
Mydosh, J. A. Spin Glasses: An Experimental Introduction (Taylor & Francis, London, 1993).
Sherrington, D. A spin glass perspective on ferroic glasses. Phys. Status Solidi B 251, 1967–1981 (2014).
Kleemann, W. & Dec, J. Ferroic superglasses: polar nanoregions in relaxor ferroelectric PMN versus CoFe superspins in a discontinuous multilayer. Phys. Rev. B 94, 174203 (2016).
Park, Y. & Kim, Y. The dielectric temperature characteristic of additives modified barium titanate having core-shell structured ceramics. J. Mater. Res. 10, 2770–2776 (1995).
Choi, S. et al. Giant electrostrain in duplex structured alkaline niobates. Chem. Mater. 24, 3363–3369 (2012).
Dong, S., Yan, L., Viehland, D., Jiang, X. & Hackenberger, W. S. A piezoelectric single crystal traveling wave step motor for low-temperature application. Appl. Phys. Lett. 92, 153504 (2008).
Ji, Y., Ding, X., Otsuka, K. & Ren, X. Glass-ferroic composite caused by crystallization of ferroic glass. Phys. Rev. B. 92, 241114 (2015).
Sun, Z. et al. Time-dependent ferroelectric transition in Pb(1-x)(Zr0.4Ti0.6)(1-x/4)O3-xLa system. Appl. Phys. Lett. 102, 222907 (2013).
Ma, C. & Tan, X. In situ transmission electron microscopy study on the phase transitions in lead-free (1-x)(Bi1/2Na1/2)TiO3-xBaTiO3 ceramics. J. Am. Ceram. Soc. 94, 4040–4044 (2011).
Fu., H. & Cohen, R. E. Polarization rotation mechanism for ultrahigh electromechanical response in single-crystal piezoelectrics. Nature 403, 281–283 (2000).
Kutnjak, K., Petzelt, J. & Blinc, R. The giant electromechanical response in ferroelectric relaxors as a critical phenomenon. Nature 441, 956–959 (2006).
Xu, G. Y., Zhong, Z., Bing, Y., Ye, Z. G. & Shirane, G. Electric-field-induced redistribution of polar nano-regions in a relaxor ferroelectric. Nat. Mater. 5, 134–140 (2006).
Li, F. et al. The origin of ultrahigh piezoelectricity in relaxor-ferroelectric solid solution crystals. Nat. Commun. 7, 13807 (2016).
Ahart, M. et al. Origin of morphotropic phase boundaries in ferroelectrics. Nature 451, 545–548 (2008).
Xu, G., Wen, J., Stock, C. & Gehring, P. M. Phase instability induced by polar nanoregions in relaxor ferroelectric system. Nat. Mater. 7, 562–566 (2008).
Cao, W. Ferroelectrics: the strain limits on switching. Nat. Mater. 4, 727–728 (2005).
Castel, E., Josse, M., Michau, D. & Maglione, M. Flexible relaxor materials: Ba2PrxNd1-xFeNb4O15 tetragonal tungsten bronze solid solution. J. Phys. Condens. Matter 21, 452201 (2009).
Yang, S. et al. Large magnetostriction from morphotropic phase boundary in ferromagnets. Phys. Rev. Lett. 104, 197201 (2010).
Bergstrom, R. Jr. et al. Morphotropic phase boundaries in ferromagnets: Tb1−xDyxFe2 alloys. Phys. Rev. Lett. 111, 017203 (2013).
Bokov, A. A. & Ye, Z. G. Recent progress in relaxor ferroelectrics with perovskite structure. J. Mater. Sci. 41, 31–52 (2006).
Acknowledgements
This work is supported by the National Natural Science Foundation of China (51431007, 51621063, 51701150, and 51831006), the Program for Changjiang Scholars and Innovative Research Team in University (IRT_17R85), the China Postdoctoral Science Foundation (2017M610637), and the Fundamental Research Funds for the Central Universities.
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Fang, M., Ji, Y., Zhang, Z. et al. Re-entrant relaxor–ferroelectric composite showing exceptional electromechanical properties. NPG Asia Mater 10, 1029–1036 (2018). https://doi.org/10.1038/s41427-018-0093-7
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41427-018-0093-7