Abstract
Current-induced effective magnetic fields offer a new pathway through spin orbit interaction (SOI) to switch magnetization and have recently attracted great interest. In the conventional heavy metal/ferromagnetic metal/oxide (HM/FM/Oxide) structure, significant efforts have been made to study the role of the HM in determining effective magnetic fields. However, very little attention has been paid to the oxide layer and its interface with FM, where the Rashba effect may affect the effective field. In this report, we present a pathway to tune the effective magnetic field by engineering the Rashba effect in a hybrid multiferroic multilayer structure. A ferroelectric oxide of BaTiO3, whose polarizations either up or down are controlled by interface engineering, was introduced into the conventional SOI multilayer with the structure of BaTiO3/CoFeB/Pt. The current-induced effective magnetic fields increase by more than 200% when the ferroelectric polarization of BaTiO3 changes from up to down. The changes in the effective magnetic field are mainly attributed to the different Rashba effective fields induced by the opposite ferroelectric polarizations. Our study offers a new path towards controlling the current-induced effective magnetic field and may pave the way for integrating other functional oxides into the spintronic devices.
Similar content being viewed by others
Introduction
Spintronics is regarded as an alternative solution beyond CMOS technology to achieve scalable and low energy-consumption electronics1, where the electrical manipulation of the magnetization is the most desirable. Spin−orbit torque (SOT) offers such a way to achieve current-induced magnetization switching2,3,4. In contrast to the conventional spin-transfer torque, which originates from a polarized current passing through a magnetized layer5, SOT is generated from a current passing through either a bulk heavy metal via strong spin Hall effect (SHE) or a structure with inversion asymmetry by the interfacial spin orbit coupling such as the Rashba effect. The current-induced SOT consists of an antidamping torque and a field-like torque represented by the equivalent effective longitudinal magnetic field HL and transverse magnetic field HT, respectively.
The most sought-after structure for achieving the magnetization switching by SOT thus far consists of an ultrathin ferromagnetic film (FM) sandwiched between a heavy metal (HM) and an oxide layer2,3, i.e., HM/FM/Oxide. Both the SHE and Rashba effect, where the SHE comes from the HM while the Rashba effect is ascribed to the inversion asymmetry across the tri-layer structure, have been considered to be the origin of current-induced magnetization switching2,3,4,6. Several HMs such as Pt, Ta, W, Hf and Au-Cu alloys, etc.2,3,7,8,9,10, have been studied to search for a larger SHE that can generate larger effective magnetic fields and thus more efficient magnetization switching in devices. Recently, the oxidization of HM and FM layers was found to play a nontrivial role in determining the SOT11,12, suggesting an important role of the Rashba effect. It is therefore expected that the oxide layer in the sandwiched structure would play an important role in the current-induced magnetization switching. However, to date, little attention has been paid to the interface between FM and oxide layers13. Furthermore, the interface might provide an alternative way to manipulate the current-induced effective magnetic field.
Due to their promising potential for application, it is highly desirable to find an effective way to tune the current-induced effective magnetic fields (HL and HT) and thus manipulate the magnetization switching14,15,16,17,18. Tuning of the effective magnetic field by a factor of four through voltage-gating has been previously achieved in a topological insulator-based structure by tuning the Fermi level position of the surface state of the topological insulator14. However, only 5% modulation by the voltage-gating can be realized in a conventional HM/FM/Oxide structure using AlOx as a dielectric layer15. A noticeable modulation effect might be available by using the ferroelectric materials, whose polarization direction can be electrically controlled. For example, the hybrid multiferroic structure with ferroelectric and ferromagnetic layers has been fabricated to attain significant magnetoelectric effect19,20,21. Further, a spin splitting through the spin orbit interaction (SOI) has been influenced by the ferroelectric polarization experimentally22,23 and theoretically24,25, which hints at the possibility of modulating the current-induced effective magnetic field in the hybrid multiferroic structure through the engineering of Rashba fields.
In this work, we fabricated a hybrid multiferroic structure, BaTiO3/CoFeB/Pt, by replacing the conventional oxide (MgO, AlOx, or HfOx) with ferroelectric BaTiO3 in the HM/FM/Oxide structure in which the perpendicular magnetic anisotropy (PMA) is still retained. The effects of different polarizations on the current-induced effective magnetic fields and magnetization switching are investigated, where different polarization directions of BaTiO3 are achieved via interface engineering.
Materials and methods
Sample preparation
Before growth of the multilayer structure, the SrTiO3 (STO) substrates were treated with buffer-HF solvent and annealed at 975 °C for 3 h to achieve TiO2 termination. For the SrO termination, a single-layer SrRuO3 was grown on the TiO2-terminated STO at 760 °C and then cooled to 640 °C, where BaTiO3 was grown. The BaTiO3 thin films were fabricated by pulsed laser deposition with a laser energy density of ~1 J/cm2 under 5 mTorr O2 environment and cooled at 10 °C/min with 200 Torr O2 in the chamber. After this, the oxide film was transferred to the sputtering chamber to in situ grow CoFeB and Pt layers, whose growth rates are 0.08 and 0.1 nm/s, respectively. All of the structures were annealed at 320 °C for 1 h to obtain the PMA.
Devices fabrication and transport measurements
The structures were patterned into the cross-bar with a channel width of 10 μm and a length of 80 μm by using the photolithography technique and ion milling. Then, 100 nm Cu with 5 nm Pt protection layer was used as electrodes. A Keithley 6221 and two lock-in amplifiers were used for the first and second harmonic measurements. The Keysight 2901A with a DC current pulse of 10 ms and a lock-in amplifier was used for the magnetization switching measurement. All the electric transport measurements were performed on a physical properties measurement system (PPMS).
Results
Ferroelectric polarization and its influence on magnetic properties
As reported in our previous work26, the preferred polarization direction of BTO can be controlled via interface engineering, i.e., controlling the termination of the STO substrate. As a result, the TiO2-terminated STO will lead to down-polarization of BTO (Fig. 1a), whereas up-polarization is preferred for the SrO termination of STO substrate (Fig. 1b). SrO termination is achieved by depositing a thin SrRuO3 (SRO) underlayer on TiO2-terminated STO prior to BTO. Panels (c) and (d) in Fig. 1 show the out-of-plane piezoresponse force microscopy (PFM) phase images, respectively, where different colors represent the opposite polarizations. The good homogeneity of phase images suggests a single domain of the single ferroelectric phase for each preferred polarization. This interface-controlled engineering was characterized by the HAADF-STEM technique. Figure 1e shows the HAADF-STEM images of a BaTiO3 film grown on top of SrO-terminated SrTiO3 via insertion of a SrRuO3 layer. From the image, it can be seen that the terminations of SrTiO3 and SrRuO3 layers are TiO2 and SrO, respectively, which are consistent with the description above.
Schematic structure of BaTiO3 grown on a TiO2-terminated SrTiO3 and b SrO-terminated SrTiO3 via insertion of a layer of SrRuO3. The red arrows represent the direction of the ferroelectric polarization of BaTiO3. The corresponding out-of-plane phase images are shown in c and d, where the different colors confirm their opposite polarization. The size scale bars are 500 nm. e HAADF-STEM images of a BaTiO3 film grown on top of SrO-terminated SrTiO3 by inserting a SrRuO3 layer
CoFeB (1.0 nm)/Pt (4.0 nm) bilayers are grown in situ on the BTO film with different polarization directions after transferring to a sputtering chamber without breaking vacuum, where the CoFeB layer directly contacts with BTO. The ferroelectric property of BTO films remains after this annealing procedure, which was confirmed by the hysteresis loops of phase and amplitude by PFM, as shown in Supplementary Figure S1. In addition to the self-polarization of BTO, all other conditions such as the growth parameters for BTO, CoFeB and Pt and the annealing procedures are identical.
As shown in Fig. 2, the magnetic easy axis of both structures is in the out-of-plane direction confirmed by superconducting quantum interference device (SQUID) and magneto-optic Kerr effect (MOKE) measurements. Moreover, we found that the different ferroelectric polarizations of BTO have nontrivial influence on the magnetic properties of CoFeB grown on top of them. The saturation magnetization Ms of CoFeB is 1212 emu/cc when the polarization points down, whereas it is 1316 emu/cc as the polarization is up. The effective magnetic anisotropy energy (in terms of Kefft) of CoFeB/Pt on BTO with polarization up (0.178 ergs/cm2), which is calculated by the integrated difference between the out-of-plane and in-plane magnetization curves, is slightly larger than that with BTO polarization down (0.171 ergs/cm2). A high anisotropy energy brings about high thermal stability and therefore requires high switching current density, whereas a low anisotropy energy lowers the writing current and therefore results in less energy consumption. The influence on magnetic anisotropy by ferroelectric polarization has been discussed theoretically27, and the Fe on the BTO with up-polarization has a larger magnetic anisotropy than that on BTO with down-polarization due to the different hybridizations among Fe, O, and Ti. This hybridization may result in orbital polarization of Fe28. Our experimental results on the magnetic anisotropy change with the polarization direction are consistent with the theoretical calculations. In Supplementary Figure S2, we also presented the polarization-dependent X-ray absorption spectra (XAS) of Fe L2,3 edge, which confirmed a different orbital polarization of Fe as the ferroelectric polarization direction changes from up to down. For a clear presentation, in the following context, BTO↑ is used to name the CoFeB/Pt bilayer grown on BTO with ferroelectric polarization up, and BTO↓ is for that grown on BTO with ferroelectric polarization down.
The MH loops by SQUID at 300 K for CoFeB/Pt bilayers grown on BaTiO3 with polarization down (a) and BaTiO3 with polarization up (b), which demonstrate the out-of-plane easy axis of both samples and that the saturated magnetization and effective anisotropy energy are influenced by the different polarizations of BaTiO3. Here, BTO↓ and BTO↑ represent the samples of CoFeB/Pt grown on BTO with polarization down and up induced by TiO2- and SrO-terminated SrTiO3, respectively
Harmonics measurements for the current-induced effective magnetic fields
Cross-bar Hall devices (Fig. 3a) of two types of structures, BTO↓ and BTO↑, were fabricated by photolithography and ion milling. The temperature-dependent anomalous Hall effect is illustrated in Supplementary Figure S3. The harmonic measurement method was employed to quantitatively evaluate HL and HT29,30,31. Considering the contribution of the planar Hall effect to the Hall voltage, the following equations are used to calculate the current-induced effective magnetic fields HL and HT30
where x = RPHE/RAHE and RPHE and RAHE are the saturation planar and anomalous Hall resistances, respectively. V1ω and V2ω are the first and second harmonic Hall voltages measured simultaneously by two lock-in amplifiers. Hx and Hy are external magnetic fields swept in the longitudinal and transverse directions during the measurement of the harmonic Hall voltage. Parabolic and linear fittings are performed on V1ω and V2ω as a function of the external field, as shown in Fig. 3b, c for the longitudinal and transverse field, respectively. HL(T),meas are obtained from the fitting results based on Eq. 1. χ is determined from the angular-dependent planar Hall resistance (see Supplementary Figure S4). The resulting effective magnetic field HL(T) can be determined from Eq. 2.
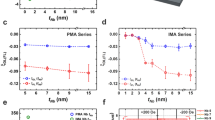
a Schematic drawing of the cross-bar device used for the measurements. During the measurements, an AC current j is injected in the x direction with the external magnetic field (HE). The current-induced effective magnetic fields (HL and HT) are reflected in the harmonic measurements. b First and c second harmonic data for the BTO↓ device with a small external magnetic field applied in the longitudinal and transverse directions, respectively, when the magnetization (M) directions of CoFeB are up. The harmonics data for down magnetization are presented in the right insets. The left insets show the corresponding measurement setups. d Calculated effective magnetic fields (HL and HT) as a function of the AC current amplitude. e, f Temperature-dependent HL and HT, respectively, of the BTO↓ and BTO↑ devices
The effective magnetic fields at 10 K for the BTO↓ structure are HL = 12.7 Oe/(107 A/cm2) and HT = 8.4 Oe/(107 A/cm2), whereas for BTO↑ HL = 4.0 Oe/(107 A/cm2) and HT = 2.2 Oe/(107 A/cm2). Both HL and HT increased by more than 200% when the ferroelectric polarization changes from up to down. As the identical CoFeB/Pt bilayers were deposited in both structures, a difference of the current-induced effective magnetic fields (both HL and HT) is not expected if the bulk SHE of Pt is the only factor affecting the changes of HL and HT, indicating that the interface between CoFeB and BTO plays a critical role, which will be discussed later. To check the influence of Joule heating, the harmonic measurements with varying AC current amplitudes were performed. As shown in Fig. 3d, the effective magnetic fields HL and HT are linearly proportional to the current amplitudes over the examined range. A similar linear dependence is observed with BTO↑, however with a different slope. The linear proportionality confirms that the Joule heating effect on the measured effective magnetic fields is negligible. Furthermore, we also excluded the influence of the anomalous Nernst effect (see Supplementary Figure S5), which is caused by a temperature gradient along the current channel if it exists.
The tuning of the polarization on the current-induced effective magnetic fields is further confirmed by the temperature-dependent harmonic measurements. Panels (e) and (f) in Fig. 3 show the derived HL and HT of the BTO↓ and BTO↑ devices, respectively. The current-induced effective magnetic fields, HL and HT, of BTO↓ are always larger than those of BTO↑ in the temperature range we studied, and the differences become smaller with increasing temperature. The temperature dependence of HT of BTO↓ is opposite to HT of BTO↑, whereas the HL of both structures increases with increasing temperature. According to \({{H}}_{{\rm L}({{T}})}/{{J}}_{\mathrm {c}} = \xi _{{\rm L}(T)}\hbar /(2e{{M}}_{\mathrm {s}}t_{{\rm FM}})\)32, where Jc is the charge current density, ξL(T) is spin torque efficiency, ћ is Planck’s constant, Ms is the saturation magnetization, and tFM is its thickness, the increase of HL upon increasing the temperature is attributed to the decrease of Ms (see Supplementary Figure S3, where the anomalous Hall resistance indicates the trend of the Ms) provided that the ξL is weakly temperature dependent. In addition, the HT/HL ratio for BTO↓ increases with decreasing temperature, whereas the HT/HL ratio for BTO↑ remains unchanged (see Supplementary Figure S6). The origin of the different behaviors in the two types of samples is discussed later.
Current-induced magnetization switching
Furthermore, the current-induced effective magnetic field is used to achieve the electrical manipulation of the magnetization. In our experimental setup, a pulse current is used to generate the effective magnetic fields, and the Hall voltage due to a small amplitude of AC current source after the pulse was recorded, which reflects the magnetization state. To obtain deterministic switching for the ferromagnetic layer with PMA, an external in-plane magnetic field is applied to break the equilibrium symmetry33. As shown in Fig. 4a, b, deterministic switching of the magnetization is achieved for both structures, i.e., changing the current direction leads to magnetization switching with a fixed in-plane magnetic field. The polarity of the switching changes upon reversing the in-plane magnetic field. These are typical features of SOT switching of PMA devices. Panels (c) and (d) in Fig. 4 summarize the switching phase diagram, i.e., the critical switching current as a function of the external magnetic field. It is found that the critical switching current for BTO↓ is smaller than that of BTO↑. The same measurements were also performed at lower temperatures (Supplementary Figure S7), which shows similar behavior.
a, b RH-I loops at various in-plane magnetic fields along the current direction for BTO↓ and BTO↑ devices, respectively. The critical currents evaluated from a and b are plotted in c and d as a function of the in-plane magnetic field. e Calculated anisotropy magnetic field from the harmonic measurements for both devices. The inset shows a typical procedure to obtain the anisotropy field. f Magnetization switching efficiency for both devices as a function of temperature
It is well-known that, in the HM/FM/Oxide systems, the effective longitudinal magnetic field HL exerts an antidamping torque to drive the magnetization switching and that the effective transverse magnetic field HT induces a field-like torque to cause precession of the magnetization, which assists in the magnetization switching, thus reducing the critical switching current34,35. Considering the nontrivial transverse magnetic field in both BTO↓ and BTO↑ structures, the equation \(\sqrt {2{{H}}_{\rm K}^2 - {{H}}_{\rm E}^2} /{{J}}_{\rm c}\) is used to evaluate the switching efficiency of the devices35, where HK is the magnetic anisotropy field, HE is the external magnetic field applied, and Jc the critical switching current. HK for the BTO↓ and BTO↑ devices is derived from the first harmonic data (inset of Fig. 4e), as shown in Fig. 4e. It can be seen that HK for BTO↑ is larger than that of BTO↓, which is consistent with that observed by SQUID and MOKE measurements. Figure 4f shows the switching efficiency of BTO↓ and BTO↑ devices as functions of temperature. The switching efficiencies of both structures increase with increasing temperature, which is consistent with the change in the HL with temperature (Fig. 3e), confirming that HL plays a dominant role in the magnetization switching process. As a result, higher switching efficiency is obtained for BTO↓ with down ferroelectric polarization, which suggests that the polarization of BTO can be used as a parameter to tune the magnetization switching. It is noted that the difference of the switching efficiency of both structures with increasing temperature is not as much as HL, which may be caused by the difference of HK as well as possible Joule heating due to the large switching current applied6.
Discussion
As demonstrated above, the different magnetic anisotropies, effective magnetic fields, and thus switching efficiencies between BTO↓ and BTO↑ confirm that the ferroelectric polarization in the BTO/CoFeB hybrid multiferroic can be used to modulate the current-induced magnetization switching. It is commonly considered that SHE, the spin memory loss/spin transparency32,36,37, and the Rashba effect play main roles in the effective magnetic field of the SOT-based magnetization switching. SHE originates from the generation of spin current in the HM layer and the diffusion into the magnetic layer, and the spin memory loss/spin transparency is related to the spin transmission efficiency at the interface between HM and FM. However, in our case, except for the ferroelectric polarization, all other experimental conditions are identical. The resistivities of both structures are almost the same as shown in Supplementary Figure S8, which further confirmed that the experiment-induced deviation can be neglected. Recently, it has been reported that the strain status of the metal layers may influence the generated SOT effective magnetic fields31,32,38. Our XRD and TEM results exhibit no difference on BTO lattice constants after insertion of an ultrathin SRO layer. With the same conditions of the CoFeB/Pt layer, it is unlikely to lead to different strain status in the two types of samples with different ferroelectric polarizations.
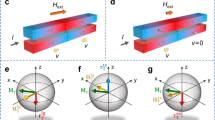
Therefore, it is natural to expect that the bottom interface BTO/CoFeB may play a role in tuning the effective magnetic fields and thus the magnetization switching efficiency. The opposite polarizations of BTO may result in different electric fields and thus a potential difference around the BTO/CoFeB interface experienced by the electrons nearby, as schematically illustrated in Fig. 5. The potential at the BTO/CoFeB interfaces may generate the effective magnetic fields via the interfacial SOI such as the Rashba effect. In the studied system with structural inversion symmetry broken along the film normal direction, the interfacial electric field E = E0z results in SO coupling of the form
where αR is known as the Rashba parameter depending on the potential drop at the interface, p is the electron momentum, and σ is the vector of the Pauli spin matrices. Equation 3 describes a Zeeman term that involves a magnetic field proportional to the electron momentum p. As shown in Fig. 5a, b, when electrons flow along the x-axis, they experience an effective magnetic field along the y-axis, BR, called the Rashba field. The magnitude of the Rashba field can be calculated from BR = 2αRkF/gμB, where kF and g are the Fermi wave vector and g factor of the carriers in the conduction channel, respectively. Its direction (along the y direction or –y direction) depends on the electric field direction. As the strength of the Rashba parameter is directly related to the interfacial potential drop (electrical field), engineering the polarization direction of the ferroelectric layer electrically modifies the system symmetry and electron occupation, which in turn controls the magnitude and direction of the Rashba effective field.
a, b BTO↓ and BTO↑ devices, respectively, where the different polarization directions are expected to result in different built-in electric fields at the BTO/CoFeB interfaces and thus different effective magnetic field BR at the bottom interfaces. Note that the effective fields due to the bulk spin Hall effect of Pt and the structural inversion asymmetry across the trilayers are not indicated
Because both SHE from Pt and the Rashba effect from interface between FE/FM are present in our structures, a simple model is proposed to separate the contribution of the Rashba effect due to the BTO polarization from the SHE. In this model, we assume that the magnitude of the contribution of Rashba effect resulting from the BTO polarization to the effective longitudinal and transverse magnetic fields are the same in BTO↓ and BTO↑ structures and their directions are opposite and that the effective magnetic fields by SHE in both structures are identical. Note that the SHE described here includes all effective fields not due to the differences in ferroelectric polarization, which may also include the Rashba effect across the trilayers2,6 related to the BTO/CoFeb and CoFeB/Pt interfaces identical for both structures. Since the magnetizations of the two structures are slightly different, the effective magnetic fields due to SHE might have a trivial difference. The detailed description of the simple model is depicted in Supplementary Information Note 1. The derived SHE contribution from Pt in terms of spin torque efficiency is ~0.08, which is in a similar range to that reported previously (Supplementary Table S1 in Supplementary Information Note 1). The effective spin torque efficiencies due to the longitudinal magnetic field from the Rashba effect are approximately 0.043 and −0.043 for the BTO↓ and BTO↑ structures at 10 K, respectively, suggesting that the magnetization switching is enhanced in the BTO↓ structure and suppressed in the BTO↑ structure. The magnitudes of the transverse field due to Rashba contributions decrease with increasing temperature (see Supplementary Figure S9), which can explain the opposite change of the measured HT with temperature in BTO↓ and BTO↑ structures (Fig. 3f). Furthermore, we have also fabricated a device based on the BTO film grown on untreated STO, which is expected to lack self-polarization. The measured effective magnetic fields, shown in Supplementary Figure S10, are between the magnitudes from the structures with opposite BTO polarizations. This further supports the scenario proposed in this work. From our model, it can be seen that the Rashba effect is able to induce both antidamping torque (longitudinal magnetic field) and field-like torque (transverse magnetic field) simultaneously, which is consistent with recent theoretical discussions39,40,41,42,43,44.
Though the measurements presented in this report were performed at low temperature, the technique is still applicable at room temperature provided there is a strong enough room temperature PMA for devices. Importantly, the demonstration of polarization-dependent modulation of current-induced magnetic fields provides opportunities for further exploration of the interplay between electrical reversal of the polarization and effective magnetic fields. It is noted that current-induced switching of a similar ferromagnetic/ferroelectric hybrid structure with a PMN-PT single-crystal substrate was recently reported18. However, it is quite different from our case as the heavy metal Pt in the structure was grown next to the PMN-PT rather than the ferromagnetic layer, and thus, it makes use of the in-plane gradient of the spin density to achieve deterministic switching of the magnetization. This effect is related to modifications of spin transport properties in the heavy metal layer, whereas in this work, the changes in effective magnetic field are not related to spin transport within the Pt layer.
In conclusion, the tuning of the current-induced effective magnetic fields has been achieved in BaTiO3/CoFeB/Pt structures with tuning of the polarization direction. This modulation effect also unambiguously demonstrates the role of the interfacial SOI with the help of the ferroelectric polarization at the conventional HM/FM/Oxide structure, which is consistent with recent studies11,39,40,45. Our findings are technologically important for the reduction of energy consumption and increase in memory density, which are the ultimate goals of spintronics research. During writing, a pulse can be applied to induce a down ferroelectric polarization with which a lower current and higher writing efficiency can be achieved, leading to lower energy consumption. An up ferroelectric polarization can be used to enhance the magnetic anisotropy, thus increasing the thermal stability of the smaller magnetic bit for a higher memory density. Therefore, our study paves the way to integrate functional oxides into SOT-based spintronics devices for future applications.
References
Wang, K. L. et al. Electric-field control of spin−orbit interaction for low-power spintronics. Proc. IEEE 104, 1974–2008 (2016).
Miron, I. M. et al. Perpendicular switching of a single ferromagnetic layer induced by in-plane current injection. Nature 476, 189–193 (2011).
Liu, L. et al. Spin-torque switching with the giant spin Hall effect of tantalum. Science 336, 555–558 (2012).
Wadley, P. et al. Electrical switching of an antiferromagnet. Science 351, 587–590 (2016).
Ralph, D. C. & Stiles, M. D. Spin transfer torques. J. Magn. Magn. Mater. 320, 1190–1216 (2008).
Yang, M. et al. Spin−orbit torque in Pt/CoNiCo/Pt symmetric devices. Sci. Rep. 6, 20778 (2016).
Pai, C. -F. et al. Spin transfer torque devices utilizing the giant spin Hall effect of tungsten. Appl. Phys. Lett. 101, 122404 (2012).
Wu, J. et al. Spin Hall angle and spin diffusion length in Au-Cu alloy. IEEE Trans. Magn. 52, 1–4 (2016).
Ramaswamy, R., Qiu, X., Dutta, T., Pollard, S. D. & Yang, H. Hf thickness dependence of spin−orbit torques in Hf/CoFeB/MgO heterostructures. Appl. Phys. Lett. 108, 202406 (2016).
Qiu, X. et al. Angular and temperature dependence of current induced spin-orbit effective fields in Ta/CoFeB/MgO nanowires. Sci. Rep. 4, 4491 (2014).
Demasius, K. U. et al. Enhanced spin−orbit torques by oxygen incorporation in tungsten films. Nat. Commun. 7, 10644 (2016).
Qiu, X. et al. Spin–orbit-torque engineering via oxygen manipulation. Nat. Nanotechnol. 10, 333–338 (2015).
Akyol, M. et al. Effect of the oxide layer on current-induced spin−orbit torques in Hf|CoFeB|MgO and Hf|CoFeB|TaOx structures. Appl. Phys. Lett. 106, 032406 (2015).
Fan, Y. et al. Electric-field control of spin–orbit torque in a magnetically doped topological insulator. Nat. Nanotechnol. 11, 352–359 (2016).
Liu, R. H., Lim, W. L. & Urazhdin, S. Control of current-induced spin−orbit effects in a ferromagnetic heterostructure by electric field. Phys. Rev. B 89, 220409 (2014).
Yan, Y. et al. Strong electrical manipulation of spin–orbit torque in ferromagnetic heterostructures. Adv. Electron. Mater. 2, 1600219 (2016).
Zhang, X. et al. Electrical control over perpendicular magnetization switching driven by spin−orbit torques. Phys. Rev. B 94, 174434 (2016).
Cai, K. et al. Electric field control of deterministic current-induced magnetization switching in a hybrid ferromagnetic/ferroelectric structure. Nat. Mater. 16, 712–716 (2017).
Morgan, T. Low energy consumption spintronics using multiferroic heterostructures. J. Phys. Condens. Matt. 28, 033001 (2016).
Vaz, C. A. F. Electric field control of magnetism in multiferroic heterostructures. J. Phys. Condens. Matt. 24, 333201 (2012).
Heron, J. T. et al. Deterministic switching of ferromagnetism at room temperature using an electric field. Nature 516, 370–373 (2014).
Lutz, P., Figgemeier, T., El-Fattah, Z. M. A., Bentmann, H. & Reinert, F. Large spin splitting and interfacial states in a Bi/BaTiO3(001) Rashba ferroelectric heterostructure. Phys. Rev. Appl. 7, 044011 (2017).
Krempaský, J. et al. Entanglement and manipulation of the magnetic and spin–orbit order in multiferroic Rashba semiconductors. Nat. Commun. 7, 13071 (2016).
Di Sante, D., Barone, P., Bertacco, R. & Picozzi, S. Electric control of the giant Rashba effect in bulk GeTe. Adv. Mater. 25, 509–513 (2013).
Narayan, A. Class of Rashba ferroelectrics in hexagonal semiconductors. Phys. Rev. B 92, 220101 (2015).
Guo, R. et al. Tailoring self-polarization of BaTiO3 thin films by interface engineering and flexoelectric effect. Adv. Mater. Interfaces 3, 1600737 (2016).
Duan, C. G. et al. Tailoring magnetic anisotropy at the ferromagnetic/ferroelectric interface. Appl. Phys. Lett. 92, 122905 (2008).
Liang, S. H. et al. Large and robust electrical spin injection into GaAs at zero magnetic field using an ultrathin CoFeB/MgO injector. Phys. Rev. B 90, 085310 (2014).
Pi, U. H. et al. Tilting of the spin orientation induced by Rashba effect in ferromagnetic metal layer. Appl. Phys. Lett. 97, 162507 (2010).
Hayashi, M., Kim, J., Yamanouchi, M. & Ohno, H. Quantitative characterization of the spin−orbit torque using harmonic Hall voltage measurements. Phys. Rev. B 89, 144425 (2014).
Jamali, M. et al. Spin−orbit torques in Co/Pd multilayer nanowires. Phys. Rev. Lett. 111, 246602 (2013).
Pai, C. F., Ou, Y., Vilela-Leão, L. H., Ralph, D. C. & Buhrman, R. A. Dependence of the efficiency of spin Hall torque on the transparency of Pt/ferromagnetic layer interfaces. Phys. Rev. B 92, 064426 (2015).
Yu, G. et al. Switching of perpendicular magnetization by spin−orbit torques in the absence of external magnetic fields. Nat. Nanotechnol. 9, 548–554 (2014).
Legrand, W., Ramaswamy, R., Mishra, R. & Yang, H. Coherent subnanosecond switching of perpendicular magnetization by the fieldlike spin−orbit torque without an external magnetic field. Phys. Rev. Appl. 3, 064012 (2015).
Taniguchi, T., Mitani, S. & Hayashi, M. Critical current destabilizing perpendicular magnetization by the spin Hall effect. Phys. Rev. B 92, 024428 (2015).
Zhang, W., Han, W., Jiang, X., Yang, S. H. & S. P. Parkin, S. Role of transparency of platinum-ferromagnet interfaces in determining the intrinsic magnitude of the spin Hall effect. Nat. Phys. 11, 496–502 (2015).
Rojas-Sánchez, J. C. et al. Spin pumping and inverse spin Hall effect in platinum: the essential role of spin-memory loss at metallic interfaces. Phys. Rev. Lett. 112, 106602 (2014).
Chowdhury, P. et al. Effect of coherent to incoherent structural transition on magnetic anisotropy in Co/Pt multilayers. J. Appl. Phys. 112, 023912 (2012).
Amin, V. P. & Stiles, M. D. Spin transport at interfaces with spin−orbit coupling: formalism. Phys. Rev. B 94, 104419 (2016).
Amin, V. P. & Stiles, M. D. Spin transport at interfaces with spin−orbit coupling: phenomenology. Phys. Rev. B 94, 104420 (2016).
Kim, K. W., Lee, K. J., Sinova, J., Lee, H. W. & Stiles, M. D. Spin−orbit torques from interfacial spin−orbit coupling for various interfaces. Phys. Rev. B 96, 104438 (2017).
Li, H. et al. Intraband and interband spin−orbit torques in noncentrosymmetric ferromagnets. Phys. Rev. B 91, 134402 (2015).
Xiao, C. & Niu, Q. Rashba torque beyond the Boltzmann regime. Phys. Rev. B 96, 035423 (2017).
Wang, X., & Manchon, A. Diffusive spin dynamics in ferromagnetic thin films with a Rashba interaction. Phys. Rev., Lett. 108, 117201 (2012).
Wang, L. et al. Giant room temperature interface spin Hall and inverse spin Hall effects. Phys. Rev. Lett. 116, 196602 (2016).
Acknowledgements
The research is partially supported by the Singapore National Research Foundation under CRP Award Nos. NRF-CRP10-2012-02 and NRF-CRP12-2013-01 and IIP award No. NRF-IIP001-001. H.Y. and J.C. are members of the Singapore Spintronics Consortium (SG-SPIN).
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lin, W., Pollard, S.D., Guo, R. et al. Tuning of current-induced effective magnetic field through Rashba effect engineering in hybrid multiferroic structures. NPG Asia Mater 10, 740–748 (2018). https://doi.org/10.1038/s41427-018-0069-7
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41427-018-0069-7
This article is cited by
-
Tuning the interfacial spin-orbit coupling with ferroelectricity
Nature Communications (2020)