Abstract
Colloids of electrically charged nanorods can spontaneously develop a fluid yet ordered liquid crystal phase, but this ordering competes with a tendency to form a gel of percolating rods. The threshold for ordering is reduced by increasing the rod aspect ratio, but the percolation threshold is also reduced with this change; hence, prediction of the outcome is nontrivial. Here, we show that by establishing the phase behavior of suspensions of cellulose nanocrystals (CNCs) fractionated according to length, an increased aspect ratio can strongly favor liquid crystallinity without necessarily influencing gelation. Gelation is instead triggered by increasing the counterion concentration until the CNCs lose colloidal stability, triggering linear aggregation, which promotes percolation regardless of the original rod aspect ratio. Our results shine new light on the competition between liquid crystal formation and gelation in nanoparticle suspensions and provide a path for enhanced control of CNC self-organization for applications in photonic crystal paper or advanced composites.
Similar content being viewed by others
Introduction
The ordered self-organization of rod-shaped has fascinated researchers since the first observation of liquid crystal (LC) formation in aqueous suspensions of tobacco mosaic virus in the 1930s1. With today’s prominent role of nanorods and their organization in a variety of advanced materials2,3, the phenomenon has also acquired key industrial relevance. Cellulose nanocrystals (CNCs) constitute a class of nanorods that currently attracts considerable attention both from academia4,5,6,7 and industry8,9,10 for reasons in addition to the fact that they can be sustainably produced from plants or other bioresources. CNCs are often conveniently approximated as cylindrical rods of crystalline cellulose with a diameter d of a few nanometers and a length L on the order of a hundred nanometers, although the true shape may be closer to an irregular twisted beam11,12. Because of the negative sulfate half-esters or other surface charges remaining from the production procedure, CNCs are easily dispersed in water. Adding their excellent mechanical properties, optical transparency, ease of chemical functionalization, and ability to form a long-range-ordered LC phase, CNCs are highly attractive for the realization of tunable, in some cases even responsive, high-performance materials with spectacular mechanical and optical properties5,9,13,14,15.
The LC phase formed by CNC suspensions is of the chiral nematic, or cholesteric, type. It was Onsager who explained how liquid suspensions of nanorods can spontaneously develop long-range orientational order—the hallmark of nematics—as a result of the gain in translational entropy overcompensating the loss in rotational entropy, provided that a sufficiently high volume fraction φ of sufficiently anisotropic nanorods is available16. He found the stability limit of the isotropic phase (disordered rods) to be φ0 = 3.3d/L, and the nematic phase that then starts forming has a rod volume fraction φ1 = 4.5d/L. If the overall rod volume fraction is between these limiting values, phase separation takes place, where the denser nematic phase sinks to the bottom and the isotropic phase floats on top15. The volume fraction Φ of the nematic phase should, according to the basic Onsager model, increase linearly from 0 to 1 as the overall rod volume fraction φ increases from φ0 to φ1.
Comparison through experiments reveals that CNC suspensions deviate into two characteristic ways. First, the real rod volume fraction φ is difficult to establish; hence, experimental work typically utilizes the corresponding mass fractions w0 (maximum mass fraction w for Φ = 0) and w1 (minimum mass fraction w for Φ = 1). In fact, because φ is the sum of the volume of the cellulose rod itself and the excluded volume induced by electrostatic repulsion between rods, the ratio between φ and w is not constant: the repulsion range decreases with increasing CNC content because of increasing screening of the rod surface charge as the CNC counterions are released into the water17. Thus, in typical plots of the nematic volume fraction Φ vs. the mass fraction w of CNC, the curve falls off sublinearly with increasing CNC content.
The second deviation—of critical importance for large-scale control of the self-organization18 and therefore for applications—is that, frequently, a completely liquid crystalline sample cannot be reached in practice because w1 > wg, the CNC mass fraction at which the system turns into a macroscopic gel, which is often considered a kinetically arrested state8,15,19,20,21,22. The rheological data that we present below confirm that the sample at w > wg is a physical gel; hence, the transition is a percolation phenomenon23, i.e., a continuous network of connected rods is established that spans the macroscopic sample and prevents the system from flowing. Because the threshold particle fraction for percolation decreases with increasing aspect ratio L/d of the particles, just like the threshold for LC formation, this relationship would suggest that any attempt to promote liquid crystallinity would also promote percolation and the related gelation. Surprisingly, our new results show that this expectation is incorrect, with far-reaching implications for the fundamental understanding of the balance between LC formation and gelation in nanoparticle suspensions as well as for the ability to apply the chiral nematic order provided by CNC suspensions in advanced materials.
By exploiting the spontaneous segregation that takes place according to the ratio L/d as the LC phase separates from the isotropic surroundings, to divide our CNC suspension into two fractions with predominantly long and short rods, we show that L/d has no impact on the onset of gelation, while it indeed strongly favors liquid crystallinity. Thus, both fractions and the original suspension have identical values of wg, but the fraction with high L/d rods shows much lower w0 and w1 values than the initial suspension. Significantly, from an applied point of view, this brings w1 well below wg, while in the original suspension, w1 ≈ wg. We have thus gained access to a large CNC mass fraction range where the complete sample is in a nonarrested equilibrium chiral nematic phase, enabling much better control of the macroscopic order18. We conclude that the gelation at wg is due to the loss of colloidal stability, as the solvent counterion concentration has reached a critical value \(c_{Na^ + }^g\), inducing linear rod aggregation, which, as a secondary phenomenon, triggers percolation regardless of the L/d of the individual rods. We corroborate this conjecture by also inducing gelation at a low CNC mass fraction by adding NaCl until \(c_{Na^ + }^g\) is reached. Atomic force microscopy (AFM) confirms the linear aggregation of CNCs upon salt addition.
Methods
Sample preparation
CNCs with Na+ counterions were purchased from USDA Forest Products lab, University of Maine (USA), and the details of their production procedure are provided at https://umaine.edu/pdc/cellulose-nano-crystals. We characterized the as-received CNCs extensively (Supplementary Information, Figures S1-S3, S7) and also determined the sulfur content, which is taken as a measure of the surface charge since this is provided by the sulfur half-ester groups (SO3−), to be 1 wt.%, as given by conductometric titration (Figure S4). The as-received suspension was diluted to w = 6 wt.% and sonicated for 70 s with an ultrasonic probe (Dr. Hielscher UP200St, 7 mm diameter titanium tip) with an energy input of 0.01 kJ/mL CNC suspension (calculation in the Supplementary Information). No further purification or filtering was done (as demonstrated by the comparison between the as-received and purified CNCs in the Supplementary Information, Figure S17). A sample series referred to as init-CNC (init = initial) with w varying from 1 to 13 wt.% was then prepared from the starting suspension by dilution with ultrapure water or the evaporation of water, as required for each target mass fraction. We left the samples standing until phase separation occurred. After 1 week, we identified the w ≈ 7 wt.% sample as having close to equal volume fractions of isotropic and LC phases (Φ = 0.5).
For fractionation, a total of 0.5 kg of sonicated init-CNC suspension was prepared at w ≈ 7 wt.%. The sample was left standing for 1 week until phase separation was visible, and the isotropic top half was then separated from the LC bottom half with a pipette. The former was concentrated, and the latter was diluted until each fraction reached Φ ≈ 0.5. The full procedure was repeated another two times each for the isotropic phase (the LC fraction in each subsequent stage was not further studied) and for the LC phase (the isotropic fraction in each subsequent stage was not further studied). The CNCs in the final fractions thus obtained are referred to as iii-CNC (threefold isotropic fractionation) and aaa-CNC (threefold anisotropic (LC) fractionation), respectively. Curves of the pH for iii-CNC and aaa-CNC are included in the Supplementary Information, Figure S9.
Considerable care was taken to obtain representative values of the diameter d, length L, and L/d from AFM experiments for each CNC fraction, as described in detail in the Supplementary Information (Figure S5). The data used in the paper are averages based on careful measurements of 300 individual rods per CNC fraction (Table S1).
Establishing the phase diagrams
A series of relevant mass fractions w were obtained by first concentrating the different CNC suspensions (init-CNC, iii-CNC, and aaa-CNC) using mechanical stirring at room temperature. Once the concentration was ~13 wt.%, we diluted aliquots with varying amounts of ultrapure water for each desired mass fraction. When phase separation was deemed complete, the volume fraction of the LC phase (Φ) was determined for each mass fraction by measuring the ratio of the height of the LC phase to that of the full sample (LC and isotropic). The anisotropic character of the LC phase was confirmed macroscopically by observation between crossed polarizers, as shown below, and the chiral nematic nature of the phase was confirmed by observation of the characteristic fingerprint textures (example in the Supplementary Information, Figure S16) in samples filled into flat capillaries and observed by a polarizing microscope. All sample vials had been standing vertically for 4 months before these measurements, which should be adequate based on previous long-term studies24.
Rheology
Rheological measurements (parallel-plate configuration) were performed in a saturated atmosphere to avoid solvent evaporation. Small-angle oscillatory shear (SAOS) measurements in the linear regime performed to determine the frequency dependence of the storage and loss moduli were directly followed by measurement of the viscosity as a function of the shear rate (flow curves). More details are provided in the Supplementary Information (Figure S15).
Results
Fractionation of CNCs
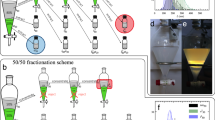
Pristine CNC suspensions are notoriously polydisperse, with rods of substantially different L/d simultaneously existing in suspension. Because a high L/d favors LC formation, as explained by Onsager, a sample with coexisting isotropic and LC phases has an increased proportion of long and slender rods in the LC phase, whereas low L/d rods segregate in the isotropic phase16,25. This LC-driven fractionation according to L/d can be confirmed experimentally by investigating the separated phases individually, as reported previously for carbon nanotubes26 and CNCs27. However, to the best of our knowledge, there is no critical study of how the CNC rod size distribution changes with repetitive separation of the phases, which is required to amplify the fractionation to an extent where the effects from the different L/d values become significant. We therefore attempted such a procedure by carrying out three consecutive separation cycles, as summarized in Fig. 1 (full details in Methods).
As demonstrated below, we found this strategy to be highly successful, although patience and time were required to complete the gravity-driven phase separation. In contrast to the case of carbon nanotubes26, the separation of CNCs could not be sped up by centrifugation. We show in the Supplementary Information (Figure S8) that centrifugation induces irreversible aggregation of CNCs, changing the phase diagram and the behavior of the suspensions. Mechanical CNC fractionation accomplished by pressing a suspension through porous filter membranes was reported in a recent study28, but the liquid crystalline behavior was not investigated (the samples were dried prior to imaging), and the rod-like aspect was not fully characterized (the particle size was studied by light scattering, a technique that generally assumes a spherical particle shape). Moreover, the electron microscopy images showed particles with L/d values much lower than what is typical for CNCs as well as a non-negligible presence of branched particles, suggesting that the filtering procedure may have induced aggregation.
Representative AFM images of the CNCs in our final fractions (iii-CNC and aaa-CNC) are presented in Fig. 2a,b, the analysis of which reveals a considerable geometrical difference (Fig. 2c–e). As expected, the fraction obtained from repeated separation of the isotropic phase contains on average shorter rods (iii-CNC) than the fraction obtained from repeated separation of the LC phase (aaa-CNC). From a population of 300 individual rods, the average length, as established by AFM (see Methods and Supplementary Information), in iii-CNC is Liii ≈ (0.17 ± 0.04) µm, whereas in aaa-CNC, Laaa ≈ (0.23 ± 0.08) µm. The aaa-CNC fraction is actually more polydisperse, with a length polydispersity of 0.36 (determined as the ratio of the standard deviation over the average length) against 0.26 for iii-CNC. Interestingly, the rod diameter remains approximately the same for all fractions, with an average of d ≈ 4 nm; hence, the fractions are effectively separated by length. The average aspect ratio (calculated as the average of L/d for 300 single rods) was 61 ± 40 for aaa-CNC and 46 ± 20 for iii-CNC.
Left: representative AFM images of the two final CNC fractions, iii-CNC (a) and aaa-CNC (b), after repeated phase separation. Right: distributions of the length L (c), diameter d (d), and L/d (e) for the two fractions, as determined from the AFM data for 300 rods (see the Supplementary Information for further details)
Equilibrium phase diagrams of aqueous CNC suspensions
The macroscopic phase separation and the phase diagrams in pure water of the initial suspension (init-CNC) and the iii-CNC and aaa-CNC suspensions are presented in Fig. 3. Prior to obtaining the photographs, the sample vials stood vertically for 4 months, resulting in separation into a lower LC phase and an upper isotropic phase for samples with an overall CNC mass fraction in the range from w0 to w1 (both of which differ between series). In this range, the relative LC volume fraction Φ increases monotonically from 0 to 1 with increasing w with the exception of iii-CNC, for which w1iii > wg. When wiii = wg, a departure from the monotonic behavior is seen with a sudden rise in the apparent LC volume fraction to Φapp = 1. This is not the true LC volume fraction but rather an artifact due to the inability of the LC phase to separate from the isotropic phase in the gelled macroscopic sample.
a Phase separation in suspensions of cellulose nanocrystals between crossed polarizers for the initial series (init-CNC), the short-rod fraction (iii-CNC), and the long-rod fraction (aaa-CNC) as a function of the CNC mass fraction w in pure water. b Quantitative plots of the volume fraction Φ of the LC phase for the three series. The error bars correspond to five different measurements per sample vial. The sample vials stood for 4 months before the photos were taken and the quantitative measurements made. The connecting lines are visual guides
The increase in the average length in the aaa-CNC sample causes a decrease in w0 from w0init ≈ 5 wt.% in the initial sample to w0aaa ≈ 3 wt.%. In the case of iii-CNC, the decrease in average length instead increases the limit of stability of the isotropic phase to w0iii ≈ 7.5 wt.%. Also, w1 is affected, shifting from w1init ≈ 11.8 wt.% in the unfractionated sample to w1aaa ≈ 6 wt.% in aaa-CNC. In the case of iii-CNC, w1 increases compared to that of init-CNC to a value greater than wg, triggering gelation, as discussed in detail below. Therefore, it is impossible to give a direct empirical value of w1iii for the suspensions of short rods. By extrapolation of the data in Fig. 3b we can, however, estimate that w1iii ≈ 13 wt.%.
Onset of gelation
As a first test of gelation, we gently turned the sample vials upside down and left them standing on their caps for 24 h, as shown in Figure S10. If the suspension remained on top (at the original bottom of the sample vial), we considered the suspension to be in a gel state. A very interesting observation in this context is that all CNC suspensions reach gelation at approximately the same CNC content of wg ≈ 12 wt.% regardless of the L/d of the rods. This shows that the change in L/d has no impact on the onset of gelation, while the common understanding based on percolation of the individual rods would suggest, as discussed above, that both LC formation and gelation should happen at a lower waaa for aaa-CNC and a higher wiii for iii-CNC. Instead, we conclude that gelation is triggered solely by reaching a threshold value of the counterion concentration \(c_{Na^ + }^g\) since the only source of ions in these samples is the CNCs themselves.
To corroborate our conjecture, we attempted to induce gelation at a substantially reduced CNC mass fraction by adding salt (NaCl) until \(c_{Na^ + } = c_{Na^ + }^g\). A similar approach has previously been used for inducing gelation, e.g., in fully isotropic suspensions of nanofibrillated cellulose with carboxyl groups at the fibril surface29 and of dye-doped CNCs30. Figure 4 shows vials with varying contents of init-CNC, iii-CNC, and aaa-CNC, photographed between crossed polarizers 3 weeks after adding an amount of NaCl that slightly surpasses the minimum required to reach \(c_{Na^ + } = c_{Na^ + }^g\) to every vial (Supplementary Information, Figures S10-S14). Twenty-four hours after salt addition, the vials were turned upside down and then left standing untouched. The experiment confirms our prediction that gelation is induced in all samples with w > 2 wt.%, irrespective of the series.
Inverted CNC suspensions (initial (a) and fractionated (b,c)) between crossed polarizers, with different CNC mass fractions w but a constant sodium ion concentration \(c_{Na^ + } \approx c_{Na^ + }^g\), adjusted by the addition of NaCl. The samples stood upside down for 2 weeks after reaching gelation by the addition of NaCl
An important further observation is that all gelled samples show birefringence, a sign of the development of long-range orientational order. In fact, the salt-induced birefringence even precedes gelation, as evidenced by the observation of birefringence in the samples in Fig. 4 with a low CNC content (w ≤ 2 wt.%) that are still fluids. We noted a similar behavior at the limit of colloidal stability in a previous study of CNC rods in solvents with varying permittivities20. The particle aggregation induced by salt addition seen in Fig. 4 thus appears to happen preferentially with rods aligned with each other. The fact that birefringence appears prior to gelation with 2 wt.% CNCs suggests that parallel rod aggregation takes place locally, generating finite linear chains with a sufficiently high effective aspect ratio to induce liquid crystalline order in small domains. However, the overall particle fraction is not yet sufficient for percolation, even at this salt-induced increased effective aspect ratio. The percolation threshold for the linear chains is apparently reached at w = 3 wt.%, as all samples at this or higher CNC contents enter the gel state in the presence of sufficient NaCl.
Figure 5 shows AFM images of init-CNC originally at w = 2 wt.% (diluted prior to AFM imaging), in the pristine state and after the addition of NaCl at two different concentrations. From these images, we observe that the rods indeed aggregate largely in parallel upon salt addition, growing into much longer chains. The average diameter of these chains is d ≈ 5.5 nm, which is not significantly larger than the diameter d ≈ 4 nm of the individual rods in the salt-free sample. The increased length and small increase in diameter suggests that aggregation takes place mostly between the extreme ends of the rods rather than through side-by-side association of the rods. After the addition of 40 mM NaCl, L/d increases from ~57 (CNCs without salt, Figure S6) to ~130.
To better quantify the above observations and characterize the gel state, we carried out SAOS rheology experiments on representative samples. Figure 6a shows the frequency dependence of the shear moduli for three different mass fractions, w = 4, 9, and 13 wt.%, of init-CNC (filled symbols). All measurements were performed in the linear regime (see the Supplementary Information).
a Viscoelastic properties: dependence of the storage (black/blue) and loss moduli (red/magenta), G’ and G”, respectively, on the probe frequency. Values below 10−7 Pa are below the reliable measuring range of the instrument. b Loss factor (tan δ) vs. CNC mass fraction w, evaluated at the lowest angular frequency in (a). Filled symbols: no NaCl. Empty symbols: NaCl added to \(c_{Na^ + } \approx c_{Na^ + }^g\)
As expected for the suspensions, the absolute values of the shear moduli increase with increasing CNC content w31. The samples with w = 4 and 9 wt.% show the rheological characteristics of a viscoelastic liquid, i.e., G” > G’ for all measured frequencies, whereas the viscoelastic properties of the sample with the highest mass fraction of w = 13 wt.% is dominated by the elastic part, i.e., G” < G’. Together with the fact that the G’ and G” curves evolve nearly parallel as a function of frequency, this suggests that the CNC suspensions undergo a transition from a liquid to a gel-like state32.
To investigate the effect of salt addition by rheology, we add NaCl to the w = 4 and 9 wt.% init-CNC samples to raise \(c_{Na^ + }\) above \(c_{Na^ + }^g\). Figure 6a shows the resulting G’ and G” curves (empty symbols). As discussed for the w = 13 wt.% sample, the horizontal evolution of the curves as well as the fact that G” < G’ for all measured frequencies indicates that these samples are gels. The transformation from a viscoelastic liquid (loss factor tan δ > 1) to a solid-like gel state (tan δ < 1) by the addition of salt is illustrated by the behavior of the loss factor depicted in Fig. 6b.
Figure 7 shows the flow curves of the five init-CNC suspensions discussed above. The low value of the zero-shear viscosity and the shear thinning behavior suggest that the CNC suspensions are soft physical gels at higher concentrations or salt contents. At higher shear rates, the gel network is destroyed by the applied shear forces.
Increasing w changes the appearance of the flow curves from an almost Newtonian shape (w = 4 wt.%) to the shape typical for polymer melts and physical gels above the yield point. All of the samples that are in the gel state (w = 4 and 9 wt.% with salt and w = 13 wt.% without salt) show a similar and almost parallel shape at higher shear rates. The clear distinction between three different regimes reported in21,22,33 is not observed. Moreover, the flow curves can be described by a power-law constitutive model. The power law exponents are shown in Table 1.
Discussion
The detection of birefringence and then gelation, in that order, with increasing counterion concentration and the observation by AFM of preferentially linear aggregates of CNCs upon salt addition together give strong evidence that predominantly linear chain formation takes place as the concentration of counterions reaches values on the order of a few tens of mM. Signs of CNC rod lengthening induced by the addition of NaCl have been reported before12,34, although for much lower concentrations of CNCs and without discussion of the consequences in terms of the macroscopic phase behavior. On the basis of small-angle neutron scattering experiments, Cherhal et al.12 detected branch-free CNC aggregation with increasing length for an intermediate ion concentration (on the order of 10 mM), while the data at 50 mM or higher suggested aggregation with branching. This matches our results relatively well, with the degree of branching at \(c_{Na^ + } \approx c_{Na^ + }^g\) in our case perhaps being lower because of a positive feedback loop made possible by the higher CNC concentration and the consequent development of long-range orientational order.
While aggregation of like-charged colloidal particles upon the addition of multivalent counterions is well understood, the theoretical framework of the phenomenon triggered by monovalent counterions is nontrivial35,36, although much experimental evidence exists with various colloidal systems, including CNC suspensions12,19,29,30,31. What is particularly surprising is the observation of chain formation with the CNCs aggregating end-to-end rather than side-by-side, at least at these comparatively high CNC mass fractions. A complete explanation may require better knowledge of the detailed CNC morphology and its charge distribution (it is likely that the surface charge at the ends is different from that on the sides) than what currently exists, but we propose the following general qualitative argument, which may be of relevance.
The end-to-end bonding of the charged rods and the formation of chains can qualitatively be explained using the DLVO theory, which is widely used to explain aggregation in aqueous dispersions37,38. According to DLVO theory, the interaction potential between two charged objects in a solvent is the sum of the Van der Waals attraction potential UVW(r) and the electrostatic repulsion potential Uel(r) due to the double layer of co- and counterions. The potential UVW(r) is negative and decreases with increasing separation between rods. Approximating the rod as a spherocylinder of radius R and total length L + 2 R, the electrostatic interaction potential between the ends of neighboring rods may be estimated using the potential for two charged spheres of radius R37,38, i.e.,
where the Debye screening length κ2 = 4πλBρ, λB is the Bjerrum length, ρ is the number density of counterions, and Z is the total surface charge. The combination of the attraction due to UVW(r) and electrostatic repulsion results in a potential barrier. If the rods can overcome this barrier, they are at a close distance where they strongly attract each other.
This mechanism can explain the aggregation of charged rods, but it is less straightforward to explain why the rods are bonded end-to-end and do not aggregate, say, side-by-side. Here, we take into account that at low \(c_{Na^ + }\), the positive counterions are more or less evenly distributed around the CNCs, and, hence, the screening is effectively independent of their location. In contrast, when \(c_{Na^ + } \approx c_{Na^ + }^g\), there is such a high concentration of counterions that a fluctuation may significantly increase the ion concentration in the gap between the ends of closely separated rods at which the interaction area is small, thereby decreasing the electrostatic repulsion and the potential barrier and resulting in attraction between the ends.
This mechanism can be illustrated using a crude estimate of the free energy of the system of two rods with a narrow gap between their ends. Let us consider a simple “two-site” model and introduce the average density ρ1 of counterions in the diffuse layer at the cylindrical part of the surface of the rod and the average density ρ2 in the gap between the spherical ends. We also introduce the corresponding average electrostatic potentials ϕ1 and ϕ2. Then, the free energy is estimated as,
where σ1 = 2 πRL is the area of the cylindrical surface, σ2 = πR2/2 is the area of the hemispherical end, and h is the effective thickness of the diffuse layer.
Minimization of this free energy yields \(\rho _1 = e^{ - e\varphi _1}\) and \(\rho _2 = e^{ - e\varphi _2/kT}e^{\omega /kT}\), where \(\omega = - \frac{{\partial U_{el}}}{{\partial \rho _2}} \propto U_{el}h\frac{{\partial \kappa }}{{\partial \rho _2}} > 0\). One notes that in general, ϕ1 ϕ2 due to the extra curvature of the spherical surface compared to the cylindrical one, and hence, ρ1 < ρ2, i.e., the repulsion (per unit area) between the ends is weaker than that between the sides of the rods, which already leads to stronger end-to-end attraction. One also notes that a fluctuating increase in Δρ1 of the ion density in the gap between the ends corresponds to a much smaller change \(\Delta \rho _2 \propto \Delta \rho _1(\frac{R}{L}) \ll \Delta \rho _1\) (assuming that the total number of ions in the diffuse layer is constant), and, hence, the screening at the cylindrical surface is not affected significantly.
The effect is strongly magnified in a self-consistent way by the factor of eω/kT in ρ2, which may result in a significant increase in the counterion concentration in the gap. As a result, the repulsion between rod ends may decrease together with the height of the corresponding potential barrier, which enables the rods to reach the “trap region” where their ends strongly attract each other. The attractive influence from van der Waals and, possibly, hydrophobic interactions is stronger in the side-by-side configuration than in the end-to-end one. However, in the side-by-side configuration, the potential barrier, determined by electrostatic repulsion, remains high, and even strong van der Waals interaction cannot overcome it, preventing side-by-side aggregation.
One also notes that the electrostatic interaction between charged surfaces at close distances has recently been considered beyond the DLVO theory for both uniform and discrete surface charge distributions39,40,41,42. According to Pezeshkian et al.39, the repulsion at close distances disappears with increasing charge discreteness, and at low temperatures, the plates always attract each other. This effect also contributes to the attraction of the rod ends.
The proposed mechanism promotes chain formation and might thus explain the observed behavior. Chains are formed as a result of a balance between the translational entropy \(S_t = \mathop {\sum }_n \rho _nln\rho _n\), where ρn is the number density of chains of length n, and the energy of the chains, \(\mathop {\sum }_n U_0n\rho _n\), where U0 is the contact interaction energy. This balance results in an exponential chain length distribution43, where the average chain length increases with increasing U0/kT. At the same time, the average alignment of the rods (the chains are approximately linear) and the appearance of birefringence can be explained by the classical Onsager theory by taking into account both the excluded volume effects and electrostatic forces.
We may now understand the gelation seen at \(c_{Na^ + } \approx c_{Na^ + }^g\) as an effect of diverging effective rod length, reducing the percolation threshold to such a low volume fraction that gelation is caused despite the low value of φ. As seen in Fig. 5, at w = 2 wt.% after the addition of salt, linear chains (CNC aggregates) of an average L/d on the order of 130 have formed. For this value, there is unfortunately no literature data regarding the rigidity percolation threshold. For hard rods of L/d = 100, Schilling et al. found the connectivity percolation threshold to be φ ≈ 0.5%44. The CNCs are not purely hard but have an attractive potential in addition to the excluded volume due to the suppression of effective electrostatic repulsion as \(c_{Na^ + }\)reaches \(c_{Na^ + }^g\). For such systems, the connectedness percolation threshold has been shown to vary by only a factor of two over a large range of stickiness45. Compared with our experimental results, it seems reasonable that attractive CNC chains with L/d ≈ 130 on average might form a gel at w > 2 wt.%. The fact that the chains are rather flexible and more kinked than the individual CNCs and possibly even branched at a high salt content very likely plays a role as well. Further investigations are needed to fully characterize the transition from a birefringent fluid suspension of linear chains to a gel in the vicinity of \(c_{Na^ + }^g\).
We note that it is also possible to have kinetic arrest into a soft glassy state with colloids of rod-shaped nanoparticles with high L/d at extremely low ion concentrations. Kang and Dhont46 reported the loss of equilibrium LC behavior for filamentous viruses beyond a critical volume fraction, yet this only happens at very low salt content. Their explanation was based on non-contact between the rods, in which the electrostatic repulsion is instead so effective at these low ion concentrations that the rods find themselves in an “electrostatic cage” if the particle volume fraction reaches a threshold value. While the macroscopic behavior of this kinetically arrested sample may appear similar, the physical mechanism is clearly different, and the condition of low salt is indeed the opposite of what we discuss here, which is the most relevant situation for CNC suspensions.
In addition to demonstrating the need for re-evaluating the reason for gelation in CNC suspensions, our study has important practical consequences for the successful preparation of high-quality materials that take advantage of the chiral nematic self-assembly offered by CNCs. Because gelation is not affected by fractionation while LC formation is, the fractionation procedure allows us to substantially extend the equilibrium LC phase range by working with aaa-CNC, which shows a 100% LC phase in equilibrium between w1 ≈ 6 wt.% and wg ≈ 12 wt.%. This is a marked improvement compared to the commercially available init-CNC, for which we need a CNC content that is very close to the onset of gelation to reach the end of the two-phase regime.
References
Bawden, F. C., Pirie, N. W., Bernal, J. D. & Fankuchen, I. Liquid crystalline substances from virus-infected plants. Nature 138, 1051–1052 (1936).
Thorkelsson, K., Bai, P. & Xu, T. Self-assembly and applications of anisotropic nanomaterials: a review. Nano Today 10, 48–66 (2015).
Njuguna, J., Pielichowski, K. & Desai, S. Nanofiller-reinforced polymer nanocomposites. Polym. Adv. Technol. 19, 947–959 (2008).
Trache, D., Hussin, M. H., Haafiz, M. K. & Thakur, V. K. Recent progress in cellulose nanocrystals: sources and production. Nanoscale 9, 1763–1786 (2017).
Giese, M., Blusch, L. K., Khan, M. K. & MacLachlan, M. J. Functional materials from cellulose-derived liquid-crystal templates. Angew. Chem. Int. Ed. 54, 2888–2910 (2015).
Dufresne, A. Nanocellulose: a new ageless bionanomaterial. Mater. Today 16, 220–227 (2013).
Klemm, D. et al. Nanocelluloses: a new family of nature-basedmaterials. Angew. Chem. Int Ed. 50, 5438–5466 (2011).
Reid, M. S., Villalobos, M. & Cranston, E. D. Benchmarking cellulose nanocrystals: from the laboratory to industrial production. Langmuir 33, 1583–1598 (2017).
Guidetti, G., Atifi, S., Vignolini, S. & Hamad, W. Y. Flexible photonic cellulose nanocrystal films. Adv. Mater. 28, 10042–10047 (2016).
Jacoby, M. Nano from the forest. Chem. Eng. News 92, 9–12 (2014).
Usov, I. et al. Understanding nanocellulose chirality and structure-properties relationship at the single fibril level. Nat. Commun. 6, 7564 (2015).
Cherhal, F., Cousin, F. & Capron, I. Influence of charge density and ionic strength on the aggregation process of cellulose nanocrystals in aqueous suspension, as revealed by small-angle neutron scattering. Langmuir 31, 5596–5602 (2015).
Fernandes, S. N. et al. Mind the microgap in iridescent cellulose nanocrystal films. Adv. Mater. 29, 1603560 (2017).
Dumanli, A. G. et al. Controlled, bio-inspired self-assembly of cellulose-based chiral reflectors. Adv. Opt. Mater. 2, 646–650 (2014).
Lagerwall, J. P. F. et al. Cellulose nanocrystal-based materials: from liquid crystal self-assembly and glass formation to multifunctional thin films. NPG Asia Mater. 6, e80 (2014).
Onsager, L. The effects of shape on the interaction of colloidal particles. Ann. N. Y. Acad. Sci. 51, 627–659 (1949).
Dong, X. M., Kimura, T., Revol, J. F. & Gray, D. G. Effects of ionic strength on the isotropic-chiral nematic phase transition of suspensions of cellulose crystallites. Langmuir 12, 2076–2082 (1996).
Park, J. H. et al. Macroscopic control of helix orientation in films dried from cholesteric liquid-crystalline cellulose nanocrystal suspensions. Chemphyschem 15, 1477–1484 (2014).
Honorato-Rios, C. et al. Equilibrium liquid crystal phase diagrams and detection of kinetic arrest in cellulose nanocrystal suspensions. Front. Mater. 3, 21 (2016). ARTN.
Bruckner, J. R., Kuhnhold, A., Honorato-Rios, C., Schilling, T. & Lagerwall, J. P. Enhancing self-assembly in cellulose nanocrystal suspensions using high-permittivity solvents. Langmuir 32, 9854–9862 (2016).
Shafiei-Sabet, S., Hamad, W. Y. & Hatzikiriakos, S. G. Ionic strength effects on the microstructure and shear rheology of cellulose nanocrystal suspensions. Cellulose 21, 3347–3359 (2014).
Urena-Benavides, E. E., Ao, G., Davis, V. A. & Kitchens, C. L. Rheology and phase behavior of lyotropic cellulose nanocrystal suspensions. Macromolecules 44, 8990–8998 (2011).
Hough, L., Islam, M., Janmey, P. & Yodh, A. Viscoelasticity of single wall carbon nanotube suspensions. Phys. Rev. Lett. 93, 168102 (2004).
Schütz, C. et al. Rod packing in chiral nematic cellulose nanocrystal dispersions studied by small-angle X-ray scattering and laser diffraction. Langmuir 31, 6507–6513 (2015).
Odijk, T. & Lekkerkerker, H. N. W. Theory of the isotropic-liquid crystal phase separation for a solution of bidisperse rodlike macromolecules. J. Phys. Chem. 89, 2090–2096 (1985).
Zhang, S. J., Kinloch, I. A. & Windle, A. H. Mesogenicity drives fractionation in lyotropic aqueous suspensions of multiwall carbon nanotubes. Nano. Lett. 6, 568–572 (2006).
Dong, X. M., Revol, J. F. & Gray, D. G. Effect of microcrystallite preparation conditions on the formation of colloid crystals of cellulose. Cellulose 5, 19–32 (1998).
Hu, Y. & Abidi, N. Distinct chiral nematic self-assembling behavior caused by different size-unified cellulose nanocrystals via a multistage separation. Langmuir 32, 9863–9872 (2016).
Fall, A. B., Lindström, S. B., Sundman, O., Ödberg, L. & Wågberg, L. Colloidal stability of aqueous nanofibrillated cellulose dispersions. Langmuir 27, 11332–11338 (2011).
Peddireddy, K. R., Capron, I., Nicolai, T. & Benyahia, L. Gelation kinetics and network structure of cellulose nanocrystals in aqueous solution. Biomacromolecules 17, 3298–3304 (2016).
Chau, M. et al. Ion-mediated gelation of aqueous suspensions of cellulose nanocrystals. Biomacromolecules 16, 2455–2462 (2015).
Winter, H. H. Gel point. Encyclopedia of Polymer Science and Technology (John Wiley & Sons, New York, 2016).
Shafiei-Sabet, S., Hamad, W. Y. & Hatzikiriakos, S. G. Rheology of nanocrystalline cellulose aqueous suspensions. Langmuir 28, 17124–17133 (2012).
Cherhal, F., Cathala, B. & Capron, I. Surface charge density variation to promote structural orientation of cellulose nanocrystals. Nord. Pulp Pap. Res. J. 30, 126–131 (2015).
Varghese, A., Rajesh, R. & Vemparala, S. Aggregation of rod-like polyelectrolyte chains in the presence of monovalent counterions. J. Chem. Phys. 137, 234901 (2012).
Zhou, S. Density functional analysis of like-charged attraction between two similarly charged cylinder polyelectrolytes. Langmuir 29, 12490–12501 (2013).
Israelachvili, J. N. Intermolecular and Surface Forces. 3rd (Academic Press, Burlington, MA, USA, 2010).
Russel, W. B., Saville, D. A. & Schowalter, W. R. Colloidal dispersions (Cambridge university press, CA, USA, 1989).
Pezeshkian, W., Nikoofard, N., Norouzi, D., Mohammad-Rafiee, F. & Fazli, H. Distribution of counterions and interaction between two similarly charged dielectric slabs: roles of charge discreteness and dielectric inhomogeneity. Phys. Rev. E 85, 061925 (2012).
Jho, Y. S., Park, G., Chang, C. S., Pincus, P. & Kim, M. W. Interaction between two inhomogeneously charged parallel surfaces in the strong coupling regime. Phys. Rev. E 73, 021502 (2006).
Naji, A., Jungblut, S., Moreira, A. G. & Netz, R. R. Electrostatic interactions in strongly coupled soft matter. Phys. A 352, 131–170 (2005).
Moreira, A. G. & Netz, R. R. Counterions at charge-modulated substrates. EPL 57, 911 (2002).
Osipov, M. A., Teixeira, P. I. & Telo da Gama, M. M. Structure of strongly dipolar fluids at low densities. Phys. Rev. E 54, 2597–2609 (1996).
Schilling, T., Miller, M. A. & Van der Schoot, P. Percolation in suspensions of hard nanoparticles: From spheres to needles. EPL 111, 56004 (2015).
Dixit, M., Meyer, H. & Schilling, T. Connectivity percolation in suspensions of attractive square-well spherocylinders. Phys. Rev. E 93, 012116 (2016).
Kang, K. & Dhont, J. K. G. Glass transition in suspensions of charged rods: structural arrest and texture dynamics. Phys. Rev. Lett. 110, 015901 (2013).
Acknowledgements
We thank T. Schilling and A. Kuhnhold for fruitful discussions. Financial support from the Luxembourg National Research Fund (FNR; project MISONANCE, grant code C14/MS/8331546) is kindly acknowledged. C. Schütz thanks the Alexander von Humboldt Foundation for financial support through a Feodor Lynen scholarship.
Author information
Authors and Affiliations
Contributions
C.H.R. performed all experiments except the rheological characterization, which was carried out by C.L. and C.S. J.B. and R.S. completed the in-depth analysis of the latter data. M.A.O. proposed the model for ion-induced chain aggregation. J.P.F.L. coordinated the study, conducted the LC physical chemistry analysis, and wrote most of the text together with C.H.R.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Honorato-Rios, C., Lehr, C., Schütz, C. et al. Fractionation of cellulose nanocrystals: enhancing liquid crystal ordering without promoting gelation. NPG Asia Mater 10, 455–465 (2018). https://doi.org/10.1038/s41427-018-0046-1
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41427-018-0046-1
This article is cited by
-
Tuning of the chiral nematic phase of cellulose nanocrystals by the adsorption of a short polymer on their surface
Cellulose (2023)
-
Large-scale fabrication of structurally coloured cellulose nanocrystal films and effect pigments
Nature Materials (2022)
-
Cellulose photonic pigments
Nature Communications (2022)
-
Chiral self-assembly of cellulose nanocrystals is driven by crystallite bundles
Nature Communications (2022)
-
Current international research into cellulose as a functional nanomaterial for advanced applications
Journal of Materials Science (2022)