Abstract
The influence of cryothermal treatment on the mechanical properties of metallic glasses with different compositions was investigated in the present work. It was found that cryothermal cycling can induce rejuvenation as well as relaxation of the metallic glasses. The local apparent Young’s modulus and its spatial distribution width on the surface of the metallic glass increase after cryothermal cycling, while in the bulk the effect depends on the glass composition. It appeared that this increase is temporary and disappears after a period of room temperature aging. This effect is connected with a large distribution of relaxation times in the metallic glasses due to their heterogeneous structure and the formation of complex native oxides on the outer surfaces of the glasses. Our findings reveal that a cryothermal cycling treatment can improve or degrade the plasticity of a metallic glass, and the atomic bond structure appears to be very important for the outcome of the treatment.
Similar content being viewed by others
Introduction
Bulk metallic glasses are materials of interest for both functional and structural applications1,2,3. However, the lack of macroscopic ductility limits their application fields4,5. Differences in the cooling rate of metallic glasses upon casting from the melt result in different final energy states of the amorphous solid6. Higher cooling rates allow freezing of the metallic glass at a higher potential energy level1, and it was established that metallic glasses on higher energy state have a higher plasticity5. Ribbon samples can be bent by 180° without fracture7. Meanwhile, there are many methods that have been developed to increase the energy level or rejuvenate metallic glasses8,9: irradiation, heavy plastic deformation, elastostatic loading, simple heating above Tg and subsequent fast cooling10, etc. Recently, another method for metallic glass rejuvenation was found11. Due to the intrinsic structural heterogeneity of metallic glasses, the spatial distribution of the properties on the nanoscale can be very wide. Heterogeneous thermal expansion or contraction upon changes in the temperature induce local stresses that are high enough for anelastic strains to occur. Cryothermal cycling appears to be an attractive and simple method for rejuvenating metallic glasses. It is non-destructive, avoids the macroscopic deformation of the sample, can be applied to samples of any shape and size, is uniform, changes the whole sample, etc. Thermal cycling is well known for polycrystalline materials with highly anisotropic thermal expansions like uranium or zinc, where it can induce superplasticity12. The method thus appears to be applicable to different classes of materials. Recently, it was found that cryothermal cycling can also be used for the synthesis of single-component supramolecular assemblies13. However, the applicability boundaries of the method for metallic glasses are still unknown. In our previous work11, we have observed a rejuvenation effect of cryothermal cycling on metallic glasses with different compositions. The effect was more pronounced for melt-spun ribbons than for bulk samples. Moreover, for Ti-based metallic glass composites14, the effect of thermal cycling was shown to be negligible.
In the present work, we applied the cryothermal cycling method to metallic glasses of three different compositions: Zr60Cu20Fe10Al10, Zr60Cu20Co10Al10, and Zr60Cu20Ni10Al10. The one thing that unites all of the alloy compositions is the presence of an element couple with a positive heat of mixing (Cu–Fe, Co, Ni). Such a composition design feature is known to induce local structural instability and increase the heterogeneity of the metallic glass15,16,17. The influence of thermal cycling on the mechanical properties of the selected metallic glasses was investigated in the present work.
Materials and methods
Metallic glassy samples were prepared by arc melting of a mixture of pure elements (99.9% purity) in an argon atmosphere and ejection casting into a copper mold. The three compositions chosen were Zr60Cu20Fe10Al10, Zr60Cu20Co10Al10, and Zr60Cu20Ni10Al10. For all compositions, the presence of a pair of elements with a positive enthalpy of mixing was the main design strategy (\( {\it{\Delta {H}}}_{\mathrm{mix}}^{\mathrm{Cu}} - {\mathrm{Fe}} = + 13\,{\mathrm{kJ/mol}},\) \({\it{\Delta {H}}}_{\mathrm{mix}}^{\mathrm{Cu}} - {\mathrm{Co}} = + 6\,{\mathrm{kJ/mol}},\) \({\it{\Delta {H}}}_{\mathrm{mix}}^{\mathrm{Cu}} - {\mathrm{Ni}} = + 4\,{\mathrm{kJ/mol}}\)). The as-cast rods with diameters of 2 mm were cut to obtain samples 4 mm in length. The ends of each sample were carefully polished to make the surfaces parallel to each other. Subsequently, the samples were subjected to cryothermal cycling. One cycle consisted of dipping the sample into liquid nitrogen for 1 min, followed by dipping it into hot (T = 320 K) ethanol, also for 1 min. The phase compositions of the samples were investigated by X-ray diffraction using a Bruker D8 diffractometer with a Cu Kα radiation source. All samples had an amorphous structure that did not change throughout the whole experimental process. The surfaces of the samples before and after treatment were analyzed by X-ray photoelectron spectroscopy (XPS). XPS spectra were recorded with the help of a Nanofab 25 (NT-MDT) electron-ion spectroscopy platform. Phase transformations were measured by differential scanning calorimetry (Perkin Elmer 8500) under a flow of purified argon. The glass transition temperatures of the samples at a 40 K/min heating rate were found to be as follows: Tg = 671 K for Zr60Cu20Fe10Al10, Tg = 676 K for Zr60Cu20Co10Al10, and Tg = 674 K for Zr60Cu20Ni10Al10. Mechanical tests were carried out with an Instron 5581 device at a strain rate of 5 × 10−4 s−1. The samples for the compression tests had 1:2 aspect ratios. To confirm the reproducibility, all compression tests were carried out at least three times. The distribution of the surface stresses upon dipping the sample into liquid nitrogen was calculated by finite element methods.
The local distribution of Young’s modulus was measured by atomic force microscopy (AFM) (AIST-NT, model SmartSPM-1000). For the AFM measurements, the surfaces were finely polished with 0.25 µm diamond paste. The average surface roughness was Ra ~2.8−3.2 nm. Quantitative nanoscale mechanical characterization was carried out using cantilevers with single-crystal diamond tips (D300, SCDprobes). The curvature radii of the tips were 4–5 nm. The spring constant of the cantilever was measured to be ~46.2 N/m by a thermal tuning method18. A single cantilever was used for one series of thermal cycling treatment experiments. The maximum force was 300 nN, which appeared to be within the elastic limit for all chosen compositions. Young’s modulus was calculated by fitting the unloading force curves by the Sneddon cone-on-flat model19,20. The error for the absolute value of Young’s modulus determined by this method is quite high, therefore we used the normalized values in the present work. The actual bulk Young’s modulus values measured by the resonant ultrasound method were in the range of 80–85 GPa. The spatial distribution of Young’s modulus was determined for each sample from a 2 × 2 µm area with 128 × 128 dots. However, due to the presence of polishing defects such as surface scratches, a reduced number of 3000 points was chosen in each case, and these points were selected from the flat areas that did not have many polishing defects. A more detailed description of the method used in the present work can be found elsewhere21.
Electron microscopy studies were carried out with a Titan G2 60–300 transmission electron microscope (TEM; FEI, the Netherlands) equipped with a high-brightness field-emission gun and a Cs image corrector. The estimated spatial resolution was approximately 0.08 nm at 300 kV. Images were acquired with a Gatan US1000 CCD camera. A dual-beam (ion beam and electron beam) system (FEI Helios 450) was employed to fabricate cross-sections of the as-cast samples as well as those cycled in liquid nitrogen (LN2). Electron-energy loss spectroscopy (EELS) experiments were performed with a post-column high-resolution energy filtering spectrometer (Gatan). The optical conditions of the microscope for EELS imaging and spectroscopy were defined to obtain a probe size of 0.2 nm with a convergence semi-angle of 10 mrad and a collection semi-angle of 12 mrad. The thickness of the areas of interest was obtained from the zero loss spectrums. Energy-dispersive X-ray (EDX) experiments were performed with an EDX RTEM (EDAX) detector by using a probe size of approximately 0.5 nm.
One of the most important tools for structural characterization of amorphous materials is the atomic radial distribution function (RDF). The RDF describes the probability of finding certain atomic pairs as a function of the pair separation and, consequently, provides short-range and medium-range structural information. In the present study, the RDFs of the as-cast and LN2-cycled samples were determined by utilizing high-resolution TEM (HRTEM). In addition to the information obtained from RDF analysis, HRTEM also provides atomic-scale imaging of the area of interest. The RDFs were directly computed from the fast Fourier transform (FFT) patterns of the HRTEM images. The results obtained from conventional selected area electron diffraction (SAED) show a similar behavior as those extracted from FFT. To evaluate the RDFs, two known software packages were used: PASAD22 and RDF TOOLS23.
Results
Cryothermal cycling can be viewed as a two-step process: contraction upon cooling and expansion upon heating. In the case of homogeneous structures, neither contraction nor expansion should induce any internal stresses, and no changes in the structure should appear after the treatment. However, due to the intrinsic heterogeneous nature of metallic glasses, a rejuvenation effect can be observed after cryothermal cycling. In the process of such a treatment, the surface of the samples should experience the strongest influence of any part of the sample because of the highest temperature gradient. In our previous work11, we ruled out any long-term surface effects, as they are insignificant in the resulting changes in the heat of relaxation. However, the results of the present work show that these conclusions might have been premature. It was discovered by atomic force resonant microscopy experiments that the statistical variation in Young’s modulus on the surface of metallic glasses is much wider than that known for crystalline materials24. This effect is caused by the existence of soft or loosely packed and hard or densely packed zones in metallic glasses. The total volume of these anelastic sites can occupy as much as a quarter of the volume of the whole sample25. Our measurements of the statistical variation in the apparent Young’s modulus on the polished surfaces of the selected metallic glasses show a similar wide distribution (Fig. 1). However, in our case, due to possible polishing defects and the existence of native surface oxides, the distribution width is larger than that found by Wagner et al24. Interestingly, thermal cycling increases the average apparent Young’s modulus as well as its surface variation width (Fig. 1a, c, e). The effect is stronger for metallic glasses that contain pairs of elements with higher positive heats of mixing, hence more heterogeneous glasses. For metallic glasses with 10 at.% Fe, the increase of the average Young’s modulus after 30 cycles is approximately 50% (Fig. 1a), which is a very large change. Such a change seems to be impossible in the bulk; however, it might occur in the near surface area. The mobility of the surface atoms is much higher than that of the atoms in the bulk. It was shown that a high atomic surface mobility might enhance the crystallization of metallic glass26. In single-crystal nanowires, the high surface mobility of the constituent elements induced large anelasticity27. It was also found that elastostatic loading and creep experiments induced structural anisotropy in metallic glasses28,29,30. In the case of cryothermal cycling, plunging of the sample into a vessel of liquid nitrogen creates an immediate temperature gradient, which creates biaxial tension in the surface plane, initiating anelastic local flow. The temperature gradient is quickly reduced by thermal diffusion; however, the low temperature allows the initial damage to be preserved. Continued cycles ultimately store even more anelastic damage, which eventually saturates. Uniaxial compression induces anisotropy, where Young’s modulus normal to the compression axis is initially smaller than the modulus parallel to the axis30. Such anisotropy in the bulk can be on the order of several percent28. The effect should be reversed under tension, and the apparent Young’s modulus change normal to the surface of the sample should be magnified by the biaxial nature of the tension. Taking these factors into account, one can assume that even for the small strains that we have induced through thermal contraction, the indentation modulus should be higher than the modulus values along the directions in the plane of the surface. These claims were partially confirmed by finite element calculations (see Supplementary Materials Figs. S1–S6), whereby tensile and compressive stresses were found in the surface of the metallic glass upon cooling in liquid nitrogen. However, the software has limitations and cannot take the anelastic effects and heterogeneity of the glasses into account.
Here, we should also take into consideration the fact that the AFM tip probed the surface of the metallic glasses under ambient conditions, and there was always a layer of native oxides on top of the glass surface31. The thickness of the native oxide layer of the selected glasses is on the order of 1 nm, and the layer has an amorphous structure32. The stiffness of the samples is quite high, and the estimated elastic deformation depth is 2–3 nm, therefore the surface oxide layer can play a significant role in the resulting effects. The surfaces of the glassy samples before and after cryothermal cycling were investigated by XPS (see Supplementary Materials Figs. S7–S9 and Tables S1–S3). It was calculated from the XPS spectra that the thickness of the surface native oxide layer was approximately 5–6 nm for all the samples. Here, it should be noted that even though the elastic deformation of the metallic glass surface in the AFM measurements is approximately 2–3 nm, the depth of the affected zone is 4–5 times larger. The surface oxides on the glasses containing Co and Ni mainly consist of Cu2O and ZrO2. However, in the case of the Zr60Cu20Fe10Al10 glass, the surface also contains iron oxides. No significant changes in the surface oxides were found after cryothermal cycling. Analysis of the XPS results also reveals that nitrogen had no influence on the surface layer.
Transmission electron microscopy measurements also confirmed the existence of the native oxide layer (Fig. 2). From the EELS (Fig. 2) and EDX (Fig. S10) maps, one can notice that the oxide layer mostly consists of zirconium oxide (Fig. 2a). Fe, Ni, and Cu are concentrated below the native oxide layer. A similar effect has been observed for the low-temperature long-term oxidation of a Ni–Nb metallic glass33. The oxide layer thickness was similar to that (5–7 nm) found from the XPS measurements. Interestingly, after the cryothermal cycling treatment, copper tends to form islands on top of the native oxide. Such behavior has also been observed in the oxidation of gold-containing metallic glasses34. The affinity of noble metals for oxygen is very low, and the bond strength is not high. As these copper islands are very thin (approximately 5 nm), they are easily removed by wiping the surface with a cloth during sample cleaning, therefore we could not observe them in the XPS measurements. Copper also tends to segregate from iron during cryothermal cycling. One can also see areas (highlighted by the dotted line) inside the glass with higher concentrations of copper (Fig. 2b). This phenomenon does not occur in the glass containing Ni (Fig. 2c).
The macroscopic thermal expansion coefficients (TEC) of pure crystalline metals and alloys with isotropic structures are not much different from the TECs of metallic glasses35. However, the TECs of both crystalline and amorphous oxide materials vary over a wide range36 up to negative values37. The difference in thermal expansion between the oxide and the metallic glass can be quite large, and oxygen covalent bonding is one of the strongest types of bonding, which explains such large average stiffening. The apparent Young’s modulus change is higher for the metallic glass with the more pronounced heterogeneous structure (the one containing Fe, hence this glass has a lower activation energy for structural changes). However, one can notice (Fig. 1a, c, e) that despite the difference in the metallic glass composition, the spatial distribution of Young’s modulus becomes wider after the cryothermal cycling treatment, which indicates that the structure of the glasses becomes more heterogeneous.
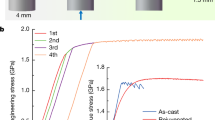
One should notice that the effect of the apparent Young’s modulus increase is not constant and disappears after a period of room temperature aging (Fig. 1b, d, f). Polishing of the Zr60Cu20Fe10Al10 metallic glass surface after 10 cryothermal cycles to a depth of approximately 300 µm results in the disappearance of the Young’s modulus increase (Fig. 1b). The average Young’s modulus inside the bulk actually decreases slightly relative to that of the as-cast state (Fig. 1b). This result leads to the conclusion that the observed effect is limited to the surface region.
This result was also confirmed by HRTEM studies of the Fe-containing glass (Fig. 3). We performed calculations of the reduced density functions from the FFT patterns obtained from the HRTEM images (Fig. 3d) and SAED patterns. This is a powerful tool for studying structural changes in metallic glassy samples. The advantage of the method is that it is possible to obtain information from selected areas in the HRTEM images. However, to achieve a better signal-to-noise ratio, the TEM lamella should be very thin. The thicknesses of the areas presented in Fig. 3 determined by EELS studies were 28 ± 2 nm (Fig. 3a) and 55 ± 2 nm (Fig. 3c), respectively. For comparison, the SAED pattern (Fig. 3b) was taken of the thicker region of the sample presented in Fig. 3a. One can notice that the RDFs, which were calculated for the as-cast sample from the FFT and SAED38 patterns, have differences in the G(r) intensities but still show the same peak positions. All the RDF peaks of the cryocycled samples shifted toward higher r values (the shift in the position of the first peak maximum is approximately 0.03 nm), which means that the average atomic bond distances increased. This result indicates that an increase in the general volume and rejuvenation occur in the Fe-containing glass.
Metallic glasses exhibit a wide range of relaxation times, which results in anelastic behavior under applied stresses. Such behavior was observed previously in nanoindentation experiments in the elastic regime39 and in the elastic cycling of metallic glasses40. The time needed for relaxation depends on the ambient temperature and the glass transition temperature of the alloy (Tg). For example, the anelastic changes in the Ce-based metallic glass (Tg = 373 K) disappeared only 6 h after the release of the stress28. In the present work, 3 days of relaxation at room temperature restored the Young’s moduli of all the investigated metallic glasses back to their as-cast values, and in the case of the Fe-containing glass the final Young’s modulus appeared to be slightly smaller than that before the treatment. However, the spatial distribution of Young’s modulus after 30 cycles and 3 days of relaxation at room temperature became narrower for all glasses. These findings indicate either the existence of unrelaxed stresses in the surface layer of the metallic glasses after the treatment or that cryothermal cycling at some point does not lead to rejuvenation but rather to relaxation of the glass.
The bulk rejuvenation effect of thermal cycling was proven by differential scanning calorimetry experiments in our previous work11. In the present work, we observed a potential relaxation effect of thermal cycling in the metallic glass surface. Can such relaxation also occur in the bulk? As mentioned before, plastic deformation is one of the methods for increasing the internal energy of metallic glasses8. The center of the shear band, which is a layer approximately 10–20 nm thick, is considered to have the highest rejuvenation effect. However, in many recent works, the shear-band-affected, or rejuvenated, layer was observed to be on the order of 10-µm thick21,41. Therefore, severe plastic deformation is considered to be one of the most effective methods for rejuvenating metallic glasses. It was recently found that metallic glasses have a low resistance against low cycle fatigue42. The inhomogeneous distribution of residual internal stresses in plastically deformed samples and the reversal of stresses on active shear bands during unloading weaken the sheared material in the bands, favoring more inhomogeneous deformation and accelerating failure as the shear bands with large offsets evolve into cracks. In the present work, we observed a decrease in the plasticity of the metallic glass samples after preliminary small plastic deformation beyond the yield point (Fig. 4). A major shear band is formed at the second loading43, and further deformation progressed by stick-slip of this major shear band (Fig. 2). However, cryothermal cycling treatment of the preliminary deformed sample almost restores the plasticity of the material to the as-cast level (Fig. 4). This restoration can be achieved only if thermal cycling has a relaxation effect on the shear band region. The excess volume generated in the shear band upon deformation is annihilated or redistributed during the thermal cycling treatment. Thus, the deformed structure formed during plastic deformation near the shear band becomes more relaxed, which prevents the easy formation of major shear bands and cracks.
A metallic glass system, in general, seeks to find an atomic configuration with the lowest energy and, in the worst-case scenario, crystallizes. However, local structural changes can increase the energy state of the system. Therefore, the effect of cryothermal cycling depends on the number of cycles. For a small number of cycles, the treatment leads to rejuvenation of the glass and an increase in the plastic strain; however, at some point, relaxation processes start to prevail, and the maximum plastic strain decreases. Rejuvenation excites the glass to higher energy states and at the same time increases the mobility of the atoms, causing the glass to relax more easily. It is quite difficult to calculate the optimal number of cycles based on only the metallic glass composition data. In our previous work11, cryothermal cycling increased the plasticity of the Zr–Cu–Fe–Al metallic glass, even after 60 cycles. The conclusion was made that the method is more effective for glasses that already have a highly heterogeneous structure. This conclusion provided the outline for the metallic glass compositions designed in the present work. However, the results of the current compression tests show that the idea of introducing energy pairs with positive heats of mixing to produce a more pronounced beneficial effect in the thermal cycling treatment works only partially. One can notice that thermal cycling has almost no effect on the maximum plastic strain in the glass containing Ni (Fig. 5), where the Cu–Ni pair has a positive enthalpy of mixing of +4 kJ/mol44. However, despite the fact that the enthalpy of mixing of the Cu–Co pair is also positive (+6 kJ/mol), thermal cycling of the Zr–Cu–Co–Al glass results in an immediate plasticity decrease in the sample. Similar to our previous results11, the metallic glass containing Fe \(\left( {{\it{\Delta {H}}}_{\mathrm{mix}}^{\mathrm{Cu} - \mathrm{Fe}} = + 13\,\mathrm{kJ/mol}} \right)\) exhibits an increase in the maximum plastic strain. However, the plastic strain does not increase indefinitely with the number of cycles, and after 30 cycles the plasticity begins to decrease. The enthalpies of mixing presented here were calculated theoretically for binary 0.5:0.5 mixtures and are, in fact, composition-dependent45, and therefore might have different values in the real glasses, although their positive sign is retained. It should also be noted here that the inability of cryothermal cycling to induce rejuvenation of the selected glasses does not mean that these or similar glasses cannot be rejuvenated by other methods46.
Discussion
Atomic bonding plays an important role in the deformation of pure metallic glasses. Metallic glasses containing metalloid elements should be treated even more carefully. Different bond structures, bond lengths, and bond strengths can have a large influence on the plasticity of metallic glasses, the degree of heterogeneity, and therefore the outcome of the cryothermal cycling treatment47,48. For example, despite having a large Poisson’s ratio, gold-based metallic glasses exhibit almost zero plasticity at room temperature and even elevated temperatures49. It was also found that Co-based and Fe-based metallic glasses containing metalloid elements exhibit only relaxation behavior upon cryothermal cycling, which has a positive effect on the magnetic properties50,51,52. Atomic bonding was found to also be important in β-relaxation processes53. β-relaxation processes are directly correlated with the shear transformation zones, and therefore with the plasticity of glasses54. It was also shown that metallic glasses with highly pronounced β-relaxation peaks can exhibit tensile plasticity55. However, there is still no generally accepted theory for β-relaxation. Yu et al.53 found that β-relaxation is more pronounced in systems with strong bonds between the constituent elements in the alloy system, while positive values or large fluctuations in the values of the enthalpy of mixing suppress β-relaxation.
In conclusion, it was established that cryothermal cycling is a universal method for triggering structural changes in metal–metal glasses, and the present work shows that the effects of these changes can be diverse. Metallic glasses of chosen compositions (Zr60Cu20Fe10Al10, Zr60Cu20Co10Al10, and Zr60Cu20Ni10Al10) behave differently under the cryothermal cycling treatment. An increase in the average apparent Young’s modulus and its magnitude distribution width on the surface of metallic glasses was found after cryothermal cycling treatment. However, this effect is not permanent and disappears after a period of relaxation at room temperature. The cryothermal cycling treatment can work as a method for rejuvenation as well as relaxation of metallic glasses. It can have a positive effect on the metallic glass plasticity; however, for some glasses, it may have no effect or even a negative one. The nature of bonding in metallic glasses appears to have a significant influence on the outcome of the treatment as well as the maximum achievable plastic strain.
References
Suryanarayana, C. & Inoue, A. Bulk Metallic Glasses, p. 565 (CRC Press, Boca Raton, USA, 2010).
Wang, W. H. Bulk metallic glasses with functional physical properties. Adv. Mater. 21, 4524–4544 (2009).
Ashby, M. F. & Greer, A. L. Metallic glasses as structural materials. Scr. Mater. 54, 321–326 (2006).
Greer, A. L., Cheng, Y. Q. & Ma, E. Shear bands in metallic glasses. Mater. Sci. Eng. R 74, 71–132 (2013).
Hufnagel, T. C., Schuh, C. A. & Falk, M. L. Deformation of metallic glasses: recent developments in theory, simulations, and experiments. Acta Mater. 109, 375–393 (2016).
Greer, A. L. & Sun, Y. H. Stored energy in metallic glasses due to strains within the elastic limit. Philos. Mag. 96 1643–1663 (2016).
Kumar, G., Desai, A. & Schroers, J. Bulk metallic glass: the smaller the better. Adv. Mater. 23, 461–476 (2011).
Sun, Y., Concustell, A. & Greer, A. L. Thermomechanical processing of metallic glasses: extending the range of the glassy state. Nat. Rev. Mater. 1, 16039 (2016).
Raghavan, R. et al. Ion irradiation enhances the mechanical performance of metallic glasses. Scr. Mater. 62, 462–465 (2010).
Saida, J., Yamada, R., Wakeda, M. & Ogata, Sh. Thermal rejuvenation in metallic glasses. Sci. Technol. Adv. Mater. 18, 152–162 (2016).
Ketov, S. V. et al. Rejuvenation of metallic glasses by non-affine thermal strain. Nature 524, 200–203 (2015).
Wu, M. Y., Wadsworth, J. & Sherby, O. D. Internal stress superplasticity in anisotropic polycrystalline zinc and uranium. Metall. Trans. A 18, 451–462 (1987).
Liu, X. et al. Transformation of dipeptide-based organogels into chiral crystals by cryogenic treatment. Angew. Chem. 129, 2704–2707 (2017).
Bu, F. et al. The effect of thermal cycling treatments on the thermal stability and mechanical properties of a Ti-based bulk metallic glass composite. Metals 6, 274 (2016).
Guo, G. Q., Yang, L. & Wu, S. Y. Structural investigation upon the high glass-forming ability in Fe-doped ZrCuAl multicomponent alloys. Intermetallics 71, 24–30 (2016).
Cheng, Y. Q. & Ma, E. Atomic-level structure and structure–property relationship in metallic glasses. Prog. Mater. Sci. 56, 379–473 (2011).
Kim, J. et al. Modulation of plastic flow in metallic glasses via nanoscale networks of chemical heterogeneities. Acta Mater. 140, 116–129 (2017).
Hutter, J. L. & Bechhoefer, J. Calibration of atomic-force microscope tips. Rev. Sci. Instrum. 64, 1868–1873 (1993).
Derjaguin, B. V., Muller, V. M. & Toporov, Yu. P. Effect of contact deformations on the adhesion of particles. J. Colloid Interf. Sci. 53, 314–326 (1975).
Sneddon, I. N. The relation between load and penetration in the axisymmetric boussinesq problem for a punch of arbitrary profile. Int. J. Eng. Sci. 3, 47–57 (1965).
Ketov, S. V., Nguyen, H. K., Trifonov, A. S., Nakajima, K. & Louzguine-Luzgin, D. V. Huge reduction of Young’s modulus near a shear band in metallic glass. J. Alloy Compd. 687, 221–226 (2016).
Gammer, C., Mangler, C., Rentenberger, C. & Karnthaler, H. P. Quantitative local profile analysis of nanomaterials by electron diffraction. Scr. Mater. 63, 312–315 (2010).
Mitchell, D. R. G. & Petersen, T. C. RDFTools: a software tool for quantifying short-range ordering in amorphous materials. Microsc. Res. Tech. 75, 153–163 (2012).
Wagner, H. et al. Local elastic properties of a metallic glass. Nat. Mater. 10, 439–442 (2011).
Dmowski, W., Iwashita, T., Chuang, C.-P., Almer, J. & Egami, T. Elastic heterogeneity in metallic glasses. Phys. Rev. Lett. 105, 205502 (2010).
Cao, C. R., Lu, Y. M., Bai, H. Y. & Wang, W. H. High surface mobility and fast surface enhanced crystallization of metallic glass. Appl. Phys. Lett. 107, 141606 (2015).
Cheng, G. et al. Large anelasticity and associated energy dissipation in single-crystalline nanowires. Nat. Nanotech. 10, 687–691 (2015).
Sun, Y. H. et al. Flow-induced elastic anisotropy of metallic glasses. Acta Mater. 112, 132–140 (2016).
Egami, T., Tong, Y. & Dmowski, W. Deformation in metallic glasses studied by synchrotron X-ray diffraction. Metals 6, 22 (2016).
Concustell, A., Godard-Desmarest, S., Carpenter, M. A., Nishiyama, N. & Greer, A. L. Induced elastic anisotropy in a bulk metallic glass. Scr. Mater. 64, 1091–1094 (2011).
Louzguine-Luzgin, D. V. et al. Bulk metallic glassy surface native oxide: its atomic structure, growth rate and electrical properties. Acta Mater. 97, 282–290 (2015).
Louzguine-Luzgin, D. V., Nguyen, H. K., Nakajima, K., Ketov, S. V. & Trifonov, A. S. A study of the nanoscale and atomic-scale wear resistance of metallic glasses. Mater. Lett. 185, 54–58 (2016).
Louzguine-Luzgin, D. V. et al. Investigation of transparent magnetic material formed by selective oxidation of a metallic glass. Thin Solid Films 531, 471–475 (2013).
Jastrow, L., Köster, U. & Meuris, M. Catastrophic oxidation of Zr-TM (noble metals) glasses. Mater. Sci. Eng. A 375–377, 440–443 (2004).
Kato, H., Chen, H.-S. & Inoue, A. Relationship between thermal expansion coefficient and glass transition temperature in metallic glasses. Scr. Mater. 58, 1106–1109 (2008).
White, G. K. Solids: thermal expansion and contraction. Contemp. Phys. 34, 193–204 (1993).
Barrera, G. D., Bruno, J. A. O., Barron, T. H. K. & Allan, N. L. Negative thermal expansion. J. Phys. Condens. Matter 17, 217–252 (2005).
Hirata, A., Hirotsu, Y., Ohkubo, T., Tanaka, N. & Nieh, T. G. Local atomic structure of Pd–Ni–P bulk metallic glass examined by high-resolution electron microscopy and electron diffraction. Intermetallics 14, 903–920 (2006).
Al-Aqeeli, N. Strengthening behavior due to cyclic elastic loading in Pd-based metallic glass. J. Alloy Compd. 509, 7216–7220 (2011).
Louzguine-Luzgin, D. V. et al. On room-temperature quasi-elastic mechanical behaviour of bulk metallic glasses. Acta Mater. 129, 343–351 (2017).
Pan, J., Chen, Q., Liu, L. & Li, Y. Softening and dilatation in a single shear band. Acta Mater. 59, 5146–5158 (2011).
Louzguine-Luzgin, D. V. et al. Influence of cyclic loading on the onset of failure in a Zr-based bulk metallic glass. J. Mater. Sci. 49, 6716–6721 (2014).
Louzguine-Luzgin, D. V., Zadorozhnyy, V. Yu, Chena, N. & Ketov, S. V. Evidence of the existence of two deformation stages in bulk metallic glasses. J. Non-Cryst. Solids 396–397, 20–24 (2014).
Takeuchi, A. & Inoue, A. Classification of bulk metallic glasses by atomic size difference, heat of mixing and period of constituent elements and its application to characterization of the main alloying element. Mater. Trans. 46, 2817–2829 (2005).
Takeuchi, A. & Inoue, A. Mixing enthalpy of liquid phase calculated by Miedema’s scheme and approximated with sub-regular solution model for assessing forming ability of amorphous and glassy alloys. Intermetallics 18, 1779–1789 (2010).
Qiang, J. & Tsuchiya, K. Composition dependence of mechanically-induced structural rejuvenation in Zr-Cu-Al-Ni metallic glasses. J. Alloy Compd. 712, 250–255 (2017).
Li, G., Borisenko, K. B. & Cockayne, D. J. H. Local structures of two metallic glasses with good plasticity. J. Phys. Conf. Ser. 241, 012066 (2010).
Lekka, Ch. E., Bokas, G. B., Almyras, G. A., Papageorgiou, D. G. & Evangelakis, G. A. Clustering, microalloying and mechanical properties in Cu/Zr-based glassy models by molecular dynamics simulations and ab-initio computations. J. Alloy Compd. 536S, S65–S69 (2012).
Ketov, S. V., Chen, N., Caron, A., Inoue, A. & Louzguine-Luzgin, D. V. Structural features and high quasi-static strain rate sensitivity of Au49Cu26.9Ag5.5Pd2.3Si16.3 bulk metallic glass. Appl. Phys. Lett. 101, 241905 (2012).
Meng, Y., Wang, Y. G., Zhu, L., Cao, C. C. & Dai, Y. D. Effect of thermal cycling treatment on local structure, thermal stability and magnetic properties of Fe80Si8.75B10Cu1.25 metallic glass. J. Non-Cryst. Solids 471, 406–409 (2017).
Zhao, C., Pan, L., Ma, X., Li, J., Liu, Q. & Wang, J. Cycle rapid cooling treatment effect on the magnetic properties and giant magnetoimpedance properties of Co-based amorphous alloy ribbons. J. Magn. Magn. Mater. 444, 198–205 (2017).
Zhukov, A. P. & Shtangeev, B. L. Cooling-induced phase transition in amorphous CoCrZr alloy. J. Appl. Phys. 73, 5716 (1993).
Yu, H. B., Samwer, K., Wang, W. H. & Bai, H. Y. Chemical influence on β-relaxations and the formation of molecule-like metallic glasses. Nat. Commun. 4, 2204 (2013).
Yu, H. B., Wang, W. H., Bai, H. Y. & Samwer, K. The β-relaxation in metallic glasses. Natl. Sci. Rev. 1, 429–461 (2014).
Yu, H. B. et al. Tensile plasticity in metallic glasses with pronounced β relaxations. Phys. Rev. Lett. 108, 015504 (2012).
Acknowledgements
This work was supported by the World Premier International Research Center Initiative (WPI), MEXT, Japan, by JSPS KAKENHI Grant Number #16K18244 and by the Ministry of Education Science of the Russian Federation in the framework of Increase Competitiveness Program of NUST “MISiS” (№ К2–2014–013 and К2-2017-089). Additional support through the European Research Council under the ERC Advanced Grant INTELHYB (grant ERC-2013-ADG-340025) is gratefully acknowledged. We also thank Prof. A. Chuvilin for technical support with the TEM experiments.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
41427_2018_19_MOESM1_ESM.docx
On cryothermal cycling as a method inducing structural changes in metallic glasses (Supplementary materials)(DOCX 5310 kb)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ketov, S.V., Trifonov, A.S., Ivanov, Y.P. et al. On cryothermal cycling as a method for inducing structural changes in metallic glasses. NPG Asia Mater 10, 137–145 (2018). https://doi.org/10.1038/s41427-018-0019-4
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41427-018-0019-4
This article is cited by
-
Deformation behavior of thermally rejuvenated Zr-Cu-Al-(Ti) bulk metallic glass
Scientific Reports (2024)
-
Nanoscopic tribological characteristics of a cryogenically cycled Zr-based metallic glass
Science China Physics, Mechanics & Astronomy (2024)
-
Ultralarge-scale anomalous phase separation discovered in a Cr-Fe-Co-Ni-Zr high-entropy metallic glass system
Science China Materials (2023)
-
Rejuvenation and Malleability Enhancement of Zr-Based Metallic Glass by Sub-Tg Annealing and Cryogenic Thermal Cycle Treatment
Journal of Materials Engineering and Performance (2023)
-
Tailoring mechanical heterogeneity, nanoscale creep deformation and optical properties of nanostructured Zr-based metallic glass
Rare Metals (2023)