Abstract
Laser-based powder-bed fusion additive manufacturing or three-dimensional printing technology has gained tremendous attention due to its controllable, digital, and automated manufacturing process, which can afford a refined microstructure and superior strength. However, it is a major challenge to additively manufacture metal parts with satisfactory ductility and toughness. Here we report a novel selective laser melting process to simultaneously enhance the strength and ductility of stainless steel 316L by in-process engineering its microstructure into a <011> crystallographic texture. We find that the tensile strength and ductility of SLM-built stainless steel 316L samples could be enhanced by ~16% and ~40% respectively, with the engineered <011> textured microstructure compared to the common <001> textured microstructure. This is because the favorable nano-twinning mechanism was significantly more activated in the <011> textured stainless steel 316L samples during plastic deformation. In addition, kinetic simulations were performed to unveil the relationship between the melt pool geometry and crystallographic texture. The new additive manufacturing strategy of engineering the crystallographic texture can be applied to other metals and alloys with twinning-induced plasticity. This work paves the way to additively manufacture metal parts with high strength and high ductility.
Similar content being viewed by others
Introduction
Metal additive manufacturing (AM), also known as metal three-dimensional (3D) printing, can produce high-strength complex geometries1 to obtain components with fine microstructures2 and achieve microstructural control within parts3. However, metal AM builds typically suffer from poor mechanical properties, such as low ductility and inconsistency, due to the presence of lack-of-fusion defects, internal pores, residual stresses, and anisotropy4, 5. Post-processing treatments are generally required to restore the desired toughness6. Selective laser melting (SLM) has been become a mainstream powder-bed fusion metal AM technique due to its refined resolution and widespread adoption7. It is commonly accepted that SLM-built parts experience a layer-wise cyclic thermal history8. Highly dense parts (>99%) can be realized by optimizing the laser scanning parameters9. They normally possess a strong <001> crystallographic texture along the build direction against the heat dissipation route10. Epitaxial growth is frequently observed11 and is hypothesized to be a prerequisite for the formation of various crystallographic textures12. Owing to the rapid cooling (~106 K/s) to ambient temperature involved in the SLM process11, elemental segregation is greatly suppressed, while large quantities of martensitic phases and dislocations are favored13. Therefore, SLM-built components tend to have higher strength than their counterparts processed by other metal AM techniques. However, the decrease in ductility accompanied with reduced toughness remains to be an unresolved issue in metal AM, especially for the SLM process.
Inspired by the various crystallographic textures11,14,15 and grain morphologies16 achieved via different scanning strategies in SLM, microstructural control within the SLM-built part holds the key to property enhancement. In addition to the common <001> crystallographic texture obtained through SLM, a few studies also attained <011> crystallographic texture along the build direction3,11,14,17. Moreover, nanometer-scale twinning (nano-twinning) is shown to be of utmost importance for ductility improvement in the latest research on metals and alloys18,19,20. Unlike conventional grain boundaries or interphase interfaces, the twin boundary energy is low, and it possesses a greater dislocation storage capacity21. Dislocations can pass through or glide along the twin boundaries by dissolving into partial dislocations21, which could simultaneously enhance both the strength and the ductility of a material.
In this work, we aim to overcome the trade-off between strength and ductility in SLM-built metals and alloys by the in situ tailoring of specific crystallographic textures and grain sizes. Stainless steel 316L (SS316L) is chosen as a representative material for this purpose because it is a popular material employed in metal AM with broad applications10,22,23. Moreover, SS316L is a face-centered cubic (FCC) metal with a relatively low stacking fault energy of ~20 mJ/m2, which favors deformation-induced twinning24. This work shows that, by utilizing a specific laser scanning strategy, a favorable fine-grained microstructure with a <011> crystallographic texture could be produced. This aids the activation of the nano-twinning mechanism during the tensile deformation of SLM-built SS316L at room temperature, which simultaneously increases the strength and ductility. This work proposes a promising solution to improve the mechanical performance of metal AM components while using less material.
Materials and methods
Sample preparation
All samples were fabricated with an SLM 250 HL machine (SLM Solutions Group AG, Lübeck, Germany). The precursor material was spherical gas-atomized SS316L powder with a size range of 20–63 μm. A dual laser system was employed, where the laser has a Gaussian profile for power inputs below 400 W and a top-hat profile for inputs up to 1 kW. The samples to test the process parameters were built with dimensions of 10 mm3, and at least two samples per parameter set were built. Standard mechanical polishing procedures were adopted and can be found elsewhere10. Both chemical (~30 min) and electrolytic (~10 s) etchings were employed with Kroll’s reagent (1–3% HF, 2–6% HNO3, and 91–97% H2O) before optical microscopic (OM) and scanning electron microscopic (SEM) examination.
X-ray diffraction (XRD) and mechanical testing
XRD analysis was conducted on a PANalytical Empyrean with Cu Kα radiation. A step size of 0.01° was used for all samples. The tensile coupon blocks were built with dimensions of 14 × 36 × 10 mm3. They were then machined to the tensile coupon size (see Supplementary Fig. 1(d)) via the electrical discharge machining method. The samples were ground with #320 grit sand paper followed by #1000 grit. Tensile tests were performed on an Instron static tester (series 5569) with a strain rate of 2.65 × 10−4/s. A contact-based extensometer was used until break. At least three samples for each set were tested.
Monte Carlo simulations
Kinetic Monte Carlo simulations were conducted with the open-source Stochastic Parallel PARticle Kinetic Simulator25,26. The Monte Carlo Potts model that involves spins (or grain identifies) on a discrete lattice was employed. The overall bond energies between adjoining unlike spins (adjacent grains) were computed as \(E = \frac{1}{2}\mathop {\sum }\limits_{i = 1}^N \mathop {\sum }\limits_{j = 1}^L (1 - \delta (q_iq_j))\), where N is the total number of lattice sites, qi and qj are the spins at lattices sites i and j, and L is the number of neighbors of each lattice site. A is the mobility factor and F is specified as \(F = F_o{\mathrm{exp}}\left( {\frac{{ - Q}}{{k_BT(t,i)}}} \right)\), where Q is the activation energy for grain boundary motion, Fo is a user defined prefatory, KB is Boltzmann’s constant, and T(t,i) is the temperature input at a specific time and location. The Monte Carlo acceptance probability of spin flip was then calculated as \(P = \left\{ {\begin{array}{*{20}{c}} {F{\mathrm{exp}}\left( {\frac{{ - \Delta E}}{{k_BT_s}}} \right)} & {if\,\Delta E > 0} \\ F & {if\,\Delta E \le 0} \end{array}} \right.\). This ensures that the overall energy of the system decreases with each calculation step and thus grain growth proceeds.
Electron back-scatter diffraction (EBSD) and transmission electron microscopic (TEM) analyses
An extra step of Struers OPS polishing was performed after the standard polishing procedures10 to prepare the samples for the EBSD experiments, which were performed on a JEOL JMS-7600F SEM equipped with an Oxford EBSD system. The step sizes used for as-built and deformed samples were 1 μm and 0.3 μm, respectively. Light etching was performed on the as-built samples to review the melt tracks. Post-deformation EBSD graphs were taken ~3 mm away from the fracture site. Data analysis was performed with the open-source software MTEX27. TEM studies were carried on a JOEL TEM 2010 at an accelerating voltage of 200 kV. The samples were prepared similarly to those in a previous study10.
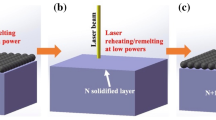
a Laser scanning strategies for single-scan and multi-scan melt pools using different laser process parameters. b The three key geometrical features (width, depth, and rear length) of a melt pool affecting grain growth. c Schematic illustration showing the formation of <001> and <011> crystallographic textures due to the different melt pool geometries. d Schematics of the two prevailing deformation mechanisms (dislocation slip and twinning) in metals and alloys. e The expected outcome of simultaneously enhanced strength and ductility for the SLM-built parts
a XRD profiles of the recycled SS316L powder and tensile coupons built at varying laser powers. b Engineering stress vs. engineering strain graphs for the various SLM-built SS316L parts. The minimum requirements for the tensile properties (including yield strength σy, ultimate tensile strength σu, and elongation ε for SS316L are indicated. c True strain hardening rate curves normalized by the shear modulus as a function of true strain in the representative 100 W, 380 W and 950 W samples
Results
Simultaneously enhanced strength and ductility
The overall SLM processing route is illustrated in Fig. 1. By manipulating the laser power and scanning strategy (Fig. 1a), the geometrical features of the melt pool varied accordingly (Fig. 1b). It would affect the crystallographic textures (Fig. 1c) formed within the built part and the deformation mechanisms (Fig. 1d) active in the deformation process, which could result in different mechanical properties, as shown in Fig. 1e. The SLM process parameters with different power inputs are given in Supplementary Table 1. Samples in this work built with 100 W power suffered from poor relative densities due to the lack-of-fusion defects caused by insufficient melting. The XRD results of the recycled SS316L powder and the SLM-built SS316L samples are displayed in Fig. 2a. Only FCC γ-phase austenite was detected in all SLM-built samples. From the XRD peak intensity distribution, we can see that the 100 W sample shows a similar polycrystalline XRD profile to that of the recycled powder. In contrast, the 200 W and 380 W samples have the strongest (200) peak, and the 570 W, 760 W and 950 W samples possess the strongest (220) peak. This suggests that they may have different crystallographic textures, which will be further elaborated by the EBSD study in the following section.
Figure 2b shows the tensile properties of SLM-built SS316L samples with varying process parameters. The mechanical requirements for SS316L based on ASTM A240/A240M28 are indicated in Fig. 2b. It is worth noting that samples with similar crystallographic textures had very close tensile performances. Thus only the 100 W, 380 W and 950 W samples will be discussed hereafter for clarity. Among all the samples, the 100 W sample had the lowest tensile strength and elongation values owing to its relatively high porosity. Its strength meets the ASTM standard, but its elongation is poor. We note that the strength of the 380 W sample far exceeds the ASTM standard. However, its elongation is not satisfactory and is still below the standard. Interestingly, the 950 W sample exhibits higher strength and better ductility than the 380 W counterpart. The increase in the true ultimate tensile strength and true strain can be up to ~16% and ~40%, respectively. Similar tensile results along the SLM build direction are shown in Supplementary Fig. 2. Figure 2c shows the work hardening rate curves normalized by a shear modulus of 74 GPa for SS316L29. All samples display a general decreasing trend, and the work hardening regimes fall within 0.01–0.03 G, which is comparable to other FCC metals with deformation twins30,31.
A closer examination of the work hardening rate graphs shows that deformation twinning started earlier for the 950 W sample at a true strain of ~0.020 compared to ~0.025 for the 380 W sample. These values correspond to the experimental twinning stresses, σtw (950 W) = ~585 MPa and σtw (380 W) = ~567 MPa, from Fig. 2b. As known, the deformation twinning stress σtw was derived from σtw = 2×γsf /(bp×maverage)32, where γsf is the stacking fault energy (~20 mJ/m2)24, bp is the Burgers vector for Shockley partial dislocation (~0.146 nm), and m is the Schmid factor. In this work, the area-normalized Schmid factors for the 950 W and 380 W samples were determined to be 0.451 and 0.459, respectively, from their EBSD maps. Therefore, the calculated twining stresses are σtw(950 W) = 607 MPa and σtw(380 W) = 597 MPa, which are in good agreement with the experimental results. Despite its earlier initiation of deformation twinning, the 950 W sample goes through a longer period of work hardening. This is mainly attributed to the higher quantity of deformation twins in the deformed 950 W sample, which can be confirmed by the post-deformation EBSD and TEM analyses.
Microstructure and crystallographic texture
Figure 3 shows that cellular microstructure is present in the 380 W and 950 W samples due to the fast cooling rates10. With different laser power inputs and laser scanning lengths, however, the size and morphology of the melt pools in the two samples drastically differed. As illustrated in Fig. 1a, the 380 W sample shows a single-scan melt pool with a Gaussian laser profile, whereas the 950 W sample shows a multi-scan melt pool with a top-hat laser profile. Figure 3a, d show the XY cross-sectional OM images of the 380 W and 950 W samples, from which the differences in laser scanning length and hatch spacing can be clearly observed. The 950 W melt pool is several times larger in size than that of 380 W, as shown in Fig. 3b, e. There exists an obvious epitaxial cellular microstructure in the 380 W sample, but we only observed an obscure non-epitaxial and misaligned cellular microstructure in the 950 W sample (Fig. 3c, f). The cellular morphologies arise from similar temperature gradient (GL) vs. solidification velocity (VL) conditions experienced by both samples33. In situ heat treatment effects from the multi-scan melt pool reduce the propensity of elemental segregation, leading to an obscure sub-grain microstructure in the 950 W sample. The black holes were generated by pitting corrosion during the etching process34. The strong Marangoni effect and the high recoil pressure result in strong convection flow within the large 950 W melt pool, which may induce misaligned cellular growth.
EBSD IPF color maps for the top view of deformed a 380 W and c 950 W samples. The respective band contrast maps superimposed with red-colored deformation twins are shown in b and d. The inverse pole figures consisting of grains with and without deformation twins parallel to the tensile direction are shown in e and g. The inverse pole figures of the as-built f 380 W and h 950 W samples parallel to the tensile direction. The dotted contour lines represent the Taylor factors. Scale bars for a, c are 50 μm
Figure 4a, b show the EBSD orientation maps of the 380 W and 950 W samples on the XZ plane. The 380 W sample has a crystallographic texture index of ~3.6 along the <001> direction, and the 950 W sample possesses a texture index of ~2.1 along the <011> direction, as computed from their corresponding inverse pole figures (IPFs), as shown in Fig. 4c, d. Despite the larger melt pool formed in the 950 W sample, it yields a much smaller average grain area of ~180 μm2 compared to that of ~310 μm2 for the 380 W sample. The melt pool boundaries in the 950 W sample are marked by black solid lines for clarity. By following the heat transfer path, it is clear that all grains were grown perpendicular to the melt pool boundaries. Moreover, fine equiaxed grains were formed on the periphery of the melt pool boundaries. Unlike the epitaxial grain growth along the build direction in the 380 W sample, a “zig-zag”, non-epitaxial growth mode is clearly observed in the 950 W sample. It is noted that the microstructures of both the 380 W and 950 W sample remain stable after heat treatment at 650 °C for 2 h, as shown in Supplementary Fig. 3.
To better understand the relationship between the melt pool geometry and the crystallographic texture, kinetic Monte Carlo simulations were conducted incorporating three key parameters, i.e., width, depth, and rear length of the melt pool geometry, as illustrated in Fig. 1b. Only the rear part of the melt pool was computed, as the front part has little effect on grain growth35. Owing to the different melt pool geometries, the grain growth directions are vastly different within each of the melt pools in the two abovementioned samples (see Fig. 1c). Figure 4e, g depict the isometric views of the grain morphologies within the melt pools of the 380 W and 950 W samples, respectively. The melt pool widths and depths were taken directly from OM observations (Supplementary Fig. 4). The rear length of the melt pool was captured either from finite element simulations or observation of its ripple pattern. The ratio of the melt pool width, height, and rear length is 6:1:35 and 2:1:3.6 for the 380 W and 950 W samples, respectively. It is apparent that grains tend to grow straight from bottom to top within the 380 W melt pool (Fig. 4f). However, in the 950 W melt pool, the grains grow perpendicular to the melt pool boundary (Fig. 4h). There is a cluster of equiaxed grains within the center of the melt pool, which prevents the columnar grains from further growth. Moreover, fine equiaxed grains are also present at the periphery of melt pool boundary. Therefore, the experimental observation of the <011> crystallographic texture in the 950 W sample is well consistent with the simulation results. Videos of the detailed simulation results of these two types of melt pools can be viewed in Supplementary Video 1 and Supplementary Video 2. In addition, the systematic simulation results regarding the influence of the melt pool geometry on the crystallographic texture can be seen in Supplementary Fig. 5.
Influence of laser power and scanning strategy
It is demonstrated that by employing a specific laser power and scanning strategy, the crystallographic texture and grain size can be engineered through an SLM process. Different tensile behavior may be observed, provided that different deformation mechanisms prevail (see Fig. 1d, e). However, the laser power is not the sole determining factor for the formation of crystallographic textures. It has been reported that a lower laser power of 400 W produces a <011> texture, whereas a higher power of 1 kW generates a <001> texture36 for the same material (SS316L). Thus a suitable scanning strategy catering to a specific laser power is the key to engineering the crystallographic texture.
Dislocation slip and deformation twinning are the two competing and complementary plastic deformation mechanisms. Deformation twinning is favored because of its superior dislocation storage capacity, which benefits work hardening and ductility enhancement21. Figure 5a, c show the XY-plane EBSD graphs of deformed 380 W and 950 W samples. Many deformation-induced twins can be observed in certain grains, which are highlighted in the band contrast maps for clarification in Fig. 5b, d. Though nanoscale twins may be absent due to the limited resolution of EBSD scanning (0.3 μm step size), the detected twins in the 380 W sample are larger but fewer in number compared to the 950 W sample. A total area of ~0.6 mm2 was examined by EBSD for the deformed 380 W and 950 W samples. The overall detected twin length in the deformed 950 W sample (~17.0 mm) is ~25% longer than that of the deformed 380 W sample (~13.6 mm).
Figure 5e, g show the corresponding IPFs of Fig. 5a, c along the tensile direction. Grains with and without deformation twins are marked by red and black dots. The dotted contour lines indicate the Taylor factor (M). It is apparent that deformation-induced twinning hardly appears when M < 2.6 and the majority of twinned grains are aligned close to the <111> orientation along the tensile direction. This is consistent with previous findings from other types of austenitic steels37,38,39. It is accepted that the activation of multiple slip systems and the presence of dislocation pile-ups are necessary to induce twinning during deformation40. Grains with a higher Taylor factor (M > 2.6) experienced a greater amount of crystallographic shear with regards to the uniaxial tension, which in turn resulted in additional strain hardening and a higher dislocation density to maintain strain compatibility with the adjoining grains41. Moreover, it is revealed that grains with a lower Taylor factor (M < 2.6) may not have sufficient slip systems and/or dislocations to induce deformation twinning. Figure 5f, h show the IPFs from the two EBSD maps of the as-built 380 W and 950 W samples in Fig. 4. It can be derived from Fig. 5f that most of the grains in the 380 W sample were unfavorable to induce deformation twinning, at least at the initial deformation stage, due to the strong <001> crystallographic texture and low value of M (<2.6) along the tensile direction. In contrast, due to the <011> crystallographic texture formed in the 950 W sample, the grains were not entirely constrained within the region of M < 2.6. Thus a larger number of deformation twins could be formed during the plastic deformation process. Moreover, as suggested by recent relevant studies, residual stress does not seem to play a significant role in the deformation process for SLM-processed SS316L42,43,44. Thus the influence of residual stress on the mechanical deformation behavior may not be a main concern in this work.
TEM study of the as-SLM-built SS316L samples reveals that more dislocations exist in the 950 W sample than in the 380 W sample (see Supplementary Fig. 6). Figure 6a shows two adjacent grains with two different orientations (<001> and <321>) in the deformed 380 W sample. No twins were observed within the <001>-oriented grain. The cubic texture of (001)[100] developed in the 380 W sample further confirms that grains with an orientation close to <001> alignment along the tensile direction are unfavorable for deformation twinning. However, within the non-<001>-oriented grains, separated single-twin lamellae with tens of nanometers in width are commonly seen in the 380 W sample (Fig. 6a–c). Moreover, Fig. 6b, c display a large number of dislocations and stacking faults between the twin lamellae, which likely strongly interact with each other during plastic deformation. In contrast, many more multiple deformation twin lamellae were observed in the deformed 950 W sample (see Fig. 6d). The multiple nano-twin lamellae and the stacking fault regions are shown in Fig. 6e. The high-resolution transmission electron microscopic image in Fig. 6f reveals the nano-twin lamellae and stacking faults on the atomic scale. Stacking faults composed of partial dislocations were formed owing to the dislocation/twin interactions19. It is evidenced that twinning is the dominant deformation mechanism in the <011>-textured 950 W sample and the formation of nano-twins could be the major reason for the simultaneously enhanced strength and ductility.
a TEM image showing two adjacent grains with <001> and <321> orientations in the deformed 380 W sample. The grain boundary (GB) is indicated. The right three arrows point to the single-twin lamellae. b TEM image showing dislocations and stacking faults between two single-twin lamellae in the deformed 380 W sample. c Enlarged TEM image of the enclosed region in b showing a nano-twin and surrounding stacking faults (SFs) along the <011> zone axis. d TEM image showing a large number of multiple twins indicated by arrows in the deformed 950 W sample along the <011> zone axis. e TEM image showing the multiple nano-twins in the deformed 950 W sample. f HRTEM image of the enclosed region in e showing the nano-twin lamellae with twin boundaries (TBs) and SFs. Scale bars for a, b, d are 200 nm, for c, e 50 nm, and for f 5 nm
Discussion
The present study reveals that the strength and ductility of SS316L can be simultaneously enhanced via an SLM process by tailoring a specific crystallographic texture. It was shown that the melt pool geometry has a significant influence on the formation of the crystallographic texture. From the previous studies on single laser tracks, we know that slow scanning generates deep but irregular melt pools, while fast scanning creates discontinuous balling phenomena35,45. Therefore, the majority of the optimized laser scanning parameters fall in between, producing regular, shallow melt pools. This in turn contributes to the formation of a <001> crystallographic texture along the build direction in SLM-built metal parts. In this work, we propose a multi-scan melt pool strategy (Fig. 1a) that can produce a stable, deep melt pool with a width-to-height ratio of 2:1 by utilizing a high-power (>400 W) laser with a top-hat profile. Accordingly, a desirable <011> crystallographic texture is formed instead of the common <001> crystallographic texture. Utilizing the kinetic Monte Carlo mesoscale simulation approach, it is shown that a long, shallow melt pool promotes the formation of <001> texture, whereas a short, deep melt pool favors the occurrence of <011> texture (see Supplementary Fig. 5). Obviously, both the experimental and simulation results demonstrate that we can effectively engineer the crystallographic textures within the SLM-processed metal parts by adjusting the melt pool geometry via different laser beam process parameters. Of particular note is that the crystallographic texture selection map shown in Supplementary Fig. 5 can also be applied to other powder-based AM processes, such as electron beam melting and laser engineered net shaping. This work provides meaningful guidance for the fabrication of complex metal parts with desired properties via microstructural engineering in a beam-based, layer-wise material deposition process.
Deformation twinning is unfavorable in the <001> orientation along the tensile direction35. However, most metal AM parts, such as the 380 W sample in this work, have a <001> crystallographic texture. Though grain rotations may occur due to intragranular compatibility during the elongation process, the deformation twinning capacity is greatly limited. In contrast, the <011> crystallographic texture that formed in the 950 W sample enables the activation of more deformation twins within the grains, particularly for the formation of nano-twins, allowing higher strains. The IPF results showed that this is the case for directions both perpendicular and parallel to the build direction. Moreover, the smaller grain size and higher amount of initial dislocation density in the 950 W sample contribute to a higher yield strength. Therefore, a higher yield strength accompanied by an earlier initiation of deformation twinning and a longer strain hardening regime due to the specific <011> crystallographic texture makes the high-power SLM-built samples stronger and tougher.
The findings of the present work will be of significance to additively manufacture other types of metallic materials into high-performance parts, especially those with a low stacking fault energy. This work also helps explain and predict the formation of certain crystallographic textures during rapid solidification processes, such as welding and laser surface modification. Engineering crystallographic textures in the microstructure via an SLM process is a promising method to overcome the long-standing strength–ductility dilemma in metallic engineering materials. With enhanced strength and ductility, metal AM parts or components will become safer when used in heavy load-bearing structures, and less material will be needed to achieve the same goal. Moreover, the use of a high-power laser can effectively improve the AM fabrication rate. These findings can help metal AM find broader industrial application.
References
Martin, J. H. et al. 3D printing of high-strength aluminium alloys. Nature 549, 365–369 (2017).
Tan, X. et al. Revealing martensitic transformation and α/β interface evolution in electron beam three-dimensional-printed Ti-6Al-4V. Sci. Rep. 6, 26039 (2016).
Geiger, F., Kunze, K. & Etter, T. Tailoring the texture of IN738LC processed by selective laser melting (SLM) by specific scanning strategies. Mater. Sci. Eng. A 661, 240–246 (2016).
Frazier, W. E. Metal additive manufacturing: a review. J. Mater. Eng. Perform. 23, 1917–1928 (2014).
Tan, X. et al. Graded microsctructure and mechanical properties of additive manufactured Ti-6Al-4V via electron beam melting. Acta Mater. 97, 1–16 (2015).
Vrancken, B., Thijs, L., Kruth, J.-P. & Van Humbeeck, J. Heat treatment of Ti6Al4V produced by selective laser melting: microstructure and mechanical properties. J. Alloy. Compd. 541, 177–185 (2012).
Lam, L. P. et al. Phase analysis and microstructure characterisation of AlSi10Mg parts produced by selective laser melting. Virtual Phys. Prototyp. 10, 207–215 (2015).
Xu, W. et al. Additive manufacturing of strong and ductile Ti–6Al–4V by selective laser melting via in situ martensite decomposition. Acta Mater. 85, 74–84 (2015).
Mumtaz, K. A., Erasenthiran, P. & Hopkinson, N. High density selective laser melting of Waspaloy®. J. Mater. Process. Technol. 195, 77–87 (2008).
Kunze, K., Etter, T., Grässlin, J. & Shklover, V. Texture, anisotropy in microstructure and mechanical properties of IN738LC alloy processed by selective laser melting (SLM). Mater. Sci. Eng. A 620, 213–222 (2015).
Sun, Z., Tan, X., Tor, S. B. & Yeong, W. Y. Selective laser melting of stainless steel 316L with low porosity and high build rates. Mater. Des. 104, 197–204 (2016).
Ishimoto, T., Hagihara, K., Hisamoto, K., Sun, S.-H. & Nakano, T. Crystallographic texture control of beta-type Ti–15Mo–5Zr–3Al alloy by selective laser melting for the development of novel implants with a biocompatible low Young’s modulus. Scr. Mater. 132, 34–38 (2017).
Haase, C. et al. Exploiting process-related advantages of selective laser melting for the production of high-manganese steel. Materials 10, 56 (2017).
Zhou, X. et al. Textures formed in a CoCrMo alloy by selective laser melting. J. Alloy. Compd. 631, 153–164 (2015).
Thijs, L. et al. Strong morphological and crystallographic texture and resulting yield strength anisotropy in selective laser melted tantalum. Acta Mater. 61, 4657–4668 (2013).
Carter, L. N., Martin, C., Withers, P. J. & Attallah, M. M. The influence of the laser scan strategy on grain structure and cracking behaviour in SLM powder-bed fabricated nickel superalloy. J. Alloy. Compd. 615, 338–347 (2014).
Thijs, L., Verhaeghe, F., Craeghs, T., Humbeeck, J. V. & Kruth, J.-P. A study of the microstructural evolution during selective laser melting of Ti–6Al–4V. Acta Mater. 58, 3303–3312 (2010).
Yu, Q. et al. Strong crystal size effect on deformation twinning. Nature 463, 335–338 (2010).
Wei, Y. et al. Evading the strength–ductility trade-off dilemma in steel through gradient hierarchical nanotwins. Nat. Commun. 5, 3580 (2014).
Li, Z., Pradeep, K. G., Deng, Y., Raabe, D. & Tasan, C. C. Metastable high-entropy dual-phase alloys overcome the strength–ductility trade-off. Nature 534, 227–230 (2016).
Lu, K., Lu, L. & Suresh, S. Strengthening materials by engineering coherent internal boundaries at the nanoscale. Science 324, 349–352 (2009).
Riemer, A. et al. On the fatigue crack growth behavior in 316L stainless steel manufactured by selective laser melting. Eng. Fract. Mech. 120, 15–25 (2014).
Yan, C., Hao, L., Hussein, A., Young, P. & Raymont, D. Advanced lightweight 316L stainless steel cellular lattice structures fabricated via selective laser melting. Mater. Des. 55, 533–541 (2014).
Obrtlík, K., Kruml, T. & Polák, J. Dislocation structures in 316L stainless steel cycled with plastic strain amplitudes over a wide interval. Mater. Sci. Eng. A 187, 1–9 (1994).
Plimpton, S., et al. Crossing the Mesoscale No-Man’s Land via Parallel kinetic Monte Carlo. Sandia Report SAND2009-6226, Sandia National Laboratories, Albuquerque, NM 87185-1316, (2009).
Rodgers, T. M., Madison, J. D., Tikare, V. & Maguire, M. C. Predicting mesoscale microstructural evolution in electron beam welding. JOM 68, 1419–1426 (2016).
Bachmann, F., Hielscher, R. & Schaeben, H. Texture Analysis with MTEX – Free and Open Source Software Toolbox., in Solid State Phenomena, edited by Klein, A. & Schwarzer, R.A. Trans. Tech. Publ., Switzerland, Vol. 160, pp. 63-68 (2010).
ASTM A240/A240M-16a. Standard Specification for Chromium and Chromium-nickel Stainless Steel Plate, Sheet, and Strip for Pressure Vessels and for General Applications. ASTM International, West Conshohocken, PA, 2016. (http://www.astm.org).
Ya, M., Xing, Y., Dai, F., Lu, K. & Lu, J. Study of residual stress in surface nanostructured AISI 316L stainless steel using two mechanical methods. Surf. Coat. Technol. 168, 148–155 (2003).
Laplanche, G., Kostka, A., Horst, O. M., Eggeler, G. & George, E. P. Microstructure evolution and critical stress for twinning in the CrMnFeCoNi high-entropy alloy. Acta Mater. 118, 152–163 (2016).
El-Danaf, E., Kalidindi, S. R. & Doherty, R. D. Influence of grain size and stacking-fault energy on deformation twinning in fcc metals. Metall. Mater. Trans. A 30, 1223–1233 (1999).
Byun, T. S. On the stress dependence of partial dislocation separation and deformation microstructure in austenitic stainless steels. Acta Mater. 51, 3063–3071 (2003).
Rosa, D. M., Spinelli, J. E., Ferreira, I. L. & Garcia, A. Cellular/dendritic transition and microstructure evolution during transient directional solidification of Pb-Sb alloys. Metall. Mater. Trans. A 39, 2161–2174 (2008).
Zhang, K., Zou, J., Grosdidier, T., Dong, C. & Yang, D. Improved pitting corrosion resistance of AISI 316L stainless steel treated by high current pulsed electron beam. Surf. Coat. Technol. 201, 1393–1400 (2006).
Liu, W. & DuPont, J. N. Effects of melt-pool geometry on crystal growth and microstructure development in laser surface-melted superalloy single crystals. Acta Mater. 52, 4833–4847 (2004).
Niendorf, T. et al. Highly anisotropic steel processed by selective laser melting. Metall. Mater. Trans. B 44, 794–796 (2013).
Gutierrez-Urrutia, I., Zaefferer, S. & Raabe, D. The effect of grain size and grain orientation on deformation twinning in a Fe–22wt.% Mn–0.6wt.% C TWIP steel. Mater. Sci. Eng. A 527, 3552–3560 (2010).
Beladi, H. et al. Orientation dependence of twinning and strain hardening behaviour of a high manganese twinning induced plasticity steel with polycrystalline structure. Acta Mater. 59, 7787–7799 (2011).
Yang, P., Xie, Q., Meng, L., Ding, H. & Tang, Z. Dependence of deformation twinning on grain orientation in a high manganese steel. Scr. Mater. 55, 629–631 (2006).
Karaman, I., Sehitoglu, H., Gall, K., Chumlyakov, Y. I. & Maier, H. Deformation of single crystal Hadfield steel by twinning and slip. Acta Mater. 48, 1345–1359 (2000).
Christian, J. W. & Mahajan, S. Deformation twinning. Prog. Mater. Sci. 39, 1–157 (1995).
Wang, Y., et al. Additively manufactured hierarchical stainless steels with high strength and ductility. Nat. Mater. 17, 63–71 (2017).
Liu, L., et al. Dislocation network in additive manufactured steel breaks strength-ductility trade-off. Mater. Today, in press (2018).
Salmi, A. & Atzeni, E. History of residual stresses durin gthe production phases of AlSi10Mg parts processed by powder bed additive manufacturing technology. Virtual Phys. Prototyp. 12, 153–160 (2017).
Yadroitsev, I., Gusarov, A., Yadroitsava, I. & Smurov, I. Single track formation in selective laser melting of metal powders. J. Mater. Process. Technol. 210, 1624–1631 (2010).
Acknowledgements
The authors acknowledge the use of the resources of the Singapore Centre for 3D Printing funded by the National Research Foundation (NRF), Singapore.
Author information
Authors and Affiliations
Contributions
X.T. conceived the idea and organized the data. Z.S. carried out the SLM fabrications, microstructural and mechanical characterization, and MC simulations. X.T. helped with the TEM observation. Z.S. and X.T. wrote the manuscript. All authors discussed the results and commented on the manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sun, Z., Tan, X., Tor, S.B. et al. Simultaneously enhanced strength and ductility for 3D-printed stainless steel 316L by selective laser melting. NPG Asia Mater 10, 127–136 (2018). https://doi.org/10.1038/s41427-018-0018-5
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41427-018-0018-5
This article is cited by
-
Multifunctional metallic nanocomposite for overcoming the strength–ductility trade-off
Scientific Reports (2024)
-
Powder-size driven facile microstructure control in powder-fusion metal additive manufacturing processes
Nature Communications (2024)
-
Machine learning enhanced analysis of EBSD data for texture representation
npj Computational Materials (2024)
-
Selective Laser Melting of Stainless Steels: A review of Process, Microstructure and Properties
Metals and Materials International (2024)
-
A Comprehensive Review on Failure Aspects of Additive Manufacturing Components under Different Loading Conditions
Journal of Failure Analysis and Prevention (2024)