Abstract
Antiferroelectrics are of interest due to their high potential for energy storage. Here, we report the discovery of pinched, polarization-vs.-electric field (P–E) hysteresis loops in the lead-free tungsten bronze ferroelectrics Ba4Sm2Ti4Nb6O30 and Ba4Eu2Ti4Nb6O30, while a broad, single P–E hysteresis loop was observed in the analogue compound Ba4Nd2Ti4Nb6O30. Pinched P–E loops are similar to antiferroelectric hysteresis loops, but in perovskites, they are mostly caused by an extrinsic, internal bias field due to defects, which block domain wall motion. We show that the pinched P–E loops are caused by an intrinsic effect, i.e., by the electric-field-induced phase transition from a non-polar incommensurate to a polar commensurately modulated crystal structure. The in situ electron diffraction results show the coexistence of commensurate polar structural modulation and incommensurate non-polar modulation during the ferroelectric transition and within the ferroelectric phase below the transition temperature. This phase coexistence is the reason for the small remanent polarization. An external electric field transforms the incommensurate component into a commensurate one, and the polarization increases. This new mechanism for pinched P–E hysteresis loops in ferroelectrics not only indicates a new direction for the development of Pb-free ferroelectric materials for energy storage but also significantly contributes to the physical understanding of ferroelectricity in materials with a tungsten bronze structure.
Similar content being viewed by others
Introduction
Ferroelectrics are a very important family of functional materials, and they have received attention from a variety of fields, including material science, condensed matter physics and electric engineering1,2,3,4,5,6,7,8. Applications of ferroelectric materials are primarily governed by their polarization response to external stimuli. Due to the nature of domains, ferroelectrics exhibit hysteresis phenomena with respect to an external electric field. Classic ferroelectrics have a single P–E hysteresis loop, which represents field-controlled transitions between two equivalent ferroelectric states with different polarization directions9. Switchable polarizations under an electric field allow ferroelectrics to be used in memory and logic devices10. In antiferroelectric compounds, two opposite polarizations arrange into two crystalline sub lattices, and the polarization vs. the electric field possesses the feature of a double P–E hysteresis loop, corresponding to the field-induced transition between the antiferroelectric and ferroelectric states11. Recently, this specific double P–E hysteresis loop has received attention due to its advantage for energy storage applications11,12,13,14. A double P–E hysteresis loop can also be observed at temperatures slightly above the Curie temperature of the first-order ferroelectric transition, indicating the electric field-induced paraelectric-ferroelectric phase transition15,16. However, in the development of ferroelectric materials, a type of “pinched” P–E hysteresis loop with a constrained remanent polarization (Pr) value has been observed in various perovskite materials, e.g., Pb(Zr,Ti)O3 solid solutions17,18,19,20,21, BiFeO3-based ceramics22,23,24, and (Bi0.5Na0.5)TiO3-based ceramics25,26,27. The main feature of the pinched P–E hysteresis loop is that the polarization, Pr, for a zero electric field is small but finite, unlike ferroelectrics (large Pr) and antiferroelectrics (zero Pr)9. Generally, the existence of pinched P–E hysteresis loops is attributed to strong domain wall pinning due to the diffusion of charged defects17,18,19,20,21,22,25. However, pinched P–E hysteresis loops can also be observed in defect-free ferroelectric materials, such as BiFeO3-based ceramics23,24 and (Bi0.5Na0.5)TiO3-based ceramics26. In some cases of BiFeO3-based ceramics, the observed pinched P–E hysteresis loops are “simply” interpreted as the double P–E hysteresis loops of antiferroelectrics, and the concomitant enhancement in the piezoelectric response is attributed to an electric-field-induced transformation from a paraelectric orthorhombic phase to a polar rhombohedral phase23. According to simulations by Xu et al.24, the pinched P–E hysteresis loops in defect-free ferroelectric materials are a result of intermediate modulated phases with an inhomogeneous dipolar pattern, which leads to the coexistence of both ferroelectric and antiferroelectric orders. Liu et al.27 reported the observation of a fine-scale intergrown microstructural phase (IGMS) within the R3c rhombohedral average structure matrix of (Bi0.5Na0.5)TiO3, and the IGMS regions form local, isolated, polar nanoregions, resulting in the high piezoelectric response and pinched P–E hysteresis loops observed in (Bi0.5Na0.5)TiO3. The pinched P–E hysteresis loops in defect-free ferroelectrics are often linked to a high piezoelectric response, but the mechanisms of these phenomena are diverse. Therefore, searching for pinched P–E hysteresis loops in more ferroelectric materials and revealing their mechanisms are of high scientific interest and importance
Pb-free ferroelectric materials have attracted increasing scientific and commercial interests due to serious environmental concerns. The structural flexibility of tungsten bronze oxides offers more opportunities for exploiting new Pb-free ferroelectric materials. The tetragonal tungsten bronze structure is composed of ten distorted octahedral sharing corners in such a way that three different interstices (2 tetragonal A1, 4 pentagonal A2, and 4 triangle C) are available for cations in the general formula (A1)2(A2)4(C)4(B1)2(B2)8O3028. In recent years, a number of Pb-free ferroelectrics with tetragonal tungsten bronze structures have been determined29,30,31,32,33,34,35,36,37,38,39,40,41,42,43. For M4R2Ti4Nb6O30 and M5RTi3Nb7O30 (M = Ba, Sr; R = rare earth), their phase transition nature and ferroelectric properties strongly depend on the cation occupation and the difference in the radius between the A2 and A1 cations29,30. M4R2Ti4Nb6O30 (M = Ba, Sr; R = Nd3+, Sm3+, Eu3+) tends to exhibit normal ferroelectric phase transitions due to its ordered structure. M2+occupies the pentagonal A2 site, and R3+ is in the tetragonal A1 sites31,32,33,34,35,36,37,38. For compositions with larger R cations, a relaxor nature is observed in Ba4Bi2Ti4Nb6O30 and Ba4La2Ti4Nb6O3032,33. For M5RTi3Nb7O30 (M = Ba, Sr; R = rare earth), relaxor ferroelectric behavior is generally observed, and it is ascribed to the cross distribution of M2+ and R3+ cations at A1 (tetragonal) sites39,40. A detailed structural study indicated that the relaxor nature is always associated with incommensurate superlattice modulation. The decrease in the R cation size increases the driving force for commensurate superlattice modulation, which dominates the normal ferroelectric nature29,30,31,32.
Here, we report the first observation of pinched P–E hysteresis loops in two new lead-free ferroelectrics with a filled tungsten bronze structure, Ba4Sm2Ti4Nb6O30 and Ba4Eu2Ti4Nb6O30, together with the analogue Ba4Nd2Ti4Nb6O30 (ferroelectric with single hysteresis loop) for comparison. The first-order ferroelectric phase transitions were confirmed by a thermal analysis and dielectric/ferroelectric characterization of all the compositions, and the ferroelectric domain structures were studied using piezoresponse force microscopy (PFM). The second harmonic generation (SHG) study reveals an on centrosymmetric structure below the Curie temperature (Tc) for all the compositions. O2-atmosphere annealing did not change the shape of the P–E hysteresis loops for all the compositions. Therefore, oxygen vacancies (the main defects that can occur during the formation of oxide ceramics) have no significant effect on the mechanism of the pinched P–E hysteresis loops. To understand the origin of the pinched P–E hysteresis loops, in situ selected area electronic diffraction (SAED) was performed, and the coexistence of commensurate modulation (polar) and incommensurate modulation (non-polar) during the ferroelectric transition and within the ferroelectric phase far below the transition temperature were detected in Ba4Sm2Ti4Nb6O30 and Ba4Eu2Ti4Nb6O30 but not Ba4Nd2Ti4Nb6O30. The pinched P–E hysteresis loop is a consequence of the electric-field-induced transition between a non-polar incommensurately modulated structure and a polar commensurately modulated phase.
Materials and methods
Materials preparation
Ba4R2Ti4Nb6O30 (R = Nd, Sm, Eu) ceramics were prepared from reagent-grade BaCO3(99.93%, Sinopharm Chemical Reagent Co., Shanghai, China), Nd2O3 (99.5%, Sinopharm Chemical Reagent Co., Shanghai, China.), Sm2O3 (99.5%, Sinopharm Chemical Reagent Co., Shanghai, China), Eu2O3 (99.5%, Sinopharm Chemical Reagent Co., Shanghai, China.), TiO2 (99.9%, Sinopharm Chemical Reagent Co., Shanghai, China) and Nb2O5 (99.99%, Sinopharm Chemical Reagent Co., Shanghai, China) raw powders by a standard solid-state reaction and sintering process. The raw powders were mixed and ball-milled in a polyethylene jar with ZrO2 media in alcohol for 24 h. The mixtures were calcined in a high-purity alumina crucible at 1500 K for 3 h. After the second grinding, the powder achieved a homogeneous granulometric distribution. Organic binders were added (10 wt% polyvinyl alcohol), and the reground powders were pressed into cylindrical compacts 12 mm in diameter and 1–2 mm thick under a pressure of approximately 98 MPa. Dense ceramics with a relative density above 96% were obtained by sintering at 1650 K for 3 h for all the compositions.
Structure and microstructure evaluations
The crystal structure was identified by powder X-ray diffraction (XRD) analysis with Cu Kα radiation (D/max 3B, Rigaku Co., Tokyo, Japan) at room temperature. The XRD analysis indicated a single phase for Ba4R2Ti4Nb6O30 (R = Sm, Eu), and a very minor second phase of Ba6Ti7Nb9O42 (5.03 wt%) was observed in Ba4Nd2Ti4Nb6O30. Piezoelectric force microscopic (PFM) images were obtained at room temperature by an atomic force microscope (Innova Microscopic, Veeco Instrument Inc., Plainview, NY, USA). The ceramic pellets were ground to a size below 0.1 mm. After surface polishing, the samples were thermally etched at 1523 K for 15 min. The bright/dark-field (BF/DF) images and the selected area electron diffraction (SAED) patterns were obtained by transmission electron microscopy (TEM, FEI Tecnai F30) operated at 300 KV and equipped with an EDAX energy dispersive spectrometer (EDS) and a Gatan image filter (GIF). The in situ TEM measurement was conducted between room temperature and 1073 K using a heating/cooling sample holder. The SAED patterns were taken when the temperature was stable at the setting temperature. The TEM equipment could not control the heating/cooling rate. The specimens for the TEM observation were prepared as follows. The EDM cutting disks were 3 mm in diameter and polished to a thickness of approximately 60–80 μm.Then, the central portions of these disks were mechanically dimpled to be approximately 10 μm thick. Finally, these specimens were precision Ar ion milled to be transparent for the TEM observation.
Second harmonic generation (SHG)
The SHG analysis was performed for the present ceramics in the temperature range from 350 to 625 K, and the heating and cooling rate was 2 K/min. The light source was a Q-switched Nd-YAG laser (7 ns pulses, 20 Hz, λ = 1064 nm). The filtered second harmonic signal behind the sample was detected by a photomultiplier and boxcar average.
Dielectric and ferroelectric characterization
The dielectric characteristics were measured with a broadband dielectric spectrometer (Turnkey Concept 50; Novocontrol Technologies, Hundsangen, Germany) over a broad temperature range (133–623 K) and frequency (10 Hz–1 MHz) range with a heating and cooling rate of 2 K/min. The thermal analysis was performed using a differential scanning calorimetry (DSC) (204F1, Netzsch, Phoenix, Arizona, USA) at a heating rate of 20 K/min in Ar. The polarization-field (P–E) hysteresis loops were evaluated at different temperatures by a Precision Materials Analyzer (RT Premier II, Radient Technologies, Inc., Albuquerque, NM, USA). The samples were immersed in silicon oil to protect the samples from breakdown due to edge discharge.
Results and discussion
The frequency dependence of the dielectric constant over a broad temperature range is shown in Fig. 1a–c. For all the compositions, the dielectric constant increases to a frequency independent maximum, indicating the ferroelectric transitions at Tc (the Curie temperature) upon heating, i.e.,~420 K for Ba4Nd2Ti4Nb6O30, ~560 K for Ba4Sm2Ti4Nb6O30, and ~590 K for Ba4Eu2Ti4Nb6O30. Meanwhile, the dielectric constant vs. temperature curves follow the Curie-Weiss law above Tc (Supplementary Figure S1). In the equation ε′ = C/(T−T0), C is the Curie constant and T0 is the Curie-Weiss temperature. A positive T0 (100.1 K) is indicated in Ba4Nd2Ti4Nb6O30, while negative T0 (−522 and −318 K) values are obtained for Ba4Sm2Ti4Nb6O30 and Ba4Eu2Ti4Nb6O30, respectively.The low temperature dielectric dispersions shown for Ba4Nd2Ti4Nb6O30 below 400 K have been reported before and attributed to the domain wall motion and structure fluctuations associated with the coupling between the polarization in the ab plane and the c axis displacement as well as the remaining random field effects32,44. The insets in Fig. 1a–c show the dielectric constant peaks tested in a heating and cooling cycle at a rate of 2 K/min, and hysteresis is observed at 31 K for Ba4Nd2Ti4Nb6O30, 48.1 K for Ba4Sm2Ti4Nb6O30, and 37.2 K for Ba4Eu2Ti4Nb6O30. The observed thermal hysteresis suggests a first-order phase transition. In the present ceramics, the tetragonal A1 sites are fully occupied by small R3+ cations, which is thought to be an important cation configuration for normal ferroelectrics29. Figure 1d–f shows the DSC curves measured for both the heating and cooling processes, and endothermic and exothermic peaks with obvious thermal hysteresis are observed for all compositions, confirming the first-order transition nature. Slightly larger hysteresis values, 37.7 K for Ba4Nd2Ti4Nb6O30, 73.5 K for Ba4Sm2Ti4Nb6O30, and 59.6 K for Ba4Eu2Ti4Nb6O30, are detected by the DSC measurement compared with those obtained from the dielectric constant curves due to the faster heating and cooling rate (20 K/min) during the DSC measurement.
a–c Temperature dependence of the dielectric constant at different frequencies: a R = Nd; b R = Sm; c R = Eu. The insets show the dielectric constant vs. temperature curves for heating and cooling cycles at 1 kHz. d–f Results of the DSC heating and cooling cycles for d Ba4Nd2Ti4Nb6O30; e Ba4Sm2Ti4Nb6O30; f Ba4Eu2Ti4Nb6O30
Figure 2a–c shows the P–E hysteresis loops with the current-electric field (J–E) curves for Ba4R2Ti4Nb6O30 (R = Nd, Sm, Eu) under different conditions. For Ba4Nd2Ti4Nb6O30 (see Fig. 2a), a linear P–E dependence is observed at 473 K (above Tc), corresponding to the paraelectric phase, and a saturated P–E hysteresis loop is observed at 293 K with a pair of J–E peaks, suggesting a classic ferroelectric nature. Upon cooling down to 193 K, the P–E hysteresis loop shrinks, while the saturated P–E hysteresis loop recovers under higher electric fields at the same temperature (see Fig. 2d). That is, the double potential wells in the free energy vs. electric field curve become deeper with the decreasing temperature, leading to the increased coercive field. Therefore, a higher field is occasionally required to switch the ferroelectric domains at lower temperatures. In Ba4Sm2Ti4Nb6O30 and Ba4Eu2Ti4Nb6O30, the situation is apparently different from that of Ba4Nd2Ti4Nb6O30. At 473 K (below the TC), obvious pinched P–E loops are observed with two pairs of J–E peaks. For Ba4Sm2Ti4Nb6O30(Fig. 2b), the polarization in a zero electric field (P0) increases from near zero (0.06 μC/cm2) to 0.55 μC/cm2 as the temperature decreases from 473 to 293 K. Meanwhile, the maximum polarization (Pm) decreases from 4.0 to 1.7 μC/cm2. When the applied electric field increases (Fig. 2e), increased P0 and Pm values are obtained, reflecting a similar increased polarization switching potential with the decreasing temperature, which is similar to the situation in Ba4Nd2Ti4Nb6O30. Similar behaviors are determined for Ba4Eu2Ti4Nb6O30 and shown in Fig. 2c,f. The synchronous increase in P0 and Pm at low temperatures causes the P–E loops to be less pinched and closer to the saturated loop, suggesting that the pinched P–E hysteresis loops become less stable and the ferroelectric phase gradually becomes stable as the temperature decreases further below TC.
For ferroelectrics with a first-order phase transition, paraelectric and ferroelectric phases coexist in the temperature range near Tc and double P–E hysteresis loops are observed, as reported for BaTiO315. Nevertheless, in the present tungsten bronzes, we discovered double P–E loops below the ferroelectric transition temperature. Double P–E hysteresis loops can arise from the pinning of ferroelectric domain walls by structural defects21. For example, in aged and lower valence-substituted lead zirconate titanate (PZT), double P–E hysteresis loops have been observed, and the polarization switching is strongly dependent on the thermal history21. However, in Ba4R2Ti4Nb6O30 (R = Sm, Eu), no volatile elements (like Pb, Bi, K,...) exists, and according to our XRD structure refinement, the Biso values for all the cations in Ba4R2Ti4Nb6O30 (R = Sm, Eu) can be scaled to a low level (Supplementary Table II). This indicates that the cation occupation follows the stoichiometry, and no cationic defects exist in the present materials. If there is a cation deficiency in the structure, a much higher Biso value will be obtained for the corresponding cation site. Therefore, cationic defects are unlikely to contribute to the polarization switching in Ba4R2Ti4Nb6O30 (R = Sm, Eu). As shown in the supplementary Figure S2, pinched P–E hysteresis loops still exist in Ba4R2Ti4Nb6O30 (R = Sm, Eu) after annealing in an O2 atmosphere, and thus, the influence of the oxygen vacancies can be neglected.
Carl and Hädtl17 studied the defect-induced pinching of P–E loops in doped PZT and explained it was due to an internal bias field Ei(t) caused by defects. According to their results, this field increases with doping, but the hysteresis-loop distortion disappears after repeated cycling. This so-called “hysteresis relaxation” obeys a time law in the form Ei(t) ∝ exp(−t/τ) and is both a field activated and thermally activated process17. In our case, the pinched loops open at lower temperatures, which excludes a thermally stimulated process.
The surface topography and room-temperature domain structure were detected by piezoelectric force microscopy (PFM). In Fig. 3a–c, the irregular grain size (approximately several micrometers) can be observed in all compositions. For one large Ba4Nd2Ti4Nb6O30 grain of ~4 μm, the dark and bright stripes contrast with the width of approximately 50 nm, indicating a ferroelectric domain structure with 180° domain walls (see Fig. 3d). For Ba4Sm2Ti4Nb6O30 and Ba4Eu2Ti4Nb6O30, dark and bright contrast patterns can also be detected in some grains, as shown in Fig. 3e, f. Since antiferroelectric domains should not have a piezo-response, these patterns correspond to the ferroelectric domain structure and confirm the ferroelectric nature of Ba4R2Ti4Nb6O30 (R = Sm, Eu). In Fig. 3e, f, the distribution of the ferroelectric domain size is not uniform. In some areas, the domain stripes are hundreds of nanometers in width, while in other areas, the widths of the domain stripes are less than 20 nm. Moreover, some broken domains with fragmented pieces could be observed, indicating destruction of the ferroelectric domain structure.
The general room-temperature crystal structure for Ba4R2Ti4Nb6O30 (R = Nd, Sm, Eu) is a tetragonal tungsten bronze structure with the space group P4bm or P4/mbm, as determined by the Rietveld refinement of the powder X-ray diffraction data using the FULLPROF program. For tetragonal tungsten bronzes, it is not possible to distinguish between the P4bm and P4/mbm space groups using XRD data since they have nearly the same best fit. However, considering their ferroelectric nature, the non-centrosymmetric P4bm space group is chosen for the structure refinement of Ba4R2Ti4Nb6O30 (R = Nd, Sm, Eu) below TC. The experimental data, calculated data, and difference are shown in supplementary Figure S3, and the refined structural parameters are summarized in Tables SI–II.
To confirm the structural symmetry of the present compounds, we studied the temperature dependence of the SHG on the reflection geometry. The results are shown in Fig. 4. The intensities of the SHG signal plotted in arbitrary units are not the same for the different samples. In fact, the differences among them are large. At room temperature, the SHG signal from Ba4Sm2Ti4Nb6O30 is several times higher than that from Ba4Nd2Ti4Nb6O30, and the SHG signal from Ba4Eu2Ti4Nb6O30 is another order of magnitude larger. The results suggest that Ba4Nd2Ti4Nb6O30 and Ba4R2Ti4Nb6O30 (R = Sm, Eu) are polar (probably ferroelectric, not antiferroelectric) below the transition temperature with a considerably large nonlinearity. A very high SHG signal in Ba4Eu2Ti4Nb6O30 shows either because of large nonlinear optic coefficients or due to the possibility of phase matching in this material.
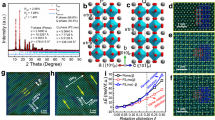
In situ TEM was conducted over a wide temperature range from room temperature up to 1073 K. The results are summarized in Fig. 5 and Supplementary Figures S4-S6. In Ba4Sm2Ti4Nb6O30, obvious ferroelectric domain structures can be observed at room temperature (Fig. 5a). The domains predominantly feature spike-like shapes that are parallel to the polar axis (c axis of the tetragonal tungsten bronze structure) according to the SAED patterns (Fig. 5c), indicating ferroelectric 180° domains. However, the size of the domains ranges from approximately 10 nm to more than 200 nm, and they are unevenly distributed, which agrees with the PFM observations. As shown in Fig. 5b–d, three types of SAED patterns are observed for Ba4Sm2Ti4Nb6O30 along the [110] zone axis at room temperature. The first SAED pattern exhibits fundamental Bragg reflections of a Tetragonal Tungsten Bronze (TTB) phase without extra reflections (Fig. 5b).The second pattern shows satellite reflections related to the commensurate superlattice modulations (Fig. 5c), while the third pattern shows the coexistence of both commensurate and incommensurate satellite reflections, indicating the intermediate modulated phase (Fig. 5d). The commensurate or incommensurate superlattice reflections are located on the (00k) [k = ±1/2, ±3/2, …] planes. The wave vector for the commensurate superlattice modulation can be expressed as q = 1/2a0* + 1/2b0* + l/2c0*, while that for the incommensurate superlattice modulation can be expressed as q = (1/4 + δ)a0*+(1/4 + δ)b0* + l/2c0*, where a0*, b0*, and c0*are the vectors in reciprocal space33,34,35, and δ is the measure of the deviation from commensurate periodicity that is defined as δ = (x − y)/(x + y), where x and y are the distance of the neighboring incommensurate superlattice spots45. The schematic diffraction patterns along the [110]TTB direction are shown in Fig. 5e.
a TEM image of a single grain with obvious 180° ferroelectric domains at room temperature. b–d Three types of SAED patterns observed along the [110] zone axis from a single grain at room temperature; b the basic tetragonal tungsten bronze structure with the space group P4bm without extra satellite reflections; c patterns with commensurate reflections; d patterns with coexisting commensurate and incommensurate reflections. The commensurate or incommensurate reflections are indicated by arrows in (c) and (d). e Schematic diffraction patterns in a [110] projection. Shaded circles are the satellite reflections of the commensurate modulation, and the open circles are the reflections of the incommensurate modulation. f–h and i–k show the variations of patterns (b) and (c), respectively, during the phase transition (Tc ~ 563 K) at (f) and (i) 523 K, (g) and (j) 553 K, and (h) and (k) 573 K
Different SAED patterns undergo different variations with temperature. In some areas with the first type of SAED patterns (Fig. 5b), as shown in Fig. 5f–h, incommensurate satellite reflections gradually arise with the increasing temperature and are obvious at 573 K, i.e., the temperature just above the phase transition temperature (Tc(R = Sm) ~ 560 K on heating). The incommensurate superlattice reflections exist up to the highest temperature we measured (~1073 K). After cooling down to room temperature, the SAED patterns for some areas return to their initial state, i.e., the fundamental Bragg reflections of the TTB phase without extra reflections. However, in some other areas (see Supplementary Figure S4), commensurate superlattice reflections appear upon heating up to approximately 573 K, and then, gradually change into incommensurate superlattice reflections between 573 and 673 K. Upon cooling, the incommensurate to commensurate superlattice modulation transition occurs between 573 and 473 K, and the commensurate superlattice reflections exist until room temperature.
For the second type of SAED pattern (Fig. 5c), as shown in Fig. 5i–k, the commensurate superlattice reflections are stable from room temperature up to 523 K. Upon heating, the incommensurate superlattice reflections appear from ~533 K and coexist with the commensurate superlattice reflections. With further increasing temperature, the commensurate superlattice reflections gradually weakened and finally disappear at ~573 K, but the intensity of the incommensurate superlattice reflections increases. In the temperature range of 533–573 K, an intermediate phase appears on heating and is the coexistence of the commensurate and incommensurate modulations. After cooling down to room temperature, the SAED patterns for some areas return to the initial state with only commensurate superlattice reflections, but for some other areas, the coexistence of the incommensurate and commensurate modulations is observed down to room temperature (Fig. 5d). Similar SAED patterns and variation features are observed in Ba4Eu2Ti4Nb6O30 (Supplementary Figure S5). In Ba4Nd2Ti4Nb6O30, commensurate and incommensurate modulations do not coexist, and only one type of SAED pattern is observed with a transition from commensurate to incommensurate reflections at approximately Tc ~ 420 K (see Supplementary Figure S6), which is consistent with the results reported by Levin et al.31. Another phenomena is that the incommensurate modulation reflections are stable until very high temperatures (~1073 K) for all the Sm and Eu samples. This is different from that in Ba4La2Ti4Nb6O30 and Ba4Nd2Ti4Nb6O30 in which the incommensurate modulations disappear at higher temperatures and manifest as an incommensurate→P4/mbm transition29,30,31. Levin et al.31 combined the room-temperature ferroelectric response and SAED patterns and suggested an orthorhombic Ima2 unit cell with the lattice parameters \({\sqrt 2 }a_{{\rm{TTB}}} \times {\sqrt 2 }b_{{\rm{TTB}}} \times { 2 }c_{{\rm{TTB}}}\) and antiphase rotations of the octahedra along the c axis for compositions with commensurate superlattice reflections and the Ama2 unit cell with the lattice parameters \(2{\sqrt 2 }a_{{\rm{TTB}}} \times {\sqrt 2 }b_{{\rm{TTB}}} \times 2c_{{\rm{TTB}}}\) and no antiphase tilting about the c axis for the incommensurate phase with δ = 0. Even if the incommensurate structure is nonpolar, SHG shows that a polar structure exists up to Tc. This is further evidence for the coexistence of both commensurate (i.e., polar) and incommensurate (i.e., nonpolar) phases up to Tc and that only their concentrations change with the temperature.
The ferroelectric or relaxor nature of the phase transition in filled tungsten bronzes is highly connected to the commensurate or incommensurate superlattice modulations. Meanwhile, the structure modulation type in the tungsten bronze Ba4R2Ti4Nb6O30 (R = rare earth cations) is generally determined by the radius difference between the Ba2+ and R3+ cations29,30,31. When larger cations such as La3+ and Bi3+are in the smaller A1 sites, a relaxor phase transition is observed in Ba4La2Ti4Nb6O30 and Ba4Bi2Ti4Nb6O30, and incommensurate superlattice modulations exist from high temperatures down to very low temperatures31,32. For small cations (R = Nd), a first-order phase transition is indicated in ferroelectric Ba4Nd2Ti4Nb6O30, and incommensurate superlattice modulations exist at T > Tc and an abrupt incommensurate to commensurate transition occurs at Tc31,32. That is, the onset of the commensurate superlattice modulation dominates the long-range polar order in filled tungsten bronzes. In Ba5NdTi3Nb7O30 with a diffuse ferroelectric transition, a low-temperature commensurate modulation changes to a high-temperature incommensurate modulation in a gradual region40, reflecting the competition between the two structural modulations, which is related to the complex configuration and random occupancy of the A sites. According to this logic, increasing the radius difference between the Ba2+ and R3+ cations should result in a more stable commensurate modulation and stronger ferroelectricity with a higher ferroelectric transition temperature. Therefore, Ba4R2Ti4Nb6O30 (R = Sm, Eu) exhibits a higher Tc than Ba4Nd2Ti4Nb6O30, but the appearance of an intermediate modulated phase weakens the ferroelectricity and dominates the pinched hysteresis loops.
The questions are why Ba4Nd2Ti4Nb6O30, which also exhibits a large thermal hysteresis, does not show a pinched hysteresis loop and why the intermediate modulated phase appears in Ba4R2Ti4Nb6O30 (R = Sm, Eu) but not in Ba4Nd2Ti4Nb6O30. We attempt to understand this phenomenon by considering the structure stabilities. Compared with Ba4Nd2Ti4Nb6O30, the smaller Sm and Eu cations in Ba4Sm2Ti4Nb6O30 and Ba4Eu2Ti4Nb6O30 decrease the tolerance factor of the A1 site (occupied by lanthanide cations) and induce larger structural distortion, resulting in a less stable tungsten bronze structure. In contrast, the appearance of incommensurate superlattice modulations in tungsten bronzes can reduce the structural energy. Therefore, the intermediate modulated phase with coexisting polar commensurate modulations and non-polar incommensurate modulations appears in Ba4Sm2Ti4Nb6O30 and Ba4Eu2Ti4Nb6O30 below Tc to reduce the structural energy and stabilize the tungsten bronze structure. Under an applied electric field, the non-polar incommensurate modulations can change into polar commensurate ones, and the field-induced ferroelectric transition can result in a double hysteresis loop. Meanwhile, the polar commensurate modulation in the intermediate phase provides a small finite polarization in a small electric field for Ba4Sm2Ti4Nb6O30 and Ba4Eu2Ti4Nb6O30. Ba4Nd2Ti4Nb6O30 does not exhibit the incommensurately modulated (i.e., nonpolar) phase below the Tc, and its ferroelectric loops are not pinched.
Comparing our results with the pinched P–E hysteresis loops reported for BiFeO3-based and (Bi0.5Na0.5)TiO3-based systems reveals some mutual features. The pinched hysteresis loops are intrinsic in nature and can be attributed to the intermediate modulated phases involving oxygen octahedral tilting. In BiFeO3-based perovskites, the intermediate modulated phases are composed of ferroelectric and antiferroelectric phases, while in tungsten bronze Ba4R2Ti4Nb6O30 (R = Sm, Eu), the intermediate modulated phases are formed by the polar commensurate and non-polar incommensurate modulations.
The relationship between the pinched hysteresis loops and the coexistence of the two structural modulations can also be understood by comparing them with the field-induced phase transition occurring in the first-order ferroelectric transition at T > Tc; i.e., where the double P–E hysteresis loops can be detected, and the existence of metastable ferroelectric states with long lifetimes are known to create pinched hysteresis loops1. Actually, the intrinsic origin of the double P–E hysteresis loops in first-order ferroelectric transitions is thermal hysteresis, which means metastable states exist during the phase transition. Normally, the thermal hysteresis of first-order ferroelectric transition is very small (several Kelvin), and T0 is also very close to Tc. This is why, in real cases (such as BaTiO3), the double P–E hysteresis loops can only be observed in a very narrow temperature region. Nevertheless, in the tungsten bronze Ba4R2Ti4Nb6O30 (R = Sm, Eu), a thermal hysteresis over tens of Kelvin is observed during the ferroelectric transition, and negative T0 values are obtained. Both factors provide good conditions for a wide temperature range of the metastable phases. Moreover, the ground states in the low electric field are paraelectric phases with zero polarization for the double P–E hysteresis loops above the Tc, while the ground states in a low electric field have a finite polarization in tungsten bronze Ba4R2Ti4Nb6O30 (R = Sm, Eu). Therefore, instead of a double P–E hysteresis loop, the pinched loops are observed.
The opening of pinched P–E hysteresis loops in high fields can be explained by the electric-field-induced transition of non-polar incommensurately modulated phases in ceramics to commensurately modulated phases. This type of phase transition is well known in other incommensurate crystals, such as thiourea46, K2SeO4, and (NH)4BeF447, but in these materials, the incommensurate structure exists only in very narrow temperature regions, and moreover, this phase transition was never used for the explanation of the pinched hysteresis loops.
Conclusion
In summary, we reported pinched P–E hysteresis loops below the first-order ferroelectric transition temperature in the tungsten bronzes Ba4Sm2Ti4Nb6O30 and Ba4Eu2Ti4Nb6O30 and revealed the intrinsic mechanisms of the pinched P–E hysteresis loops. A metastable intermediate modulated phase with coexisting polar commensurate and non-polar incommensurate modulations appears in both Ba4Sm2Ti4Nb6O30 and Ba4Eu2Ti4Nb6O30 below and during the ferroelectric transition to reduce the structural energy due to the smaller Sm and Eu cations. Consequently, the field-induced transition from non-polar incommensurate modulation to polar commensurate modulation results in the double P–E hysteresis loop. The small remanent polarization in the pinched hysteresis loop is attributed to the phase coexistence. The large thermal hysteresis of the ferroelectric transition in Ba4Sm2Ti4Nb6O30 and Ba4Eu2Ti4Nb6O30 provides good conditions for the metastable intermediate modulated phase to have large lifetimes. Moreover, the relatively higher structural energy is also an important factor for the appearance of incommensurate modulation. Since the pinched hysteresis loops are similar to antiferroelectric loops, our discovery opens up a new avenue for the development of Pb-free ferroelectric materials for energy storage.
References
Lines, M. E. & Glass, A. M. Principle and applications of ferroelectrics and related materials. (Clarendon, Oxford, 1977).
Haertling, G. H. Ferroelectric ceramics: history and technology. J. Am. Ceram. Soc. 82, 797–818 (1999).
Cross, L. E. Relaxor ferroelectrics. Ferroelectrics 76, 241–267 (1987).
Saito, Y. et al. Lead-free piezoceramics. Nature 432, 84–87 (2004).
Liu, W. F. & Ren, X. B. Large Piezoelectric effect in Pb-free ceramics. Phys. Rev. Lett. 103, 257602 (2009).
Kutnjak, Z., Petzelt, J. & Blinc, R. The giant electromechanical response in ferroelectric relaxors as a critical phenomenon. Nature 44, 956–959 (2006).
Scott, J. F. Room-temperature multiferroic magnetoelectrics. NPG Asia Mater. 5, e72 (2013).
Oh, Y. S., Luo, X., Huang, F.-T., Wang, Y. & Cheong, S.-W. Experimental demonstration of hybrid improper ferroelectricity and the presence of abundant charged walls in (Ca,Sr)3Ti2O7 crystals. Nat. Mater. 14, 407–413 (2015).
Jin, L., Li, F. & Zhang, S. Decoding the fingerprint of ferroelectric loops: comprehension of the material properties and structures. J. Am. Ceram. Soc. 97, 1–27 (2014).
Scott, J. F. Applications of modern ferroelectrics. Science 315, 954–959 (2007).
Hao, X., Zhai, J., Kong, L. B. & Xu, Z. A comprehensive review on the progress of lead zirconate-based antiferroelectric materials. Prog. Mater. Sci. 63, 1–57 (2014).
Tagantsev, A. K. et al. The origin of antiferroelectricity in PbZrO3. Nat. Commun. 4, 2229 (2013).
Liu, C. et al. Energy storage and polarization switching kinetics of (001)-oriented Pb0.97La0.02(Zr0.95Ti0.05)O3 antiferroelectric thick films. Appl. Phys. Lett. 108, 112903 (2016).
Zhao, L., Liu, Q., Gao, J., Zhang, S. & Li, J. F. Lead-free antiferroelectric silver niobate tantalate with high energy storage performance. Adv. Mater. 29, 1701824 (2017).
Merz, W. J. Double Hysteresis loop of BaTiO3 at the Curie point. Phys. Rev. 91, 513–517 (1953).
Srivastava, N. & Weng, G. J. A theory of double hysteresis for ferroelectric crystals. J. Appl. Phys. 99, 054103 (2006).
Carl, K. & Hardtl, K. Electrical aftereffects in Pb(Ti,Zr)O3ceramics. Ferroelectrics 17, 473–486 (1978).
Rojac, T., Drnovsek, S., Bencan, A., Malic, B. & Damjanovic, D. Role of charged defects on the electrical and electromechanical properties of rhombohedral Pb(Zr,Ti)O3 with oxygen octahedra tilts. Phys. Rev. B 93, 014102 (2016).
Robert, G., Damjanovic, D. & Setter, N. Preisach modeling of ferroelectric pinched loops. Appl. Phys. Lett. 77, 4413–4414 (2000).
Granzow, T., Suvaci, E., Kungl, H. & Hoffmann, M. J. Deaging of heat-treated iron-doped lead zirconate titanate ceramics. Appl. Phys. Lett. 89, 262908 (2006).
Tan, Q., Li, J. X. & Viehland, D. Role of lower valent substituent-oxygen vacancy complexes in polarization pining in potassium-modified lead zirconate titanate. Appl. Phys. Lett. 75, 418 (1999).
Rojac, T., Kosec, M., Budic, B., Setter, N. & Damjanovic, D. Strong ferroelectric domain-wall pinning in BiFeO3 ceramics. J. Appl. Phys. 108, 074107 (2010).
Kan, D. et al. Universal behavior and electric-field-induced structural transition in rare-earth-substituted BiFeO3. Adv. Fun. Mater. 20, 1108–1115 (2010).
Xu, B., Paillard, C., Dkhil, B. & Bellaiche, L. Pinched hysteresis loop in defect-free ferroelectric materials. Phys. Rev. B 94, 140101(R) (2016).
Cao, W. et al. Defect dipole induced large recoverable strain and high energy-storage density in lead free Na0.5Bi0.5TiO3-based systems. Appl. Phys. Lett. 108, 202902 (2016).
Kitanaka, Y. et al. Polarization twist in perovskite ferrielectrics. Sci. Rep. 6, 32216 (2016).
Liu, Y. et al. Response of intergrown microstructure to an electric field and its consequences in the lead-free piezoelectric bismuth sodium titanate. J. Solid State Chem. 187, 309–315 (2012).
Jamieson, P. B., Abrahams, S. C. & Bernstein, J. L. Ferroelectric tungsten bronze-type crystal structures. II. Barium sodium niobate Ba4+xNa2−2xNb10O30. J. Chem. Phys. 50, 4352–4363 (1969).
Zhu, X. L., Li, K. & Chen, X. M. Ferroelectric transition and low-temperature dielectric relaxations in filled tungsten bronzes. J. Am. Ceram. Soc. 97, 329–338 (2014).
Zhu, X. L. et al. A crystal-chemical framework for relaxor versus normal ferroelectric behavior in tetragonal tungsten bronzes. Chem. Mater. 27, 3250–3261 (2015).
Levin, I. et al. Coupling between octahedral tilting and ferroelectric order in tetragonal tungsten bronze-structured dielectrics. Appl. Phys. Lett. 89, 122908 (2006).
Stennett, M. C. et al. Dielectric and structural studies of Ba2 MTi2Nb3O15(BMTNO15, M = Bi3+, La3+, Nd3+, Sm3+, Gd3+…) tetragonal tungsten bronze-structured ceramics. J. Appl. Phys. 101, 104114 (2007).
Bovtun, V. et al. Relaxor-like behavior of lead-free Sr2LaTi2Nb3O15 ceramics with tetragonal tungsten bronze structure. J. Appl. Phys. 101, 054115 (2007).
Zhu, X. L. & Chen, X. M. Thermal hysteresis of ferroelectric transition in Sr4R2Ti4Nb6O30 (R=Sm and Eu) tetragonal tungsten bronzes. Appl. Phys. Lett. 96, 032901 (2010).
Zhu, X. L. & Chen, X. M. Ferroelectric properties and polarization dynamics in Ba4Sm2Ti4Ta6O30 tungsten bronze ceramics. Appl. Phys. Lett. 108, 152903 (2016).
Feng, W. B., Zhu, X. L., Liu, X. Q. & Chen, X. M. Crystal structure, ferroelectricity and polar order in Ba4R2Zr4Nb6O30 (R=La, Nd, Sm) tetragonal tungsten bronze new system. J. Mater. Chem. C 5, 4009–4016 (2017).
Michau, D., Simon, A. & Maglione, M. Lead-free relaxor thin films of tungsten bronze symmetry. J. Phys. D: Appl. Phys. 42, 075407 (2009).
Josse, M. et al. The Ba2LnFeNb4O15 ‘‘tetragonal tungsten bronze’’: towards RT composite multiferroics. Solid State Sci. 11, 1118–1123 (2009).
Zhu, X. L., Liu, X. Q. & Chen, X. M. Crystal structure and dielectric properties of Sr5RTi3Nb7O30 (R=La, Nd, Sm, and Eu) tungsten bronze ceramics. J. Am. Ceram. Soc. 94, 1829–1836 (2011).
Mao, M. M., Li, K., Zhu, X. L. & Chen, X. M. Incommensurate and commensurate modulations of Ba5RTi3Nb7O30 (R = La, Nd) tungsten bronzes and the ferroelectric domain structures. J. Appl. Phys. 117, 134108 (2015).
Rotaru, A., Arnold, D. C., Daoud-Aladine, A. & Morrison, F. D. Origin and stability of the dipolar response in a family of tetragonal tungsten bronze relaxors. Phys. Rev. B 83, 184302 (2011).
Gardner, J. et al. Relaxor-to-ferroelectric crossover and disruption of polar order in “empty” tetragonal tungsten bronzes. Chem. Mater. 28, 4616–4627 (2016).
Gardner, J. & Morrison, F. D. Manipulation of polar order in the “empty” tetragonal tungsten bronzes: Ba4-xSrxDy0.67Nb10O30, x = 0, 0.25, 0.5, 1, 2, 3. Appl. Phys. Lett. 109, 072901 (2016).
Zhu, X. L., Chen, X. M., Liu, X. Q. & Li, X. G. Ferroelectric phase transition and low-temperature structure fluctuations in Ba4Nd2Ti4Nb6O30 tungsten bronze ceramics. J. Appl. Phys. 105, 124110 (2009).
Bursill, L. A. & Lin, P. J. Incommensurate superstructures and phase-transition of strontium barium niobate (SBN). Acta Cryst. B. 43, 49–56 (1987).
Moudden, A. H., Svensson, E. C. & Shirane, G. Electric-field-induced commensurate phase in deuterated thiourea. Phys. Rev. Lett. 49, 557–560 (1982).
Hudák, O. Influence of external electric-field on incommensurate-commensurate phase-transition in K2SeO4 and (NH4)2BeF4 crystals .1. static properties. J. Phys. C: Solid State Phys. 16, 2641–2658 (1983).
Acknowledgements
This work was supported by the National Science Foundation of China under grant No. 51332006 (X.M.C.), the Ministry of Science and Technology of China under grant No. 2015CB654601 (X.M.C.), the Czech Science Foundation (Project No. 15-08389S), and the Czech Ministry of Education (Project No. LD15014).
Author information
Authors and Affiliations
Contributions
K.L. performed most of the experiments. X.L.Z. analyzed the data and co-directed the research work. X.Q.L. conducted the XRD analysis. X.M. conducted the TEM analysis with the help of M.S.F. J.K. performed the SHG analysis. S.K. supervised the SHG analysis and contributed greatly to the theoretical analysis. X.M.C. directed the research work. All authors contributed to the discussion of the results and preparation of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare that they have no conflict of interest.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Li, K., Zhu, X.L., Liu, X.Q. et al. Electric-field-induced phase transition and pinched P–E hysteresis loops in Pb-free ferroelectrics with a tungsten bronze structure. NPG Asia Mater 10, 71–81 (2018). https://doi.org/10.1038/s41427-018-0013-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41427-018-0013-x