Abstract
The development of microbial networks is central to ecosystem functioning and is the hallmark of complex natural systems. Characterizing network development over time and across environmental gradients is hindered by the millions of potential interactions among community members, limiting interpretations of network evolution. We developed a feature selection approach using data winnowing that identifies the most ecologically influential microorganisms within a network undergoing change. Using a combination of graph theory, leave-one-out analysis, and statistical inference, complex microbial communities are winnowed to identify the core organisms responding to external gradients or functionality, and then network development is evaluated against these externalities. In a plant invasion case study, the winnowed microbial network became more influential as the plant invasion progressed as a result of direct plant-microbe links rather than the expected indirect plant–soil–microbe links. This represents the first use of structural equation modeling to predict microbial network evolution, which requires identification of keystone taxa and quantification of the ecological processes underpinning community structure and function patterns.
Similar content being viewed by others
Introduction
Microorganisms profoundly influence human life and global biogeochemical cycles [1], yet the dynamics of how groups of microbes or, networks, develop across space, time, or experimental treatments are enigmatic due to complex interactions between community members [2, 3]. Though important studies exist (e.g., see refs. [4,5,6]), network analysis of dynamic communities is hindered because the number of samples in sequencing data are typically much smaller than the number of taxa in each sample (known as the “small n large p” problem) hindering the calculation of association measures and downstream analyses [7]. One solution is to remove rare species under the assumption that they add noise to multivariate analyses [8]. However, there is considerable evidence that some rare taxa can have important ecological roles in complex communities [9, 10], and hence removing rare taxa risks systemic misinterpretation of the data [11]. Data refinement must retain ecologically relevant taxa while reducing the total number of organisms to avoid eliminating key microbial taxa during data reduction.
Co-occurrence networks are fundamental tools for understanding microbial community pattern and process [5, 12]. Large metagenomic datasets generated from rapidly advancing sequencing technologies [13, 14] are amenable to co-occurrence network construction, which allows study of the microbial interactions imbedded in these datasets [4, 15]. Microbial network dynamics are driven by a plethora of interactions among their members, as well as by environmental and host factors, such as immunological processes in gut microbiota [16] or plant community dynamics [17]. Microbe–microbe relationships exert considerable influence over a range of host–microbe interactions—they can support health, promote disease, and/or dictate resilience and resistance [18, 19]. To evaluate holistic hypotheses about the interactions of highly complex, dynamically changing networks with hosts or environmental gradients requires the construction of testable hypothesis in a multivariate environment. To do so, it is required that one has a coherent network that can be linked to external drivers and functions.
To meet this challenge, we developed an iterative data winnowing process for inferring community development across gradients of extrinsic variables, which identifies the most influential microorganisms within a co-occurrence network, and the subsequent statistical processes to characterize how influential microorganism interact with experimental manipulations. The process draws on three distinct mathematical processes: (1) ranking the ecological importance of taxa across a range of centralities from graph theory to capture a range of biological interactions, and to mitigate against mathematical artifacts and overly restrictive definitions of importance; (2) permutational analysis of variance (PERMANOVA)-based sensitivity analysis to identify key taxa responding to the gradient stimulus; and (3) structural equation modeling to test hypothesized causal links between microbial networks and the external gradient of interest. We winnowed the soil microbial community of a natural grassland undergoing smooth brome (Bromus inermis Leyss) invasion and predicted microbial network evolution across an invasion gradient. We demonstrate that the data winnowing approach is broadly applicable over changes in environmental conditions and as such can link microbial network development to extrinsic factors or functions.
Keystone taxa in microbial communities
Microbial keystone taxa are defined as highly connected taxa (or nodes) that individually or in a subgraph (or module) exert a considerable influence on microbiome structure and functioning regardless of their abundance across space and time [20]. Network analysis is a means of inferring keystone taxa from microbial communities [4, 20]. Graph theory metrics like betweenness, degree, closeness, and eigenvector centrality capture different aspects of node importance and statistically identify keystone taxa in several studies [21, 22]. Degree centrality is the summed number of links per node, or the total number of shared connections with other taxa. Betweenness centrality is the number of shortest paths between all other taxa that pass through a focal taxon [23]. Taxa with high betweenness are those that share connections between modules that do not share many intra-module connections, representing a potential pathway for resource sharing between modules [24]. Closeness centrality represents the relative distance of a focal taxon to all other taxa in the network; identifying taxa that are close (based on some measure of association like r or maximal information coefficient) to many other taxa. Closeness is essentially a global centrality version of degree, as it incorporates distance information from all taxa in the network [23]. Eigenvector centrality measures the tendency for a focal taxon to share connections with other taxa that have connections with many other taxa. Taxa with a high eigenvector—well-connected taxa connected with other well-connected taxa—may be good indicators of subgraphs (or modularity) in co-occurrence networks [25]. Combinations of local and global centrality measures have been shown to collectively identify keystone taxa with 85% accuracy [5], and therefore a union of centrality measures is a more effective means of isolating keystone taxa than use of a single centrality measure [20].
Network prediction in model systems
Keystone taxa perform important ecological processes [22, 26, 27], but such network-based inferences need to be complemented with experimental evidence showing the impact of the keystone taxa on microbial structure and function. However, co-occurrence networks are based on the covariance of microbes across samples, thereby confounding typical methods of contrasting treatments to identify key drivers of network development [28]. Though recently developed methods assess if networks differ [28, 29], we are still unable to link how/why networks differ along extrinsic factors such as environmental gradients. Structural equation modeling (SEM), a multivariate statistical approach that tests putative causal relationships against experimental data [30, 31], has potential to address this shortcoming. SEM is theory oriented and capable of testing a network of causal hypotheses by allowing evaluation of simultaneous influences rather than individual (bivariate) causes [32, 33]. SEM has yielded powerful insights into microbial metabolites as drivers of soil organic carbon accumulation [34], pathogens and disease progression [35], and microbe–plant community dynamics [17]. Yet, to our knowledge, SEM has not been used to predict the evolution of microbial networks, which requires identification of keystone taxa/modules and quantification of the ecological processes underpinning spatial-temporal patterns in community structure and function [12].
To model causal hypotheses about microbial co-occurrence networks, we drew upon a well-characterized microbial dataset, consisting of archaeal, bacterial, and fungal co-occurrences in a smooth brome-invaded fescue grassland [17, 36, 37]. Smooth brome invasion lowers plant species diversity in grasslands [38] and increases nitrogen availability [36]. Together, this initiates a cascade of soil community changes including (1) suppression of dominant bacterial species allowing rare species to increase in abundance [37], and (2) increased bacterial diversity that leads to reduced fungal diversity [17]. Calculation of co-occurrence networks from soil samples collected along a gradient of smooth brome invasion allowed us to build upon a previously proposed causal conceptual framework [37] and explore the rules governing microbial network assembly as brome becomes more dominant.
Materials and methods
The dataset consisted of 16S ribosomal RNA (rRNA) gene analysis of bacterial and archaeal operational taxonomic units (OTUs), internal transcribed spacer (ITS) fungal OTUs [37], plant roots identified using the trnL intron [39], and environmental data that were collected from the soil A and B horizons in 60 plots in a natural grassland undergoing invasion by the forage grass smooth brome (Bromus inermis (Leyss.) [40] (see Piper et al. [37] for field collection protocols). Briefly, to ensure even sampling across the full range of the brome invasion (0, 40–50, 51–85, and >85%), each plot had 14–16 samples in each of four classes of smooth brome shoot abundance. Sampling locations were determined using the random point generator in ArcMap (ESRI, Redlands, CA, USA). Within each plot, we assessed plant species cover and gathered grass, forb, shrub, and litter biomass. Smooth brome biomass was collected separately from other grass species. From each soil sample we quantified pH, soil organic carbon, total soil nitrogen, and litter carbon/nitrogen ratio, among other environmental data [36].
Plant roots identified from DNA extracts of mixed-species root samples
Plant roots, especially in grasslands, can be challenging to study due to the difficulty of separating roots to species based on morphology. To overcome this challenge, we used the trnL intron to develop a reliable method for estimating root identity and abundance in grasslands [39, 41]. The details of this process are available in Lamb et al. [39].
Bacteria, archaea, and fungi from DNA extracts of soil samples
To identify and quantify composition of bacteria and archaea, and fungal composition, we used 16S rRNA and ITS gene sequencing and bioinformatics processing, respectively, to obtain OTU feature tables for each domain [17]. We sequenced bacteria on the Ion Torrent platform (Contango Strategies, Saskatoon, SK, Canada) using the universal 16S rRNA 515F/806R primer set that amplifies a 291-bp fragment near the bacterial v4 region [42]. Archaea were sequenced on the 454 FLX titanium platform (Roche, Branford, CT, USA) using A344F/A589R primers [43]. These archaea amplicon libraries were sequenced from the forward primer at Genome Quebec. Similarly, fungal and archaeal diversity were assessed via triplicate reactions using ITS1F and ITS4 primers [44, 45] for fungi.
The pipelines for both the 16S and ITS datasets were similar except for minor adjustments made to accommodate the differences in sequencing platform. Subsampling was required due to a varied read distribution; we subsampled to a number of reads that would provide analytical power but retained the most samples. Owing to this strategy, some samples were excluded from the analysis due to very low read numbers [37]. Taxonomic assignment of OTUs was achieved using a naive Bayesian classifier implemented in mothur against the Greengenes 2011 database [46,47,48]. We calculated community evenness using Evar [49] and species richness as the total number of OTUs in each sample. The majority of the pipeline was conducted using the mothur software package version 1.32.1 [47]. The details of this process are available in Mamet et al. [17] and Piper et al. [37].
Feature selection identifies keystone microbiota within invaded grasslands
We used an automated network co-occurrence approach to reduce the number of taxa included in our downstream analyses (Fig. 1). Here we leveraged the well-curated microbial metagenomic dataset [17, 37] described above on which to test our feature selection algorithm. We combined the OTU matrices (6747 bacteria, 1339 archaea, and 4014 fungi; N = 12,100 OTUs × 109 samples) into a single dataset to use as input for the first step of the winnowing pipeline. To assign an occurrence probability to absent species and reduce the influence of zeroes in the data, we add-one smoothed the data to shift some probabilities from observed to not observed OTUs.
Conceptual diagram of the general winnowing and network prediction algorithms for microbial taxa with example results using degree centrality. Abundance data were conditioned using Laplace (add-1) smoothed [65] to reduce the undue influence of absent or rare species on subsequent network analyses (step 1). Correlation matrices were generated using maximal information coefficient (MIC) [50] (step 2). Centrality metrics drawn from graph theory highlight different aspects of changing microbial populations (step 3) [66] (see Supporting Information for results of the other centrality measures). Winnowed microbial communities were ordered by decreasing centrality (step 4) and a certain number selected (step 5) based on area under the curve (AUC) sensitivity analysis of the metric of interest. The selected operational taxonomic units (OTUs) were evaluated by treatment effect (i.e., brome-invaded versus natural grasslands; step 6) by testing the homogeneity of multivariate dispersions within groups using permutational analysis of variance (PERMANOVA) [52] at 5% AUC intervals. The F-statistic was scaled from 0 to 1 and spline-smoothed (solid line) to facilitate comparisons among the datasets. The dashed line indicates standard deviation calculated within a 5% moving window. Closed circles indicate retained taxa. Points were plotted at 1% intervals around each cut-off point. The number of sequentially ordered OTUs were selected to maximize the F-statistic and minimize the standard deviation (e.g., 99 OTUs in blue text). To test the consistency of the selection procedure, we ran a sensitivity analysis to evaluate the effect of parameter selection on the winnowing process conditioning for each centrality measure (select j OTUs per iteration; step 7). BW betweenness, CL closeness, DG degree, EV eigenvector. To generate the data used for the structural equation modeling (SEM), we iterated the winnowing pipeline in a leave-one-out procedure to quantify the contribution of each sample plot to abundance and centrality for each OTU (n = number of samples; steps 8–9). We used the sum of all OTU abundance-centrality distances to origin (step 10) as an endogenous variable in our SEM. Winnowed OTUs are represented by enlarged points with black outlines in the abundance versus occupancy plot
We used the maximal information coefficient (MIC) to generate an adjacency matrix among all OTUs. MIC describes the relationship between paired variables, regardless of presence or absence of linearity [50], and hence is ideally suited to microbial data. MICs were generated using the python package “minepy” v. 1.2.2 [51]. To predict ecological relationships among microorganisms from abundance data, we generated degree, closeness, betweenness, and eigenvalue centralities for each OTU based on MIC adjacency matrix value ≥0.2. A low MIC threshold of 0.2 was chosen to avoid excluding any potentially interesting OTUs (as indicated by centrality) prior to the winnowing pipeline, while maintaining a reasonable number of relationships in the dataset. Each centrality measure was ordered and used to locate a maximum treatment effect between invaded and natural grasslands by iteratively adding OTUs based on increasing centrality metrics to a PERMANOVA using the R package “vegan” v. 2.5–2 [52, 53]. We included OTUs at 1% contribution intervals to the total area under the curve (AUC) of the centrality metric and generated a series of PERMANOVA F-statistics as a measure of treatment effect. Because F-statistics were multimodal and highly variable for low AUCs (suggesting selecting OTUs from this region may not be based on stable F-statistics), we employed a conservative approach and interpreted the maximum treatment effect to be where a peak in F-statistic corresponded with low variance as indicated by a moving standard deviation at 5% intervals.
Here we used the winnowing algorithm to determine the most important OTUs in terms of centrality in a complete community. This method may or may not capture OTUs that are important in subgraphs (modules), but possess relatively low centrality measures in the complete graph including all OTUs. One method to find potentially influential subgraph OTUs could be to select subsets of OTUs in an iterative procedure that regenerates the graph after each selection (i.e., sampling without replacement) and repeats the subset selection to obtain a list of OTU importance at both the graph and subgraph scales. To assess the sensitivity of this method to: (1) number of OTUs selected per winnowing iteration, (2) chosen centrality measure (degree, closeness, betweenness, eigenvector), and (3) correlation type (MIC, Spearman), we selected 5 base-2 targets to compare for agreement among OTU lists for different correlation and centrality metrics. We compared OTU lists generated by selecting 20, 22, 24, and 26 OTUs per iteration without replacement to a 27 list. Similarity among lists was assessed using the Jaccard similarity index [54]. The Jaccard similarity index is used for comparing the similarity and diversity of sample sets—the index measures similarity between finite sample sets and is defined as the size of the intersection divided by the size of the union of the sample sets.
Structural equation modeling of microbial networks during smooth brome invasion
Using a comprehensive list that included a compilation of all winnowed OTUs generated from the four centrality measures, we generated a dataset that included sample, OTU “importance” (i.e., centrality), and abundance. To do this, we ran a leave-one-out analysis where each sample was sequentially left out with replacement and then rebuilt the network without the left-out sample in order to quantify the centrality and abundance for each OTU among the samples—achieved by summation of each OTU contribution to sample centrality and abundance. This resulted in a matrix of centrality × sample for each centrality measure that was then used in subsequent SEM of microbial network evolution under smooth brome invasion.
We used these data to build upon the SEM framework developed by Piper et al. [37], in which they assessed how smooth brome influenced bacterial diversity during smooth brome invasion of natural grasslands. Here we wanted to build on this model to test if we could predict the evolution of microbial networks during smooth brome invasion. SEMs allow the exploration of networks of simultaneous influences, rather than individual causes [17, 31]. The method is thus appropriate for supporting causal interpretations at the system (for example, brome–edaphic–microbial network connectivity) rather than the individual level (for example, brome–network). Before fitting the SEM, we used general linear models with a quadratic term to check for nonlinear relationships among exogenous (solely explanatory) and endogenous (can be both response and explanatory) variables; no nonlinearities were found. To equalize variances we standardized variables by dividing raw values by their group maximum. Improved model fit was assessed based on reduced χ2 and Akaike information criterion. Models were fit using the R package “lavaan” v. 0.6–1 [55].
Here we tested three potential causal pathways through which smooth brome may influence microbial network development, via: (1) bacterial alpha diversity (richness or evenness), (2) bacterial alpha diversity and direct plant linkages, (3) bacterial alpha diversity and direct soil linkages, and/or (4) bacterial alpha diversity and both direct plant and soil linkages (see Supplementary Figs. S7–S10).
k-clique community analysis
As an independent test of winnowing robustness (i.e., do the winnowed OTUs represent a real sub-group within the microbial community), we quantified the connectivity of the winnowed community using k-clique analysis [56]. A k-clique community represents the union of all k-cliques (complete subgraphs or modules of size k) that can be reached from each other through a series of adjacent k-cliques (where adjacency = sharing k–1 nodes) [57, 58]—referred to as the clique percolation method [57]. This method first requires locating all cliques (maximal complete subgraphs) of the entire network, and then identifying the communities by carrying out a standard component analysis of the clique–clique overlap matrix [56]. The methodology is described further by Palla et al. [56] and the code is available at https://networkx.github.io/documentation/networkx-1.10/reference/generated/networkx.algorithms.community.kclique.k_clique_communities.html.
All analyses were performed using python (https://www.python.org/) and R v. 3.5.1 [59].
Results
Putative keystone taxa within microbial co-occurrence networks
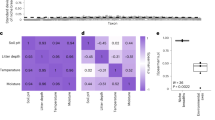
The first step of the winnowing pipeline involved Laplace (add-1) smoothing the data to compensate for zero values. We generated co-occurrence networks from MIC [50] adjacency matrices derived from OTU abundance tables (Fig. 1). We considered |MIC| ≥ 0.2 as representing a viable connection between OTUs (Supplementary Fig. S1). Ordered plots of betweenness, degree, closeness, and eigenvector centralities indicated near negative exponential or power distributions of centrality metrics (Fig. 1 and Supplementary Fig. S2). By iteratively adding OTUs of decreasing centrality to sequential PERMANOVAs between brome-invaded natural grasslands for each ordered centrality, we detected 10–112 influential OTUs from each centrality measure (Fig. 1 and Supplementary Fig. S2), for a total of 115 unique taxa that were deemed influential according to these criteria (Fig. 2 and Supplementary Table S1). The unique taxa consisted of 90 bacteria and 25 fungi, but no archaea—consistent with previous work that found that archaea did not strongly respond to invasion or influence other members of the microbial community [17].
Structural equation model of smooth brome interactions with soil properties, bacterial diversity, and microbial network connectivity along a brome cover gradient. The winnowed network is based on the union of centralities (degree, betweenness, closeness, and eigenvector; n = 115 operational taxonomic units (OTUs)). Each node in the network represents an OTU and each edge represents a pairwise association based on maximal information coefficient (MIC) >0.6. MIC values <0.6 are not represented visually to avoid overwhelming readers with superfluous detail that may obscure visual assessment of the graphs. Edge thickness increases with increasing MIC and node sizes correspond to degree. Structural equation modeling (SEM) co-variates are colored by origin (light green represents vegetation and brown represents soils). Solid arrows indicate notable effect sizes (P < 0.10, dashed lines P > 0.10), where the thickness of the arrow represents the strength of the relationship (green indicates positive, red negative relationships). Standardized path coefficients are shown next to pathways. Node color represents k-clique membership within the winnowed dataset. k-cliques are complete subgraphs of k-nodes [57, 60] and represent a validation of subgraph membership within the winnowed community. Full results for the models are presented in Supplementary Tables S2 and S3 and Supplementary Figs. S7–S11
We determined that the winnowing procedure differed among centrality metrics, though it was relatively insensitive to differing selection magnitudes (Fig. 1 and Supplementary Fig. S3a). Mean Jaccard similarity (intersection over union of OTU lists between the initial and subset runs) ranged from 75% for closeness to 94% for degree.
Increased network connectivity with smooth brome invasion
We recreated networks highlighting the winnowed OTUs for each smooth brome cover category. The magnitude and frequency of co-occurrence connections increased with smooth brome cover (Fig. 2 and Supplementary Figs. S3–S6). Microbial network degree centrality increased more than 12-fold between fescue and fully brome-invaded grasslands as median MIC increased by 12% and the number of strong connections (MIC ≥ 0.6) nearly doubled. Thus, the winnowed network became more connected as smooth brome became more dominant.
Prediction of core microbial networks
Of the 115 OTUs in the winnowed community (90 bacteria, 25 fungi), 89 bacteria and 19 fungi (94%) belonged to the same k-clique (i.e., complete subgraph; Fig. 2 and Supplementary Fig. S4), indicating robust selection of the core community using the winnowing pipeline. k-cliques are complete subgraphs of k-nodes [57, 60] and represent a validation of subgraph membership within the winnowed community. The winnowed community consisted of 13 bacterial and 2 fungal phyla (Supplementary Table S1). Increasing smooth brome abundance increased alpha diversity (evenness and richness) of observed bacterial taxa, which augmented connectivity of the winnowed network (Fig. 2, Supplementary Figs. S7–S11 and Tables 2–3). Brome aboveground biomass (shoots) directly decreased network connectivity. Smooth brome controls on microbial network development were more pronounced near the soil surface (i.e., in the A horizon) (Supplementary Figs. S7–S11) and SEMs with both direct plant effects (brome shoots) and indirect via bacterial alpha diversity were the most important drivers of changes in microbial network structure.
Discussion
The prediction of complex, dynamically changing microbial networks allows us to build mechanistic models that link community composition and biotic/abiotic factors to ecological functioning in metagenomic datasets. Feature selection based on ecological importance orthogonal to abundance can help researchers winnow the community down to microbes that are strongly responding to externalities regardless of abundance. The winnowed community may then be used in downstream hypothesis-driven analyses of network evolution among treatments.
Our data winnowing and causal hypothetical modeling approach combines feature selection using co-occurrence networks with structural equation modeling to characterize keystone OTUs and predict network evolution along gradients or among treatment effects. Identifying the causal links between microbial (e.g., archaea, bacteria, and fungi) and macrobial (e.g., smooth brome) systems provides the rationale for future manipulative experiments to identify the molecular mechanisms of smooth brome’s control of microbial networks. Such a combined SEM/manipulative approach is an important tenet in ecology, especially for assessing functional consequences of above- and below-ground interactions in changing ecosystems and predicting effects of global change [12]. Here we assessed how microbial network assemblage and structure changed in response to plant invasion. The winnowing approach may be applied by researchers in any field—whether it be exploring immunology in the human microbiome [61], linking animal behavior with pathogens [62], or managing the soil microbiome to improve crop production [63, 64].
There is no one-size-fits-all solution for mitigating the “small n large p” problem in metagenomic and microbiome studies. Our method addresses this problem for experimental designs involving treatments or environmental gradients. Notably, our method is adaptable to a wide range of input data, which will make it readily functional with higher-resolution datasets (e.g., single-nucleotide variants) as they become available. In our example we used SEM to link external factors to microbial network development; however, the winnowing approach could also be used with other popular statistical approaches such as generalized linear mixed modeling or additive modeling to link graph metrics to fixed or random experimental factors. This study provides the analytical platform for researchers to explore how interactions encoded within microbial networks link to the outside environs, be they eukaryotic hosts or edaphic factors.
Data availability
Processed sequencing data have been deposited into the Dryad Digital Repository at https://doi.org/10.5061/dryad.00b1d. These data include abundance and taxonomy for archaea, bacteria, and fungi, as well as environmental data. Steps 1–3 of the winnowing pipeline have been automated online at https://winnowing.usask.ca/ and the R and Python code for steps 4–10 are available at https://github.com/sua474/winnowing-pipeline-merged. A full port of the winnowing pipeline into a Python library is currently underway.
References
Whitman WB, Coleman DC, Wiebe WJ. Prokaryotes: the unseen majority. Proc Natl Acad Sci USA. 1998;95:6578–83.
Pocock MJO, Evans DM, Fontaine C, Harvey M, Julliard R, McLaughlin Ó, et al. (2016) Chapter two - the visualisation of ecological networks, and their use as a tool for engagement, advocacy and management. In: Woodward G, Bohan DA (ed) Advances in ecological research. Academic Press, London UK. p. 41–85.
Steele JA, Countway PD, Xia L, Vigil PD, Beman JM, Kim DY, et al. Marine bacterial, archaeal and protistan association networks reveal ecological linkages. ISME J. 2011;5:1414.
Barberán A, Bates ST, Casamayor EO, Fierer N. Using network analysis to explore co-occurrence patterns in soil microbial communities. ISME J. 2012;6:343–51.
Berry D, Widder S. Deciphering microbial interactions and detecting keystone species with co-occurrence networks. Front Microbiol. 2014;5:1–14.
Freilich S, Kreimer A, Meilijson I, Gophna U, Sharan R, Ruppin E. The large-scale organization of the bacterial network of ecological co-occurrence interactions. Nucleic Acids Res. 2010;38:3857–68.
Faust K, Raes J. Microbial interactions: from networks to models. Nat Rev Microbiol. 2012;10:538.
McCune B, Grace JB, Urban DL. Analysis of ecological communities. Gleneden Beach: MjM Software Design; 2002.
Lynch MDJ, Neufeld JD. Ecology and exploration of the rare biosphere. Nat Rev Microbiol. 2015;13:217–29.
Cao Y, Larsen DP, Thorne RS. Rare species in multivariate analysis for bioassessment: some consideration. J North Am Benthol Soc. 2001;20:144–53.
Shade A, Jones SE, Caporaso JG, Handelsman J, Knight R, Fierer N, et al. Conditionally rare taxa disproportionately contribute to temporal changes in microbial diversity. mBio. 2014;5:e01371–14.
Ramirez KS, Geisen S, Morriën E, Snoek BL, van der Putten WH. Network analyses can advance above-belowground ecology. Trends Plant Sci. 2018;23:759–68.
Caporaso JG, Lauber CL, Walters WA, Berg-Lyons D, Huntley J, Fierer N, et al. Ultra-high-throughput microbial community analysis on the Illumina HiSeq and MiSeq platforms. ISME J. 2012;6:1621–4.
Caporaso JG, Kuczynski J, Stombaugh J, Bittinger K, Bushman FD, Costello EK, et al. QIIME allows analysis of high-throughput community sequencing data. Nat Methods. 2010;7:335–6.
Goldford JE, Lu N, Bajić D, Estrela S, Tikhonov M, Sanchez-Gorostiaga A, et al. Emergent simplicity in microbial community assembly. Science. 2018;361:469–74.
Coyte KZ, Schluter J, Foster KR. The ecology of the microbiome: networks, competition, and stability. Science. 2015;350:663–6.
Mamet SD, Lamb EG, Piper CL, Winsley T, Siciliano SD. Archaea and bacteria mediate the effects of native species root loss on fungi during plant invasion. ISME J. 2017;11:1261–75.
Faust K, Sathirapongsasuti JF, Izard J, Segata N, Gevers D, Raes J, et al. Microbial co-occurrence relationships in the human microbiome. PLoS Comput Biol. 2012;8:e1002606.
Wei Z, Yang T, Friman V-P, Xu Y, Shen Q, Jousset A. Trophic network architecture of root-associated bacterial communities determines pathogen invasion and plant health. Nat Commun. 2015;6:8413.
Banerjee S, Schlaeppi K, Van Der Heijden MGA. Keystone taxa as drivers of microbiome structure and functioning. Nat Rev Microbiol. 2018;16:567–76.
Jiang Y, Li S, Li R, Zhang J, Liu Y, Lv L, et al. Plant cultivars imprint the rhizosphere bacterial community composition and association networks. Soil Biol Biochem. 2017;109:145–55.
Banerjee S, Kirkby CA, Schmutter D, Bissett A, Kirkegaard JA, Richardson AE. Network analysis reveals functional redundancy and keystone taxa amongst bacterial and fungal communities during organic matter decomposition in an arable soil. Soil Biol Biochem. 2016;97:188–98.
Newman M, Barabási AL, Watts DJ. The structure and dynamics of networks, vol. 19. Princeton: Princeton University Press; 2011.
Dallas TA, Han BA, Nunn CL, Park AW, Stephens PR, Drake JM. Host traits associated with species roles in parasite sharing networks. Oikos. 2019;128:23–32.
Layeghifard M, Hwang DM, Guttman DS. Disentangling Interactions in the microbiome: a network perspective. Trends Microbiol. 2017;25:217–28.
Lupatini M, Suleiman AKA, Jacques RJS, Antoniolli ZI, de Siqueira Ferreira A, Kuramae EE. et al. Network topology reveals high connectance levels and few key microbial genera within soils. Front Environ Sci. 2014;2:10
Wang H, Wei Z, Mei L, Gu J, Yin S, Faust K, et al. Combined use of network inference tools identifies ecologically meaningful bacterial associations in a paddy soil. Soil Biol Biochem. 2017;105:227–35.
Li A, Cornelius SP, Liu Y-Y, Wang L, Barabási A-L. The fundamental advantages of temporal networks. Science. 2017;358:1042–6.
Xiao Y, Angulo MT, Friedman J, Waldor MK, Weiss ST, Liu Y-Y. Mapping the ecological networks of microbial communities. Nat Commun. 2017;8:2042.
Grace JB. Structural equation modeling and natural systems. Cambridge: Cambridge University Press; 2006.
Grace JB, Schoolmaster DR, Guntenspergen GR, Little AM, Mitchell BR, Miller KM, et al. Guidelines for a graph-theoretic implementation of structural equation modeling. Ecosphere. 2012;3:1–44.
Pearl J. Causality: models, reasoning and inference. New York: Cambridge University Press; 2009.
Pearl J. The causal foundations of structural equation modeling. In: Hoyle RH editor. Handbook of structural equation modeling. New York: Guilford Press; 2012. p. 68–91.
Zhang Z, Liang S, Wang J, Zhang X, Mahamood M, Yu J, et al. Tillage and crop succession effects on soil microbial metabolic activity and carbon utilization in a clay loam soil. Eur J Soil Biol. 2018;88:97–104.
Quigley BL, Carver S, Hanger J, Vidgen ME, Timms P. The relative contribution of causal factors in the transition from infection to clinical chlamydial disease. Sci Rep. 2018;8:8893.
Piper CL, Lamb EG, Siciliano SD. Smooth brome changes gross soil nitrogen cycling processes during invasion of a rough fescue grassland. Plant Ecol. 2015;216:235–46.
Piper CL, Siciliano SD, Winsley T, Lamb EG. Smooth brome invasion increases rare soil bacterial species prevalence, bacterial species richness and evenness. J Ecol. 2015;103:386–96.
Wilson SD, Pinno BD. Environmentally-contingent behaviour of invasive plants as drivers or passengers. Oikos. 2013;122:129–35.
Lamb E, Winsley T, Piper CL, Freidrich SA, Siciliano SD. A high-throughput belowground plant diversity assay using next-generation sequencing of the trnL intron. Plant Soil. 2016;404:361–72.
Otfinowski R, Kenkel NC, Catling PM. The biology of Canadian weeds. 134. Bromus inermis Leyss. Can J Plant Sci. 2007;87:183–98.
Hiiesalu I, Öpik M, Metsis M, Lilje L, Davison J, Vasar M, et al. Plant species richness belowground: higher richness and new patterns revealed by next-generation sequencing. Mol Ecol. 2012;21:2004–16.
Caporaso JG, Lauber CL, Walters WA, Berg-Lyons D, Lozupone CA, Turnbaugh PJ. et al. Global patterns of 16S rRNA diversity at a depth of millions of sequences per sample. Proc Natl Acad Sci USA. 2011;108:4516–22.
Teske A, Sørensen KB. Uncultured archaea in deep marine subsurface sediments: have we caught them all? ISME J. 2007;2:3–18.
Gardes M, Bruns TD. ITS primers with enhanced specificity for Basidiomycetes‐application to the identification of mycorrhizae and rusts. Mol Ecol. 1993;2:113–8.
Manter DK, Vivanco JM. Use of the ITS primers, ITS1F and ITS4, to characterize fungal abundance and diversity in mixed-template samples by qPCR and length heterogeneity analysis. J Microbiol Methods. 2007;71:7–14.
McDonald D, Price MN, Goodrich J, Nawrocki EP, DeSantis TZ, Probst A, et al. An improved Greengenes taxonomy with explicit ranks for ecological and evolutionary analyses of bacteria and archaea. Isme J. 2011;6:610.
Schloss PD, Westcott SL, Ryabin T, Hall JR, Hartmann M, Hollister EB, et al. Introducing mothur: open-source, platform-independent, community-supported software for describing and comparing microbial communities. Appl Environ Microbiol. 2009;75:7537–41.
Wang Q, Garrity GM, Tiedje JM, Cole JR. Naïve Bayesian classifier for rapid assignment of rRNA sequences into the new bacterial taxonomy. Appl Environ Microbiol. 2007;73:5261–7.
Smith B, Wilson JB. A consumer’s guide to evenness indices. Oikos. 1996;76:70–82.
Reshef DN, Reshef YA, Finucane HK, Grossman SR, McVean G, Turnbaugh PJ, et al. Detecting novel associations in large data sets. Science. 2011;334:1518–24.
Albanese D, Filosi M, Visintainer R, Riccadonna S, Jurman G, Furlanello C. minerva and minepy: a C engine for the MINE suite and its R, Python and MATLAB wrappers. Bioinformatics. 2013;29:407–8.
Anderson MJ. A new method for non-parametric multivariate analysis of variance. Austral Ecol. 2001;26:32–46.
Oksanen J, Blanchet FG, Friendly M, Kindt R, Legendre P, McGlinn D, et al. (2018). vegan: Community Ecology Package. R package version 2.5-2. https://cran.r-project.org/package=vegan. Accessed 17 June 2018.
Jaccard P. Nouvelles Recherches Sur La Distribution Florale. Bull De la Société Vaud Des Sci Nat. 1908;44:223–70.
Rosseel Y. lavaan: an R package for structural equation modeling. 2012. 2012;48:36.
Palla G, Derényi I, Farkas I, Vicsek T. Uncovering the overlapping community structure of complex networks in nature and society. Nature. 2005;435:814.
Derényi I, Palla G, Vicsek T. Clique percolation in random networks. Phys Rev Lett. 2005;94:160202.
Everett MG, Borgatti SP. Analyzing clique overlap. Connections. 1998;21:49–61.
R Core Team. R: a language and environment for statistical computing. Vienna: R Foundation for Statistical Computing; 2018.
Bollobás B. Random graphs. 2 ed. Cambridge: Cambridge University Press; 2001.
Cho I, Blaser MJ. The human microbiome: at the interface of health and disease. Nat Rev Genet. 2012;13:260.
Ezenwa VO, Gerardo NM, Inouye DW, Medina M, Xavier JB. Animal behavior and the microbiome. Science. 2012;338:198.
Fierer N. Embracing the unknown: disentangling the complexities of the soil microbiome. Nat Rev Microbiol. 2017;15:579.
P2IRC. Plant Phenotyping and Imaging Research Centre (P2IRC). Saskatoon: University of Saskatchewan; 2017.
Manning CD, Raghavan P, Schütze H. Introduction to information retrieval. Cambridge: Cambridge University Press; 2010.
Newman MEJ, Barabási AL, Watts DJ. The structure and dynamics of networks. Princeton: Princeton University Press; 2006.
Acknowledgements
We thank Carl Gutwin and Gurjot Bhatti for help with the infrastructure that we used to process the data. Candace Piper aided in the experimental design along with Tristrom Winsley for bioinformatic analysis. Syed Umair Aziz compiled the R and python code onto GitHub. This work is supported by a grant from the Plant Phenotyping and Imaging Research Centre (P2IRC) to BLH, EGL, KS, and SDS. P2IRC is a digital agriculture research center funded by the Canada First Research Excellence Fund (CFREF) from the Natural Sciences and Engineering Research Council (NSERC), managed by the Global Institute for Food Security (GIFS), and located at the University of Saskatchewan (U of S).
Author information
Authors and Affiliations
Contributions
SDM, SDS, and KS designed the approach and interpreted the results. ER and MB implemented the method and generated results, with input from SDS and KS. SDM analyzed the data. EGL contributed data. SDS and KS supervised the study with input from EGL and BLH. All authors drafted and approved the manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
About this article
Cite this article
Mamet, S.D., Redlick, E., Brabant, M. et al. Structural equation modeling of a winnowed soil microbiome identifies how invasive plants re-structure microbial networks. ISME J 13, 1988–1996 (2019). https://doi.org/10.1038/s41396-019-0407-y
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41396-019-0407-y
This article is cited by
-
Drought and vegetation restoration lead to shifts in soil microbial diversity and co-occurrence networks in California coastal prairie
Plant and Soil (2024)
-
The Review of Ecological Network Indicators in Graph Theory Context: 2014–2021
International Journal of Environmental Research (2022)
-
Native tree root exudates promote tolerance of simulated herbivory of an invasive tree via altered functional traits
Plant and Soil (2022)
-
Enterococcus faecium are associated with the modification of gut microbiota and shrimp post-larvae survival
Animal Microbiome (2021)
-
Development of fungal-mediated soil suppressiveness against Fusarium wilt disease via plant residue manipulation
Microbiome (2021)