Abstract
The size and biogeochemical impact of the subseafloor biosphere in oceanic crust remain largely unknown due to sampling limitations. We used reactive transport modeling to estimate the size of the subseafloor methanogen population, volume of crust occupied, fluid residence time, and nature of the subsurface mixing zone for two low-temperature hydrothermal vents at Axial Seamount. Monod CH4 production kinetics based on chemostat H2 availability and batch-culture Arrhenius growth kinetics for the hyperthermophile Methanocaldococcus jannaschii and thermophile Methanothermococcus thermolithotrophicus were used to develop and parameterize a reactive transport model, which was constrained by field measurements of H2, CH4, and metagenome methanogen concentration estimates in 20–40 °C hydrothermal fluids. Model results showed that hyperthermophilic methanogens dominate in systems where a narrow flow path geometry is maintained, while thermophilic methanogens dominate in systems where the flow geometry expands. At Axial Seamount, the residence time of fluid below the surface was 29–33 h. Only 1011 methanogenic cells occupying 1.8–18 m3 of ocean crust per m2 of vent seafloor area were needed to produce the observed CH4 anomalies. We show that variations in local geology at diffuse vents can create fluid flow paths that are stable over space and time, harboring persistent and distinct microbial communities.
Similar content being viewed by others
Introduction
The igneous ocean crust contains 2% of the fluid volume of the overlying global ocean [1] and an estimated 1.5 Pg of microbial carbon [2]. Diverse chemolithotrophic Epsilonbacteraeota living in the global ocean crust at deep-sea hydrothermal vents contain an estimated 1.4–2.7 Gg C and produce 0.045–1.4 Tg of organic C yr−1, suggesting that microbes in the shallow hydrothermal subseafloor are a relatively small standing stock which turns over rapidly [3]. However, quantifying the biogeochemical impact of subseafloor microbes in the anoxic zones of oceanic crust remains a challenge. At Axial Seamount in the northeastern Pacific Ocean (Fig. 1), low-temperature (<50 °C) diffuse hydrothermal fluids steadily emanate from cracks in the basaltic seafloor and contain biogenic CH4 and culturable methanogenic microbes [4,5,6,7,8]. Both molecular and culture-based analyses of these fluids showed that the predominant methanogens present are thermophilic Methanothermococcus and hyperthermophilic Methanocaldococcus species [6, 9,10,11,12]. They are among the most common high-temperature methanogens found globally in hydrothermal vents [13,14,15] and hot subsurface petroleum reservoirs [16,17,18,19].
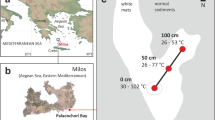
Map of Axial Seamount and the sampling locations. The hydrothermal sampling sites were along the southeastern rim of the caldera. The outline of the 2011 lava flow is from Caress et al. [42]. The inset shows the location of Axial seamount in the NE Pacific Ocean. The map is based on MBARI autonomous underwater vehicle bathymetry (2 m grid) overlain on shipboard multibeam bathymetry (20 m grid)
Communities of methanogens and other microbes at individual vents at Axial Seamount are distinct and persistent over time, demonstrating that the subseafloor habitat consists of stable localized microbial communities that reflect their local environment [12, 20, 21]. However, the inaccessibility of the igneous subsurface makes it difficult to measure the total number of active methanogens that inhabit the subseafloor at each vent site, the environmental factors shaping the composition of these microbial communities, and their biogeochemical impact on the diffuse fluids exiting the seafloor into the overlying ocean. One approach for quantitatively assessing these questions is reactive transport modeling. However, developing models of subsurface microbial growth relies on correctly parameterizing the growth kinetics of the resident microbes. The Methanothermococcus and Methanocaldococcus species dominant at Axial grow primarily by combining 4H2 and CO2 to produce CH4 and 2H2O. Microcosm incubations of diffuse vent fluids from Axial Seamount demonstrated that methanogenesis at 55 °C and 80 °C does not use formate or acetate and was limited by H2 availability rather than anabolic needs such as nitrogen, vitamins, or trace metals [8]. Therefore, these two genera of methanogens are ideal for reactive transport modeling using H2 concentration and temperature as the primary variables.
To predict the minimum threshold of H2 needed for growth, three Methanocaldococcus spp. were grown previously in a gas-purged batch reactor at different H2 concentrations to determine their H2 Monod kinetics for growth [6]. This threshold predicted the presence or absence of hyperthermophilic methanogens in various global hydrothermal systems based on H2 availability. However, a chemostat is necessary to estimate CH4 production rates by methanogens at different H2 concentrations. In this study, CH4 production rates and Monod kinetics at varying H2 concentrations were determined using a chemostat for Methanocaldococcus jannaschii and Methanothermococcus thermolithotrophicus. Arrhenius growth constants at varying temperatures were also determined using Balch tubes. These data were used to parameterize a reactive transport model describing the growth and transport of M. jannaschii and M. thermolithotrophicus beneath the seafloor, along with H2, heat, and Mg2+, from the high-temperature source fluid and diluted with seawater until the fluid reached the temperature observed on the seafloor. The model was applied to two physically distinct deep-sea hydrothermal vent sites at Axial Seamount. This work highlights the potential of coupling pure culture laboratory studies of environmental processes with reactive transport modeling and field observations to determine the size and nature of biogeochemical processes in environments that are otherwise difficult to access.
Methods
Chemostats
Methanocaldococcus jannaschii DSM 2661 [22] and Methanothermococcus thermolithotrophicus DSM 2095 [23] were purchased from the Deutsche Sammlung von Mikroorganismen und Zellkulturen GmbH (DSMZ, Braunschweig, Germany). For chemostat growth, M. jannaschii was grown at 82 and 65 °C and M. thermolithotrophicus was grown at 65 and 55 °C in a 2-L bioreactor with a working volume of 1.5 L. The growth medium was modified DSM 282 medium [22]. The medium was reduced with 0.025% each of Na2S•9H2O and cysteine-HCl, stirred at 300 rpm, and sparged with 7.5 mL min−1 CO2 and varying flow rates of H2 and N2 to bring the total gas flow rate to 70 mL min−1, or to 100 mL min−1 for the highest H2 concentrations. The medium was maintained at pH 6.0 ± 0.1 by the automatic addition of 0.25 mM HCl.
The organisms were grown in batch phase prior to initiating the chemostat until they reached late logarithmic growth phase. The growth medium in the bioreactor was replaced with fresh sterile medium from an 18.5 L reservoir that was sparged with N2 and heated to the same temperature as the bioreactor. The dilution rate of the chemostat matched the batch-phase growth rate of the organism for the temperature and H2 concentration provided until steady-state conditions were reached (assumed to be after three full replacements of the medium based on longer test runs). The chemostat was operated such that all the H2 input into the reactor was consumed by the cells and the H2 output concentration was below the level of detection. Cell concentrations were determined using a Petroff-Hausser counting chamber and phase-contrast light microscopy. The headspace gas of the bioreactor was sampled directly using a Hamilton gas-tight syringe through a septum. The gas concentrations in the liquid medium were measured by anoxically transferring 20 mL of medium into a sealed 60 mL serum bottle that was pre-flushed with N2, allowing the gases to equilibrate into the headspace. The concentration of CH4 in the headspace was measured using a gas chromatograph (Shimadzu GC-17A) with a flame-ionization detector and a molecular sieve 5A column at 120 °C. The concentration of H2 was also measured using a gas chromatograph (Shimadzu GC-8A) with a thermal conductivity detector and an Alltech Haysep DB 100/120 column at 120 °C. The gas flow rate into the bioreactor was measured using a bubble meter. The cell-specific CH4 production rate was calculated from the sum of the CH4 concentration in the headspace times the gas flow rate and the CH4 concentration in the medium times the medium dilution rate, which was normalized by the total cell concentration in the reactor. Each measurement was taken in duplicate, and the dilution rate was changed midway through each chemostat run to determine the effect of changing the growth rate of the organisms on the rate of CH4 production.
To determine the effect of temperature on growth, growth rate was determined for cells incubated between 84 and 45 °C for M. jannaschii and between 68 and 30 °C for M. thermolithotrophicus. Cells were grown in modified DSM 282 medium as described above in Balch tubes sealed with butyl rubber stoppers and containing 2 atm (100 kPa added pressure at room temperature) of H2:CO2 (80%:20%) headspace. At various time points during growth, the cell concentration in the tubes was determined as described above. The growth rate was determined from a best-fit curve through the exponential portion of cell growth. The 95% confidence interval of the growth rate was determined using analysis of covariance (ANCOVA) [24].
Model description
A major challenge in developing the reactive transport model for methanogen growth is the lack of information on the size and configuration of the subsurface hydrothermal mixing zone. While numerical models using Darcy flow through a porous medium have captured the dominant features of hydrothermal circulation over the scale of an entire vent field or ridge system (i.e., 1–10 km) [25, 26], such models lack the resolution necessary to describe fluid flow at the scale of an individual vent, where flow is most likely controlled by the unique configuration of cracks and fissures feeding an outflow [27, 28]. Therefore, we took a simpler approach, whereby the flow was parameterized (rather than modeled using Darcy flow), but mass conservation was maintained.
The model describes the growth of methanogens in a high-temperature end-member fluid devoid of Mg2+ that is transported along a flow path and progressively diluted with seawater until it exits the seafloor. To represent fluid transport, the model considered a one-dimensional flow path consisting of a series of n boxes (Fig. 2). High-temperature hydrothermal fluid, lacking Mg2+, entered the first box with the fluid composition of the high-temperature end-member, then flowed from box-to-box, and at each box was progressively diluted with an equal amount of 2 °C seawater. Because the true length of the flow path is unknown, the model is non-dimensionalized with respect to space, such that the sum of all the box volumes is equal to one and represents the total volume of the subsurface mixing zone feeding the vent outflow. The total residence time of fluid in the system is set by the spatially non-dimensionalized fluid flux exiting the seafloor (Q′vt), which has units of time−1 and can be thought of as a dilution factor that defines the timescale of hydrothermal fluid circulation. The residence time fluid spends at different temperatures along the flow path is controlled by both Q′vt and the volume of each individual box along the flow path. To simplify the specification of box volumes, the volume of each box is given by the following formula:
where V is the box volume, n is the total number of boxes, x is a non-dimensional variable describing the position along the flow path and varies from 0 at the high-temperature end-member to 1 at the point where fluid is venting into the deep ocean, and xb is a shape parameter describing the geometry of the subsurface mixing zone. The shape parameter allowed the model to transition between two different mixing regimes. If xb >> 1, then the flow path resembled a linear crack or straight pipe (Fig. 2a). If xb << 1, then the flow path spread out as it rose, approximating an expanding plume percolating through the ocean crust (Fig. 2b). The fluid flux, Q′vt, and the shape parameter, xb, were treated as tuning parameters that were adjusted to understand how flow characteristics influence the chemical concentrations and the microbial populations present in venting fluids. While Q′vt sets the timescale of fluid flow, the shape parameter, xb, determined the relative amount of time spent at various temperatures along the flow path. All model parameters and boundary conditions are provided as Supplementary Material.
The model state variables were concentration of CH4, [CH4] (μmol kg−1), concentration of H2, [H2] (μmol kg−1), concentration of a thermophilic methanogen with M. thermolithotrophicus growth kinetics, [Mthe] (cells L−1), concentration of a hyperthermophilic methanogen with M. jannaschii growth kinetics, [Mjan] (cells L−1), concentration of Mg2+, [Mg2+] (mmol kg−1), and temperature, T (K). Temperature was calculated assuming pure mixing and was given by the following equation,
where fht is the fraction of high-temperature fluid in the box determine from the Mg2+ content of the venting fluid assuming 0 mmol Mg2+ kg−1 in the hydrothermal end-member, Tht is the temperature of the hydrothermal end-member fluid, Tsw is the temperature of seawater, and Cp,ht and Cp,sw are the heat capacities of hydrothermal end-member fluid and seawater, respectively. During hydrothermal circulation, Mg2+ is removed from solution within hours at high temperatures and the Mg2+ content of diffuse fluids indicates how much hot, zero-Mg2+ end-member is in the fluid [29].
The rest of the variables were described by the following system of differential equations for each box i, which were solved using the method-of-lines. The model was implemented in the R software environment using the package ReacTran [30].
where Q is fluid flux. Methane production (RCH4) is calculated by:
where vmax is the maximum rate of cell-specific CH4 production, KH2 is the half-saturation constant for cell-specific CH4 production, and Tmax is the optimum growth temperature of the methanogen. A conversion factor of 10−9 is used to convert νmax, which in Table S3 is expressed in terms of fmol cell−1 h−1 to μmol cell−1 h−1.
Growth rate for methanogens is given by,
where A is the Arrhenius constant and Ea is the activation energy.
Field constraints on the reactive transport model
Field measurements of Methanocaldococcus species, Methanothermococcus species, CH4, and H2 concentrations in exiting fluids at individual diffuse vents were used to constrain the modeled subseafloor methanogen abundance, CH4 production, and the shape function of fluid mixing for each vent. Dissolved inorganic carbon (DIC) was also measured in the fluids to ensure that it was not growth limiting. Thirty-seven diffuse hydrothermal fluid samples were collected from Marker 113 and Marker 33 (Fig. 1) in 2013, 2014, and 2015 using the deep-sea remotely operated vehicles Jason II and ROPOS (Table S1) as previously described [8, 12]. The concentration of Methanocaldococcus and Methanothermococcus cells in the diffuse hydrothermal fluids was estimated from the product of the proportion of these organisms in annotated metagenomic sequence read counts [12] and the total cell counts [8] (Table S1).
There was no high-temperature hydrothermal venting within 0.5 km of Marker 113 or Marker 33 that could provide hydrothermal end-member gas concentrations. Therefore, high-temperature end-member H2 concentrations for these sites were estimated based on a trend of end-member H2 and end-member Cl− for the closest high-temperature vents at Axial Seamount. The end-member Cl− concentration of Marker 113 is ~100 mmol kg−1 and that of Marker 33 is ~ 400 mmol kg−1 (from extrapolation of diffuse fluid Cl− to zero Mg2+). Temperature and chlorinity for the high-temperature end members were determined from the relationship of Mg2+ and temperature (or chlorinity) and extrapolated to zero Mg2+ concentration. The nearest high-temperature vents with similar Cl− end-members are Diva vent (end-member Cl− 200 mmol kg−1, end-member H2 400–970 µmol kg−1) and El Guapo vent (end-member Cl− 400 mmol kg−1 and end-member H2 120–470 µmol kg−1). End-member H2 concentrations at Marker 113 and Marker 33 were assigned values of 950 and 300 μmol kg−1, respectively. These end-member H2 values for the diffuse vent sites reflect the fact that Marker 113 has a vapor-dominated source with higher gas content than the source for Marker 33.
Results
H2 Monod kinetics for methanogenesis
M. jannaschii was grown in 11 separate chemostat runs and M. thermolithotrophicus in 9 separate chemostat runs at varying H2 concentrations, dilution rates, and temperatures (Table S2). The cell-specific CH4 production rates were not distinguishable based on dilution rate or growth temperature at each H2 concentration examined, so the Monod kinetics data were pooled for each organism (Fig. 3a). For M. jannaschii, the maximum CH4 production rate (Vmax) was 43 ± 5 fmol CH4 cell−1 h−1 (± standard error) and the KS for H2 was 37 ± 15 µM. For M. thermolithotrophicus, the Vmax was 24 ± 3 fmol CH4 cell−1 h−1 and the KS for H2 was 27 ± 12 µM. The growth rates of both organisms in a closed system (Balch tubes) were measured over their growth temperature range to determine their Arrhenius constants (Table S3). For M. jannaschii, the activation energy (Ea) was 86.3 kJ mol−1 and the pre-exponential factor (A) was 9.16 × 1012 h−1. For M. thermolithotrophicus, the Ea was 73.8 kJ mol−1 and A was 3.36 × 1011 h−1 (Fig. 3b).
a Rates of methanogenesis as a function of H2 concentration and b growth rates as a function of 1/T for M. jannaschii (red solid circle) and M. thermolithotrophicus (blue solid circle). Monod kinetic parameters (KH2, vmax) were determined from the data in plot (a) and the Arrhenius parameters (A, Ea) were determined from the data in plot (b). The error bars in panel (b) represent 95% confidence intervals
Reactive transport modeling
The parameter Q′vt set the timescale or average residence time of fluid circulation through the hydrothermal system. If this parameter was large, then the residence time was short and there was not enough time spent at optimal growth conditions for a population to develop. Any microbes that might be present were simply washed out and H2 and CH4 followed conservative mixing between high-temperature source fluid and seawater. If Q′vt was small, then the residence time was long and there was enough time for methanogen populations to establish in the fluid during its transport through the system. Any H2 present in the fluid was converted to CH4, producing significant H2 and CH4 anomalies from conservative mixing.
The pipe-like and expanding-plume models shown in Fig. 4 had identical final H2 and CH4 concentrations (Fig. S1), but the ratio of hyperthermophilic-to-thermophilic methanogens varied significantly. For fluid flow through a straight-pipe-like model, the hyperthermophile Methanocaldococcus dominated the system by consuming all the H2 prior to any significant growth of the thermophile Methanothermococcus (Fig. 4a). Fluid flow was constrained by the walls of the pipe, so as seawater was entrained into the pipe, mass conservation accelerated the flow, leaving the thermophiles more sensitive to washout than the hyperthermophiles. Alternatively, if the cross-sectional area increases along the vertical flow path, as in the expanding plume model, the thermophile Methanothermococcus dominated the system (Fig. 4b). The exact transition between the dominance of the two types of methanogens depended on the residence time, composition, and temperature of the end-member fluids.
General reactive transport model results for straight-pipe (a) and expanding-plume (b) models. Lateral cross-sections depicting each model are shown on the left. The estimated concentration of M. jannaschii and M. thermolithotrophicus cells and the geometry of the flow path are shown on the right. The fluid temperatures at steps 0 and 1 are 84.6 and 26.7 °C, respectively
The reactive transport model was applied to two sites of diffuse venting at Axial Seamount. The aqueous H2 and CH4 concentrations in exiting diffuse fluids were 0.1–2.6 μmol kg−1 of fluid and 13–40 μmol kg−1 of fluid at Marker 33 and Marker 113, respectively, indicating H2 consumption and CH4 production relative to conserved end-member mixing [12]. The DIC concentrations were 4.5–15.1 mmol kg−1 of fluid at these sites and were not considered limiting to methanogenesis. At Marker 113, 15–31% of annotated metagenomic sequences were assigned to known methanogenic genera, primarily thermophilic Methanothermococcus species, based on metagenomic and culture-dependent analyses (Table S1) [8, 12]. The estimated concentrations of Methanothermococcus and Methanocaldococcus cells in exiting vent fluids based on metagenomic analyses were 1.9 ± 0.7 × 108 cells L−1 (± standard error) and 2.9 ± 0.9 × 107 cells L−1, respectively. In contrast, at Marker 33, only 2–5% of annotated metagenomic sequences were assigned to known methanogenic genera, primarily hyperthermophilic Methanocaldococcus species (Table S1) [8, 12]. The estimated concentrations of Methanothermococcus and Methanocaldococcus cells in these exiting vent fluids, based metagenomic analyses, were 1.2 ± 0.3 × 106 and 1.2 ± 0.3 × 107 cells L−1, respectively.
To fit the model, both the fluid flux (Q′vt) and shape parameter (xb) were adjusted until the H2 and CH4 concentrations and ratio of thermophiles to hyperthermophiles fit those observed in the vent fluid outflow (Fig. 5). The model closely reproduced the H2 and CH4 concentrations observed and methanogens estimated in the vent fluid outflow. For Marker 113 and Marker 33, the residence times of fluid below the surface were 33 and 29 h, respectively. Parameter values and boundary conditions used for the simulations are provided in Table S4.
Field data and reactive transport model results for Marker 33 and Marker 113 at Axial Seamount. Model fits compared to field observations from 2013, 2014, and 2015 for Marker 33 (top row, a–d) and Marker 113 (bottom row, e–h). The first column (a, e) shows H2 concentrations vs. the conservative tracer Mg2+. The solid line shows the model fit and the dashed line the conservative abiotic mixing line. The shaded gray area shows the geometry of the mixing zone needed to produce the fit. The second column (b, f) shows CH4 concentrations vs. Mg2+. The third column (c, g) shows estimated methanogen cell concentrations from field measurements for the thermophilic (blue solid circle) and hyperthermophilic (red solid circle) methanogens and the modeled cell abundances. The fourth column (d, h) shows how the methanogen population is divided between thermophile and hyperthermophiles as estimated from the metagenomic data in Fortunato et al. [12] for each of the years compared to the model fit over all years
Discussion
Methanocaldococcus and Methanothermococcus species almost exclusively use H2 and CO2 as their carbon and energy sources. Some Methanothermococcus spp. can use formate in lieu of H2 and CO2 [23, 31], but microcosm enrichments using diffuse fluids from Axial Seamount that were spiked with formate or acetate instead of H2 did not result in CH4 production at 55 or 80 °C [8]. These attributes make these methanogens amenable to modeling based on H2 availability. Previous Monod kinetics determined for Methanocaldococcus spp. in a batch reactor generally predicted which hydrothermal vent fluid chemistries could support the reproduction of these methanogens [6]. However, growth and CH4 production in a chemostat at constant H2 flux rates were needed to estimate biomass production and the biogeochemical impact of high-temperature methanogens in the subseafloor. This study expanded the temperature range of these measurements by including a Methanothermococcus species. The KS and minimum H2 threshold for CH4 production measured in this study in the chemostat for M. jannaschii and M. thermolithotrophicus were slightly lower than the growth kinetic values measured previously for three Methanocaldococcus species grown in a batch reactor [6].
Comparing the fitted model domains for Marker 113 and Marker 33, the shape function for Marker 113 was more expanding plume-like while that for Marker 33 was more pipe-like. Although the average residence time of hydrothermal circulation was similar for both vents, the local residence time in the optimal growth ranges for Methanothermococcus and Methanocaldococcus differed due to the hydrology of the flow paths. The plume-like hydrology of Marker 113 resulted in a shorter residence time for hotter fluid compared to cooler fluid, favoring Methanothermoccus, while the pipe-like geometry of Marker 33 had a longer residence time at the hotter temperatures favoring Methanocaldococcus. This trend is similar to that observed for these two vent sites using metagenomic analyses, where mesophilic Epsilonbacteraeota were predominant at Marker 113 while thermophilic Epsilonbacteraeota were predominant at Marker 33 [12].
The reactive transport model was non-dimensional, which permitted estimates of residence times but not the extent or volume of the subsurface biotope associated with each vent. If fluid flux estimates are known, then the model could be rescaled to estimate the subsurface volume and methanogen abundance (details of these calculations are described in the Supplementary Material). While diffuse fluid flux measurements at Marker 113 and Marker 33 are not available, Pruis and Johnson [32] used a hydrologically-sealed sampler to estimate the diffuse fluid flux in the ASHES vent field at Axial Seamount (Fig. 1), ~2 km from Marker 113 and Marker 33, where fluids emanate from a collection of similarly small (<5 cm width) fractures. The fluid flux estimate was 48 m3 m−2 y−1. Assuming this fluid flux rate for Marker 113 and Marker 33, our model predicted that each vent hosts 0.4–1.3 × 1011 methanogen cells m−2 of vent seafloor surface area (Table S5). Assuming an effective porosity of 10–30% [32], the methanogens would occupy only 1.8–18 m3 of ocean crust m−2 of vent seafloor surface area (Table S5). From this, the depth below the seafloor at which methanogen growth begins can be estimated (see Supplemental Materials). For Marker 33 where xb = 100, methanogen growth begins 1.8–18 mbsf depending upon the porosity. For Marker 113 where xb = 1, methanogen growth begins somewhere between 3 and 28 mbsf (Fig. S2). This result was consistent with previous field observations suggesting that the subsurface populations feeding these vents are predominately local features [12, 22, 33] drawing on nearby subsurface microbial populations, rather than large-scale subsurface hydrothermal fluid circulation patterns. The degree to which these local hot spots of microbial activity represent the overall subsurface biotope of Axial Seamount is unknown.
The 29–33 h subseafloor residence times of the diffuse fluids at Axial Seamount were comparable to the 17–41 h resident time estimate for microbes in a diffuse vent Crab Spa at 9°50ʹ East Pacific Rise hydrothermal vent site [3]. We similarly found that a relatively small but highly productive microbial standing stock in the subseafloor at vents likely accounts for the biogeochemical alteration and biomass output from subseafloor vent chemoautotrophs. Unlike Crab Spa where there was net CH4 consumption in the diffuse fluids [3], there was net biogenic CH4 production in our two diffuse vent fluids at Axial Seamount, demonstrating that in certain circumstances methanogens can represent a significant proportion of the total primary productivity.
One possible caveat for our model was that it only considered microbial growth in the fluid phase and not growth of microbes attached to surfaces. Hyperthermophiles, including M. jannaschii, produce biofilms and form attachments to hydrothermal minerals [34, 35]. The microbial mat and centimeter-scale flocculent material that was flushed from the seafloor immediately following a volcanic eruption at Axial and elsewhere [10, 36, 37] suggests that subsurface microbes attach to one another and to solid surfaces, most likely to prevent washout from the system. Incorporating biofilms into the model introduces additional parameters, such as the attachment strength and surface area available for colonization. For the Marker 113 model, the CH4 anomaly observed in the diffuse fluid matched the concentration of methanogens present in the vent outflow. This suggests that the methanogen population at this vent could exist in the fluid phase given the estimated residence times of the fluid at thermophilic growth temperatures. In contrast, the number of hyperthermophilic methanogens needed to produce the modeled CH4 anomaly at Marker 33 was much higher than the numbers observed in the diffuse fluid outflow (Fig. 4b). The ‘missing’ hyperthermophilic methanogens could be living in a subsurface biofilm.
Another possible caveat for our model is that it assumes a constant growth yield (i.e., amount of cell mass produced per mol of CH4 produced) across varying H2 concentrations and temperatures. In this study, M. jannaschii and M. thermolithotrophicus were grown in the chemostat at maximum cell concentrations such that all the available H2 in the reactor was consumed, which closely resembles the complete depletion of H2 in diffuse vent fluids exiting the seafloor. However, when M. jannaschii was grown in a chemostat at 80–83 μM H2 and 10-fold lower cell concentrations such that excess H2 was observed in the headspace, the growth yield (Yp/CH4) dropped ~10-fold and the cell-specific CH4 production rate increased to ~ 500 fmol CH4 cell−1 h−1 [38]. Growth yields also increased in laboratory studies in the hydrogenotrophic thermophile Methanothermobacter thermoautotrophicus and the mesophile Methanococcus maripaludis when H2 was limiting [39,40,41]. Therefore, the ‘missing’ hyperthermophilic methanogens at Marker 33 may also be due to excess H2 availability and low hyperthermophilic methanogen growth yields at hyperthermophilic temperatures that lead to much higher CH4 production rates per cell. In this study, the cell-specific CH4 production rates are conservative and the estimated number of total methanogens at each Axial vent in this study should be considered upper limits. This means that the population of methanogen cells necessary to support substantial methane anomalies could be even smaller than we have predicted.
Conclusion
This study used two representative methanogens as tracers of subsurface fluid circulation and microbial production at two diffuse vents at Axial Seamount. By combining laboratory-derived methanogen growth kinetics with reactive transport modeling and in situ observations, the population size of methanogens, the volume of crust occupied by these organisms, the fluid residence time, and the nature of subsurface mixing were estimated. Results suggest that the methanogen population at each vent was relatively small and local, occupying as little as 2 m3 of subsurface crust and consisting of 0.4–1.3 × 1011 total methanogen cells m−2 of vent area. The model showed that the differences in the methanogen populations at Marker 113 and Marker 33 can be explained by differences in the geometry of the subsurface hydrology. Therefore, small-scale variation in the geologic fabric of the upper crust can create varied fluid flow paths fixed in space that harbor persistent and distinct microbial communities, whose metabolic activity produces microbial and chemical signatures at seafloor vents.
References
Johnson HP, Pruis MJ. Fluxes of fluid and heat from the oceanic crustal reservoir. Earth Planet Sci Lett. 2003;216:565–74.
Bar-On YM, Phillips R, Milo R. The biomass distribution on Earth. Proc Natl Acad Sci USA. 2018;115:6505–11.
McNichol J, Stryhanyuk H, Sylva SP, Thomas F, Musat N, Seewald JS, et al. Primary productivity below the seafloor at deep-sea hot springs. Proc Natl Acad Sci USA. 2018;115:6756–61.
Butterfield DA, Roe KK, Lilley MD, Huber JA, Baross JA, Embley RW, et al. Mixing, reaction and microbial activity in the sub-seafloor revealed by temporal and spatial variation in diffuse flow vents at Axial Volcano. In: Wilcock WSD, DeLong EF, Kelley DS, Baross JA, Cary SC, editors. The subseafloor biosphere at mid-ocean ridges. Washington, DC: American Geophysical Union; 2004. p. 269–89.
Mehta MP, Baross JA. Nitrogen fixation at 92 °C by a hydrothermal vent archaeon. Science. 2006;314:1783–6.
Ver Eecke HC, Butterfield DA, Huber JA, Lilley MD, Olson EJ, Roe KK, et al. Hydrogen-limited growth of hyperthermophilic methanogens at deep-sea hydrothermal vents. Proc Natl Acad Sci USA. 2012;109:674–9. 13
Stewart LC, Jung JH, Kim YT, Kwon SW, Park CS, Holden JF. Methanocaldococcus bathoardescens sp. nov., a hyperthermophilic methanogen isolated from a volcanically active deep-sea hydrothermal vent. Int J Syst Evol Microbiol. 2015;65:1280–3.
Topçuoğlu BD, Stewart LC, Morrison HG, Butterfield DA, Huber JA, Holden JF. Hydrogen limitation and syntrophic growth among natural assemblages of thermophilic methanogens at deep-sea hydrothermal vents. Front Microbiol. 2016;7:1240.
Huber JA, Butterfield DA, Baross JA. Temporal changes in archaeal diversity and chemistry in a mid-ocean ridge subseafloor habitat. Appl Environ Microbiol. 2002;68:1585–94.
Meyer JL, Akerman NH, Proskurowski G, Huber JA. Microbiological characterization of post-eruption “snowblower” vents at Axial Seamount, Juan de Fuca Ridge. Front Microbiol. 2013;4:153.
Fortunato CS, Huber JA. Coupled RNA-SIP and metatranscriptomics of active chemolithoautotrophic communities at a deep-sea hydrothermal vent. ISME J. 2016;10:1925–38.
Fortunato CS, Larson B, Butterfield DA, Huber JA. Spatially distinct, temporally stable microbial populations mediate biogeochemical cycling at and below the seafloor in hydrothermal vent fluids. Environ Microbiol. 2018;20:769–84.
Takai K, Gamo T, Tsunogai U, Nakayama N, Hirayama H, Nealson KH, et al. Geochemical and microbiological evidence for a hydrogen-based, hyperthermophilic subsurface lithoautotrophic microbial ecosystem (HyperSLiME) beneath an active deep-sea hydrothermal field. Extremophiles. 2004;8:269–82.
Perner M, Kuever J, Seifert R, Pape T, Koschinsky, Schmidt K, et al. The influence of ultramafic rocks on microbial communities at the Logatchev hydrothermal field, located 15°N on the Mid-Atlantic Ridge. FEMS Microbiol Ecol. 2007;61:97–109.
Flores GE, Campbell JH, Kirshtein JD, Meneghin J, Podar M, Steinberg JI, et al. Microbial community structure of hydrothermal deposits from geochemically different vent fields along the Mid-Atlantic Ridge. Environ Microbiol. 2011;13:2158–71.
Orphan VJ, Taylor LT, Hafenbradl D, DeLong EF. Culture-dependent and culture-independent characterization of microbial assemblages associated with high-temperature petroleum reservoirs. Appl Environ Microbiol. 2000;66:700–11.
Dahle H, Garshol F, Madsen M, Birkeland NK. Microbial community structure analysis of produced water from a high-temperature North Sea oil-field. Antonie Van Leeuwenhoek. 2008;93:37–49.
Lewin A, Johansen J, Wentzel A, Kotlar HK, Drabløs F, Valla S. The microbial communities in two apparently physically separated deep subsurface oil reservoirs show extensive DNA sequence similarities. Environ Microbiol. 2014;16:545–58.
Okpala GN, Chen C, Fida T, Voordouw G. Effect of thermophilic nitrate reduction on sulfide production in high temperature oil reservoir samples. Front Microbiol. 2017;8:1573.
Huber JA, Mark Welch DB, Morrison HG, Huse SM, Neal PR, Butterfield DA, et al. Microbial population structures in the deep marine biosphere. Science. 2007;318:97–100.
Opatkiewicz AD, Butterfield DA, Baross JA. Individual hydrothermal vents at Axial Seamount harbor distinct subseafloor microbial communities. FEMS Microbiol Ecol. 2009;70:413–24.
Jones WJ, Leigh JA, Mayer F, Woese CR, Wolfe RS. Methanococcus jannaschii sp. nov., an extremely thermophilic methanogen from a submarine hydrothermal vent. Arch Microbiol. 1983;136:254–61.
Huber H, Thomm M, König H, Thies G, Stetter KO. Methanococcus thermolithotrophicus, a novel thermophilic lithotrophic methanogen. Arch Microbiol. 1982;132:47–50.
Zar JH. Biostatistical analysis, 3rd ed. Upper Saddle River, NJ: Prentice-Hall, Inc.; 1996.
Coumou D, Driesner T, Geiger S, Paluszny A, Heinrich CA. High-resolution three-dimensional simulations of mid-ocean ridge hydrothermal systems. J Geophys Res Solid Earth. 2009;114:B07104.
Craft KL, Lowell RP. A boundary layer model for submarine hydrothermal heat flows at on-axis and near-axis regions. Geochem Geophys Geosyst. 2009;10:Q12012.
Larson BI, Houghton JL, Lowell RP, Farough A, Meile CD. Subsurface conditions in hydrothermal vents inferred from diffuse flow composition, and models of reaction and transport. Earth Planet Sci Lett. 2015;424:245–55.
Lowell RP, Houghton JL, Farough A, Craft KL, Larson BI, Meile CD. Mathematical modeling of diffuse flow in seafloor hydrothermal systems: the potential extent of the subsurface biosphere at mid-ocean ridges. Earth Planet Sci Lett. 2015;425:145–53.
Seyfried WE Jr., Mottl MJ. Hydrothermal alteration of basalt by seawater under seawater-dominated conditions. Geochim Cosmochim Acta. 1982;46:985–1002.
Soetaert K, Herman PM. A practical guide to ecological modelling: using R as a simulation platform. Medford, MA: Springer Science & Business Media; 2008.
Takai K, Inoue A, Horikoshi K. Methanothermococcus okinawensis sp. nov., a thermophilic, methane-producing archaeon isolated from a Western Pacific deep-sea hydrothermal vent system. Int J Syst Evol Microbiol. 2002;52:1089–95.
Pruis MJ, Johnson HP. Tapping into the sub-seafloor: examining diffuse flow and temperature from an active seamount on the Juan de Fuca Ridge. Earth Planet Sci Lett. 2004;217:379–88.
Akerman NH, Butterfield DA, Huber JA. Phylogenetic diversity and functional gene patterns of sulfur-oxidizing subseafloor Epsilonproteobacteria in diffuse hydrothermal vent fluids. Front Microbiol. 2013;4:185.
van Wolferen M, Orell A, Albers SV. Archaeal biofilm formation. Nat Rev Microbiol. 2018;16:699–713.
Wirth R, Luckner M, Wanner G. Validation of a hypothesis: colonization of black smokers by hyperthermophilic microorganisms. Front Microbiol. 2018;9:524.
Haymon RM, Fornari DJ, Von Damm KL, Lilley MD, Perfit MR, Edmond JM, et al. Volcanic eruption of the mid-ocean ridge along the East Pacific Rise crest at 9° 45–52ʹN: direct submersible observations of seafloor phenomena associated with an eruption event in April, 1991. Earth Planet Sci Lett. 1993;119:85–101.
Juniper SK, Martineu P, Sarrazin J, Gélinas Y. Microbial-mineral floc associated with nascent hydrothermal activity on CoAxial Segment, Juan de Fuca Ridge. Geophys Res Lett. 1995;22:179–82.
Topçuoğlu BD, Meydan C, Nguyen TB, Lang SQ, Holden JF. Growth kinetics, carbon isotope fractionation, and gene expression in the hyperthermophile Methanocaldococcus jannaschii during hydrogen-limited growth and interspecies hydrogen transfer. Appl Environ Microbiol. 2019; https://doi.org/10.1128/AEM.00180-19.
Schönheit P, Moll J, Thauer RK. Growth parameters (K s, µmax, Y s) of Methanobacterium thermoautotrophicum. Arch Microbiol. 1980;127:59–65.
Morgan RM, Pihl TD, Nölling J, Reeve JN. Hydrogen regulation of growth, growth yields, and methane gene transcription in Methanobacterium thermoautotrophicum ΔH. J Bacteriol. 1997;179:889–98.
Costa KC, Yoon SH, Pan M, Burn JA, Baliga NS, Leigh JA. Effects of H2 and formate on growth yield and regulation of methanogenesis in Methanococcus maripaludis. J Bacteriol. 2013;195:1456–62.
Caress DW, Clague DA, Paduan JB, Martin JF, Dreyer BM, Chadwick Jr WW, et al. Repeat bathymetric surveys at 1-metre resolution of lava flows erupted at Axial Seamount in April 2011. Nat Geosci. 2012;5:483–8.
Acknowledgements
We thank Susan Merle, Andra Bobbitt, and Bill Chadwick for providing the site map. We thank the captains and crews of the R/V Falkor, R/V Thompson, and R/V Brown as well as the ROV ROPOS and JASON groups. Lisa Zeigler Allen, Giora Proskurowski, Kevin Roe, and Begüm Topçuoğlu provided critical support in sample collection and experimental design and execution. This is C-DEBI contribution number 464.
Funding
This work was funded by the Gordon and Betty Moore Foundation grant GBMF 3297 to JAH, JFH, JJV, and DAB; the NASA Earth and Space Science Fellowship Program grant NNX11AP78H to LCS and JFH; NSERC Discovery grant to CKA, a Fulbright New Zealand-Ministry of Research, Science and Technology Graduate Award to LCS; NSF grant OCE-1547004 to JFH, NSF Grant OCE-1546695 to DAB, NSF grants GEO-1451356 and GEO-1238212 to JJV, the NSF Center for Dark Energy Biosphere Investigations (C-DEBI) grant OCE-0939564 to JAH, and by University of Washington Joint Institute for Study of the Atmosphere and Oceans, NOAA Cooperative Agreement NA15OAR4320063. The data collected in this study includes work supported by the Schmidt Ocean Institute during cruise FK010-2013 aboard R/V Falkor.
Author information
Authors and Affiliations
Contributions
LCS, CKA, and JFH designed the study; field sampling was conducted by LCS, CKA, CSF, BL, DAB, JAH, and JFH; lab analyses were done by LCS, CSF, and JFH; modeling was done by CKA, JJV, and JFH; the manuscript was written by LCS, CKA, and JFH with contributions from all coauthors.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Stewart, L.C., Algar, C.K., Fortunato, C.S. et al. Fluid geochemistry, local hydrology, and metabolic activity define methanogen community size and composition in deep-sea hydrothermal vents. ISME J 13, 1711–1721 (2019). https://doi.org/10.1038/s41396-019-0382-3
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41396-019-0382-3
This article is cited by
-
Geography, not lifestyle, explains the population structure of free-living and host-associated deep-sea hydrothermal vent snail symbionts
Microbiome (2023)
-
Mcr-dependent methanogenesis in Archaeoglobaceae enriched from a terrestrial hot spring
The ISME Journal (2023)
-
Desulfovulcanus ferrireducens gen. nov., sp. nov., a thermophilic autotrophic iron and sulfate-reducing bacterium from subseafloor basalt that grows on akaganéite and lepidocrocite minerals
Extremophiles (2022)