Abstract
Calorimetry of single biological entities remains elusive. Suspended microchannel resonators (SMRs) offer excellent performance for real-time detection of various analytes and could hold the key to unlocking pico-calorimetry experiments. However, the typical readout techniques for SMRs are optical-based, and significant heat is dissipated in the sensor, altering the measurement and worsening the frequency noise. In this manuscript, we demonstrate for the first time full on-chip piezoelectric transduction of SMRs on which we focus a laser Doppler vibrometer to analyze its effect. We demonstrate that suddenly applying the laser to a water-filled SMR causes a resonance frequency shift, which we attribute to a local increase in temperature. When the procedure is repeated at increasing flow rates, the resonance frequency shift diminishes, indicating that convection plays an important role in cooling down the device and dissipating the heat induced by the laser. We also show that the frequency stability of the device is degraded by the laser source. In comparison to an optical readout scheme, a low-dissipative transduction method such as piezoelectricity shows greater potential to capture the thermal properties of single entities.
Similar content being viewed by others
Introduction
Micro- and nanoelectromechanical systems (M/NEMS) have long been established as physical sensors. While such devices can be operated in static mode through surface-stress effects1,2, their operation as resonators in dynamic mode offers a wider range of applications3. In this latter configuration, the magnitude of interest is the resonance frequency of the device, and the performance and stability are better when the mechanical losses are low (high quality factor). The great promise shown by resonant beam sensors has rapidly attracted interest for applications in the biological field4. Nevertheless, the study of biological samples typically implies a liquid environment. Immersing the resonant beams in fluid leads to a degradation of the quality factor due to viscous drag, especially for flexural beams5.
An elegant solution to this issue was brought to the microscale by Burg and Manalis6, where a microfluidic channel was made part of a resonant beam6. These so-called suspended microchannel resonators (SMRs) were later encapsulated in vacuum, showing quality factors up to three orders of magnitude higher than the same resonator immersed in liquid7. Therefore, the use of SMRs reduces damping, and thus one can reach better sensitivities8. Over the years, applications of SMRs have diversified: measurement of the pressure9, density10,11, and viscosity12 of homogeneous samples or characterization of the mass, density, volume, growth rate, and deformation of populations of cells13,14.
A field that remains elusive is the calorimetry study of single biological entities. Typically, biocalorimetry experiments study tissue aggregates or multiple analytes together15,16. The community indeed lacks tools to measure the thermal properties of single biological entities, which have been reported only a few times17,18,19. SMRs are a great candidate to become such a tool.
However, to exploit the full sensing potential of these devices, the transduction strategy needs to be optimized. Most of the SMRs presented in the literature are actuated with a piezo-ceramic shaker12,13 or, in some cases, electrostatically6,20. On the one hand, the latter option can be implemented on a chip, but then the device cannot operate over its full dynamic range (either weak actuation or strong nonlinearity). On the other hand, using a shaker requires attaching the chip to the piezo-ceramic slab, inevitably making the system bulkier. We recently showed the piezoelectric (PZE) actuation of SMRs, which is integrated on-chip, is linear, and allows for large amplitudes to be reached21.
Regarding detection, the most commonly used measurement methods are optical-based, whether they consist of optical levers6, interferometers10, or laser Doppler vibrometers9,12,22. Although they offer excellent performance, those solutions are bulky, generally costly, and time-consuming to set up. In addition, a portion of the laser power is absorbed by the SMR; therefore, heating the SMR and shifting the resonance frequency. This effect strongly depends on the position of the laser during measurement and the laser power fluctuations due to heat-induced local stresses at the laser position23,24. For this reason, some groups have developed optical-free readout methods, such as piezoresistive25,26, PZE through quartz tuning fork coupling27, or electrostatic11 methods. A more exhaustive list of the existing transduction techniques for SMRs can be found in our recently published review28.
In this manuscript, we present for the first time full-on-chip PZE transduction of flexural SMRs with integrated electrodes. This transduction mechanism offers notable advantages; for example, the electrodes are directly integrated on the chip, and the operation of the devices dissipates little power. Our experimental setup allows us to compare the measurement noise between PZE transduction and an alternative detection scheme29. Indeed, we show that focusing a laser source on the beam creates a shift in the resonance frequency due to the local temperature increase of the SMR. This effect is modulated by the flow rate of the liquid within the microfluidic channel: a higher flow rate accelerates the cooling of the SMR and reduces the heat-induced frequency shift. We also compare the frequency stability in different situations and show that focusing the laser on the device significantly degrades its performance. We show that for our devices, avoiding the use of heat absorption within the transduction is preferential to reach better frequency stability and, as such, improve the sensitivity of the resonators. PZE SMRs also show potential for pico-calorimetry applications.
Results and discussion
It is well known that the resonance frequency of SMRs depends on their effective mass and thus varies with the density of the fluid flowing inside the channels10,11,21. The temperature behavior of such devices as operated with PZE actuation and optical readout, empty and fluid-filled, was previously described29. However, in that former experiment, the readout laser heated the SMRs and thus affected the operating temperature of the device. With full PZE transduction, we can remove the laser-heating effect and have more control over the experiment. We do this by encapsulating the devices in vacuum in a dedicated interface and by then sweeping the temperature of the chip between 25 and 50 °C. Each temperature set point is stabilized by a thermoelectric temperature controller (ILX Lightwave LDT-5910C, Newport, USA), implemented with proportional integral derivative (PID) control. The controller reads the temperature from a thermistor located inside the metallic fluidic connector and consequently adjusts the current input of a Peltier module in direct contact with the interface. After changing each set point, we wait for ~5 min for the temperature to be uniform on the chip. The frequency is monitored with a phase-locked loop (PLL) control from a lock-in amplifier (UHFLI, Zurich Instruments, Switzerland).
Figure 1 shows the relative frequency shifts of a 250-μm- and a 500-μm-long SMR filled with deionized water, measured with full PZE transduction. As expected, when the temperature increases, the resonance frequency of the SMR follows the same trend. Indeed, the density of the water is inversely proportional to the temperature and decreases at a faster rate than the Young’s modulus of the resonator’s structural material. It is notable that the data are valid for any SMR length. The responsivity of the device with respect to the temperature only depends on the ratio of the cross-sectional areas of the solid and the fluid of the SMR29. Figure 1 also shows great agreement in the comparison of our experimental data to a finite-element analysis simulation without fitting parameters.
Resonance frequency of the first mode of a 250-μm- and a 500-μm-long SMR filled with deionized water, as a function of temperature applied using uniform heating. Even though the Young’s modulus of the structural material decreases with decreasing temperature, making the device more compliant, the resonance frequency change is dominated by the decreasing density of the water
Following this initial characterization, we investigate the heat that is transferred to the filled SMR from our optical detection system, consisting of a laser Doppler vibrometer (LDV OFV-5000 with OFV-551, Polytec, Germany). This allows us to estimate how much the laser readout affects the previously published results29. To do this, we focus the laser at the tip of the SMR and switch it on and off repeatedly and for different periods of time (5, 10, and 20 s) while tracking the frequency. The laser power was determined independently with a power meter (PM100D, ThorLabs, USA) and was ~645 μW.
We repeat this procedure at different input pressures within the microfluidic channel, as shown in Fig. 2. The liquid pressure is measured by a pressure sensor on the fluidic line before the connection to the interface. The pressure is applied using a syringe pump (Low-Pressure module, CETONI GmbH) controlled by a PID loop operated through dedicated commercial software (Qmix Elements, CETONI GmbH).
While the resonance frequency of the SMR is continuously detected via piezoelectric transduction, the laser beam is focused on the tip of the beam and switched on and off repeatedly. We observe a positive frequency shift when the laser turns on and a recovery of the baseline after shut-off. The magnitude of the shift does not depend on the illumination time. The experiment is performed at different input pressures and lasts ~1 h
As shown in Fig. 2, when the beam collides with the SMR, a positive shift in resonance frequency is immediately detected. This effect looks similar to that of a uniform increase of 20 °C in the temperature of the system, if compared to Fig. 1. The resonance frequency reverts back to its original value as soon as the laser beam is switched off. We do not acknowledge any significant difference in the resonance frequency shifts depending on how fast the laser is switched on and off and how long it is kept on. We attribute this behavior to a temporary and local change in the water density as it is heated up by the laser. As the laser shuts off, the flow of water inside the SMR carries away excessive heat, and the system returns to the initial conditions.
As we increase the fluidic pressure, we notice two things: (i) a reduction in the frequency baseline, which is attributed to the resonance frequency dependence on pressure9 and (ii) a reduction in the shift (Fig. 2) due to laser illumination. This latter effect is a clear evidence that the water acts as a cooling medium via convection and that it is possible to enhance the cooling efficiency through a higher flow rate.
The first effect shows a reduction in the baseline frequency between the beginning of the experiment at 0 bar pressure and the end at ~1.5 bar. We can characterize the pressure responsivity of our SMR: −24 p.p.m./bar. Our understanding is that the input pressure creates an expansion of the channel volume, leading to an increased effective mass. Since the frequency shift is negative, it seems that this effect dominates over the stiffening of the beam. Nevertheless, this effect is negligible when compared to the effect of laser illumination.
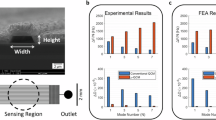
In this paper, we present experiments that use SMRs of two different lengths (250-µm- and 500-µm-long) found on different chips, each of which has different channel lengths. In particular, the 250-µm-long SMR (device A) is part of a channel with two resonators, while the 500-µm-long SMR (device B) is part of a channel with six resonators. Therefore, the fluidic resistances of the microchannels are different, and the same pressure does not provide the same flow rate in each of the chips. To appropriately compare the effect of laser heating and convection cooling on the different devices, we plot the measurements with respect to the flow rate instead of the input pressure, which is experimentally fixed, since the measurements are performed in a pressure-controlled setup. To appropriately calculate the flow rate, we first divide the applied pressure at the inlet by the fluidic resistance of the respective channel. According to their geometrical dimensions, the channel of device A features a fluidic resistance of ~5.26 bar/(µl/min), whereas the channel of device B has a resistance ~1.46 times higher due to the additional length. To determine the dimensions of each channel, we used the experimentally determined values after cutting through an SMR via focused ion beam technology and observed its cross-sectional dimensions with a scanning electron microscope. The details of the measurements are available in the Supplementary information. To fine-tune the flow rates, we use the results of finite-element modeling (FEM) transient simulations of the stabilization of temperature in our system compared to experimental results. Benefiting from our PLL tracking of the frequency, we can study the time constant of the transition. Looking closer at the apparently abrupt changes in frequency that are seen in Fig. 2, we can indeed see exponential decay behavior, which can be fitted to extract the time constant for each event (see Supplementary information). Figure 3 shows the extracted time constants vs flow rate, both in absolute and relative terms. Importantly, the values of these time constants are dependent on the thermal conductivity, cross-sectional dimensions, and flow rate. Thus, it is possible to use the comparison between the experiment and simulation to (i) determine that the thermal conductivity of our silicon nitride is κSiN ≈ 4 W/(mK) and (ii) fine-tune the values of the fluidic resistances mentioned above, which are Rf,250 μm = 5.26 bar/(µl/min) (same as estimated from dimensions) and Rf,500 μm = 8.63 bar/(µl/min) (12% larger than estimated from dimensions).
The time constant τ of the frequency transition when the laser is switched on is studied for both devices. The time constant is decreasing with increasing flow rate, confirming that higher fluid velocity in the channel is more efficient to cool down the SMR. The two devices behave similarly, with the absolute time constant of the 500-μm-long SMR being 3.5 to 3.75 times higher than that of the 250-μm-long SMR (τ scales with the square of the length)
The behavior shown in Fig. 3 can be explained considering three sources of heat dissipation in the system: (i) conduction through the ls-SiNx, (ii) conduction through the water, and (iii) convection in the water due to the flow. As the devices are operated in vacuum (0.01 Pa pressure), convection and conduction to the air around the device are neglected. We also neglect the effect of thermal radiation because the temperature changes are not very large (see further discussion below). We notice that the FEM results show a planarization of the value of the thermal response time for flow rates below 20 nl/min (Fig. 3). At lower flow rate values, conduction dominates, and thus no dependence on the flow rate is seen. For the range of flow rate values that we use in experiments, convection due to the internal liquid is the dominant mechanism for heat transfer.
Using the adjusted values for the fluidic resistances, we can also plot the relative frequency shift for each SMR under study as a function of the flow rate, which we show in Fig. 4. We overlap the experimental results (scattered data, with error bars) with the results from an FEM simulation using modal analysis with the stationary thermal state as a boundary condition. The matching between the FEM and experimental results is remarkable. We can see how for flow rates <20 nl/min, the simulated response flattens out, as was the case for the thermal response times. For larger flow rates, the frequency shift decreases in magnitude when the flow rate increases. For example, in device A, a flow rate of 280 nl/min corresponds to a frequency 44% lower than in the case of no flow rate. As discussed above, the flow rates for each device are different because the fluidic resistances are different. For device B, it is not possible to reach higher flow rates because otherwise, the required input pressure could break the inlet membrane.
Effect of fluidic flow on the local heating induced by the laser focused on the cantilever’s tip. Each point represents the relative frequency shift caused by a change in laser state (on/off), normalized to the maximum shift (with no flow rate). Experiment data and simulations are shown for two devices of two different chip configurations. There is a decrease in the frequency shift with respect to the flow rate, illustrating a more efficient cooling of the device as the fluid velocity increases. Insets: Device A has a length of 250 μm and is part of a 2-SMR array, while Device B extends for 500 μm, being part of a more complex 6-SMR array
The last interesting question that remains is whether the laser-heating effect, which affects the value of the resonance frequency, also affects our ability to determine this frequency. To evaluate that, we measure the frequency stability and calculate the Allan deviation, which is directly proportional to the sensitivity of a given resonating sensor and is the recognized tool to assess device performance in the M/NEMS community30. For this experiment, we keep the flow rate at a constant value of ~50 nl/min, and we track the resonance frequency with a PLL (bandwidth 100 Hz). We recorded the frequency for 5 min under three distinct conditions: without any external light contribution, with the standard white light for microscope illumination focused on the beam, and with both the white light and the LDV laser focused. Figure 5 depicts the Allan deviation in the three different cases. We notice that additional light contributions are detrimental to the device performance. In particular, switching on the LDV detection scheme worsens the stability by two orders of magnitude (with an integration time of 1 s). This result indicates that the performance of SMRs is greatly reduced when an optical readout is implemented. To reach ultimate levels of detection, it seems that adopting on-chip, built-in readout techniques, such as piezoresistive or PZE techniques, would yield higher sensitivities.
Allan deviation of a 500-μm-long SMR with water flowing at ~50 nl/min (input pressure 370 mbar). A minimum deviation below 20 p.p.b. with integration times between 2 and 4 s is achieved when all external light contributions are removed. In contrast, the LED (for cantilever imaging) and the laser contribute significantly to the noise of the resonator
In this manuscript, we demonstrate for the first time full on-chip PZE transduction of flexural SMRs. This detection scheme allows us to analyze the back-action of an alternative and widely used optical detection method—laser Doppler vibrometry—on our device. We show that the laser beam brings a significant amount of heat, measured with the resonance frequency shift, to the SMR. The extent of the frequency shift can be controlled by the flow rate of the fluidic analyte, indicating that convection is a significant mechanism of heat dissipation. We even observe that a significant improvement in frequency noise is attained when no external light illuminates the SMR.
Although on-chip PZE transduction increases the complexity of the fabrication and adds to the effective mass of the SMR, the advantages outweigh the drawbacks since we gain frequency stability (compensating for the increase in effective mass) and simplify the overall experimental setup, which can mean a paradigm shift for the field of calorimetry of single cells.
Materials and methods
The structural material of the PZE SMRs used in this work is low-stress silicon nitride (ls-SiNx). The devices consist of singly-clamped beams with cross-sectional dimensions of ~7 × 30 μm2 and lengths of 250 or 500 μm. From inlet to outlet, the microfluidic channel runs through several SMRs located in series with the channel, but physically organized in parallel (see Fig. 6a). In each resonator, the embedded channel forms a U-turn at the tip of the beam, and its dimensions are ~10 ×5 μm2. More accurate dimensions can be found in the Supplementary information. As shown in Fig. 6a, each resonator features a 25-nm-thick platinum ground electrode. A 300-nm-thick layer of PZE material, aluminum nitride, was deposited and covered with another layer of platinum (50 nm) forming the top electrode. These two layers were subsequently patterned, creating two separate fingers for independent actuation and detection of the SMRs. More details about the fabrication of those devices can be found elsewhere21,31. After the wafer was cleaved, the chips were interfaced and encapsulated by a custom-made microfluidic connector also serving as a vacuum chamber29.
We perform the dynamic characterization of our devices using the Zurich Instrument lock-in amplifier. We start by sending a harmonic signal to one top electrode while recording the output signal from the other top electrode (their ground is common), and we do this while sweeping the signal’s frequency around the resonance frequency of the device. Figure 6c shows frequency sweeps of the PZE signal measured at the detection electrode for actuation voltages from 500 mV to 2 V. We can see that the resonance peak is buried in a large background; the linear increase of the signal level away from resonance as well as the small phase change across the resonance are problematic for suitable detection. This large background level is due to the design and fabrication choices: the electrode tracks cover a large area on the wafer, and the polysilicon layer used as a sacrificial material to fabricate hollow channels is heavily doped with conducting POCl3. Both points contribute to a very large parasitic feedthrough capacitance. A detailed electrical layout depicts the situation in Fig. 6b (in black), where Cf1 represents the feedthrough capacitance between the actuation and detection electrodes. Within this schematic, the motional current coming from the SMR (im) is superimposed with a parasitic current if1, which is directly proportional to the magnitude of Cf1. Since the inherent linearity of PZE detection makes it difficult to implement most of the methods for background cancellation32,33, we decide to balance, away from resonance, the current at the output point. This strategy has been used in the past for different transduction techniques34,35,36,37,38. We implement it by connecting a second resonator on the same chip, but operating at a different resonance frequency with respect to the device to detect. We feed this second device a harmonic signal at the same frequency and amplitude as the driving signal, but with a phase shift of ~180°. By doing this (in gray in Fig. 6b), we remove most of the background from the output point. This can be seen in detail in Fig. 6b (in gray), where a second parasitic current if2 reduces the background from the output point. By carefully tweaking the amplitude and phase of V2(ω), we can reduce the contribution of if1 to the output current of the resonator of interest by more than three orders of magnitude. Therefore, we can see a much higher signal-to-background ratio than in the unbalanced configuration, as is shown in Fig. 6d. The amplitude now portrays a resonance peak standing well above the background, and the phase undergoes a 180° phase shift; these characteristics allow the device to be operated within PLL to easily track the resonance frequency over extended periods of time.
a Colored scanning electron microscope image of an array of two SMRs, 250 and 500 μm long, with their integrated PZE electrodes on top. The microfluidic channel is represented in purple, the bottom contact in orange, and the top contacts in cyan. b Electrical drawing of the balancing bridge circuit implemented to lower the level of parasitic background. c Frequency sweep of the amplitude and phase of a 250-μm-long SMR filled with deionized water without balancing circuit, for different actuation voltages. The signal-to-background ratio is ~1.012. d Same frequency sweep using the balanced bridge configuration. The signal-to-background ratio is greatly enhanced and >30
References
Wu, G. et al. Bioassay of prostate-specific antigen (PSA) using microcantilevers. Nat. Biotechnol. 19, 856–60 (2001).
Ndieyira, J. W. et al. Nanomechanical detection of antibiotic-mucopeptide binding in a model for superbug drug resistance. Nat. Nanotechnol. 3, 691–6 (2008).
Tamayo, J., Kosaka, P. M., Ruz, J. J., San Paulo, A. & Calleja, M. Biosensors based on nanomechanical systems. Chem. Soc. Rev. 42, 1287–311 (2013).
Arlett, J. L., Myers, E. B. & Roukes, M. L. Comparative advantages of mechanical biosensors. Nat. Nanotechnol. 6, 203–15 (2011).
Sader, J. E. Frequency response of cantilever beams immersed in viscous fluids with applications to the atomic force microscope. J. Appl. Phys. 84, 64–76 (1998).
Burg, T. P. & Manalis, S. R. Suspended microchannel resonators for biomolecular detection. Appl. Phys. Lett. 83, 2698–2700 (2003).
Burg, T. P. et al. Weighing of biomolecules, single cells and single nanoparticles in fluid. Nature 446, 1066–9 (2007).
Olcum, S. et al. Weighing nanoparticles in solution at the attogram scale. Proc. Natl Acad. Sci. USA 111, 1310–1315 (2014).
Khan, M. F., Knowles, B., Dennison, C. R., Ghoraishi, M. S. & Thundat, T. Pressure modulated changes in resonance frequency of microchannel string resonators. Appl. Phys. Lett. 105, 013507 (2014).
Malvar, O. et al. Highly sensitive measurement of liquid density in air using suspended microcapillary resonators. Sensors 15, 7650–7 (2015).
Alveringh, D., Wiegerink, R. J. & Lotters, J. C. Integrated pressure sensing using capacitive coriolis mass flow sensors. J. Microelectromech. Syst. 26, 653–661 (2017).
Khan, M. F. et al. Online measurement of mass density and viscosity of pL fluid samples with suspended microchannel resonator. Sens. Actuators B 185, 456–461 (2013).
Cermak, N. et al. High-throughput measurement of single-cell growth rates using serial microfluidic mass sensor arrays. Nat. Biotechnol. 34, 1052–1059 (2016).
Shaw Bagnall, J. et al. Deformability of tumor cells versus blood cells. Sci. Rep. 5, 18542 (2015).
Braissant, O. et al. Isothermal microcalorimetry accurately detects bacteria, tumorous microtissues, and parasitic worms in a label-free well-plate assay. Biotechnol. J. 10, 460–468 (2015).
Krenger, R., Lehnert, T. & Gijs, M. A. M. Dynamic microfluidic nanocalorimetry system for measuring Caenorhabditis elegans metabolic heat. Lab Chip 18, 1641–1651 (2018).
Inomata, N., Toda, M. & Ono, T. Highly sensitive thermometer using a vacuum-packed Si resonator in a microfluidic chip for the thermal measurement of single cells. Lab Chip 16, 3597–3603 (2016).
Chien, M.-H., Brameshuber, M., Rossboth, B. K., Schütz, G. J. & Schmid, S. Single-molecule optical absorption imaging by nanomechanical photothermal sensing. Proc. Natl Acad. Sci. USA 115, 11150–11155 (2018).
Gaiduk, A., Yorulmaz, M., Ruijgrok, P. V. & Orrit, M. Room-temperature detection of a single molecule’s absorption by photothermal contrast. Science 330, 353–356 (2010).
Modena, M. M., Wang, Y. & Burg, T. P. Resolution enhancement of suspended microchannel resonators by mass correlation analysis. Lab Chip 14, 342–350 (2014).
De Pastina, A., Maillard, D. & Villanueva, L. G. Fabrication of suspended microchannel resonators with integrated piezoelectric transduction. Microelectron. Eng. 192, 83–87 (2018).
Calmo, R. et al. Monolithic glass suspended microchannel resonators for enhanced mass sensing of liquids. Sens. Actuators B 283, 298–303 (2018).
Pini, V. et al. Shedding light on axial stress effect on resonance frequencies of nanocantilevers. ACS Nano 5, 4269–75 (2011).
Larsen, T. et al. Position and mode dependent optical detection back-action in cantilever beam resonators. J. Micromech. Microeng. 27, 035006 (2017).
Lee, J. et al. Suspended microchannel resonators with piezoresistive sensors. Lab Chip 11, 645–51 (2011).
Gagino, M. et al. Suspended nanochannel resonator arrays with piezoresistive sensors for high-throughput weighing of nanoparticles in solution. ACS Sensors https://doi.org/10.1021/acssensors.0c00394 (2020).
Lee, D. et al. Pulled microcapillary tube resonators with electrical readout for mass sensing applications. Sci. Rep. 6, 33799 (2016).
De Pastina, A. & Villanueva, L. G. Suspended micro/nano channel resonators: a review. J. Micromech. Microeng. 30, 043001 (2020).
Maillard, D., De Pastina, A., Larsen, T. & Villanueva, L. G. Modular interface and experimental setup for in-vacuum operation of microfluidic devices. Rev. Sci. Instrum. 90, 045006 (2019).
Schmid, S., Villanueva, L. G. & Roukes, M. L. Fundamentals of nanomechanical resonators. Fundam. Nanomech. Resonators. 1–175 (Springer, 2016).
De Pastina, A. PZE‐Transduced Suspended Microchannel Resonators for Sensing Applications. Ph.D. thesis (2018).
Bargatin, I., Myers, E. B., Arlett, J., Gudlewski, B. & Roukes, M. L. Sensitive detection of nanomechanical motion using piezoresistive signal downmixing. Appl. Phys. Lett. 86, 133109 (2005).
Sazonova, V. et al. A tunable carbon nanotube electromechanical oscillator. Nature 431, 284–7 (2004).
Ekinci, K. L., Yang, Y. T., Huang, X. M. H. & Roukes, M. L. Balanced electronic detection of displacement in nanoelectromechanical systems. Appl. Phys. Lett. 81, 2253–2255 (2002).
Feng, X. L., White, C. J., Hajimiri, A. & Roukes, M. L. A self-sustaining ultrahigh-frequency nanoelectromechanical oscillator. Nat. Nanotechnol. 3, 342–6 (2008).
Dukic, M., Adams, J. D. & Fantner, G. E. Piezoresistive AFM cantilevers surpassing standard optical beam deflection in low noise topography imaging. Sci. Rep. 5, 16393 (2015).
Villanueva, L. G. et al. Surpassing fundamental limits of oscillators using nonlinear resonators. Phys. Rev. Lett. 110, 177208 (2013).
Toledo, J. et al. Piezoelectric MEMS resonators for monitoring grape must fermentation. In 27th Micromechanics and Microsystems Europe Workshop (MME 2016), Vol. 757, 01202027 (2016).
Acknowledgements
We acknowledge financial support from Swiss SNF grant 200020_184935. We also thank the ATME mechanical workshop at EPFL for the manufacturing of the interface connector and chamber and the Center of MicroNanoTechnology (CMi) at EPFL for their support and help in the fabrication of the devices.
Author information
Authors and Affiliations
Contributions
D.M. and L.G.V. designed the experiment. A.D.P. and D.M. fabricated the devices; D.M. performed the experiments. D.M., A.M.A., and L.G.V. performed the simulations. D.M., A.D.P., and L.G.V. wrote the paper.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no competing interests.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Maillard, D., De Pastina, A., Abazari, A.M. et al. Avoiding transduction-induced heating in suspended microchannel resonators using piezoelectricity. Microsyst Nanoeng 7, 34 (2021). https://doi.org/10.1038/s41378-021-00254-1
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41378-021-00254-1
This article is cited by
-
Advanced operation of heated fluidic resonators via mechanical and thermal loss reduction in vacuum
Microsystems & Nanoengineering (2023)
-
Measuring nanoparticles in liquid with attogram resolution using a microfabricated glass suspended microchannel resonator
Microsystems & Nanoengineering (2022)
-
Adaptive under-actuated control for capacitive micro-machined ultrasonic transducer based on an accurate nonlinear modeling
Nonlinear Dynamics (2022)
-
Cellular and biomolecular detection based on suspended microchannel resonators
Biomedical Engineering Letters (2021)