Abstract
A wearable energy harvester technology is developed for generating electricity from the movement of human joints. A micro-electroplated ferromagnetic nickel cantilever is integrated with a piezoelectric element and bonded on a flexible substrate. Based on the magnetic interaction between the magnetized cantilever and a magnet on the substrate, a novel vertical-vibration frequency-up-conversion (FUC) structure is formed to generate stable amounts of electric energy per cycle from the horizontal substrate stretching/rebounding. The two ends of the flexible substrate are attached on both sides of a limb joint to transform joint rotation into substrate stretching. During limb movement, the flexible substrate is horizontally stretched and rebounded, causing the cantilever to vertically release from and return to the magnet, thereby exciting the piezoelectric cantilever into resonant generation. Since the horizontal low-frequency limb movement is perpendicular to the vertical high-frequency resonance, the stretch has little influence on the resonance of the cantilever. Thus the generated energy is always stable within a wide frequency range of limb movements. The performance of the novel harvester is experimentally verified using a stretching/rebounding movement cycle, where the cycle corresponds to the frequency range of 0.5–5.0 Hz. Within one stretching/rebounding movement cycle, the generated electric energy is stable in the approximate range of 0.56–0.69 μJ for the whole frequency range. Two flexible harvesters are worn on the human elbow and knee for a body kinetic energy harvesting test. Considerable power can always be generated under typical low-frequency limb movements, such as squatting, walking, jogging, and fast running, where the peak-to-peak generated voltages are always approximately 4.0 V. Additionally, energy harvesting under two-directional area stretching is also realized by adjusting the FUC structure layout. The flexible-substrate harvester is promising for various wearable applications.
Similar content being viewed by others
Introduction
Wearable devices are highly demanded for various microsystem applications, such as health care, medical rehabilitation, athletic training, and outdoor equipment1,2. Conventional wearable devices are mainly powered by batteries and thus have a limited working time period. Energy renewal or battery recharge for the devices is too inconvenient to satisfy “plug and play”3,4. To address this issue, the self-powered scheme, in which the device’s power is supplied by an attached wearable energy harvester, is increasingly attracting attention5. The basis of such a self-powered scheme lies in the fact that the human body contains abundant kinetic energy sources during limb movements, such as joint rotation6,7,8,9.
The conversion from kinetic energy to electric energy can be accomplished via piezoelectric, electromagnetic, and electrostatic effects10,11,12. Since conventional kinetic harvesters normally utilize resonant structures, e.g., cantilevers, only movements or vibrations near the resonant frequency can be efficiently harvested, thus hindering operation for a wide frequency band13,14. Many technical efforts have been made to broaden the frequency band, such as the use of multimode coupling, bi-stable structures, and stoppers15,16,17. However, wearable harvesters are normally miniature in size and feature a much higher frequency response of hundreds of Hz than the sub-Hz to several Hz slow-speed movement of human limbs18. Therefore, it is necessary to find a way, e.g., frequency-up-conversion (FUC), to bridge the great frequency disparity19,20. Galchev et al. proposed an interesting parametric frequency-increased generator for FUC generation under low-frequency vibrations21. The device consists of a large inertial mass and two generator structures placed on either side of the inertial mass for high-frequency oscillation. The inertial mass snaps back and forth between the two generator structures due to a magnetic attracting force. As the force on the inertial mass overwhelms the holding magnetic force, the inertial mass detaches, and the generator structures can generate electric energy. When the vibration amplitude is larger than the size of the device, the FUC scheme helps to break through the vibration displacement limit of the device. Hence, the FUC structure realizes more effective electric generation than conventional linear harvesters. Takahashi et al. proposed another kind of attraction-based FUC energy harvester in which an electrostatic attracting force is used for frequency conversion22. Additionally, impact-based FUC harvesters have been reported, which usually consist of sliding balls that physically impact high-frequent resonators for energy generation23,24. Since the free sliding structures can effectively absorb energy from ambient vibrations, these kinds of FUC harvesters are suitable for electricity generation under wideband vibrations21,23,24.
Triboelectric flexible harvesters have recently been developed for generating energy from body movement, where free electrons can be induced by the rubbing between a dielectric material and an electrode25,26,27. Novel woven structures of triboelectric flexible harvesters have also been developed, which show great potential in large-scale and low-cost applications28. Based on a single-friction-surface scheme, transparent triboelectric generating sheets are very convenient for self-powered portable applications, where light human finger touching can induce considerable energy generation29. Moreover, the triboelectric generation technique has been widely used to convert wind energy, tide energy, etc. into electric power30.
In this study, a tiny wearable energy harvester is proposed and developed for efficiently generating stable energy from low-frequency limb movement. In the harvester, a micro-electroplated nickel ferromagnetic cantilever and a magnet are individually bonded on a flexible substrate, and in the initial state, they are attracted into contact. When the substrate is elongated owing to limb stretching, the cantilever releases from the magnet to resonate. When the substrate rebounds back due to limb retraction, the cantilever is pulled back to the magnet to form a clamped-supported beam that will resonate again in a higher resonance mode. With a piezoelectric thin film attached to the surface, the device can be excited into resonant generation twice within one limb movement cycle. Since the low-frequency horizontal stretching/rebounding movement of the substrate is frequency up-converted into a vertical high-frequency resonance, the harvester can freely resonate and generate stable electric power during each cycle of limb movement. The design, simulation, micro-fabrication, and wearable testing results of the novel flexible-substrate harvester will be detailed in the following.
Materials and methods
Structure design
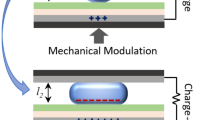
Figure 1a shows a cross-sectional schematic of the proposed wearable energy harvester. An NdFeB magnet and a micromachined nickel cantilever are individually fixed by gluing them to a polydimethylsiloxane (PDMS) film, serving as a flexible substrate, via two glass pedestals. A lead-zirconate-titanate (PZT) piezoelectric ceramic film is bonded to the top surface of the cantilever, with conductive silver paste as the bonding media layer.
a Cross-sectional view of the energy harvester. b Schematic of the flexible-substrate stretching process that causes the cantilever release from the magnet and free resonance/generation at the up-conversion frequency. c Schematic of the flexible-substrate rebounding process that causes pull-in again of the cantilever end to generate electricity at the higher clamped-supported mode up-conversion frequency
Figure 1b, c illustrate the FUC harvesting scheme within one elongation/rebounding cycle of the flexible substrate. In the initial state, the end of the ferromagnetic cantilever is pulled into contact with the magnet. When the PDMS substrate is stretched out, the piezoelectric cantilever will abruptly release from the magnet to cause free resonance/generation at its resonant frequency for a while, and then the resonance is attenuated to zero due to damping. When the substrate rebounds, the magnet will attract the cantilever again. When the magnetic force surpasses the restoring force of the cantilever, the magnetized nickel cantilever will impact and pull-in onto the magnet to form a beam with one end clamped and the other simply supported. Excited by the impact, the beam will resonate at a much higher resonant frequency than previously. The flexible device can be worn on a human joint, with both ends of the substrate adhered to the two sides of the joint. As the joint continuously rotates, the releasing/pull-in cycle will repeat. The horizontal stretching and the vertical resonance are perpendicular, and the slow movement and the high-speed resonance are disparate in frequency. In other words, the two kinetic behaviors cannot couple and influence each other. Therefore, the power generation efficiency can remain stable during one cycle. Based on this FUC generating scheme, the ultra-low frequency (e.g., sub-Hz to several Hz) limb movement can trigger a high-frequency efficient energy generating resonance at hundreds of Hz.
Analysis and simulation
The two FUC processes are individually calculated, with the assumption that, during pull-in, the cantilever is changed to a clamped-supported beam that has one end fixed and the other simply supported. Using the Rayleigh approximation method, the vibration-wave mode that satisfies the boundary conditions can be assumed as
where i is the order number of the model. The first three modes (i.e., i = 1, 2, and 3) are included in the solution, as they can ensure the analysis precision31. For the resonant cantilever schematically shown in Fig. 1b, the coefficient qi in Eq. (1) can be determined as
where β1 = 1.875, β2 = 4.694, and β3 = 7.855. In contrast, the qi of the clamped-supported beam [shown in Fig. 1c] is
where β1 = 3.927, β2 = 7.069, and β3 = 10.210. Supplementary Information details the deduction steps for both the mode shapes and the relevant coefficients. The mass and stiffness matrix can be defined as32
where m(x) and YI(x) are the distributed density and the bending stiffness along the length direction, respectively33. The subscripts m and n stand for the order number of the model.
Using the Eigen-value problem formula
where ωi is the ith order angular frequency, and the practically behaved vibration modes φi(x) can be calculated by superposing all the three assumed modes in
In practice, the piezoelectric film does not fully cover the whole substrate, which substantially influences the distributed stress and generated voltage. In this case, Eq. (7) can be used for precisely calculating φi(x).
The first three modes of the cantilever and the beam are shown in Fig. 2a, b, respectively. The deflection of the two kinds of vibration structures can be solved using
a The cantilever and b the clamped-supported beam. The normalized time-domain output voltage after cantilever release is shown in (c), compared to that after pull-in shown in (d). Finite element simulation results for the release process are shown in terms of the (e) displacement, f normalized voltage waves, and g normalized voltage spectrum. For the pull-in process, the finite element simulation results are shown in terms of (h) displacement, i normalized voltage waves, and j normalized voltage spectrum
Then, with Ui replaced by φi, M and K in Eqs. (4) and (5) are diagonalized. After diagonalization, the electromechanical coupled dynamic equation and Kirchhoff’s law of the circuit loop can be used to establish an equivalent circuit model as
where ri, Mi, Di, and Ki are the displacement, mass, damping coefficient, and stiffness of the ith mode diagonal components, respectively. Di can be obtained using \(D_i{\mathrm{ = }}2\zeta \sqrt {M_iK_i}\), where ζ is the damping ratio. v is the output voltage across load resistor RL. The capacitance CP of the piezoelectric film can be calculated as \(C_{\mathrm{p}} = bL_{\mathrm{p}}\varepsilon /h_{\mathrm{P}}\) . θi is the piezoelectric coupling factor, which can be deduced from the piezoelectric constitutive equation29. The material and geometric parameters of the piezoelectric cantilever are listed together in Table 1
.
The normalized output voltage waves of the cantilever and the beam obtained using Eqs. (9) and (10) are shown in Fig. 2c, d, respectively. The low-frequency human movement is frequency up-converted into high-frequency resonant electricity.
Since the cantilever anchor on the flexible substrate is still compliant, the PDMS substrate somewhat influences the resonance of the cantilever. To obtain a more precise solution, the COMSOL finite element analysis software is used to simulate the complex vibration process, which includes the interaction between the flexible substrate and the stiff cantilever. Figure 2e shows the three-dimensional (3D) model for transient z axis displacement during the cantilever release. Figure 2f, g show the time-domain normalized voltage wave shape and the normalized frequency spectrum of the voltage during release. The observed peak at 200 Hz shows the resonant frequency of the cantilever. Similarly, Fig. 2h–j show the displacement, normalized voltage wave shape, and normalized frequency spectrum of the pull-in process. The much higher frequency peak at 2358 Hz corresponds to the resonance of the clamped-supported beam.
When the magnet is laid right under the cantilever, the magnetic force should surpass the restoring force of the cantilever such that the cantilever is attracted to the magnet. After the cantilever is attached to the magnet, the other parts of the magnetized cantilever structure have a magnetic interaction with the magnet. Fortunately, this magnetic interaction does not greatly influence the electric energy generation of the pull-in and release processes. Both the calculation and simulation show that, after the free end of the cantilever is attached to the magnet, the single-side clamped cantilever is changed to a clamped-supported beam, and its spring constant will increase by >45 times. In this case, the interfering magnetic interaction becomes much weaker compared to the stiffened spring restoring force; thereby, the influence on the resonant mode and frequency is very small. However, when the substrate is stretched, the magnet horizontally moves far from the end of the cantilever (shown in Fig. 1b), and the magnetic force exerted on the cantilever end will rapidly reduce to further weaken the aforementioned magnetic influence.
The space distance between the beam and the magnet should be small to ensure that the magnetic force can be larger than the restoring force of the cantilever. Under such a condition, the pull-in process and FUC electric generation can be realized. At the opposite extreme, the space should be large enough to ensure reliable release of the cantilever from attachment to the magnet. Additionally, the thickness of the cantilever anchor (almost equal to the space distance) should be thick enough to satisfy the mechanical clamping condition. After calculation and simulation, the 7740# Pyrex-glass anchor is designed with a 4 mm thickness and an area of 4 × 2 mm2, as shown in Fig. 1a.
Fabrication
The fabrication flow chart shown in Fig. 3 will be detailed as follows.
-
a.
A Cr/Au layer (300/3000 Å) is sputtered onto a 4-inch silicon wafer to form the seed layer for the following micro-electroplating.
-
b.
After the adhesion promoter (OminCoatTM) is spin-coated, 90 μm-thick SU8-3050 photoresist is spin-coated and patterned using photolithography.
-
c.
Then an 84 μm-thick nickel film is micro-electroplated. The electroplating solution mainly consists of 300 g/l Ni(NH2SO3)2, 30 g/l NiCl2.6H2O and 30 g/l H3BO3. To form the nickel film with a low stress and a smooth surface, the electroplating conditions are set as follows: pH = 3.25, temperature = 50 °C, current density = 9 mA/cm2, and plating time of 22 h34.
-
d.
After removal of the SU8 photoresist, the substrate silicon is etched off using KOH with a 42% concentration at 85 °C to release the formed nickel film. Then conductive silver resin (H20E) is screen-printed on the surface of the nickel film. A PZT ceramic sheet (already with metal electrode films on the double sides) is bonded at the cantilever root to form the piezoelectric cantilever.
-
e.
A PDMS substrate (60 × 15 × 1.5 mm3) is fabricated by solidification in a mold and is then peeled out.
-
f.
The PDMS surface is modified using an oxygen-plasma treatment to enhance the bonding strength with the glass35,36.
-
g.
Two square glass pedestals are attached on the plasma-treated PDMS substrate to achieve spontaneous bonding.
-
h.
Another glass block and a small piece of NdFeB magnet are bonded on the glass pedestals using an ultraviolet (UV) light-assisted bonding glue.
-
i.
The piezoelectric cantilever is finally fixed on the glass block via the UV light-assisted bonding glue.
a A seed layer is sputtered on a wafer. b A photoresist layer is spin-coated and patterned. c A nickel film is electroplated. d The nickel film is released. Then, a PZT ceramic sheet is bonded. e A PDMS substrate is fabricated. f The PDMS is plasma treated. g Glass pedestals are attached on the PDMS. h Another glass block and a magnet are bonded on the two pedestals, respectively. i The piezoelectric cantilever is fixed on the glass block.
Results and discussion
The scanning electron microscopic (SEM) image in Fig. 4a shows a cross-sectional view of the electroplated 84-μm-thick nickel film on the silicon substrate. Figure 4b shows the scanned surface morphology of the nickel film obtained using an atomic force microscope (AFM). The surface roughness is generally <0.8 μm. SEM images of the PDMS surface before and after the plasma treatment are compared in Fig. 4c, d. The plasma treatment can roughen the PDMS surface (roughness ≈ 1.0 μm) and generate high-density chemical groups for firm bonding with glass. The photograph in Fig. 4e shows the fabricated energy harvester. Figure 4f, g show the stretching and rebounding states of the energy harvester. By horizontally stretching the PDMS film, the change of the distance between the two glass pedestals is normally <0.8 mm.
a SEM image showing a cross-sectional view of the nickel film. b AFM scanned surface morphology of the nickel film. c SEM of the PDMS surface. d SEM of the PDMS surface after the plasma treatment. e Photograph of the fabricated energy harvester, with the inset showing the simple support by the magnet of the attracted cantilever end. f, g The release and pull-in states of the energy harvester
The test setup is schematically shown in Fig. 5. A wave-form generator (Agilent 33120A) is used to excite a vibration shaker (JZK-5) to repeatedly stretch the flexible harvester. The two sides of the PDMS substrate are fixed on the shaker and a standard tensiometer. A standard accelerometer is also installed on the shaker to monitor the acceleration of the shaker movement. A data acquisition unit (NI USB-6003, 16 bit) is used to record the three transient signals from the accelerometer, the harvester, and the tensiometer. The harvester is loaded with a 40-kΩ matching resistor.
Figure 6a shows the time-domain voltage generated under a series of low frequencies from 0.5 to 5.0 Hz. The stretching force and stretching movement acceleration are tested using the tensiometer and accelerometer, producing the results shown in Fig. 6b, c, respectively. To ensure the uniformity of the stretching-induced strain throughout the test, the maximum amplitude of the stretching force is kept as 2.0 N. The pre-stretch force of 2 N is designed to ensure that the PDMS film is always in the tensile state. The maximum acceleration is always kept at <1 × g, which corresponds with limb movements. Figure 6d shows the generated peak-to-peak voltage Vp-p, which is always in the stable range from 7.5 V to 6.7 V when the frequency decreases from 5.0 Hz to 0.5 Hz. Figure 6e shows both the root-mean-square voltage (Vrms) and the averaged power within the same frequency range. The relation of the power and frequency is quite linear, which indicates that identical energies are generated in one stretching/rebounding cycle. Our proposed wearable harvester can generate stable and efficient electric energy. Figure 6f shows the test result for voltage waves during one stretching/rebounding cycle, clearly demonstrating the two parts for the cantilever release process and the pull-in process. Figure 6g shows the relation between the averaged electric energy generated in one cycle and the stretching/rebounding movement frequency. In the whole frequency range from 0.5 Hz to 5.0 Hz, the generated energy within one movement cycle always remains in the stable range of 0.56–0.69 μJ. Taking the one-cycle generation of 0.69 μJ as an example, the generated average electric energy during release and pull-in is 0.48 and 0.21 μJ, respectively. Figure 6h is the normalized voltage spectrum for the release process. The peak at 253 Hz indicates the resonant frequency of the cantilever. Figure 6i shows the normalized voltage spectrum for the pull-in process. The peak near the much higher resonant frequency of 1852 Hz corresponds to the clamped-supported beam after pull-in. The testing results well verify the simulation results in Fig. 2g, j. The majority of the mechanical energy from the shaker vibration is absorbed by the PDMS to form the horizontal stretching. Only a very small part of the mechanical energy from the shaker is provided to the piezoelectric cantilever for vertical vibration and electric generation. Excluding the stretched PDMS substrate, the energy conversion efficiency of the cantilever–magnet interaction/generation structure is calculated to be approximately 9%. This device’s operation scheme is different from those of most inertial vibrating harvesters. Herein body-movement-induced horizontal substrate stretch is transformed into vertical vibration of the cantilever, i.e., the two movement directions are perpendicular. The cantilever longitudinal direction is along the in-plane direction of the structure for easy fabrication of the device chip. In future work, we will try to improve the device configuration to obtain a higher energy generation efficiency.
Time-domain test results of the generated voltage (a), stretching force (b), and stretching movement acceleration (c) for the stretching frequency range of 0.5–5.0 Hz. Frequency-domain test results of Vp-p (d), Vrms, and power (e) for the frequency range of 0.5–5.0 Hz are also given. Test results for two voltage waves within one stretching cycle. g Frequency-dependent averaged electric energy in one movement cycle. The generated energy from the cantilever release process and pull-in process is separately indicated. h, i The normalized voltage spectrum for the release process and the pull-in process, respectively
Figure 7a–f show the voltage generation test results when the harvester is connected to different electrical loads. Herein the frequency is fixed as 5.0 Hz. Figure 7a shows the generated Vp-p and the average power for varied resistors. The matching resistor is 40 kΩ, which should be the same as the inner resistance of the harvester. The open-loop voltage is approximately 15 V. Figure 7b shows the charging/storage properties of the harvester, where a 2.1 μF tantalum capacitor is connected through a full-wave rectifier. After 5 s of charging, the voltage across the capacitor is 1.6 V, and the averaged power is 0.54 μW. Figure 7c shows that the stretched harvester successfully lights seven red light-emitting diodes (LEDs) in parallel. Figure 7d is the time-domain voltage across the LEDs, indicating that the harvester can quickly reach the 1.7 V threshold voltage of the LEDs to switch them on. The reliability of the device is also tested. Figure 7e shows the generated voltage waves during 2000 continuous cycles of stretching/rebounding of the flexible device. Since the generated power at the beginning and end of the test is 0.69 and 0.68 μJ, respectively, the change of the generated power is only 1.4%. Thus the generated power always remains stable throughout the test. Figure 7f shows the obtained relation of the stress and stain for the PDMS substrate obtained by testing the relation of the force and displacement. When the strain reaches the maximum of 0.5 (i.e., the length of the substrate increases 3 cm), no cracks occurs. As long as the strain does not exceed 0.1, which satisfies the requirement of most limb movements, the displacement of the substrate can be linear with the stretching force, and the Young’s modulus remains as 2.06 MPa.
a Generated Vp-p and averaged power vs. load resistance. b Time-domain voltage waves during the charging process of the harvester to a capacitor that is across a full-wave rectifier. c Seven red LEDs in parallel are lit by the harvester. d The voltage across the LEDs is quickly switched on, where the threshold voltage of the LED is approximately 1.7 V. e Test results for voltage waves during 2000 continuous cycles of stretching/rebounding. f Test results for the stress–stain relation of the PDMS substrate
As shown in Fig. 8a, two harvesters are individually attached to the elbow and knee of a person moving on a treadmill to demonstrate a practical wearable application. The magnified views of Fig. 8b, c show that the two wearable harvesters are mounted just under the joints of the elbow and the knee. For each harvester, the two ends of the PDMS substrate are taped to the two sides of the joint. Once the joint rotates, the device will undergo the cycled release/pull-in process. When the elbow or knee bends along with the limb’s movement, the substrates are stretched, and the harvesters are in the release state. When the two limbs return, the harvesters’ states are changed to pull-in. To ensure the occurrence of the two generation processes, the minimum bending angles of the elbow and the knee are 40° and 30°, respectively. In the experiment, two 40 kΩ matching resistors are connected to the two harvesters. The generated voltage waves for the harvesters at the elbow and the knee (both loaded with matching resistors) are shown in Fig. 8d, e, respectively. Typical limb movements, such as knee bending during a squat (once per 1.5 s.), walking (at the speed of 1-2 m/s), jogging (3–4 m/s), and fast running (5–6 m/s), are tested. A stable voltage can be always generated, with the device on the elbow generating a Vp-p of approximately 7.5 V and the device on the knee generating a Vp-p of approximately 4.0 V. The tested powers for different movements are listed in Table 2.
a Photograph showing a practical wearable application where two flexible harvesters are attached on a human elbow and knee. b, c Magnified views of the devices on the elbow and knee, respectively. d, e Test results for the voltage waves generated from the devices on the elbow and knee, respectively. The generated results are, sequentially, from joint bending (only for knee), walking, jogging, fast running, and walking again
Moreover, the proposed FUC generating scheme can be used to achieve two-directional stretching energy harvesters, which are often required in wearable applications. Figure 9a schematically shows the 3D structure of a two-directional harvester, where two magnets are individually laid under the two vertex points of the cantilever free end. When the stretch is not along the cantilever length direction, the flexible substrate will be transversely lengthened, and the distance between the two magnets will be enlarged to cause the release of the cantilever. In this way, the harvester can generate electric energy regardless of what in-plane direction the external stretch is in. Figure 9b shows the fabricated two-directional harvester and the test results of the generated voltage waves when the stretch is along the cantilever length direction (indicated with the red arrow). Figure 9c, d are the voltage generation results for the stretch directions with deviations from the cantilever length direction of 45° and 90°, respectively. The generated Vp-p is stable and always >4 V for the three stretching directions, where the stretched displacement is unchanged.
a Schematic of the two-directional energy harvester for in-plane stretching along various directions. b–d When the stretching direction is along the device length direction, 45° inclined from the device length direction, and perpendicular to the device length direction, respectively; photographs of the harvester (on the left side) and the voltage waves generated during stretch (on the right side) are given
Unlike most reported FUC harvesters, which usually transform the kinetic energy of inertial structures to electric power, the emphasis of the herein developed wearable FUC energy harvester is to transform horizontal low-frequency stretching movement into vertical high-frequency resonance for energy generation. Therefore, the device is suitable for usage with body movements, such as limb joint bending. The harvester demonstrates a good flexible-structure response to low-frequency movement and stable electric power generation within the per-cycle movement. Additionally, the achieved two-directional stretching energy harvesters in this study can potentially be attached to special clothes. However, it is difficult to weave the device into tissue structures. Currently, wearing the device by attaching the harvester to the opposite sides of a limb joint is somewhat inconvenient. In future work, we will try to improve the flexible-device packaging technique.
CONCLUSION
This study proposes and develops a novel wearable energy harvester that frequency up-converts low-frequency human limb movements into the high-frequency electric generating resonance of a piezoelectric cantilever. Since the horizontal stretch of the flexible substrate has little influence on the vertical electric generating resonance, the harvester features stable electric energy generation in the sub-Hz to several Hz wide joint movement frequency range. In every limb movement cycle, the Vp-p and electric energy can remain stable even if the limb movement frequency changes within the range of sub-Hz to several Hz. The test results and human body wearable experiments have verified the usability of the flexible harvester. Additionally, a two-directional energy harvester for in-plane stretching in any direction is achieved using the same FUC scheme. The flexible-substrate harvesters have potential wearable applications.
References
Sue, C. Y. & Tsai, N. C. Human powered MEMS-based energy harvest devices. Appl. Energy 93, 390–403 (2012).
Shaikh, F. K. & Zeadally, S. Energy harvesting in wireless sensor networks: a comprehensive review. Renew. Sustain. Energy Rev. 55, 1041–1054 (2016).
Khaligh, A., Zeng, P. & Zheng, C. Kinetic energy harvesting using piezoelectric and electromagnetic technologies—state of the art. IEEE Trans. Ind. Electron. 57, 850–860 (2010).
Xu, S. et al. Self-powered nanowire devices. Nat. Nanotechnol. 5, 366–373 (2010).
Saha, C. R. et al. Electromagnetic generator for harvesting energy from human motion. Sens. Actuators A Phys. 147, 248–253 (2008).
Pillatsch, P., Yeatman, E. M. & Holmes, A. S. A piezoelectric frequency up-converting energy harvester with rotating proof mass for human body applications. Sens. Actuators A Phys. 206, 178–185 (2014).
Ylli, K. et al. Energy harvesting from human motion: exploiting swing and shock excitations. Smart Mater. Struct. 24, 025029 (2015).
Niu, S. et al. A universal self-charging system driven by random biomechanical energy for sustainable operation of mobile electronics. Nat. Commun. 6, 8975 (2015).
Lee, M. et al. Self-powered environmental sensor system driven by nanogenerators. Energy Environ. Sci. 4, 3359–3363 (2011).
Roundy, S. & Wright, P. K. A piezoelectric vibration based generator for wireless electronics. Smart Mater. Struct. 13, 1131–1142 (2016).
Beeby, S. P. et al. A micro electromagnetic generator for vibration energy harvesting. J. Micromech. Microeng. 17, 1257–1265 (2007).
Hillenbrand, J., Pondrom, P. & Sessler, G. M. Electret transducer for vibration-based energy harvesting. Appl. Phys. Lett. 106, 1457 (2015).
Erturk, A., Hoffmann, J. & Inman, D. J. A piezomagnetoelastic structure for broadband vibration energy harvesting. Appl. Phys. Lett. 94, 254102–254102-3 (2009).
Harne, R. L. & Wang, K. W. A review of the recent research on vibration energy harvesting via bistable systems. Smart Mater. Struct. 22, 023001 (2013).
Tang, Q. & Li, X. Two-stage wideband energy harvester driven by multimode coupled vibration. IEEE/ASME Trans. Mechatron. 20, 115–121 (2014).
Cottone, F., Vocca, H. & Gammaitoni, L. Nonlinear energy harvesting. Phys. Rev. Lett. 102, 080601 (2008).
Moss, S. et al. A broadband vibro-impacting power harvester with symmetrical piezoelectric bimorph-stops. Smart Mater. Struct. 20, 045013 (2011).
Renaud, M., et al. Scavenging energy from human body: design of a piezoelectric transducer. In International Conference on Solid-StateSensors, Actuators and Microsystems. 5–9 June 2005. Seoul, South Korea. 784–787 (2005).
Galchev, T., Aktakka, E. E. & Najafi, K. A piezoelectric parametric frequency increased generator for harvesting low-frequency vibrations. J. Microelectromech. Syst. 21, 1311–1320 (2012).
Tang, Q. et al. Wireless alarm microsystem self-powered by vibration-threshold-triggered energy harvester. IEEE Trans. Ind. Electron. 63, 2447–2456 (2016).
Galchev, T., Kim, H. & Najafi, K. Micro power generator for harvesting low-frequency and nonperiodic vibrations. J. Microelectromech. Syst. 20, 852–866 (2011).
Takahashi, T., et al. Vertical capacitive energy harvester positively using contact between proof mass and electret plate - stiffness matching by spring support of plate and stiction prevention by stopper mechanism. Ed. Tariq Samad. In IEEE International Conference on MICRO Electro Mechanical Systems, IEEE, Estoril, Portugal. 1145–1148 (2015).
Lu, Y. et al. A nonlinear MEMS electrostatic kinetic energy harvester for human-powered biomedical devices. Appl. Phys. Lett. 107, 429–2244 (2015).
Halim, M. A. & Park, J. Y. A non-resonant, frequency up-converted electromagnetic energy harvester from human-body-induced vibration for hand-held smart system applications. J. Appl. Phys. 115, 1457 (2014).
Fan, F. R., Tian, Z. Q. & Wang, Z. L. Flexible triboelectric generator. Nano Energy 1, 328–334 (2012).
Hou, T. C. et al. Triboelectric nanogenerator built inside shoe insole for harvesting walking energy. Nano Energy 2, 856–862 (2013).
Zi, Y. et al. Triboelectric-pyroelectric-piezoelectric hybrid cell for high-efficiency energy-harvesting and self-powered sensing. Adv. Mater. 27, 2340–2347 (2015).
Zhou, T. et al. Woven structured triboelectric nanogenerator for wearable devices. ACS Appl. Mater. Interfaces 6, 14695–14701 (2014).
Meng, B. et al. A transparent single-friction-surface triboelectric generator and self-powered touch sensor. Energy Environ. Sci. 6, 3235–3240 (2013).
Xi, Y. et al. Multifunctional TENG for blue energy scavenging and self‐powered wind‐speed sensor. Adv. Energy Mater. 7, 1602397 (2017).
Elvin, N. G. & Elvin, A. A. A general equivalent circuit model for piezoelectric generators. J. Intell. Mater. Syst. Struct. 20, 3–9 (2009).
Hobeck, J. D. & Inman, D. J. A distributed parameter electromechanical and statistical model for energy harvesting from turbulence-induced vibration. Smart Mater. Struct. 23, 115003 (2014).
Erturk, A. & Inman, D. J. A distributed parameter electromechanical model for cantilevered piezoelectric energy harvesters. J. Vib. Acoust. 130, 1257–1261 (2008).
Prioteasa, P. et al. Electrodeposition of nickel for fabrication of microfluidic pumps. Rev. Chim. Buchar. Orig. Ed. 64, 275–280 (2013).
Tan, S. H. et al. Oxygen plasma treatment for reducing hydrophobicity of a sealed polydimethylsiloxane microchannel. Biomicrofluidics 4, 32204 (2010).
Zhou, J. et al. Surface modification for PDMS-based microfluidic devices. Electrophoresis 33, 89 (2012).
Acknowledgements
This work was supported in part by the Chinese 863 Program under Grant 2015AA043502; MOST of China (2016YFA0200800); the National Natural Science Foundation of China Projects under Grants 91323304, 61234007, and 61321492; the International Science and Technology Cooperation Program of China under Grant 2013DFG62830; and the National Key Technology Research and Development Program under Grant 2015BAZ05750.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Li, K., He, Q., Wang, J. et al. Wearable energy harvesters generating electricity from low-frequency human limb movement. Microsyst Nanoeng 4, 24 (2018). https://doi.org/10.1038/s41378-018-0024-3
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41378-018-0024-3
Keywords
This article is cited by
-
Multimodal MEMS vibration energy harvester with cascaded flexible and silicon beams for ultralow frequency response
Microsystems & Nanoengineering (2023)
-
Numerical and experimental evaluation of the magnetic interaction for frequency up-conversion in piezoelectric vibration energy harvesters
Meccanica (2022)
-
Spray-coated electret materials with enhanced stability in a harsh environment for an MEMS energy harvesting device
Microsystems & Nanoengineering (2021)
-
Wearable multi-sensing double-chain thermoelectric generator
Microsystems & Nanoengineering (2020)
-
A piezoelectric cantilever-beam energy harvester (PCEH) with a rectangular hole in the metal substrate
Microsystem Technologies (2020)