Abstract
Laser state active controlling is challenging under the influence of inherent loss and other nonlinear effects in ultrafast systems. Seeking an extension of degree of freedom in optical devices based on low-dimensional materials may be a way forward. Herein, the anisotropic quasi-one-dimensional layered material Ta2PdS6 was utilized as a saturable absorber to modulate the nonlinear parameters effectively in an ultrafast system by polarization-dependent absorption. The polarization-sensitive nonlinear optical response facilitates the Ta2PdS6-based mode-lock laser to sustain two types of laser states, i.e., conventional soliton and noise-like pulse. The laser state was switchable in the single fiber laser with a mechanism revealed by numerical simulation. Digital coding was further demonstrated in this platform by employing the laser as a codable light source. This work proposed an approach for ultrafast laser state active controlling with low-dimensional material, which offers a new avenue for constructing tunable on-fiber devices.
Similar content being viewed by others
Introduction
Ultrafast fiber lasers are becoming more popular as bulk laser alternatives, with applications in micromachining1,2,3, biomedicine4,5, ultrafast physics6,7,8,9, multiphoton microscopy10,11,12, and spectroscopy13,14. Many innovations and applications require tunable ultrafast laser parameters, including wavelength, intensity, pulse width, laser state (LS), etc15. Due to complex nonlinear effects within the ultrafast system, it is still a great challenge for laser state active controlling (LSAC) of ultrafast fiber lasers. LSAC has been reported in nonlinear ultrafast systems such as traditional nonlinear polarization rotation (NPR) by adjusting the polarization controller (PC) to change the intracavity parameters. However, this approach has limitations in modulation bandwidth and environmental stability16,17. A fundamental way to achieve stable LSAC is to increase the tunability of fiber-based devices. Low-dimensional materials (LDMs) with the quantum confinement effect exhibit unique optoelectronic properties, providing new opportunities for generation of ultrafast lasers18,19,20,21,22,23,24,25,26,27. The ultrafast lasers based on LDMs exhibits decent performance in pulse width and spectra28,29,30,31 while the LS controlling is elusive. Even though LS controlling can be achieved by regulating pump power32,33,34 or thickness of saturable absorber (SA)35, it typically suffers from low effectiveness and lack of dynamic mechanism.
LDMs with anisotropic crystal structure provide an additional degree of freedom for light modulation by polarization control, offering opportunity for tunable optoelectronic devices36. Recently, anisotropic LDMs have been harnessed in polarization-sensitive optoelectronic devices such as photodetectors37,38 and polarized light-emitting diodes39,40. However, their application in ultrafast photonics has yet to be reported by exploiting their prominent polarization-sensitive absorption. Layered materials with broadband photoresponse and high air stability are required for their application in ultrafast photonics. As a ternary anisotropic van der Waals material, Ta2PdS6 features high air stability because of strong d2sp3 hybridization between chalcogen atoms and group-10 precious elements41. Furthermore, its band gap varies from nearly 0 eV to 1.0 eV with different thicknesses, resulting in broadband photoresponse in optoelectronic applications18.
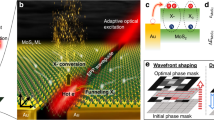
In this work, the stable LSAC ultrafast dynamics platform is demonstrated by using a high-quality quasi-one-dimensional (1D) Ta2PdS6 “0−1”-switcher, as shown in Fig. 1. The twin-detector experiment reveal that the quasi-1D anisotropic Ta2PdS6 presents distinct nonlinear polarization optical response. A “0−1”-switcher performing steady LSAC between conventional soliton (CS) and noise-like pulse (NLP) has been achieved based on polarization control. The numerical simulation elucidates the dynamical processes of CS (“0”) and NLP (“1”) states. The digital coding applicability has been further demonstrated in this platform. These findings pave the way for tunable ultrafast laser devices based on anisotropic LDMs.
Results
Polarization-dependent optical response in anisotropic layered Ta2PdS6
Ta2PdS6 was a stable layered material with reduced in-plane symmetry (Fig. 2a)18. Single-crystal Ta2PdS6 were synthesized via a chemical vapor transport (CVT) approach (see Methods and Fig. S1a in Supporting Information) and the analysis of the elements together with microscopic morphology demonstrated the expected atomic ratio and high quality (Figs. S1 and S2, Supporting Information). The obtained crystals and flakes typically appear needle-like morphology, manifesting their quasi-1D structure (Fig. 2b and Fig. S1b in Supporting Information). High-resolution transmission electron microscopy in Fig. S1c (Supporting Information) further reveals the microscopic structure anisotropy. As demonstrated by angle-resolved photoemission spectroscopy (ARPES) and Fourier transform infrared (FTIR) absorption spectrum in Fig. 2c, d, Ta2PdS6 has a narrow bandgap of ~0.21 eV, rendering its wide band absorption in the infrared regime.
a The crystal structure of Ta2PdS6 observed along the b-axis. b Low-magnification TEM image of quasi-1D Ta2PdS6. c ARPES measurement of the Ta2PdS6 crystal. d FTIR spectrum of the Ta2PdS6. e The polarized Raman spectra of Ta2PdS6. f The direction-dependent optical properties of Ta2PdS6. g The polarization-dependent transmission at various incidence powers. h The polarization contrast at various maximum transmitted powers. i Ta2PdS6 nonlinear transmission versus energy intensity at various tilt angles. j The saturation intensity and modulation depth of Ta2PdS6 for various tilt angles. k The nonsaturable loss of Ta2PdS6 for various tilt angles
Anisotropic optical responses were expected from the reduced in-plane symmetry. Polarized Raman spectra of Ta2PdS6 flake (Fig. 2e and Fig. S3 in Supporting Information) show anisotropic Raman intensities corresponding to the typical \({A}_{g}\) and \({B}_{g}\) vibrational modes42, indicating the polarization-sensitive phonon vibrations. The UV-Vis-NIR spectrum in Fig. S4 (Supporting Information) reveals the broad-band absorption from Ta2PdS6 with approximately 62% at 1560 nm, which is chosen in the subsequent pulsed laser experiments. The polarized optical absorption of the Ta2PdS6 was first theoretically simulated (See Methods)43. The results in Fig. 2f illustrate a prominent polarization-dependent absorption characteristic of Ta2PdS6 at 1.56 μm (corresponding to about 0.8 eV). The anisotropic transmittance of Ta2PdS6 was measured experimentally with a wavelength of 1.56 μm (see Methods and Fig. S5a in Supporting Information). The polarization-dependent transmitted power for Ta2PdS6 changes under incident powers of 3.9 mW, 6.7 mW, and 10.5 mW, respectively, as shown in Fig. 2g. The polarization-dependent absorption properties of Ta2PdS6 exhibited different maximum transmitted powers of 1.4 mW, 2.4 mW, and 3.7 mW, respectively. The transmittance is sensitive to the polarization of the incident light and the polarization contrasts increase with pump power (Fig. 2h), which offers an extra degree of freedom to regulate pulsed laser performance.
The polarization-dependent saturable absorption of Ta2PdS6 was further investigated by the all-fiber twin-detector configuration (see Methods and Fig. S5b in Supporting Information). In the experiment, the light polarization was altered by tilting the angle of the PC from 0° to 180° with a step of 45°. We note that the rotation angle of the PC does not directly reflect the direction of the laser polarization state. Nevertheless, the large tilt angles offer a convenient way to change the optical polarization in the following ultrafast laser experiments. As shown in Fig. 2i, the nonlinear transmittance differs with the tilt angles of PC. The key parameters of SA were fitted by
where the \(T(I)\) is the transmittance rate, \(I\), \(\varDelta R\), \({I}_{s}\), and \({T}_{ns}\) are the input intensity, the modulation depth, saturation intensity, and nonsaturable loss, respectively. As shown in Fig. 2j, both the saturation intensity and the modulation depth depend on the tilt angle. The high modulation depth (over 31%) of Ta2PdS6, benefits its application as SA for ultrafast pulse generation. Specifically, the nonsaturable loss exhibits a significant variation with the maximum saturation absorption loss of about 65.8% at the tilt angle of 0° and the minimum saturation loss of about 56.3% at the tilt angle of 180° (Fig. 2k). Since the saturable absorption results from the Pauli blocking principle7 (Fig. S6, Supporting Information), the polarization-dependent nonsaturable loss variation in the quasi-1D layered materials offers new opportunities for regulating nonlinear absorption behavior.
Ultrafast fiber lasers with CS and NLP states
Ta2PdS6-based ultrafast fiber lasers were constructed by integrating Ta2PdS6 precisely in the center of the fiber end face by a fully dry transfer process (see Methods and Fig. S5c in Supporting Information). Atomic force microscopy measurements indicate that the thickness of the Ta2PdS6 is about 40 nm with good flatness. To verify its ability to generate ultrashort pulses, the Ta2PdS6 was removed from the ring cavity or a linear polarizer was utilized in place of the Ta2PdS6, and no ultrafast pulse output phenomenon was observed by adjusting the state of the PC and the pump power values. Firstly, the CS LSs were successfully generated in the Ta2PdS6-based fiber laser. The threshold pump power from continuous wave to CS state was 200 mW, as unambiguously demonstrated by the change of the optical spectrum with the pumping power (Fig. 3a). The laser can supply steady CS pulses within the pump power range of 200−830 mW and the maximum average output power was 37 mW with a corresponding slope efficiency of about 4.5% (Fig. S7a, Supporting Information). The spectrum of CS mode was centered at 1558.9 nm with a 3 dB bandwidth of 5.9 nm (Fig. 3a). The pulse-to-pulse separation of 70.9 ns and repetition frequency of 14.1 MHz (Fig. S7b, Supporting Information) match well with the cavity length, indicating that the fiber laser works in a mode-locked state. A pulse duration of 697 fs was extracted from the autocorrelation trace data (Fig. 3b), further corroborating the laser working in the typical conventional soliton regime. The spike of the basic repetition frequency was located at 14.1 MHz without side peaks, and a signal-to-noise ratio (SNR) was about 57 dB measured by the radio frequency (RF) spectrum, indicating high stability of CS operation (Fig. 3c). The laser under CS mode was further recorded for more than 720 h under ambient conditions with fixed experimental conditions and no significant degradation of the central wavelength and spectral width was observed, as shown in Fig. 3d and Fig. S7c (Supporting Information), proving its long-term stability.
a Spectral evolution under different pump power and optical spectrum of CS at 830 mW. b Autocorrelation trace. c The RF spectrum of the CS state laser. d The central wavelength and 3 dB bandwidth of CS spectra obtained at various time durations. e Spectral evolution under different pump power and optical spectrum of NLP at 830 mW. f Autocorrelation trace of NLP state laser at 830 mW. g NLP base and spike width versus pump power. h The central wavelength and 3 dB bandwidth of NLP spectra obtained at various time durations
Additionally, NLP LS can also be successfully generated in the same Ta2PdS6-based fiber laser by adjusting the PC tilt angle. The spectral variation of the NLP state (Fig. 3e) demonstrates a more pronounced spectral broadening of the NLP state than the CS state. Figure 3e also shows the detailed characteristics of the NLP state output spectrum at a maximum pumping power of 830 mW, with the spectrum centered at 1562.1 nm and a 3 dB bandwidth of 27.5 nm. The average output power of NLP state operation varies with the absorbed pump power, as shown in Fig. S8a (Supporting Information). The pump power threshold was 450 mW, and the effective power operating range was 450−830 mW. The maximum average output power of the NLP state was 45 mW with a corresponding slope efficiency of 6.1%. The typical pulse train was obtained at pump powers of 450−830 mW, corresponding to a round trip time of approximately 70.9 ns (Fig. S8b, Supporting Information), the same as the CS mode due to the identical laser configuration. Figure 3f shows the autocorrelation trace data for a pump power of 830 mW. It is worth noting that the base width and spike width change with the pump power of NLP state operation. As the pump power increases, the spike width decreases from 151 to 98 fs, and the base width increases from 14.9 to 21.4 ps when pump power increases from 450 to 830 mW (Fig. 3g), which is a typical characteristic of NLP state operation. The RF spectra of the NLP state (Fig. S8d, Supporting Information) show the sharp peak of the fundamental repetition rate of 14.1 MHz and the SNR of ~55 dB, indicating high stability of NLP operation. No significant degradation of the central wavelength and spectral width was observed in the measured spectral properties (Fig. 3h and S8e, Supporting Information) under long-time NLP state operation, indicating that the laser has the potential for long-term stable operation.
The threshold of stable CS state is 200 mW, while the NLP state is 450 mW. This is difference also in the noise performance between CS and NLP states. The phase noise of the CS state decreases as the frequency increases monotonically from 1 Hz to 10 KHz, as demonstrated in Fig. 4a. The timing jitter of the CS state is calculated to be about 45.44 ps in the frequency range of 1 Hz−1 MHz at the pump power of 830 mW (Fig. 4b), further demonstrating the good stability of the laser pulse. The power spectral density curve of phase noise of NLP state appeared only when the pump power reached 500 mW (Fig. 4c), which can be attributed to the characteristics of NLP, i.e., a cluster formed by a series of sub-pulses with randomly distributed amplitudes and durations. The timing jitter is calculated to be about 60.40 ps at the frequency range of 1 Hz−1 MHz (Fig. 4d), which is inferior to that in the CS state. To further characterize the variation of the NLP state, the dispersive Fourier transformation (DFT) technique was employed (see Methods and Fig. S5d in Supporting Information). Typical experimental results based on the DFT technique (Fig. 4e) show that the spectral mapping of the stretched NLP is different at each instant. In this experiment, the real-time DFT spectral measurements were analyzed to provide a spectral characterization of the dynamics of the NLP state, as shown in Fig. 4f. Compared to spectrometer measurements, the flanks of NLP spectra measured by the DFT technique vary from shot to shot, but the bandwidth is essentially constant. For additional information, six frames of a typical shot-to-shot spectral trajectory are shown in Fig. 4g, which clearly illustrates the evolution of the NLP spectra. The strongest peaks of the spectrum alternate at center wavelengths and the sideband evolution is muddled. The results further demonstrate the wave packet nature of the NLP state, whose internal structure is a series of pulses with randomly distributed amplitudes and durations.
a The phase noise characteristics of the CS state laser. b The timing jitter of CS under pump power of 830 mW. c The phase noise characteristics of the NLP state laser. d The timing jitter of NLP under pump power of 830 mW. e Typical experimental results based on the DFT technique. f DFT recording of single-shot spectra over 25 consecutive round trips. g The six typical frames of NLP spectra based on the DFT technique
“0−1”- LSAC in ultrafast fiber lasers by polarization control
By adjusting the PC, we successfully achieved a stable CS LS output in the pump power of 200−830 mW and a stable NLP LS output in the pump power of 450-830 mW, as shown in Fig. 5a. In the pump power range of 450 mW to 830 mW, it is possible to achieve switching between the two LSs (CS-NLP) at a constant pump power just by adjusting the tilt angles of PC (refer to Supplementary Video). The spectra of soliton and NLP at a maximum pump power of 830 mW are illustrated in Fig. 5b. The CS operation was located at 1558.9 nm with a 3 dB spectral width of 5.9 nm while the NLP at 1562.1 nm with 3 dB spectrum bandwidth of 27.5 nm. Their state stability further strengthens the reliability of conversion between the two photonic states of the Ta2PdS6-based ultrafast fiber laser. We recorded changes in the output spectrum of the laser for a continuous conversion operation (adjust the tilt angles of PC) over a period of 3.5 h (seven operations, each run lasting 0.5 h), as demonstrated in Fig. 5c. The spectra of the two pulse states are essentially unchanged before and after conversion, as well as being very smooth over the 3.5 h running time, demonstrating the LSAC stability of the Ta2PdS6-based ultrafast fiber laser. It further illustrates the reliability of the results of the relative polarization analysis of saturable absorption. The phenomenon of conversion between NLP and other soliton states was observed in NPR fiber lasers16,17. However, the generation of LSAC in ultrafast lasers based on real saturable absorbers (SAs) is more compact and convenient.
a Ultrafast fiber laser conversion demonstration. b The soliton and NLP spectra. c The output spectrum of a Ta2PdS6-based ultrafast fiber laser for a continuous conversion operation. d Spectral and temporal evolutions of CS-NLP LSs conversion across 3500 consecutive round trips. e A“NUDT” is encoded digitally
The mode switch effect is attributed to the polarization-sensitive nonlinear absorption behavior, originating from the anisotropic LDMs. Numerical simulation was performed based on a generalized nonlinear Schrödinger equation (see Methods for details). Figure S9a (Supporting Information) shows the evolutionary process of the CS with the round-trip (RT) of 500, when the \(\varDelta R\), and \({T}_{ns}\) are taken as 0.22 MW cm1, 32.2%, and 65.8%, respectively, and the dynamics of the simulated spectra and pulses match the typical CS characteristics (Figs. S10a, S10b, Supporting Information). After modulation of the nonlinear parameters of the Ta2PdS6 “0−1”-switcher by changing the PC, the \(\varDelta R\), \({I}_{s}\), and \({T}_{ns}\) are set as 0.21 MW cm1, 31.2%, and 56.3% while other parameters remain constant. As illustrated in Fig. S9b (Supporting Information), the dynamics of the simulated spectra and pulses match the typical NLP characteristics, and the spectral profile and pulse autocorrelation trace are shown in Figs. S10c and S10d (Supporting Information). Furthermore, the Ta2PdS6 “0−1”-switcher-based regulation also causes changes in the intensity of the intracavity nonlinear effects, where the solitons split into multiple pulses due to soliton quantization effects. Consequently, the evolutionary process of the CS (“0”)-NLP (“1”) state conversion happens in the system (seven operations, each RT of 500), which is consistent with the experimental results (Fig. 5d).
The stable conversion of different pulse states in a single ultrafast fiber laser system has the potential for extended applications, such as communications coding and optical switching. The conversion of CS (“0”) and NLP (“1”) is displayed on the oscilloscope by the intensity of the pulse signal with a level difference of about 0.02 V (Fig. S11a, and Supplementary Video). The application of digital coding can be realized by receiving the optical signal through the photoelectric detector. The optical binary codes of NUDT (01001110010101010100010001010100, an abbreviation from the National University of Defense Technology) can be obtained by the Ta2PdS6 “0-1”-switcher, as shown in Fig. 5e. In this work, the adjustment of the PC is manually controlled, and the maximum switching frequency that can be achieved is in the order of a few Hz. By time domain analysis, the time interval between the two luminescent state transitions is about 42 μs, as shown in Fig. S11b (Supporting Information). As a result, It can be expected that the dual-state switching frequency can reach the kHz magnitude by introducing a mechanically tunable motorized device. Combined with the steady conversion and stable operation of the CS and NLP states, tunable photonics devices based on anisotropic materials are expected to offer new prospects in ultrafast laser applications.
Discussion
In summary, the quasi-1D layered Ta2PdS6 with anisotropic optical absorption was investigated to modulate the property of nonlinear absorption as SA. Both steady-state CS (“0”) and NLP (“1”) pulsed laser modes were achieved by altering the polarization of light. The CS state produces an ultrashort pulse with a pulse width of 697 fs and a pulse energy of 2.62 nJ. NLP state operation yielded pulses with spike widths as short as 98 fs. Additionally, the noise features and long-term stability for both two modes have been systematically investigated. A Ta2PdS6 “0-1”-switcher was further demonstrated and explained by numerical simulation. LSAC laser was used as a codable light source to demonstrate their application for digital coding. The findings demonstrate that anisotropic quasi-1D layered materials are an efficient optical modulator for LSAC, which will pave the way for developing tunable ultrafast photonic devices.
Materials and methods
Synthesis of Ta2PdS6 Single Crystals
By using the iodide as the transport agent, the high-quality single crystals of Ta2PdS6 were synthesized via a CVT method. The 0.3 g of high purity Ta, Pd, and S, and 120 mg of iodide were sealed in a 20 cm-long vacuum quartz tube under a vacuum of 10−6 Torr and placed in a two-zone furnace. The source end is then slowly heated to 875 °C and the other end is kept at 730 °C to maintain a relatively low temperature with the source end. The heating process held for 168 h. The furnace is then naturally cooled to room temperature. Shiny silver needle-like single crystals of Ta2PdS6 are obtained at the cold end of the tube.
Characterizations
ARPES data were gathered by a DA30L analyzer with energy resolution and angular resolution set to 20 meV and 0.2°, respectively. XPS measurement was carried out on a spectrometer outfitted with a monochromatic Al Kα X-ray source (1486.6 eV) that operates at 100 W. Raman data were measured by a Raman spectrometer (Lab RAM HR 800) with a laser wavelength of 532 nm. STEM images were obtained on the instruments (Thermo Scientific, Themis Z) operating at 300 kV. UV-vis-NIR spectrophotometry (UV-3600 Plus, SHIMADZU) was performed to study the absorption property of the Ta2PdS6.
Theoretically simulated of polarized optical absorption
The following formula was employed to simulate the direction-dependent optical properties43:
where the ε1(ω) and ε2(ω) represent the real and imaginary parts of the dielectric function, respectively. The imaginary part ε2(ω) of the dielectric function can be obtained by evaluating the momentum matrix elements between the occupied and unoccupied states using the following expression:
where Ω represents the volume, α, and β are the Cartesian components, eα, and eβ represent the unit vectors, v, and c correspond to the matrix elements of the transition from the valence band state (uvk) to the conduction band state (uck), εck and εvk signify for the energy of the conduction and valence band, respectively. The real part ε1(ω) of the dielectric function can be derived from the imaginary part using the Kramer-Kronig relationship, expressed as:
where P represents the principal value of the integral.
Experimental setup for polarization absorption of Ta2PdS6
The light source was a 1.56 μm homemade laser, and the emitted light was passed through a collimator and then through a polarized beam splitter. The beam was then passed through a half-wave plate and onto the Ta2PdS6 sample. The polarization state of the light was changed by turning the half-wave plate and the change in transmitted power was measured with a power meter (PM).
Experimental setup for the measurement of the nonlinear polarization optical response
The structure of the measurement system consists of a homemade 1.56 μm seed laser (pulse width: 260 fs; repetition frequency: 13.0 MHz) and an erbium-doped fiber amplifier. The laser beam is divided into two paths by a 50:50 optical coupler (OC): contrasting path and test path. In the contrasting path, the power is measured using a PM 1. In the test path, the intensity of the laser interaction with the material can be varied by adjusting the amplifier pump, and the power is measured with PM 2 after the laser has passed through the sample. Furthermore, a polarization-independent isolator (ISO) and a PC are added to the optical path of measurement to simply simulate the nonlinear optical response of Ta2PdS6 “0-1”-switcher after polarization changes caused by the tilt angles of PC in the laser cavity and the adjustment position change (tilt angle with 0°, 45°, 90°, 135°, and 180°) of PC.
Experimental setup of Ta2PdS6-based ultrafast fiber laser
The device diagram of the fiber laser is shown in Fig. S5b (Supporting Information). A laser diode (LD, maximum output power of 830 mW) with a center wavelength of 980 nm was selected as the pump light source, and the light source is coupled to the cavity through a 980/1550 wave division multiplexer (WDM). The gain medium of the fiber laser was a 2.4-m-long EDF (dispersion coefficient of 28 ps2·km−1) to achieve the inversion of particle numbers. The PC was used to adjust the polarization state in the laser cavity, and the ISO was used to control the unidirectional transmission of light. The 2:8 OC coupled 80% of the laser into the WDM and output 20% of the laser. All optical fibers were SMF (dispersion coefficient of −23 ps2·km−1). The total length of the laser cavity is about 14.6 m with a total dispersion of about −0.21 ps2.
Experimental setup of the DFT
The schematic of the real-time detection system based on the DFT technique is shown in Fig. S5d (Supporting Information). The laser source is a Ta2PdS6-based ultrafast fiber laser constructed for our experiment. The laser source was tuned to the NLP output state, and the laser light output was split into two paths via an optocoupler. One path (the reference volume) is used to record the evolution of the instantaneous intensity pattern of the pulse. The signal from the other path is fed into an approximately 10.4 km long normal SMF to time-stretch the pulse (~230 ps2) for DFT-based spectral measurements44. The signals from the two paths were detected by two identical high-speed photodetectors (PD1 and PD2) and recorded on a real-time oscilloscope at a sampling rate of 5 GS s−1 and a bandwidth of 1 GHz. The resolution of the corresponding DFT measurements was about 0.2 ns.
Simulation
The numerical simulation was performed to model the LS evolution dynamics based on generalized nonlinear Schrödinger equation45:
where \(\psi (z,t)\), \(z\), \({\beta }_{2}\), \(\gamma\), and \({\varOmega }_{g}\) are the slow pulse electric field envelope, propagation coordinate, second-order dispersion, Kerr nonlinearity coefficients, and bandwidth of the gain, respectively. The gain coefficient \(g\) is given by the following equation.
where \({g}_{0}\), \({E}_{p}\), and \({E}_{s}\) are the small signal gain, pulse energy, and gain saturation energy, respectively. The Ta2PdS6-based mode-locking method can be modeled by the instantaneous nonlinear transfer function of Eq.(1). The numerical model is solved with a split-step Fourier method, and the initial input pulse is a weak Gaussian pulse. The other parameters are matched to the experimental conditions, and the specific parameters are as follows: erbium-doped fiber (EDF) = 2.4 m, single-mode optical fibers (SMF) = 12.2 m, \({E}_{s}\) = 100 pJ, \({\varOmega }_{g}\) = 30 nm, \(\gamma\) = 5 W−1·km−1; \({g}_{0}\) = 2.9 m−1, \({\beta }_{2}\)= 28 ps2·km−1 for EDF; \({g}_{0}\) = 0, \({\beta }_{2}\) = −23 ps2·km−1 for SMF.
Data availability
The data that support the plots within this paper and other findings of this study are available within this article and its Supplementary Information file, and are also available from the corresponding author upon request.
Code availability
The code that supports the findings of this study is available from the corresponding author on request.
References
Kerse, C. et al. Ablation-cooled material removal with ultrafast bursts of pulses. Nature 537, 84–88 (2016).
Li, J. Q. et al. Nanoscale multi-beam lithography of photonic crystals with ultrafast laser. Light Sci. Appl. 12, 164 (2023).
Tan, D. Z., Zhang, B. & Qiu, J. R. Ultrafast laser direct writing in glass: thermal accumulation engineering and applications. Laser Photonics Rev. 15, 2000455 (2021).
Dipalo, M. et al. Intracellular action potential recordings from cardiomyocytes by ultrafast pulsed laser irradiation of fuzzy graphene microelectrodes. Sci. Adv. 7, eabd5175 (2021).
Santos, H. D. A. et al. Ultrafast photochemistry produces superbright short-wave infrared dots for low-dose in vivo imaging. Nat. Commun. 11, 2933 (2020).
Kim, K. et al. Massively parallel ultrafast random bit generation with a chip-scale laser. Science 371, 948–952 (2021).
Bao, Q. L. et al. Atomic-layer graphene as a saturable absorber for ultrafast pulsed lasers. Adv. Funct. Mater. 19, 3077–3083 (2009).
Xue, X. X. et al. Dispersion-less Kerr solitons in spectrally confined optical cavities. Light Sci. Appl. 12, 19 (2023).
Hamdi, S. et al. Superlocalization reveals long-range synchronization of vibrating soliton molecules. Phys. Rev. Lett. 128, 213902 (2022).
Hoover, E. E. & Squier, J. A. Advances in multiphoton microscopy technology. Nat. Photonics 7, 93–101 (2013).
Zheng, C. et al. De-scattering with excitation patterning enables rapid wide-field imaging through scattering media. Sci. Adv. 7, eaay5496 (2021).
Zhu, X. Y. et al. Real-time whole-brain imaging of hemodynamics and oxygenation at micro-vessel resolution with ultrafast wide-field photoacoustic microscopy. Light Sci. Appl. 11, 138 (2022).
Leone, S. R. & Neumark, D. M. Probing matter with nonlinear spectroscopy. Science 379, 536–537 (2023).
Ding, T. et al. Measuring the frequency chirp of extreme-ultraviolet free-electron laser pulses by transient absorption spectroscopy. Nat. Commun. 12, 643 (2021).
Balla, P. et al. Ultrafast serrodyne optical frequency translator. Nat. Photonics 17, 187–192 (2023).
Kobtsev, S. et al. Generation of double-scale femto/pico-second optical lumps in mode-locked fiber lasers. Opt. Express 17, 20707–20713 (2009).
Zhang, D. M. et al. From multiple solitons to noise-like pulse in a passively mode-locked erbium-doped fiber laser. Opt. Commun. 504, 127468 (2022).
Yu, P. et al. Ternary Ta2PdS6 atomic layers for an ultrahigh broadband photoresponsive phototransistor. Adv. Mater. 33, 2005607 (2021).
Wang, Q. B. et al. Broadband saturable absorption in germanene for mode-locked Yb, Er, and Tm fiber lasers. Nanophotonics 11, 3127–3137 (2022).
Liu, J. T. et al. High output mode-locked laser empowered by defect regulation in 2D Bi2O2Se saturable absorber. Nat. Commun. 13, 3855 (2022).
Ma, W. L. et al. In-plane anisotropic and ultra-low-loss polaritons in a natural van der Waals crystal. Nature 562, 557–562 (2018).
Liu, S. D. et al. Laser switching characteristics of enriched (7,5) single-walled carbon nanotubes at 640 nm. Carbon 191, 433–438 (2022).
Yu, Q. et al. Femtosecond ultrafast pulse generation with high-quality 2H-TaS2 nanosheets via top-down empirical approach. Nanoscale 13, 20471–20480 (2021).
Dai, Y. P. et al. Controllable synthesis of narrow-gap van der waals semiconductor Nb2GeTe4 with asymmetric architecture for ultrafast photonics. ACS Nano 16, 4239–4250 (2022).
Deng, H. Q. et al. Mode-locking pulse generation based on lead-free halide perovskite CsCu2I3 micro-rods with high stability. J. Mater. Chem. C. 11, 1696–1703 (2023).
Li, L. et al. Ternary transition metal dichalcogenides for high power vector dissipative soliton ultrafast fiber laser. Laser Photonics Rev. 16, 2100255 (2022).
Yang, Z. X. et al. Few-layer Ti3CN MXene for ultrafast photonics applications in visible band. J. Materiomics 9, 44–55 (2023).
Sun, J. X. et al. Ag/MXene composite as a broadband nonlinear modulator for ultrafast photonics. ACS Photonics 10, 3133–3142 (2023).
Lyu, W. H. et al. Fabrication and applications of heterostructure materials for broadband ultrafast photonics. Adv. Opt. Mater. 11, 2300124 (2023).
Zhao, X. L. et al. Integration and applications of nanomaterials for ultrafast photonics. Laser Photonics Rev. 16, 2200386 (2022).
Fu, B. et al. MXenes: synthesis, optical properties, and applications in ultrafast photonics. Small 17, 2006054 (2021).
Xu, N. N. et al. Tellurene-based saturable absorber to demonstrate large-energy dissipative soliton and noise-like pulse generations. Nanophotonics 9, 2783–2795 (2020).
Ma, W. Z. et al. Graphdiyne-decorated microfiber based soliton and noise-like pulse generation. Nanophotonics 10, 3967–3977 (2021).
Mansor, M. et al. Tungsten trioxide nanocomposite for conventional soliton and noise-like pulse generation in anomalous dispersion laser cavity. Nanotechnol. Rev. 12, 20220535 (2023).
Dong, Z. K. et al. Conventional soliton and noise-like pulse generated in an Er-doped fiber laser with carbon nanotube saturable absorbers. Appl. Sci. 10, 5536 (2020).
Seo, S. B. et al. Completely anisotropic ultrafast optical switching and direction-dependent photocarrier diffusion in layered ZrTe5. Adv. Opt. Mater. 11, 2201544 (2023).
Yuan, H. T. et al. Polarization-sensitive broadband photodetector using a black phosphorus vertical p–n junction. Nat. Nanotechnol. 10, 707–713 (2015).
Pi, L. J. et al. Highly in-plane anisotropic 2D PdSe2 for polarized photodetection with orientation selectivity. Adv. Funct. Mater. 31, 2006774 (2021).
Chang, T. Y. et al. Black phosphorus mid-infrared light-emitting diodes integrated with silicon photonic waveguides. Nano Lett. 20, 6824–6830 (2020).
Wang, J. Y. et al. Polarized light-emitting diodes based on anisotropic excitons in few-layer ReS2. Adv. Mater. 32, 2001890 (2020).
Zhao, Y. D. et al. High-electron-mobility and air-stable 2D layered PtSe2 FETs. Adv. Mater. 29, 1604230 (2017).
Loudon, R. The Raman effect in crystals. Adv. Phys. 50, 813–864 (2001).
Gajdoš, M. et al. Linear optical properties in the projector-augmented wave methodology. Phys. Rev. B 73, 045112 (2006).
Goda, K. & Jalali, B. Dispersive fourier transformation for fast continuous single-shot measurements. Nat. Photonics 7, 102–112 (2013).
Wu, X. Q. et al. Farey tree and devil’s staircase of frequency-locked breathers in ultrafast lasers. Nat. Commun. 13, 5784 (2022).
Acknowledgements
We sincerely appreciate Prof. Xiao Wang and Dr. Xiaoxin Yang from the Institute of Technology for Carbon Neutrality, Shenzhen Institute of Advanced Technology, Chinese Academy of Sciences for their help in the simulation of the polarized optical absorption. This research was supported by the Jiangsu Province Key Research and Development Program (Grant No. BE2021007-3, BE2023009-5), the National Natural Science Foundation of China (Grant No. 62035015, 62061136013), the Postgraduate Scientific Research Innovation Project of Hunan Province (Grant No. QL20230006), the Hubei Province Key Laboratory of Systems Science in Metallurgical Process (Grant No. Y202208), and the Open Fund of Key Laboratory for Intelligent Nano Materials and Devices of the Ministry of Education NJ2023002 (Grant No. INMD-2023M06). J.W. acknowledges the support from the CAS Young Talent program under Grant No. E3291305. The support from the Vacuum Interconnected Nanotech Workstation (Nano-X) of Suzhou Institute of Nano-tech and Nano-bionics (SINANO), Chinese Academy of Sciences is also acknowledged.
Author information
Authors and Affiliations
Contributions
Z.Y., Q.Y., J.W., J.W., P.Z. and K.Z. conceived and designed the project. Z.Y. carried out the experiments and numerical simulations. Q.Y. and Y.Z. prepared the materials and performed the characterizations. Q.Y. and H.D. helped with the laser experiments. W.W., T.X., S.Y. and L.Z. helped with the numerical simulations. L.H., J.Z., J.L. and Z.J. helped with the data analysis. Z.Y. drafted the paper. All authors read and contributed to the manuscript.
Corresponding authors
Ethics declarations
Conflict of interest
The authors declare no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Yang, Z., Yu, Q., Wu, J. et al. Ultrafast laser state active controlling based on anisotropic quasi-1D material. Light Sci Appl 13, 81 (2024). https://doi.org/10.1038/s41377-024-01423-3
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41377-024-01423-3