Abstract
Hot charge carriers (HC) are photoexcited electrons and holes that exist in nonequilibrium high-energy states of photoactive materials. Prolonged cooling time and rapid extraction are the current challenges for the development of future innovative HC-based optoelectronic devices, such as HC solar cells (HCSCs), hot energy transistors (HETs), HC photocatalytic reactors, and lasing devices. Based on a thorough analysis of the basic mechanisms of HC generation, thermalization, and cooling dynamics, this review outlines the various possible strategies to delay the HC cooling as well as to speed up their extraction. Various materials with slow cooling behavior, including perovskites and other semiconductors, are thoroughly presented. In addition, the opportunities for the generation of plasmon-induced HC through surface plasmon resonance and their technological applications in hybrid nanostructures are discussed in detail. By judiciously designing the plasmonic nanostructures, the light coupling into the photoactive layer and its optical absorption can be greatly enhanced as well as the successful conversion of incident photons to HC with tunable energies can also be realized. Finally, the future outlook of HC in optoelectronics is highlighted which will provide great insight to the research community.
Similar content being viewed by others
Introduction
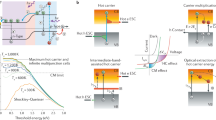
The quest for a sustainable society has promoted rapid research progress and stride in the field of optoelectronics. With a skyrocketing increase in the energy demand, there is an urgent need for a highly efficient, cost-effective, and environmentally stable energy technology to foster the rapid development of emerging scenarios like nearly zero-energy buildings, solar vehicles, portable electronic devices, ultrafast lasers, sensors, light-emitting diodes (LEDs), and photocatalytic devices. Several factors, such as production cost, price of precursor materials, and their toxicity, need to be carefully considered by the respective stakeholders. However, power conversion efficiency (PCE) is the key criterion that has been typically tackled by the scientific community in the last few decades. In 1961, Shockley and Queisser demonstrated a theoretical PCE limit (33.8%) in solar cells1. This limit has been already surpassed with the effective employment of the multijunction concept, whereby multiple semiconductor layers, with bandgaps tuned to broaden the coverage of the solar spectrum, are combined in the same device2,3. The energy of the solar photons lies in the range between 0.5 and 3.5 eV. The photons with energy below the bandgap of the photoactive material are not absorbed while those with energy above the bandgap, create electron and hole (e–h) pairs with excess kinetic energy equal to the difference between the incident photon energy and the bandgap energy of the material4,5. These (e–h) pairs are referred to as hot charge carriers (HC). In conventional solar cells, the excess energy of photons over the bandgap is wasted as heat. The general description of the solar cells working mechanism, charge collection, and energy loss is presented in Fig. 16.
The figure is taken from ref. 32 and modified
The effective utilization of such excess energy can be achieved by two alternative processes, namely (i) enhancing the photo-voltage by extracting the HC before their quick cooling, or (ii) increasing the photocurrent by producing one or two more e–h pairs through impact ionization7. The first process refers to the hot-carrier solar cells (HCSCs)8 and the second one is known as multiple exciton generation (MEG) or carrier multiplication (see the section “HC cooling and multiple exciton generation (MEG)”)9. HC extraction is an unconventional and innovative approach to overcome the unavoidable energy losses in solar cells. As a result, HC enable boosting the PCE towards the Shockley–Queisser (S–Q) limit and beyond. The concept is based on the thermal isolation of HC and phonons (so that they may stay at different temperature regimes10), followed by their selective extraction to the external circuit through efficient energy-selective contacts (ESCs).
Considering the theoretical S–Q limit of single-junction solar cells (under 1 and 100 Sun illuminations), there is still plenty of room for sophisticated device architectures and new materials. Since the first theoretical concept introduced by Ross and Nozik in 1982 on HC solar energy converters, many researchers across the globe struggled with developing a proof-of-concept device architecture4. The collection of excited charges in femto- to picosecond time regime, before their subsequent cooling toward the respective conduction band, is a daunting challenge for the practical application of this concept into a fully functional device11.
HC are soaked in a fluid of phonons and at first glance, it is very difficult to isolate them from such a highly unstable fluid. In his book about the energy losses by the charge carriers in solar cells, Ridley highlights that “Interest in semiconductor physics generally focuses on properties consequent on the quantum transitions made by electrons and holes, but many of these transitions involve the emission of phonons, and therefore it is pertinent to ask what happens to these phonons”12. The strong interaction of HC with acoustic and optical phonons, the scattering of these phonons from the nanostructure and boundaries, and their contribution to the thermal conductivity are important processes that need to be addressed.
The schematics of photoexcitation, along with HC generation and the sequential process of their thermalization and recombination, are illustrated in Fig. 2a. The cooling of HC in their respective conduction and valence energy bands (hot electrons in CB and hot holes in VB, respectively) takes place through the generation of phonons (Fig. 2b)13. The PCE of HC can be extended up to 67%, close to that of tandem cells at 1 Sun irradiation (Fig. 2c), and can even reach up to ≈75% using 100 sun concentrators, where the electronic temperature increases up to 3000 K (Fig. 2d). This highlights the importance of this new type of device (HCSCs).
a The sequential process of HC, starting from excitation till recombination. b The cooling of HC in their respective bands of unequal curvatures (as different carrier effective mass). c The new generation solar cells with efficiency above the S–Q limit. d Under irradiation of 1 and 100 suns concentration (i.e., low-concentrator photovoltaics) the ultimate efficiency of HC solar cells, at different charge carrier temperatures, plotted versus their photoabsorber bandgap. A conventional solar cell is represented by the lowermost curve, while the vertical dashed lines correspond to the bandgap of halide perovskite materials. “A” in ASnI3 and APbI3 corresponds to methylammonium (MA), formamidinium (FA), and cesium (Cs) ions. The figures are adopted with permission from (a, b) ref. 14 and (c, d) ref. 26
Compared to multijunction solar cells that require various stacked layers of different semiconductors, HCSC is composed of only three layers, i.e., an absorber and two ESC layers (for extraction of hot electrons and hot holes, respectively)14,15. This simple architecture can achieve similar PCE as that of multijunction photovoltaics (PV). Studies on HC have been also extended to various other important applications beyond PV, such as photocatalysis16, photodetection17, and light emission18.
The advent of a new class of photoactive materials with outstanding optoelectronic properties, namely halide perovskites, has created exciting research avenues uncovering new technological applications. Perovskite materials have been extensively studied in the context of photon absorption and separation/collection of charge carriers, leaving the HC generation, thermalization, and extraction aspects almost unexplored.
On the other hand, metallic nanostructures (typically Ag, Au, and Cu) can also produce HC. When the frequency of incident light matches the intrinsic oscillation of free electrons in the metallic nanostructure, the electrons oscillate collectively, which is known as surface plasmon resonance (SPR)19,20. The generation of HC is one of the energy-releasing mechanisms of these plasmons as they undergo ultrafast dephasing in femto- to picosecond timescale. The fundamental understanding of excitation, generation, and successful extraction of these plasmonic HC as well as their futuristic use in photodetection, sensing, photochemical, and PV applications are the hot research topic these days. Deepening the knowledge on higher excited energy states, as well as HC, will not only enable the development of sophisticated ultrafast spectroscopy techniques but will also open new research directions for a number of energy conversion applications based on enhanced light intensities, hence making the realization of future HC optoelectronics possible.
This review addresses the fundamental concept of HC generation in photoactive materials, with a special focus on their thermalization and cooling phenomenon (see section “HC generation, thermalization, and relaxation phenomena”). Section “HC in organic–inorganic halide perovskites” highlights the key properties of HC in perovskite materials followed by the effect of material morphology and structure on the HC behavior. The design and performance of efficient energy-selective contacts for perovskites and other semiconductor materials are discussed in the section “Working principals of HC solar cells”. Furthermore, the basic plasmonic effects in the most common plasmonic materials, as well as their energy loss mechanisms in terms of HC generation, are elucidated in the section “Plasmonic HC and their applications in other optoelectronic devices”, which also show their effective use in futuristic energy-efficient applications, such as ultrafast photochemical reactors, hot-electron transistors (HET), detectors, and lasing devices. Finally, in the section “Outlook for HC in future optoelectronic devices”, we highlight the most promising research perspectives and directions for HC science and applications.
HC generation, thermalization, and relaxation phenomena
In the photoexcitation process, an incident photon, whose energy is equal to or higher than the bandgap energy (Eg) of the targeted materials, imparts its energy to the valence band electron of the photoabsorber material and excites it to the higher energy level (conduction band). The excited electrons in the conduction band leave a positive charge behind in the valance band, termed as an excited hole. These excited species are collectively called “excitons” or “free charge carriers”. However, if the excitation energy is far higher than Eg, the charge carriers jump to even higher energy states, termed as energy sub-bands, which are above the conduction band minimum (CBM) and below the valence band maximum (VBM) for excited electrons and excited holes, respectively. The highly excited charge carriers are hot electrons and hot holes, collectively termed as HC, as shown in Fig. 4 (see ref. 21). HC convert their excess energy to heat upon de-excitation. The distribution of the excess energy between the HC is described by the following equations22:
where m*e and m*h are the effective masses of electron and hole, respectively. ΔEe is the energy difference between the conduction band and the initial energy of photogenerated electrons, and ΔEh is the energy difference between the valence band and photogenerated holes (see Fig. 3, Eqs. (1) and (2)).
In this image, “HC” refers to hot electrons. A similar phenomenon takes place for hot holes as well. a Absorption of high-energy photons by a photoabsorber. b Electrons from the valence band maximum (VBM) of an absorber material jump to energy states higher than conduction band minimum (CBM). The detailed phenomenon of HC is presented in (c): (i) carrier–carrier scattering, (ii) the thermalization of HC to occupy energy states through Fermi–Dirac distribution, (iii) cooling through their interaction with LO phonons, and (iv) finally the loss of their energy to attain lattice temperature. d The charge carrier either transfer to the electron-transport layer (ETL) or recombination takes place
The HC, generated through photoexcitation, subsequently cool down by carrier–carrier collision, scattering between HC and lattice phonons, causing significant energy losses (thermal cooling). The general mechanism of HC generation and cooling is summarized in Fig. 3. The scattering continues until the energy of HC is less than the longitudinal optical (LO) phonon energy. The emitted LO phonons from the electron–LO–phonon scattering decay into daughter acoustic phonons or transverse optical phonons, which decay further within 100 ps. The thermally cooled HC are now available to be transferred to the charge transport layers (hole-transport layer, HTL, or electron-transport layer, ETL) or lose the remaining part of their energy through recombination. The detailed mechanism of HC generation and their subsequent thermalization and cooling processes are illustrated in Fig. 4a–d.
The HC relaxation process is composed of two stages. In the first stage, the HC are far from the equilibrium, and the collisions start between the HC (electron–electron and hole–hole collision) or through impact ionization and Auger recombination if their concentration is high (>1018 cm−3)23,24. This stage is attained very rapidly (<100 fs) and is referred to as “thermal equilibration” or “carrier thermalization”22. The temperature of these species generally reaches from 2500 to 4500 K under 1 and 100 sun illumination, respectively22,25. The second stage of HC relaxation starts with their equilibration with the lattice through carrier–phonon inelastic interaction until the temperature of both lattice and HC becomes equal. The process is referred to as “carrier-cooling” and occurs at the picosecond timescale. Finally, the equilibration ends with the complete relaxation of the system. Electrons and holes are now available in their respective energy bands for either transfer to the charge transport layers (in the case of PV devices) or for recombining through radiative or nonradiative processes.
Two important clarifications need to be made before discussing the HC and the related energy dissipation phenomena in more detail: (i) for the calculation of the energy loss rate per charge carrier, the ultrafast community has standardized and fixed the minimum value of HC temperature to 600 K. In fact, below 600 K the cooling rate of HC is sufficiently slow, which may underestimate the results; (ii) due care must be considered when reporting the values of HC lifetime because every spectroscopic instrument, such as those required to carry out the time-resolved photoluminescence (TRPL) or transient absorption (TA) characterization, has its own temporal response that may influence the value of HC intrinsic lifetime. The detailed processes of HC relaxation are elaborated in the following sub-sections.
Pathways during thermalization and cooling of HC
As explained by Li et al., in higher excited energy states, the HC redistribute their energy and relax through various pathways to attain the thermal equilibrium with the lattice26. The energy relaxation process is explained by the concepts of “carrier thermalization” and “carrier cooling”.
The carrier thermalization occurs very rapidly (<100 fs) and is governed by carrier–carrier elastic collisions in which the HC equilibrate among themselves. However, when the HC concentration is high due to the high excitation density of the incident light, an equilibration process also occurs through an impact ionization and Auger recombination5,24. The HC scattering is generally proportional to the square of their concentration (electrons or holes)27 that leads to the renormalization of HC or it interacts with the valence band electrons (in the case of hot electrons) known as the Auger recombination. Auger recombination is not a loss mechanism but rather a reverse process and, once the energy is released, the free charge carriers are re-heated again5. The energy renormalization process results in a Fermi–Dirac distribution of the hot species that reaches a higher temperature than their lattice5. These hot species interact amongst themselves by carrier–carrier interactions and intervalley scattering to achieve a Fermi–Dirac energy distribution (separately for hot electrons and hot holes)14. A separate temperature is assigned to hot electrons and hot holes, which reflects the distribution of kinetic energy in their respective charge carrier population. The equilibrated HC occupy energy states according to the Fermi–Dirac statistics with a temperature assigned as carrier temperature, Tc (Te and Th for electrons and holes, respectively) that is larger than the lattice temperature (TL)28. This distribution is maintained by the carrier–carrier interactions to randomize the carrier distribution in k-space, where the k-space randomization is affected by the interaction rate. An interested reader may refer to refs. 25,29 for further detailed insights. Although, the hot species attain an equilibrium among themselves, they are far from equilibrium when compared to the lattice, and no phonon generation has yet taken place at this stage.
The carrier-cooling stage, taking place after carrier thermalization, starts with the equilibration of thermalized carriers with the crystalline lattice mainly through inelastic carrier–phonon interactions.5 The excess kinetic energy is transferred from the carriers to the phonons, in which the carrier cooling and the lattice heating take place until both reach the thermal equilibrium22.
Mechanisms for optical phonon emission
Because of the local electrostatic distortion, the Fröhlich interaction starts between the electrons and phonons and results in the formation of polarons5. Furthermore, the electron energy loss takes place through the emission of an optical phonon, which decays further to an acoustic phonon that reheats the free electrons5. The generalized process of HC generation and the possible scattering of HC are depicted in Fig. 5.
The numerical labels indicate each specific process, namely (1) exciton generation, (2) hot electrons reflection at the ESC, (3) electron–electron collision, (4) impact ionization, (5) sub-bandgap photons reabsorbed by free electrons, (6) emission of optical phonon, (7) re-absorption of optical phonon, (8) quasi-ballistic transport of HC, (9) tunneling of HC from the photoabsorber to the interfacial contact. The figure is taken with permission from ref. 5
This process continues with phonon emission as long as the TC of HC is higher than that of the phonons30. TC is extracted from the high-energy tail of the TA spectra using the Maxwell Boltzmann function (Eq. (3)). In halide perovskites, the effective masses of an electron and hole are roughly the same (m*e = 0.19 m0, m*h = 0.25 m0, where m0 is the rest mass of an electron)24,26,31, and thus the temperature of hot electrons and hot holes are approximately equal26.
where, ΔA is a transient absorption, \({\Delta}E\,(E_f - E)\) i.e., E–Ef > KBT, TC is the HC temperature and KB is the Boltzmann constant.
Mechanism of phonon decay
The dominant way of heat dissipation, observed in polar compounds such as GaAs, occurs through Fröhlich interactions or Fröhlich scattering, which is governed by long-range coulombic potential. The initial rate of the intervalley carrier–LO phonon scattering is given by the following equation
where E represents the energy above the CBM, mef is the electron effective mass, \(\eta _{BE\left( {\omega ,T} \right)} = \frac{1}{{e^{\frac{{\hbar \omega }}{{k_BT}} - 1}}}\) is the phononic equilibrium population at T (temperature) with phonon frequency ω, \(\varepsilon _\infty \,and\,\varepsilon _s\) are the dielectric constants at low- and high-frequency (static) constants. The same equation can be written for the hole cooling process in the valence band. Thus, the energy relaxation rate is given by \(\left\langle\frac{{{\mathrm{d}}E}}{{{\mathrm{d}}_t}}\right\rangle = \frac{{\hbar \omega }}{{\tau _{e - {\mathrm{LO}}}}}\) by neglecting the re-absorption of the phonons. The cooling of HC (electrons) continue by LO phonon emission until their energy is less than the energy of an LO phonon (\(\hbar \omega _{{\mathrm{LO}}}\)) above the CBM. Interaction of the hot electrons with the acoustic phonons also takes place, but mainly around the Brillouin zone center, and exhibits negligible energy exchange while primarily imparting the momentum equilibration. LO phonons exhibit low thermal conductivity and the heat dissipation is mainly due to acoustic phonons. The lattice anharmonicity is responsible for the further decay of optical phonons to acoustic phonons. At temperatures <1000 K, there are four prominent decay mechanisms found in various materials14. In the cubic crystalline structure of zinc blend or diamond, three decays mechanisms are found: (i) Klemens decay mechanism, (ii) Ridley decay mechanism, and (iii) a decay mechanism through Valle´e–Bogani channel, and (iv) the fourth decay mechanism called Barman–Srivastava (Fig. 6b), is found in hexagonal materials (e.g., wurtzite structure). Generally, the electron–LO phonon scattering occurs in the time range of 1 ps, followed by the emission through acoustic phonons. Hence, the charge carriers become available for transfer to ESC or recombination (radiative or nonradiative).
a The predominant routes of phonon decay start from their origin center as LO phonons and progressively turn into lower energy acoustic phonons that are responsible for the dissipation of heat. b The four types of decay mechanisms are depicted as Klemens, Ridely, Vallee–Bogani, and Barman–Sirvastava. The figures are taken with permission from ref. 13
HC in organic–inorganic halide perovskites
Organic–inorganic metal halide perovskites have attained a top position in photovoltaic research due to their extraordinary optoelectronic properties, facile synthesis routes, and convenient device fabrication processes. Among these properties is slow HC cooling28,31, which is paramount for the new generation of HCCs to surpass the S–Q limit32. Recent experimental results revealed that the bulk lead halide perovskite materials showed slower HC dynamics at an excess excitation energy of 1.4 eV (∼0.4 ps)33 as compared to most of the other inorganic semiconductors (∼0.1 ps)34. The various intrinsic properties of perovskite materials that are responsible for prolonging the HC thermalization time are shown in Fig. 7.
Polaron formation in perovskites and its size effect on HC cooling
The polaron concept was first introduced by Landau, and its self-energy and effective mass were investigated later35. A polaron originates from the interaction of a charge (electron or hole) with its surrounding atoms. Typically, in a polar semiconductor or an ionic crystal, the conducting charge carrier, together with its self-induced polarization cloud, forms a quasi-particle known as polaron (Fig. 8a)36. As compared to the bare charge particle, physically, a polaron is characterized by its newly modified properties, such as the polaron binding energy Ep, its effective mass m*, and its response to the externally applied electric and magnetic field (e.g., DC mobility and optical absorption coefficient). These very peculiar properties lead to a strong change in the electrical and thermal properties of the materials37.
Two distinct types of polarons, small polaron and large polaron, are found in two- or three-dimensional systems. The type of polaron formation depends on the electron–lattice interaction, which is of primary importance. A large polaron forms due to the long-range Coulombic interactions between a charge carrier and a solid ion. Competing effects then determine the radius of the large polaron. By contrast, a small polaron can form when a short-range electron–lattice interaction, such as the deformation-potential interaction, is dominant38. Specifically, due to the excess charge in a deformable solid, the electron–phonon coupling becomes sufficiently strong so that a self-trapped polaron formation is found. For a strong electron–phonon coupling in highly polar and ionic crystalline solids, two driving forces are responsible for the polaron formations, namely (i) the long-range Coulombic potential (VLR) between the ionic lattice and the excess electron (screen hole), and (ii) the short-range deformation potential (VSR) due to the variation in local bonding by the excess charge. VLR is given by the following Eq. (5)
where r is the vector distance between an ionic site and electron, \(\varepsilon _0\) is the permittivity in vacuums, \(\varepsilon _{r( \propto )}\) and \(\varepsilon _{r(0)}\) are the high-frequency and static dielectric constants, respectively and \(e\) is the electron charge. In the case of Si or GaAs, the two dielectric constants are the same (\(\varepsilon _{r(0)} \approx \varepsilon _{r( \propto )}\)), hence the value of \(V^{{\mathrm{LR}}}\) is negligible. However, in ionic solids, the value of \(\varepsilon _{r(0)}\) is twice that of \(\varepsilon _{r( \propto )}\), thus making the long-range Coulombic potential significant. If VLR is higher than VSR, the size of the polarization cloud (coherent length, Lcoh) is larger than the unit cell dimension (Lcoh > a). This results in the formation of a large polaron. In the case of small polaron formation, VSR is higher than VLR (Lcoh < a)39. The electronic and optical properties of large and small polarons are significantly different. The transport in large polarons is coherent with their high mobility (µ > 1 cm2 V−1 s−1) and the transport resembles the coherent transport of a free charge carrier in a conductor. However, mobility decreases with a decrease in temperature (\(\frac{{\partial \mu }}{{\partial T}} < 0\)). In contrast, the transport in small polarons is incoherent with far lower mobility (µ ≪ 1 cm2 V−1 s−1) and increases with the increasing temperature (\(\frac{{\partial \mu }}{{\partial T}} > 0\))38. Lu et al. theoretically explained the polaron formation and their dynamics in organic semiconductors40. The large polaron is also defined as the shallow bound state that arises from the Coulombic interaction between the electron and the polarizable lattice. Similarly, small polarons are strongly localized wave functions within a chemical bond.
The unique crystal structure of organic–inorganic lead halide perovskite is a hybrid framework-like structure composed of two interpenetrating structures, (i) a sublattice of inorganic Pb halide corner-shared octahedra (PbX6)4− to form a 3D crystalline network with \(PbX_3^ -\) stoichiometry, and (ii) a sublattice of an organic cation (A+), commonly CH3NH3+, to fill the cubo-octahedral void between the inorganic sublattice and to balance the charge (Fig. 8b). The peculiar nature of this hybrid structure lies in such a way that both valence and conduction bands for charge transport are formed by the inorganic sublattice. This structure gives rise to two main properties, namely dynamic disorder and intrinsic softness. The dynamic disorder is reflected by various phenomena, such as the anharmonicity and broadening in far-infrared (far-IR) and low-frequency Raman spectra, the disorder in nuclear magnetic resonance (NMR) and X-ray or neutron scattering, and liquid-like responses in dielectric function or fs-ps responses41,42. Intrinsic softness is shown by lower Young’s moduli (i.e., ten times lower than Si and GaAs)42. Thus, the organic sublattice serves as charge screening and charge localization by modulating the electrostatic landscape experienced by the charge carriers39.
The dipole nature of organic molecule (CH3NH3+) introduces polar potential and ferroelectricity in halide perovskite structures. The fast rotations of this organic molecule and also the soft inorganic sublattice affect the carrier transport by electron–phonon coupling43,44. With a relatively strong electron–phonon coupling, large polaron formation is observed, which develops pseudo-free dressed carriers that screened from other free carriers and defects to avoid recombination and trapping. This results in a long lifetime and diffusion length39. These large polarons spread over a hundred unit cells due to their weak long-range Coulombic interaction and small lattice distortion of LO phonons. The HC longer lifetime (>100 ps) observed at low excitation density (<1018 cm−3) might be attributed to the screening of these large polarons. At high excitation density (>1018 cm−3), the overlapping of the polarons is responsible for the “phonon bottleneck” effect.
The formation of a small polaron is usually facilitated by the presence of lattice defects that initiate the charge trapping process with a negative impact on the transport of charge carriers as well as on the overall device efficiency39,45. Therefore, the effects of polarons on the charge transport properties need to be revealed in order to synthesize and design semiconductors for efficient optoelectronic devices.
HC dynamics in perovskites at high- and low-carrier densities
Before analyzing in more detail the effects of high- and low-carrier density on HC dynamics, it is worth discussing how to calculate their density and the power or energy loss rate of HC. Spectroscopic techniques, such as TRPL and TA, are typically used to study the HC dynamics in nanocrystals (NCs) and thin films. Specifically, these techniques allow researchers to study the momentum and kinetic energy of the excited states along with their transient inhabitants (i.e., HC) and also provide essential information about the electronic states and the electronic structures of photoactive materials.
In a typical spectroscopic experiment, a laser beam of a selected power (typically in microwatt scale) is focused onto a small spot on the sample to excite it. The pump fluence (F) can be calculated as \({{F}} = {{EA}}^{ - 1}\), where E is energy and A is the spot size in cm2. Energy can be calculated as \({{{\mathrm{E}}}} = {{{\mathrm{power}}}} \times {{{\mathrm{time}}}}(f^{ - 1})\) where time is the repetition time of the used pulse, i.e., the inverse of frequency (\(f^{ - 1}\)). The carrier’s density calculations (n0 cm−3) in perovskite films has been reported by Dursun et al.46 as
where j is the laser pump fluence and its unit is µJ cm−2 (equivalent to the number of photons/cm2) and can be calculated as E = n‧h‧c/λ), and \(\alpha\) is the absorption coefficient at the excitation wavelength. The power loss rate of HC can be calculated by fitting the TA spectra and using the following equation47
where KB is Boltzmann constant, TC and TL are the temperatures of HC and lattice, respectively. Different cooling dynamics in perovskite films and NCs have been observed at different carrier densities or pump fluences. The rather complex interplay of HC cooling dynamics depends not only on the intrinsic properties but also on several additional factors, such as (i) the excitation energy, i.e., pump energy, with typically higher excess energy leading to a longer carrier’s lifetime, (ii) the initial HC density, where the higher density usually follows a longer cooling time trajectory, and (iii) HC energy loss rate, which is typically lower at lower HC temperature13.
At low pump fluence where the carrier concentration is <1018 cm−3, the cooling dynamics can be explained by Eq. (7). However, at high pump fluence (carrier concentration after the excitation >1018 cm−3), the cooling trend deviates from the equation due to the appearance of two phenomena, Auger recombination and phonon bottleneck effect that decrease the cooling rate. The effect of the initial carrier density and excitation energy on HC dynamics in perovskite bulk film and NCs has been extensively investigated by various researchers13,46,47. Li et al. studied the effect of pump fluence on carriers cooling in MAPbBr3 NCs and bulk film, where the higher initial temperature at high pump fluence, as well as the slower cooling rate, has been observed for NCs as compared to bulk film (Fig. 9a)13. The smaller TC of the bulk film showed ultrafast cooling of HC and is beyond the temporal resolution of the TA equipment used in the experiment. Similarly, there is a rapid energy distribution through elastic scattering, i.e electron–hole scattering, at low pump fluence and electron–electron scattering at high pump fluence is responsible for lower-temperature regime and higher cooling rate26. Higher excitation fluence generates higher TC and also a slower cooling rate is observed. The initial rapid cooling rate until 600‒700 K is attributed to the strong carrier–LO–phonon coupling, which establishes thermal equilibration between HC and LO phonons. Beyond 600 K a lower cooling rate to the band edges is observed due to thermal equilibrium between LO phonons and acoustic phonons26,47. Chen et al. studied the same cooling rate in organic halide perovskite NCs, which is attributed to carriers-phonon couplings at higher and lower-temperature regimes (Fig. 9d). The steep red line in Fig. 9d indicates that the carriers’ temperature is higher than LO phonon, while the blue line corresponds to the regime where there is equilibration between LO phonon and HC. The thermal energy between electron and LO phonon moves back and forth, and the process sometimes is known as phonon energy up-conversion48. The breakpoint between the two regimes occurs at 600 K. Beyond that temperature, LO phonons give away their energy to acoustic phonons and this usually takes place at a timescale of 3–5 ps47. In polar semiconductors, slow carrier cooling is observed at higher excitation intensity or higher carrier density. Thus, in these semiconductors, three to four orders of slow cooling is attributed to hot LO-phonon botttleneck30,49. At higher laser fluence, multiple exciton states are occupied and they lead to higher carrier density as well as higher temperature. The lifetime of HC in MAPbI3 film reaches ≈60 ps until 600 K, which is about two times higher than the lifetime at low pump fluence50. The HC cooling time regime in hybrid perovskites is 100 times longer than that of GaAs film and CdS microplates26.
a The temperature of HC versus the delay time for MAPbBr3 NCs and bulk film. b, c represent the influence of various excitation densities on HC temperature on perovskite film, where higher initial carrier density corresponds to delay in cooling time. d Power loss in CsPbBr3 NCs as a function of inverse temperature, where the red line and blue line correspond to HC temperature higher than lattice LO phonons and the equilibrium established between both entities, respectively. e Slow cooling of organic lead halide perovskite in which the influence of various pump energies on HC cooling is observed. Higher energy corresponds to slow cooling. The figures are taken with permission from (a) ref. 46, (c) ref. 50 and (d, e) ref. 47
Similarly, an increase in the excitation energy results in higher temperature, as shown in Fig. 9e. The excess excitation energy above the bandgap of the targeted material corresponds to TC according to the energy relation E = 13/2KBTC, and it is equally distributed between both carriers (electron and holes). Lower excitation energy will result in a temperature decrease of the resultant HC. Finally, the HC cool down to the band edge and are available for collection or recombination (Fig. 2b). These results provide an insight into HC dynamics in high and low excitation densities, which can be beneficial for selecting the appropriate selective contacts for an efficient charge extraction.
Modifications in chemical composition and their effect on HC dynamics
Extensive research efforts have been directed toward tailoring the HC dynamics by doping and using various chemical modifications, such as cation (A+) and halogen (X−) modifications in organic–inorganic lead halide perovskite materials48,50,51,52,53 Xing et al. studied the effect of HC cooling dynamics and extractions in Zn-doped CsPbI2Br at low photoexcitation level (1017 cm−3). The Zn-doped perovskite showed a reduced HC cooling rate, three times smaller than undoped perovskite, which is due to the improved film morphology and lower defect density. In addition, the nonadiabatic coupling between conduction bands and the introduction of relaxation channels due to Zn are mainly responsible for slow carrier cooling and fast extraction at interface53. Madjet et al. simulated the theoretical radiative relaxation dynamics of HC in lead halide perovskites and outlined how relaxation time depends on the halogen composition. The effect of cation modification on HC dynamics in perovskites was studied by using nonadiabatic molecular dynamic (NA–MD) combined with density functional theory. Due to the larger nonadiabatic coupling in the valence band states as compared to the coupling in the conduction band states, the hot holes relax faster than hot electrons, which is further attributed to the low recombination rates in the perovskite systems52.
Cation modification is a simple and easy method to prolong the HC lifetime in lead halide perovskite materials. In a similar study, an increase in chlorine (Cl) concentration leads to slower HC relaxation dynamics which is due to nonadiabatic electronic coupling that arises from charge-state localization around the Cl atom. In addition, in a work by Talbert et al. the effect of bromide content in MAPbI3-xBrx on the excited states and HC dynamics was probed54. With an increase in Br concentration, there is not much effect on auger recombination, but the rapid thermalization of HC was observed due to enhanced electron–phonon coupling. A strong hot-phonon bottleneck effect has been observed for pure MAPbI3, which indicates a long HC lifetime, while an increase in Br substitution in crystal lattice suppresses the phonon bottleneck effect. Figure 10a shows the substantial rapid thermalization with an increase in Br contents in mixed-halide perovskites.
a The rapid thermalization of HC with increasing Br concentration can be seen, which indicates the strong electron–phonon coupling that in fact reduces the phonon bottleneck effect. b The dependence of HC cooling on cation nature where FA and MA cations are more prone to charge carrier–phonon coupling compared to Cs counterpart. c Energy and density of states of phonons in MAPbBr3 (16 modes) and CsPbBr3 (9 modes) and d the band structure of all inorganic perovskite (CsPbX3, X = Cl, Br, I) crystal showing the highest valence band (VB1) and lowest conduction band (CB1) and their energy of states. The figures are taken with the permission from (a) ref. 54, (b) ref. 47, (c) ref. 58, and (d) ref. 51
In recent years, A-site cation engineering of the ABX3 perovskite structure, with A being e.g., formamidinium (FA), methylammonium (MA), and/or inorganic (e.g., Cs) cation, has been a hot topic for the study of HC dynamics, and many interesting fundamentals have been revealed by ultrafast spectroscopy techniques47,48,51,55. Due to defect tolerance, nanostructure, quantum confinement, and excellent charge transport properties, the low-dimensional halide perovksite [e.g., quantum dots (QDs), nanocrystals (NCs), nanowires (NWs), and nanorods (NRs)] have gained much research attention. Recently, long-range exciton diffusion length (>10 µm) has been observed in MAPbBr3 NC film that has shown a superior exciton carrier mobility (10 cm2 V−1 s−1) which is much higher than 3D perovskite film56. Chen et al. related the HC relaxation dynamics to the cation engineering in lead halide perovskite (MAPbBr3) NCs and observed longer HC cooling time for inorganic (Cs) cation-based perovskite compared to the other organic counterparts (MA and FA) (Fig. 10b)47. The fast motion of the organic cations (MA and FA) induces stronger electron–phonon interaction and coupling as compared to Cs57. As a result, enhanced HC cooling is achieved for organic cation-based perovskites. Among the three selected cations (i.e., MA, FA, and Cs), FA showed the fastest relaxation dynamics. This was ascribed to its strongest interaction with the PbX framework as compared to the other two cations. The intrinsic thermal conductivity of the material has also an impact on HC lifetime, and longer lifetimes are displayed for materials with lower thermal conductivity. Hopper et al. studied the HC relaxation of different lead halide perovskite systems by fs TA spectroscopy, where he studied the effect of cation and halide composition (e.g., FAPbI3, FAPbBr3, MAPbI3, MAPbBr3, and CsPbBr3) on the HC temperature and relaxation dynamics58. The inorganic cation (Cs) showed the longest HC relaxation and prolonged cooling time compared to other configurations, which was attributed to a smaller specific heat capacity59,60 and fewer optical phonon modes in Cs-based halide perovskites (9 optical phonon modes for CsPbBr3 and 16 for MAPbBr3) as shown in Fig. 10c. The valence band (VB) and conduction band (CB) are mostly occupied by lead and the incorporation of halogen can affect the bandgap as well as density of states (DOS) of organic–inorganic perovskite. In CsPbX3 when X sequentially altered from Cl to I, there is a change from 3p to 5p, observed in valence orbital that corresponds to a decrease in perovskite bandgap. The effect of halide modification on the band structure in Cs-based halide perovskites can be seen in Fig. 10d, where the lowest bandgap (1.83 eV) is achieved with the iodide substitution. Intrinsic thermal conductivity in perovskite materials is relatively lower as compared to other semiconductors, which has a positive impact on HC dynamics by prolonging their lifetime61. The single and polycrystalline MAPbI3 perovskites were also studied, displaying ultralow thermal conductivities of 0.5 WmK−1 and 0.3 WmK−1, respectively. The lower phononic group velocities and anharmonicity were responsible for such a slow thermal conductivity62.
These results will guide future works on how the phonon modes in different materials affect the relaxation mechanism and dynamics of HC relaxation. HC dynamics are mostly cationic dependant where organic cation (FA and MA)-based perovskite shows faster thermalization as compared to inorganic (Cs) perovskite. The HC cooling times of various perovskite compositions are summarized in Table 1.
HC cooling and multiple exciton generation (MEG)
HC typically possess an amount of energy equal to the difference between the bandgap of the photoactive material and the incident photon energy. However, if this excess photon energy exceeds a certain threshold limit (two times Eg), the MEG process takes place, which yields two or more excitons9,63. MEG has been proposed as a promising and feasible method for capturing the energy of HC and boosting the light conversion beyond the S–Q limit7,64. MEG can be promoted in semiconductor NCs compared to their bulk counterparts7. Fortunately, the slow HC cooling in perovskites makes them highly suitable for MEG, which has led to discoveries of the underlying physics of the MEG phenomena9,65,66.
After the excitation of HC, the carrier thermalization and cooling processes depend on the properties of the HC and the band structure of the photoabsorber. In optoelectronic applications, the carrier scattering rates determine the fundamental limits of carrier transport and electronic coherence.
Quasi-ballistic HC diffusion
By combining TA with spatial microscopy, researchers such as Sung et al.67,68 and Guo et al.69 showed that HC can diffuse extremely fast compared to the cooled carriers. While the cooled carriers may require a few hundred ps to few nanoseconds to travel across a 500 nm thick perovskite layer, the HC can travel at near a ballistic speed with a traveling distance of 150 nm within the first 20 fs68, and 600 nm overall before cooling down69. This implies that the excess energy of the hot electrons can act like kinetic energy. By improving the perovskite quality via reduction and passivation of traps, this ballistic transport can be further enhanced67. These results suggest much better chances for functional HC as the HC extraction is otherwise limited to the carriers close to the extraction interface.
Working principals of HC solar cells
To handle the major PV loss mechanisms due to the fast thermalization and cooling of HC, it is important to understand the working principle of these novel types of devices, namely HCSCs. To implement the ideal and theoretical model of HC to a working device, two parameters are of crucial importance; (i) long cooling time and (ii) ultrafast and efficient extraction of HC before their cooling. This innovative HC solar cell design was proposed since 1982 by various eminent researchers4,5,15,70 and is equivalent to a conventional solar cell, where an absorber is sandwiched between the two very thin carrier extraction layers followed by external electrodes, as shown in Fig. 11.
\(\mu _e^c\) and \(\mu _h^c\) are the chemical potential energies for hot electrons and holes, respectively, and \(\mu _{eh}^c\) is their separation. The figure is taken with permission from ref. 14
The basic operation of a HC solar cell is to utilize the temperature gradient established between the HC (TC) and the lattice (TL) to get higher voltages than are otherwise obtainable in a conventional PV cell4. ESCs extract HC with specific energies (Ee for hot electrons and Ep for hot holes) with an energy window of δE from the absorber. The bandwidth of the energy selective window (ESW) has to be narrow, less than kBTL, in order to prevent the HC from relaxing to the lower states and cooling down isentropically to TL. The open-circuit voltage of the device is given by Eq. (4),
where ∆Eeh is the energy separation of the ESCs. However, in a conventional solar cell, the equation reduces to \(eV_{{\mathrm{OC}}} = {\Delta}\mu\) as the HC relax to TL. In conventional PV devices, there is much emphasis on particle extraction rather than energy extraction25.
Physics of the energy-selective contacts for the HC extraction
The selection of an ideal and effective ESC is difficult as it acts as a tunneling barrier with a resonant energy level of width \({\Delta}E_{{\mathrm{ESC}}}\) (\(\delta {{E}}_{{{{\mathrm{ESC}}}}} < < k_BT\)) allowing only a narrow range of charges to tunnel through it. However, the HC beyond the aforementioned energy have a high probability to reflect back into the absorber. The isentropic extraction of the HC through the ESC prevents the mixing of HC with colder ones during their transfer and thus minimizes the increase in entropy. Figure 12 illustrates this process.
Hot carriers in other semiconductors and energy-selective contacts
The theoretical concept of HC extraction from a wide-bandgap material with narrow conduction and valence band through an ESC membrane was introduced by Würfel15. According to that concept, 85% efficiency can be achieved via the exclusion of the electron–phonon scattering mechanism in the absorber material. Various nanostructures such as quantum dots (QDs), quantum wells (QWs), and nanowires (NWs) were suggested as appropriate candidates for ESCs8,16,71,72. Later, the experimental evidence of HC extraction was achieved by using 4–7 nm thick Si QDs array which was sandwiched between two SiO2 layers (with the thickness of 5 nm each) (Fig. 13a)73,74,75. This array acts as a medium with double-barrier resonant tunneling for HC extraction. Similarly, Su et al. simulated HC by using QDs and QWs as the ESC where the former showed significantly improved efficiency and performance8, and the experimental evidence by the same author supported his simulation data76. The parameter of conductance of ESC using QDs and QWs was neglected previously. Since then it has been shown that a resonant tunneling diode (RTD) with QDs and QWs may be negatively affected by both high or too low conductance77. However, plenty of experimental research has been done to prove the concept of resonant tunneling using QDs and QWs28,72. A similar demonstration of a proof of concept of hot-electron extraction has been presented based on resonant tunneling from a narrow bandgap GaAs (absorber) to a wider bandgap AlGaAs (collector) through a double-barrier QWs of AlAs/GaAs structure78,79. The device temperature ranged from 93 to 213 K where the electron–phonon interaction was negligible. However, promising results can be achieved by optimizing the barrier thickness, selection of appropriate absorber with slow carrier-cooling rates, and reducing dimensionality from 3D to 2D. The schematics and proof of concept are shown in Fig. 13b. Recently, in 2019, Dimmock et al. showed an enhanced HC extraction through resonant tunneling using semiconductor QWs as ESC80. A few nanometer thick metallic layer (chromium) was used as the photoabsorber on GaAs substrate and by altering the thickness of the metallic film, the absorption of incident light was enhanced that resulted in the generation of HC. The two different mechanisms, tunnelling and thermionic emission of hot charge extraction from metal to semiconductor were studied. All these materials discussed above are relatively wide-bandgap materials (i.e Eg > 1 eV). However, theoretical maximum power conversion efficiency for HC can be achieved with low-bandgap materials (i.e Eg < 0.5 eV)8,24 and single nanowires with unidirectional morphology81. In this context, InP was used as the ESC to harvest photogenerated hot electrons from a single NW of InAs (Eg = 0.39 eV)82. The author has claimed an increase in short circuit current by adopting certain strategies and modifications in the NW such as variation in diameter, surface passivation, and modification in the ESC that showed an enhancement of the current collection.
a 2–4 nm Si quantum dots are sandwiched between SiO2 layers. b Hot electrons resonant tunneling concept where the hot electrons with resonant tunneling energy easily cross the barrier while those with non-resonant energy reflect back to the absorber. The concept was experimentally proven with GaAs as the absorber and AlGaAs as the hot-electron collector. c InAs/GaAs layered based quantum dot solar cells: (i) the schematics of stacking InAs/GaAs quantum dot layers, (ii and iii) the InAs QD layers are embedded in a GaAs matrix, (iv) stacking multiple QD layers enhances both current and voltage of the device, and d a single nanowire-based HC solar cell: (i) the device cross-section taken with the scanning electron microscope (SEM), (ii) energy band diagram showing three steps in the current generation (ISC) process as electron–hole pair photo-generation, their diffusion and charge transfer and, (iii) the energy band diagram under VOC condition. The figures are taken with permission from (a) ref. 73, (b) ref. 78, (c) ref. 71, and (d) ref. 82
The schematics of a single NW solar cell are presented in Fig. 13d. Very recently in 2019, Harada et al. demonstrated the successful extraction of HC in an InAs/GaAs QDs superlattice solar cell by employing successive layers of QD lattices, which increased the photo-absorption, current, and voltage of the device compared to a single QD lattice71. Table 2 represents various types of ESCs used for HC extraction in conventional semiconductors and organic-inorganic halide perovskites.
Although perovskites have demonstrated slow HC cooling and are considered a game-changer for the future of HCSCs, they require a proper understanding of suitable and efficient ESCs that can strongly couple their energy bands with those of the perovskite absorber13,83,84,85. Recently, researchers have employed various forms of carbon such as graphene and C60 as ESCs in perovskite solar cells, which have not only improved the current densities but also the stability of the devices. In 2017, Li et al. was the first to use a thin absorber layer of 4,7-diphenyl-1,10-phenanthroline (B-Phen) as the ESC with perovskite and studied the dynamics and extraction of HC in a system of MAPbBr3 NCs coated with a B-Phen, demonstrating efficient hot-electron extraction from the perovskite13. The B-Phen has high electron mobility, narrow electron bandwidth13 and a suitable molecular structure for strong coupling of its higher LUMO to the CBM of the perovskite (Fig. 14a). The HC extraction efficiency (ƞhot) reaches up to 75% at low pump fluence but reduces to 58% when pump fluence is increased, which is attributed to the back electron transfer from the B-Phen into the perovskite. The perovskite NCs prevailed over their bulk counterpart when it came to the charge extraction efficiency (Fig. 14c). It has been observed that ƞhot reduces from 75 to 15% as the excess HC energy reduces from 0.7 to 0.1 eV, which is clear evidence that B-Phen has a strong coupling with the perovskite and only the HC with high temperature and energy have been extracted.
a The schematics of HC generation and their extraction with an illustration of the flat energy band alignment of B-Phen absorber and perovskite NCs. b the dependence of the pump energy on HC extraction using a 35 nm thin B-Phen layer in which hot electrons with higher excitation energy can be extracted efficiently. c The HC extraction efficiency versus the B-Phen layer thickness for both the perovskite bulk film and NCs at 3.1 eV photoexctation. Higher extraction of HC was observed for NCs. The figures are taken with permission from ref. 13
Recently, in 2019, Lim et al. revealed the formation of an interfacial junction between a perovskite absorber (MAPbI3) and B-Phen, which is responsible for the electron-back transfer to the absorber at higher pump fluence84. Instead of using conventional ultrafast spectroscopy, they deployed pump-push probe (PPP) spectroscopy, which has been used for probing the excited states by re-exciting the carrier population above the LUMO of the absorber with the push pulse after the initial pump. PPP has the ability to circumvent the various complexities that arise because of the multiband excitation and density-dependent multiparticle effects to probe the lifetime of the excited state84. At 3.1 eV pump pulse, the HC are not fully extracted by B-Phen, and thus no quenching is seen (Fig. 14b). However, a 1.98 eV push probe successively transfers HC to B-Phen. The reason for this hindrance in a complete HC transfer might be caused by an interfacial Schottky barrier formed at the interface of the two materials (perovskite and B-Phen) and a single pump fluence of even 3.5 eV cannot overcome the barrier. Wang et al. reported a new device design (MAPbI3/Au/TiO2/FTO) in which photoexcited hot electrons were extracted under one sun steady-state illumination. Hot electrons traversed ballistically through Au film and transferred to Au-TiO2 interface86. These innovative findings pave the way for exploring efficient ESCs for highly efficient HCSCs.
Researchers have also observed an ultrafast charge transfer from a thick film of metal halide perovskites to the electron- and hole-accepting layers (ETL and HTL, respectively) by monitoring the transient absorption spectra of perovskite-ETL/HTL systems in the near-infrared (NIR) region, where the transient spectra of a pristine perovskite film differed greatly from the spectra of perovskite-ETL/HTL systems87,88. This difference in the signal was attributed to the ultrafast charge transfer in fs timescale while the charge carriers are still hot. However, these results were later challenged by the findings showing that the NIR TA spectra of perovskite films primarily originate from the photoinduced change in reflectance and thin-film interference, not from a change in absorption89. The interference of the pristine film and the resulting TA spectra are modified by the presence of ETL or HTL. Thus, no charge extraction takes place and perceived HC transfer is nothing but likely a mischaracterization of the TA signal. Adding an ETL/HTL would therefore modify the thin-film interference of the pristine film and the resulting TA spectra even if no charge extraction took place, and the perceived HC transfer was likely a mischaracterization of the signal.
Plasmonic HC and their applications in other optoelectronic devices
For centuries, scientists have been fascinated by the interaction between incident light and matter. In properly designed metallic nanostructures (typically Au, Ag, and Cu), if the frequency of incident light matches with that of the free electrons, the collective oscillations of the electrons are triggered in a confined region90. This oscillation reaches its maximum amplitude at a specific wavelength known as the localized surface plasmon resonance (LSPR) (Fig. 15a) and the surface plasmon polaritons (SPPs). The collective oscillation is called a plasmon. The LSPR is damped either radiatively through re-emission of a photon or by the nonradiative decay, also named as Landau damping, by the generation of HC within the plasmonic nanostructures91,92. The generation and decay processes of HC in a plasmonic nanostructure are displayed in Fig. 15a–d. The Landau damping is a quantum mechanical phenomenon in which the LSPR quantum is transferred to a single-electron–hole pair excitation at an ultrafast timescale (1‒100 fs) (Fig. 15b). Finally, HC redistribute their energy and the heat is transferred to the surrounding environment.
a Photoexcitation of the local surface plasmons and enhanced light absorption. b HC generation through Landau damping (1‒100 fs) and their subsequent decay through photon re-emission or by carrier multiplication. c HC redistribute their energy quickly (100 fs‒1 ps) through carrier–carrier scattering processes. d Finally, heat is transferred out of the metallic structure to the surroundings at a relatively long timescale (100 ps–1 ns). Electronic states are represented by gray areas, the hot holes and hot electrons are presented in orange and purple colors, respectively. The figures are taken with permission from ref. 149
Thus, typically a plasmon dephases quickly and the energy decays via four different routes, namely (i) HC generation, (ii) near-field electromagnetic field enhancement (non-radiatively), (iii) far-field light scattering (radiatively), and (iv) plasmonic heat effects (Fig. 16)93,94. The ratio of each of these routes depends on the morphology as well as the surrounding medium of the plasmonic nanostructure.
In recent years, extensive research has been done to exploit the novel aspects of plasmonic HC in carefully synthesized and designed metallic nanostructures to effectively exploit the decay energy into various outstanding applications91,93,95. Some potential applications include enhanced infrared absorption from a near-field enhancement effect known as the surface-enhanced Raman scattering effect (SERS), enhanced light trapping far-field radiation effect, cancer therapy with plasmons, water splitting and other photoconversion routes for photochemistry, photovoltaics, photodetection, and sensing96,97 applications. Various applications of HC are explained in detail for better understanding and development of future optoelectronic devices.
HC-mediated photochemical reactions
During the photoexcitation of metallic nanoparticles, the oscillation of the plasmonic electrons results in the confinement of photon energy at the metallic surface over a longer period of time compared to the unconfined photons that travel at speed of light, therefore tremendous accumulation of photon intensity and highly energetic hot electrons are created at the surface of the nanoparticle98,99. When adsorbate molecules or semiconductors are directly attached to a metal nanostructure, hot electrons can be captured and extracted to the adsorbates or semiconductors before thermalization. The effect of light illumination on the distribution of hot electrons and their self-scattering (electron–electron scattering) and interaction with phonons have been theoretically studied as well as experimentally explored for plasmonic nanostructures19. Due to the rapid relaxation through self-scattering, only a very small portion of the plasmonic hot electrons can overcome the interfacial energy barrier for the indirect charge transfer process. The hot-electron injection process is in competition with the electron–electron scattering process. Besides the back transfer of electrons taking place at the interface, the self-scattering and the scattering with phonons are some of the basic reasons that the indirect transfer process shows a very low efficiency (typically < 2%). There are two possible ways for plasmons to decay in the metal/adsorbate system; one is a direct pathway (the generated hot electrons are transferred to the LUMO of the attached molecule) and the other is an indirect pathway (the hot electrons are generated in the LUMO of the attached molecule and leave a hot hole behind in the metal)100. The direct pathway of the plasmon decay is also termed as the chemical interface damping (CID)101. Apart from the thermalization of HC through their conventional scattering process, there is another way for their thermalization in metals called chemical interface scattering (CIS), in which a hot charge carrier upon transferring to the adsorbate moiety leaves a portion of its energy behind and transfers back to the metal again. This portion of the energy vibrationally excites the adsorbate, transforms it into a hot adsorbate102 and turns the hot adsorbate into a transient energy reservoir that prolongs the HC lifetime from fs to ps, thus making them perfectly available for a chemical reaction102. The various timescales for the hot-electron generation, as well as their relevant transfer to the adsorbate or semiconductor, are illustrated in Fig. 17 (see refs. 100,101,102,103).
Note that SC stands for semiconductor, e stands for electron and CID & CIS refer to the chemical interface damping and the chemical interface scattering, respectively. The idea of the figure has been taken from ref. 102, modified and redrawn
Similarly, HC generation and their vital role in photocatalytic behaviors in metal, metal–semiconductor, and hybrid nanostructures have been widely accepted104. In a typical catalytic reaction, the HC either directly or indirectly transfer to the adsorbate molecule or semiconductor. Indirect transfer suffers large energy losses due to the HC self-scattering and scattering with phonons. However, a direct transfer required a suitable and empty hybridized orbital of an adsorbate or semiconductor with strong interaction105. The excitation mechanism presented by plasmon chemistry is shown in Fig. 18106. In direct intramolecular excitation, when the adsorbate molecule attached to the metal surface, is excited resonantly with LSP, there is a direct transition occurs between frontier electronic states of adsorbate (Fig. 18a-i). In direct excitation, the charge transfers between metal and adsorbate states (Fig. 18a-ii) thus HC transfer from metal to adsorbate molecule through inelastic tunnelling (Fig. 18a-iii). Local heating generates through decay of LSP involve in the reduction of the activation barrier and vibrational excitation of adsorbate molecules (Fig. 18a-iv).
a The excitation mechanisms in plasmonic-induced reactions representing (i) direct intramolecular excitation, (ii) excitation between metal and adsorbate, (iii) HC transfer to adsorbate, and (iv) local heat generation through the decay of localized surface plasmons that cause vibrational excitation. b The interfacial chemistry and charge transfer mechanism of thiolated Au/TiO2 excited through X-rays and visible light radiations. c Illustration of the experimental setup and plasmon-induced disassociation of a single O2 molecule when it adsorbed on Ag surface and d HC transferred to hybridized π* states of O2 molecule and potential energy curve for O2 molecular dissociation. The Figures are taken with permission from (a, c, d) ref. 106 and (b) ref. 107
A strong motivation towards the replacement of fossils fuels, photoreduction of available stocks of H2O (water splitting) and CO2 have been a matter of interest for a long time. As compared to water splitting, the photoreduction of CO2 is a more challenging and complex process. However, plasmonic HC can facilitate the photoreduction of CO2 attached at the surface of a metal oxide. Recently, Chu et al. performed a theoretical simulation of the photoexcited electron-induced CO2 reduction at the surface of a rutile TiO2105. Due to the excitation of specific vibrational modes, the CO2 molecule can trap hot electrons and dissociate to form CO within 30–40 fs. However, the transient life of the CO2 molecule is very short (10‒15 fs), which is due to the strong hybridization of the CO2 orbitals with the TiO2 (rutile 110 surface) electronic band. However, the time limit for the photoreduction may vary for other metal oxides. Similarly, HC transfer at metal/metal oxide interfacial heterojunction has been thoroughly investigated due to the widespread applications in phototherapy, photocatalysis, sensing, and removal of hazardous pollutants. Au/TiO2 is one such example: the hot electrons in Au can initiate the photoreduction while the hot holes are left in the valence band of TiO2, which were used in oxidative degradation of thiol-ligand (L-glutathione capping ligands) attached to the Au surface (Fig. 18b)107. The reaction mechanism of the photo-redox reaction, where the plasmon generates and initiates the redox cycle, is still unclear. Because these reactions generate HC, strong electric fields, and heat by excitation and decay processes, it is unclear which factor is controlling the mechanism.
Very recently, chemists have studied the governing factors responsible for the plasmon-induced chemical reactions and explored “why shining light on silver nanoparticles causes oxygen molecules, attached to their surfaces to break off”106. Christopher et al. investigated the HC-mediated plasmon-induced oxidation of various chemical moieties chemisorbed on the Ag surface108. Similarly, others have studied the same mechanism responsible for the plasmon-induced activation or disassociation of an O2 molecule109,110. However, Seemala et al. found that the disassociation of the O2 molecule attached to Ag is due to the interaction of the localized surface plasmon (LSP) and the molecule rather than HC involved111. Therefore, to clarify the fundamental mechanism of this reaction, Kazuma et al. studied a single-molecule chemisorbed on the Ag surface by using a scanning tunneling microscope (STM) combined with a light illumination source106. The experimental setup is illustrated in Fig. 18c in which the Au tip was positioned on the target molecule and excites through LSP. Using a combination of theoretical calculations and experimental results, they revealed that although there is a contribution of hot electrons, however, hot holes transfer is the dominant mechanism of the O2 disassociation108. The coupled structure that forms due to the molecule–metal chemical interaction is the source of the HC transfer to the antibonding molecular orbital of a strongly hybridized oxygen. The schematics for a plasmonic-induced HC-mediated O2 reaction mechanism with a potential energy surface has been illustrated in Fig. 18d in which the transfer of the hot holes to the strongly hybridized π* states of the adsorbed O2 molecule is detailed. These simulations and experimental studies proved that the HC transfer and the degree of hybridization between the metal state and the metal oxide’s surface are the principal mechanisms of the molecular excitation by LSPs.
In plasmonic photocatalysis, the generation of HC and their importance in photochemical reactions through metal–semiconductor hybrid materials have been extensively investigated104,112,113,114. Zhou et al. studied the role of HC in plasmonic photocatalysis of ammonia (NH3) by using plasmonic antenna reactor (AR) photocatalyst of copper ruthenium (Cu-Ru) surface alloy that composed of Cu nanoparticles (NPs) and Ru reactor sites112. The conventional thermal decomposition of NH3 for the production of H2 requires high temperature because of the high thermal activation energy (Ea) of 1–2 eV to achieve the turnover frequency (1 NH3 molecule/active metal site/second)115. However, by using AR, the reaction rate was higher as compared to the Cu and Ru NPs alone, and an enhancement of the turnover frequency (>15%) was also achieved. The decomposition of ammonia upon excitation has been investigated as a function of excitation wavelength and intensity112 (Fig. 19a). It was observed that without any external heating (high temperature), the plasmonic surface with the AR photocatalyst gave the highest decomposition rate of NH3 at an illumination of 9.6 Wcm−2.
a The quantification analysis of reaction mechanism with and without HC generation in terms of light intensity and wavelength in hydrogen production and b the schematics of the experiment where a single-molecule junction was established between a grounded nanodevice and the STM probe, alongside the HC generation and their distribution. The figures are taken with permission from (a) ref. 112 and (b) ref. 113
The energy distribution of the plasmon-generated HC in the metallic nanostructures is highly important for the design and development of highly active plasmon-driven applications116.
Reddy et al. investigated the steady-state energy distribution of the HC with STM by creating a single molecular junction (quaterthiophene, tetracyanoethylene or 3,4 thylenedioxythiophene) between an Au thin film (6–13 nm) and the Au tip of the STM (Fig. 19b)113. By employing various biasing voltages, the current–voltage characteristics were elucidated with and without plasmonic excitations, which allowed them to calculate the energy distribution of the HC. According to their findings, the film thickness, the molecular type, and the distance between the STP tip and Au film are the crucial factors that contribute towards the HC current and their energy distribution above the Fermi level. An increase in the thickness of the Au film (13 nm) reduced the HC generation by 43% as compared to a thinner Au film (6 nm).
Overall, the fundamental understanding of HC generation, energy distribution, transfer, and energy decay mechanism are crucially required for the development of highly efficient and sensitive plasmonic photocatalytic applications, and there is still much left to know about the HC generation through the surface plasmonic polariton. Various important topics are still under investigation, including for example the energy losses due to the vibrations of the adsorbate molecule, the interfacial energy loss by the electron–electron scattering, and the contribution of both thermal and plasmonic HC on the plasmonic catalysis.
HC in transistors and photodetectors
The development of transistors operating in the high-frequency region (terahertz, THz) is the key requirement for future imaging, sensing, and communication applications such as the next-generation autonomous vehicles and wireless communication systems117,118. Currently, for such applications, high-electron-mobility transistors are designed by using III‒IV semiconductor heterostructures in which lateral charge transport is governed by field-effect modulation119,120. However, there is a hindrance in further improving these devices due to the technical and physical issues related to the lateral scaling of the channel. Hence, as an alternative to lateral field-effect transistors, hot-electron transistors are a suitable vertical design composed of an ultrathin base layer, which facilitates transverse ballistic transport of hot electrons. The typical device architecture consists of three terminals (emitter, base, and collector) and, under a base-to-emitter polarization condition, the hot electrons are injected from the emitter to the base region. If the base thickness is shorter than the mean free path, the hot electrons can transit through the base region without any energy loss (ballistic transport)121,122. These THz transistors rely on a channel material that can accommodate high carrier densities suitable for low-contact resistance123,124.
Giannazzo et al. used graphene in a junction with an AlxGa1-xN/GaN heterostructure and evaluated the hot-electron injection efficiency from the AlGaN/GaN into the graphene base region122. They achieved a high on-state current density (Jc) of 1 Acm−2. Similarly, Liu et al. recently observed ambipolar HC transport for the first time in a newly proposed device architecture of a HET transistor for the efficient collection of HC121. The typical device structure consists of an extra thin (~1 nm) layer by layer stacking of graphene, hexagonal boron nitride and Tungsten diselenide. They achieved nearly lossless ambipolar transport of both hot holes and hot electrons through an extra thin base (Fig. 20a, b) and almost 100% collection efficiency. This very high collection efficiency is due to several reasons, such as (1) long HC lifetime and less carrier–phonon interactions in the graphene, (2) high-energy and high-injection levels reduce the chances of HC backscattering at the collector’s barrier, and (3) efficient charge transfer due to a clean interface and strong adhesion between the different stacked layers.
a The HET device design on a flexible substrate showing the electrical connections, along with the optical image, TEM image of the real device and the energy band diagram representing the HC energetics and b the collection efficiencies of HC under various bias conditions. The figures are taken with permission from ref. 121
The device architecture with the thin graphene base not only enhanced the efficiency limit of the HET but also provided a platform for the fundamental understanding of HC dynamics in these high-frequency devices. However, in graphene-based heterostructures, the scattering of HC has a negative impact on the charge transfer properties, especially scattering due to the field injection of hot holes. The reason for the HC scattering even in an ultrashort (10 nm) gate is still a topic to be addressed125. Perovskite materials with longer quasi-ballistic transport, HC lifetime, and easy fabrication process are a strong hope for the development of hot-electron transistors.
In optical communication, high-speed photodetectors are an important component that converts the optical photons into electrical signals126. Specifically, photodetectors are able to detect photoelectrons from a metal surface over a Schottky barrier or an oxide tunnel barrier127. The presence of a Schottky barrier (∅B) limits the motion of HC through metal/metal oxide interface and the efficient injection of hot electrons into the semiconductor remains a major challenge. Besides, HC must have enough energy to overcome this barrier, and their momentum should be in the perpendicular direction to the interface. Thus, both energy and momentum are the two primary requirements, as they are the main causes of the low extraction efficiency of HC128. The embedding of optical nanoantennas within the semiconductor facilitates the HC extraction throughout the surface of nanoantenna and circumvents this issue. Knight et al. fabricated a rectangular array of Au nanorods (optical antenna) on a silicon substrate, which generates hot electrons via plasmon decay17. The energy band diagram of the optical antenna diode is presented in Fig. 21a. A detectable photocurrent was produced via the absorption of light by the metal (Au) nanorods and the generation of hot electrons that emit over the Schottky barrier. These plasmonic nanoantennas have the capability of detecting light below the bandgap of the semiconductor (in this case, Si) even without a voltage bias. Although multiple antenna arrays could make an efficient on-chip spectrometer, the current device can only absorb 0.01% of the photons. A further enhancement in the efficiency could be achieved by optimization of the materials and structural morphology.
a The energy band diagram of an optical antenna diode showing the photoexcitation and injection of hot electrons into the Si over the Shottky barrier (∅B), thus contributing to the photocurrent generation. b–i: The schematic of the sandwiched heterostructure device with an Au grating/MoS2/Al2O3/Au/Si, and b-ii a cross-section image of the MIM structure of a real device. c A diagram showing the band alignment of the Au grating and MoS2 monolayer where the plasmonic hot electrons were excited by a 780 nm pump laser, and by crossing the Schottky barrier they are injected to MoS2 monolayer, where the induced variation in the filled states is monitored by a 650 nm probe pulse. d The detailed schematics of a complete device model and experimental setup of a graphene photoemitter: (i–iii) the mechanisms of the hot-electron generation and scattering, the hot-electron emission prior to cooling, the field emission of thermal electrons, and (iv–vi) the continuous wave-laser photoemission by the waveguide mechanism of an integrated monolayer of graphene. The figures are taken with permission from (a) ref. 17, (b, c) ref. 140, and (d) ref. 131
Similarly, graphene has been explored as an extraordinary plasmonic material due to its long lifetime and exceptional optical confinement with comparatively low losses129. In presence of static electric potential, the electrons in graphene can reflect, refract, and interfere in similar manner like electromagnetic waves in dielectrics. Photon-like behavior of charge carriers in graphene 2D morphology makes this material an excellent candidate for exploitation of electron optics130. The waveguide photoemission by using graphene monolayer has been experimentally tested in the work of Rezaeifar et al., where the probability of the photoemission was enhanced before the thermalization of the hot electrons131. At room temperature, the HC effect in graphene is prominent because of the relatively large electron–electron relaxation rate in comparison to its electron–phonon relaxation rate, which enables the fast and sensitive THz detection through photothermoelectric effect132,133,134,135. However, the important challenge in graphene is to increase its absorption. Plasmonic photodetection may greatly enhance the spectral range and sensitivity of the currently available light-harvesting devices. Due to their extraordinary performance and upscaling ability graphene-based mid-infrared and THz detectors are recently much focused136,137. Cai et al. introduced graphene-based THz detectors that worked at room temperature138,139. Fabrication of large-area arrays of graphene microribbons that were oriented perpendicularly on SiC substrate greatly enhanced the absorption efficiency in THz range.
HC generation through plasmonic oscillation, especially by the interaction of LSP and the SPP, is a complex phenomenon. In a recent study, Shan et al. proposed a new device design to observe the generation of HC through a strong coupling of LSP and SPP140. The proposed new metal-insulator-metal (MIM) heterostructure (Fig. 21b), in which molybdenum selenide (MoS2) serves as a heterojunction, showed strong coupling between the LSP and SPP that synergize to produce plasmonic HC. The electrons are excited by a 760-nm pump laser, and by crossing the Schottky barrier these electrons are injected into the MoS2 layer where they are monitored by a probe pulse of 650 nm (Fig. 21c). In contrast to the LSP that release their energy radiatively by emitting a photon, the SPP decay non-radiatively, leading to high photon-carrier conversion efficiency. However, in practice, these carriers generated by the SPP decay have not enough energy to cross the potential barrier between the metal and the semiconductor which results in low output yield. Thus, instead of transformation into useful electrical energy, the photon absorbed by the SPP are mostly converted to charge carriers which exhausted as heat140. The properties of LSP and SPP can be synergize to produce plasmonic HC. In this coherent energy exchange mechanism, the photons radiated by the relaxation of the LSP are reabsorbed by the SPP and thus usable in HC generation. In the work by Shan et al.140, the ultrafast (≈40 fs) transfer of hot electrons from the Au grating to the MoS2 monolayer achieved an external quantum yield of 1.65%.
The outstanding performance of perovskites in plasmonic devices
The heterostructure that consists of metal and semiconductor NPs are employed in plasmon-induced hot-electron devices. At the metal–semiconductor interface, the efficiency of plasmon-hot-electron conversion strongly determines the performance of these devices. replacement of a conventional chalcogenide semiconductor (II–IV, e.g., CdS and CdSe) with a perovskite (CsPbBr3) has substantially improved the efficiency of the plasmon-hot-electron conversion at the Ag–CsPbBr3 interface141. The quantum efficiency (energy resonant transfer) of the device was enhanced up to ≈15%, which is attributed to the fast (<100 fs) transfer of HC at the interface. As compared to other conventional semiconductors with similar bandgaps, the large absorption cross-section of CsPbBr3 NCs and the large and strong oscillation strength of the intraband transition are responsible for efficient plasmon-hot-electron conversion at the metal/perovskite interface142. Similarly, compared to the ballistic transport length (85 nm) of GaAs grown through molecular beam epitaxy143, perovskite (MAPbI3) can achieve a much longer length (>200 nm) despite of their economical low-temperature and solution-processable fabrication67,69. Hence, for designing the ultrathin base layer of the HET, perovskites can be suitable candidates due to the longer ballistic transport length. The enhanced efficiency (~50 ± 18%) of the plasmonic-induced HET and the long-living charge-separated energy states prove a promising potential in the employment of the nano-heterostructures with the metal–perovskite semiconductor to further improve the performance of the hot-carrier optoelectronic devices. Recently, Gu et al. fabricated a MAPbI3–Au-based photodetector in which the generation of HC is promoted through the enhanced field of LSPR144. Due to the enhanced electromagnetic field and the suppressed electron–hole recombination, the MAPbI3–Au-based photodetector showed a very short response time and a large photocurrent.
Although the noble metals (Au, Ag, etc.) are well-known for their plasmonic effects, their direct contact with the perovskite may induce degradation, which is a serious limitation on the device lifetime of the noble metal–perovskite hybrid structures144. However, metal nitrides (TiN and ZrN) have also been successfully incorporated as plasmonic nanostructures. Mohsen et al. recently developed a model using COMSOL multiphysics simulation, which showed that by decorating perovskite (MASnI3) with core–shell nanostructures of ZRN/SiO2, an unprecedented increase in efficiency up to 20% could be achieved145. In this simulated architecture, the core–shell structure acts as a nanoantenna with an effective coupling of the SPR to the underlying perovskite layer, substantially increasing the optical absorption of the perovskite.
The timescale of the plasmonic HC functionality ranges from fs to ps (<10 ps) before the thermal equilibration. However, the timescales for various applications such as photochemical reactions, efficient HC collection in transistors, sensing, and detection, are much longer (fs‒ps) than the lifetime of the plasmonic HC. Therefore, their fast and efficient extraction from the photoabsorber or the plasmonic material needs to be addressed in the future. Nonetheless, the highly efficient plasmon-hot-electron conversion can be applied to further improve the emerging technology of HC optoelectronic devices based on perovskite semiconductors.
Outlook for HC in future optoelectronic devices
The fundamental understanding of HC generation, thermalization, and cooling phenomena has not only explored the basic science of higher molecular states but also opened new pathways for the use of HC in a variety of innovative applications. For the successful collection of these highly energetic and unstable species, one needs to understand the energy decay processes of their self-scattering, scattering with phonons, and finally interactions with the lattice phonons. The ultrashort time span of these energy decay processes plays a vital role in determining the energy distribution of HC, their probability of transferring into nearby acceptor levels for efficient extraction, collection, or taking part in the chemical reaction, and finally designing a suitable device architecture. Although the increased confinement in a finite nanoparticle will definitely increase the HC lifetime due to the bottleneck effect, a highly efficient energy-selective contact is still vital for any final device. The factors that have a strong impact on the efficiency and can be tuned further to enhance the performance of HC optoelectronic devices are (i) HC relaxation time (τrel), which has the largest impact on improving the efficiency. τrel should have a similar timescale as the radiative recombination, i.e 10‒100 ps, and the PCE could be increased up to 50 % if a timescale of 1 ns is achieved; (ii) heat dissipation characteristics, which can be considered in terms of the thermalization rate Qth. Qth is recommended to be greater than 1 WK−1 cm−2 for a substantial HC contribution; (iii) HC equilibration time, and (iv) HC extraction time. Nevertheless, the effective and successful implementation of these concepts in a working device still remains a challenge for the future.
Perovskite materials have shown extraordinary performances in various optoelectronic devices, and they possess intrinsic extraordinary properties of slow cooling, reduced heat dissipation, efficient charge transport characteristics, and tuneable energy band alignment with other interfacial semiconductor or metallic nanostructures. Perovskites can be further explored for futuristic HC optoelectronic devices. As the HC lie in a pool of lattice phonons and the interaction with the phonons result in heat dissipation, one can think of introducing a suitable blocking mechanism at each stage of the thermal relaxation such as a thermal isolation between the phonons and the HC populations, the up-conversion of acoustic phonons to optical phonons and the reduction of the density of states (DOS) of the phonons. However, the effective temperature of the crystal lattice will be increased by employing such strategies, and how to modify the currently available perovskite materials for such a scenario, these are the questions for the future which need to be thoroughly addressed.
In addition to the importance of the photoexcited HC in high-efficiency photovoltaic applications, plasmonic HC are also expected to deliver new fundamental intuition into various dynamic processes at the interfaces and on the metallic surfaces, such as chemical reactions, desorption of molecules, and many more. The new strategies of embedding optical nanoantenna within semiconductor and the use of canonical metallic nanotips near the surface of semiconductors enable better HC generation and also employed for the enhancement of HC extraction at the interface. Their role in other applications such as photodetection, hot-electron transistors, lasing applications, and light-harvesting have been noteworthy. The efficiency of the new energy technologies, such as the hydrogen-based fuel cells, could be improved by the successful utilization of HC, which would enhance the chemical reactions. Besides the other energy loss mechanisms governing these conventional materials such as the HC self-scattering and scattering with phonons, there is another new route of their thermalization termed as the chemical interface damping also known as the ultrafast chemical interface scattering, which has been found in metal/adsorbate or metal–semiconductor hybrid systems. Although various landmark achievements have been secured, the enhancement in the device efficiency is generally weak in traditional hybrid nanostructures due to the low yield of HC along with their lower utilization rate. Similarly, the emergence of the layered perovskite materials and their ability to incorporate various cations, metals, and halides, could provide an ideal platform to investigate the generation of both photoexcited and plasmonic HC. The various coupling phenomena such as photon–phonon, photon–exciton, and electron–phonon will pave the way to explore the fundamental science and future technologies.
With the advances in device fabrication and characterization using ultrafast laser spectroscopy techniques, the HC optoelectronic applications are ripe for scientific breakthroughs. Insights into the HC dynamics in the higher energy states not only help conceptualizing new ground-breaking optoelectronic devices but also remain a hot fundamental research topic in the future.
References
Shockley, W. & Queisser, H. J. Detailed balance limit of efficiency of p-n junction solar cells. J. Appl. Phys. 32, 510–519 (1961).
Torabi, N. et al. Progress and challenges in perovskite photovoltaics from single- to multi-junction cells. Mater. Today Energy 12, 70–94 (2019).
Green, M. A. Tracking solar cell conversion efficiency. Nat. Rev. Phys. 2, 172–173 (2020).
Ross, R. T. & Nozik, A. J. Efficiency of hot-carrier solar energy converters. J. Appl. Phys. 53, 3813–3818 (1982).
König, D. et al. Hot carrier solar cells: principles, materials and design. Phys. E: Low.-Dimensional Syst. Nanostruct. 42, 2862–2866 (2010).
Alharbi, F. H. & Kais, S. Theoretical limits of photovoltaics efficiency and possible improvements by intuitive approaches learned from photosynthesis and quantum coherence. Renew. Sustain. Energy Rev. 43, 1073–1089 (2015).
Nozik, A. J. Quantum dot solar cells. Phys. E: Low.-Dimensional Syst. Nanostruct. 14, 115–120 (2002).
Su, S. H. et al. Hot-carrier solar cells with quantum well and dot energy selective contacts. IEEE J. Quantum Electron. 51, 4800208 (2015).
Li, M. J. et al. Low threshold and efficient multiple exciton generation in halide perovskite nanocrystals. Nat. Commun. 9, 4197 (2018).
Luque, A. & Martí, A. Electron–phonon energy transfer in hot-carrier solar cells. Sol. Energy Mater. Sol. Cells 94, 287–296 (2010).
Luque, A. & Martí, A. Theoretical Limits of Photovoltaic Conversion and New-Generation Solar Cells. in Handbook of Photovoltaic Science and Engineering (eds. Luque, A. & Hegedus, S.) 2nd edn. 113–151 (John Wiley & Sons, 2003).
Ridley, B. K. Quantum Processes in Semiconductors 5th edn. (Oxford University Press, USA, 2013).
Li, M. J. et al. Slow cooling and highly efficient extraction of hot carriers in colloidal perovskite nanocrystals. Nat. Commun. 8, 14350 (2017).
Kahmann, S. & Loi, M. A. Hot carrier solar cells and the potential of perovskites for breaking the Shockley–Queisser limit. J. Mater. Chem. C. 7, 2471–2486 (2019).
Würfel, P. Solar energy conversion with hot electrons from impact ionisation. Sol. Energy Mater. Sol. Cells 46, 43–52 (1997).
Ni, X. et al. InGaN staircase electron injector for reduction of electron overflow in InGaN light emitting diodes. Appl. Phys. Lett. 97, 031110 (2010).
Knight, M. W. et al. Photodetection with active optical antennas. Science 332, 702–704 (2011).
Mukherjee, S. et al. Hot electrons do the impossible: plasmon-induced dissociation of H2 on Au. Nano Lett. 13, 240–247 (2013).
Dubi, Y. & Sivan, Y. “Hot” electrons in metallic nanostructures—non-thermal carriers or heating? Light.: Sci. Appl. 8, 89 (2019).
Tan, S. J. et al. Plasmonic coupling at a metal/semiconductor interface. Nat. Photonics 11, 806–812 (2017).
Shi, J. J. et al. From ultrafast to ultraslow: charge-carrier dynamics of perovskite solar cells. Joule 2, 879–901 (2018).
Nozik, A. J. Spectroscopy and hot electron relaxation dynamics in semiconductor quantum wells and quantum dots. Annu. Rev. Phys. Chem. 52, 193–231 (2001).
Esipov, S. E. & Levinson, Y. B. The temperature and energy distribution of photoexcited hot electrons. Adv. Phys. 36, 331–383 (1987).
Fu, J. H. et al. Hot carrier cooling mechanisms in halide perovskites. Nat. Commun. 8, 1300 (2017).
Tsai, C. Y. The effects of intraband and interband carrier-carrier scattering on hot-carrier solar cells: a theoretical study of spectral hole burning, electron-hole energy transfer, Auger recombination, and impact ionization generation. Prog. Photovoltaics: Res. Appl. 27, 433–452 (2019).
Li, M. J. et al. Slow hot-carrier cooling in halide perovskites: prospects for hot-carrier solar cells. Adv. Mater. 31, 1802486 (2019).
Feng, Y. et al. Investigation of carrier-carrier scattering effect on the performance of hot carrier solar cells with relaxation time approximation. Appl. Phys. Lett. 102, 243901 (2013).
Konovalov, I., Emelianov, V. & Linke, R. Hot carrier solar cell with semi-infinite energy filtering. Sol. Energy 111, 1–9 (2015).
Hirst, L. C. & Ekins-Daukes, N. J. Fundamental losses in solar cells. Prog. Photovoltaics: Res. Appl. 19, 286–293 (2011).
Joshi, P. P., Maehrlein, S. F. & Zhu, X. Y. Dynamic screening and slow cooling of hot carriers in lead halide perovskites. Adv. Mater. 31, 1803054 (2019).
Price, M. B. et al. Hot-carrier cooling and photoinduced refractive index changes in organic–inorganic lead halide perovskites. Nat. Commun. 6, 8420 (2015).
Green, M. A. Third generation photovoltaics: ultra-high conversion efficiency at low cost. Prog. Photovoltaics: Res. Appl. 9, 123–135 (2001).
Xing, G. C. et al. Long-range balanced electron- and hole-transport lengths in organic-inorganic CH3NH3PbI3. Science 342, 344–347 (2013).
Jailaubekov, A. E. et al. Hot charge-transfer excitons set the time limit for charge separation at donor/acceptor interfaces in organic photovoltaics. Nat. Mater. 12, 66–73 (2013).
Landau, L. D. & Pekar, S. I. The effective mass of the polaron. in Collected Papers of L.D. Landau (ed. D. Ter Haar) Vol. 53, 478–483 (Oxford: Pergamon, 1965).
Lu, N. D. et al. A review for polaron dependent charge transport in organic semiconductor. Org. Electron. 61, 223–234 (2018).
Franchini, C. et al. Polarons in materials. Nat. Rev. Mater. 6, 560–586 (2021).
Emin, D. Optical properties of large and small polarons and bipolarons. Phys. Rev. B 48, 13691–13702 (1993).
Zhu, X. Y. & Podzorov, V. Charge carriers in hybrid organic–inorganic lead halide perovskites might be protected as large polarons. J. Phys. Chem. Lett. 6, 4758–4761 (2015).
Lu, N., Li, L., Geng, D. & Liu, M. A review for polaron dependent charge transport in organic semiconductor. Org. Electron. 61, 223–234 (2018).
Even, J., Carignano, M. & Katan, C. Molecular disorder and translation/rotation coupling in the plastic crystal phase of hybrid perovskites. Nanoscale 8, 6222–6236 (2016).
Miyata, K., Atallah, T. L. & Zhu, X. Y. Lead halide perovskites: crystal-liquid duality, phonon glass electron crystals, and large polaron formation. Sci. Adv. 3, e1701469 (2017).
Zheng, F. et al. Rashba spin–orbit coupling enhanced carrier lifetime in CH3NH3PbI3. Nano Lett. 15, 7794–7800 (2015).
Frost, J. M., Whalley, L. D. & Walsh, A. Slow cooling of hot polarons in halide perovskite solar cells. ACS Energy Lett. 2, 2647–2652 (2017).
Mahata, A. & Meggiolaro, D. & De Angelis, F. From large to small polarons in lead, tin, and mixed lead–tin halide perovskites. J. Phys. Chem. Lett. 10, 1790–1798 (2019).
Dursun, I. et al. Why are hot holes easier to extract than hot electrons from methylammonium lead iodide perovskite? Adv. Energy Mater. 9, 1900084 (2019).
Chen, J. S. et al. Cation-dependent hot carrier cooling in halide perovskite nanocrystals. J. Am. Chem. Soc. 141, 3532–3540 (2019).
Yang, J. F. et al. Acoustic-optical phonon up-conversion and hot-phonon bottleneck in lead-halide perovskites. Nat. Commun. 8, 14120 (2017).
Shi, H. F. et al. Strong hot-phonon bottleneck effect in all-inorganic perovskite nanocrystals. Appl. Phys. Lett. 116, 151902 (2020).
Yang, Y. et al. Observation of a hot-phonon bottleneck in lead-iodide perovskites. Nat. Photonics 10, 53–59 (2016).
Zhang, P. L. et al. Ultrafast interfacial charge transfer of cesium lead halide perovskite films CsPbX3 (X = Cl, Br, I) with different halogen mixing. J. Phys. Chem. C. 122, 27148–27155 (2018).
Madjet, M. E. A. et al. Enhancing the carrier thermalization time in organometallic perovskites by halide mixing. Phys. Chem. Chem. Phys. 18, 5219–5231 (2016).
Wei, Q. et al. Effect of zinc-doping on the reduction of the hot-carrier cooling rate in halide perovskites. Angew. Chem. Int. Ed. 60, 10957–10963 (2021).
Talbert, E. M. et al. Bromine substitution improves excited-state dynamics in mesoporous mixed halide perovskite films. Nanoscale 9, 12005–12013 (2017).
Minda, I. et al. Ultrafast charge dynamics in mixed cation–mixed halide perovskite thin films. ChemPhysChem 19, 3010–3017 (2018).
Giovanni, D. et al. Origins of the long-range exciton diffusion in perovskite nanocrystal films: photon recycling vs exciton hopping. Light.: Sci. Appl. 10, 2 (2021).
Ghosh, S. et al. Phonon coupling with excitons and free carriers in formamidinium lead bromide perovskite nanocrystals. J. Phys. Chem. Lett. 9, 4245–4250 (2018).
Hopper, T. R. et al. Ultrafast intraband spectroscopy of hot-carrier cooling in lead-halide perovskites. ACS Energy Lett. 3, 2199–2205 (2018).
Xie, H. Y. et al. All-inorganic halide perovskites as potential thermoelectric materials: dynamic cation off-centering induces ultralow thermal conductivity. J. Am. Chem. Soc. 142, 9553–9563 (2020).
Haque, A. et al. Halide perovskites: thermal transport and prospects for thermoelectricity. Adv. Sci. 7, 1903389 (2020).
Qian, X., Gu, X. K. & Yang, R. G. Lattice thermal conductivity of organic-inorganic hybrid perovskite CH3NH3PbI3. Appl. Phys. Lett. 108, 063902 (2016).
Pisoni, A. et al. Ultra-low thermal conductivity in organic–inorganic hybrid perovskite CH3NH3PbI3. J. Phys. Chem. Lett. 5, 2488–2492 (2014).
Kroupa, D. M. et al. Enhanced multiple exciton generation in PbS|CdS janus-like heterostructured nanocrystals. ACS Nano 12, 10084–10094 (2018).
Zhou, Q. H. et al. Highly efficient multiple exciton generation and harvesting in few-layer black phosphorus and heterostructure. Nano Lett. 20, 8212–8219 (2020).
Manzi, A. et al. Resonantly enhanced multiple exciton generation through below-band-gap multi-photon absorption in perovskite nanocrystals. Nat. Commun. 9, 1518 (2018).
de Weerd, C. et al. Efficient carrier multiplication in CsPbI3 perovskite nanocrystals. Nat. Commun. 9, 4199 (2018).
Sung, J., Macpherson, S. & Rao, A. Enhanced ballistic transport of charge carriers in alloyed and K-passivated alloyed perovskite thin films. J. Phys. Chem. Lett. 11, 5402–5406 (2020).
Sung, J. et al. Long-range ballistic propagation of carriers in methylammonium lead iodide perovskite thin films. Nat. Phys. 16, 171–176 (2020).
Guo, Z. et al. Long-range hot-carrier transport in hybrid perovskites visualized by ultrafast microscopy. Science 356, 59–62 (2017).
Green, M. A. Third generation photovoltaics: solar cells for 2020 and beyond. Phys. E: Low.-Dimensional Syst. Nanostruct. 14, 65–70 (2002).
Harada, Y. et al. Hot-carrier generation and extraction in InAs/GaAs quantum dot superlattice solar cells. Semiconductor Sci. Technol. 34, 094003 (2019).
Hirst, L. C. et al. Experimental demonstration of hot-carrier photo-current in an InGaAs quantum well solar cell. Appl. Phys. Lett. 104, 231115 (2014).
Conibeer, G. J. et al. Selective energy contacts for hot carrier solar cells. Thin Solid Films 516, 6968–6973 (2008).
Shrestha, S. K., Aliberti, P. & Conibeer, G. J. Energy selective contacts for hot carrier solar cells. Sol. Energy Mater. Sol. Cells 94, 1546–1550 (2010).
Aliberti, P. et al. Study of silicon quantum dots in a SiO2 matrix for energy selective contacts applications. Sol. Energy Mater. Sol. Cells 94, 1936–1941 (2010).
Yagi, S. & Okada, Y. Fabrication of resonant tunneling structures for selective energy contact of hot carrier solar cell based on III–V semiconductors. in 35th IEEE Photovoltaic Specialists Conference (PVSC 2010) (ed. John D. Meakin) 1213–1216 (IEEE, Honolulu, Hawaii, USA, 20–25 June, 2010).
Takeda, Y. et al. Resonant tunneling diodes as energy-selective contacts used in hot-carrier solar cells. J. Appl. Phys. 118, 124510 (2015).
Dimmock, J. A. R. et al. Demonstration of a hot-carrier photovoltaic cell. Prog. Photovoltaics: Res. Appl. 22, 151–160 (2014).
Dimmock, J. A. R. et al. Optoelectronic characterization of carrier extraction in a hot carrier photovoltaic cell structure. J. Opt. 18, 074003 (2016).
Dimmock, J. A. R. et al. A metallic hot-carrier photovoltaic device. Semiconductor Sci. Technol. 34, 064001 (2019).
O’Dwyer, M. F., Humphrey, T. E. & Linke, H. Concept study for a high-efficiency nanowire based thermoelectric. Nanotechnology 17, S338–S343 (2006).
Limpert, S. et al. Single-nanowire, low-bandgap hot carrier solar cells with tunable open-circuit voltage. Nanotechnology 28, 434001 (2017).
O’Keeffe, P. et al. Graphene-induced improvements of perovskite solar cell stability: effects on hot-carriers. Nano Lett. 19, 684–691 (2019).
Lim, S. S. et al. Hot carrier extraction in CH3NH3PbI3 unveiled by pump-push-probe spectroscopy. Sci. Adv. 5, eaax3620 (2019).
Jiménez-López, J. et al. Improved carrier collection and hot electron extraction across perovskite, C60, and TiO2 interfaces. J. Am. Chem. Soc. 142, 1236–1246 (2020).
Wang, G. et al. An internally photoemitted hot carrier solar cell based on organic-inorganic perovskite. Nano Energy 68, 104383 (2020).
Piatkowski, P. et al. Direct monitoring of ultrafast electron and hole dynamics in perovskite solar cells. Phys. Chem. Chem. Phys. 17, 14674–14684 (2015).
Jiménez-López, J. et al. Hot electron injection into semiconducting polymers in polymer based-perovskite solar cells and their fate. Nanoscale 11, 23357–23365 (2019).
Pasanen, H. P. et al. Refractive index change dominates the transient absorption response of metal halide perovskite thin films in the near infrared. Phys. Chem. Chem. Phys. 21, 14663–14670 (2019).
Yan, H. Plasmons dragged by drifting electrons. Nature 594, 498–499 (2021). (2021).
Zhan, C. et al. From plasmon-enhanced molecular spectroscopy to plasmon-mediated chemical reactions. Nat. Rev. Chem. 2, 216–230 (2018).
Zhang, H. & Govorov, A. O. Optical generation of hot plasmonic carriers in metal nanocrystals: the effects of shape and field enhancement. J. Phys. Chem. C. 118, 7606–7614 (2014).
Tang, H. B. et al. Plasmonic hot electrons for sensing, photodetection, and solar energy applications: a perspective. J. Chem. Phys. 152, 220901 (2020).
Gellé, A. & Moores, A. Plasmonic nanoparticles: photocatalysts with a bright future. Curr. Opin. Green. Sustain. Chem. 15, 60–66 (2019).
Besteiro, L. V. et al. The fast and the furious: ultrafast hot electrons in plasmonic metastructures. Size Struct. matter Nano Today 27, 120–145 (2019).
Li, J. T. et al. Solar hydrogen generation by a CdS-Au-TiO2 sandwich nanorod array enhanced with au nanoparticle as electron relay and plasmonic photosensitizer. J. Am. Chem. Soc. 136, 8438–8449 (2014).
Wei, Q. L., Wu, S. Y. & Sun, Y. G. Quantum-sized metal catalysts for hot-electron-driven chemical transformation. Adv. Mater. 30, 1802082 (2018).
Schuller, J. A. et al. Plasmonics for extreme light concentration and manipulation. Nat. Mater. 9, 193–204 (2010).
Ciracì, C. et al. Probing the ultimate limits of plasmonic enhancement. Science 337, 1072–1074 (2012).
Lee, S. Y. et al. Tuning chemical interface damping: interfacial electronic effects of adsorbate molecules and sharp tips of single gold bipyramids. Nano Lett. 19, 2568–2574 (2019).
Therrien, A. J. et al. Impact of chemical interface damping on surface plasmon dephasing. Faraday Discuss. 214, 59–72 (2019).
Zhang, Y. C. et al. Surface-plasmon-driven hot electron photochemistry. Chem. Rev. 118, 2927–2954 (2018).
Bauer, C. et al. Ultrafast chemical interface scattering as an additional decay channel for nascent nonthermal electrons in small metal nanoparticles. J. Chem. Phys. 120, 9302–9315 (2004).
Fu, X. Q. et al. Hot carriers in action: multimodal photocatalysis on Au@SnO2 core–shell nanoparticles. Nanoscale 11, 7324–7334 (2019).
Chu, W. B. et al. CO2 photoreduction on metal oxide surface is driven by transient capture of hot electrons: ab initio quantum dynamics simulation. J. Am. Chem. Soc. 142, 3214–3221 (2020).
Kazuma, E. et al. Single-molecule study of a plasmon-induced reaction for a strongly chemisorbed molecule. Angew. Chem. Int. Ed. 59, 7960–7966 (2020).
Yang, C. et al. Hot carrier transfer-induced photodegradation at a thiolated Au/TiO2 interface under X-ray irradiation. J. Phys. Chem. C. 124, 22212–22220 (2020).
Christopher, P., Xin, H. L. & Linic, S. Visible-light-enhanced catalytic oxidation reactions on plasmonic silver nanostructures. Nat. Chem. 3, 467–472 (2011).
Huang, Y. F. et al. Activation of oxygen on gold and silver nanoparticles assisted by surface plasmon resonances. Angew. Chem. Int. Ed. 53, 2353–2357 (2014).
Zhang, Q. F. & Wang, H. Mechanistic insights on plasmon-driven photocatalytic oxidative coupling of thiophenol derivatives: evidence for steady-state photoactivated oxygen. J. Phys. Chem. C. 122, 5686–5697 (2018).
Seemala, B. et al. Plasmon-mediated catalytic O2 dissociation on Ag nanostructures: hot electrons or near fields? ACS Energy Lett. 4, 1803–1809 (2019).
Zhou, L. et al. Quantifying hot carrier and thermal contributions in plasmonic photocatalysis. Science 362, 69–72 (2018).
Reddy, H. et al. Determining plasmonic hot-carrier energy distributions via single-molecule transport measurements. Science 369, 423–426, https://doi.org/10.1126/science (2020).
Ahn, W. et al. Energy-tunable photocatalysis by hot carriers generated by surface plasmon polaritons. J. Mater. Chem. A 7, 7015–7024 (2019).
Amano, A. & Taylor, H. The decomposition of ammonia on ruthenium, rhodium and palladium catalysts supported on alumina. J. Am. Chem. Soc. 76, 4201–4204 (1954).
Govorov, A. O., Zhang, H. & Gun’ko, Y. K. Theory of photoinjection of hot plasmonic carriers from metal nanostructures into semiconductors and surface molecules. J. Phys. Chem. C. 117, 16616–16631 (2013).
Takida, Y. et al. Sensitive terahertz-wave detector responses originated by negative differential conductance of resonant-tunneling-diode oscillator. Appl. Phys. Lett. 117, 021107 (2020).
Rappaport, T. S. et al. Wireless communications and applications above 100 GHz: opportunities and challenges for 6G and beyond. IEEE Access 7, 78729–78757 (2019).
Rode, J. C. et al. Indium phosphide heterobipolar transistor technology beyond 1-THz bandwidth. IEEE Trans. Electron Devices 62, 2779–2785 (2015).
del Alamo, J. A. Nanometre-scale electronics with III–V compound semiconductors. Nature 479, 317–323 (2011).
Liu, W. et al. Approaching the collection limit in hot electron transistors with ambipolar hot carrier transport. ACS Nano 13, 14191–14197 (2019).
Giannazzo, F. et al. High-performance graphene/AlGaN/GaN schottky junctions for hot electron transistors. ACS Appl. Electron. Mater. 1, 2342–2354 (2019).
Li, M. Y. et al. How 2D semiconductors could extend Moore’s law. Nature 567, 169–170 (2019).
Shoron, O. F. et al. Prospects of terahertz transistors with the topological semimetal cadmium arsenide. Adv. Electron. Mater. 6, 2000676 (2020).
Chen, Y., Li, Z. & Chen, J. Abnormal electron emission in a vertical graphene/hexagonal boron nitride van der Waals heterostructure driven by a hot hole-induced auger process. ACS Appl. Mater. Interfaces 12, 57505–57513 (2020).
Fang, Y., Armin, A., Meredith, P. & Huang, J. Accurate characterization of next-generation thin-film photodetectors. Nat. Photonics 13, 1–4 (2019).
Akbari, A. & Berini, P. Schottky contact surface-plasmon detector integrated with an asymmetric metal stripe waveguide. Appl. Phys. Lett. 95, 021104 (2009).
Schuck, P. J. Hot electrons go through the barrier. Nat. Nanotechnol. 8, 799–800 (2013).
Woessner, A. et al. Highly confined low-loss plasmons in graphene–boron nitride heterostructures. Nat. Mater. 14, 421–425 (2015).
He, Y. et al. Guided modes in a graphene barrier waveguide. Superlattices Microstructures 85, 761–767 (2015).
Rezaeifar, F. et al. Hot-electron emission processes in waveguide-integrated graphene. Nat. Photonics 13, 843–848 (2019).
Breusing, M., Ropers, C. & Elsaesser, T. Ultrafast carrier dynamics in graphite. Phys. Rev. Lett. 102, 086809 (2009).
Winzer, T., Knorr, A. & Malic, E. Carrier multiplication in graphene. Nano Lett. 10, 4839–4843 (2010).
Graham, M. W. et al. Photocurrent measurements of supercollision cooling in graphene. Nat. Phys. 9, 103–108 (2013).
Alonso-González, P. et al. Acoustic terahertz graphene plasmons revealed by photocurrent nanoscopy. Nat. Nanotechnol. 12, 31–35 (2017).
Guo, Q. S. et al. Efficient electrical detection of mid-infrared graphene plasmons at room temperature. Nat. Mater. 17, 986–992 (2018).
Bandurin, D. A. et al. Resonant terahertz detection using graphene plasmons. Nat. Commun. 9, 5392 (2018).
Cai, X. H. et al. Sensitive room-temperature terahertz detection via the photothermoelectric effect in graphene. Nat. Nanotechnol. 9, 814–819 (2014).
Cai, X. H. et al. Plasmon-enhanced terahertz photodetection in graphene. Nano Lett. 15, 4295–4302 (2015).
Shan, H. Y. et al. Direct observation of ultrafast plasmonic hot electron transfer in the strong coupling regime. Light.: Sci. Appl. 8, 9 (2019).
Huang, X. Y. et al. Efficient plasmon-hot electron conversion in Ag–CsPbBr3 hybrid nanocrystals. Nat. Commun. 10, 1163 (2019).
Yakunin, S. et al. Low-threshold amplified spontaneous emission and lasing from colloidal nanocrystals of caesium lead halide perovskites. Nat. Commun. 6, 8056 (2015).
Hayes, J. & Levi, A. Dynamics of extreme nonequilibrium electron transport in GaAs. IEEE J. Quantum Electron. 22, 1744–1752 (1986).
Gu, Q. C. et al. Plasmon enhanced perovskite-metallic photodetectors. Mater. Des. 198, 109374 (2021).
Mohsen, A. A. et al. Refractory plasmonics enabling 20% efficient lead-free perovskite solar cells. Sci. Rep. 10, 6732 (2020).
Zhu, H. M. et al. Screening in crystalline liquids protects energetic carriers in hybrid perovskites. Science 353, 1409–1413 (2016).
Kang, M. G. et al. Holstein polaron in a valley-degenerate two-dimensional semiconductor. Nat. Mater. 17, 676–680 (2018).
Fu, Y. P. et al. Metal halide perovskite nanostructures for optoelectronic applications and the study of physical properties. Nat. Rev. Mater. 4, 169–188 (2019).
Brongersma, M. L., Halas, N. J. & Nordlander, P. Plasmon-induced hot carrier science and technology. Nat. Nanotechnol. 10, 25–34 (2015).
Acknowledgements
This work was financially supported by the Shanghai Science and Technology Innovation Action Plan, Belt & Road Young Scientist Program (Grant No. 19160745500). P.V. and H.P. thank Jane & Aatos Erkko Foundation (project “ASPIRE”) for funding. This work is part of the Academy of Finland Flagship Programme, Photonics Research and Innovation (PREIN), Decision No. 320165.
Author information
Authors and Affiliations
Contributions
I.A. conceptualize and wrote the draft, Y.Z. participated in conception and design, L.S. contributed in drafting section “Plasmonic HC and their applications in other optoelectronic devices”, P.V. and H.P. participated equally in drafting the article and revised it critically, P.M. and M.H. contributed equally in final revisions, corrections, and editing.
Corresponding authors
Ethics declarations
Conflict of interest
The authors declare no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ahmed, I., Shi, L., Pasanen, H. et al. There is plenty of room at the top: generation of hot charge carriers and their applications in perovskite and other semiconductor-based optoelectronic devices. Light Sci Appl 10, 174 (2021). https://doi.org/10.1038/s41377-021-00609-3
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41377-021-00609-3
This article is cited by
-
Recent Advances on Solution-phase Synthesis of Metal Chalcohalide Nanocrystals
Korean Journal of Chemical Engineering (2024)
-
Photoinduced large polaron transport and dynamics in organic–inorganic hybrid lead halide perovskite with terahertz probes
Light: Science & Applications (2022)
-
A Facile In Situ Hydrothermal Etching Method to CaTiO3/TiO2 Heterostructure for Efficient Photocatalytic N2 Reduction
Catalysis Letters (2022)