Abstract
Semiconductor nanowire field-effect transistors represent a promising platform for the development of room-temperature (RT) terahertz (THz) frequency light detectors due to the strong nonlinearity of their transfer characteristics and their remarkable combination of low noise-equivalent powers (<1 nW Hz−1/2) and high responsivities (>100 V/W). Nano-engineering an NW photodetector combining high sensitivity with high speed (sub-ns) in the THz regime at RT is highly desirable for many frontier applications in quantum optics and nanophotonics, but this requires a clear understanding of the origin of the photo-response. Conventional electrical and optical measurements, however, cannot unambiguously determine the dominant detection mechanism due to inherent device asymmetry that allows different processes to be simultaneously activated. Here, we innovatively capture snapshots of the photo-response of individual InAs nanowires via high spatial resolution (35 nm) THz photocurrent nanoscopy. By coupling a THz quantum cascade laser to scattering-type scanning near-field optical microscopy (s-SNOM) and monitoring both electrical and optical readouts, we simultaneously measure transport and scattering properties. The spatially resolved electric response provides unambiguous signatures of photo-thermoelectric and bolometric currents whose interplay is discussed as a function of photon density and material doping, therefore providing a route to engineer photo-responses by design.
Similar content being viewed by others
Introduction
Photodetection relies on the ability to convert absorbed photons into a stable electrical signal.1 Photocurrent generation at terahertz (THz) frequencies in semiconducting nanostructures can be mediated by different physical mechanisms such as the bolometric effect,2,3,4 photo-thermoelectric effect (PTE),1,5,6 photovoltaic effect,7 galvanic effect,8,9 and excitation of plasma waves (PWs).10,11,12,13
InAs nanowires (NWs) have proven to be an efficient active material for the development of state-of-the-art field-effect transistors (FETs) operating as room-temperature (RT) THz photodetectors14,15 due to their high electron mobility16,17 (up to 6000 cm2 V−1 s−1), attofarad (aF) capacitance,16,17 and high saturation velocity18 (~1.3 107 cm s−1 at a field of 16 kV cm−1), which can easily enable high transconductance at low gate voltages and high cut-off frequencies18 (~1 GHz). Furthermore, their narrow bandgap and degenerate Fermi-level pinning allow for the easy formation of stable ohmic contacts, which become increasingly important as the transistor is scaled down.
While in the last few years, the dependences of the THz detection performance of semiconductor NW photodetectors on material-related parameters (NW doping,19 carrier concentration, geometry, and/or material choice) have been widely investigated,20 a systematic study of the physical mechanisms at the base of RT photodetection is still lacking.
Present assumptions indeed only rely on what can be indirectly inferred by mapping the gate-tunable conductivity through transport experiments, analysis of photo-responses in antenna-integrated devices,21 or on-chip photocurrent pump-probe studies.22
Mapping the spatial distribution of the photocurrent in an active material conversely represents an unambiguous way to discriminate the dominant process controlling photodetection since individual physical mechanisms correspond to distinctive profiles of the light-induced photocurrent.
Scanning photocurrent microscopy based on far-field optics has been successfully applied in the last few years to investigate local photocurrents induced by visible and near/mid-infrared illumination in one-dimensional (1D) nanostructures such as NWs13,23 and nanotubes.24,25,26
The extension of photocurrent microscopy to the THz frequency range, an interesting frontier for the rapidly emerging development of micro- and nanosources,22,27 nanodetectors,14,20,25,28 modulators29,30,31 and metamaterials,32 has been, however, traditionally hindered by the diffraction limit. Overcoming this limitation, near-field techniques can have a tremendous impact on engineering the aforementioned technologies with progressively improved performances and functionalities.
Near-field optical microscopy has shown amazing potential in the last few years for investigating optoelectronic properties of nanoscale materials and devices, thanks to its unique capabilities of inspecting charge carrier density13,33,34,35,36,37 and plasmon–polariton38,39,40,41 and phonon–polariton42,43,44 modes45 with unprecedented spatial resolution. Furthermore, near-field microscopy can allow mapping of the spatial variation and the bias dependence of local currents induced by light illumination, therefore tracking the photocarrier transport and electronic band bending in electronic and photonic nanodevices.
Very recently, scattering-type scanning near-field optical microscopy (s-SNOM) has been exploited at THz frequencies to map photocurrents in graphene46 with sub-diffraction spatial resolution, exploiting lightning-rod effects in a metal-coated atomic force microscopy (AFM) tip illuminated by the THz output of a bulky, table-top, gas laser.47
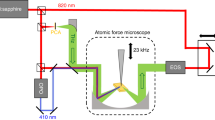
Here, we conceive and devise a compact, portable, scanning near-field system that functions at THz frequencies and is capable of simultaneously performing photocurrent nanoscopy48,49,50,51,52,53,54,55,56,57,58,59 and detectorless near-field imaging60 of a 1D NW field-effect nanodetector with ~35 nm spatial resolution, which corresponds to a wavelength fraction <λ/3000. The system comprises a continuous-wave (CW) THz quantum cascade laser (QCL) coupled to s-SNOM and is here innovatively exploited to trace and map, unambiguously, the physical mechanisms inducing light detection at THz frequencies.
Results
Our samples employ Au-catalysed InAs NWs slightly doped with Se grown by chemical beam epitaxy (CBE) following a bottom-up approach.61 The resulting crystalline phase is wurtzite, and the InAs NWs exhibit {110} facets and hexagonal cross-sections with lengths ∼2.5 µm and radii ∼40 nm. Following the fabrication procedure described in the “Methods” section, the individual NWs are integrated in lateral-gated FETs.
Figure 1a shows scanning electron microscopy (SEM) images of two prototypical devices, each consisting of a single NW-FET with source (S), drain (D), and gate (G) contacts as indicated. The two devices, denoted NW1 and NW2, differ in the gate-NW distance d (dNW1 = 210 nm, dNW2 = 267 nm) and the channel length l (lNW1 = 1.95 µm and lNW2 = 0.86 µm). In both cases, the gate length W (WNW1 = 1 µm and WNW2 = 328 nm) is smaller than the FET channel length. The FETs are primarily characterized through transport experiments, showing a stable ohmic behaviour, on–off current ratios higher than 10 (NW1) and 3 (NW2), and a lack of gate leakage through the SiO2/Si substrate (see Supporting Information).
a Scanning electron microscopy (SEM) images of InAs NW field-effect transistors labelled NW1 and NW2, with source (S), drain (D), and gate (G) contacts indicated. b The conductivity σ of NW1 (black line) and NW2 (red line) measured at room temperature applying drain-to -source voltage of VDS = 2 mV for NW1 and VDS = 5 mV for NW2, reported as a function of the gate voltage VG.
The conductivity σ of the two devices as a function of the gate voltage VG is reported in Fig. 1b. The resistivities ρ at VG = 0 V are ρ0NW1 ∼ 3 mΩ m−1 and ρ0NW2 ∼ 1.2 mΩ m−1, and the transconductances g in the linear regime are gNW1 = 1.6 mS m−1 and gNW2 = 13 mS m−1. We estimate the capacitance C between the lateral gate and the NWs for the two devices as CNW1 = 41 aF and CNW2 = 12 aF by numerical simulation based on a finite element method (FEM) using the AC/DC module of commercial software (Comsol Multiphysics). The carrier mobility µ in the two NWs can be extracted from the gate capacitance using the Wunnicke metrics62 as µ = gl2/(CVDS), giving µNW1 = 740 cm2 V−1 s−1 and µNW2 = 505 cm2 V−1 s−1 for the two devices. From the current dependence at the applied VDS, we estimate the carrier density at zero gate voltage ne = (μeρ0)−1, where e is the electron charge, obtaining the following estimations for the two devices: neNW1 = 3 × 1016 cm−3 and neNW2 = 1 × 1017 cm−3. The local modulation provided by the gate enables us to investigate the photo-response as a function of the carrier density with an expected carrier density modulation on the order of 1016 cm−3 V−1.
The near-field photocurrent measurements are performed by combining scanning near-field THz nanoscopy with the electrical read-out at the S and D contacts of the FET, as sketched in Fig. 2a. The output of a THz-QCL emitting at 2.7 THz, operating in CW and linearly p-polarized, is focused on the 10 nm radius PtIr-coated AFM tip of an s-SNOM instrument, with a 30° incident angle relative to the sample surface. The AFM tip couples to the incident THz light, which is funnelled at its apex63 and interacts with the approached sample. While performing a raster scan of the sample, we simultaneously monitor the topography with an infrared laser focused on the AFM probe cantilever and the D–S electrical signal. Specifically, we detect the D–S photovoltage ΔV when no VDS is applied (VDS = 0 V) using a high input impedance (R = 100 MΩ), low-noise voltage amplifier, or, alternatively, the photocurrent ΔI for a finite VDS by using a low input impedance (R = 50 Ω), low-noise (50 fA) transimpedance amplifier.
a Sketch of the photocurrent nanoscopy experiment. A THz-QCL coupled to the AFM tip of an s-SNOM photo-excites a single InAs NW integrated into a FET. Source (S), drain (D), and gate (G) contacts are marked on the graph. In the experiment, the S–D signal is monitored together with the sample topography. b, c Simulated local increases in the electron Te (b) and lattice Tph (c) temperatures with respect to the room-temperature To = 296 K induced by photoexcitation in a 1.4 µm long NW with a diameter of 80 nm and its centre at x = 0 as a function of the position x along the NW axis and of the position xtip of the tip scanning the sample. d, e Simulated photocurrent profiles induced by the bolometric (d) and PTE (e) effects as a function of the tip position xtip. The slightly positive shift of xtip at which the photocurrent value crosses zero reflects the near-field photoexcitation with the CW THz-QCL field funnelled by the AFM tip, which is illuminated from one side of the NW with a 30° incident angle.
Near-field photoexcitation with the CW THz-QCL field, impinging on the AFM tip with a 30° angle with respect to the sample plane, is funneled onto the NW, introducing an asymmetry along the NW axis and producing strongly localized heating in the NW caused by THz photon absorption via intraband transitions. Conversely, interband absorption can be discarded considering that the ∼356 meV energy gap of InAs64 largely exceeds the THz photon energy (11.2 meV). The absorbed heat results in finite gradients of both Te and Tph along the NW axis that depend on the AFM tip position.
To predict the temperature profiles during a sample scan, we first simulate the electromagnetic field distribution along an NW via FEM simulation as a function of the tip position xtip, and then we extract the power loss map (see Supporting Information). Interestingly, the simulated THz field power peaks below the tip apex and at the NW/electrode interfaces. The Te and Tph corresponding to a given xtip, i.e., to a given distribution of the THz field, are then estimated by solving a 1D heat-diffusion model along the NW, including heat exchange with the substrate65 (see Fig. 2b, c). Details on the thermal constants employed in the simulation are given in the Supporting Information. While the retrieved Te profiles along the NW axis peaked at xtip (see Fig. 2b), the Tph, which describes the lattice temperature increase due to the coupling with the hot electron bath, presents a broader profile that is less dependent on xtip and peaked at the NW centre. The photocurrent signal at each xtip value is finally calculated from these temperature profiles, assuming thermally driven effects, i.e., bolometric and PTE photocurrents. The bolometric (IB) and thermoelectric (IPTE) photocurrents as a function of xtip are reported in Fig. 2d, e following the expressions:
where σ is the electrical conductivity, Se is the Seebeck coefficient, and x spans the NW length l. The two effects exhibit consistently different photocurrent profiles.
The expected near-field IB photocurrent profile (Fig. 2d) resembles the bell-shaped trend of Tph, with a maximum near the NW centre and constant polarity. In contrast, the PTE voltage VPTE and the current IPTE = σVPTE exhibit a sign change along the NW, with zero signal near the NW centre. The bolometric current IB results from the variation of σ with Tph, as quantified by the bolometric coefficient dσ/dT. In contrast to PTE, IB could also arise when the device is homogeneously heated (∇T = 0) and depends only on the temperature variation with respect to the dark condition (To = 296 K). The polarity depends on the sign of the bolometric coefficient, which is negative (positive) for a degenerate (nondegenerate) semiconductor.
The PTE response instead emerges thanks to the combination of a finite Te gradient induced by the local photoexcitation and to a spatially varying Seebeck coefficient Se. For the InAs NWs, a Seebeck coefficient SeNW ∼ 150 μV K−1 is extrapolated from the transfer characteristics (see Supporting Information), in good agreement with the recently determined temperature dependence of the transport properties of InAs NWs.66 On the other hand, the Au electrodes have SeAu ∼ 0 μV K−1, so the interface electrodes/NW acts as a thermocouple, able to translate temperature gradients into an electrical signal. When the tip is at the centre of the NW, the two opposite PTE currents, originating at the S and D electrodes, cancel out, resulting in a clearly zero signal (Fig. 2e). The maximum PTE signal appears at a finite distance from the metal/NW interface since the difference (Te−To) reaches its minimum on the metallic electrodes. The photovoltaic mechanism is not considered for InAs NWs because the THz incident photon energy is not compatible with interband transition photo-exciting electron–hole pairs. As expected, simulations confirm that the different photodetection mechanisms that can come into play in InAs NWs correspond to clearly distinguishable near-field photocurrent profiles.
To perform photocurrent nanoscopy experiments, we operate our s-SNOM tip in tapping mode, with an oscillating frequency Ω. To isolate the components of the electrical signals due to the near-field photoexcitation, i.e., those induced solely by the light scattered by the tip, the signals are demodulated at high harmonics of the tapping frequency Ωn = nΩ, i.e., at the order n in the range n = 2–5. First, we collect near-field maps while setting VDS = 0 V on sample NW1, with S grounded and collecting ΔV at the D electrode, as sketched in Fig. 3a. ΔV is the superposition of signals oscillating at the tapping frequency Ω and at its harmonics ΔVn: ΔV = Σ5n=0 ΔVn = ∆V0 + ∆V1 + ∆V2 + …; the second-order (n = 2) component ∆V2 is shown in Fig. 3c for different values of VG. A finite value is reported only when the tip scans the portion of the NW that is not covered by the metallic electrodes. Indeed, the THz near-field is screened by the metal contacts and fails to photo-excite the portion of NW buried beneath. The horizontal cut of each individual photovoltage map, taken by averaging over 50 nm (5 pixels) around the NW centre (as identified by the topographic image in Fig. 3a), is shown in Fig. 3e.
THz near-field photocurrent maps. a, b Sketches of the applied fields on the FET channel of NW1 with an applied VDS = 0 V (a) and of NW2 with VDS = 1 mV (b) together with the topographic maps (in greyscale) of the two FETs. c Near-field second-order photovoltage ∆V2 maps of NW1 with VDS = 0 V and at different gate voltages in the range VG = 0–7 V. d Near-field second-order photocurrent maps ∆I2 of NW2 with VDS = 1 mV and VG in the range 0–6 V. e ∆V2 profiles of NW1 at different VG values as obtained by averaging the horizontal cuts of the maps in panel c over a 50 nm range around the NW1 centre. f ∆I2 profiles of NW2 at different VG values obtained by averaging horizontal cuts of the maps in panel d over a 50 nm range around the NW2 centre. The flat, nearly zero, photocurrent region in panel e reflects the gate-induced screening of the THz field at the centre of the NW
In the maps and line profiles, the photovoltage exhibits a phase change along the NW; it increases in amplitude approaching the contacts and becomes negligible at the NW centre, as expected when photodetection is governed by the PTE. Moreover, the signal progressively increases with VG, while the position of the zero signal along the NW axis remains practically unperturbed. Since VDS = 0 V, we can only probe the photovoltage signal that is directly generated by photoexcitation, as in the case of the PTE or PW excitation, but we are not sensitive to any photo-induced variation of the conductivity, i.e., to any bolometric effect.
Accordingly, we repeat the same measurements on NW2 as sketched in Fig. 3b while applying VDS = 1 mV at the S contact, corresponding to a DC dark current of ∼5 nA. The near-field maps and line profiles, corresponding to the second-order (n = 2) component of the photocurrent ∆I2, are shown in Fig. 3d and f, respectively. Since the signal is acquired from D, a positive photocurrent corresponds to a current flowing from S to D. At VG = 0 V, as we illuminate NW2 with THz light, we observe a ∆I2 signal with constant polarity along the whole NW, with only small intensity modulations, which resembles the expected response for the bolometric effect, plotted in Fig. 2d. Since the number of carriers contributing to the conduction is not affected by THz-light absorption, the conductance change associated with the observed bolometric photocurrent can be ascribed to a temperature-induced mobility variation. Interestingly, by increasing VG above the pinch-off (VG > 2.5 V), the photocurrent maps drastically change, and the phase jump, distinctive of the PTE, reappears. The enhancement of the PTE, which eventually dominates at high carrier densities, overwhelming the bolometric response, is encoded in the dependence of Se on the carrier density ne, which determines the increase with VG. To elucidate the interplay between the bolometric effect and the PTE, we explore the dependence of the photocurrent signal in NW2 in two opposite regimes: when the photo-response is dominated by the PTE (VG = 6 V) and when the bolometric effect is dominant (VG = 0 V). Figure 4 shows the ∆I2 maps and the related horizontal cuts as a function of the incident THz field power P and as a function of VDS. The incident power is progressively increased by varying the bias applied to the THz-QCL heterostructure, and it is measured with a calibrated power meter (Thomas Keating THz Absolute Power & Energy Meter System) placed at the entrance of the s-SNOM instrument. To better quantify how the incident power affects the retrieved near-field signals, we integrated the horizontal line profiles, extrapolating the area underneath. In the PTE regime (Fig. 4a–f), the signal increases with the incident power (see Fig. 4e) and remains almost constant while varying VDS up to VDS = 10 mV (see Fig. 4f). Conversely, in the bolometric regime, see Fig. 4g–l, the near-field photocurrent increases linearly, both with the incident THz power (see Fig. 4k) and with VDS (see Fig. 4l).
Evolution of the retrieved photocurrent signals. a, b Second-order photocurrent ΔI2 maps of NW2 in the PTE regime (gate voltage VG = 6 V) as a function of the incident THz power P at fixed source–drain bias VDS = 5 mV (a) and as a function of VDS at a fixed P of 100 µW (b). c, d ΔI2 linear profiles in the PTE regime extracted by averaging horizontal cuts of panels a and b in a 50 nm range around the NW centre. e–h Integrated areas in the PTE regime underneath the ΔI2 profiles shown in panels c and d. g, h ΔI2 maps of NW2 in the bolometric regime (gate voltage VG = 0 V) as a function of P at a fixed VDS of 10 mV (g) and as a function of VDS at a fixed P of 100 µW (h). i, j ΔI2 linear profiles in the bolometric regime, extracted by averaging horizontal cuts of panels g and h in a 50 nm range around the NW centre. k, l Integrated areas in the bolometric regime underneath the ΔI2 profiles shown in panels 4i-4j
In addition to thermally driven effects, PW photoexcitation could generate ΔV and ΔI signals via the Dyakonov–Shur rectification51 due to the capacitive coupling between the S and D contacts and the AFM tip. Since this coupling depends on the relative distance between the tip and the electrodes, it is influenced by tip tapping. Accordingly, the PW photo-response can, in principle, contribute to the demodulated signal at n = 2. The signal profile and photocurrent versus VG expected for the PW excitation is the same as that for the PTE,67 meaning that a phase change is expected at the NW centre. However, the PW photo-response is expected to increase with the applied VDS because of the forced injection of electrons in the FET channel and the enhanced asymmetry induced by the IDS current.11,68 Accordingly, the lack of dependence on VDS in the regime where we observe the phase change (Fig. 4d) clearly indicates that the PW effect is here negligible and overwhelmed by the PTE response.
In all the explored conditions, the PTE photocurrent is at least four times more intense than the bolometric photocurrent; however, due to the different dependences on VDS, the bolometric contribution can eventually become comparable to the PTE current even at high carrier density (VG above the pinch-off) if VDS is sufficiently high. This is clearly probed by measuring the VG-dependent photocurrent maps at VDS = 10 mV (see Supplementary Information). At gate voltages VG = 4 V and VDS = 10 mV, the two physical effects (photo-thermoelectric and bolometric) become comparable, leading to a higher detected total photocurrent at the expense of a mixed detection regime. The dominant role of the PTE is not surprising considering the giant thermoelectric response demonstrated in InAs NWs.66
Detectors relying on the PTE can operate without the application of any current; conversely, for bolometers, the detector current represents an additional source of noise. To take advantage of the strong PTE response of InAs NWs, the coupling elements used to funnel the THz light into the nanoscale active region can be designed to favour the formation of thermal gradients through asymmetric photoexcitation of the active element. This is achieved by using a nanoscale antenna with one arm coupled to the gate and the other to the source or drain electrode.
The carrier density has a paramount role in defining the mechanism that dominates the photocurrent generation in InAs NWs at THz frequencies and can be quantitatively determined from measurements of nano-optical properties.13,35,69
To this aim, we exploit the capability of THz-QCL to serve both as a powerful source and as a phase-sensitive detector to monitor the change in field scattered by the InAs NW as a function of the applied VG. The THz light, back-scattered by the AFM tip, eventually returns into the laser cavity, perturbing its emission via the self-mixing effect.61,70 We isolate the near-field contribution to the back-scattered light by monitoring the QCL contact voltage VQCL and demodulating it at Ωn. The sn signal from InAs NWs has generally lower intensity than those captured from the undoped Si substrate and from the gold electrodes, as seen in the map of the second-order component s2 in Fig. 5b and the corresponding topography (Fig. 5a), where the NW appears as a dark stripe bridging the much brighter gold contacts. The self-mixing signal s2 is a function of the length Lext of the external cavity defined by the AFM tip and by the laser emission facet such that self-mixing fringes can be acquired by changing Lext with a delay line in the optical path. The fringes collected at three different spots on the sample corresponding to the NW, substrate, and electrodes are shown in Fig. 5d. The phase of the back-scattered field (φn) is directly related to the phase of the self-mixing fringes.
Detectorless near-field optical microscopy. a Topography of the NW1 nanowire. b Self-mixing intensity maps demodulated at 2Ω (s2) at different VG values scaled to the substrate value and normalized to the value measured at the gold contacts. The maps are acquired at fixed Lext = 33.5 μm, corresponding to the maximum of the individual self-mixing fringes on gold electrodes. c s2 line profiles obtained by integrating horizontal cuts of the s2 maps in a 50 nm range around the NW1 centre and at different VG values. d Self-mixing fringes as a function of the external cavity length Lext at VG = 0 V. Individual curves correspond to different positions on the sample, marked as coloured crosses in panel a: blue for the gold electrode, red for NW1, and black for the substrate. e Self-mixing fringes acquired at a fixed position on NW1 as a function of the external cavity length Lext for different gate voltages VG. f Amplitude s2 (black) and phase φ2 (blue) of the second-order demodulation self-mixing signal of panel e as a function of the carrier density ne estimated from the transconductance curve assuming a constant mobility (open triangles), together with the predictions of Eq. (4) (solid lines). The experimental s2 values are scaled by a factor of 0.55 μV−1 to match the model at VG = 1 V. Better agreement between the experiment and model is observed for carrier densities ne scaled by a factor of 1.6 (full triangles)
By scanning the sample, we observe a change in the amplitude and degree of asymmetry of the self-mixing fringes due to the variation in the scattered intensity, which is fed back into the laser cavity. The self-mixing contrast is evaluated by subtracting the signal from the substrate and by normalizing the maps to the value retrieved on the gold electrodes. The line profiles are extracted by averaging the horizontal cuts of the maps of Fig. 5b in a 50 nm range centred on the NW. Negligible variations are seen by changing the current flowing in the NW with VDS (see Supporting Information). In contrast, as ne increases with VG, we observe a clear change in the near-field contrast at a fixed Lext (see Fig. 5b, c). This change can be attributed to variations in the dielectric permittivity ε of the NW with carrier density ne, as described by the Drude model.
The field scattered by the tip is indeed related to the incident field by the complex-valued scattering coefficient \(\sigma _{\mathrm s} = (1 + r_{\mathrm p})^2\alpha _{{\mathrm {eff}}}\), where rp is the Fresnel coefficient accounting for the reflection by the sample surface and αeff is the effective polarizability that depends on the sample-tip near-field interaction and is the function ε. We can expand the second-order scattered signal s2 in ε in the framework of the point dipole moment model,71 as detailed in the “Methods” section, to trace the changes in s2 to the dependence of ε on ne.
In the investigated carrier density range, the model predicts a small variation in the signal amplitude and a consistent shift of the phase of the scattered field. To disentangle the effects of carrier injection on the phase (φ2) and amplitude (s2) of the scattered field, we acquire the self-mixing signal of NW1 as a function of Lext at different gate voltages, as reported in Fig. 5e. While s2 remains barely unchanged at VG values up to 6 V, a phase drift is observed, a signature of a signal depletion at increasing VG in the maps, at constant Lext in Fig. 5b. The phase shift can be attributed to the photoexcitation of plasmon resonance of the NW,13 whose frequency matches the probe photon energy at carrier densities on the order of 1017 cm−3. To compare the observed trend with predictions based on the Drude model of ε of the InAs NW (see “Methods”), we evaluate the carrier density ne corresponding to the applied VG from the transconductance curve in the range VG = 1–6 V while assuming constant mobility (Fig. 5f). The signal amplitude s2 is normalized to the predicted value for VG = 1 V to rule out any dependence on the acquisition parameters (alignment, self-mixing parameters, THz coupling to the tip). The model predicts the observed trends of signal amplitude and phase, but it indicates that ne is overestimated. A better agreement is reached by dividing the extracted ne values by a factor of 1.6, meaning that the carrier mobility is slightly underestimated here (see Fig. 5f).
The carrier density ne corresponding to the applied VG is determined from the transconductance curve in the range VG = 1–6 V, assuming constant mobility. More carriers are injected in the NW, more the plasmon resonance of the NW13 approaches the probe photon energy, resulting in a phase shift of the field scattered back into the QCL to produce the self-mixing signal. To rule out any dependence of the absolute value of s2 on the acquisition parameters (alignment, self-mixing parameters, THz coupling to the tip), the signal reported in Fig. 5f is normalized to the predicted value for VG = 1 V (green open circle).
The THz response at 2.7 THz shows a strong dependence on the carrier density ne34 in the range 1016–1018 cm−3, and the trend of the self-mixing signal of the NW indicates that at VG up to 6 V, the gating effect is not saturated, as it can occur when the charge carriers in the NW shell screen the gate potential, and we are then still able to inject carriers into the NW. Finally, by exploiting the imaging capability of s-SNOM, we observe that the self-mixing signal in Fig. 5b, c varies along the NW axis, exhibiting a minimum contrast near the D contact, which could be induced by local variations in the carrier density caused by crystal impurities.
Discussion
In conclusion, we exploit photocurrent nanoscopy at THz frequencies to identify the photodetection mechanisms in InAs NW FETs. Once the radiation of a THz QCL source impinges on the s-SNOM AFM tip, we capture snapshots of the photocurrent flowing in the strongly subwavelength NW section, and we retrieve clear signatures of two thermally driven processes: the PTE and the bolometric effect. The interplay between these two mechanisms is discussed as a function of the carrier density, VDS and incident THz power.
Interestingly, at VDS = 0 V, the PTE dominates at high carrier density. Such a condition is extremely advantageous in engineering RT photodetectors combining low noise-equivalent powers (NEPs) and high speeds. Indeed, the zero-bias operation reduces dominant noise sources such as flicker noise, shot noise, and generation-recombination noise, owing to the absence of a static current. Moreover, the high carrier density operation entails a reduction of the channel resistance (the NW can be operated at its maximum conductivity state), which, in turn, results in a proportional reduction in the overall RC time constant. Eventually, the positive correlation between the device temperature and the Seebeck coefficient, given by the Mott relation, makes the PTE mechanism ideal for RT operation. On the other hand, to take full advantage of the bolometric detection mechanism, low temperatures are preferable because of the reduced lattice thermal conductivity, and suitable device architectures capable of minimizing the thermal exchange between the NW and its surroundings, such as suspended NW architectures, should be employed. The achieved results provide a route for engineering THz RT photodetectors with larger NEPs and inherently high speeds, which could be attained by favouring the formation of light-induced thermal gradients along the NW axis to exploit the highly efficient photo-thermoelectric response of InAs NWs and by the inherently small (attofarad) capacitance. In InAs NWs, knowledge of the local photocurrent can be used to select the ideal position of the lateral gate in a planar NW geometry, where the gate is coupled to one of the arms of a dipole antenna.14 In turn, this choice can simultaneously maximize the photocurrent and determine the dominant detection mechanism. By maximizing the photocurrent, the NEP can be reduced.21,72
On the other hand, it is well known that a specific detection mechanism directly affects both the NEP and the response time of a detector, and this is valid for different material platforms.73,74,75 Indeed, a device operating via the PTE, not requiring a direct bias through the channel (unlike what happens in a bolometer65,73,75), is less prone to a number of noise sources, as mentioned before: flicker noise, generation-recombination noise and shot noise all scale with increasing current, eventually dominating the noise figure of a bolometer even at RT. Therefore, THz photocurrent nanoscopy measurements indicate a way to reduce NEP by identifying a route to selectively activate the PTE.
Selective activation of the PTE detection mechanism would also allow increasing the detection speed, which, in a thermally driven THz photo-response, is limited by the efficiency of the energy transfer between incoming photons and the photo-detecting system. In the case of the PTE, the photo-detecting system is the electronic thermal distribution that is modified by the absorption of a photon.65 The characteristic timescale of the photo-response is then given by the electronic specific heat, which limits the rise-time of the signal, and by the electron cooling rate (mainly towards the phonon bath). On the other hand, the bolometric effect is driven by a change in the lattice temperature, which occurs subsequent to the formation of a temperature gradient in the electronic distribution,65 i.e., the lattice temperature changes as a consequence of the increase in the electronic temperature, in agreement with the model described in Fig. 2.
The proposed THz nanoscopy investigation will open up research opportunities in many application domains: real-time pulsed imaging and time-of-flight tomography; time-resolved THz spectroscopy of gases, complex molecules and cold samples; coherent control of quantum systems; quantum optics, where high-power pulses can drive molecular samples out of equilibrium and ultrafast detectors can capture such an effect; metrology; and ultra-high-speed communications, where THz frequency carriers will become increasingly more important in the quest for higher bandwidth data communications and finally can promise extraordinary impacts on the market for biomedical imaging, security and process control. The photocurrent distributions and polarities corresponding to the two effects are consistently different, making photocurrent nanoscopy a very valuable tool in investigating photo-conduction in low-dimensional materials.
Furthermore, we demonstrate that a detectorless s-SNOM system built with a THz-QCL can serve as a multimodal near-field microscope, providing complementary information on optical properties via self-mixing interferometry. The strong dependence of the THz scattered intensity makes this technique particularly useful to probe the Drude response to THz fields for charge carrier densities in the 1016–1018 cm−3 range.
Materials and methods
Sample fabrication
Au-catalysed n-doped InAs NWs are grown by CBE on InAs (111) substrates using trimethylindium and tertiarybutylarsine and ditertiarybutylselenide as metal-organic precursors. As-grown InAs NWs have an average length of 2.3 ± 0.5 μm and radii in the 40–120 nm range. NW FETs are realized with standard nano-fabrication methods. NWs are transferred from the growth substrate to the host substrate via dry transfer. The host substrate is a 350-μm-thick intrinsic silicon wafer capped by 500 nm SiO2. Individual NWs are then geometrically analysed with SEM imaging, and electrical contacts are defined by aligned electron beam lithography. Before metal evaporation, a chemical wet passivation step is performed on the exposed NW areas. The ammonium polysulfide (NH4)2Sx solution, employed for this step, removes the oxide layer that covers the NW before metallization, thus ensuring Ohmic metal-semiconductor contacts. The lateral-gated FETs are then finalized by the thermal evaporation of a 10/100 nm Cr/Au layer and lift-off.
Near-field microscopy
The THz-QCL is mounted in a liquid helium continuous-flow cryostat with a polymethylpentene window and maintained at a fixed heat sink temperature of 13 K. The emitted THz beam is collimated using a 90° off-axis parabolic mirror with an effective focal length of 50 mm. The collimated THz beam is fed into the entrance optical port of a commercial near-field microscope (NeaSNOM, Neaspec, Martinsried, Germany). The optical path length is varied using a delay line, with a linear translation stage having a 30 nm precision. In the microscope, a second paraboloid mirror with an equivalent focal length of 25 mm focuses the beam onto a PtIr tip (RMN-25PtIr300B-H10) having a nominal apex radius of 10 nm and a shank length of 80 μm that is resonant at tapping frequency Ω = 20 (±30%) kHz. The laser polarization lies in the plane containing the tip to efficiently induce an oscillating dipole in the tip. The metallized AFM probe in close proximity to the NW can influence the potential in the transistor channel and thus photocurrent generation by screening the gate field. To minimize this impact, we do not electrically ground the metal cladding of the tip. To maximize the sensitivity to coherent optical feedback, in the self-mixing measurements, the QCL is driven in a continuous wave at the current I = 780 mA (J = 256 A cm−2), which is just 5% higher than the threshold current density (Jth = 240 A cm−2), using a highly stable current generator (Lightwave Electronics, mod. QCL 2000). To perform photocurrent nanoscopy, the QCL is driven in a continuous wave with a current in the range I = 780–830 mA. The THz radiation scattered by the sample is collected by the same focusing parabolic mirror and coupled back to the laser cavity along the same incident optical path. The voltage modulation across the QCL terminals produced by the self-mixing effect is pre-amplified using a low-noise amplifier (DL Instruments, mod. 1201) and demodulated up to the highest harmonic order (n = 5) allowed by the electronic card of the NeaSNOM. The average optical path length from the QCL front facet to the tip is 60 cm. Approach curves reveal that the second harmonics (n = 2) of the electrical signals are already free from far-field background contribution (see Supporting Information), and they are chosen as experimental result metric.
Near-field self-mixing signal and carrier density estimation
In the framework of the point dipole moment model,63,71,76 the effective probe polarizability αeff can be expressed in terms of the electrostatic coefficient α, which is the dipole-polarizability, and β, which is the quasi-static reflection coefficient:
where h is the sample-probe distance and R is the tip radius. To estimate the second-order scattering contribution to the s-SNOM signal s2, we consider the second-order expansion of αeff at a power of h, which is varied with a sinusoidal function at a frequency equal to the tapping frequency. The second-order coefficient is
We can expand Eq. (3) in the dielectric constant ε of the NW considering that \(\beta = \frac{{(\varepsilon - 1)}}{{\varepsilon + 1}}\) and that for a metal-coated tip \(\alpha = \frac{{(\varepsilon - 1)}}{{\varepsilon + 2}} \approx 1\). The expression of the complex-valued s2 simplifies as
The permittivity is described by the Drude model as\(\varepsilon = \varepsilon _\infty ( {1 - \frac{{\omega _{\mathrm {pl}}^2}}{{\left( {\omega ^2 - \frac{{i\omega }}{\tau }} \right)}}} )\), where the high-frequency dielectric constant ε∞ = 13.13 as in ref. 13; ωpl is the plasma frequency, which depends on the carrier density \(\omega _{{\mathrm {pl}}} = \sqrt {\frac{{4\pi n_{\mathrm e}}}{{\varepsilon _\infty m^\ast }}}\); m* is the carrier effective mass (=0.023me); me is the free electron mass; τ = 10 fs is the Drude scattering time as in ref. 13 and ne is the carrier density tuned with the lateral gate.
References
Koppens, F. H. L. et al. Photodetectors based on graphene, other two-dimensional materials and hybrid systems. Nat. Nanotechnol. 9, 780–793 (2014).
Andrews, D. H., Milton, R. M. & DeSorbo, W. A fast superconducting bolometer. J. Opt. Soc. Am. 36, 518–524 (1946).
Jones, R. C. The general theory of bolometer performance. J. Opt. Soc. Am. 43, 1–14 (1953).
Richards, P. L. Bolometers for infrared and millimeter waves. J. Appl. Phys. 76, 1–24 (1994).
Cai, X. H. et al. Sensitive room-temperature terahertz detection via the photothermoelectric effect in graphene. Nat. Nanotechnol. 9, 814–819 (2014).
Lu, X. W. et al. Progress of photodetectors based on the photothermoelectric effect. Adv. Mater. 31, 1902044 (2019).
Somma, C. et al. High-field terahertz bulk photovoltaic effect in lithium niobate. Phys. Rev. Lett. 112, 146602 (2014).
Ganichev, S. D. et al. Spin-galvanic effect. Nature 417, 153–156 (2002).
Plank, H. & Ganichev, S. D. A review on terahertz photogalvanic spectroscopy of Bi2Te3-and Sb2Te3-based three dimensional topological insulators. Solid-State Electron. 147, 44–50 (2018).
Dyakonov, M. & Shur, M. Detection, mixing, and frequency multiplication of terahertz radiation by two-dimensional electronic fluid. IEEE Trans. Electron Devices 43, 380–387 (1996).
Knap, W. et al. Field effect transistors for terahertz detection: physics and first imaging applications. J. Infrared Millim. Terahertz Waves 30, 1319–1337 (2009).
Knap, W. et al. Nanometer size field effect transistors for terahertz detectors. Nanotechnology 24, 214002 (2013).
Arcangeli, A. et al. Gate-tunable spatial modulation of localized plasmon resonances. Nano Lett. 16, 5688–5693 (2016).
Vitiello, M. S. et al. Room-temperature terahertz detectors based on semiconductor nanowire field-effect transistors. Nano Lett. 12, 96–101 (2012).
Ravaro, M. et al. Detection of a 2.8 THz quantum cascade laser with a semiconductor nanowire field-effect transistor coupled to a bow-tie antenna. Appl. Phys. Lett. 104, 83116 (2014).
Dayeh, S. A. et al. High electron mobility InAs nanowire field-effect transistors. Small 3, 326–332 (2007).
Ford, A. C. et al. Diameter-dependent electron mobility of InAs nanowires. Nano Lett. 9, 360–365 (2009).
Takahashi, T. et al. Parallel array InAs nanowire transistors for mechanically bendable, ultrahigh frequency electronics. ACS Nano 4, 5855–5860 (2010).
Viti, L. et al. Se-doping dependence of the transport properties in CBE-grown InAs nanowire field effect transistors. Nanoscale Res. Lett. 7, 159 (2012).
Vitiello, M. S. et al. One dimensional semiconductor nanostructures: an effective active-material for terahertz detection. APL Mater. 3, 26104 (2015).
Viti, L. et al. Nanowire terahertz detectors with a resonant four-leaf-clover-shaped antenna. Opt. Express 22, 8996–9003 (2014).
Erhard, N. et al. Ultrafast photocurrents and THz generation in single InAs-nanowires. Ann. Phys. 525, 180–188 (2013).
Graham, R. et al. Electric field dependent photocurrent decay length in single lead sulfide nanowire field effect transistors. Nano Lett. 11, 717–722 (2010).
Allen, J. E., Hemesath, E. R. & Lauhon, L. J. Scanning photocurrent microscopy analysis of Si nanowire field-effect transistors fabricated by surface etching of the channel. Nano Lett. 9, 1903–1908 (2009).
Ahn, Y., Dunning, J. & Park, J. Scanning photocurrent imaging and electronic band studies in silicon nanowire field effect transistors. Nano Lett. 5, 1367–1370 (2005).
Xia, F. N. et al. Photocurrent imaging and efficient photon detection in a graphene transistor. Nano Lett. 9, 1039–1044 (2009).
Trukhin, V. N. et al. Terahertz generation by GaAs nanowires. Appl. Phys. Lett. 103, 072108 (2013).
Peng, K. et al. Single nanowire photoconductive terahertz detectors. Nano Lett. 15, 206–210 (2015).
Degl’Innocenti, R. et al. All-integrated terahertz modulators. Nanophotonics 7, 127–144 (2018).
Baig, S. A. et al. An ultrafast switchable terahertz polarization modulator based on III-V semiconductor nanowires. Nano Lett. 17, 2603–2610 (2017).
Docherty, C. J. et al. An ultrafast carbon nanotube terahertz polarisation modulator. J. Appl. Phys. 115, 203108 (2014).
Shi, J. H. et al. THz photonics in two dimensional materials and metamaterials: properties, devices and prospects. J. Mater. Chem. C 6, 1291–1306 (2018).
Huber, A. J. et al. Terahertz near-field nanoscopy of mobile carriers in single semiconductor nanodevices. Nano Lett. 8, 3766–3770 (2008).
Stiegler, J. M. et al. Nanoscale free-carrier profiling of individual semiconductor nanowires by infrared near-field nanoscopy. Nano Lett. 10, 1387–1392 (2010).
Berweger, S. et al. Near-field control and imaging of free charge carrier variations in GaN nanowires. Appl. Phys. Lett. 108, 073101 (2016).
Liewald, C. et al. All-electronic terahertz nanoscopy. Optica 5, 159–163 (2018).
Jung, L. et al. Quantification of carrier density gradients along axially doped silicon nanowires using infrared nanoscopy. ACS Photonics 6, 1744–1754 (2019).
Kawata, S. Near-Field Optics and Surface Plasmon Polaritons (Springer, Berlin, Heidelberg, 2001).
Chen, J. N. et al. Optical nano-imaging of gate-tunable graphene plasmons. Nature 487, 77–81 (2012).
Fei, Z. et al. Infrared nanoscopy of dirac plasmons at the graphene-SiO2 interface. Nano Lett. 11, 4701–4705 (2011).
Fei, Z. et al. Gate-tuning of graphene plasmons revealed by infrared nano-imaging. Nature 486, 82–85 (2012).
Li, P. N. et al. Hyperbolic phonon-polaritons in boron nitride for near-field optical imaging and focusing. Nat. Commun. 6, 7507 (2015).
Huber, A. et al. Near-field imaging of mid-infrared surface phonon polariton propagation. Appl. Phys. Lett. 87, 081103 (2005).
Renger, J. et al. Resonant light scattering by near-field-induced phonon polaritons. Phys. Rev. B 71, 075410 (2005).
Low, T. et al. Polaritons in layered two-dimensional materials. Nat. Mater. 16, 182–194 (2017).
Alonso-González, P. et al. Acoustic terahertz graphene plasmons revealed by photocurrent nanoscopy. Nat. Nanotechnol. 12, 31–35 (2017).
Schiefele, J. et al. Coupling light into graphene plasmons through surface acoustic waves. Phys. Rev. Lett. 111, 237405 (2013).
Hsu, J. W. P. et al. Near-field scanning optical microscopy imaging of individual threading dislocations on relaxed GexSi1-x films. Appl. Phys. Lett. 65, 344–346 (1994).
Buratto, S. K. et al. Imaging InGaAsP quantum-well lasers using near-field scanning optical microscopy. J. Appl. Phys. 76, 7720–7725 (1994).
Goldberg, B. B. et al. Near-field optical studies of semiconductor heterostructures and laser diodes. IEEE J. Sel. Top. Quantum Electron. 1, 1073–1081 (1995).
Richter, A. et al. Optical near-field photocurrent spectroscopy: a new technique for analyzing microscopic aging processes in optoelectronic devices. Appl. Phys. Lett. 69, 3981–3983 (1996).
McNeill, C. R. et al. Direct photocurrent mapping of organic solar cells using a near-field scanning optical microscope. Nano Lett. 4, 219–223 (2004).
Gu, Y. et al. Near-field scanning photocurrent microscopy of a nanowire photodetector. Appl. Phys. Lett. 87, 43111 (2005).
Mueller, T. et al. Role of contacts in graphene transistors: a scanning photocurrent study. Phys. Rev. B 79, 245430 (2009).
Rauhut, N. et al. Antenna-enhanced photocurrent microscopy on single-walled carbon nanotubes at 30 nm resolution. ACS Nano 6, 6416–6421 (2012).
Mauser, N. & Hartschuh, A. Tip-enhanced near-field optical microscopy. Chem. Soc. Rev. 43, 1248–1262 (2014).
Mauser, N. et al. Antenna-enhanced optoelectronic probing of carbon nanotubes. Nano Lett. 14, 3773–3778 (2014).
Grover, S. et al. Limits on the bolometric response of graphene due to flicker noise. Appl. Phys. Lett. 106, 051113 (2015).
Woessner, A. et al. Near-field photocurrent nanoscopy on bare and encapsulated graphene. Nat. Commun. 7, 10783 (2016).
Giordano, M. C. et al. Phase-resolved terahertz self-detection near-field microscopy. Opt. Express 26, 18423–18435 (2018).
Gomes, U. P. et al. Controlling the diameter distribution and density of InAs nanowires grown by Au-assisted methods. Semicond. Sci. Technol. 30, 115012 (2015).
Wunnicke, O. Gate capacitance of back-gated nanowire field-effect transistors. Appl. Phys. Lett. 89, 083102 (2006).
Keilmann, F. & Hillenbrand, R. Near-field microscopy by elastic light scattering from a tip. Philos. Trans. R. Soc. A 362, 787–805 (2004).
Vurgaftman, I., Meyer, J. R. & Ram-Mohan, L. R. Band parameters for III-V compound semiconductors and their alloys. J. Appl. Phys. 89, 5815–5875 (2001).
Low, T. et al. Origin of photoresponse in black phosphorus phototransistors. Phys. Rev. B 90, 081408 (2014).
Roddaro, S. et al. Giant thermovoltage in single InAs nanowire field-effect transistors. Nano Lett. 13, 3638–3642 (2013).
Bandurin, D. A. et al. Dual origin of room temperature sub-terahertz photoresponse in graphene field effect transistors. Appl. Phys. Lett. 112, 141101 (2018).
Delgado-Notario, J. A. et al. Sub-THz imaging using non-resonant HEMT detectors. Sensors 18, 543 (2018).
Govyadinov, A. A. et al. Quantitative measurement of local infrared absorption and dielectric function with tip-enhanced near-field microscopy. J. Phys. Chem. Lett. 4, 1526–1531 (2013).
Rakić, A. D. et al. Sensing and imaging using laser feedback interferometry with quantum cascade lasers. Appl. Phys. Rev. 6, 021320 (2019).
Cvitkovic, A., Ocelic, N. & Hillenbrand, R. Analytical model for quantitative prediction of material contrasts in scattering-type near-field optical microscopy. Opt. Express 15, 8550–8565 (2007).
Viti, L. et al. HBn-encapsulated, graphene-based, room-temperature terahertz receivers, with high speed and low noise. Nano Lett. 20, 3169–3177 (2020).
Freitag, M. et al. Photoconductivity of biased graphene. Nat. Photonics 7, 53–59 (2013).
Tielrooij, K. J. et al. Generation of photovoltage in graphene on a femtosecond timescale through efficient carrier heating. Nat. Nanotechnol. 10, 437–443 (2015).
Viti, L. et al. Efficient Terahertz detection in black-phosphorus nano-transistors with selective and controllable plasma-wave, bolometric and thermoelectric response. Sci. Rep. 6, 20474 (2016).
Knoll, B. & Keilmann, F. Enhanced dielectric contrast in scattering-type scanning near-field optical microscopy. Opt. Commun. 182, 321–328 (2000).
Acknowledgements
This work was supported by the European Research Council through the ERC Consolidator Grant (681379) SPRINT, by the European Union through the H2020-MSCA-ITN-2017, TeraApps (765426) grant, partially by the SUPERTOP project of the QuantERA ERA-NET Cofund in Quantum Technologies and by the FET-OPEN project. M.S.V. acknowledges partial support from the second half of the Balzan Prize 2016 in applied photonics delivered to Federico Capasso. The authors acknowledge fruitful discussions with A. Tomadin.
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Pogna, E.A.A., Asgari, M., Zannier, V. et al. Unveiling the detection dynamics of semiconductor nanowire photodetectors by terahertz near-field nanoscopy. Light Sci Appl 9, 189 (2020). https://doi.org/10.1038/s41377-020-00425-1
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41377-020-00425-1
This article is cited by
-
Near-field detection of gate-tunable anisotropic plasmon polaritons in black phosphorus at terahertz frequencies
Nature Communications (2024)
-
Manipulating hyperbolic transient plasmons in a layered semiconductor
Nature Communications (2024)
-
Field-resolved high-order sub-cycle nonlinearities in a terahertz semiconductor laser
Light: Science & Applications (2021)
-
High-frequency rectifiers based on type-II Dirac fermions
Nature Communications (2021)