Abstract
Optical metasurfaces have become versatile platforms for manipulating the phase, amplitude, and polarization of light. A platform for achieving independent control over each of these properties, however, remains elusive due to the limited engineering space available when using a single-layer metasurface. For instance, multiwavelength metasurfaces suffer from performance limitations due to space filling constraints, while control over phase and amplitude can be achieved, but only for a single polarization. Here, we explore bilayer dielectric metasurfaces to expand the design space for metaoptics. The ability to independently control the geometry and function of each layer enables the development of multifunctional metaoptics in which two or more optical properties are independently designed. As a proof of concept, we demonstrate multiwavelength holograms, multiwavelength waveplates, and polarization-insensitive 3D holograms based on phase and amplitude masks. The proposed architecture opens a new avenue for designing complex flat optics with a wide variety of functionalities.
Similar content being viewed by others
Introduction
Optical metasurfaces are planar nanostructured devices that provide versatile platforms for manipulating the wavefront of light with subwavelength resolution1,2. Several configurations have been demonstrated for controlling the amplitude3,4,5, phase1,6,7, and polarization8,9 of light. Due to their thin form factor and compatibility with integrated circuit fabrication, metasurface lenses10,11, beam splitters12,13, and waveplates8,9 could be attractive replacements for conventional optical elements in certain applications. While success has been achieved in thickness reduction relative to traditional refractive elements, designing metasurfaces with independent control over phase, amplitude, and polarization remains a challenge. It is also desirable to control these properties over broad bandwidths or at multiple wavelengths. While complete control over phase and polarization at a particular wavelength has been demonstrated14, independent control of phase and amplitude15,16,17,18 has been achieved only at the expense of a polarization-dependent response. Several approaches have been investigated to achieve multiwavelength phase control using spatially multiplexed resonators19,20,21,22,23,24, but this generally leads to efficiency degradation due to space filling limitations and resonator cross-talk. Ultimately, the limited design freedom associated with a single resonator layer imposes limits on device functionality.
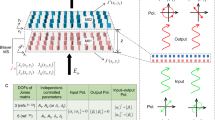
In this work, we explore a bilayer metasurface architecture with the goal of increasing the design space for metaoptics. We have previously used this architecture to realize multiwavelength lenses using layers composed solely of nanopost resonators25. Here, we use bilayers that comprise various combinations of nanoposts, nanodisks, and rectangular nanopillars to increase the available design space. In this approach, each unique unit cell geometry provides a unique design freedom, and when combined, these geometries enable independent control over any two of the following three properties: amplitude, phase, and polarization. The proposed approach also enables any one of these properties to be independently controlled at two different wavelengths. This freedom is used to realize metaoptics with a wide range of functionalities, including multiwavelength holograms, multiwavelength waveplates, and 3D holograms.
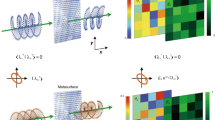
A schematic of our general approach is shown in Fig. 1. We start with independent control of the phase at two different wavelengths, which is achieved by using nanopost unit cells in both layers (Fig. 1a). The nanopost unit cell enables 2π phase coverage while maintaining high transmission, which, in the bilayer format, can be used to encode independent phase-only holograms at two different wavelengths. Independent control of the polarization at two different wavelengths can be achieved by utilizing polarization-sensitive resonators in both layers (Fig. 1b). This combination can be used to design independent waveplates operating at each wavelength. Finally, the design space can be further enlarged by using two dissimilar resonator geometries. For instance, independent phase and amplitude control can be achieved by combining a nanopost geometry for phase control and a strongly resonant nanodisk geometry for amplitude control, as shown in Fig. 1c. While previous phase-only meta-holograms have suffered from speckle noise and a limited depth of focus, such amplitude and phase holograms enable clearer 2D, as well as 3D, holograms. Furthermore, the use of bilayer metasurfaces enables amplitude and phase control that is independent of the polarization, unlike in single-layer designs, whose operation is restricted to circularly polarized light of a particular handedness15,16,17. We believe that the increased engineering freedom provided by bilayer metasurfaces will open new avenues for the development of a wide range of planar multifunctional metaoptics.
a Illustration of a multiwavelength hologram. The metasurface is designed to achieve independent phase modulation at two wavelengths. b Illustration of a multiwavelength waveplate using a combination of two polarization-sensitive rectangular nanopillar geometries. The bilayer metasurface functions as a half-wave plate and a quarter-wave plate at two different, and independent, wavelengths. c Schematic of a metaoptic for producing a 3D hologram with on-axis evolution. The bilayer metasurface comprises nanodisks and nanoposts to enable polarization-insensitive control over both amplitude and phase
Results
Metaoptics for multiwavelength phase control
The proposed bilayer metasurfaces for multiwavelength phase control are based on high-contrast transmit arrays made of silicon (Si) nanoposts with a high aspect ratio. The nanoposts, which can be modeled as truncated waveguides, serve as ideal building blocks for phase modulation due to their high transmission efficiency, localized resonances, and low sensitivity to the angle of incidence10. To begin, we explore multiwavelength phase control by cascading two layers of cylindrical nanoposts while keeping them uncoupled in the vertical direction. Figure 2a shows a schematic of the corresponding unit cell embedded in a layer of polydimethylsiloxane (PDMS). The independent variation of the nanopost radii (r1 and r2) in each layer provides independent phase control at two different illumination wavelengths. Here, we have arbitrarily selected working wavelengths of 1180 and 1680 nm. The height of the Si nanoposts is 750 nm, and they are arranged in a square lattice with a period of 600 nm. To mitigate wavefront divergence between the layers, the nanoposts are placed in close proximity along the z direction but remain uncoupled (Fig. S1), such that the transmission coefficient of the bilayer can be assumed to be the product of the transmission coefficients (t1 and t2) of each individual layer. The independent control of the radii in each layer allows one to independently specify the spatial phase profile at each wavelength. Figure 2b and c show the required radii in layer 1 (r1) and layer 2 (r2), along with the corresponding transmission values (Fig. 2d and e), for achieving all combinations of ϕ(λ1) (the phase at 1180 nm) and ϕ(λ2) (the phase at 1680 nm); the deviation between the designed and ideal phases is presented in Fig. S2. These design plots can be used to quickly select the structural parameters of each layer to achieve arbitrary and independent phase profiles at the two wavelengths of interest.
a Schematic of a bilayer metasurface unit cell consisting of amorphous silicon nanoposts vertically stacked in close proximity. The nanoposts have a height of 750 nm and are arranged in a square lattice with a period of 600 nm and embedded in a PDMS layer. The transmission coefficient (t) of the bilayer is calculated as the product of the transmission coefficients of each individual layer (t1 and t2). b, c Design plots showing the corresponding radii in layer 1 (r1) and layer 2 (r2), as indicated by the color bars, for achieving all possible combinations of ϕ(λ1) (the phase at 1180 nm) and ϕ(λ2) (the phase at 1680 nm). d, e Corresponding transmission values (|t1t2|2) at 1180 nm d and 1680 nm e
We have previously used this architecture to realize multiwavelength lenses25; here, we extend the approach to the more arbitrary phase profiles found in holograms. A phase-only low-k hologram consisting of two different Vanderbilt University logos projected at the wavelengths of 1180 and 1680 nm (Fig. 3b) has been designed using the Gerchberg–Saxton algorithm26. The holographic metasurface has a size of 500 μm, and the images are designed to be displayed in the Fraunhofer region (see the design details in Supplementary Section 1). The fabrication involved traditional lithography and etching followed by metasurface transfer and bonding. A schematic illustration of the fabrication flowchart is shown in Fig. 3a. The first layer of the metasurface was defined using electron beam lithography (EBL) and reactive ion etching (RIE) followed by encapsulation in a thin layer of diluted PDMS to allow close stacking of the second layer. The nanostructures of the second layer were created on a 300 nm-thick germanium (Ge) sacrificial layer using the same procedures used for the first layer, followed by release through wet etching of the Ge layer. The second layer was then aligned and bonded to the first layer using a 2D material transfer tool. The details of the fabrication and alignment setups are presented in Supplementary Sections 2 and 3 and Supplementary Fig. S3. Figure 3c shows a scanning electron microscope (SEM) image of the Si nanoposts after RIE. Optical images of the metasurface doublet and the alignment marks in each layer (inset) are shown in Fig. 3d. Both layers are clearly visible under a ×20 optical microscope, indicating a separation smaller than the focal depth of the objective, which is 5.8 μm.
a Schematic illustration of the fabrication steps. The first layer of Si nanostructures was defined on a silica substrate and embedded in a thin layer of PDMS. The second layer was transferred into PDMS and bonded with the first layer. b Schematic of the bilayer hologram consisting of two independent Vanderbilt logos projected at two independent wavelengths. c SEM image of the Si nanoposts before PDMS spin coating. d Optical images of the bonded metaoptic and the alignment marks in each layer (inset). e, f Simulated e and captured f images produced under illumination wavelengths of 1180 and 1680 nm
The metasurface was characterized using an unpolarized supercontinuum laser that was passed through a monochromator. To reduce the beam diameter, a lens (f = 200 mm) was used to partially focus the beam onto the sample, and the images produced by the metasurface were directly recorded on a near-infrared camera (for the details of the optical systems, see the “Methods” section and Supplementary Fig. S4). To evaluate the design, the transmission of the bilayer metasurface was calculated as a direct product of the designed transmission through each individual layer. The simulated far-field images are shown in Fig. 3e. The absence of unwanted diffraction orders indicates excellent multiwavelength phase coverage. The measured images are presented in Fig. 3f, showing good agreement with the simulations and an absence of twin images, such as those observed in previous work on multiwavelength holograms21,22 based on spatially multiplexed metasurfaces. The intense spots in the center are primarily due to the beam overfilling the metasurface, which results in additional zero-order diffraction. The reduced image quality compared with the simulations is attributed to the lateral misalignment of the layers, which is estimated to be 3 μm (see Supplementary Fig. S5). The misalignment tolerance is expected to be improved by employing a larger holographic metasurface, under the assumption of the same maximum diffraction angles.
While it is difficult to gauge the hologram efficiency due to the prohibitively large simulation domain and the beam overfilling in the experiment, we can quantify the diffraction efficiency of similar devices. To accomplish this, a wavelength-multiplexed grating was designed to deflect incident light at 1180 and 1680 nm to −15° and 15°, respectively. The grating has a size of 200 μm, and the metasurfaces are separated by 3 μm (for the details of the simulation, see the Supplementary Methods and Supplementary Fig. S6). The device was simulated using a finite-difference time-domain (FDTD) solver (MEEP)27, and the absolute efficiency was calculated as the ratio of the power diffracted into the desired order over the total power incident on the device. The calculated transmission is 81.4% at 1180 nm and 83% at 1680 nm, and the relative diffraction efficiencies are 59% at 1180 nm and 61% at 1680 nm, resulting in absolute efficiencies of 48.1% and 50.3% at 1180 and 1680 nm, respectively. These efficiencies are consistent with the theoretical and experimental efficiencies of multilayer metalenses25 based on the same architecture.
Metaoptics for multiwavelength polarization control
The proposed approach can be further extended to achieve independent polarization conversion at multiple wavelengths. To achieve this, polarization-sensitive rectangular nanopillars were selected because their length and width can be independently tuned to achieve polarization-dependent phase retardance. As a proof of concept, we designed a bilayer metasurface that functions as a half-wave plate at a wavelength of 1200 nm and a quarter-wave plate at 1600 nm. Figure 4a shows a schematic of the unit cell of this metasurface. The resonators are oriented at a 45° rotation, and the length and width (u, v) are designed to be (400, 280) and (320, 200) nm for each layer, resulting in phase retardances between the long and short axes of π and π/2 for the wavelengths of 1200 and 1600 nm, respectively. Figure 4b and c show the simulated transmission and phase retardances, respectively, at 1200 nm. The metaoptic has a polarization conversion efficiency (\(\left| {t_{xy}} \right|^2\)) of over 80% and a phase retardance of π between wavelengths of 1180 and 1230 nm. Figure 4d and e show the simulated transmission amplitudes and phases, respectively, at 1600 nm for the x and y polarizations. At 1616 nm, we observe a transmission of 47.5% for both polarizations while maintaining a π/2 phase difference, resulting in conversion from linearly to circularly polarized light with 95% efficiency. To numerically determine the polarization state, we extracted the ellipticity, tan(χ), by calculating the Stokes parameters (for the details of the calculation, see the “Methods” section), revealing an ellipticity of larger than 0.8 from 1565 to 1670 nm (Fig. 4d). While this functionality could have been achieved using an unstructured material with substantial dispersion, the true advantage of the proposed approach is that any combination of waveplates can be readily realized by modifying the widths and lengths of the nanopillars in each layer. To illustrate this freedom, we present a design graph for achieving all combinations of half-wave and quarter-wave plates at the wavelengths of 1200 and 1600 nm in Fig. 4f (additional details regarding the transmission and ellipticity can be found in Supplementary Fig. S7).
a Schematic of the rectangular nanopillar unit cell. The metasurface is designed to function as a half-wave plate and a quarter-wave plate at 1200 and 1600 nm, respectively. The resonators have a height of 750 nm and are arranged in a square lattice and oriented at 45° with respect to the x-axis. The lengths and widths (u, v) are (400, 280) and (320, 200) in the bottom and top layers, respectively. b, c Simulated transmission profiles for the x and y polarizations b and phase delays for the short and long axes c at wavelengths near 1200 nm. d, e Simulated transmission amplitude and ellipticity (tan(χ)) profiles d and phases e for the x and y polarizations at wavelengths near 1600 nm. f Design graph for achieving all combinations of waveplates at the two considered wavelengths. The x and y axes correspond to the half-wave and quarter-wave plate cases at 1200 and 1600 nm, respectively, and the colors represent the designed nanopillar widths and lengths, as indicated in the legend on the right
Metaoptics for polarization-insensitive phase and amplitude control
Finally, we explore the use of the proposed bilayer architecture to achieve complete control over amplitude and phase. In the past amplitude and phase meta-holography, amplitude modulation has been achieved through polarization conversion15,16,17, resulting in an efficiency loss due to polarization sensitivity. Here, we use a bilayer metasurface composed of polarization-insensitive elements for phase and amplitude modulation. Wavefront control is achieved by assigning phase modulation to one layer and amplitude modulation to the other. Amplitude modulation is achieved by utilizing Si nanodisks that support fundamental Mie resonances at the wavelength of operation, and the spectral positions of the resonances can be adjusted by changing the nanodisk radius. In previous work, similar resonators have been used to achieve Huygens surfaces28, perfect reflectors29, and polarizing beam splitters13. Here, we have designed the nanodisks to operate near the magnetic dipole resonance, with a transmission amplitude that is controlled by tuning the structures to work either at or away from the resonance. A schematic of the unit cell is shown in Fig. 5a; the nanodisks have a height and period of 440 and 600 nm, respectively. Figure 5b shows the transmission amplitude and phase as functions of the nanodisk radius at a wavelength of 1400 nm, demonstrating 100% amplitude modulation along with a phase change of π. The second layer is used to implement the designed phase functions by means of cylindrical nanoposts with a larger aspect ratio than that of the nanodisks. Figure 5c shows a schematic of the second-layer unit cell, which is used for phase modulation. The nanoposts have a height of 750 nm and a period of 600 nm, and the corresponding transmission amplitude and phase as functions of the nanopost radius are presented in Fig. 5d. The transmission dips highlighted in gray were excluded from the design database, resulting in 2π phase coverage and an average transmission of 96%.
a Schematic of the Si nanodisk that serves as the unit cell for the bottom layer. The disks have a height of h1 = 440 nm and are arranged in a square lattice with a period of P = 600 nm. b Simulated transmission amplitude \(\left| {t_1} \right|\) and phase \(\angle t_1\) as functions of the disk radius. c Schematic of the nanopost that serves as the unit cell for the second layer. The nanoposts have a height of h2 = 750 nm. d Simulated transmission amplitude \(\left| {t_2} \right|\) and phase \(\angle t_2\) as functions of the post radius. e Schematic of the bilayer metasurface. The bottom layer is used for amplitude modulation (\(\left| t \right|\)), and the top layer is used for phase modulation \((\angle t_2)\). The total phase profile of the bilayer metasurface is \(\angle t_1 + \angle t_2.\) f, g, h Designed phase pattern f, along with an optical microscope image g and an SEM image h of the top metasurface. i The designed amplitude profile. j, k Optical j and SEM k images of the bottom metasurface. All phases and amplitudes are calculated for λ = 1400 nm
As a proof of concept, we designed a 3D hologram (600 μm × 600 μm) to display a clock evolving along the z-axis. The design of the holographic plate involves three types of 3D holograms. The two hands of the clock are designed to rotate in opposite directions with different angular speeds along the z-axis, while the outer frame remains in focus over an extended depth of view (for the details of the hologram design, see Supplementary Section 1). Figure 5f–h show the designed phase profile (Fig. 5f) along with corresponding optical (Fig. 5g) and SEM (Fig. 5h) images of the nanopost metasurface. The designed amplitude profile is presented in Fig. 5i. Optical and SEM images of the fabricated metasurface are shown in Fig. 5j and k, respectively. The optical images illustrate the substantial difference between the two metasurfaces and indicate that the global distribution of the unit cells is correct. Note that the nanodisks (layer 1) used for amplitude modulation also introduce a phase shift, and thus, the phase profile of the nanopost layer (layer 2) is designed to compensate for this variation.
Discussion
Figure 6a shows the simulated on-axis evolution of the hologram from z = 0.9 mm to z = 2.7 mm based on the designed phase and amplitude patterns from Fig. 5f and i. To determine the performance of the fabricated device, the metasurface was characterized using a collimated and unpolarized monochromatic beam. The incident wavelength was tuned slightly to 1330 nm to achieve the best performance, and image slices were recorded at various distances using a ×20 objective paired with a tube lens (f = 200 mm). The real images acquired at the various on-axis planes are presented in Fig. 6b and show good agreement with the simulation. It should be noted that the intensity maps have been slightly saturated to reveal clear outlines in the images. The lower contrast and resolution in the measured images are mainly due to the strong structural sensitivity of the nanodisk layer, resulting in errors in the amplitude mask, as illustrated in Fig. S8. To illustrate the role of misalignment, we also realized 3D holograms based on two layers of waveguide-based nanopillars (Fig. S10), which permit polarization-sensitive amplitude and phase control (see Fig. S10 for details). In this case, the structural sensitivity is quite low, and as a result, the far-field images (Fig. S10n) show an absence of background noise and good agreement with the simulation. While better control over the nanodisk size should alleviate the background noise, high-resolution polarization-independent greyscale transmission masks can also be achieved using high-energy beam-sensitive (HEBS) glass30,31.
In conclusion, we have demonstrated a bilayer metasurface architecture with various combinations of unit cells to increase the available design space for metaoptics. This approach can be further extended using other sets of unit cell geometries to achieve independent control over other combinations of properties, as demonstrated in Supplementary Figs. S9 and S10. Metasurfaces sensitive to the angle of incidence32 could also be incorporated into the platform for applications, such as holographic storage and augmented reality displays. While we have combined independent metasurfaces here, the proposed fabrication techniques can also be utilized to prepare more complex metaoptics with interacting layers, including topology-optimized devices33 and bianisotropic metasurfaces34,35. Further improvements in performance are also expected if design optimization methods36,37,38,39 are employed.
Materials and methods
Simulation
The transmission coefficient of the array of Si nanoposts was determined using an open-source rigorous coupled-wave analysis (RCWA) solver40. The nanoposts, with a height of 750 nm, were arranged in a square lattice with a lattice constant of 600 nm and embedded in a layer of PDMS. The index of the PDMS was set to 1.4, and the refractive index values of the Si (3.55 and 3.47 at 1180 and 1680 nm, respectively) were obtained using ellipsometry. The complex transmission coefficient was calculated using a plane wave at normal incidence, and nanopost radii that corresponded to dips in transmission were excluded from the design database. The same method was used to obtain the transmission coefficients of nanodisks and rectangular nanopillars. The details of the hologram design are presented in Supplementary Section 1.
Ellipticity calculation
The polarization state of the quarter-wave plate was numerically determined by using the Stokes parameters:
where txx and txy are the transmission coefficients for copolarization and cross polarization, respectively, and Δφ is their phase difference, \(\angle t_{xy} - \angle t_{xx}\). The ellipticity χ can be expressed in terms of the Stokes parameters as follows: \(\sin \left( {2\chi } \right) = \frac{{S_3}}{{S_0}}\).
Measurement
The multiwavelength hologram was characterized using the setup shown in Fig. S4a. The samples were illuminated using a collimated supercontinuum laser (Fianium WhiteLase) that was passed through a monochromator (CornerstoneTM 130 1/8 m). To reduce the beam size, a lens (AC254-200-C-ML, f = 200 mm) was placed in front of the device to partially focus the light. The far-field hologram images were recorded using an InGaAs NIR camera (Xeva-1.7-640).
The 3D clock hologram was characterized using a custom imaging system with a ×20 objective (Mitutoyo Plan Apo, NA = 0.4) paired with a tube lens (f = 200 mm). The device was mounted on a translation stage and moved along the axial direction to measure the on-axis evolution of the hologram, as shown in Fig. 6b. A schematic of the characterization system is shown in Fig. S4.
References
Yu, N. F. et al. Light propagation with phase discontinuities: generalized laws of reflection and refraction. Science 334, 333–337 (2011).
Yu, N. F. & Capasso, F. Flat optics with designer metasurfaces. Nat. Mater. 13, 139–150 (2014).
Walther, B. et al. Spatial and spectral light shaping with metamaterials. Adv. Mater. 24, 6300–6304 (2012).
Butt, H. et al. Carbon nanotube based high resolution holograms. Adv. Mater. 24, OP331–OP336 (2012).
Huang, K. et al. Ultrahigh-capacity non-periodic photon sieves operating in visible light. Nat. Commun. 6, 7059 (2015).
Chong, K. E. et al. Polarization-independent silicon metadevices for efficient optical wavefront control. Nano Lett. 15, 5369–5374 (2015).
Wang, L. et al. Grayscale transparent metasurface holograms. Optica 3, 1504–1505 (2016).
Kruk, S. et al. Broadband highly efficient dielectric metadevices for polarization control. APL Photon. 1, 030801 (2016).
Yu, N. F. et al. A broadband, background-free quarter-wave plate based on plasmonic metasurfaces. Nano Lett. 12, 6328–6333 (2012).
Arbabi, A. et al. Subwavelength-thick lenses with high numerical apertures and large efficiency based on high-contrast transmitarrays. Nat. Commun. 6, 7069 (2015).
Khorasaninejad, M. et al. Metalenses at visible wavelengths: diffraction-limited focusing and subwavelength resolution imaging. Science 352, 1190–1194 (2016).
Khorasaninejad, M. et al. Efficient polarization beam splitter pixels based on a dielectric metasurface. Optica 2, 376–382 (2015).
Slovick, B. A. et al. Metasurface polarization splitter. Proc. R. Soc. A 375, 20160072 (2017).
Arbabi, A. et al. Dielectric metasurfaces for complete control of phase and polarization with subwavelength spatial resolution and high transmission. Nat. Nanotechnol. 10, 937–943 (2014).
Overvig, A. C. et al. Dielectric metasurfaces for complete and independent control of optical amplitude and phase. Preprint at https://arxiv.org/pdf/1903.00578.pdf (2019).
Song, X. et al. Selective diffraction with complex amplitude modulation by dielectric metasurfaces. Adv. Opt. Mater. 6, 1701181 (2018).
Lee, G. Y. et al. Complete amplitude and phase control of light using broadband holographic metasurfaces. Nanoscale 10, 4237–4245 (2018).
Wang, Q. et al. All-dielectric meta-holograms with holographic images transforming longitudinally. ACS Photon. 5, 599–606 (2018).
Arbabi, E. et al. Multiwavelength metasurfaces through spatial multiplexing. Sci. Rep. 6, 32803 (2016).
Arbabi, E. et al. Multiwavelength polarization-insensitive lenses based on dielectric metasurfaces with meta-molecules. Optica 3, 628–633 (2016).
Huang, Y. W. et al. Aluminum plasmonic multicolor meta-Hologram. Nano Lett. 15, 3122–3127 (2015).
Wan, W., Gao, J. & Yang, X. D. Full-color plasmonic metasurface holograms. ACS Nano 10, 10671–10680 (2016).
Lin, D. M. et al. Photonic multitasking interleaved Si nanoantenna phased array. Nano Lett. 16, 7671–7676 (2016).
Wang, B. et al. Visible-frequency dielectric metasurfaces for multiwavelength achromatic and highly dispersive holograms. Nano Lett. 16, 5235–5240 (2016).
Zhou, Y. et al. Multilayer noninteracting dielectric metasurfaces for multiwavelength metaoptics. Nano Lett. 18, 7529–7537 (2018).
Gerchberg, R. W. & Saxton, W. O. A practical algorithm for the determination of phase from image and diffraction plane pictures. Optik 35, 237–246 (1972).
Oskooi, A. F. et al. MEEP: a flexible free-software package for electromagnetic simulations by the FDTD method. Comput. Phys. Commun. 181, 687–702 (2010).
Decker, M. et al. High-efficiency light-wave control with all-dielectric optical Huygens’ metasurfaces. Adv. Opt. Mater. 3, 813–820 (2014).
Moitra, P. et al. Experimental demonstration of a broadband all-dielectric metamaterial perfect reflector. Appl. Phys. Lett. 104, 171102 (2014).
Kovalskyy, A. P. et al. Chalcogenide glass e-beam and photoresists for ultrathin grayscale patterning. J. Micro/Nanolithogr. MEMS MOEMS 8, 043012 (2009).
Kley, E. B. et al. Adapting existing e-beam writers to write HEBS-glass gray-scale masks. In Proc. SPIE 3633, Diffractive and Holographic Technologies, Systems, and Spatial Light Modulators VI, 35–45 (SPIE, San Jose, CA, United States, 1999). https://www.spiedigitallibrary.org/conference-proceedings-of-spie/3633/1/Adapting-existing-e-beam-writers-towrite-HEBS-glass-gray/10.1117/12.349333.full.
Kamali, S. M. et al. Angle-multiplexed metasurfaces: encoding independent wavefronts in a single metasurface under different illumination angles. Phys. Rev. X 7, 041056 (2017).
Lin, Z. et al. Topology-optimized multilayered metaoptics. Phys. Rev. Appl. 9, 044030 (2018).
Pfeiffer, C. et al. High performance bianisotropic metasurfaces: asymmetric transmission of light. Phys. Rev. Lett. 113, 023902 (2014).
Pfeiffer, C. & Grbic, A. Bianisotropic metasurfaces for optimal polarization control: analysis and synthesis. Phys. Rev. Appl. 2, 044011 (2014).
Molesky, S. et al. Inverse design in nanophotonics. Nat. Photon. 12, 659–670 (2018).
Jensen, J. S. & Sigmund, O. Topology optimization for nano-photonics. Laser Photon. Rev. 5, 308–321 (2011).
Callewaert, F. et al. Inverse-designed broadband all-dielectric electromagnetic metadevices. Sci. Rep. 8, 1358 (2018).
Han, A. L. et al. Inverse design of optical elements based on arrays of dielectric spheres. Appl. Opt. 57, 1437–1446 (2018).
Liu, V. & Fan, S. H. S4: A free electromagnetic solver for layered periodic structures. Comput. Phys. Commun. 183, 2233–2244 (2012).
Acknowledgements
Y.Z., H.Z., and J.V. acknowledge support received from the Office of Naval Research under award N00014-18-1-2563 and from the National Science Foundation under award ECCS-1351334. H.W. and G.G. acknowledge support received from the National Science Foundation under award DMR-1410940. Part of the fabrication process was conducted at the Center for Nanophase Materials Sciences, which is a DOE Office of Science User Facility.
Authors’ contributions
Y.Z. performed the design, fabrication, and characterization of the metasurfaces. I.I.K. performed the materials growth procedures and patterned the metasurfaces. H.W. and G.G. assisted in metasurface alignment and bonding. H.Z. assisted in the reactive ion etching and imaging of the metasurfaces. J.V. helped develop the ideas and concepts presented here and assisted in writing the manuscript.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhou, Y., Kravchenko, I.I., Wang, H. et al. Multifunctional metaoptics based on bilayer metasurfaces. Light Sci Appl 8, 80 (2019). https://doi.org/10.1038/s41377-019-0193-3
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41377-019-0193-3
This article is cited by
-
Acetylene/argon mixture plasma to build ultrathin carbon bridge of CFx/C/MnO2 for high-rate lithium primary battery
Rare Metals (2024)
-
Scattering exceptional point in the visible
Light: Science & Applications (2023)
-
Integrated metasurfaces for re-envisioning a near-future disruptive optical platform
Light: Science & Applications (2023)
-
Polychromatic full-polarization control in mid-infrared light
Light: Science & Applications (2023)
-
Advances in optical metalenses
Nature Photonics (2023)