Abstract
Implicit summation is a technique for the conversion of sums over intermediate states in multiphoton absorption and the high-order susceptibility in hydrogen into simple integrals. Here, we derive the equivalent technique for hydrogenic impurities in multi-valley semiconductors. While the absorption has useful applications, it is primarily a loss process; conversely, the non-linear susceptibility is a crucial parameter for active photonic devices. For Si:P, we predict the hyperpolarizability ranges from χ(3)/n3D = 2.9 to 580 × 10−38 m5/V2 depending on the frequency, even while avoiding resonance. Using samples of a reasonable density, n3D, and thickness, L, to produce third-harmonic generation at 9 THz, a frequency that is difficult to produce with existing solid-state sources, we predict that χ(3) should exceed that of bulk InSb and χ(3)L should exceed that of graphene and resonantly enhanced quantum wells.
Similar content being viewed by others
Introduction
Multiphoton absorption requires a high intensity, and was first observed shortly after the invention of the laser using impurities in solids1 and alkali vapor2. Although multiphoton absorption is useful for metrology and modulators, and can be enhanced where there is near-resonance of an intermediate state as in the case of Rb3, it is essentially a loss process contributing an imaginary part to the non-linear susceptibility. The corresponding real part is responsible for a great variety of wavelength conversion processes such as harmonic generation, first observed in quartz4 and later in atomic vapors5 including alkalies6. THz multiphoton absorption has been shown to be very large in hydrogenic shallow impurities in semiconductors, even without intermediate state resonances7, due to the large dielectric screening and low effective mass. Here, we predict giant values for the real part of the THz non-linear susceptibility for doped silicon and germanium. This finding opens access to novel applications for these materials in THz photonics. For example, tripling the output of a 2–4 THz quantum cascade laser through third-harmonic generation would fill the frequency gap currently only filled by larger, more expensive systems. We show that a good efficiency can be obtained for third-harmonic generation with doped silicon and germanium. Our theory can be readily applied to any donor in any semiconductor host where the effective mass approximation is valid, and our discussion makes it clear that a giant value of χ(3) is expected for donors with a small binding energy in a host with a large dielectric constant and small effective mass.
The theory developed in this paper is appropriate for frequencies both near to and far from loss-inducing resonances, including the effects of effective mass anisotropy, multi-valley interactions and the central cell correction. The method could easily be applied to other systems with complicated potentials, such as multi-quantum wells. Although this work focuses on perturbative harmonic generation, we anticipate that shallow impurities may also be useful for non-perturbative high-harmonic generation (HHG)8,9 taking advantage of the excellent control over the carrier-envelope phase of few-cycle pulses in this THz regime, which can be used to enhance HHG10.
Results
The implicit summation technique
From Nth-order perturbation theory7,11 the N-photon absorption (NPA) transition rate may be written as
where \(I_a = E_H^2/\hbar a_B^2\), aB is the Bohr radius, EH the Hartree energy, and αfs the fine structure constant. M(N) is a dimensionless transition matrix element, and Im is the intensity of the light in the medium with relative dielectric permittivity εr. The lineshape function Γ(N)(ω) has unit area. For silicon and germanium donors, the factors inside the bracket are renormalized, and of particular importance here Ia is ten orders of magnitude smaller for silicon than it is for hydrogen. This is apparent from the formulae of the Hartree energy and Bohr radius for donors in these materials: \(E_H = m_t(e^2/4\pi \epsilon _0\varepsilon_r \hbar )^2\), and \(a_B = 4\pi \epsilon _0\varepsilon_r \hbar ^2/m_te^2\), where mt is the transverse effective mass and \(\varepsilon_r\) the dielectric constant12. Both germanium and silicon have a small mt and large \(\varepsilon_r\), raising the Bohr radius and lowering the binding energy. The wavefunction is therefore significantly larger than that of alkali atoms, leading to an enhanced dipole matrix element and hence a substantially stronger interaction with light.
The details of the spectrum given by Eq. (1) are controlled by M(N), which is influenced in silicon by the indirect valley structure, the anisotropic effective mass, and the donor central cell correction potential. Our main aim here is to calculate these effects. For single-photon absorption (N = 1) between states |ψg〉 (the ground state) and |ψe〉 (the excited state), \(M^{(1)} = \left\langle {\psi _e\left| {{\boldsymbol{\epsilon }}.{\boldsymbol{r}}} \right|\psi _g} \right\rangle /a_B\), where \({\bf{\epsilon }}\) is a unit vector in the polarization direction, and Eq. (1) reduces to Fermi’s golden rule. For two-photon absorption,
in the E.r gauge, which may be written as M(2) = 〈ψe|ζG1ζ|ψg〉 where \(\zeta = {\boldsymbol{\epsilon }}.{\boldsymbol{r}}/a_B\),
and ω = ωeg/N. The states |j〉 are intermediate states, and along with |ψe〉 & |ψg〉 they are eigenstates of \(H\left| j \right\rangle = \hbar \omega _j\left| j \right\rangle\), where H is the Hamiltonian in the dark. For general multiphoton absorption,
The summation in Eq. (2) can be avoided11 by noticing that (H − Wn)Gn = EH, where Wn = ℏωg + nℏω, and ω = ωeg/N as already mentioned, and by using the completeness relation \(\mathop {\sum}\nolimits_j {\left| j \right\rangle \left\langle j \right|} = 1\). In other words,
Rewriting Eq. (3), M(N) = 〈ψe|ζ|ψN−1〉 where |ψ0〉 = |ψg〉 and |ψn〉 is the solution of the partial differential equation (PDE) \(G_n^{ - 1}\left| {\psi _n} \right\rangle = \zeta \left| {\psi _{n - 1}} \right\rangle\). Instead of finding M(N) by repeated application of Eq. (2), which requires infinite sums (that might be reduced down to a few terms if there are obvious resonances), we may now use Eq. (4) and the PDE at each stage, which can be simpler.
The Nth-order susceptibility far from any multiphoton resonances may also be calculated using the Nth-order perturbation theory13. For example, the “resonant” term in the third-order susceptibility, χ(3)(3ω), is
where e is the electron charge, and n3D is the concentration. χ(3) may be written in a similar form to Eqs (1) and (3), and for Nth order,
where C(N) = 〈ψg|ζGN…G2ζG1ζ|ψg〉 is a dimensionless matrix element that may be found in a similar way to M(N), either by repeated application of Eq. (2)—as has been done previously for alkali metal vapors6—or by using the implicit summation method of Eq. (4) with the only difference being ω ≠ ωeg/N. The antiresonant terms13 and other non-linear processes, such as sum-frequency generation, can be calculated with simple modifications to Wn at each step.
Multi-valley theory for donors in silicon and germanium
In this section, we develop the multi-valley theory for the nonlinear optical processes of donors based on the effective mass approximation (EMA). For simplicity of presentation, we describe the derivation for silicon; the case of germanium is discussed in the Supplementary Materials. It will become apparent that our theory is readily applicable to any donor in any host as long as the EMA is reliable.
To apply the method to donors, we require |ψg〉, ωg, |ψe〉, ωe and H|ψn〉. Silicon and germanium are indirect with equivalent conduction band minima (valleys) near the Brillouin zone edge; each minimum is characterized by a Fermi surface that is a prolate ellipsoid with transverse & longitudinal effective masses, mt,l. According to the Kohn-Luttinger effective mass approximation14, the state |ψj〉 of a shallow donor can be decomposed into slowly varying hydrogenic envelope functions, one for each valley, modulated by plane-wave functions corresponding to the crystal momenta at the minima, kμ (and a lattice periodic function that is unimportant here). We write \(\psi _j({\boldsymbol{r}}) = \mathop {\sum}\nolimits_\mu {e^{i{\boldsymbol{k}}_\mu .{\boldsymbol{r}}}F_{j,\mu }({\boldsymbol{r}})}\) where Fj,μ(r) is the slowly varying envelope function. We have neglected the lattice periodic part, uμ(r), of the Bloch functions for the simplicity of presentation. A rigorous derivation with uμ(r) included is provided in the Supplementary Materials, but it does not lead to any change in the final equations for the envelope functions (Eqs (7) and (8) below).
We separate the potential into the slowly varying Coulomb term of the donor V(r), and a rapidly varying term due to the quantum defect that is short range, U(r), referred to as the central cell correction (CCC). Within the EMA, the kinetic energy term in the Hamiltonian operates only on the envelope function, and the EMA Schrodinger equation may be written as
where H0 includes the Coulomb potential V(r): \(E_H^{ - 1}H_0 = - \frac{1}{2}a_B^2\left[ {\partial _x^2 + \partial _y^2 + \gamma \partial _z^2} \right] - a_Br^{ - 1}\) using a valley-specific coordinate system (x, y, z where z is the valley axis, i.e., the valley-frame is rotated relative to the lab-frame of x1, x2, x3). The kinetic energy has cylindrical symmetry because γ = mt/ml ≠ 1, and V(r) and U(r) are spherical and tetrahedral respectively. H0 produces wave functions that are approximately hydrogen-like, and U(r) mixes them to produce states that transform as the A1, E and T2 components of the Td point group.
We take U(r) to be very short range, and we neglect the small change in the envelope functions over the short length scale 2π/|kμ|. Premultiplying Eq. (6) by \(e^{ - i{\boldsymbol{k}}_{\mu \prime }.{\boldsymbol{r}}}\) and averaging over a volume (2π/|kμ|)3 around r, the Schrodinger eqn now reads \(\left[ {H_0 - \hbar \omega _j} \right]F_{j,\mu }({\boldsymbol{r}}) + \mathop {\sum}\nolimits_{\mu \prime } {U_{\mu \mu \prime }\delta ({\boldsymbol{r}})F_{j,\mu \prime }({\boldsymbol{r}})} = 0\), where δ(r) is the Dirac delta function, and \(U_{\mu \mu \prime } = {\int} {d{\boldsymbol{r}}{\kern 1pt} e^{i({\boldsymbol{k}}_{\mu \prime } - {\boldsymbol{k}}_\mu ).{\boldsymbol{r}}}U({\boldsymbol{r}})}\). For an A1 state, all the envelope functions have the same amplitude at r = 0, hence, \(\mathop {\sum}\nolimits_{\mu \prime } {U_{\mu \mu \prime }\delta ({\boldsymbol{r}})F_{j,\mu \prime }({\boldsymbol{r}})} = - U_{cc}\delta ({\boldsymbol{r}})F_{j,\mu }({\boldsymbol{r}})\), where \(U_{cc} = - \mathop {\sum}\nolimits_{\mu \prime } {U_{\mu \mu \prime }}\). It is found experimentally that for E and T2 states, the CCC has a rather small effect, and so we neglect it. Since H0 has cylindrical symmetry, the component of angular momentum about the valley axis is a conserved quantity, i.e., Fj,μ(r) = eimϕfj,m,μ(r, θ), where m is a good quantum number, and now fj,m,μ is a 2D function only. Substituting into the Schrodinger eqn, premultiplying by e−im′ϕ and finally integrating over ϕ, the eigenproblems are
where \(H_0^{(m)} = H_0 + E_Ha_B^2m^2\)/2(r sin θ)2. We solve Eq. (7) using a 2D finite element method (FEM) (see Supplementary Materials).
We focus on silicon, in which case the valley index, μ, runs over (±1, ±2, ±3), where 1, 2, 3 are the three crystal axes, and we let the light be polarized along a crystal axis, x1, by way of illustration; the calculation for germanium and other polarization directions is described in the Supplementary Materials. For the μ = ±1, ±2, ±3 valleys, aBζμ = z, x, y = r cos θ, r sin θ cos ϕ, r sin θ sin ϕ, respectively, because each has its coordinate rotated so that z is the valley axis. Following the expansion of ψj in terms of the fj,m,μ, we write the intermediate state functions as \(\psi _n({\boldsymbol{r}}) = \mathop {\sum}\nolimits_{m,\mu } {e^{im\phi }e^{i{\boldsymbol{k}}_\mu .{\boldsymbol{r}}}f_{n,m,\mu }(r,\theta )}\), substitute them into \(G_n^{ - 1}\psi _n = \zeta \psi _{n - 1}\), premultiply by \(e^{ - i{\boldsymbol{k}}_{\mu \prime }.{\boldsymbol{r}}}\), average over a volume of (2π/|kμ|)3, premultiply by e−im′ϕ, and finally, integrate over ϕ. Since f0,0,μ = fg,0,μ for all μ, we find that fn,m,3 = i−mfn,m,2 and fn,m,−μ = fn,m,μ, and
where \({\cal{D}} = U_{cc}\delta ({\boldsymbol{r}})\delta _{m,0}/3\) and δm,0 is the Kronecker delta. In the above equations we drop the valley-specific coordinates in fn,m,μ for notational simplicity, and the coordinates in \(H_0^{(m)}\) and the right hand side are understood to belong to the valley of the envelope function that they act on.
It is evident that Eq. (8) are not coupled by Ucc when the envelope function is zero at the origin. The ground state |ψ0〉 = |ψg〉 has only m = 0 components, and it has even parity. Therefore, |ψ1〉 has odd parity according to Eq. (8), so the Ucc coupling term is suppressed. By the same logic, the Ucc coupling is only non-zero for even n and m = 0. In the case of \(\left| {f_{n,m,1}} \right\rangle\), there is only dipole coupling to the functions with the same m, while for \(\left| {f_{n,m,2}} \right\rangle\) the dipole coupling is to states with Δm = ±1. The latter couplings are identical, so fn,−m,μ = fn,m,μ. Figure 1 shows how the intermediate states are coupled by dipole excitation and the CCC.
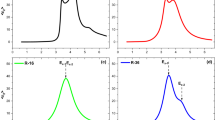
Equation (8) can be solved by sequential application of the 2D FEM15. To test our numerical calculation we first compute C(3) for hydrogen, and each of the resonant and antiresonant terms is shown in Fig. 2. Their sum is shown in Fig. 3, and we find excellent agreement within 0.2% of the previous result obtained from a Sturmian coulomb Green function in ref. 16.
Contributions to C(3) from the resonant and anti-resonant terms for hydrogen: 〈ψ0|ζG3ζG2ζG1ζ|ψ0〉 (blue), 〈ψ0|ζG−1ζG2ζG1ζ|ψ0〉 (yellow), 〈ψ0|ζG−1ζG−2ζG1ζ|ψ0〉 (green), and 〈ψ0|ζG−1ζG−2ζG−3ζ|ψ0〉 (red). At ω = 0, the two terms containing G−2 have opposite signs to the two terms with G2, and the sum tends to 222
A hydrogenic atomic vapor (Rb) is shown for comparison (data from ref. 6). Labels indicate the excited state for 3ω = ωeg resonances and one 2ω resonance. The top axis applies only to Si:P and indicates the frequency in THz
Discussion
Giant third-order nonlinear susceptibility
Since silicon and germanium donors have an isotropic potential in an isotropic dielectric, the lowest-order nonlinear response is determined by χ(3). The χ(3) spectrum for each (including the antiresonant terms) is shown in Fig. 3. We took the parameters for silicon obtained from spectroscopic17 and magneto-optical measurements12,18, which are γ ≈ 0.208, aB ≈ 3.17 nm and EH ≈ 39.9 meV. The parameters for germanium are γ ≈ 0.0513, aB ≈ 9.97 nm and EH ≈ 9.40 meV19. Resonances occur when 3ω = ωeg, labeled according to |ψe〉, and there are also sign-changes at which |χ(3)| goes to zero. In the range of frequency shown, we also observe a two-photon resonance for 1sA1 → 1sE, which is an obvious illustration of the need for a multivalley theory. There is no 3ω resonance with 1sT2 within the approximations made above in which there is no intervalley dipole coupling. The effect of Ucc on χ(3) and the NPA matrix element is shown in Fig. 4. The low-frequency response of C(3) is illustrated at 100 GHz. Two higher-frequency curves are included, with both far from 3ω resonances, half way between the 2p0 and 2p± resonances, and between the 3p0 and 3p±. We choose these average frequencies since χ(3) for Si:P varies slowly around them (see Fig. 3) and hence would not be sensitive to small experimental variations in the light frequency. For the 2p-average frequency, the 2ω resonance with the 1sE produces a coincidental zero-crossing for Si:Bi. Example results for the intermediate state wave functions produced in the calculation are shown in Fig. 5. The state |ψ2〉 is much larger in extent (and in magnitude) than |ψ0〉, and the extra node in the radial dependence due to the contribution of 2s is visible at about 5 nm. Similarly, the state |ψ3〉 is much larger in extent (and in magnitude) than |ψ1〉.
The abscissa is the binding energy of the ground state (which is 31.5 meV at Ucc = 0), \(\bar \omega _{2p} = (\omega _{2p_0} + \omega _{2p_ \pm })/2 - \omega_g\) is the average transition frequency to the 2p levels, and likewise for \(\bar \omega _{3p}\). The binding energies of the Group V shallow donors are indicated in the left panel. The resonance and zero-crossing in the left panel, as well as the peaks in the 2p0 (3PA) and 2sA1 (4PA) matrix element on the right are due to the (2ω) resonance with the intermediate 1sE state
The square bracket in Eq. (5) gives the scaling of χ(N) from hydrogenic atoms in vacuum to hydrogenic impurities in semiconductors, just as that in Eq. (1) does for w(N), and as before, the much smaller Ia greatly increases the strength of the non-linearity. For example, the low-frequency limit of the hyperpolarizability χ(3)/n3D for Si:P is much larger than that for hydrogen or alkali metal vapors such as Rb6, as shown in Fig. 3.
Some of the highest values of χ(3) have been reported for solids, e.g., 2.8 × 10−15 m2/V2 for InSb20 and 2 × 10−16 m2/V2 for GaTe21. To convert the hyperpolarizability to a bulk χ(3) value requires the concentration. To match InSb with Si:P at low frequency where C(3) ≈ 1 (Fig. 4) (and χ(3)/n3D = 2.9 × 10−38 m5/V2) requires a donor density of n3D = 1017 cm−3 (where the donor–donor distance is 10aB). At high frequency, the hyperpolarizability is much higher, but the density should be lower to avoid inhomogeneous concentration broadening of the nearby excited levels. For example, C(3) ≈ 20 between the 2p0 and 2p± resonances at \(\omega = \bar \omega _{2p}/3 = 2\pi \times 3.2\,{\text{THz}}\) (Fig. 4), and we match InSb at a density of n3D = 5 × 1015 cm−3 at which concentration the 2p lines are well resolved22. If 3ω is moved even closer to the 2p± resonance (or if the resonance is tuned with a magnetic field18), then χ(3) could easily exceed InSb. Losses due to dephasing by phonon scattering may become important if the time spent in the intermediate states exceeds the phonon lifetime. Since the inverse of the former is given approximately by the detuning (ΔfΔt ≥ 1/2π) and the inverse phonon-limited width (1/πT2 = 1 GHz23,24), then this loss is negligible for much of the spectrum. At 50 GHz below the 2p± line so that such losses may be ignored, C(3) ≈ 200, and χ(3) is an order of magnitude above InSb.
We are not aware of any larger values for bulk media, but higher “bulk” values have been reported for 2D systems such as graphene and MoS2 for which χ(3)L data are divided by an interaction thickness L to obtain χ(3); in particular, reports for graphene range from 10−19 25,26 to 10−15 m2/V2 27 for near-IR excitation and up to 10−10 m2/V2 in the THz region under resonant enhancement by landau levels in a magnetic field28. A recent experiment with single-layer graphene at room temperature reports a remarkably high value of 1.7 × 10−9 m2/V2 for the THz third-order nonlinear susceptibility29. In the case of coupled quantum wells (QW), large values of χ(3) may be engineered through resonances, as demonstrated up to 10−14 m2/V2 30. However, since the non-linear effect is limited by the interaction length, the 2D χ(3)L is probably a better figure of merit in these cases. For THz field-enhanced graphene with 50 layers, χ(3)L = 9 × 10−20 m3/V2 28, and for single-layer graphene χ(3)L = 5.1 × 10−19 m3/V2 29, or χ(3)L = 1.4 × 10−18 m3/V2 for resonant coupled QWs30. Even higher values are predicted for doped QWs up to χ(3)L = 5 × 10−17 m3/V2 31. To match this value with Si:P at \(\omega = \bar \omega _{2p}/3 = 2\pi \times 3.2\,{\text{THz}}\) and n3D = 5 × 1015 cm−3 (see above) would require a sample thickness of L = 2 cm. Obviously, the required thickness can be significantly reduced when close to resonance, or for germanium.
Efficient third-harmonic generation
The non-linear susceptibility is important for predicting the strength of frequency conversion processes such as third-harmonic generation (3HG), and we use this as an example application to investigate the utility of the medium. A solution for the amplitude of the generated wave produced by 3HG, neglecting absorption, is given by32. Converting to irradiance in MKS units,
where Iin is the irradiance of the input pump wave at frequency fin, and n is the geometric mean of the refractive indexes for the input and output waves, and n2D = n3DL. Note that the isotropy mentioned earlier means that the polarization of the input and output waves must be parallel. We ignored a factor for the phase matching, which is unity if the length of the sample L ≪ Lc, where the coherence length Lc = πc/(3ωin[nout − nin]). Si:P at room temperature has a nearly constant n = 3.4153 in the range from 1 THz to 12 THz33, leading to typical values of Lc ≈ 10 cm. The factor x = 6.9 × 1023 W/cm2 × THz × cm−2 for silicon. For comparison, germanium has x = 9.2 × 1019 W/cm2 × THz × cm−2.
To illustrate the possible applications of this high χ(N), we note that two types of THz diode lasers are available, the quantum cascade laser (QCL) from 0.74 THz34 to 5.4 THz35 with output powers of up to a few W36,37, and the hot hole (p-Ge) laser38,39 with a similar range and power. However, there is a large gap in the availability of solid-state sources from about 5 THz to about 12 THz40, where the GaAs Reststrahlen band renders laser operation impossible. This is an important region for quantum qubit applications41,42,43,44. Currently, the gap is only filled by larger, more expensive systems (difference frequency generators and free electron lasers). Tripling the output of 2–4 THz QCLs would fill the gap, but their output powers are far smaller than those typical for a pump laser in standard tripling applications, so a giant non-linearity is critical. At \(\omega = \bar \omega _{2p}/3 = 2\pi \times 3.2\,{\text{THz}}\), C(3) ≈ 20, so for n2D = 1016 cm−2 (see above), a 1% predicted conversion may be obtained with 100 kW/cm2, and by moving to 50 GHz below the 2p± resonance this value could be brought down to 10 kW/cm2, which is just about achievable with a well focussed QCL, and would thus provide enough output for spectroscopy applications. A nonlinear process that may possibly reduce the 3HG efficiency is multiphoton ionization45 since it reduces the population of the donors in the ground state. When \(\omega = \bar \omega _{2p}/3\), for example, a four-photon absorption takes the electron to the continuum. We estimate this ionization in Si:P using the implicit summation method and find that the rate is w = 3.17 s−1 for Iin = 10 kW/cm2. This result simply means that the pulses must be kept significantly shorter than a second to avoid significant ionization.
In summary, we calculated the absolute values of the THz non-linear coefficients for the most common semiconductor materials, lightly doped silicon and germanium, which are available in the largest, purest and most regular single crystals known. The values we obtain for off-resonance rival the highest values obtained in any other material even when resonantly enhanced, and the material could gain new applications in THz photonics. We also predict the highly efficient third-harmonic generation of THz light in doped silicon and germanium. Our multi-valley theory for nonlinear optical processes of donors in silicon and germanium can be readily applied to any donor in any semiconductor host in which the effective mass approximation is reliable.
Materials and methods
Details of the finite element computation used for solving the coupled partial differential equations (Eq. (8)) are provided in the Supplementary Material.
Data availability
Data for Nguyen Le et al. Giant non-linear susceptibility of hydrogenic donors in silicon and germanium, https://doi.org/10.5281/zenodo.3269481. The data underlying this work is available without restriction.
References
Kaiser, W. & Garrett, C. G. B. Two-photon excitation in CaF2: Eu2+. Phys. Rev. Lett. 7, 229–231 (1961).
Abella, I. D. Optical double-photon absorption in cesium vapor. Phys. Rev. Lett. 9, 453–455 (1962).
Saha, K. et al. Enhanced two-photon absorption in a hollow-core photonic-band-gap fiber. Phys. Rev. A 83, 033833 (2011).
Franken, P. A. et al. Generation of optical harmonics. Phys. Rev. Lett. 7, 118–119 (1961).
Ward, J. F. & New, G. H. C. Optical third harmonic generation in gases by a focused laser beam. Phys. Rev. 185, 57–72 (1969).
Miles, R. & Harris, S. Optical third-harmonic generation in alkali metal vapors. IEEE J. Quantum Electron. 9, 470–484 (1973).
Van Loon, M. A. W. et al. Giant multiphoton absorption for THz resonances in silicon hydrogenic donors. Nat. Photonics 12, 179–184 (2018).
Vampa, G. et al. Theoretical analysis of high-harmonic generation in solids. Phys. Rev. Lett. 113, 073901 (2014).
Beaulieu, S. et al. Role of excited states in high-order harmonic generation. Phys. Rev. Lett. 117, 203001 (2016).
Haworth, C. A. et al. Half-cycle cutoffs in harmonic spectra and robust carrier-envelope phase retrieval. Nat. Phys. 3, 52–57 (2007).
Gontier, Y. & Trahin, M. On the multiphoton absorption in atomic hydrogen. Phys. Lett. A 36, 463–464 (1971).
Li, J. et al. Radii of Rydberg states of isolated silicon donors. Phys. Rev. B 98, 085423 (2018).
Boyd, R. W. Nonlinear Optics. 3rd edn, 640. Academic Press, New York (2008).
Kohn, W. & Luttinger, J. M. Theory of donor states in silicon. Phys. Rev. 98, 915–922 (1955).
The Mathematica FEM code used in this paper is available at, https://github.com/lehnqt/chi3.git.
Mizuno, J. Use of the sturmian function for the calculation of the third harmonic generation coefficient of the hydrogen atom. J. Phys. B: At. Mol. Phys. 5, 1149–1154 (1972).
Ramdas, A. K. & Rodriguez, S. Review article: spectroscopy of the solid-state analogues of the hydrogen atom: donors and acceptors in semiconductors. Rep. Prog. Phys. 44, 1297–1387 (1981).
Murdin, B. N. et al. Si:P as a laboratory analogue for hydrogen on high magnetic field white dwarf stars. Nat. Commun. 4, 1469 (2013).
Faulkner, R. A. Higher donor excited states for prolate-spheroid conduction bands: a reevaluation of silicon and germanium. Phys. Rev. 184, 713–721 (1969).
Yuen, S. Y. & Wolff, P. A. Difference-frequency variation of the free-carrier-induced, third-order nonlinear susceptibility in n-InSb. Appl. Phys. Lett. 40, 457–459 (1982).
Susoma, J. et al. Second and third harmonic generation in few-layer gallium telluride characterized by multiphoton microscopy. Appl. Phys. Lett. 108, 073103 (2016).
Thomas, G. A. et al. Optical study of interacting donors in semiconductors. Phys. Rev. B 23, 5472–5494 (1981).
Steger, M. et al. Shallow impurity absorption spectroscopy in isotopically enriched silicon. Phys. Rev. B 79, 205210 (2009).
Greenland, P. T. et al. Coherent control of Rydberg states in silicon. Nature 465, 1057–1061 (2010).
Woodward, R. I. et al. Characterization of the second- and third-order nonlinear optical susceptibilities of monolayer MoS2 using multiphoton microscopy. 2D Mater. 4, 11006 (2017).
Karvonen, L. et al. Rapid visualization of grain boundaries in monolayer MoS2 by multiphoton microscopy. Nat. Commun. 8, 15714 (2017).
Säynätjoki, A. et al. Rapid large-area multiphoton microscopy for characterization of graphene. ACS Nano 7, 8441–8446 (2013).
König-Otto, J. C. et al. Four-wave mixing in landau-quantized graphene. Nano Lett. 17, 2184–2188 (2017).
Hafez, H. A. et al. Extremely efficient terahertz high-harmonic generation in graphene by hot Dirac fermions. Nature 561, 507–511 (2018).
Sirtori, C. et al. Giant, triply resonant, third-order nonlinear susceptibility \(\chi _{3\omega }^{(3)}\) in coupled quantum wells. Phys. Rev. Lett. 68, 1010–1013 (1992).
Yildirim, H. & Aslan, B. Donor-related third-order optical nonlinearites in GaAs/AlGaAs quantum wells at the THz region. Semicond. Sci. Technol. 26, 085017 (2011).
Shen, Y. R. The Principles of Nonlinear Optics. 3rd edn, 576. Wiley-Interscience, New York, 2002.
Chick, S. et al. Metrology of complex refractive index for solids in the terahertz regime using frequency domain spectroscopy. Metrologia 55, 771 (2018).
Scalari, G. et al. Magnetically assisted quantum cascade laser emitting from 740GHz to 1.4THz. Appl. Phys. Lett. 97, 081110 (2010).
Wienold, M. et al. Frequency dependence of the maximum operating temperature for quantum-cascade lasers up to 5.4 THz. Appl. Phys. Lett. 107, 202101 (2015).
Li, L. et al. Terahertz quantum cascade lasers with >1 W output powers. Electron. Lett. 50, 4309 (2014).
Li, L. H. et al. Multi-Watt high-power THz frequency quantum cascade lasers. Electron. Lett. 53, 799 (2017).
Pfeffer, P. et al. p-type Ge cyclotron-resonance laser: Theory and experiment. Phys. Rev. B 47, 4522–4531 (1993).
Hübers, H. W., Pavlov, S. G. & Shastin, V. N. Terahertz lasers based on germanium and silicon. Semicond. Sci. Technol. 20, S211–S221 (2005).
Ohtani, K., Beck, M. & Faist, J. Double metal waveguide InGaAs/AlInAs quantum cascade lasers emitting at 24 μm. Appl. Phys. Lett. 105, 121115 (2014).
Saeedi, K. et al. Optical pumping and readout of bismuth hyperfine states in silicon for atomic clock applications. Sci. Rep. 5, 10493 (2015).
Litvinenko, K. L. et al. Coherent creation and destruction of orbital wavepackets in Si:P with electrical and optical read-out. Nat. Commun. 6, 6549 (2015).
Chick, S. et al. Coherent superpositions of three states for phosphorous donors in silicon prepared using THz radiation. Nat. Commun. 8, 16038 (2017).
Stoneham, A. M. et al. Letter to the editor: optically driven silicon-based quantum gates with potential for high-temperature operation. J. Phys.: Condens. Matter 15, L447–L451 (2003).
Bebb, H. B. & Gold, A. Multiphoton ionization of hydrogen and rare-gas atoms. Phys. Rev. 143, 1–24 (1966).
Acknowledgements
We acknowledge financial support from the UK Engineering and Physical Sciences Research Council [ADDRFSS, Grant No. EP/M009564/1] and EPSRC strategic equipment grant no. EP/L02263X/1.
Author information
Authors and Affiliations
Contributions
N.H. Le and B.N. Murdin worked on the multivalley theory and the finite element calculation of the third-order susceptibility. B.N. Murdin and G.V. Lanskii calculated the third-harmonic generation efficiency. B.N. Murdin, N.H. Le and G. Aeppli wrote the manuscript. All authors contributed to the discussion of the results.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Le, N.H., Lanskii, G.V., Aeppli, G. et al. Giant non-linear susceptibility of hydrogenic donors in silicon and germanium. Light Sci Appl 8, 64 (2019). https://doi.org/10.1038/s41377-019-0174-6
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41377-019-0174-6
This article is cited by
-
Highly efficient THz four-wave mixing in doped silicon
Light: Science & Applications (2021)
-
The multi-photon induced Fano effect
Nature Communications (2021)