Abstract
A digital-coding programmable metasurface (DCPM) is a type of functional system that is composed of subwavelength-scale digital coding elements with opposite phase responses. By configuring the digital coding elements, a DCPM can construct dynamic near-field image patterns in which the intensity of each pixel of the image can be dynamically and independently modulated. Thus, a DCPM can perform both spatial and temporal modulations. Here, this advantage is used to realize multichannel direct transmissions of near-field information. Three points are selected in the near-field region to form three independent channels. By applying various digital phase codes on the DCPM, independent binary digital symbols defined by amplitude codes (namely, weak and strong amplitudes) are transmitted through the three channels. The measured near-field distributions and temporal transmissions of the system agree with numerical calculations. Compared with the conventional multichannel transmission, the proposed mechanism achieves simultaneous spatial and temporal modulations by treating DCPM as an energy radiator and information modulator, thereby enduing DCPM with high potential in near-field information processing and communications.
Similar content being viewed by others
Introduction
With the rapid growth in the number of devices that are in use, the fifth generation (5G) of communication will involve communications not only between humans but also between objects and between humans and objects. Hence, in addition to improving the network capacity and the spectrum efficiency, establishing additional communication modes is an evolution direction of 5G. Device-to-device (D2D) communication is a type of communication technology that can directly transmit and receive information between terminals; hence, it can reduce the burden on the base stations and decrease the end-to-end delay, improve the spectrum efficiency and reduce the transmission power of the terminals. However, the communication systems that are based on the classical superheterodyne architecture can no longer satisfy the requirements of modern communications due to the high complexities, high cost, and large volumes. Furthermore, the digitization of modern communication systems has evolved from baseband to radio frequency links and antennas. Therefore, more flexible hardware architectures, new types of information, and innovative breakthroughs in the theories of information and communication are urgently needed for satisfying the substantial demands of 5G for “huge capacity, huge connections, and extensive applications”.
Metamaterial1,2, which is a type of artificial material, has been demonstrated to control macroscopic phenomena of electromagnetic (EM) waves, such as negative reflections3,4, perfect lenses5, and invisible cloaks6,7,8,9,10. Microscopic phenomena, such as molecular spontaneous emission11 and bound states in the continuum12, can also be manipulated by metamaterials. After years of development, metamaterials have been fully developed in various morphologies, from acoustic waves13 to light14. A metasurface is a two-dimensional morphology of metamaterials. According to a generalized version of Snell’s law15, the manipulation of EM waves does not necessarily require bulky gradient metamaterials, which typically have a size of several wavelengths according to effective medium theory16; instead, the manipulations can be realized within the subwavelength scale. Many types of metasurfaces have been proposed for controlling the phases17,18,19, amplitudes20,21,22,23, and polarizations24,25,26,27,28,29 of EM wave fronts and for novel applications such as holographic imaging30,31,32, vortex beams33,34,35 and conversions of propagation waves, and surface waves36,37. Active metasurfaces have also been proposed for manipulating the EM waves in various frequency regimes38,39,40,41.
With further research, digital coding metasurfaces (DCMs)42,43,44,45 were proposed for designing more functional devices and/or systems, thereby introducing metasurfaces into informatic fields46,47, in which the digital coding metasurface can manipulate EM waves by arranging the states of digital elements instead of designing effective medium parameters. Moreover, digital coding programmable metasurfaces (DCPMs) were proposed for performing dynamic spatial modulations48,49,50. A DCPM is a type of artificial encoded aperture that is constructed of digital elements and digital coding information is written into the aperture by independently applying a driven voltage on each digital element. Hence, a DCPM can control EM waves dynamically in a programmable way. However, only far-field EM features (e.g., radiation and scattering patterns) of DCMs and DCPMs have been explored in the literature42,43,44,45,46,47,48,49,50. According to Fresnel diffraction theory, the aperture field is related to the diffracted field via the Fourier transform. Therefore, spatial modulations of near fields can be realized by configuring the digital coding schemes of DCPMs, which have higher information capacities.
Since the aperture codes of a DCPM change over time, the digital coding mechanism naturally involves temporal operations. Hence, for each position on the near-field plane, the amplitudes and phases of near fields can be modulated in the time domain by sequentially changing the aperture codes. Therefore, DCPMs can perform near-field modulations in both the space and time domains, which can be used to directly transmit near-field information through multiple channels. To interpret the mechanism, a near-field communication system with multiple channels is established using a DCPM. Three points are selected in the near-field region to form three independent channels. By applying space-time digital codes on a DCPM, independent binary symbols are transmitted through the three channels. The measured near-field distributions and temporal transmissions of the system accord with the numerical calculation results. As the spatial and temporal modulations are directly realized by a DCPM, the presented mechanism of multichannel transmission of near-field information will enrich the modes of 5G communication and improve the mechanisms of near-field information processing and communications.
Results
Near-field patterns that correspond to various coding schemes
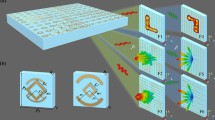
A conceptual diagram of the multichannel transmission system is presented in Fig. 1a. The presented DCPM consists of 400 elements. Figure S4 presents the detailed structure of an element and the simulated scattering coefficients. Each element can render either of two types of states, which possess opposite reflection phases and similar reflection amplitudes. Hence, the aperture configurations of a DCPM can be described by a matrix of binary phase codes. By applying specially designed phase codes, a DCPM can focus the EM fields at arbitrary specified points and the field intensities at these points can be controlled independently. If one denotes the strong field intensity as digital symbol “1” and the weak field intensity as digital symbol “0”, these points will function as multiple transmission channels of binary symbols. To continuously transmit the binary digital symbols, the DCPM can be configured sequentially via a series of coding schemes, which are stored in a field-programmable gate array (FPGA) in advance. As a result, different binary symbols can be transmitted at different near-field points, thereby realizing multichannel direct transmission of near-field information.
a The coding schemes are stored in a field-programmable gate array (FPGA) in advance and are recalled to sequentially configure DCPM so that the near field will be modulated in the space and time domains. As a result, distinct information can be transmitted through each channel. a(i)–h(i) The simulated results. a(ii)–h(ii) The measured results
By combining spatial and temporal modulations, a multichannel transmission system can be realized by using a DCPM. Photos of the fabricated DCPM are shown in Fig. S1. The near-field patterns of the system are presented in the lower part of Fig. 1, in which each pattern has been normalized to its maximum value. The left two columns are calculated results and the right two columns are measured results. The intensities of three points are modulated independently by changing the coding schemes of the DCPM. If high intensity represents symbol “1” and lower intensity symbol “0”, then the three points form three transmission channels and binary digital symbols can be transmitted through these channels.
Because the presented multiple channels are realized by rearranging the near-field energies at three channels, the amplitudes of the symbols may fluctuate in the space and time domains. In the space domain, the imbalanced energy of the channels is caused by factors such as the asymmetry of the coding scheme and the fabrication errors. The symbol “1” may differ in amplitude among the three channels due to this imbalanced energy. In the time domain, there is an inherent imbalance among the channels. If only one channel transmits the symbol “1”, the signal intensity of this channel is stronger than that of each channel if all three channels transmit the symbol “1”. Because the energy is focused on a single channel rather than being distributed among three channels, the amplitude of a symbol in the same channel will depend on the combination of symbols in the three channels.
Channel strengths and transmission efficiencies
To evaluate the fluctuations of the channel strengths, the near fields are integrated around the focal point within an integral area, in which the field values are higher than 10% of the value at the focal point. All the channel strengths are normalized to a fixed value, which is obtained by integrating the values of near-field pattern “010”. Figure 2a–c presents the normalized channel strengths. If only one channel transmits symbol “1”, the channel strength is stronger compared to the cases in which two or three channels transmit symbol “1”. Hence, the number of channels affects the strengths of the channels. As the independent channels are established by focusing the near-field energy, the channel strengths can be increased by enlarging the aperture of the DCPM. The squares of the sums of the channel strengths are defined as the transmission efficiencies in Fig. 2d. The transmission efficiencies are unaffected by the combinations of symbols in the three channels; hence, increasing or reducing the number of channels will not affect the total energy that is transmitted by the DCPM. To analyze the effect of multiple channels on the receiving performance, Fig. S2 compares various numbers of channels in terms of the bit error rate (BER). The results in Fig. S2 demonstrate that the multiple channels that are produced by DCPMs can contribute to the reduction of BER.
a The channel efficiency of channel 1. b The channel efficiency of channel 2. c The channel efficiency of channel 3. d The transmission efficiency. The horizontal ordinate in each figure represents combinations of binary symbols in the three channels. The red digits represent the transmitted symbols in the corresponding channel
Multichannel transmission of symbols
The results of the following transmission experiments demonstrate that the DCPM can transmit different near-field symbols among channels. To receive the symbols, a general signal processing board was used to sample the signal at each channel. For convenience of sampling, the carrier waves of the transmitted signals were converted from 10 GHz to 3 MHz. The period of each symbol is 2 μs and the sampling frequency is 31.44 MHz. Hence, each period of the signal will be sampled by 63 times. The digital receiver can record 400 sampling points. The left column of Fig. 3 presents the sampled signals in three independent channels. However, after Hilbert transformations (the middle column of Fig. 3) and threshold decisions (the right column of Fig. 3), the extracted envelopes of the signals demonstrate that the sampled signals are exactly the signals that were transmitted by the DCPM; therefore, the DCPM can perform both spatial and temporal modulations on the near fields. Hence, multichannel direct transmissions of near-field information are realized using the DCPM.
Discussion
For spatial modulations, the fabricated DCPM was measured in a near-field microwave anechoic chamber. Figure S1 presents a photograph of the measuring environment. In the procedure of measuring the near fields, the DCPM was placed on a wood platform and a waveguide probe was positioned 600 mm away from the DCPM to record the near-field pattern with a step size of 0.018 mm. All measurements were automatically controlled by the software system of the anechoic chamber. For convenience of measurement, the aperture codes of the DCPM were held constant during each measurement. The centers of the measuring plane and the DCPM were aligned for all measurements. The three channels were selected to be horizontally distributed to alleviate the shielding effects. For temporal modulations, the DCPM was configured sequentially via a series of coding schemes and a general signal processing board was used as a digital receiver to sample the signals that were recorded by the waveguide probe. Figure S2 presents a schematic diagram of the multichannel transmission process. The waveforms of the signals were recorded by the software of the general signal processing board, as presented in Fig. 3.
From both calculations and measurements, we observe the fluctuations in the space and time domains. However, they are not sufficiently violent for hindering the identification of symbols. Typically, the receivers of communication systems have sufficient dynamic ranges for covering the fluctuations. In the presented experiments, the period of the transmitted symbols is selected as 2 μs for convenience of sampling. The minimum period of the transmitted symbols is determined by the fastest switching time of the DCPM. The main limiting factor of the speed of the DCPM is the switching time of the Positive-Intrinsic-Negative (PIN) diode and the DC feeding method. In the present work, all units of the DCPM are controlled by a digital circuit board (e.g., FPGA) in parallel; hence, the switching time of the whole aperture is very close to the switching time of a single PIN diode. The fastest switching time of the DCPM is 25 ns according to the test. However, short periods may result in larger errors in the transmitted symbols. Hence, the period of the transmitted symbols must balance the rate and accuracy of the symbols.
In conclusion, the dynamic property of DCPMs is used to realize multichannel direct transmission of near-field information. Spatial modulations are performed on the near fields to form three transmission channels and independent binary amplitude modulations are performed on each channel to transmit distinct digital information. Both spatial and temporal modulations are achieved by directly configuring a DCPM. Comparing with the conventional multichannel transmissions, the new transmission mechanism does not require phase shifters for the spatial modulations or baseband modulators for the temporal modulations. These advantages endow DCPMs with high potential in near-field information processing and high-capacity communications.
Materials and methods
Spatial modulations
First, the capacity of a DCPM for performing near-field spatial modulations is investigated. As an example, six focal points are defined arbitrarily on a near-field plane that is 600 mm away from the DCPM. Figure 4 shows the specified points and the corresponding binary phase code matrix of the DCPM. According to the near-field pattern, six focal points appear at the specified positions. In addition to the focal points, other complex near-field patterns can be realized by configuring the DCPM. In Fig. S5, the near-field pattern is defined as the shape of the letter “T”. Both the calculations and measurements show a letter “T” on the near-field plane, thereby demonstrating that DCPM can distribute near-field patterns in an arbitrary way. For all the near-field patterns, the derivations of the matrix of binary phase codes are detailed in Fig. S6.
Based on the spatial modulations, multiple channels for the near-field transmission can be physically established. For convenience of testing, three points are specified as three transmission channels. When the DCPM focus the energy at one point, the digital symbol “1” will be transmitted through the corresponding channel; otherwise, the digital symbol “0” will be transmitted. To independently transmit binary digital symbols through the three channels, eight types of coding schemes for the DCPM are needed. The correspondences between the coding schemes and the transmitted symbols in the three channels are presented in Fig. 5a–h.
Temporal modulations
For temporal modulations, one can specify a series of coding schemes for the DCPM for transmitting a series of binary symbols. As an example of independent temporal modulations, periodic bytes that each contain four binary symbols are specified in the three channels: “1010”, “0110”, and “0001” in channel 1, channel 2, and channel 3, respectively. Figure 5i shows the timing sequence of the coding schemes that will be used to configure the DCPM for the transmission of the specified binary symbols of each channel. Figure 5j presents the corresponding signal waveforms of the three channels. The carrier wave is defined at 10 GHz; hence, the signals will be amplitude-modulated sinusoidal waves. Because each coding scheme of the DCPM remains unchanged for 2 μs, the transmitted symbol will also last for 2 μs. For the transmitted signals, high amplitude represents symbol “1”, while low amplitude represents symbol “0”. The envelopes of the signals in the three channels correspond to the transmitted binary symbols.
References
Pendry, J. B., Schurig, D. & Smith, D. R. Controlling electromagnetic fields. Science 312, 1780–1782 (2006).
Pendry, J. B. et al. Transformation optics and subwavelength control of light. Science 337, 549–552 (2012).
Smith, D. R., Pendry, J. B. & Wiltshire, M. C. K. Metamaterials and negative refractive index. Science 305, 788–792 (2004).
Shelby, R. A., Smith, D. R. & Schultz, S. Experimental verification of a negative index of refraction. Science 292, 77–79 (2001).
Pendry, J. B. Negative refraction makes a perfect lens. Phys. Rev. Lett. 85, 3966–3969 (2000).
Schurig, D. et al. Metamaterial electromagnetic cloak at microwave frequencies. Science 314, 977–980 (2006).
Li, J. S. & Pendry, J. B. Hiding under the carpet: a new strategy for cloaking. Phys. Rev. Lett. 101, 203901 (2008).
Ergin, T. et al. Three-dimensional invisibility cloak at optical wavelengths. Science 328, 337–339 (2010).
Xu, L., Xiong, Z. & Chen, H. Y. Analysis of a conformal invisible device. Front. Phys. 13, 134203 (2018).
Chu, H. C. et al. A hybrid invisibility cloak based on integration of transparent metasurfaces and zero-index materials. Light. Sci. Appl. 7, 50 (2018).
Ginzburg, P. et al. Spontaneous emission in non-local materials. Light. Sci. Appl. 6, e16273 (2017).
Kirill, K., Bogdanov, A. & Kivshar, Y. Meta-optics and bound states in the continuum. Science Bulletin. https://doi.org/10.1016/j.scib.2018.12.003 (2018).
Cao, W. K. et al. Asymmetric transmission of acoustic waves in a waveguide via gradient index metamaterials. Science Bulletin. https://doi.org/10.1016/j.scib.2019.01.002 (2019).
Zeng, B. B. et al. Hybrid graphene metasurfaces for high-speed mid-infrared light modulation and single-pixel imaging. Light. Sci. Appl. 7, 51 (2018).
Yu, N. F. et al. Light propagation with phase discontinuities: generalized laws of reflection and refraction. Science 334, 333–337 (2011).
Liu, R. P. et al. Description and explanation of electromagnetic behaviors in artificial metamaterials based on effective medium theory. Phys. Rev. E 76, 026606 (2007).
Huang, L. L. et al. Helicity dependent directional surface plasmon polariton excitation using a metasurface with interfacial phase discontinuity. Light. Sci. Appl. 2, e70 (2013).
Wan, X. et al. A broadband transformation-optics metasurface lens. Appl. Phys. Lett. 104, 151601 (2014).
Wan, X. et al. Planar bifunctional Luneburg-fisheye lens made of an anisotropic metasurface. Laser Photonics Rev. 8, 757–765 (2014).
Yu, Y. F. et al. High-transmission dielectric metasurface with 2π phase control at visible wavelengths. Laser Photonics Rev. 9, 412–418 (2015).
Wan, X. et al. Independent modulations of the transmission amplitudes and phases by using Huygens metasurfaces. Sci. Rep. 6, 25639 (2016).
Minatti, G. et al. Synthesis of modulated-metasurface antennas with amplitude, phase, and polarization control. IEEE Trans. Antennas Propag. 64, 3907–3919 (2016).
Kim, T. T. et al. Amplitude modulation of anomalously refracted terahertz waves with gated-graphene metasurfaces. Adv. Opt. Mater. 6, 1700507 (2018).
Song, X. et al. Selective diffraction with complex amplitude modulation by dielectric metasurfaces. Adv. Opt. Mater. 6, 1701181 (2018).
Wan, X. et al. Horn antenna with reconfigurable beam-refraction and polarization based on anisotropic huygens metasurface. IEEE Trans. Antennas Propag. 65, 4427–4434 (2017).
Mueller, J. P. B. et al. Metasurface polarization optics: independent phase control of arbitrary orthogonal states of polarization. Phys. Rev. Lett. 118, 113901 (2017).
Aydin, K. et al. Broadband polarization-independent resonant light absorption using ultrathin plasmonic super absorbers. Nat. Commun. 2, 517 (2011).
Grady, N. K. et al. Terahertz metamaterials for linear polarization conversion and anomalous refraction. Science 340, 1304–1307 (2013).
Jiang, S. C. et al. Controlling the polarization state of light with a dispersion-free metastructure. Phys. Rev. 4, 021026 (2014).
Wei, Q. S. et al. Broadband multiplane holography based on plasmonic metasurface. Adv. Opt. Mater. 5, 1700434 (2017).
Huang, L. L. et al. Three-dimensional optical holography using a plasmonic metasurface. Nat. Commun. 4, 2808 (2013).
Ye, W. M. et al. Spin and wavelength multiplexed nonlinear metasurface holography. Nat. Commun. 7, 11930 (2016).
Yue, F. Y. et al. Vector vortex beam generation with a single plasmonic metasurface. ACS Photonics 3, 1558–1563 (2016).
Zhang, Y. C. et al. Generating focused 3D perfect vortex beams by plasmonic metasurfaces. Adv. Opt. Mater. 6, 1701228 (2018).
Liu, Z. X. et al. Generation of arbitrary vector vortex beams on hybrid-order Poincaré sphere. Photonics Res. 5, 15–21 (2017).
Sun, S. L. et al. Gradient-index meta-surfaces as a bridge linking propagating waves and surface waves. Nat. Mater. 11, 426–431 (2012).
Liu, S. et al. Negative reflection and negative surface wave conversion from obliquely incident electromagnetic waves. Light. Sci. Appl. 7, 18008 (2018).
Cong, L. Q. et al. All-optical active THz metasurfaces for ultrafast polarization switching and dynamic beam splitting. Light. Sci. Appl. 7, 28 (2018).
Papaioannou, M. et al. All-optical dynamic focusing of light via coherent absorption in a plasmonic metasurface. Light. Sci. Appl. 7, 17157 (2018).
Yin, X. H. et al. Beam switching and bifocal zoom lensing using active plasmonic metasurfaces. Light. Sci. Appl. 6, e17016 (2017).
Zhang, J. J. et al. Integrated spoof plasmonic circuits. Science Bulletin. https://doi.org/10.1016/j.scib.2019.01.022(2019).
Cui, T. J. et al. Coding metamaterials, digital metamaterials and programmable metamaterials. Light. Sci. Appl. 3, e218 (2014).
Liu, S. et al. Anisotropic coding metamaterials and their powerful manipulation of differently polarized terahertz waves. Light. Sci. Appl. 5, e16076 (2016).
Liu, S. et al. Convolution operations on coding metasurface to reach flexible and continuous controls of terahertz beams. Adv. Sci. 3, 1600156 (2016).
Cui, T. J. Microwave metamaterials. Natl. Sci. Rev. 5, 134–136 (2018).
Cui, T. J., Liu, S. & Li, L. L. Information entropy of coding metasurface. Light. Sci. Appl. 5, e16172 (2016).
Cui, T. J., Liu, S. & Zhang, L. Information metamaterials and metasurfaces. J. Mater. Chem. C. 5, 3644–3668 (2017).
Wan, X. et al. Field-programmable beam reconfiguring based on digitally-controlled coding metasurface. Sci. Rep. 6, 20663 (2016).
Li, L. L. et al. Electromagnetic reprogrammable coding-metasurface holograms. Nat. Commun. 8, 197 (2017).
Cui, T. J. Microwave metamaterials-from passive to digital and programmable controls of electromagnetic waves. J. Opt. 19, 084004 (2017).
Acknowledgements
This work was supported by Fund for International Cooperation and Exchange of National Natural Science Foundation of China (61761136007), the National Key Research and Development Program of China (2017YFA0700201, 2017YFA0700202, 2017YFA0700203), the National Natural Science Foundation of China (61631007, 61571117, 61501112, 61501117, 61522106, 61731010, 61735010, 61722106, 61701107, and 61701108), the 111 Project (111-2-05) and Zhishan Young Scholar Program of Southeast University.
Author’s contributions
X.W. conducted the analytical modeling, numerical simulations, sample fabrication, and measurements. Q.Z., W.X., H.H., C.K.X., and Q.X. conducted parts of the fabrications and measurements. As principle investigator of the project, T.J.C. conceived the idea, suggested the designs, and planned, coordinated, and supervised the work. All authors contributed to the preparation and writing of the manuscript.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wan, X., Zhang, Q., Yi Chen, T. et al. Multichannel direct transmissions of near-field information. Light Sci Appl 8, 60 (2019). https://doi.org/10.1038/s41377-019-0169-3
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41377-019-0169-3