Abstract
Achieving strong coupling between plasmonic oscillators can significantly modulate their intrinsic optical properties. Here, we report the direct observation of ultrafast plasmonic hot electron transfer from an Au grating array to an MoS2 monolayer in the strong coupling regime between localized surface plasmons (LSPs) and surface plasmon polaritons (SPPs). By means of femtosecond pump-probe spectroscopy, the measured hot electron transfer time is approximately 40 fs with a maximum external quantum yield of 1.65%. Our results suggest that strong coupling between LSPs and SPPs has synergetic effects on the generation of plasmonic hot carriers, where SPPs with a unique nonradiative feature can act as an ‘energy recycle bin’ to reuse the radiative energy of LSPs and contribute to hot carrier generation. Coherent energy exchange between plasmonic modes in the strong coupling regime can further enhance the vertical electric field and promote the transfer of hot electrons between the Au grating and the MoS2 monolayer. Our proposed plasmonic strong coupling configuration overcomes the challenge associated with utilizing hot carriers and is instructive in terms of improving the performance of plasmonic opto-electronic devices.
Similar content being viewed by others
Introduction
Surface plasmons (SPs), as the collective oscillation of free electrons at the interface between dielectric and metal layers1, have aroused tremendous interest in diverse fields, such as solar energy conversion, superresolution, high harmonic generation, near-field imaging, and nonlinear phenomena2,3,4,5,6,7,8,9. As nonpropagating SPs, localized surface plasmons (LSPs) can either dephase radiatively by re-emitting photons or decay by Landau damping to form energetic electron−hole pairs10,11. These pairs are nonthermal, and their intense collisions can redistribute accumulated energy in hundreds of femtoseconds, developing into hot carriers that obey a Fermi−Dirac-like distribution with an increased effective temperature2,3. If these hot carriers are exported at a rate faster than energy dissipation by electron−phonon scattering, they can be collected and utilized in external circuits for opto-electronic devices such as photodetectors12,13,14,15,16,17,18,19,20,21,22,23,24,25,26. To realize this application, two critical challenges must be overcome: the large radiative rate of LSPs and the rapid relaxation of the hot carriers.
In contrast to LSPs, surface plasmon polaritons (SPPs) relax almost nonradiatively even at rough surfaces, leading to a higher photon-to-carrier conversion efficiency27,28. However, such carriers with lower energies have a low probability of crossing the potential barrier between a metal and semiconductor, which leads to a low output yield in practice29. In addition, the lack of vertical momentum and interfacial reflection also block the exportation of SPP-generated carriers29. Photons absorbed by SPPs are hence mostly exhausted as heat rather than transformed into exploitable electrical energy.
Here, we consider that the distinct properties of LSPs and SPPs may synergize to produce plasmonic hot carriers. In the weak coupling regime, the interaction between two oscillators only introduces a perturbation to their original properties; thus, SPPs exert little influence on the intrinsic radiative damping of LSPs. However, the energy levels of hybrid polaritons can be greatly altered when oscillators strongly interact with each other in a phenomenon called strong coupling, in which Rabi splitting can be experimentally observed as a distinguishable characteristic of the energy spectrum30,31,32,33,34,35,36. When the coupling strength exceeds the decoherence rate of the original oscillator, strong coupling occurs30, and the energy exchange between the oscillators becomes the dominant relaxation channel. It has been proven that the resonant radiative rate of harmonic oscillators can be modulated in the strong coupling regime37,38,39, which is conducive to addressing the radiation damping bottleneck in the exploitation of hot carriers decayed from LSPs37.
In this article, we propose a metal−insulator−metal (MIM) sandwiched heterostructure, where an MoS2 monolayer is employed to constitute a Schottky heterojunction with an Au grating on top and serves as an acceptor to harvest hot electrons that decay from LSPs. Stemming from the strong coupling between LSPs and SPPs, hot electron transfer at this heterojunction can be facilitated by coherent energy exchange and the perpendicular enhanced electric field, which decreases the radiative rate of the LSPs and accelerates the exportation of hot electrons. The physical insight presented in this work paves the way to construct plasmonic hot carrier devices with improved performance in the future.
Results
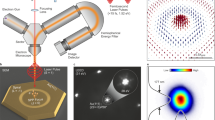
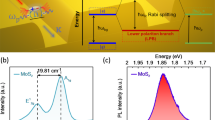
Figure 1a shows a schematic of our Au grating/MoS2/substrate sandwiched structure, where the substrate consists of a 20 nm Al2O3 spacer and a 50 nm Au layer evaporated on a Si/SiO2 wafer. Scanning electron microscopy (SEM) images of the heterostructures with different grating periods are shown in Fig. 1b and Figure S1. The electronic band alignment diagram of the Au grating and MoS2 monolayer is illustrated in Fig. 1c, which also sketches the transfer process of the plasmonic hot electrons. These electrons are excited by a 780 nm pump laser. After crossing the Schottky barrier, they are injected into the MoS2 monolayer underneath and induce a variation in the filled states therein, which is monitored by a 650 nm probe pulse. In the experiment, the 20 nm Al2O3 layer can prevent hot carriers that decay from SPPs from tunneling into the MoS2 monolayer, although most carriers are distributed in the low-energy region and can hardly cross the Schottky barrier. As the energy of the pump laser (1.59 eV) is lower than the bandgap of the MoS2 monolayer, excitons cannot be directly excited. Therefore, it is safe to consider that the detected transient absorption signal is only induced by the injection of hot electrons that decay from LSPs, indicating the direct observation of plasmonic hot electron transfer.
a Schematic of the Au grating/MoS2/Al2O3/Au/Si sandwiched heterostructure. b Cross-sectional SEM view of a typical MIM heterostructure, imaged at a 52° tilted angle. The inset shows a top-view SEM image for gratings with a 700 ± 5 nm period. The gray area corresponds to the substrate, while the dark gray represents the MoS2 monolayer. c The band alignment diagram of the Au grating and MoS2 monolayer. Plasmonic hot electrons were pumped at 780 nm, and the transient absorption of the A exciton in the MoS2 monolayer was monitored by a 650 nm probe pulse. d Experimentally measured reflectance spectra of the MoS2 monolayer, Au grating and Au grating/MoS2 at the substrate with a 600 ± 5 nm grating period (solid lines). Reflectance spectra with plasmonic structures were also simulated by the finite-difference time-domain (FDTD) method (dashed lines), which show good agreement with the measurements. SEM scanning electron microscopy
Figure 1d shows plots of the measured reflectance spectra of a pristine MoS2 monolayer, bare Au grating array and hybrid Au grating/MoS2 structure at the substrate. Two absorption peaks were observed at 605 nm (B exciton) and 654 nm (A exciton) for the pristine MoS2 monolayer (olive line). Regarding the bare Au grating (magenta line), three obvious resonances appeared at 615, 725, and 823 nm. For the hybrid Au grating/MoS2 structure (orange line), the third resonance peak was redshifted by approximately 25 nm due to the change in the surrounding dielectric medium. From the above results, we can see that the third resonance is primarily due to LSPs, while the first two resonances mainly result from SPPs40. In fact, all of these resonances are coupled polaritons that hybridize between LSPs and SPPs along either the –x (SPP1) or +x (SPP2) axes (Figure S2). In Fig. 1d, the dashed lines are FDTD simulation results for the bare Au grating array and Au/MoS2 hybrid structure, which are in good agreement with the experimental results (see Materials and methods for details).
It is well known that a steady-state reflectivity measurement is an efficient way to investigate strong coupling. Figure 2a, b shows the measured and simulated reflectance spectra of Au/MoS2 hybrids with Au grating periods ranging from 600 to 750 nm, where the three plasmon resonances behave in a similar fashion. The magnetic field distribution of these resonances for a grating period of 700 nm was calculated in Fig. 2c. It is apparent that the mode at 704 nm (798 nm) is dominated by SPPs propagating along the +x (−x) axis, and the third resonance is mainly due to LSPs. Similar results can be obtained from the electric field distribution in Figure S3 and Supplementary Section 1.
a Measured reflectance spectra of the Au grating/MoS2/substrate with grating periods of 600, 650, 700, and 750 nm. b Simulated reflectance spectra of the corresponding samples in (a). c Simulated magnetic field distribution at the resonances for the sample with a 700 nm grating period. d The simulated grating-period-dependent reflectance of the sandwiched structures, which exhibits classic Rabi splitting. Ψi (i = 1, 2, 3) are eigenstates of the Hamiltonian. e Simulated (hollow triangles), measured (filled dots), and theoretical (solid lines) resonance energies as a function of the grating period. The dotted line shows the constant dispersion relation of the uncoupled localized surface plasmons, while the dashed and dash-dotted lines denote the dispersions of the uncoupled SPPs propagating along the –x (SPP1) and +x (SPP2) axes, respectively. SPP surface plasmon polariton
Figure 2d shows the simulated reflectance mapping for grating periods ranging from 550 to 1000 nm, where two clear energy anticrossings appear. These avoided crossings correspond to Rabi splitting and demonstrate strong coupling between the uncoupled modes. A coupled oscillator model was successfully used to study the observed strong coupling41,42,43. In our case, the Hamiltonian H can be written as
where ELSPs, ESPP1 and ESPP2 are the resonance energies of the uncoupled LSP, SPP1, and SPP2 states, and Vi (i = 1, 2, 3) represent the coupling strengths between these states. Ψi (i = 1, 2, 3) are defined as eigenstates of H with the lowest, middle, and highest eigenenergies. They are also mixtures of uncoupled modes and can be expressed as
where cij (j = 1, 2, 3) are coefficients.
To solve the Hamiltonian, the dispersion relations of the uncoupled LSPs, SPP1, and SPP2 are plotted in Fig. 2e as dotted, dashed, and dash-dotted lines, respectively, from which we can see that the LSP resonance energy (ELSPs = 1.46 eV) remains constant as the grating period changes. For the uncoupled SPP modes, their dispersion relations can be obtained from the equation
where \(K_{{\mathrm {spp}}} = \frac{\omega }{c}\sqrt {\frac{{\varepsilon _1\varepsilon _2}}{{\varepsilon _1 + \varepsilon _2}}}\) is the SPP wavevector, ε1 (ε2) is the dielectric permittivity of the Au (dielectric) layer, \(K_x = \frac{\omega }{c}\sin \theta\) is the horizontal wavevector component of the incident light, m is an integer and P corresponds to the grating period. For such an air/Al2O3/Au interface, the dispersion relation of the SPPs cannot be directly described by a classic model of two semi-infinite layers. However, the actual dispersion can be acquired from a modified model, in which an effective medium with a wavelength-dependent refractive index is introduced (Figure S4 and Supplementary Section 2).
With the fitting parameters Vi (i = 1, 2, 3) equal to 0.075, 0.075, and 0.06 eV, respectively, theoretical results based on the coupled oscillator model were calculated. The results are shown as red solid lines in Fig. 2e. V1 = V2 means that the coupling strength between the LSPs and SPP1 equals that between the LSPs and SPP2, which may be attributed to m = 1 for both SPP1 and SPP2. The simulated (hollow triangles), measured (filled dots), and theoretical (solid lines) results are in excellent agreement, as demonstrated in Fig. 2e, which implies that strong coupling between the LSPs and SPPs occurs in our proposed MIM heterostructures.
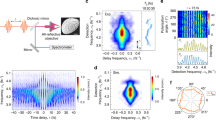
To investigate the dynamics of plasmonic hot electron transfer in the strong coupling regime between the LSPs and SPPs, femtosecond pump-probe measurements in a reflection configuration were carried out. Figure 3a presents differential reflection spectra ΔR/R0(t) of the heterostructure with a 700 nm Au grating period (red dots) and reference samples, which include a bare Au grating array on the substrate (blue), a pristine MoS2 monolayer on the substrate (green) and the substrate (gray). The pump had a wavelength of 780 nm and a fluence of 7.5 μJ/cm2, and 650 nm probe pulses with a fluence of 0.75 μJ/cm2 were used to detect the transient absorption of the A exciton in the MoS2 monolayer. For the bare Au grating array on the substrate, no transient differential reflection signal appears, proving that plasmonic hot electron relaxation cannot induce ultrafast signals in this case. One of the causes of this phenomenon could be the low pump and probe fluences in our experiments, which are two orders of magnitude weaker than those used in typical pump-probe measurements of metallic electron relaxations44. This reason is verified in Figure S5 and Supplementary Section 3, in which the pump fluence is enhanced by two orders of magnitude. The other reason is the pump wavelength of 780 nm pump, which is chosen to excite SP resonances rather than interband transitions of Au that have larger absorption cross-sections44.
a Differential reflection spectra of the Au grating/MoS2/substrate (red dots) and control samples of the Au grating, MoS2 monolayer and substrate for a pump fluence of 7.5 μJ/cm2. The red line is a fitting curve for the descent of ΔR/R0(t) with a biexponential function. The inset shows details of the rising process with normalization. The data shown in gray represent the interferometric autocorrelation function for the pump pulses, from which the upper envelope with a full width at half-maximum of ~130 fs is taken as the IRF. The red line in the inset was obtained by convoluting the IRF and the actual electron injection function. b Pump-fluence-dependent transient absorption spectra of the heterostructure. The scale bar corresponds to the intensity of the ultrafast signals. c The maximum amplitude of ΔR/R0(t) as a function of pump fluence. The red line is a fitting curve with the saturation formula of Eq. (4). d Fast and slow decay lifetimes varying with pump fluence. e Ultrafast pump-probe spectra of the Au grating/MoS2/substrate for different grating periods pumped at 780 nm with 7.5 μJ/cm2. f Excited (injected) electron densities derived from the peak amplitudes of ΔR/R0(t). The red dots represent the grating-period-dependent densities of electrons injected into the MoS2 monolayer pumped at 780 nm, while the blue dots correspond to the densities of electrons excited directly at the pump wavelength of 400 nm. IRF instrument response function
The ultrafast signal only emerges in the Au grating/MoS2/substrate heterostructure, revealing that the variation in the occupancy in MoS2 arises from plasmonic hot electron injection. As the injected hot electrons fill unoccupied states in the conduction band of MoS2 and rapidly relax to the exciton level, the absorbance of the A exciton with the pump is lower than that without the pump. Thus, the transfer process can be represented by the rising edge of ΔR/R0(t), as shown in the inset. The injection time was estimated to be approximately 40 fs by deconvoluting the signal with the instrument response function (IRF) (see Supplementary Section 5 for the detailed deconvolution process). The red line in the inset was obtained by convoluting the IRF and the actual electron injection function, which can well reproduce the experimentally measured transient differential signal. Then, the decay of transferred hot electrons occurs during the descent of ΔR/R0(t). The decay process can be well fitted with a biexponential function and is caused by electron−electron and electron−phonon scattering.
The pump fluence dependence of the ultrafast signal was studied in Fig. 3b, and the maximum amplitudes of the spectra were extracted in Fig. 3c. The peak amplitude increases and gradually saturates as the fluence increases, and the relationship can be fitted by
where f and fsat are the pump fluence and the saturation value, respectively. When the fluence exceeds 10 μJ/cm2, the peak of ΔR/R0(t) is greatly influenced by the saturation effect. This phenomenon could be caused by a mass accumulation of transferred hot electrons because these electrons repel like charges and prevent further injection into the MoS2 monolayer. Different from the saturating trend of the peak amplitude, the decay processes in the transient absorption spectra are independent of the pump fluence, as shown in Fig. 3d, and can be fitted by biexponential functions with average parameters of 210 fs and 5.5 ps, which are attributed to the lifetimes of electron−electron and electron−phonon interactions.
Apart from the transfer timescale, the injected hot electron density is another important factor. As ultrafast signals arise from variations in occupation number in the MoS2 monolayer, the largest intensity of ΔR/R0(t) can in principle represent the density of excited (injected) electrons. At a pump wavelength of 780 nm, ultrafast signals arise from the injection of plasmonic hot electrons. As a result, the densities of the electrons transferred into MoS2 cannot be directly evaluated by the absorbance of MoS2. To derive the densities in this case, a quantitative relationship between the densities and peak amplitudes of ΔR/R0(t) needs to be established first. To obtain this relation, transient absorption spectra pumped at 400 nm were measured, because ultrafast signals originate from the direct excitation of electrons in the valence band of MoS2 in this case. Therefore, the excited electron density can be calculated from the absorbance of the MoS2 monolayer. At a pump wavelength of 400 nm with 7.5 μJ/cm2, the excited electron density equals 1.47 × 1012 cm−2 with a corresponding peak amplitude of ΔR/R0(t) of 0.08% (Figure S6). Based on this result, a linear relationship between the density and peak amplitude was eventually established (see Supplementary Section 6 for details). The density of injected hot electrons pumped at 780 nm, which was derived from the peak amplitude in Fig. 3a, was estimated as 3.55 × 1011 cm−2.
Moreover, to further confirm the active role of SPs in injecting hot electrons, ultrafast transient absorption measurements of samples pumped at 780 nm for various grating periods were performed, as shown in Fig. 3e. Based on their peak amplitudes, the transferred electron densities were calculated similarly in Fig. 3f. The density reaches a maximum for a grating period of 700 nm because strong coupling occurs therein and the resonance peak of Ψ2 (the eigenstate with the middle eigenenergy) is closer to the pump wavelength than the resonances of the other grating periods (Fig. 2a). In contrast, the excited electron density hardly changes with the grating period when the pump wavelength is 400 nm, as illustrated in Fig. 3f and Figure S7, in which case the plasmonic modes cannot be resonantly excited. This distinct grating period dependence at different pump wavelengths is ascribed to the diverse origins of the occupancy number variation in MoS2.
From the above results, plasmonic hot electron transfer from the Au grating to the MoS2 monolayer was directly observed in the strong coupling regime, in which the injection time and density were approximately 40 fs and 3.55 × 1011 cm−2, respectively, for a pump fluence of 7.5 μJ/cm2.
The injection efficiency is an important factor in carrier transfer studies. In our work, there is also significant evidence to prove the contribution of strong coupling in advancing plasmonic hot electron transfer. Here, we reveal the effect of strong coupling by comparing experimental and theoretical electron injection yields. The external quantum yield η is defined as the ratio of transferred electron densities to incident photon densities. To obtain a maximum yield in the experiment, the pump wavelength was altered, as shown in Fig. 4a. The resonance wavelength of Ψ2 is 813 nm for the 700 nm grating period, and the peak of η follows the resonance, reaching its largest value of 1.65% at the pump wavelength of 810 nm.
a Transferred hot electron densities and corresponding η for the heterostructure with a 700 nm grating period at different pump wavelengths. b Branches of Ψ2 (|c21|2, |c22|2, and |c23|2) as a function of the grating period. c The simulated absorbance of the heterostructures with grating periods of 600, 650, 700, and 750 nm. For a grating period of 700 nm, the absorbance is approximately 0.4 when Ψ2 is resonantly excited. d A diagrammatic model proposed to describe the physical processes in the strong coupling regime between LSPs and surface plasmon polaritons. Coherent energy exchange is represented by the dashed lines labeled by ① and ②. The processes labeled as ③ and ④ denote the radiative and nonradiative relaxation channels of the LSPs, respectively. LSP localized surface plasmon
To estimate theoretical efficiencies, we first calculated all branches of Ψi (i = 1, 2, 3) (|cij|2) for different grating periods in Fig. 4b and Figure S8 according to the coupled oscillator model. For a grating period of 700 nm, the LSP branches (|ci1|2) are approximately 85, 6, and 10% in Ψi (i = 1, 2, 3), respectively, in agreement with the magnetic field distribution in Fig. 2c. Since Ψ2 is near-resonant with a 780 nm pump, its fractions are analyzed in detail in Fig. 4b. It is interesting to note that SPP1 dominates Ψ2 and the LSPs only contribute 6% for a 700 nm grating period, which implies that the LSPs are launched with 6% of the energy in Ψ2.
Next, we evaluate the theoretical injection efficiency of hot electrons induced by the LSPs individually. Before transferring into MoS2, many steps must occur for the LSPs to generate hot electrons. First, pump pulses couple to Ψ2 with an absorbance of approximately 40% (Fig. 4c), and only 6% of the coupled energy is used to stimulate LSPs. In practice, both hot electrons and holes are excited, all of which are distributed in a range of energy and momentum. Assuming that hot electrons attain half of the energies and all are injected into MoS2, the efficiency is 1.2% (=40% × 6% × 50%) when considering the steps up to now, which equals the measured yield when pumped at 780 nm. However, in fact, only energetic hot electrons with enough vertical momentum are capable of crossing the Schottky barrier17,29. In addition, they must overcome interfacial reflection and recombination with defects at the interface before finally transferring into MoS2. This comparison result suggests that η should much less than the measured value if hot electrons are solely produced by the LSPs.
Based on the analysis above, we propose a model to depict the mechanism as illustrated in Fig. 4d, in which strong coupling between plasmonic modes is the ultimate reason for the elevated η. In the strong coupling regime, the energies of uncoupled oscillators are coherently exchanging31. In this case, photons emitted by the radiative damping of LSPs are reabsorbed into SPPs by coherent energy exchange (①). As uncoupled SPPs with prolonged lifetimes are almost relaxed nonradiatively, their captured energies can be stored for a relatively long time. Thereafter, the intrinsic energies of the SPPs and reabsorbed energies can also be delivered to the LSPs through coherent energy exchange (②), experiencing radiative (③) and nonradiative (④) relaxations once again. The net result is that the original energies stored in the SPPs and radiation energies of the LSPs are recycled to produce hot carriers rather than being exhausted as heat or radiating into free space directly, such that the inaccessible energies in the SPPs are utilized and radiative damping in the LSPs is suppressed. In the strong coupling regime, the enhanced electric field surrounding MoS2 at resonance is another element that facilitates hot electron transfer. The electric field induced by image charges in the Au grating and Au film provides hot electrons with requisite vertical momenta for crossing the Schottky barrier. In such a picture, LSPs and SPPs collaborate excellently to take full advantage of unavailable energies for generating hot carriers in the strong coupling regime.
Discussion
In summary, by virtue of femtosecond pump-probe spectroscopy, direct plasmonic hot electron transfer from an Au grating to an MoS2 monolayer was successfully observed in an MIM structure in the strong coupling regime. Plasmonic hot electron transfer occurs at ~40 fs with a maximum η of 1.65%. Strong coupling between LSPs and SPPs generates plasmonic hot electrons from energy and momentum. Coherent energy exchange allows photons radiated by the decay of LSPs to be reabsorbed by SPPs and originally unavailable energies stored in SPPs to participate in generating hot carriers. In this picture, low-loss SPPs that are nonradiative in nature function as an “energy recycle bin”: capturing, storing and delivering radiative energies of the LSPs. Due to the intense electric field induced by image charges in the MIM structure, the perpendicular momenta required for crossing the Schottky barrier are provided. Ascribed to strong coupling, the complementary aspects of LSPs and SPPs overcome the intrinsic drawbacks of individual plasmonic modes in exploiting hot carriers. The insight presented in this work is also applicable to other metal-2D semiconductor, metal-molecular and metal-organic semiconductor systems. The spectral range of strong coupling can also be modulated in the near-infrared region by tuning the geometry and size, which holds great prospects for improving the performance of plasmonic hot carrier devices in fields involving photoconversion.
Materials and methods
Sample preparations
The Au film (50 nm) and Al2O3 layer (20 nm) were deposited on an Si/SiO2 wafer by electron beam evaporation sequentially. The CVD-grown MoS2 monolayer was then transferred onto the prepared substrate with the wetting transfer method. The MoS2 monolayer grown on an Si/SiO2 wafer was first spin-coated with poly(methyl methacrylate) (PMMA) and baked on a hot plate (180 °C) for 5 min. It was then etched in KOH solution for 6 h to strip the film from the wafer. Next, the film was removed and transferred to deionized water to rinse off impurities. This cleaning process was repeated three times. The film was then transferred onto the prepared substrate and heated for 5 min on a 100 °C hot plate. The PMMA on the film was dissolved with acetone steam that was produced by heating acetone at 150 °C. An MoS2 monolayer was eventually left on the substrate. Au gratings 40 nm in thickness and 85 ± 5 nm in width were fabricated using electron beam lithography and electron beam evaporation methods. To obtain a cross-sectional SEM image, the heterostructure was etched by a focused ion beam.
Reflectance measurements
A hyperspectral imaging system (Cytoviva HISV3) was adapted to perform the reflectance measurements. Reflectance spectra were recorded by the spectrometer (Horiba iHR550) with a ×10 objective (Olympus MPlanFL, NA = 0.25). Relative reflectivity was utilized to represent the reflectance spectra, which was obtained by dividing the reflected intensity of the sample by that of the substrate. Nonpolarized white light passed through a linear polarizer (Thorlabs LPNIRE100-B) with the polarization direction along the x-axis. As the normal incident white light was confined by the objective, the in-plane wavevector kx was not zero despite the value being small compared with the momentum provided by gratings. However, this issue could not be neglected as it resulted in a splitting of uncoupled SPP modes (SPP1 and SPP2).
Finite-difference time-domain (FDTD) simulations
The FDTD method was employed to simulate the reflectance spectra and electromagnetic field distributions of heterostructures. The relative permittivities of the Au and MoS2 monolayers were taken from the literature45,46, and the refractive index of Al2O3 was taken as 1.77. The incident angle of TM-polarized light was set at 3° because oblique incidence with an angle of θ ~ 3° can supply a similar in-plane wavevector to simulate the influence of objective confinement. Bloch boundary conditions were used in the x direction, symmetric boundaries were applied in the y direction and perfectly matched layer boundaries were used in the z direction.
Femtosecond pump-probe measurements
Typical femtosecond transient absorption spectra measurements in a reflection configuration were carried out. The mode-locked oscillator (Tsunami 3941C-25XP) generated 800 nm femtosecond pulses with a repetition rate of 80 MHz and a pulse duration of ~73 fs. The output laser was split into two parts. One part was used as the pump and chopped at 1500 Hz, while the other part was focused onto photonic crystal fiber (Newport SCG-800) to generate supercontinuum white light extending from 550 to 1400 nm. The probe was then selected with a 650 ± 10 nm bandpass filter (Thorlabs). The pump pulses passed through a linear polarizer (Thorlabs LPNIRE100-B), with the polarization direction along the x axis. The reflected probe pulses were collected by a high-sensitivity photomultiplier (Thorlabs PMM02) and were converted into electric signals. The spot size of the focused probe was approximately 2 µm. The delay time between the pump and probe pulses was controlled by a stepper linear stage (Newport M-ILS150PP). Differential reflection signals ∆R/R0(t) = (R − R0)/R0 were acquired by subtracting the reflectivity of the probe with pump pulses (R) from that without the pump (R0).
References
Barnes, W. L., Dereux, A. & Ebbesen, T. W. Surface plasmon subwavelength optics. Nature 424, 824–830 (2003).
Brongersma, M. L., Halas, N. J. & Nordlander, P. Plasmon-induced hot carrier science and technology. Nat. Nanotechnol. 10, 25–34 (2015).
Clavero, C. Plasmon-induced hot-electron generation at nanoparticle/metal-oxide interfaces for photovoltaic and photocatalytic devices. Nat. Photonics 8, 95–103 (2014).
Knight, M. W., Sobhani, H., Nordlander, P. & Halas, N. J. Photodetection with active optical antennas. Science 332, 702–704 (2011).
Zhong, J. H. et al. Probing the electronic and catalytic properties of a bimetallic surface with 3 nm resolution. Nat. Nanotechnol. 12, 132–136 (2016).
Kim, S. et al. High-harmonic generation by resonant plasmon field enhancement. Nature 453, 757–760 (2008).
Kawata, S., Inouye, Y. & Verma, P. Plasmonics for near-field nano-imaging and superlensing. Nat. Photonics 3, 388–394 (2009).
Wurtz, G. A. et al. Designed ultrafast optical nonlinearity in a plasmonic nanorod metamaterial enhanced by nonlocality. Nat. Nanotechnol. 6, 107–111 (2011).
Baida, H. et al. Ultrafast nonlinear optical response of a single gold nanorod near its surface plasmon resonance. Phys. Rev. Lett. 107, 057402 (2011).
Hartland, G. V. Optical studies of dynamics in noble metal nanostructures. Chem. Rev. 111, 3858–3887 (2011).
Manjavacas, A., Liu, J. G., Kulkarni, V. & Nordlander, P. Plasmon-induced hot carriers in metallic nanoparticles. ACS Nano 8, 7630–7638 (2014).
Tan, S. J. et al. Plasmonic coupling at a metal/semiconductor interface. Nat. Photonics 11, 806–812 (2017).
Giugni, A. et al. Hot-electron nanoscopy using adiabatic compression of surface plasmons. Nat. Nanotechnol. 8, 845–852 (2013).
Wu, K., Chen, J., McBride, J. R. & Lian, T. Efficient hot-electron transfer by a plasmon-induced interfacial charge-transfer transition. Science 349, 632–635 (2015).
Harutyunyan, H. et al. Anomalous ultrafast dynamics of hot plasmonic electrons in nanostructures with hot spots. Nat. Nanotechnol. 10, 770–774 (2015).
Furube, A., Du, L. C., Hara, K., Katoh, R. & Tachiya, M. Ultrafast plasmon-induced electron transfer from gold nanodots into TiO2 nanoparticles. J. Am. Chem. Soc. 129, 14852–12853 (2007).
Li, W. & Valentine, J. G. Harvesting the loss: surface plasmon-based hot electron photodetection. Nanophotonics 6, 177–191 (2017).
Yu, Y. et al. Ultrafast plasmonic hot electron transfer in Au nanoantenna/MoS2 heterostructures. Adv. Funct. Mater. 26, 6394–6401 (2016).
Kang, Y. M. et al. Plasmonic hot electron induced structural phase transition in a MoS2 monolayer. Adv. Mater. 26, 6467–6471 (2014).
Hoang, C. V. et al. Interplay of hot electrons from localized and propagating plasmons. Nat. Commun. 8, 771 (2017).
Kim, M., Lin, M. H., Son, J., Xu, H. X. & Nam, J. M. Hot-electron-mediated photochemical reactions: principles, recent advances, and challenges. Adv. Opt. Mater. 5, 1700004 (2017).
Wen, X. L., Xu, W. G., Zhao, W. J., Khurgin, J. B. & Xiong, Q. H. Plasmonic hot carriers-controlled second harmonic generation in WSe2 bilayers. Nano Lett. 18, 1686–1692 (2018).
Fang, Z. Y. et al. Graphene-antenna sandwich photodetector. Nano Lett. 12, 3808–3813 (2012).
Sobhani, A. et al. Narrowband photodetection in the near-infrared with a plasmon-induced hot electron device. Nat. Commun. 4, 1643 (2013).
Li, W. & Valentine, J. Metamaterial perfect absorber based hot electron photodetection. Nano Lett. 14, 3510–3514 (2014).
Li, W. et al. Circularly polarized light detection with hot electrons in chiral plasmonic metamaterials. Nat. Commun. 6, 8379 (2015).
Sundararaman, R. et al. Theoretical predictions for hot-carrier generation from surface plasmon decay. Nat. Commun. 5, 5788 (2014).
Bernardi, M., Mustafa, J., Neaton, J. B. & Louie, S. G. Theory and computation of hot carriers generated by surface plasmon polaritons in noble metals. Nat. Commun. 6, 7044 (2015).
Narang, P., Sundararaman, R. & Atwater, H. A. Plasmonic hot carrier dynamics in solid-state and chemical systems for energy conversion. Nanophotonics 5, 96–111 (2016).
Törmä, P. & Barnes, W. L. Strong coupling between surface plasmon polaritons and emitters: a review. Rep. Prog. Phys. 78, 013901 (2015).
Vasa, P. et al. Real-time observation of ultrafast Rabi oscillations between excitons and plasmons in metal nanostructures with J-aggregates. Nat. Photonics 7, 128–132 (2013).
Groß, H., Hamm, J. M., Tufarelli, T., Hess, O. & Hecht, B. Near-field strong coupling of single quantum dots. Sci. Adv. 4, eaar4906 (2018).
Kleemann, M.-E. et al. Strong-coupling of WSe2 in ultra-compact plasmonic nanocavities at room temperature. Nat. Commun. 8, 1296 (2017).
Thomas, R. et al. Plexcitons: the role of oscillator strengths and spectral widths in determining strong coupling. ACS Nano 12, 402–415 (2018).
Chen, H. J. et al. Plasmon–molecule interactions. Nano Today 5, 494–505 (2010).
Zheng, D. et al. Manipulating coherent plasmon–exciton interaction in a single silver nanorod on monolayer WSe2. Nano Lett. 17, 3809–3814 (2017).
Zeng, P. et al. Photoinduced electron transfer in the strong coupling regime: waveguide-plasmon polaritons. Nano Lett. 16, 2651–2656 (2016).
Rodriguez, S. R. K., Murai, S., Verschuuren, M. A. & Rivas, J. G. Light-emitting waveguide-plasmon polaritons. Phys. Rev. Lett. 109, 166803 (2012).
Konrad, A., Kern, A. M., Brecht, M. & Meixner, A. J. Strong and coherent coupling of a plasmonic nanoparticle to a subwavelength fabry–pérot resonator. Nano Lett. 15, 4423–4428 (2015).
Chu, Y. Z. & Crozier, K. B. Experimental study of the interaction between localized and propagating surface plasmons. Opt. Lett. 34, 244–246 (2009).
Liu, W. J. et al. Strong exciton–plasmon coupling in MoS2 coupled with plasmonic lattice. Nano Lett. 16, 1262–1269 (2016).
Cade, N. I., Ritman-Meer, T. & Richards, D. Strong coupling of localized plasmons and molecular excitons in nanostructured silver films. Phys. Rev. B 79, 241404 (2009).
Bellessa, J. et al. Exciton/plasmon polaritons in GaA/Al0.93Ga0.07As heterostructures near a metallic layer. Phys. Rev. B 78, 205326 (2008).
Su, M. N. et al. Optomechanics of single aluminum nanodisks. Nano Lett. 17, 2575–2583 (2017).
Johnson, P. B. & Christy, R. W. Optical constants of the noble Metals. Phys. Rev. B 6, 4370–4379 (1972).
Liu, J. T., Wang, T. B., Li, X. J. & Liu, N. H. Enhanced absorption of monolayer MoS2 with resonant back reflector. J. Appl. Phys. 115, 193511 (2014).
Acknowledgements
This work was supported by the National Key Research and Development Program of China (Grant No. 2017YFA0205700), National Basic Research Program of China (Grant Nos. 2015CB932403, 2017YFA0206000), National Science Foundation of China (Grant Nos. 11674012, 61422501, 11374023, 61521004 and 21790364), Beijing Natural Science Foundation (Grant No. L140007), Foundation for the Author of National Excellent Doctoral Dissertation of PR China (Grant No. 201420), National Program for Support of Top-notch Young Professionals (Grant No. W02070003) and Ministry of Education Singapore under Grant No. MOE2015-T2-2-043.
Author information
Authors and Affiliations
Contributions
Z.F. supervised the project. Y.Y. and H.S. performed the experiments. H.S. and Y.Y. established the theoretical model and carried out the simulations. All authors discussed the results and wrote the manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Supplementary Information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Shan, H., Yu, Y., Wang, X. et al. Direct observation of ultrafast plasmonic hot electron transfer in the strong coupling regime. Light Sci Appl 8, 9 (2019). https://doi.org/10.1038/s41377-019-0121-6
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41377-019-0121-6
This article is cited by
-
Real-time observation of two distinctive non-thermalized hot electron dynamics at MXene/molecule interfaces
Nature Communications (2024)
-
High performance artificial visual perception and recognition with a plasmon-enhanced 2D material neural network
Nature Communications (2024)
-
Phonon-assisted upconversion in twisted two-dimensional semiconductors
Light: Science & Applications (2023)
-
Sub-picosecond collapse of molecular polaritons to pure molecular transition in plasmonic photoswitch-nanoantennas
Nature Communications (2023)
-
Interface-engineered Au@MoS2 core-shell heterostructures with superior hot-carrier transfer dynamics for plasmonics and optoelectronics
Science China Materials (2023)