Abstract
The established international 2°C target stipulates that global warming should be limited to below 2°C compared with pre-industrial periods; this has emerged as the most prominent interpretation of how to avoid dangerous climate change. The 2°C target was confirmed and made legally binding in the Paris agreement at the “climate summit” (Conference of Parties 21, COP21) in December 2015. But despite agreement on the target, greenhouse-gas emissions are unlikely to fall soon and fast enough to meet the target, raising the question of whether this target needs to be revised or reinterpreted, and also of why there is insufficient cooperation toward emissions reduction despite the risk of dangerous climate change. Previous theoretical and experimental research has suggested that cooperation towards emissions reduction is undermined by uncertainty about the threshold marking the transition to dangerous climate change. However, even if the threshold and hence the location of the target are known precisely, uncertainty ensues because of an unknown risk that arises from missing the collective target. How humans deal with this risk has not been investigated experimentally. Here we investigate how individuals behave under different risk scenarios if a collective target is missed. We perform economics experiments framed as a collective-risk social dilemma and directly examine the extent to which human subjects trade pay-out reduction for risk. We show that a reduced assessed risk arising from missing the collective target leads to reduced contributions towards the target; but that risk reduction causes the subjects almost to maximize their individual pay-out by balancing the effort to reach the target against the risk posed by missing it. We provide quantitative support for the argument that group contributions toward the collective target can be interpreted as proportional to mitigated warming. We conclude that reinterpretation of the 2°C target as less strict causes additional warming. However, our subjects deal effectively with a risk of dangerous climate change that they assess to depend gradually on global warming. Our results suggest that, if the additional warming is judged to be acceptable, a less strict interpretation of the 2°C target might support finding a trade-off between the effort put into climate mitigation and the risk of dangerous climate change.
Similar content being viewed by others
Introduction
The 2°C climate target stipulates that globally averaged surface warming should be limited to less than 2°C above pre-industrial levels (Rijsberman and Swart, 1990; WBGU, 1995; Ott et al., 2004; Tol, 2007; Ramanathan and Feng, 2008; Randalls, 2010; Cointe et al., 2011; Jaeger and Jaeger, 2011; Moellendorf, 2011). The 2°C target has emerged as the most prominent candidate (Randalls, 2010; Cointe et al., 2011; Jaeger and Jaeger, 2011) for fulfilling the mandate by the United Nations Framework Convention on Climate Change (UNFCCC) to “prevent dangerous anthropogenic interference with the climate system” (UNFCCC, 1992). However, meeting a temperature target alone cannot comprehensively avoid dangerous interference (Steinacher et al., 2013; IPCC, 2014); furthermore, some fundamental critique of the 2°C target has been levied (Shaw, 2010; 2013). Nevertheless, a legally binding international adoption of the 2°C target has emerged as a central outcome of the 2015 Conference of Parties 21 (COP21) in Paris (COP21, 2015).
The 2°C target implies a reduction in greenhouse-gas emissions from about 2020 onward; by 2050 emissions must fall to a level of 50% or less of the year-2000 emissions (IPCC, 2007; Allen et al., 2009; Meinshausen et al., 2009; IPCC, 2013). Despite the success of the COP21 climate summit in Paris in 2015, including the continued and now binding commitment to the 2 °C target, this target appears increasingly unlikely to be met, due to continually increasing emissions (Geden, 2013; Guivarch and Hallegatte, 2013; Peters et al., 2013; Stocker, 2013; Geden and Beck, 2014; Peters et al., 2017). Investigating how individuals behave under different risk scenarios if a collective target, interpreted as the 2 °C climate target, might be missed is the objective of our article.
The spectre of missing the target has caused discussions about potential policy consequences such as target modification (Geden, 2013; Guivarch and Hallegatte, 2013; Geden and Beck, 2014). The 2°C target is unlikely to be relaxed by policymakers, both because he or she might fear losing credibility (Geden, 2013) and because the target characterizes the level of ambition and hence might still formulate what is desirable (Guivarch and Hallegatte, 2013). On the other hand, a policymaker’s credibility might also be damaged by pursuing a target that is patently unrealistic—that lack of realism might undermine the negotiation process, and he or she might be seen as politically unsuccessful (Guivarch and Hallegatte, 2013). Faced with these conflicting tendencies, the political process is more likely to favour reinterpretation over revision of the 2°C target (Geden, 2013), for example by accepting a temporary or even a permanent overshoot while keeping the target nominally intact. Such an overshoot—in strict terms, missing the target—invokes an increased risk of dangerous climate change (IPCC, 2014). With the international climate negotiation process in mind, we here investigate by means of experimental economics how the assessment of the risk arising from missing a collective target, interpreted as the 2°C target, influences the effort undertaken by groups of subjects to reach the target.
We use the framework of the collective-risk social dilemma that we established previously (Milinski et al., 2008) to investigate the dilemma inherent in avoiding dangerous climate change: Will a group of people reach a collective target through individual contributions when everybody suffers individually if the target is missed? The dilemma arises because every player can gain only if the group reaches the target, requiring sufficient cooperation (fair-share or even altruistic contributions). But cooperation is undermined by free-riding—the hope that others will compensate one’s own less-than-fair contributions, a compensation that causes the group to reach the target while maximizing the particular individual’s profit. If too much free-riding occurs, because of too frequent emphasis on immediate self-interest, the collective target is missed and everyone loses (Milinski et al., 2008).
The collective-risk social dilemma has characteristic features that, taken together, distinguish it from other social dilemmas and other instances of decision-making under uncertainty (Milinski et al., 2008): (i) people have to make decisions repeatedly before the outcome is evident, (ii) investments are lost (that is, no refunds), (iii) the effective value of the public good (in this case, the prevention of dangerous climate change) is unknown, and (iv) the remaining private good is at risk if the target sum is not collected. The climate game involves investing in a public good, not in order to realize a gain but to avoid a loss. The collective-risk social dilemma has been used as the workhorse to study various collective problems faced by humans (Wang et al., 2009; Wang et al., 2010; Milinski et al., 2011; Tavoni et al., 2011; Abou Chakra and Traulsen, 2012; Chen et al., 2012a,b; Santos et al., 2012; Burton-Chellew et al., 2013; Hilbe et al., 2013; Jacquet et al., 2013; Abou Chakra and Traulsen, 2014; Chen et al., 2014; Du et al., 2014; Freytag et al., 2014; Vasconcelos et al., 2014; Dannenberg et al., 2015; Bynum et al., 2016; Hagel et al., 2016; Milinski et al., 2016). Here, we add a crucial component by experimentally investigating the behavioural consequences of differing assessed risk levels if the 2°C climate target is missed.
Subjects receive an initial endowment and then play a pre-determined number of rounds; in each round they decide whether or not to invest from their endowment into a climate account. If at the end of the game a group of subjects has collectively invested enough into the climate account to reach a pre-determined target sum, each subject receives in cash whatever is left of his or her individual endowment. However, if the target sum is not reached collectively, each subject loses with a certain probability whatever is left of his or her endowment. The contribution to the climate account is interpreted as an effort to mitigate climate change by reducing greenhouse-gas emissions. Reaching the target sum is interpreted as preventing dangerous climate change, whereas the loss of the remaining endowment—should it happen—is interpreted as the occurrence of dangerous climate change.
In Milinski et al. (2008), the risk of incurring dangerous climate change remained constant until the target sum was reached and then dropped abruptly to zero. But in reality the risk of dangerous climate change is expected to vary more gradually with the effort to reduce greenhouse-gas emissions. Here we include this effect through two different treatments that use the same target sum, but employ a gradual dependence of the risk on the group contribution to the climate account. The risk is zero for contributions equal to or higher than the target sum; the target sum and thus the location of the threshold are always known to the participants.
Uncertainty about the location of the threshold were previously investigated theoretically (Barrett, 2013; Barrett and Dannenberg, 2014), in one-shot experiments sometimes including communication among subjects (Barrett and Dannenberg, 2012; Barrett and Dannenberg, 2014), and in the collective-risk social dilemma (Dannenberg et al., 2015). All of these studies represented threshold uncertainty through a range of values, each to be randomly chosen with the same probability after the experiment; range and probability could either be known or unknown to the subjects. By contrast, there is no uncertainty about the threshold in our experiments, and the subjects in our treatments have been directly informed about the risk at any collective investment level (see below). Thus, our study allows us to examine directly the extent to which human subjects trade pay-out reduction for risk.
The gradual dependence of risk on group contributions also differs substantially from the design of Milinski et al. (2011), who introduced an intermediate target into the collective-risk social dilemma. If their intermediate target was not met, the average risk amounted to a 10% loss of the endowment, simulating climate events before dangerous climate change could occur. However, the sharp dependence of the risk of simulated dangerous climate on the group contribution remained. Here we represent that the risk of dangerous climate change, which in the experiment is mimicked through a complete loss of the remaining endowment, is likely to depend gradually on the effort to reduce greenhouse-gas emissions.
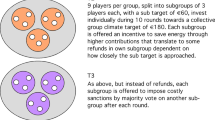
In particular, we argue that despite the extensive scientific uncertainty (IPCC, 2013), we can interpret the group contribution to the climate account as being proportional to the achieved mitigation of further global anthropogenic temperature rise (see Methods in Supplementary Information). As a consequence, we can interpret a set target sum of €120 as mitigating warming by 3 °C and thus meeting the 2°C target (see Methods in Supplementary Information). To reach this target sum as a group, each of the six subjects per group must on average contribute €20, half of the initial endowment. Failure to reach the target sum of €120 mimics that insufficient mitigation has incurred the risk of dangerous climate change and its consequent potential damages. Hence, if a group collects less than €120 over the ten rounds, each subject loses what is left over from the initial endowment, with a probability that differs among three different treatments.
Treatment 1 (T1) assigns a loss probability of 90% for every sum collected over the ten rounds that is below a target sum of €120 (Fig. 1a). We interpret the collection of €120 as reaching the 2°C climate target. This is the treatment we have investigated earlier (Milinski et al., 2008); it has the clearly unrealistic interpretation that there exists a sharp boundary between a high risk and no risk of dangerous climate change.
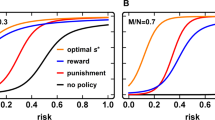
Loss probability (left) and average expected winnings per subject (right), as a function of group investment over ten rounds, for Treatment 1 (T1, a and d), Treatment 2 (T2, b and e), and Treatment 3 (T3, c and f). The maximum of the average expected winnings per subject occurs at the target sum of €120 in T1 and T2 and at €113.3 in T3 (asterisks; see Methods).
Treatment 2 (T2) assigns a loss probability of 90% for every sum collected over ten rounds that is below €80 (Fig. 1b); between €80 and €120, loss probability decreases linearly from 90% to 0. This treatment introduces a more gradual and thus more realistic transition from a high to no risk of dangerous climate change. Furthermore, T2 stresses the role of a climate target as a focal point for climate negotiations (Jaeger and Jaeger, 2011), by introducing a second focal point. The €80 focal point can be interpreted as a warming of 3 °C above pre-industrial, assuming that climate change mitigation is proportional to the effort (see Methods in Supplementary Information). Treatment 2 is thus interpreted such that dangerous climate change would occur with 90% probability for any warming above pre-industrial levels by 3 °C or more.
Treatment 3 (T3) specifies that the loss probability decreases linearly from 90% to 0 as the sum collected increases from €0 to €120 (Fig. 1c). This treatment is interpreted such that any amount of climate-change mitigation leads to a proportional reduction in the risk of dangerous climate change.
We interpret the group contribution after ten rounds as achieving a certain level of climate-change mitigation. Thus, we investigate how actors deal with the uncertainty in the risk of dangerous climate change that is incurred by warming. Our conceptual starting point is that actors’ responses to the climate-change-mitigation challenge are based not on the real risk, which might be unknown to them, but on the assessed risk. Our three treatments could hence represent that, no matter what the real risk, assessment of risk by the actors in climate-change mitigation corresponds to three different profiles. In an alternative interpretation, formally different but leading to similar conclusions, the probability of dangerous climate change depends on future warming in a way that is very uncertain. We hence explore various functional dependencies and communicate that dependency to our subjects. In this alternative interpretation, the subjects’ risk assessment is accurate.
Irrespective of which of the two interpretations is chosen, the assessment of a risk that depends gradually on climate-change mitigation, as it does in T2 and T3, implies an imperative to meet exactly the €120 or 2°C target that is weaker than the imperative is for T1. It is in this sense that the 2°C climate target is reinterpreted; it is not replaced by a new, less stringent target, which would be politically unpalatable (Geden, 2013).
As is the case for all economics experiments including all studies cited in this article, the present one must be regarded as a “proof of principle”, investigating the causal effect of one variable of interest in an otherwise stable scenario. This approach leaves out most of the natural complexity, the inclusion of which would render such a study untreatable. This is the strength but of course also the limitation of any experimental approach.
Our results suggest that a lower assessed risk arising from missing the 2°C climate target would lead to additional warming. On the other hand, the groups balance this lower assessed risk of simulated dangerous climate change against the effort to avoid it.
Results
Maximizing expected winnings
Investments reduce the remaining endowment but also the risk of losing it. For each treatment there is thus an optimal group investment that maximizes the final expected winnings (social optimum). In T1 and T2 the expected winnings as a function of group investment over ten rounds are maximized at the target sum of €120 (Fig. 1d, e), whereas in T3 the maximum occurs at a group investment of €113.3 (Fig. 1f; see Methods in Supplementary Information). In T1 the expected winnings decrease monotonically with the group investment until just before the target sum is reached. In T2 the winnings decrease monotonically until the sum of €80 is reached and then increase until the target sum is reached. In T3 the expected winnings increase for any amount up to the maximum at a collected sum of €113.3. Treatment T2 thus has two different focal points that the subjects might aim for: €120, which provides a zero risk, and €80, above which contributions cause an increase in expected winnings. Treatment T3 likewise has two focal points, €120 with zero risk and €113.3 with the maximum expected winnings, although it is unlikely that the subjects have identified the maximum during the experiment. Nonetheless, the subjects in T3 might intuit that they reach a point of diminishing returns at a collective contribution lower than the point of the maximum. As the expected-winnings curve flattens, a given further enhancement in expected winnings comes at an ever higher expense in contribution, something that might be unattractive as a strategy given the uncertainty in the other subjects’ behaviour. A theoretical analysis of T3 has shown (Hagel et al., 2016) that at the social optimum, the expected pay-out for an individual player decreases if this player unilaterally increases his or her contribution, whereas the symmetric Nash equilibrium (at which any change in contribution by any player would confer no benefit to this player) lies at much lower average contributions than the social optimum (Hagel et al., 2016).
Group investments
Average group investments over ten rounds are substantially higher in T1 (€119.8±2.1; mean±sem) than those in T2 (€111.6±1.9) and T3 (€87.3±4.6). These differences are significant in an overall comparison among treatments (Kruskal–Wallis, χ2= 24.02, nT1, nT2, nT3= 11, P<0.001; the group of six subjects is the statistical unit throughout; all tests are two-tailed) as well as when compared pairwise (Wilcoxon rank sum test, nT1, nT2, nT3=11, WT1 versus T2= 102, PT1 versus T2= 0.0069; WT1 versus T3= 120.5, PT1 versus T3< 0.001; WT2 versus T3= 119, PT1 versus T2< 0.001). Part of the difference in group investment over ten rounds arises from a higher frequency of selfish acts (individual contribution of €0 per round) and a lower frequency of altruistic acts (individual contribution of €4 per round) in T3 (see subsection “Free-riders” and Methods in Supplementary Information).
The average group investment over ten rounds in T1 (€119.8±2.1) matches the social optimum of €120 (maximum expected winnings) almost precisely (Table 1). However, all four groups that miss the target sum lose the savings of their endowment. The average investment in T2 (€111.6±1.9) is significantly less than the €120 needed for maximum expected winnings (Wilcoxon signed rank test, V= 2, nT2= 11, P= 0.0066; Fig. 1e). However, the loss probability is reduced to 18.8% on average, and eight out of ten groups that miss the target sum receive their savings. The average investment in T3 (€87.7±4.6) is likewise significantly less than the €113.3 needed for maximum expected winnings (Wilcoxon signed rank test, V= 0, nT2= 11, P= 0.0038; Fig. 1f). However, the loss probability is reduced to 24.2% on average, and seven out of eleven groups that miss the target sum of €120 receive their savings.
Pay-out per subject
The average pay-out per subject, including those who lose their savings when the target sum of €120 is missed, differs significantly among the treatments, with €12.4, €17.4, and €16.8 in T1, T2 and T3, respectively (Kruskal–Wallis, χ2= 6.30, nT1, nT2, nT3= 11, P= 0.043). The pairwise differences are, however, statistically significant only for the comparison of T1 and T2 (Wilcoxon rank sum test, WT1 vs. T2= 22, nT1, nT2= 11, PT1 versus T2= 0.011). We speculate that the groups in T2 and T3 play relatively successfully by defining their strategy intuitively rather than being aware of the optimum. In T1, which has a higher loss probability overall (Fig. 1), the subjects are less successful. The lower average pay-out in T1 can be traced back to the four groups that miss the target, if only narrowly, and lose their remaining endowment. Such irrational behaviour has already been observed in previous experiments (for example, Milinski et al., 2008) and is the worst possible outcome of a game—savings are reduced without lowering the risk.
Reaching the target sum
Among all treatments, there is a significant difference in the number of groups that reach the target sum of €120 (Fisher exact test, nT1, nT2, nT3= 11, P= 0.0016); the number of groups are seven, one, and zero in T1, T2 and T3, respectively (Fig. 2). Whereas the pairwise differences between T1 and T2 as well as between T1 and T3 are significant (Fisher exact test, nT1, nT2, nT3=11, PT1 versus T2= 0.024, PT1 versus T3= 0.0039), the pairwise difference between T2 and T3 is not significant (Fisher exact test, nT2, nT3=11, PT2 versus T3= 1).
Group investments collected over ten rounds (dots) and their empirical frequency distribution (violins, in intervals of €3), for treatments T1 (blue), T2 (green), and T3 (brown). The frequency distribution is derived using non-parametric kernel density. Larger dots represent duplicate outcomes. The dashed lines represent the 2°C climate target at a target sum of €120 and the 3°C focal point at an additional focal point at €80.
Although €80 is introduced as a second focal point only in T2, €80 are collected as a trend faster in T1, on average at round number 7.3±0.2, compared to round number 7.6±0.2 in T2 (Wilcoxon rank sum test, WT1 versus T2= 44, nT1, nT2= 11, PT1 versus T2= 0.29; Fig. 3). In T3, the sum of €80 is collected on average at round number 8.9±0.3, significantly different from the other treatments (Wilcoxon rank sum test, nT1, nT2, nT3=11, WT1 versus T3= 8, PT1 versus T3< 0.001, WT2 versus T3= 11.5, PT2 versus T3= 0.0014; for groups that do not pass the €80 threshold until after round 10, the round number of passing the €80 threshold is conservatively set to 10; Fig. 3). Thus, for reaching the second focal point of €80 group contribution, interpreted here as mitigating warming by 2°C and corresponding to a climate focal point of 3 °C (see Methods in Supplementary Information), T2 and T3 do not constitute more effective alternatives to T1.
Free-riders
We define as free-riders those subjects who over ten rounds contribute less than their fair share of €20. The average number of free-riders per group in T3 (4.55±0.28) differs significantly from that in T1 (2.18±0.26; Wilcoxon rank sum test, WT1 versus T3= 4.5, nT1, nT3= 11, PT1 versus T3< 0.001) and T2 (2.45±0.16; Wilcoxon rank sum test, WT2 versus T3= 2.5, nT2, nT3= 11, PT2 versus T3< 0.001). However, the average numbers of free-riders per group are similar in T1 and T2 (Wilcoxon rank sum test, WT1 versus T2= 46, nT1, nT2= 11, PT1 versus T2= 0.3). The collective deficit that free-riders produce per group (deviation from fair share) is also similar in T1 (€–14.55±1.91) and T2 (€–15.64±1.98; Mann-Whitney U-test, nT1, nT2= 11, z= –0.2670, PT1 versus T2= 0.8), whereas the collective surplus that fair players produce per group (deviation from fair share) differs significantly between T1 (€15.27±2.04) and T2 (€7.46±1.87; z= –2.472, PT1 versus T2= 0.013).
The higher group investments in T1 compared with those in T2 thus result from the more generous behaviour of the fair players in T1, whereas free-riders behave similarly. The strict simulated climate target in T1 motivates fair players more effectively to avoid a loss than when the target is seen as less strict, as it is in T2. The fair players respond to the stricter target in T1 by enhancing their effort, whereas the free-riders do not react (Milinski et al., 2016).
Discussion and conclusions
The alternative risk scenarios that are represented by T2 and T3 in our experiments reinterpret rather than revise the 2°C target (Geden, 2013). The value of 2°C is present in all treatments through the target sum of €120, above which the loss probability is 0. However, the risk arising from missing the target differs among treatments, implying differing consequences of an overshoot in warming. Whether such a reinterpretation, possibly accepting a permanent overshoot, is considered effective depends on which of two alternative perspectives is taken. The first perspective defines efficacy as achieving a limitation of warming to below 2°C compared to pre-industrial. The different treatments then correspond to different assessment by the subjects of the risk invoked by missing the 2°C target. The subjects reach the target sum more often in T1 than in either of T2 or T3, and they achieve a more substantial interpreted mitigation of warming in T1 than in T2 or T3. Assuming proportionality between group effort and mitigated warming, the average group contributions correspond to limiting the warming to 2.0, 2.2, and 2.8°C in T1, T2, and T3, respectively. The most effective strategy thus emerges in T1, which implements the assessment that any overshoot of the 2°C target invokes a high risk of dangerous climate change. Thus, a reinterpretation of the 2°C climate target is likely to cause stronger warming. Our finding that contributions toward the target are reduced if risk depends gradually on the target is consistent with earlier results stating that an uncertain location of the threshold, implemented through threshold uncertainty (Barrett and Dannenberg, 2012; Barrett, 2013; Barrett and Dannenberg, 2014; Dannenberg et al., 2015), reduces the effort to reach the target. Viewed from this first perspective, insisting less strictly on the 2°C target as in T2 and T3 is undesirable.
However, there exists a second perspective from which to interpret our results. This perspective defines efficacy as the optimal balance between the effort to avoid dangerous climate change and the risk posed by it. Differences among treatments then depict the uncertainty in assessing that risk. In T2 and T3, the subjects have played relatively successfully by achieving an average pay-out of €17.4 and €16.8, respectively, not too far from the maximum possible pay-out of €20.0 and €20.1, respectively. By contrast, the subjects are less successful in T1 with its higher overall risk level. The average pay-out is €12.4, substantially below the maximum of €20.0; this low average pay-out indicates that the groups could not establish sufficient cooperation despite the high risk.
Choosing between the two perspectives formulated here is not only a scientific matter of but also one of value judgement. This value judgement concerns how to deal with the substantial uncertainty in the connection between anthropogenic warming and the risk of dangerous climate change. A position averse to that risk would stipulate that the first perspective be applied and a reinterpretation of the 2°C climate target be rejected—all the more so if one takes into account that climate change invokes risks that cannot be quantified by a single temperature target (Steinacher et al., 2013; IPCC, 2014). By contrast, a position assuming that a warming greater than 2°C does not necessarily cause dangerous climate change would stipulate that the negotiation gridlock of the 2°C climate target can be overcome by reinterpreting the target and accepting an overshoot (Geden, 2013).
If—and this is a big caveat—the behaviour of our subjects is representative of the world’s governments trying to avoid dangerous climate change, our experiments suggest that a lower assessed risk arising from missing the 2°C climate target is likely to lead to stronger warming. If that assessment of a lower risk is justified—perhaps because 2°C warming does not sharply divide between high and no risk and also because “acceptable risk” depends on individual value judgements—the risk posed by dangerous climate change is balanced in our experiments against the effort to avoid it if the 2°C target is reinterpreted as being less strict.
Data Availability
The datasets analysed during the current study are available in the Harvard Dataverse repository, doi:10.7910/DVN/XFGQEX.
Additional Information
How to cite this article: Hagel K, Milinski M and Marotzke J (2017) The level of climate-change mitigation depends on how humans assess the risk arising from missing the 2°C target. Palgrave Communications. 3:17027 doi: 10.1057/palcomms.2017.27.
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Abou Chakra M and Traulsen A (2012) Evolutionary dynamics of strategic behavior in a collective-risk dilemma. Plos Computational Biology; 8 (8): e1002652.
Abou Chakra M and Traulsen A (2014) Under high stakes and uncertainty the rich should lend the poor a helping hand. Journal of Theoretical Biology; 341, 123–130.
Allen MR et al. (2009) Warming caused by cumulative carbon emissions towards the trillionth tonne. Nature; 458 (7242): 1163–1166.
Barrett S (2013) Climate treaties and approaching catastrophes. Journal of Environmental Economics and Management; 66 (2): 235–250.
Barrett S and Dannenberg A (2012) Climate negotiations under scientific uncertainty. Proceedings of the National Academy of Sciences; 109 (43): 17372–17376.
Barrett S and Dannenberg A (2014) Sensitivity of collective action to uncertainty about climate tipping points. Nature Climate Change; 4 (1): 36–39.
Burton-Chellew MN, May RM and West SA (2013) Combined inequality in wealth and risk leads to disaster in the climate change game. Climatic Change; 120 (4): 815–830.
Bynum A, Kline R and Smirnov O (2016) Passive non-participation versus strategic defection in a collective risk social dilemma. Journal of Theoretical Politics; 28 (1): 138–158.
Chen X, Szolnoki A and Perc M (2012a) Averting group failures in collective-risk social dilemmas. EPL; 99 (6): 68003.
Chen X, Szolnoki A and Perc M (2012b) Risk-driven migration and the collective-risk social dilemma. Physical Review E; 86 (3): 036101.
Chen X, Zhang Y, Huang T-Z and Perc M (2014) Solving the collective-risk social dilemma with risky assets in well-mixed and structured populations. Physical Review E; 90 (5): 052823.
Cointe B, Ravon P-A and Guérin E (2011) 2 °C: the history of a policy-science nexus. IDDRI Working Papers No.19/11 Paris, France: IDDRI Working Papers N°19/11.
COP21. (2015) 'Adoption of the Paris Agreement', https://unfccc.int/resource/docs/2015/cop21/eng/l09r01.pdf. Accessed 27 June 2016.
Dannenberg A, Loschel A, Paolacci G, Reif C and Tavoni A (2015) On the provision of public goods with probabilistic and ambiguous thresholds. Environmental and Resource Economics; 61 (3): 365–383.
Du J, Wu B and Wang L (2014) Climate collective risk dilemma with feedback of real-time temperatures. EPL; 107 (6): 60005.
Freytag A, Gueth W, Koppel H and Wangler L (2014) Is regulation by milestones efficiency enhancing? An experimental study of environmental protection. European Journal of Political Economy; 33, 71–84.
Geden O (2013) Modifying the 2 °C Target. SWP Research Paper: SWP Research Paper 5, Stiftung Wissenschaft und Politik.
Geden O and Beck S (2014) Renegotiating the global climate stabilization target. Nature Clim. Change; 4 (9): 747–748.
Guivarch C and Hallegatte S (2013) 2C or not 2C? Global Environmental Change - Human and Policy Dimensions; 23 (1): 179–192.
Hagel K, Abou Chakra M, Bauer B and Traulsen A (2016) Which risk scenarios can drive the emergence of costly cooperation? Scientific Reports; 6.
Hilbe C, Abou Chakra M, Altrock PM and Traulsen A (2013) The evolution of strategic timing in collective-risk dilemmas. Plos One; 8 (6): e66490.
IPCC. (2007) Climate change 2007: The physical science basis. In: Solomon S et al. (eds). Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge University Press: Cambridge, UK, New York.
IPCC. (2013) Summary for Policymakers. In Stocker TF et al. (eds). Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge University Press: Cambridge, UK, New York, pp 3–29.
IPCC. (2014) Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. IPCC: Geneva, Switzerland.
Jacquet J, Hagel K, Hauert C, Marotzke J, Röhl T and Milinski M (2013) Intra- and intergenerational discounting in the climate game. Nature Climate Change; 3 (12): 1025–1028.
Jaeger CC and Jaeger J (2011) Three views of two degrees. Regional Environmental Change; 11 (1, Suppl): S15–S26.
Meinshausen M et al. (2009) Greenhouse-gas emission targets for limiting global warming to 2 degrees C. Nature; 458 (7242): 1158–1162.
Milinski M, Hilbe C, Semmann D, Sommerfeld R and Marotzke J (2016) Humans choose representatives who enforce cooperation in social dilemmas through extortion. Nature Communications; 7, 10915.
Milinski M, Röhl T and Marotzke J (2011) Cooperative interaction of rich and poor can be catalyzed by intermediate climate targets. Climatic Change; 109 (3–4): 807–814.
Milinski M, Sommerfeld RD, Krambeck H-J, Reed FA and Marotzke J (2008) The collective-risk social dilemma and the prevention of simulated dangerous climate change. Proceedings National Academy of Sciences; 105 (7): 2291–2294.
Moellendorf D (2011) A normative account of dangerous climate change. Climatic Change; 108 (1-2): 57–72.
Ott K et al. (2004) Reasoning Goals of Climate Protection. Specification of Article 2 UNFCCC. Report for the Federal Environmental Agency, Berlin, Germany.
Peters GP et al. (2013) COMMENTARY: The challenge to keep global warming below 2 degrees C. Nature Climate Change; 3 (1): 4–6.
Peters GP et al. (2017) Key indicators to track current progress and future ambition of the Paris agreement. Nature Clim. Change; 7 (2): 118–122.
Ramanathan V and Feng Y (2008) On avoiding dangerous anthropogenic interference with the climate system: Formidable challenges ahead. Proceedings of the National Academy of Sciences of the United States of America; 105 (38): 14245–14250.
Randalls S (2010) History of the 2 degrees C climate target. Wiley Interdisciplinary Reviews - Climate Change; 1 (4): 598–605.
Rijsberman FR and Swart RJ (1990) Targets and Indicators of Climatic Change. Stockholm Environment Institute: Stockholm, Sweden.
Santos FC, Vasconcelos VV, Santos MD, Neves PNB and Pacheco JM (2012) Evolutionary dynamics of climate change under collective-risk dilemmas. Mathematical Models and Methods in Applied Sciences; 22 (supp01): 1140004.
Shaw C (2010) The dangerous limits of dangerous limits: Climate change and the precautionary principle In: Carter B and Charles N (eds). Nature, Society and Environmental Crisis. Wiley-Blackwell: Walden, MA, pp 103–123.
Shaw C (2013) Choosing a dangerous limit for climate change: Public representations of the decision making process. Global Environmental Change-Human and Policy Dimensions; 23 (2): 563–571.
Steinacher M, Joos F and Stocker TF (2013) Allowable carbon emissions lowered by multiple climate targets. Nature; 499 (7457): 197.
Stocker TF (2013) The closing door of climate targets. Science; 339 (6117): 280–282.
Tavoni A, Dannenberg A, Kallis G and Loeschel A (2011) Inequality, communication, and the avoidance of disastrous climate change in a public goods game. Proceedings of the National Academy of Sciences of the United States of America; 108 (29): 11825–11829.
Tol RSJ (2007) Europe's long-term climate target: A critical evaluation. Energy Policy; 35 (1): 424–432.
UNFCCC. (1992) United Nations Framework Convention on Climate Change. United Nations: New York.
Vasconcelos VV, Santos FC, Pacheco JM and Levin SA (2014) Climate policies under wealth inequality. Proceedings of the National Academy of Sciences of the United States of America; 111 (6): 2212–2216.
Wang J, Fu F and Wang L (2010) Effects of heterogeneous wealth distribution on public cooperation with collective risk. Physical Review E; 82 (1): 016102.
Wang J, Fu F, Wu T and Wang L (2009) Emergence of social cooperation in threshold public goods games with collective risk. Physical Review E; 80 (1): 016101.
WBGU. (1995) Szenario zur Ableitung globaler CO 2 -Reduktionsziele und Umsetzungsstrategien - Stellungnahme zur ersten Vertragsstaatenkonferenz der Klimarahmenkonvention in Berlin (Scenario for deducing CO 2 reduction targets and implementation strategies - position for the first conference of the parties of the FCCC in Berlin) Dortmund: Wissenschaftlicher Beirat der Bundesregierung Gobale Umweltveränderungen, http://www.wbgu.de/sondergutachten/sg-1995-co2-reduktion/.
Acknowledgements
We thank the students from the universities Kiel and Hamburg for their participation, and H. Brendelberger and S. Dobler for logistic support. Thanks are also due to N. Maher and the reviewers for carefully reading the manuscript, which helped us to improve our paper. This study was supported by the Max Planck Society for the Advancement of Science; K.H. received funding through the International Max Planck Research School for Evolutionary Biology.
Author information
Authors and Affiliations
Contributions
J.M. conceived the study, K.H., M.M., and J.M. designed research, K.H. programmed the game by the experimental software z-Tree, K.H. and M.M. performed research, K.H. analysed data, K.H., M.M. and J.M. wrote the paper. All authors commented on the interpretation of the results and on the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Supplementary information
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Hagel, K., Milinski, M. & Marotzke, J. The level of climate-change mitigation depends on how humans assess the risk arising from missing the 2°C target. Palgrave Commun 3, 17027 (2017). https://doi.org/10.1057/palcomms.2017.27
Received:
Accepted:
Published:
DOI: https://doi.org/10.1057/palcomms.2017.27
This article is cited by
-
Staring at the Abyss: a neurocognitive grounded agent-based model of collective-risk social dilemma under the threat of environmental disaster
Journal of Economic Interaction and Coordination (2022)
-
The economic interaction between climate change mitigation, climate migration and poverty
Nature Climate Change (2020)