Abstract
We live in a complex economic system where externalities play a key role in fostering growth in complexity through increasing interdependence of interacting agents. This study tests this hypothesis for the case of Colombia. We ask whether knowledge externalities lead to growth in economic complexity. If yes, which variety of knowledge externalities—Marshall-Arrow-Romer (MAR), Porter or Jacobs? Results from our empirical investigation uphold the MAR theories of externalities or intra-industrial externalities, which are maximized with high local specialization1 and local monopoly. A pattern of convergence in economic complexity of Colombian municipalities emerges from our results, supporting Schumpeterian growth theories, which advocate that knowledge externalities drive convergence. This is in line with the recent macroeconomic trends of the Colombian economy, which is suffering from “Dutch disease” leading to a contraction in its domestic economy. We show that knowledge externalities are a mechanism through which convergence dynamics are brought about and fostered in the domestic economy.
Similar content being viewed by others
Introduction
The study of complex systems has brought a renewed focus on the role of externalities. The “divergence between social and private costs or benefits” affecting other agents in the system or other subsystems necessitates the understanding of the whole system to which they are endogenous. Brewer (1973) suggests the following in his analysis of social systems: “Because social systems exhibit properties of organized complexity (our emphasis), perturbations at one point in a structure may have effects elsewhere. Participants often perceive these effects as occurring ‘outside’ of their particular system, and almost as often, are surprised by these externalities”. Footnote 1
More recently, Antonelli (2011) argues that the “new growth theory” that builds upon Arrow’s (1962) legacy fails to appreciate the endogenous, idiosyncratic and dynamic character of knowledge spilloversFootnote 2. Starting from this gap in the literature, the motivation of this study is then twofold: on one hand, it attempts an in-depth analysis of the notion of externalities and on the other, it attempts to understand their role in a “complexity framework”. We focus on each of these three characteristics (endogeneity, idiosyncrasy and dynamism) in proposing such a framework. Specifically, we test if knowledge externalities lead to growth in economic complexity.
The literature on positive knowledge externalities has drawn particular attention towards their role in fostering growth, particularly in cities (Jacobs, 1970; Bairoch and Braider, 1991; Glaeser et al., 1992). While this is simultaneously situated in the broader literature of Economic Geography, a complexity-angle might lend new insights into the same. Other scholars have vouched for them even more forcefully as “engines of growth” (Romer, 1986; Lucas, 1988). All these theories deal with technological externalities, whereby innovations and improvements occurring in one firm increase the productivity of the other firms without full compensation (Glaeser et al., 1992). Accordingly, knowledge externalities are expected to facilitate the recombination of different bits of productive knowledge that lead to growth.
The key idea of this article is that availability of knowledge externalities (as a specific type of externality) leads to growth (positive or negative) in complexity. In this sense, they are a complexity fostering mechanism, albeit not the only one. We shall test this hypothesis by regressing complexity growth—as measured by the Regional Economic Complexity Index (RECI)—on the system’s characteristics (or available “variety”) that are conducive for knowledge spillovers as per endogenous growth theories. Furthermore, we investigate which variety of knowledge spillovers leads to complexity growth in the case of Colombia: Marshall-Arrow-Romer (MAR), Jacobs or Porter.
The literature stands indecisive as to which variety of knowledge externalities are most important for economic growth—which can together be referred to as the theories of dynamic externalities (Glaeser et al., 1992)—for they explain economic growth in the region, in comparison to the theories of static externalities which focus on why industry specializes and its choice of location. Location externalities are discussed by Lichtenberg (1960), Henderson (1986,1991), Arthur (1990), and Rotemberg and Saloner (2000), among others. Another group of static externalities—urbanization externalities—are discussed by Lichtenberg (1960), Murphy et al. (1988) and Krugman (1990, 1991).
Since it is often not possible to directly observe the origin and scale of externalities in a complex economic system, we infer their existence and variety from the conditions that must hold true for them to be available in the system. Which is to say that if knowledge externalities are available, (a) diversity of the economic base of the region and; (b) local competition within the geographical area under investigation should be significant predictors of growth in economic complexity.
On a broad note, we seek to test the following model:
Given that the extent and impact of externalities is very difficult to trace in a complex system (because of its intricate interdependencies and in particular, emergent behaviour), the direct measurement of externalities is a challenging task. The chain of causality is extremely hard to trace, if not completely lost. Hence, we explicitly assume that knowledge spillovers are not directly observable and infer their presence through the system’s characteristics.
The next section clarifies the meaning of a complex system and our working definition of economic complexity, listing key characteristics of complex systems, before turning to the dynamics of complexity growth.
Understanding economic complexity
Definition
The literature on the applications of complexity science to economics contains no strict definition of “complexity”. The term “complexity” ultimately refers to the connective structure (or lack thereof) of a system (Foster, 2005). What distinguishes complex systems is the way they exhibit emergent self-organizing behaviour, driven by co-evolutionary interactions, and an adaptive capacity that enables them to rearrange their internal structure spontaneously (Martin and Sunley, 2007). Complexity arises whenever a system—technical, social, or natural—has multiple interdependent parts. The human body, bees in a hive, a soccer team, and international banking are all examples of complex systems—they consist of many components and interdependencies that can change unpredictably and frequently (Sull and Eisenhardt, 2015). This resonates closely with Antonelli’s (2011) criticism of the new growth theories, emphasizing the idiosyncratic character of knowledge spillovers in complex systems, which themselves exhibit such behaviour.
There is, however, a broad consensus on the characteristics that identify a particular system as complex or not. Johnson (2007) defines complexity science as “the study of the phenomena which emerge from a collection of interacting objects” Footnote 3 listing the following features/components, which characterize any complex system: (a) The system contains a collection of many interacting “agents”; (b) The agents’ behaviour is affected by memory or “feedback”; (c) The agents can adapt their strategies according to their history; (d) The system is typically “open”; (e) The system appears to be “alive”; (f) The system exhibits “emergent phenomena”, which are generally surprising, and may be extreme; (g) The emergent phenomena typically arise in the absence of a central controller and (h) The system shows a complicated mix of ordered and disordered behaviour.
With these characteristics in mind, it is not hard to see that we live in a complex system—the global economy—and equally complex sub systems like national economies. While a simple example of a stock market crash easily exemplifies all of these features simultaneously; this study emphasizes one fundamental aspect of complex systems: the interdependence of agents, which is fostered through interactions. And were it for the lack of direct interactions, as one might argue in the case of externalities where the action of one economic agent affects the other, there is one thing that is flowing through the system that makes it complex: information Footnote 4. The result is a system that appears to be “alive” or as if with a life of its own. Hence, interdependencies between interacting agents is a necessary condition for complexity behaviour to arise within a system. Once the economy or an ecosystem is identified as a complex system, modelling complexity can take the form of taking into account these interdependencies to understand economic phenomena and predict economic outcomes. Importantly, the degree of complexity of the system depends on the scale we analyse it at.
Economic complexity is, thus, the study of interdependencies among interacting economic agents in all spheres of economic activity.
Measuring economic complexity
The application of complexity science to economics is relatively new, compared to other disciplines (for example, biology). So far, no one measure of economic complexity can be credited with being the most robust one, exactly because what makes a system complex also makes it unpredictable and idiosyncratic, embedding various levels interdependencies which are challenging to model. Accordingly, a good measure of economic complexity would then be the one that can explicitly takes in account the interdependencies in the system. For not only the agents in the system are important, but equally important are the linkages between them, and these linkages cannot be the property of any one individual (Antonelli, 2011).
This invariably calls for a networks-based analysis of the system. Indeed, Networks Theory has become the basic warehouse of complexity science just as the IS-LM framework for the general equilibrium models.
This study adapts the Economic Complexity Index (ECI) as a proxy for the measurement of economic complexity. A very specific formulation of economic complexity, where “the complexity of an economy is related to the multiplicity of useful knowledge embedded in it; expressed in the composition of its productive output and reflected in the structures that emerge to hold and combine knowledge” (Hausmann et al., 2014); it analyses and infers the knowledge embedded in networks of individuals and organizations as reflected in the mix of products an economy is able to make. In other words, the ECI reflects the total amount of productive knowledge in an economy.
Why is the growth of economic complexity good for an economy? The literature has established that the way countries progress is by slowly moving up the value chains – from low complexity to high complexity products. Variety growth is then required for the long term continuation of economic development (Saviotti and Frenken, 2008). Or, in other words economic growth has a direction. Countries commonly considered as developed are extremely diversified, exporting a large variety of products from very simple to very complex. At the same time countries generally considered “less developed” export only the products also exported by the majority of other countries (Cristelli et al., 2013). Hausmann et al. (2014) claim that the complexity of the country is a more robust predictor of growth (measured in GDP per capita) compared to traditional measures like human capital (years of schooling), governance and institutional quality, natural resource endowment and so on. A host of empirical works have confirmed the relationship between ECI and GDP growth (Mejía, 2011; Regional Economic Outlook, 2015). Hence, increase in economic complexity is a necessary (but not sufficient) condition for the growth of economies.
Figure 1 shows the relationship between GDP per capita and ECI for 128 countries. Countries where natural resource exports are larger than 10% of GDP (red) tend to be significantly richer than what would be expected given the complexity of their economies, while countries where natural resource exports are lower than 10% of GDP (blue) have a combined R-square of 0.75. In other words, the Economic Complexity Index accounts for 75% of the variance. ECI correlates strongly with the income of both groups. Source: Hausmann et al. (2014), reproduced from the Atlas of Economic Complexity. This figure is covered by a Creative Commons Attribution-ShareAlike 3.0 Unported License.
The question is all the more important for developing countries and emerging economies. Although we only analyze the case of Colombia in this particular study, similar analysis can be undertaken for any country. Several other countries in the region have experienced a decline in diversification and complexity over recent years, including large or fast-growing economies, such as Brazil, Mexico, Chile and Peru. The findings are then relevant for the entire Latin American region which suffers from a relatively narrow economic base with strong dependence on commodity exports compared to advanced economies and the newly industrialized Asian countries (which can be thought of as a reference point for successful economic convergence), but similar to what is observed among other emerging markets and developing economies (Regional Economic Outlook, 2015).
The dynamics of complexity growth
What does it mean for economic complexity to grow or evolve? How do we know if a system is more/less complex over time? How can we compare two systems in terms of their relative complexities? The answers to these questions require a dynamic understanding of complexity.
The next section discusses how the literature in the past 100 years has witnessed an emerging consensus on the role of positive knowledge externalities in regional economic growth. Since we explicitly start with the assumption that the economy depicts the characteristics of a complex system, we now ask: How does the complexity of a system grow? Keeping in mind Hausmann et al.’s formulation of economic complexity presented in Section 2.2, growth in complexity is, accordingly, the growth in the total amount of productive knowledge in the economy. From the literature, we know that knowledge grows through re-combinatory processes where new knowledge builds on previous knowledge.
Hence, if indeed economic complexity or the total amount of productive knowledge in the economy grows over time, there has to be a mechanism to foster complexity growth. This study suggests that externalities (both positive and negative)—the divergence between private and social costs/benefits which then become part of the utility/production function of the agents it affects—are one such mechanism, for it creates ever increasing interdependencies between agents and various subsystems.
How are externalities a complexity fostering mechanism?
On a broad note, the presence of externalities means that the impact of the actions of one economic agent has direct or indirect bearings on the other agents in the system. Increasing interdependence is caused by the presence of external effects in the system and is in fact, the consequence of the presence of externalities. Externalities are thus, endogenous to the system. They arise from the system, impacting its macro structure and in turn yield newer and greater external effects. As Brian Arthur says, “the system is constantly reinventing itself”. And given that interdependence of agents is a key feature of a complex system, greater interdependence is invariably associated with higher interactions, resulting in greater spillovers. A city is an excellent example of a complex system where production is highly specialized and no one agent is completely self-sufficient. Greater the density of population in a city, higher the number of interactions among agents.
Knowledge externalities in economic thought: a brief summary of the literature
Positive externalities largely focuses on the role of knowledge spillovers in economic growth and the challenges in appropriation of knowledge, thus calling for policy support in terms of direct investment or subsidies, along with strict property rights.
The nature of information (or knowledge) as an economic good has been elaborated upon by Arrow (1962) as limited by the three classical reasons for the failure of perfect competition to achieve optimality in resource allocation: indivisibilities, non-appropriability and uncertainty.
This challenge of information/knowledgeFootnote 5 “appropriability” or the inevitable “divergence between private and social costs/benefits” has been explored in the literature over the decades. Knowledge externalities directly contribute to economic growth of the local region in terms of the knowledge (technological or otherwise) that the agents receive from others without paying for it, thanks to the very nature of knowledge which is not fully appropriable. This means that not all agents have to pay the full cost of acquiring knowledge, making this positive externality available in the system. At the same time, previous knowledge is a necessary input for creating new knowledge. We create new knowledge by standing on the shoulders of the giants (Antonelli et al., 2015). Importantly, the degree of the available knowledge spillovers depends on the relative geographical proximity to the producer of knowledge (Jaffe et al., 1993; Audretsch and Feldman, 2004); spillovers are stronger in close proximity to knowledge producers. Firms are able to appropriate only a fraction of the knowledge they produce, which then spills over into the system. The insight comes from Griliches (1979) who highlighted the role of positive knowledge externalities as the divergence between social and private returns on R&D expenditures (Antonelli, 2011). Accordingly, greater knowledge spillovers can be expected in dense areas, characterized by high interactions.
The varieties of knowledge externalities and expected coefficients
The debate in the literature concerning spillovers that are key to the growth of economic systems, mainly focuses on three varieties of it: MAR, Porter and Jacobs. MAR externalities are maximized with high local specialization and local monopoly, while according to Jacobs (1970), knowledge externalities are most easily available between industries, while local competition plays an important role in the early adoption of new technology. Porter (1990), on the other hand, favours specialization along with local competition. Although all of them have implications for economic growth, the theories of dynamic knowledge externalities differ along two lines: first, they differ in whether knowledge spillovers come from within the industry or from other industries; second, they differ in their predictions of how local competition affects the impact of these knowledge spillovers on growth (Glaeser et al., 1992).
Introduced by Marshall (1890), and subsequently developed by Arrow (1962) and Romer (1986), “MAR externalities” were consolidated by Glaeser et al. (1992) in their search for dynamic externalities as a factor explaining growth of city-industries in the United States. The Marshallian thesis emphasizes the concentration of an industry in a geographical region that allows knowledge to spill over between firms within the industry as Audretsch and Feldman (2004) quotes Krugman (1991) in his proposing a new theory of economic geography: “What is the most striking feature of the geography of economic activity? The short answer is surely concentration... production is remarkably concentrated in space”. At the same time, MAR theories favours local monopoly over local competition as monopoly rights provide innovators the economic incentive for further innovation. Porter, on the other hand, favours local competition over local monopoly. According to him, it is competition that provides the incentive to innovate (firms compete to survive). He favours specialization over diversification. Jacobs, in her theories concerning growth of cities, argues that it is the cross-fertilization of ideas across industries that sets the stage for knowledge spillovers to flow. Jacobs (1970) believes that the most important knowledge transfers come from outside the core industry (Glaeser et al., 1992).
In summary, MAR externalities are maximized with high local specialization and local monopoly while according to Jacobs (1970), knowledge externalities are most easily available between industries with local competition playing an important role in the early adoption of new technology. Porter (1990), on the other hand, favours specialization along with local competition.
Accordingly, in our empirical investigation, we expect negative signs of the coefficients of Diversity and Competition in case MAR externalities are available in the system. On the other hand, we expect positive coefficients of Diversity and Competition in case the system is characterized by Jacobs externalities. Porter externalities is an intermediate case, where we expect a negative coefficient of Diversity and a positive coefficient of Competition. Table 1 provides a quick summary of the types of knowledge externalities and the expected signs of the coefficients of Diversity and Competition corresponding to each.
The empirical evidence on the famed “MAR versus Jacobs” debate remains very context specific. For example, Van der Panne (2004) finds evidence in the favour of Marshallian specialization in the Dutch case, where regional innovativeness is investigated through innovation counts, with high “local competition” within an industry playing a negative role in its innovativeness. Similarly, Henderson (1986) finds evidence for increase in factor productivity because of specialization in Brazil. In contrast, Glaeser et al. (1992) find evidence that supports inter-industrial spillovers for the case of 170 U.S. cities, consistent with Jacobs’ views.
Paci and Usai (1999) find evidence supporting both Specialization (Marshall) and Diversity (Jacobs) externalities at the same time, in the case of Italy. Antonelli et al. (2015) conclude the same for their study of patent data from 27 European Union countries, using the “size of the regional stock of knowledge” as a proxy for Marshall externalities and ECI as a proxy for Jacobs externalitiesFootnote 6.
Convergence or divergence driven by knowledge externalities
A related stream of literature on technological convergence or divergence (and their causes and dynamics thereof) is readily applicable to this study. It explores the possibility of convergence of productivity among firms, thanks to the knowledge externalities available from more productive firms to the less productive ones. These are the so-called Schumpeterian growth models, where convergence is expected from knowledge spillovers. For instance, Fung (2005) shows that R&D expenditures being the same, the followers in technology will eventually catch up with the leaders, because they receive knowledge spillovers from the leaders.
Another stream of literature builds on the neoclassical growth models pioneered by Solow (1956), where convergence is a result of decreasing returns in physical or human capital accumulation. Antonelli (2011) discusses the process of technological convergence among firms through knowledge recombination, which exploits complementary technologies (moving more and more towards the periphery of the core technologies), with diminishing returns to recombination that eventually set in. Hence, both sets of growth models discuss convergence but with different factors leading to it. Accordingly, we only check for the Schumpeterian explanation of a possible convergence in our study, which occurs due to the availability of knowledge externalities.
Since ECI is, in fact, a measure of the total amount of knowhow in an economy (technological or otherwise), as reflected in its product composition, we maintain that the literature on technological convergence or divergence has key insights to offer. Accordingly, we seek to find evidence suggestive of either variety of knowledge externalities and understand their role in the growth of complexity in Colombia.
Economic complexity and knowledge externalities in Colombia: empirical evidence
Colombia provides an interesting case study for economic complexity growth. The country witnessed a steady GDP growth over the past few years (one of the highest in Latin America; 6.9% in 2007) albeit suffering from a painful depression in 1999. In our study, we seek to analyse growth in economic complexity of Colombia from 1997 to 2011. Although we envision a probable impact of the recession in the years immediately following it, we think that the period spanning 12 years from 1999 to 2011 is also expected to have provided adequate time for economic recovery. As a historically agrarian economy, the industry is Colombia is less mature compared to its American and European counterparts over the period of 1997–2011. During the same years and more recently too, the Colombian economy has seen a boom in the export of petroleum oils (crude and refined) and coal briquettes leading to an appreciation in its currency and contraction of its domestic economy (in terms of employment, output as well as exports from non-natural resource sectors), thus presenting a classic case of “Dutch disease”.
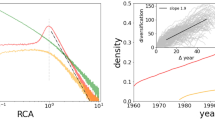
Figure 2 illustrates the share of fuels and manufactures exports as a percentage of merchandise exports of Colombia from 1962–2011. Clearly, the percentage share of fuel exports by Colombia is rapidly increasingly, simultaneously crowding out manufactures exports, particularly in recent years.
We believe that these are important dynamics of the Colombian economy that should serve as the broader context in which the study can be situated, even though we only concern ourselves with the manufacturing sector of Colombia. More specifically, our thrust remains on understanding the domestic dynamics as evident from knowledge externalities rather than broader macroeconomic trends which have, nevertheless, been analysed by various other studies. There is a broad consensus in the literature that the Colombian economy is undergoing a process of deindustrialization (Botta et al., 2014). The average RECI growth in Colombian municipalities (the geographical unit for our analysis) from 1997–2011 is in fact, negative at −0.38. This is in line with the trend of boom in natural resource exports and an overall decline in manufacturing sector exports (Fig. 2). The “Convergence hypothesis” is discussed as a possible explanation of such a trend in the conclusion.
Figure 3 provides a comparative picture of Colombia’s exports in years 1997 and 2011 respectively. Panel A depicts the exports data as a Tree-map while Panel B is a Product Space visualization. The trend of increasing specialization or reduced diversification of Colombia’s export basket is clearly evident, even though the volume of trade grew five-fold over this period. Source: Hausmann et al. (2014), reproduced from the Atlas of Economic Complexity. This figure is covered by a Creative Commons Attribution-ShareAlike 3.0 Unported License.
Data
Construction of the data set
Years of observation
The panel dataset studied is derived from the Annual Manufacturing Survey or Encuesta Anual ManufactureraFootnote 7 of Colombia on output, employment, wages and number of firms per municipality per ISIC 4-digit industry classification (revision 3) for all years from 1995–2013.Footnote 8 The largest difference in economic complexity is intuitively assumed to be observed over longer periods, allowing sufficient time for new and highly complex industries to emerge and develop. In other words, structural change can only be witnessed in the medium or the long term. Which is why longer the time frame, the more meaningful the comparison is expected to be.
Our dataset compares years 1997 and 2011, rather than 1995 and 2013 because of the non-availability of data on certain industries in years 1995–1996. This is clear from Fig. 4. Also, the year 2012 witnessed the transition from the 3-digit industry classification to 4-digit classification, resulting in some significant outliers. Hence, 1997 and 2011 will serve as our years of comparison in this study.
Figure 4 plots the available data on all 2-digit level manufacturing industries, 1995–2011. Year 1995 and 1996 have been dropped from the dataset because of the non-availability of data on industries 15–30 as per the ISIC 2-digit classification.
Choice of municipalities
The largest spillovers or externalities are expected in the biggest municipalities. For if indeed it is true that knowledge externalities are available because of interactions among agents, stronger evidence should be available in areas where there are greater number of interactions (Jacobs, 1970, 1984; Glaeser et al., 1992), thus justifying the creation of a subset of the largest municipalities. Smaller municipalities with a small number of workers are less interesting for our study. We let the data speak for itself in this case. A quick look at Fig. 5 highlights that the top 50 municipalities (ranked by the number of employees) is an appropriate sample for testing our hypothesis.
Figure 5 ranks all municipalities (total <250) by employment or the total number of workers (across all manufacturing industries) in each municipality, where the municipality with the highest employment is ranked 1. Clearly, there is a huge difference between the biggest and the smallest municipality, with Bogotá, D.C. being the biggest municipality and Valledupar being the smallest municipality in Colombia in terms of employment across all manufacturing industries in 1997.
Setting the cut off at the 50 biggest municipalities in 1997, we obtain a matrix of 1100 observations (50 municipalities × 22 industries). These 50 municipalities are then matched with their 2011 entries—only retaining data on these 50 municipalities in order to study the complexity dynamics in the same municipalities over time. Accordingly, we obtain a matrix of 1100 observations for 2011 as well.
Aggregation by industry
Since the original data is disaggregated at the 4-digit industry code—which is required for calculating the RECI—we aggregate the variables “output”, “wages”, “employment” and “number of firms” up to the 2 digit classification of industries which is then used for calculating our “Competition” and “Diversity” indexes. As a result, we obtain the values of these variables per municipality per 2-digit industry. This municipality-industry data is subsequently used to test the hypothesis: Are inter or intra industrial externalities (from the available “urban variety” and local competition during the base year) significant predictors of change in complexity over time?
Since our data is at the lowest available geographical level of disaggregation (municipalities), it arguably lends a very close look at the dynamics occurring at the regional level. This stands in contrast with Glaeser et al.’s, 1992 paper where they create “cities” by aggregating American counties for testing the conditions for knowledge spillovers. At the same time, our study retains all 22 industries which constitute “manufacturing” (according to the ISIC 4-digit classification), as against only the 6 fastest growing city-industries in Glaeser et al., 1992.
Description of the data
To get a better sense of the data, descriptive statistics of key variables are briefly summarized in this section.
Table 2 provides a summary of the variables. The values of RECI—our dependent variable—range between −9.407 and 4.620 with mean value of −0.384 and standard deviation of 2.548. The negative mean of RECI growth underlines an average fall in the complexity of Colombian municipalities. Explanatory variable average “Diversity” of a municipality assumes values between 0.057 and 0.213, where the most diverse municipality has the smallest value and the least diverse municipality has the highest value. The mean of variable average Diversity is 0.135 with a standard deviation of 0.047. The second explanatory variable average “Competition” in a municipality across all industries has minimum value of 0.046 and maximum value of 9.835, with a mean of 2.841 and standard deviation of 2.119. Higher values of this variable point towards greater competition across all industries in a municipality. A detailed discussion of all variables and their construction follows later in this section.
Tables 3 and 4 compare the five largest and five smallest municipalities by total employment in 1997 to their subsequent total employment in 2011, respectively. Notably, all of them saw a significant decrease in their employment from 1997 to 2011 except for two of the smallest municipalities in our sample (El Cerrito and Cajicá). This is in line with the macroeconomic trends in the Colombian economy, which is witnessing a contraction in manufacturing sector employment and exports.
Table 5 lists the ten largest municipality-industries by their output (in Colombian pesos) in 1997 in our sample. With the data at municipality-industry 2-digit levelFootnote 9 for each year, it gives a descriptive picture of the biggest industries with their respective municipalities. “Food products and beverages” in Bogotá, D.C. is the biggest municipality-industry in Colombia in 1997. As the table shows, it is also the biggest municipality-industry in Cali, Medellín and Barranquilla, thus appearing 4 times in the list in total. “Chemical and chemical products” is the second biggest municipality-industry in Bogotá, D.C. and the fourth largest in Cali. The remaining four largest municipality-industry are “Coke, refined petroleum products and nuclear fuel” (Barrancabermeja), “Motor vehicles, trailers and semi-trailers” (Bogotá, D.C.), “Textiles” (Bogotá, D.C.) and “Rubber and plastics products” (Bogotá, D.C.). Their respective outputs are listed in table 5.
Tables 6 and 7 list the five municipalities that witnessed the highest RECI growth from 1997 to 2011 and the five municipalities that witnessed the lowest RECI growth over the same period.
RECI growth
Contrary to intuition, the average complexity of the 50 largest municipalities in Colombia actually reduces from 0.071 in 1997 to 0.051 in 2011. This means a −0.38 growth in RECI. This can be understood as the decrease over time in the number of products, and how complex they are in turn, that Colombia produces competitively (as measured by RECI), rather than decrease in the growth rate of municipalities in terms of their GDP. Indeed, the municipalities might in fact be growing, but with a decreasing diversity in their product basket.
Figure 6 plots the RECI values of municipalities under all years of observation. An emergent convergence trend is visible, starting in year 2002 and particularly remarkable around year 2003 following all the way to year 2010.Footnote 10
Construction of the variables
ECI
We adapt the ECI proposed by Hausmann et al. (2014) as the RECI for our study, as in Farra et al. (2015). Although most studies have used the index for country level analysis (measuring what a country competitively exports with RCA>1), it can easily be adapted for any geographical unit (measuring what a region competitively produces with RCA>1). Given that it is increasingly recognized that the engines of national economic performance are sub-national technology districts that are characterized by strong ties between regional actions (Scott, 1993; Storper, 1995 and Feldman, 1999), we argue that our study design (anchored at the municipality level) provides a more rigorous assessment of the availability of knowledge externalities.
Formally:
Define a Matrix Mrp that is I if a region r produces product p, and 0 otherwise. Diversity and Ubiquity are measured as the sum of rows and columns of this matrix.
These two measures are simultaneously used to correct the other. For a given region, calculate the average ubiquity of the products it exports and the average diversity of the regions that produce those productsFootnote 11 . This can be expressed as follows:
Inserting (4) into (3), to obtain:
Rewriting:
where,
Equation (7) is satisfied when This, in turn, is the eigenvector of which is associated with the largest eigenvalue. This eigenvector is a vector of 1s, hence the eigenvector associated with the second highest eigenvalue captures the largest amount of variance in the system. This is Hidalgo-Hausmann (HH) measure of economic complexity.
Thus, RECI is defined as
(where < > represents an average, stdev stands for the standard deviation)
And: =Eigenvector of associated with the second largest eigenvalue.
The absolute values of RECI are then used to rank regions in terms of their relative complexity vis-a-vis other regions. Higher complexity renders a region a higher rank in RECI and lower rank corresponds to lower complexity. The region with the highest RECI value is ranked 1 and so on.
For the purposes of this study, a measure of change in complexity over time is sought. The RECI value corresponding to each municipality is only meaningful in relation to all other municipalities over time. Hence, we normalize RECI values of both base year (1997) and the current year (2011) by their mean by dividing each value of RECI by the mean value of the distribution. We then calculate the growth rate of RECI from 1997 to 2011 for each municipality using normalized RECI values. This is our measure of RECI growth. It can be expressed as follows:
where RECI’ are normalized by their means.
Competition
This index calculates how competitive each industry is in each municipality. The study adapts Glaeser et al.’s (1992) measure of local competition in a municipality as the number of firms per worker in an industry in a given municipality relative to the number of firms per worker in this industry in all 50 Colombian municipalities in our sample.
where “Colombia industry” refers to the 50 Colombian municipalities in our sample and not the total number of municipalities in Colombia.
We then take the average of the “Competition” in each municipality-industry, to arrive at the average competition in each municipality across all industries. This ensures that the analysis is at the same level—municipality—as the other variables in our regression equationFootnote 12.
One of the benefits of using this index is that it is calculated in relation to the national (sample) average; in other words, it normalizes local competition with the national average. This “correction” is extremely useful when applied to a developing country manufacturing dataset because many industries are still in their infant stageFootnote 13 .
Competition hence, represents number of firms per worker per industry per municipality compared to the sample average (50 biggest municipalities). Average Competition represents the number of firms per worker (across all industries) in the municipality in question, compared with the sample average. Accordingly, greater average competition represents more firms per worker in a municipality and vice versa. This measure ranges between 0.04 and 9.83 in our dataset.
Diversity
The current study devises a new variable of “diversity in production” for each municipality (not to be confused with the diversity statistic that goes in the construction of RECI). Just like the RECI and Average Competition, “Diversity” is calculated at the level of municipality.
We calculate this variable is by taking the ratio of the output of a single industry in a municipality relative to the total output of that municipality across all industries, thus arriving at a vector of relative shares of all industries in a municipality. Since we do not have any information about the distribution of such a vector, we simply take the standard deviation of this distribution. The result is a unique value for each municipality that we use as a measure of the “diversity” of a municipality. The closer this value is to 0, the more diverse the municipality and the farther it is from 0, the less diverse the municipality. The limit cases would be a municipality whose output is say, equally split between all 22 industries and a municipality all of whose output comes from one industry. In the former case, the standard deviation of such a distribution (1/22, 1/22, 1/22…) would be 0, whereas in the latter case, the standard deviation of a municipality all of whose output comes from one industry (1, 0, 0…) would be 0.213.
Suppose we are calculating the diversity of the ith municipality with n number of industries where the share of each industry’s output is denoted by and OT is the total output of the ith municipality, then, formally:
Figure 7 plots the number of municipalities against their respective diversity values, for 1997 and 2011 respectively to lend a visual sense to the distribution of the variable, Diversity.
The key strength of this measure is its intuitive appeal; the standard deviation accounts for the “spread of the distribution” of the relative share of each industry in a geographical area under consideration. The index simultaneously accounts for the presence of an industry (however small or large, as long as it generates some output) while preserving information regarding the relative output of each industry in the total manufacturing output of the geographical area.
In a host of related studies, alternative variables have been used by scholars for measuring specialization, diversity and competition. Paci and Usai (1999) use the production specialization index (PS) and a separate production diversity index (PD). Van der Panne (2004) employs the same PS and PD indexes from Paci and Usai (1999) along with “Competition” measured on similar lines as Glaeser et al. (1992). These studies maintain that a geographical region can be simultaneously diverse and specialized in a particular industry. Similar analysis can be undertaken for our study. A variable for “Specialization” can be added, which would check for industry-level specialization within a municipality, for example. However, it would likely necessitate aggregating the data into bigger geographical units than municipalities to allow for this variability.Footnote 14
One criticism of the regression model can be a potential endogeneity problem as a certain measure of “diversity” goes in the construction of the RECI, and another is one of the key explanatory variables in our regression model. To address this, the most important thing to consider is the following: where the HH variable of “diversity” is the simple summation of the total number the products that a municipality produces (with higher values representing greater diversity), our variable of diversity is the standard deviation of the distribution of the relative shares of each industry in a given municipality (with lower values representing greater diversity and higher values representing lower diversity). By using growth in RECI as our dependent variable (rather than the absolute values of RECI in 2011), a possible endogeneity problem should stand corrected as we are only measuring the change in complexity as our dependent variable.
Control variable—Normalized RECI, 1997
The normalized RECI of the base year (1997)—the variable NormRECI1997—serves as an important control in the RECI-growth regression model. Controlling for the complexity of the municipalities in the base year facilitates the measurement of the pure impact of externalities, which in turn is because of average Diversity and average Competition within the municipalities. At the same time, the relationship between base RECI values and RECI growth is clarified by the coefficient of this variable. This helps in identifying the general trend of complexity growth in Colombian municipalities, thus lending a bigger picture view.
RECI-growth regression model
The study uses regression analysis to test the stated hypothesis: Do knowledge externalities lead to growth in economic complexity of Colombian municipalities?
The general model is as follows:
Where, RECIgrowth is the dependent variable—a proxy for measuring growth in economic complexity in the system. Diversity and Competition are the two explanatory variables, representing the characteristics (or the available variety in the system) which make available dynamic knowledge externalities and NormRECI1997 is the normalized (by mean) RECI of the base year (1997) in our analysis, starting from which we infer which variety of knowledge externalities—if at all—were available in Colombian municipalities. It serves as a key control in the model, but not only. Its coefficient also points out (as we shall see in the results) the unexpected but interesting and explicable negative relationship between RECIgrowth and RECI 1997 (base year) values. θ is the error term.
Table 8 summaries the results of the linear regressionFootnote 15 models. The following points summarize the results
-
1
The significant negative coefficient of DiversityFootnote 16 points towards the inverse relationship between the average Diversity of the manufacturing base of Colombian municipalities in 1997 and RECI growth. Note that the range of the variable Diversity is 0.057 to 0.213 in our sample while the coefficient of Diversity ranges between −21.132 to −2.195 in our regression models. Hence, whether the municipalities were more or less diverse in 1997, there is a negative relationship between RECI growth and the diversity of municipalities.
-
2
The significant negative coefficient of Competition underlines that higher the number of firms per worker in 1997, lower the RECI growth. However, note that Competition is not a significant explanatory variable after controlling for Diversity (models 3 and 4).
-
3
The significant negative coefficient of RECI1997 depicts an inverse relationship between RECI 1997 and growth of RECI: municipalities which had high RECI values in 1997 have a low RECI growth and municipalities which had low RECI values in 1997 witnessed high RECI growth. This is the most interesting finding of the study and indicate a convergence pattern in Colombian municipalities. Note that this is our control variable in regression model 4.
-
4
The negative signs of the “Diversity” and “Competition” coefficients provide evidence in support of MAR externalities. The results are robust and statistically significant (except Competition in models 3 and 4) even after controlling for RECI 1997.
Discussion of the results
The results presented above allow us to arrive at some tentative conclusions, keeping in mind the specific proxy we use for measuring economic complexity. This article attempts to measure the role of knowledge externalities on the growth of economic complexity as inferred from the Diversity and Competition of a region. In so doing, we develop a new variable for measuring the diversity of the economic base of a region. The evidence—suggestive of MAR or intra-industrial variety of externalities—is useful for understanding Colombia’s industrial development and agglomeration dynamics in its manufacturing sector.
The first possible theoretical explanation of the results can be that specialization is important for the effective transmission of productive knowledge in the early stages of development of industries when firms tend to co-locate (Glaeser et al., 1992). Accordingly, our results are in contrast with the works of Glaeser (1992) and Antonelli et al. (2015) who found that greater economic diversity and local competition (and hence the availability of Jacobs externalities) played a key role in the growth of American cities and production of new knowledge in European regions respectively, which are mature manufacturing economies.
Another possible explanation can be a mean reversion effect operating at the sub-national level in Colombia. If the initial level of diversity was too high for Colombian municipalities to sustain (given that production requires a set of complementary inputs), a fall in RECI can be reasonably expected. Indeed, Fig. 6 shows a clear convergence towards (what we can be called) the “mean” RECI value of municipalities from 2003 onwards, particularly the time period between 2005–2010. In the growth literature, the effect is well known and evidence for growth reversion to mean has been presented in various studies (Pritchett and Summers, 2014; Regional Economic Outlook, 2015).
An interesting pattern of convergence emerges from the results. Municipalities that had high economic complexity have low RECI growth and vice versa. We run an additional model to seek further evidence on this convergence pattern. We regress RECI 2011 on RECI 1997, while controlling for Diversity and Competition. Table 9 summarizes the regression results.
There is a highly significant negative correlation between RECI 2011 and RECI 1997: municipalities that had high complexity in 1997 have lower complexity in 2011. This confirms the convergence pattern among municipalities. These results can be reasonably expected as these municipalities belong to the same country.
Further, it may be that knowledge externalities affect not only the complexity of the municipality they originate from, but also the complexity of other municipalities through inter-municipality spillovers. This can be the logical extension of the current study.
Convergence, in turn, can be because of three possible reasons:
-
1
Diminishing marginal returns on Competition and Diversity the amount of knowledge externalities they are able to generate (for high complexity municipalities).
-
2
Imitation by low complexity municipalities. Fung (2005) shows that R&D expenditures being the same, the followers in technological knowledge will catch up with the leaders as they receive knowledge spillovers from the leader.
-
3
Increased absorptive capacity of low complexity municipalities. Cohen and Levinthal (1989) find that intra-industry spillovers may encourage equilibrium industry R&D investment. Building on which, Aghion and Jaravel (2015) argue that the notion of absorptive capacity has important implications for convergence and divergence due to knowledge spillovers. The absorptive capacity of the low complexity municipality “in self-reinforcing feedback cycles can result in either convergence or divergence” (Aghion and Jaravel, 2015).
Panel regression model
One limitation of the analysis presented above is that it does not account for the unobserved heterogeneity between municipalities. We hence undertake a panel data analysis in this section while including municipality fixed effects and municipality wages and employment as controls. Essentially, we aim to remove the effect of time-invariant characteristics unique to each municipality from the regression analysis. The simplest way forward then would be to include n–1 dummies (where n=the number of municipalities; 50 in our sample) in the regression model. However, that’s too many units of observation and too few time periods. Including 49 additional intercepts sacrifices a lot of degrees of freedom, leaving the model susceptible to picking more noise than signal. Hence, we prepare a smaller sample of the 10 biggest municipalities in Colombia in 1997, with data on each year, from 1997–2011 to test our hypothesis that knowledge externalities are a significant predictor of the economic complexity of a region. These municipalities (in the order of size, starting from the biggest) are: Bogotá, D.C., Medellín, Cali, Barranquilla, Itagüí, Yumbo, Manizales, Bucaramanga, Palmira and Cartagena de Indias. We also include wages and employment as controls in the model. Table 10 provides a summary of the variables.
An important consideration for panel data regression is choosing the right estimator. We use the Durbin-Wu-HausmanFootnote 17 test for fixed versus random effects model. The test checks the difference between the coefficients of a fixed effects model and a random effects model. Since the χ2 test (7.88) yields a value greater than the p-value (0.019) when we run the Hausman test, we reject the null hypothesis that the difference in the fixed and random effect coefficients is zero. This means that the difference in the coefficients is statistically significant and we would have to use a fixed effects model. Table 11 reports the results of the panel regression analysis.
The significant positive coefficient of Diversity provides evidence for Jacobs externalities, where higher the diversity in production in a given region, greater the complexity over time. This can also be interpreted as “unrelated variety” being crucial for complexity growth. The coefficient of Competition is insignificant in all variations of the fixed effects model. Model 4 controls for the mean wages and mean employment in each municipality (the most restrictive model) and in fact, shows a stronger impact of Diversity on RECI. The coefficient of Diversity increased to 6.055.
Discussion of the results
The linear regression model (with RECI growth as the independent variable) including 50 biggest municipalities in 1997 provides evidence for a convergence pattern favoring MAR externalities. On the other hand, with a panel data approach over the same time period (including data from all years but restricting the sample to 10 biggest municipalities), we still find the coefficient of diversity to be highly significant, although this time with a positive coefficient indicative of Jacobs externalities. The fixed effects model confirms evidence in favour of the stated hypothesis that the system characteristics (available variety)—generating specific externalities—is an important determinant of complexity growth. The two results are easy to reconcile. They state that the top 10 municipalities witnessed diversity based externalities (which is expected, given that the biggest municipalities have the most number of industries represented and hence greater possibility of horizontal spillovers), while when we broaden the sample that accounts for the top 50 municipalities, to understand long term effects, the overall diversity coefficient is negative, thus providing evidence for MAR externalities. This is in line with the fall in the economic complexity of Colombia over the years under investigation as it continues to specialize in natural resource based production and exports. We do not present the results of the panel regression involving all 50 municipalities in our sample, since such a specification is expected to pick more noise than signal, but as per our expectation, the coefficient of diversity is negative. In other words, the effect of the negative diversity (or specialization in production) of the next 40 municipalities (after the top 10) is stronger than the effect of the positive diversity coefficient of the top 10 municipalities, so the overall coefficient is negative. Even though there might be Jacob externalities (unrelated variety) available in the 10 biggest municipalities by employment, the overall trend is clearly convergent towards declining complexity in Colombia.
Conclusion and policy considerations
Externalities are the entry point to economic complexity (Antonelli, 2011). They lead to growth in economic complexity because they increase the interdependence of interacting agents in the system.
In the case of Colombia, which witnessed a fall in its economic complexity from 1997–2011, our empirical tests provide evidence in favour of MAR externalities (greater specialization and less competition) as the coefficients of our explanatory variables have a negative sign. In particular, the negative relationship between RECI growth and RECI 1997 underlines a convergence pattern where municipalities ranking high in RECI in 1997 saw the lowest RECI growth and vice versa. The same is true for the panel regression model even though the 10 biggest municipalities have Jacobs externalities available within and between them. These are very interesting findings from a Complex Systems perspective and can be explained by the rich neo-classical and Schumpeterian literatures on convergence dynamics. The neoclassical growth theories attribute convergence to diminishing returns on physical or human capital accumulation, while the Schumpeterian thesis attributes convergence to knowledge spillovers. Even though we have evidence that clearly points towards diminishing returns on Competition and Diversity in Colombian municipalities, further analysis would be required to confirm the neo-classical hypothesis. On the other hand we have, in fact, checked for the Schumpeterian dynamics of convergence through knowledge externalities and indeed a trend of convergence between municipalities is evident.
This stands in conformity with the macroeconomic trends in the Colombian economy which has witnessed extraordinary FDI flows (US$16.1 billion in 2014 alone), with a large part targeted at its natural resource extraction sector, with decreasing employment in and exports from manufacturing and agriculture sectors (UNCTAD, 2015). In light of the Colombian Dutch disease, the municipalities show a trend of convergence towards lower levels of economic complexity due to knowledge spillovers both within and between municipalities. The added value of this study lies in an in-depth analysis of the role knowledge externalities play in complexity dynamics and that, at the lowest level of geographical disaggregation (municipalities). The results have important implications for policies aimed at building resilience through diversification of the economic base of the country. We show that spillovers—albeit growth enhancing—may not always be a positive force in the long term health of the economy. They form an important mechanism that drives the macroeconomic dynamics in the economy, regardless of the direction of change. The literature so far only explores their positive contribution to economic growth which is, arguably, only one side of the coin. Such an understanding is made possible because our explanatory variable is RECI rather than the conventional “output growth” or “productivity growth”.
While indeed the Colombian economy is growing, its negative trend in complexity growth is detrimental for its manufacturing sector which is in fact, contracting as evident from the results. The crowding out of non-commodity exports is undesirable, perhaps because the manufacturing sector has greater externalities for long-run growth (Frankel, 2012). Colombia, however, is not the sole example of such decreasing complexity driven by commodity boom; various economies have suffered from Dutch disease or the “natural resource curse” (Norway, Ireland, Chile and so on). An important question is whether the country already has good institutions at the time that oil or other minerals are discovered, in which case it is more likely to be put to use for the national welfare instead of the welfare of an elite (Frankel, 2012). Given that the Colombian government foresees a reduction in the production of oil from 2017 onwards, it might be wise for Colombia to use natural resource revenues to support a clear diversification strategy that could, at least partially, rebalance the development strategy it has followed so far (Botta et al., 2014).
“Looking ahead, the key to improving longer-term growth prospects is to prioritize structural reforms and harness knowledge spillovers from greater openness, while preserving sound macroeconomic frameworks” (Regional Economic Outlook, 2015).
Data availability
The datasets generated during and/or analysed during the current study are not publicly available as they are internal to the Center for International Development at Harvard University; they are available from the corresponding author on reasonable request.
Additional information
How to cite this article: Sahdev NK (2016) Do knowledge externalities lead to growth in economic complexity? Empirical evidence from Colombia. Palgrave Communications. 2:16086 doi: 10.1057/palcomms.2016.86.
Notes
Note that we do not add a separate variable to measure “Specialization” and at the same time, neither is specialization the reciprocal of our “Diversity” variable. The results we present point towards the availability of MAR externalities as inferred from the system’s characteristics, rather than a direct measurement of knowledge spillovers. This necessitates careful handling of the two concepts.
Note that we use the terms “knowledge externalities” and “knowledge spillovers” interchangeably throughout the paper. Strictly speaking, these are “externalities” because agents receive knowledge without paying for its full cost. But at the same time, the literature seems to prefer the term “spillovers”. This might be due to the following line of argument: Knowledge spillovers do not require any transaction between the producers and the recipients of the external effects: they can be considered the characteristic of the “atmosphere” of the districts in which firms are based (Antonelli, 2011).
A common example of this crowd response is a financial market or the housing market where the spontaneous formation of a crowd of people who wish to sell—and hence effectively competing for buyers—can lead to a market crash in which the price falls dramatically in a short time.
For a fascinating discussion on the topic, see “The Information” (2011) by James Gleick. We envision future research work on the topic.
Over the last few decades, the difference between information and knowledge has become clear. Briefly, information can be defined as “organized data”, “data endowed with relevance and purpose” or “interpreted data”, whereas knowledge can be defined with the notions of empiricism and rationalism, that is, knowledge can only reside in one’s mind and is the result of human experience and reflection based on a set of beliefs that are at the same time individual and collective. The high complexity of knowledge (as compared to information) lies in the critical role of human beings in processing, creating, carrying and using it.
One possible criticism of using ECI as a proxy for Jacobs externalities can be that the ECI contains much more information about the economic complexity of a region than the mere availability of inter-industrial externalities, as is assumed by Antonelli et al. (2015). In fact, ECI seeks to explain the total amount of productive knowledge contained in an economy as expressed in the country’s industrial composition. (Hausmann et al., 2014)
EAM is aimed at capturing the regional distribution and geographical concentration or dispersion of industrial activity in Colombia.
As per ISIC industry classification for all economic activity, classification numbers 15–39 constitute “manufacturing” activities. Hence, services are not included in this study. An interesting topic for future research can be to study whether knowledge externalities across services sector (or the whole array of economic activities) in Colombia lead to greater economic complexity over time.
Since we are interested in looking at inter-industry/intra-industry knowledge externalities as a predictor of growth in economic complexity, we aggregate the variables to arrive at 2-digit industry level classification even though the dataset details ISIC values at the 4-digit level of classification for each industry in each municipality which is too disaggregated for the purposes of this study.
Three outliers have been removed to facilitate the visualization.
Note that Hausmann et al. (2014) define a parallel measure for products - called the Product Complexity Index (PCI) - by calculating the average diversity of the regions that make those products and the average ubiquity of the other products that these regions make.
Both RECI and Diversity are unique values computed for each municipality – characteristic of a Colombian municipality and not a municipality-industry.
Other than Glaeser et al.’s (1992) formulation of market competition, the Herfindahl-Hirschman Index (HHI) is an accepted measure of market concentration and competition among market participants. However, the HHI is applicable at the level of each industry (in a region), rather than the region as a whole (municipality in this case). Secondly, HHI assigns weights to the share of each firm by a simple squaring of its relative market share. We argue that this measure, when applied to regions where industry is still in its infant stage, presents a distorted picture of the market (not to mention governance and institutional factors) particularly if simply averaged out for all industries in a given region. Thirdly, the HHI hinges upon the clear recognition of an industry (which in turn is subject to the problem of substitutability of products) which might be challenging at a broad level of classification as in our study. Finally, an obvious problem with defining a market is choosing its geographical scope. For example, a smaller municipality bordering a bigger one, might effectively be a single market for a particular industry, but applying the HHI would distort this. We opine that Glaeser et al.’s (1992) formulation is better suited for our study, for its simplicity and low dependence on the above mentioned variables.
Paci and Usai (1999) proposed a Production Diversity Index (PD), which can be compared to our proposed Diversity index. Essentially, PD calculates the reciprocal of the Gini coefficient based on the share of employment ordered ascendingly by size (x axis) and the share of industries in a given region (y axis). This is the essentially the Competition index proposed by Glaeser et al. (1992) that we adapt in the current study. As is apparent from the empirical literature on externalities, the choice of the variables is ultimately, a subjective decision.
Note that we tested the results by fitting Generalized Linear Models as well, and found them to be robust up to three decimal points. The significance of the coefficients stands unaffected.
The highly significant Diversity coefficient (even after controlling for base RECI values) confirms of our claim that the proposed “Diversity” index is able to capture the available variety in the system at the base year. Since the index is based on the relative share in output of all industries in a municipality, it is a confirmation of the thesis that the output composition has crucial bearing on generating knowledge spillovers. In other words, the output has additional predictive content—effectively, the knowledge intensity of goods—compared with other simple diversification indexes (Regional Economic Outlook, 2015), which in turn rely on different variables for their construction.
The test evaluates the consistency of an estimator when compared to an alternative, less efficient, estimator which is already known to be consistent.
References
Aghion P and Jaravel X (2015) Knowledge spillovers, innovation and growth. The Economic Journal; 125 (583): 533–573.
Antonelli C ed (2011) Handbook on the Economic Complexity of Technological Change. Edward Elgar Publishing: Cheltenham, UK.
Antonelli C, Crespi F, Ospina C and Scellato G (2015) Knowledge complexity, Jacobs externalities and innovation performance in European regions. BRICK, Collegio Carlo Alberto working paper, University of Turin: Turin, Italy.
Arrow K (1962) Economic welfare and the allocation of resources for invention. In: Universities-National Bureau Committee for Economic Research, Committee on Economic Growth of the Social Science Research Council (ed). The Rate and Direction of Inventive Activity: Economic and Social Factors. Princeton University Press, pp 609–626.
Arthur WB (1990) “Silicon valley” locational clusters: When do increasing returns imply monopoly? Mathematical Social Sciences; 19 (3): 235–251.
Audretsch DB and Feldman MP (2004) Knowledge spillovers and the geography of innovation. Handbook of Regional and Urban Economics; 4, 2713–2739.
Bairoch P and Braider C (1991) Cities and Economic Development: From the Dawn of History to the Present. University of Chicago Press: Chicago.
Botta A, Godin A and Missaglia M (2014) Finance, foreign (direct) investment and dutch disease: the case of Colombia. Economia Politica; 33 (2): 265–289.
Brewer GD (1973) Analysis of Complex Systems: An Experiment and Its Implications for Policymaking. RAND Corporation: Santa Monica, CA.
Cohen WM and Levinthal DA (1989) Innovation and learning: The two faces of R & D. The Economic Journal; 99 (397): 569–596.
Cristelli M, Gabrielli A, Tacchella A, Caldarelli G and Pietronero L (2013) Measuring the intangibles: A metrics for the economic complexity of countries and products. PloS One; 8 (8): e70726.
Farra F et al. (2015) Diversification of Kazakhstan’s economy: A capability-based approach. Whiteshield Partners.
Feldman MP (1999) The new economics of innovation, spillovers and agglomeration: A review of empirical studies. Economics of Innovation and New Technology; 8 (1-2): 5–25.
Foster J (2005) From simplistic to complex systems in economics. Cambridge Journal of Economics; 29 (6): 873–892.
Frankel JA (2012) The Natural Resource Curse: A Survey of Diagnoses and some Prescriptions, HKS Faculty Research Working Paper Series RWP12-014, John F. Kennedy School of Government, Harvard University.
Fung MK (2005) Are knowledge spillovers driving the convergence of productivity among firms? Economica; 72 (286): 287–305.
Glaeser EL, Kallal HD, Scheinkman JA and Shleifer A (1992) Growth in Cities. Journal of Political Economy; 100 (6): 1126–1152.
Griliches Z (1979) Issues in assessing the contribution of research and development to productivity growth. The bell Journal of Economics; 10 (1): 92–116.
Hausmann R, Hidalgo CA, Bustos S, Coscia M, Simoes A and Yildirim MA (2014) The Atlas of Economic Complexity: Mapping Paths to Prosperity. MIT Press: Cambridge, MA.
Henderson JV (1986) Efficiency of resource usage and city size. Journal of Urban Economics; 19 (1): 47–70.
Henderson JV (1991) Urban development: Theory, fact, and illusion. Oxford University Press, https://ideas.repec.org/b/oxp/obooks/9780195069020.html.
Jacobs J (1970) The Economy of Cities, Jonathan Cape: London, p 268.
Jacobs J (1984) Cities and the Wealth of Nations. Random House: New York.
Jaffe AB, Trajtenberg M and Henderson R (1993) Geographic localization of knowledge spillovers as evidenced by patent citations. The Quarterly journal of Economics; 108 (3): 577–598.
Johnson NF (2007) Two’s Company, Three is Complexity: A Simple Guide to the Science of all Sciences. Oneworld: Oxford, UK.
Krugman P (1990) Increasing Returns and Economic Geography; No. w3275 National Bureau of Economic Research: Cambridge, MA.
Krugman P (1991) Cities in Space: Three Simple Models; No. w3607 National Bureau of Economic Research: Cambridge, MA.
Lucas RE (1988) On the mechanics of economic development. Journal of Monetary Economics; 22 (1): 3–42.
Lichtenberg RM (1960) One-Tenth of a Nation: National Forces in the Economic Growth of the New York Region. Harvard University Press: Cambridge, MA.
Marshall A (1890) 1920 Principles of Economics. Palgrave Macmillan: London.
Martin R and Sunley P (2007) Complexity thinking and evolutionary economic geography. Journal of Economic Geography.
Mejía JF (2011) Export Diversification and Economic Growth: An Analysis of Colombia’s Export Competitiveness in the European Union’s Market. Springer Science & Business Media: Springer-Verlag Berlin Heidelberg, Germany.
Murphy KM, Shleifer A and Vishny RW (1988) Industrialization and the big push, Working paper no. 2708, National Bureau of Economic Research.
Paci R and Usai S (1999) Externalities, knowledge spillovers and the spatial distribution of innovation. GeoJournal; 49 (4): 381–390.
Porter M (1990) Competitive advantage of nations. Competitive Intelligence Review; 1 (1): 14–14.
Pritchett L and Summers LH (2014) Asiaphoria Meets Regression to the Mean; No. w20573 National Bureau of Economic Research: Cambridge, MA.
Regional Economic Outlook: Western Hemisphere Northern Spring, Southern Chills. (2015) World Economic and Financial Surveys. International Monetary Fund: Washington DC, pp 67–77.
Romer PM (1986) Increasing returns and long-run growth. The Journal of Political Economy; 94 (5): 1002–1037.
Rotemberg JJ and Saloner G (2000) Competition and human capital accumulation: a theory of interregional specialization and trade. Regional Science and Urban Economics; 30 (4): 373–404.
Saviotti PP and Frenken K (2008) Export variety and the economic performance of countries. Journal of Evolutionary Economics; 18 (2): 201–218.
Scott AJ (1993) Technopolis: High-Technology Industry and Regional Development in Southern California. University of California Press: Berkeley.
Solow RM (1956) A contribution to the theory of economic growth. The Quarterly Journal of Economics; 70 (1): 65–94.
Storper M (1995) Regional technology coalitions: An essential dimension of national technology policy. Research Policy; 24: 895–911.
Sull D and Eisenhardt KM (2015) Simple rules: How to Thrive in a Complex World. Houghton Mifflin Harcourt: New York.
UNCTAD (2015) World investment report 2015, Reforming international investment governance, http://unctad.org/en/PublicationsLibrary/wir2015_en.pdf.
Van der Panne G (2004) Agglomeration externalities: Marshall versus Jacobs. Journal of Evolutionary Economics; 14 (5): 593–604.
Acknowledgements
The author is grateful to Ricardo Hausmann, Cristiano Antonelli, Benjamin Coriat and Frank Neffke for their advice and Luis Espinoza, Juan Tellez, Andres Gomez, Michele Coscia, Jose Ramon, Sebastian Bustos, Forrest Rogers-Marcovitz and Federico Bassi for their helpful comments.
Author information
Authors and Affiliations
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Sahdev, N. Do knowledge externalities lead to growth in economic complexity? Empirical evidence from Colombia. Palgrave Commun 2, 16086 (2016). https://doi.org/10.1057/palcomms.2016.86
Received:
Accepted:
Published:
DOI: https://doi.org/10.1057/palcomms.2016.86