Abstract
Multiferroics and magnetoelectrics with coexisting and coupled multiple ferroic orders are materials promising new technological advances. While most studies have focused on single-phase or heterostructures of inorganic materials, a new class of materials called metal–organic frameworks (MOFs) has been recently proposed as candidate materials demonstrating interesting new routes for multiferroism and magnetoelectric coupling. Herein, we report on the origin of multiferroicity of (CH3)2NH2Mn(HCOO)3 via direct observation of ferroelectric domains using second-harmonic generation techniques. For the first time, we observe how these domains are organized (sized in micrometer range), and how they are mutually affected by applied electric and magnetic fields. Calculations provide an estimate of the electric polarization and give insights into its microscopic origin.
Similar content being viewed by others
Introduction
The coexistence of ferromagnetism and ferroelectricity, i.e., multiferroicity (MF), is desirable for device applications, such as actuators, switches, magnetic field sensors, or new types of electronic memory devices.1–6 However, this coexistence and possible coupling, i.e., magnetoelectricity (ME), tends to be rare in single-phase materials.7 An alternate method is to engineer heterostructures of different magnetic and ferro/piezoelectric materials, which can show coupled MF and ME via strain coupling or exchange coupling.8,9
Recently, a different approach has been pursued, where organic and inorganic components are combined into a single-phase hybrid material. Metal–organic frameworks (MOFs) are a new class of hybrid crystalline materials comprising extended ordered networks formed from organic linkers and metal cations. MOFs show unique properties arising from their organic–inorganic duality.10 They not only display an unprecedented variety of physical properties and potential applications (gas storage, exchange/separation, catalysis, drug delivery, optics, magnetism are only a few examples), but the possibility of having an essentially infinite number of new materials by varying the inorganic/organic components.11 In particular, dense MOFs exhibiting a perovskite structure similar to their inorganic counterparts have shown MF and ME properties.12–21
Here, we focus on [(CH3)2NH2]Mn(COOH)3, a Mn-MOF with the ABX3 perovskite architecture, where A is [(CH3)2NH2]+, the dimethylammonium (DMA) cation, B is Mn2+, and X is the HCOO−, formate ion.22 It was the first MOF reported to be a multiferroic.12 Hereafter, we refer to it as DMAMnF (dimethyl-ammonium-Mn-formate). The Mn ions exhibit magnetic ordering below 8 K. It was initially reported to show an antiferroelectric phase transition at 180 K. Later, it was demonstrated that DMAMnF shows a spontaneous ferroelectric polarization that depends on magnetic field23 in the paramagnetic phase when cooled through the ferroelectric phase transition temperature Tc (180 K) in an external electric field. However, the switching of the electric polarization was not established, which contributed to our impetus for this undertaking. It is presently controversial whether the magnetic properties are affected by the 180 K phase transition, with one paper reporting a subtle change in the magnetic susceptibility versus temperature and the EPR signal at the the ferroelectric transition, and another paper suggesting that these effects can be attributed to impurities and experimental artifacts.24
In this work, we show that it is indeed possible to switch the direction of electric polarization in DMAMnF by applying an external electric field and that we can control the magnitude of the electric polarization with magnetic field. Electric polarization in DMAMnF varies depending upon its cooling history, which could be associated with the slow ordering of its disordered central cations, as seen in nuclear magnetic resonance measurement done by Besara et al.19 on it’s zinc analog. It could also be owing to the twinning that accompanies the lowering of symmetry through the ferroelectric phase transition. Here, for the first time, we are also able to image the ferroelectric domains of a multiferroic MOF, utilizing the second-harmonic generation (SHG) signal, highly sensitive to the loss of a center of symmetry in the ferroelectric state. Using single-crystal neutron-scattering measurements, as well as computational studies, we explain the origin of the ferroelectric polarization, and suggest guidelines for further polarization enhancement.
Experiments
The electric polarization of DMAMnF has been investigated by means of pyroelectric current and optical SHG measurements. Here, a brief description of the material synthesis procedure and experimental setups is given, together with an overview of the main results obtained by the two experimental techniques.
Experimental details
The crystal structure of DMAMnF, below 180 K, has a monoclinic Cc polar space group with cell parameters of a=14.315 Å, b=8.311 Å, c=8.914 Å and β=120.651° (see Supplementary Information for the crystallographic information file from single-crystal neutron data collected at 25 K). The unit cell contains four formula units. The octahedrally coordinated Mn2+ ions are connected by the formate HCOO− bridges, forming the ReO3 type anionic [Mn(HCOO)3] framework, with the [(CH3)2NH2] groups in the cubic-octahedral cavities. The N atom of the DMA cation sits in a single crystallographic position. According to our calculations, the distance between the N atom of DMA and the O atoms of the closest formate anion is 2.82 Å and is in agreement with single-crystal neutron data (see Supplementary Information for the crystallographic information file). The Mn cations occupy a distorted octahedral environment with six different Mn-O distances, from 2.16 Å to 2.25 Å. Other structural parameters, such as bond lengths and bond angles, are in agreement with data reported by Sanchez-Andujar et al., within a few percent.18
Electric polarization
Figure 1a shows the electric polarization in DMAMnF as a function of temperature. An electric field is applied while cooling through Tc, then the field is removed and the data are collected on warming. In the resulting data, we observe a finite electric polarization at low temperatures that sharply drops to zero at Tc, which coincides with the order–disorder structural transition temperature. Upon reversal of the electric field applied during cooling, the direction of the polarization reverses, as expected for a true ferroelectric. The electric polarization seems to saturate below 100 K at a value of about 0.55 μC/cm2. We do not, however, observe a reversal of the electric polarization when applying electric fields below Tc. This is not unusual for a millimeter-sized single crystal. Further measurements on thin films would allow us to apply larger electric fields and test whether the electric polarization can be reversed below Tc.
(a) Reversal of electric polarization with the reversal of electric field. (b) Magnetoelectric (ME) coupling in DMAMnF (dimethyl-ammonium-Mn-formate). Electric polarization was measured after cooling the sample in a voltage of 600 V (1 KV/cm). Three numbers refer to the magnetic field during cooling, the temperature that the sample was cooled to, and the magnetic field during the measurement.
Figure 1b shows, in the same experimental conditions, the effect of an externally applied magnetic field, applied after cooling and during warming. The electric polarization of DMAMnF is clearly enhanced by the interaction with the magnetic field. Furthermore, depending on the cooling history, there appears to be a change in the value of electric polarization: cooling to 40 K produced an electric polarization of 0.55 μC/cm2 compared with 0.70 μC/cm2 when the sample was cooled to 4 K in an external electric field. Let us note, here, that this value is about one order of magnitude lower than what is expected from ab initio calculations (see next sections), thus suggesting that below the phase transition, the DMA+ cations are not fully ordered. This could be due to twinning, to glass-like behavior akin to that seen in the zinc analog of DMAMnF,19 or to the formation of the observed multi-domain structure as described in the next section. In fact, in the zinc analog, the rotational motions of the methyl groups begin to randomly freeze at 40 K leading to a glass-like structure at 4 K, as revealed by the nuclear magnetic resonance measurements. Different relaxation pathways were observed around the structural phase transition as a result of this effect.19
The anomalous electric polarization increase in DMAMnF when cooled to 4 K is related to a strengthening of the ordering process that starts at 180 K. It is interesting, though, that the enhancement in electric polarization with an external magnetic field as high as 13 T is similar in both the 40 K (41%) and 4 K (37%) cases. As DMAMnF is a weak ferromagnet with a magnetic ordering temperature of 8.9 K, this means that the enhancement in electric polarization with magnetic field occurs in the paramagnetic state of the material.
SHG measurements
We used SHG to investigate, in greater detail, the nature of the observed ferroelectric state in DMAMnF. This investigation was, in particular, aimed at addressing the discrepancy between the measured polarization and that predicted theoretically. In this respect, SHG imaging is a powerful tool for detecting possible inhomogeneities and domains that might explain this discrepancy. The second-order contribution to the electric polarization generated in a material is proportional to the square of the electric field of the incident light wave of frequency ω (see Supplementary Material for details). This gives rise to a non-linear, i.e., frequency-doubled, 2ω, response.25 In an electric-dipole approximation, all even-order nonlinear optical effects are non-vanishing only in non-centrosymmetric media. Therefore, for the SHG process to occur, an inversion-symmetry-breaking of the magnetically and/or electrically ordered phase of a material is required. This extreme sensitivity of SHG to such a symmetry breaking makes it a very powerful tool for investigating the multiferroic phase in many different crystals and heterostructures.26–29 The microscopic origin of the symmetry breaking occurring in our samples is explained in the section “Ferroelectric properties”.
To probe the paraelectric-to-ferroeletric transition observed in the section “Electric polarization”, a temperature scan was carried out. This is shown in Figure 2a. As expected, the SHG signal is vanishingly small above the phase transition temperature, and easily detectable below that temperature, when the material is in the ferroelectric state.
The second-harmonic generation (SHG) dependence on temperature is shown (a). Note that the measurement shows clear hysteretic behavior when the temperature is cycled although there is no external field applied. (b–d) The SHG image of the same sample area (with no field applied) is shown at 150 K, i.e., below both critical temperatures. After each measurement, the sample temperature is increased above the critical temperature and then back to 150 K: the domain pattern is found to change. The grayscale is consistent for the three panels, i.e., the overall SHG signal from that sample region is lower for (d), higher for (c), and intermediate for (b).
We observe a clear hysteretic behavior only driven by the temperature, i.e., in the absence of any external electric or magnetic field.30 The hysteretic interval is marked by two critical temperatures at about 160 and 172 K. Moreover, we observe an anomalous increase of the SHG signal during the warming phase close to the transition temperature.
By using a microscope objective for collecting the SHG signal, we can visualize possible inhomogeneities in the lateral spatial distribution of the SHG signal. Indeed Figures 2b–d clearly show the presence of brighter domains against darker regions, indicating the formation of ferroelectric domains. Panels b–d show the SHG image of the same sample area (with no external electric field) at 150 K, i.e., below both of critical temperatures. These images are recorded in a temporal sequence. After each measurement, the sample temperature is increased above the critical temperature of 172 K and then lowered back to 150 K: and the domain pattern is found to change. Note that no qualitative difference is observed in the pattern, when the temperature variations are limited to a range below the critical temperature. The grayscale is consistent for the three panels, i.e., the SHG signal integrated over all the image area is lower for panel d, higher for c and intermediate for b.
The variation of the domain pattern after each cycle clearly demonstrates that the observed domains are intrinsic to the material and not a trivial effect caused by light interference (speckle). These images demonstrate the spontaneous formation of polar domains in DMAMnF below the transition temperature.
In a different set of experiments, we have tried to modify the spatial distribution of these domains and to fully saturate the sample’s electric polarization. We were only able to partially do this. As explained in detail in the Supplementary Material, also when applying the strongest available electric field of 3.3 kV/cm, we could not achieve a homogeneous polar state of the sample.
The presence of these domains and the absence of a uniform polarization below the critical temperature, also in the presence of an external electric field applied during cooling may explain why the experimentally observed electric polarization is found to be smaller than the theoretically expected value (see below).
Theoretical results
Ferroelectric properties
Since the experiments show the presence of ferroelectricity, we have performed numerical calculations in order to (i) determine the stability of the acentric phase with respect to the centric phase, (ii) estimate the ferroelectric polarization and shed light on the microscopic mechanism.
We started our calculations from experimental crystallographic data, optimizing the structure until Hellmann–Feynman forces were smaller than 0.02 eV/Å. Kohn–Sham equations were solved using the projector-augmented (PAW) method.31,32 For the exchange-correlation functional, we used the Heyd–Scuseria–Ernzerhof hybrid functional as implemented in VASP.33 The energy cutoff for the plane wave expansion was set to 400 eV; a 2×4×4 Monkhorst–Pack grid of k-points was used. The ferroelectric polarization was calculated according to the Berry phase theory.34
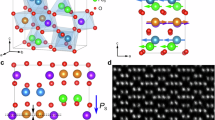
DMAMnF crystallizes in the monoclinic space group Cc and its pseudosymmetric centric structure has space group symmetry C2/c. Here, pseudosymmetric means that small-amplitude atomic distortions connect the two space groups. The amplitude of the atomic distortion can be parametrized by λ. We recall that the C–N bonds of the DMA+ cation are polar owing to the atomic electronegativity difference between N and C. Simple geometrical considerations show that the DMA+ cation is polar with the cation dipole moment belonging to the N–C plane. For λ=0, the dipoles are antiferroelectrically ordered and the polarization is zero. For λ=1, they tilt by a small tilting angle with respect to the b axis, or equivalently, they ‘rotate’ by the same angle, around a rotation axis, passing through the C–C atoms. Analogously, the λ=−1 state can be reached by a tilting/rotation of an opposite angle (see Figure 3). Therefore, the DMA+ cations deviate by only a small tilting angle with respect to antiferroelectric arrangements, giving rise to a small uncompensated ferroelectric component. As already pointed out in Ref. 13, the presence of tilting of the molecular cations giving rise to an uncompensated polarization is not unusual in hybrid−organic compounds.
(a) Spatial arrangement of the DMA+ cations in the antiferroelectric (AFE) and ferroelectric (FE) states, with polarization positive (+P) or negative (−P) along the polar direction. (b) Energy profiles as a function of the polar distortion (λ) from the AFE to FE states. (c) Modulus of the polarization as a function of the polar distortion.
The ferroelectric state is lower in energy with respect to the reference centric structure by 330 meV/(ABX3 f.u.). Therefore, our calculations support the conclusion that the ferroelectric state is more stable than the centric structure. This is in agreement with the experimental findings of a polar stable phase of this compound. It is interesting to see that the variation of the total energy from the centric (λ=0) to the polar structure (λ=1) as a function of the amplitude of the polar distortion (λ; Figure 3) shows a double-well energy profile characteristic of a ferroelectric material. The presence of polar molecular cations in a crystalline framework gives rise to a new mechanism for the onset of ferroelectricity that has no analog in inorganic compounds. Rather, it bears some similarity to the family of liquid crystals, where dipolar units are embedded in a liquid. Here, dipolar units are embedded in a crystalline framework. It is worth noting that this mechanism is suitable for ferroelectricity engineering by substituting A-cations having different intrinsic dipole moments.13 The overall polarization in the unit cell depends on both the dipole moment of the A-group as well as on the tilting angle of the organic cations with respect to a reference antiferroelectric alignment. Our estimate of the polarization in DMAMnF is as large as 7.3 μC/cm2, while the highest experimental electric polarization we have measured is ~1 μC/cm2, as shown in Figure 1b. It is possible that the saturation polarization for a DMAMnF thin film sample could be closer to the theoretical value, as larger electric fields can be applied.
SHG spectra
Our theoretical calculations also provide insight into SHG of such complex hybrid organic–inorganic material. The linear and second-order optical response have been calculated applying the formalism developed in refs 35–40 and implemented in the exciting code.41Ground-state calculations were carried out using a 2×4×4 k-point grid and RmtGmax=4 (with the corresponding effective plane-wave energy cutoff Gmax=72.5 eV). The LSDA42 eigenvalues were rigidly corrected using a “scissor”-operator of 2.43 eV to reproduce the Heyd–Scuseria–Ernzerhof33 bandgap of 3.9 eV calculated using VASP.34 Calculations of the optical spectra were performed on a 4×6×6 shifted k-point mesh. The resulting linear and second-order response spectra of the ferroelectric phase are presented in Figure 4. Although being in general rather similar for all diagonal tensor components, the dielectric function exhibits a clear anisotropy for some high-intensity peaks, which could be attributed to a different nature of the involved transitions. Interestingly, two peaks at ≈8 eV and ≈13 eV are common for all diagonal components. This behavior can be understood from the nature of these peaks due to transitions between Mn 3d and O 2p orbitals together with the highly symmetric local (octahedral) environment of Mn atoms. The highest intensity is observed at ≈15 eV for the zz-component. This peak has a ‘plasmon’-like feature (the corresponding real part of the tensor component turns to zero at this energy) and is attributed to s-p transitions on carbon atoms bridging MnO6 octahedra. The second-order susceptibility tensor has been calculated for all 14 symmetry-allowed tensor components. Only three of them have pronounced intensities, i.e., xzz, zyy, and xxx, with the major peak at ≈7.5 eV. Our analysis identifies this peak as originating mainly owing to the frequency doubling (2ω resonances) corresponding to the interband transitions, that are responsible for the dominant peak in the linear response spectra at 15 eV.
The linear (top) and second-order (bottom) optical response spectra in the polar phase. Dashed line corresponds to the estimated/calculated (3.9 eV) bandgap. The second-order spectra are shown only for the high-intensity tensor components. Shadow area demonstrates the superposition of all the tensor components.
Summary
In summary, we show that DMAMnF is ferroelectric below 180 K, as a result of an order–disorder structural phase transition. The electric polarization can be controlled and switched by a poling electric field. Furthermore, we confirm that the compound shows significant enhancement of the electric polarization by applied magnetic fields. On the basis of the electric polarization data and SHG domain imaging, we suggest that the ordering process in DMAMnF continues until at least 4 K. This is the first time that SHG has been applied to image ferroelectric domains in an MOF. Theoretical modeling showing that the large polarization originates from the tilting of the A cation dipole moment opens new avenues for engineering ferroelectricity in this versatile class of compounds. Given the magnetic-field-induced enhancement of the ferroelectric polarization, it may be possible to use these materials for magnetodielectric applications and sensors.
Materials and Methods
Synthesis
Crystals of DMAMnF were synthesized according to the procedure described in ref. 12. Briefly, 5 mmol of MnCl2. 6H2O were mixed in a 60 ml 1:1 solution of dimethylformamide and water. The reaction mixture was heated to 413 K, leading to in situ synthesis of formate anion and dimethylammonium cation. A clear reaction solution was decanted and transparent cubic crystals were obtained after 2 days of room temperature crystallization.
Electric polarization
Electric polarization was obtained by measuring the pyroelectric current with a Keithley 6517A electrometer on a single crystal with cubic morphology. Silver paste contacts were made and connected to a capacitance bridge using platinum wires. For the data shown in Figure 1, a single crystal was poled by cooling through Tc in 600 V (1 KV/cm) and then grounding the two leads of the sample before collecting the pyroelectric current data on warming. The electric polarization was determined by integrating the pyroelectric current with time. No electric field was applied during the measurement on warming. The measurements were performed using a custom coaxial probe in a Quantum Design Physical Property Measurement System with the sample chamber filled with a small amount of Helium gas for thermalization. Magnetic fields of up to 13 T were applied once the sample was cooled to base temperature, and left on during during data collection.
SHG imaging
An ultrafast frequency-tunable laser pulse (~130 fs, 1 kHz) with a typical pulse energy of 4 μJ and 1300 nm wavelength was focused on the sample with fluence equal to 3 mJ/cm2. The sample was placed in a He-cryostat and cooled to well below Tc. The SHG signal, generated in the sample in transmission geometry, was then filtered and imaged on a CCD camera. The spatial resolution of this setup is ~1 μm. The sample position has been recorded by linear white-light images taken together with the SHG images. All the measurements herein presented were performed on single crystals. Further details about the experimental setup for SHG imaging can be found in ref. 25.
References
Fiebig, M. Revival of the magnetoelectric effect. J. Phys. D Appl. Phys 38, R123 (2005).
Cheong, S. W. & Mostovoy, M. Multiferroics: a magnetic twist for ferroelectricity. Nat. Mat 6, 13–20 (2007).
Spaldin, N. A. & Fiebig, M. The renaissance of magnetoelectric multiferroics. Science 309, 391–392 (2005).
Catalan, G. & Scott, J. F. Physics and applications of bismuth ferrite. Adv. Mat 21, 2463–2485 (2009).
Chu, Y.-H. et al. Electric-field control of local ferromagnetism using a magnetoelectric multiferroic. Nat. Mat 7, 478–482 (2008).
Gajek, M. et al. Tunnel junctions with multiferroic barriers. Nat. Mat 6, 296–302 (2007).
Hill, N. A. Why are there so few magnetic ferroelectrics? J. Phys. Chem. B 104, 6694–6709 (2000).
Jain, P. et al. Synthetic magnetoelectric coupling in a nanocomposite multiferroic. Sci. Rep. 5, 9089 (2015).
Catalan, G., Seidel, J., Ramesh, R. & Scott, J. F. Domain wall nanoelectronics. Rev. Mod. Phys. 84, 119–156 (2012).
Cheetham, A. K. & Rao, C. N. R. There's room in the middle. Science 318, 58–59 (2007).
Murray, L. J., Dinca, M. & Long, J. R. Hydrogen storage in metal-organic frameworks. Chem. Soc. Rev 38, 1294–1314 (2009).
Jain, P. et al. Multiferroic behavior associated with an order-disorder hydrogen bonding transition in metal-organic frameworks (MOFs) with the perovskite ABX3 architecture. J. Am. Chem. Soc 131, 13625–13627 (2009).
Di Sante, D., Stroppa, A., Jain, P. & Picozzi, S. Tuning the ferroelectric polarization in a multiferroic metal-organic framework. J. Am. Chem. Soc 135, 18126–18130 (2013).
Jain, P., Dalal, N., Toby, B., Kroto, H. & Cheetham, A. K. Order-disorder antiferroelectric phase transition in a hybrid inorganic-organic framework with the perovskite architecture. J. Am. Chem. Soc 130, 10450–10451 (2008).
Tian, Y. et al. Cross coupling between electric and magnetic orders in a multiferroic metal-organic framework. Sci. Rep 4, 6062 (2014).
Tian, Y. et al. Electric control of magnetism in a multiferroic metal-organic framework. Phys. Status Solidi Rapid Res. Lett. 8, 91–94 (2014).
Maczka, M. et al. Temperature- and pressure-induced phase transitions in the metal formate framework of [ND4][Zn(DCOO)3] and [NH4][Zn(HCOO)3]. Inorg. Chem. 53, 9615–9624 (2014).
Sanchez-Andujar, M. et al. First-order structural transition in the multiferroic perovskite-like formate [(CH3)2NH2][Mn(HCOO)3]. CrystEngComm 16, 3558–3566 (2014).
Besara, T. et al. Mechanism of the order-disorder phase transition, and glassy behavior in the metal-organic framework [(CH3)2NH2]Zn(HCOO)3 . Proc. Natl Acad. Sci. USA 108, 6828–6832 (2011).
Sanchez-Andujar, M. et al. Characterization of the order-disorder dielectric transition in the hybrid organic-inorganic perovskite-like formate Mn(HCOO)3[(CH3)2NH2]. Inorg. Chem 49, 1510–1516 (2010).
Pato-Doldan, B. et al. Coexistence of magnetic and electrical order in the new perovskite-like (C3N2H5)[Mn(HCOO)3] formate. RSC Adv 3, 22404–22411 (2013).
Wang, X. Y., Gan, L., Zhang, S. W. & Gao, S. Perovskite-like metal formates with weak ferromagnetism and as precursors to amorphous materials. Inorg. Chem. 43, 4615–4625 (2004).
Wang, W. et al. Coupling in the paramagnetic state of a metal-organic framework. Sci. Rep. 3, 2024 (2013).
Abhyankar, N., Sylvain Bertaina, S. & Dalal, N. S. On Mn2+ EPR probing of the ferroelectric transition and absence of magnetoelectric coupling in dimethylammonium manganese formate (CH3)2NH2Mn(HCOO)3, a metal-organic complex with the Pb-free perovskite framework. J. Phys. Chem. C 119, 28143–28147 (2015).
Fiebig, M., Pavlov, V. V. & Pisarev, R. V. Second-harmonic generation as a tool for studying electronic and magnetic structures of crystals: review. J. Opt. Soc. Am. B 22, 96–118 (2005).
Meier, D. et al. Observation and coupling of domains in a spin-spiral multiferroic. Phys. Rev. Lett. 102, 107202 (2009).
Lottermoser, T. H., Meier, D., Pisarev, R. V. & Fiebig, M. Giant coupling of second-harmonic generation to a multiferroic polarization. Phys. Rev. B 80, 100101R (2009).
Günter, T. et al. Spatial inhomogeneities at the LaAlO3/SrTiO3 interface: evidence from second harmonic generation. Phys. Rev. B 86, 235418 (2012).
Rubano, A. et al. Optical second harmonic imaging as a diagnostic tool for monitoring epitaxial oxide thin-film growth. Appl. Surf. Sci. 327, 413–417 (2015).
Lottermoser, T. & Fiebig, M. Magnetoelectric behavior of domain walls in multiferroic. Phys. Rev. B 70, 220407 (R) (2004).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169 (1996).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).
Heyd, J., Scuseria, G. E. & Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 118, 8207–8215 (2003).
King-Smith, R. D. & Vanderbilt, D. Theory of polarization of crystalline solids. Phys. Rev. B 47, 1651 (1993).
Ambrosch-Draxl, C. & Sofo, J. O. Linear optical properties of solids within the full-potential linearized augmented planewave method. Comp. Phys. Commun. 175, 1–14 (2006).
Hughes, J. L. P. & Sipe, J. E. Calculation of second-order optical response in semiconductors. Phys. Rev. B 53, 10751 (1996).
Sipe, J. E. & Ghahramani, E. d. Nonlinear optical response of semiconductors in the independent-particle approximation. Phys. Rev. B 48, 11705 (1993).
Sipe, J. E. & Shkrebtii, A. I. Interpretation of Raman spectra of disordered and amorphous carbon. Phys. Rev. B 61, 53337 (2000).
Rashkeev, S. N., Lambrecht, W. R. L. & Segall, B. Efficient ab initio method for the calculation of frequency-dependent second-order optical response in semiconductors. Phys. Rev. B 57, 3905 (1998).
Sharma, S., Dewhurst, J. K. & Ambrosch-Draxl, C. Linear and second-order optical response of III-V monolayer superlattices. Phys. Rev. B 67, 165332 (2003).
Gulans, A. et al. Exciting: a full-potential all-electron package implementing density-functional theory and many-body perturbation theory. J. Phys. Condens. Matter 26, 363202 (2014).
Perdew, J.-P. & Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 45, 13244 (1992).
Acknowledgements
P.J. and V.S.Z. were funded by the U.S. Dept. of Energy via the LANL LDRD program. P.J. would also like to acknowledge the support of the U.S. National Science Foundation I2CAM International Materials Institute Award, Grant DMR-1411344. A.S. and D.P. acknowledges support from SPIN-CNR SEED project PAQSE001 “Metal-organic frameworks, new routes to multiferroicity and magnetoelectricity”. A.S. thanks the High-End Foreign Expert program hosted by Shanghai University and Special Program for Applied Research on Super Computation of the NSFC-Guangdong Joint Fund (the second phase). A.R. acknowledges funding from the European Union (FP7-PEOPLE-2012-CIG, PCIG12-GA-2012-326499-FOXIDUET). A.K.C. thanks the ERC for an Advanced Investigator Award. This work has benefited from the use of the Lujan Neutron Scattering Center (Los Alamos National Laboratory). Los Alamos National Laboratory is operated by Los Alamos National Security LLC under DOE Contract DE-AC52-06NA25396. The NHMFL facilities are funded by the U.S. National Science Foundation through Cooperative Grant No. DMR-1157490, the State of Florida, and the U.S. Department of Energy. MM and MF thank the SNSF for support from projects 20PC21_155659/1 and 200021_147080/1.
Author information
Authors and Affiliations
Contributions
All the authors contributed to the research, results analysis, and manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no conflict of interest.
Additional information
Supplementary Information accompanies the paper on the npj Quantum Materials website (http://www.nature.com/npjquantmats)
Supplementary information
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Jain, P., Stroppa, A., Nabok, D. et al. Switchable electric polarization and ferroelectric domains in a metal-organic-framework. npj Quant Mater 1, 16012 (2016). https://doi.org/10.1038/npjquantmats.2016.12
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/npjquantmats.2016.12
This article is cited by
-
Magnetic field-temperature phase diagram of multiferroic (NH4)2FeCl5·H2O
npj Quantum Materials (2019)
-
Lead-free Single-molecule Switching Material with Electric, Optical, Thermal Triple Controllable Multifunction Based on Perovskite-like Crystal and Flexible Thin Film
Scientific Reports (2017)
-
Competing magnetostructural phases in a semiclassical system
npj Quantum Materials (2017)
-
Impulse voltage control of continuously tunable bipolar resistive switching in Pt/Bi0.9Eu0.1FeO3/Nb-doped SrTiO3 heterostructures
Applied Physics A (2017)