Abstract
In this article we have investigated the electrical control of the exchange coupling (J) between donor-bound electrons in silicon with a detuning gate bias, crucial for the implementation of the two-qubit gate in a silicon quantum computer. We found that the asymmetric 2P–1P system provides a highly tunable exchange curve with mitigated J-oscillation, in which 5 orders of magnitude change in the exchange coupling can be achieved using a modest range of electric field (3 MV/m) for ~15-nm qubit separation. Compared with the barrier gate control of exchange in the Kane qubit, the detuning gate design reduces the gate density by a factor of ~2. By combining large-scale atomistic tight-binding method with a full configuration interaction technique, we captured the full two-electron spectrum of gated donors, providing state-of-the-art calculations of exchange energy in 1P–1P and 2P–1P qubits.
Similar content being viewed by others
Introduction
Donor qubits in silicon are promising candidates for spin-based quantum computation as they have exceptionally long T1 (refs 1, 2, 3) and T2 times4–6 and offer both electron and nuclear spins for encoding quantum information5–8 utilising commonly used silicon device technology. With recent demonstration of single qubits in silicon with both electronic and nuclear spins of donors,5,7 the next biggest challenge is to demonstrate two-qubit gates based on the exchange interaction. Ideally, the exchange coupling J in a two-qubit gate needs to be tuned electrically by several orders of magnitude between an ‘Off’ and an ‘On’ state within a small and realisable bias range. To achieve this, the popular Kane architecture uses a J-gate between two phosphorus donors to tune the J-coupling. Recently A-gates that tune the hyperfine interaction for individual qubits have been demonstrated.9 However, in the long run such a J- and A-gate architecture leads to a high gate density, requiring ultra-small gate widths to minimise electrical cross-talk between gates, and precise donor positioning relative to gates. Moreover, the tunability of the exchange coupling is limited both by the electric field range the J-gate can produce and by the field ionisation of the electrons to the surface. Previous calculations have also shown that the J-coupling oscillates as a function of donor separation due to crystal momentum states,10 and is therefore sensitive to atomic-scale placement errors. All these issues lead to severe constraints in the implementation of a two-qubit gate in donors.
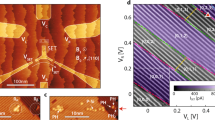
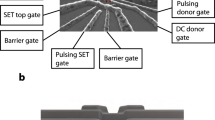
In this work, we introduce an alternative design for an exchange gate in a two-qubit donor system, which allows flexibility in device fabrication and in tuning the exchange coupling. In principle, this new design can (1) eliminate the need for additional J-gates between the donors, (2) function with a range of donor separations, (3) provide an ~5 orders of magnitude J-tunability within a modest E-field range of ~3 MV/m and lowered ‘Off’ state exchange and (4) mitigate the J-oscillations with donor separations. This design can also benefit from improved addressability2 and longer T1 times,3 and can be used in conjunction with the two-qubit scheme proposed in ref. 11. This design can therefore overcome some of the experimental obstacles for realising a two-qubit gate in silicon. To perform these state-of-the-art calculations of exchange energy in donor qubits, we have combined atomistic full-band electronic structure calculations, electrostatic device simulations of experimentally realisable device architecture and a two-electron full configuration interaction (FCI) technique over a lattice of 1.7 million atoms. The calculations therefore describe the detailed two-electron spectrum of donor qubits over large E-field ranges accounting for both crystal effects and electron–electron exchange and correlation effects.12 By studying double quantum dots in silicon,13 we find that an asymmetric 2P–1P system outperforms the symmetric 1P–1P system in exchange controllability with detuning gates. Analogous to exchange tuning in double quantum dots,14,15 we envision a (1,1) to (2,0) charge transition in both 1P–1P and 2P–1P qubits as a function of a lateral electric field that provides the energy detuning. (The charge configuration of the system is denoted as (M,N), where M indicates the number of electrons on the left dot, and N the right dot.) As the electron bound to one donor is pulled to the other by the electric field, the exchange coupling can be engineered from a small value in the (1,1) state to a large value in the (2,0) state due to the large spatial overlap of the wavefunctions in the latter. Such an electric field can be applied from either top gates (Figure 1b) in a metal-oxide-semiconductor device or from in-plane gates realised by scanning tunnelling microscope-based lithography (Figure 1c).13 Placed on either side of the donor qubits, the detuning gates eliminate the need for a sensitive tunnel barrier control by the J-gate. Instead, this design realises a tilt in the potential landscape of the two qubits, as shown in Figure 1d,e, and therefore relaxes the more stringent engineering requirements of donor separations and gate widths of the Kane architecture, leading to a reduced overall gate density in the computer.
Control of exchange in donor-based qubits separated by ~15 nm. (a) Kane’s two-qubit donor device with J-gate.8 (b) A metal-oxide-semiconductor device with top detuning gates. (c) A scanning tunnelling microscope-patterned device with in-plane detuning gates. (d, e) Schematic potential energy profiles of the two-qubit system without and with the detuning electric field , showing a tilt in potential energy along the separation direction in e.
Results
In Figure 2a we show the computed exchange coupling (J, defined in the Materials and Methods section) between two donor-bound electrons as a function of donor separation along two high-symmetry crystallographic directions [100] and [110]. We consider two cases: (1) a symmetric two-qubit system of 1P–1P8 (black triangles and squares); and (2) an asymmetric two-qubit system of 2P–1P along the lines of refs 2,13 in which we consider two representative locations of the donors inside the 2P cluster, shown in Figure 2b as 2P(A) and 2P(B). The exchange coupling as a function of 2P–1P separation for these two spatial configurations of the 2P cluster is labelled as 2P(A) (blue curves) and 2P(B) (magenta curves) in Figure 2a. In Figure 2b, the squares represent the silicon atoms on the (001) plane and the filled circles represent the substituting P atoms. In all the cases, the exchange coupling decreases exponentially with increasing separation in both the [100] and the [110] directions, attaining ~1,000 GHz for separation ~5 nm and a few tens of MHz for ~15 nm. This is expected as the wavefunction overlap between the qubits decreases as the separation increases. The exchange coupling of the 2P–1P qubits is found to be slightly larger than that of the 1P–1P qubits even without an electric field. This is somewhat counter-intuitive considering the fact that a 2P system provides a stronger confinement for the electron and should minimise the overlap with the 1P electron. However, because of the asymmetry of the confinement potential, the 2P cluster is already slightly detuned towards the (2,0) state with larger wavefunction overlap, resulting in a larger exchange. The exchange can be reduced below the 1P–1P value due to the smaller Bohr radius of the 2P wavefunction in this case by applying a negative detuning bias, as shown later.
Separation dependence of exchange coupling. (a) The exchange coupling of 1P–1P and 2P–1P qubits in silicon as a function of inter-qubit separation along the [100] and [110] crystallographic axes without any applied electric fields. (b) Two-studied 2P cases with different donor locations on a (001) plane in silicon. The squares are the silicon atoms on the (001) atomic plane and the filled circles are the substituting P atoms.
The exchange coupling of the 1P–1P qubits in the [110] direction (black triangles) exhibits oscillations as a function of donor separation. This has been observed in earlier works based on the Kohn–Luttinger effective mass Heitler–London method,10,16 and has been attributed to the interference between the wavefunctions of the six conduction band valleys of silicon. In the [100] direction, we do not observe the J-oscillations as predicted by the Kohn–Luttinger effective mass theory, which is consistent with ref. 17 due to effective mass anisotropy captured by our atomistic tight-binding method.
It is interesting to note that the J-oscillations are strongly mitigated in all the 2P–1P cases along both [100] and [110] separation. In fact, we considered two different 2P cluster configurations, 2P(A) and 2P(B), to verify this. In 2P(A), the intra-cluster P donors are separated by a0 times an integer in both [100] and [010], and in 2P(B) by a0/2 times an odd integer. These two cases are thus representatives of the donors separated by a whole unit cell and a half unit cell. Relative to this 2P cluster, if the 1P distance is varied along [100] or [110], the J-oscillations should appear in analogy with the 1P–1P system. However, as shown in Figure 2a, we observe strongly suppressed J-oscillations in all the 2P–1P cases due to a number of factors such as reduction of Bohr radius, valley repopulation and contribution of excited orbital states, which are analysed in more detail in the Supplementary Information. Hence, the 2P–1P unit is a more fault-tolerant system for fabrication and control than the 1P–1P unit. Now that we have explored the range of exchange energies that can be accessed in donor qubits for various donor separations, we investigate the electric field control of exchange in the 1P–1P and 2P–1P systems. Figure 3 shows the exchange energies as a function of the electric field for 10- and 15-nm qubit separations, respectively. We consider an electric field range of −2 to 2 MV/m, consistent with typical E-fields realised in scanning tunnelling microscope-patterned donor devices. In general, the exchange curves show a transition from a low value to a large value for a charge transition from (1,1) to (2,0) for the 2P–1P curves. This is because when the two electrons are localised on separate qubits, the spatial overlap of the wavefunction is small, and so is the J-coupling. As a 2P–1P system is slightly detuned towards the 2P cluster at zero field, a negative electric field further decreases the wavefunction overlap so that the exchange coupling is decreased. A positive field pulls both the electrons gradually to one qubit, such that the spatial overlap increases, and so does the exchange. In the extreme (2,0) regime when both electrons are on the left qubit, the electric field has little effect on the overlap, and the exchange coupling levels off. For the 2P–1P exchange curve at a 15-nm separation, the exchange coupling is observed to vary from 11.6 MHz to 1,310 GHz over a field range of −2 to 0.9 MV/m, resulting in over 5 orders of magnitude tunability. The ‘Off’ state (at −2 MV/m) is ~1 order of magnitude lower than that of the 1P–1P case at a 15-nm separation (the circled blue curve at 0 MV/m).
Electric field induced exchange in donors. Exchange energy as a function of an electric field along the separation axis for a 1P–1P and a 2P–1P system with inter-dot separations of 10 and 15 nm. The 2P(B) configuration is used (shown in Figure 2b).
We note that within the 2 MV/m field range, only the 2P–1P cases exhibit significant exchange tunability in Figure 3. The 1P–1P case only shows a change from 113.4 to 578.6 MHz (5 times) over 2 MV/m for a 15-nm separation distance. As the 2P cluster has two core nuclear charges with one bound electron, it is easier to shuttle an extra electron to this system aided by the net attractive potential of the core. In the 1P–1P case, the electron–electron repulsive energy is stronger because of the charge neutrality of each qubit, and a larger E-field is needed to reach the (2,0) regime. The calculations show that for E<2 MV/m, the (2,0) regime is never reached in the 1P–1P case if the separation is <15 nm. In addition, as such a system is symmetric, either a positive or a negative field will increase the exchange coupling. It can be seen that qubit pairs with larger separations exhibit larger tunability. This is because the same electric field causes a larger potential drop between the qubits if their separation is larger, and hence provides a larger detuning energy. We also note that the exchange curves show that the transition to the (2,0) regime is smoother if the separation distance is less. This is due to the stronger molecular hybridisation of closely spaced qubit pairs.
After comparing the 1P–1P and 2P–1P cases in Figure 3, one can see that a 2P–1P system with a 15-nm separation provides a promising two-qubit unit of a silicon quantum computer, yielding 5 orders of magnitude exchange tunability. In our simulations with uniform electric fields, we are unable to go to the high-field regime for the 1P–1P case, as high fields induce a triangular quantum well at the lateral domain boundaries causing electron localisation in the surface states.18 However, larger exchange energies can possibly be realised even in the 1P–1P case with large spatially varying E-fields from detuning gates as shown in Figure 1b,c. In Supplementary Information, we show that the exchange coupling of a 1P–1P system can be tuned by a factor of 50 using surface-detuning gates. We also compare the exchange tunability of corresponding cases to the original Kane architecture with J-gate and show the proposed detuning scheme in this manuscript is superior. These simulations include electrostatic simulations with the Sentaurus technology computer-aided design tool (TCAD) (Synopsys Sentaurus Semiconductor TCAD Software, Mountain View, CA, USA) coupled to the tight-binding-FCI method.
We now study the promising 2P–1P system for a 15-nm separation in more detail, including the two-electron energy spectrum and the singlet and triplet wavefunctions at various electric fields. Figure 4a demonstrates the two-electron total energies of several lowest singlet (black curves) and triplet (blue curves) states as a function of the electric field, relative to the top of the valence band energy at the midpoint of the two qubits. The lowest black solid lines are the (1,1) and (2,0) singlet states. They mix at low electric fields and anti-cross at ~0.7 MV/m, which marks the symmetry point of the (1,1) to (2,0) charge transition. The lowest (1,1) triplet state represented by the blue dotted line has little dependence of the electric field until 0.9 MV/m, indicating that it is decoupled from other triplet states. A sharp transition occurs at 0.9 MV/m, beyond which the energies of singlet and triplet states have a linear dependence on the electric field, indicating the occupation regime of a (2,0) charge configuration where the lowest states of the two qubits are no longer tunnel-coupled. Figure 4b shows the weight of the lowest (2,0) Slater determinant in the ground-state singlet of the 2P–1P system as a function of the electric field. As can be seen, the weight changes from a small probability 3×10−6 to ~1, indicating a charge transition from (1,1) to (2,0). This (2,0) probability can be measured by a charge sensor, as in experiments with double quantum dots-based singlet–triplet qubits.14,19 Thus, the same control scheme of ref. 14 can be utilised to realise singlet–triplet-based donor qubits with electrical manipulation of J.
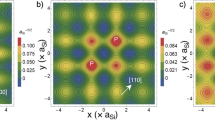
Electric field dependence of singlet and triplet states. (a) The total energy of the lowest few singlet and triplet states of a 2P–1P system with a 15-nm inter-qubit separation as a function of electric field. (b) Probability of the (2,0) state with both electrons on 2P as a function of electric field. (c) Two-electron density of the lowest singlet (S) and triplet (T0) states at three electric field values, showing a transition from (1,1) to (2,0).
In Figure 4c, we show the two-electron density of the lowest singlet and triplet states computed from the FCI wavefunctions at three different E-fields. At E=0, the singlet and triplet states look similar as they are both in the (1,1) charge configuration. The stronger confinement in the 2P cluster on the left is responsible for a smaller wavefunction extent. At E=0.7 MV/m, the (1,1) singlet mixes with the (2,0) singlet and the electron density gradually shifts to the 2P cluster. However, because of spin blockade, the triplet still remains in the (1,1) configuration, with almost negligible change in the wavefunction. At high-enough electric fields of 1 MV/m, both the singlet and the triplet are in the (2,0) regime, as verified by the electron densities being localised in the 2P cluster.
Discussion
In summary, we have shown that a detuning gate control of the J-coupling in donors can relax the stringent requirements of including additional J-gates to control the exchange coupling needed to realise a two-qubit gate in silicon. In addition, the use of an asymmetric 2P–1P qubit pair can yield tunability of the exchange by 5 orders of magnitude over a modest field range (3 MV/m) with an even lower ‘Off’ state exchange than the corresponding 1P–1P qubits. Combined with long T1 times of donor clusters,3 improved addressability of 2P–1P qubits,2 and operation schemes of ref. 11 the proposed design helps in the experimental realisation of the much sought after two-qubit gate with donors in silicon. The calculations of detuning controlled exchange coupling also helps in realising highly tunable singlet–triplet qubits.14
Materials and Methods
Previous works have calculated the exchange energy between two donor-bound electrons in silicon as a function of separation R using the effective mass approximation and the Heitler–London formalism,10,16 which is valid in the regime of small wavefunction overlap (R>5 nm). Control of exchange with the Kane J-gate was also calculated in refs 16,20 from the effective mass approximation-based Heitler–London method. However, this method becomes inaccurate at modest gate biases when the wavefunction overlap increases. The Heitler–London method also ignores contributions of doubly excited configurations that increase with reduced separations or increasing fields. More recently, the exchange coupling was calculated in a 1P–1P system from effective mass approximation-based molecular orbital and configuration interaction approaches for separation distances larger than 7.5 nm (ref. 21) and modest electric fields.22 All these works are based on the Kohn–Luttinger form of the donor wavefunctions,23 which provides a very specific solution to the two-electron problem, and cannot provide a full description of the (1,1) to (2,0) charge transition in which strong Stark effect causes mixing of the lowest states with many excited states.18 The atomistic configuration interaction method used here goes beyond these approximations to include the Stark effect, large wavefunction overlap and electron–electron exchange and correlations. In this work, we use a large-scale atomistic tight-binding method that describes the crystal as a linear combination of atomic orbitals, and captures the full-energy spectrum of a donor in silicon, including the conduction band valley degrees of freedom, the valley-orbit interaction,24 the Stark shift of the donor orbitals,18 and real and momentum space images of the donor obtained by scanning tunnelling microscope experiments.25 Using the atomistic wavefunctions, we compute the two-electron states of donor and donor clusters in the presence of an electric field from an FCI technique. The same method has been successful in solving the challenging problem of the D− state (the two-electron state of a single donor) without any fitting parameters and providing a charging energy of 45 meV (ref. 26) compared with the 44-meV experimental value.27 The method is described in detail in Supplementary Information.
The FCI technique is an exact way to solve the multi-electron problem only limited by the number of one-electron basis functions used. The method diagonalises the multi-electron Hamiltonian in the basis of all Slater determinants constructed from the single-electron states of the system. Each Slater determinant represents a multi-electron anti-symmetric wavefunction for a particular arrangement of the electrons among the basis orbitals. In addition to the ground state, the method also captures the excited multi-electron spectra. The exchange coupling J in the two-electron case can be obtained from the difference between the lowest triplet energy (ET) and singlet energy (ES) divided by the Planck’s constant h, as J=ΔEST/h=(ET−ES)/h.15
References
Morello, A. et al. Single-shot readout of an electron spin in silicon. Nature 467, 687–691 (2010).
Büch, H., Mahapatra, S., Rahman, R., Morello, A. & Simmons, M. Y. Spin readout and addressability of phosphorus-donor clusters in silicon. Nat. Commun. 4, 2017 (2013).
Hsueh, Y.-L. et al. Spin-lattice relaxation times of single donors and donor clusters in silicon. Phys. Rev. Lett. 113, 246406 (2014).
Muhonen, J. T. et al. Storing quantum information for 30 seconds in a nanoelectronic device. Nat. Nanotechnol. 9, 986–991 (2014).
Pla, J. J. et al. A single-atom electron spin qubit in silicon. Nature 489, 541–545 (2012).
Saeedi, K. et al. Room-temperature quantum bit storage exceeding 39 minutes using ionized donors in silicon-28. Science 342, 830–833 (2013).
Pla, J. J. et al. High-fidelity readout and control of a nuclear spin qubit in silicon. Nature 496, 334–338 (2013).
Kane, B. E. A silicon-based nuclear spin quantum computer. Nature 393, 133–137 (1998).
Laucht, A. et al. Electrically controlling single-spin qubits in a continuous microwave field. Sci. Adv. 1, e1500022 (2015).
Koiller, B., Hu, X. & Sarma, S. D. Exchange in silicon-based quantum computer architecture. Phys. Rev. Lett. 88, 027903 (2001).
Kalra, R., Laucht, A., Hill, C. D. & Morello, A. Robust two-qubit gates for donors in silicon controlled by hyperfine interactions. Phys. Rev. X 4, 021044 (2014).
Sherrill, C. D. & Schaefer, H. F. III The configuration interaction method: advances in highly correlated approaches. Adv. Quantum Chem. 34, 143–269 (1999).
Weber, B. et al. Spin blockade and exchange in Coulomb-confined silicon double quantum dots. Nat. Nanotechnol. 9, 430–435 (2014).
Petta, J. R. et al. Coherent manipulation of coupled electron spins in semiconductor quantum dots. Science 309, 2180–2184 (2005).
Rahman, R., Nielsen, E., Muller, R. P. & Carroll, M. S. Voltage controlled exchange energies of a two-electron silicon double quantum dot with and without charge defects in the dielectric. Phys. Rev. B 85, 125423 (2012).
Wellard, C. J., Hollenberg, L. C. L., Kettle, L. M. & Goan, H.-S. Voltage control of exchange coupling in phosphorus doped silicon. J. Phy.: Condens. Matter 16, 5697 (2004).
Pica, G., Lovett, B. W., Bhatt, R. N. & Lyon, S. A. Exchange coupling between silicon donors: the crucial role of the central cell and mass anisotropy. Phys. Rev. B 89, 235306 (2014).
Rahman, R. et al. Orbital Stark effect and quantum confinement transition of donors in silicon. Phys. Rev. B 80, 165314 (2009).
Shulman, M. D. et al. Demonstration of entanglement of electrostatically coupled singlet-triplet qubits. Science 336, 202–205 (2012).
Wellard, C. J. et al. Electron exchange coupling for single-donor solid-state spin qubits. Phys. Rev. B 68, 195209 (2003).
Kettle, L. M., Goan, H. S. & Smith, S. C. Molecular orbital calculations of two-electron states for P-donor solid-state spin qubits. Phys. Rev. B 73, 115205 (2006).
Gonzalez-Zalba, M. F. et al. An exchange-coupled donor molecule in silicon. Nano Lett. 14, 5672–5676 (2014).
Kohn, W. & Luttinger, J. M. Theory of donor states in silicon. Phys. Rev. 98, 915 (1955).
Rahman, R. et al. Gate-induced g-factor control and dimensional transition for donors in multivalley semiconductors. Phys. Rev. B 80, 155301 (2009).
Salfi, J. et al. Spatially resolving valley quantum interference of a donor in silicon. Nat. Mater. 13, 605–610 (2014).
Tankasala, A., Wang, Y., Klimeck, G. & Rahman, R. Atomistic configuration interaction simulations of two-electron states of donors in silicon. APS March Meeting 2015, Vol. 60, No. 1, San Antonio, TX, USA, 2–6 March 2015. A37.00011.
Rahman, R. et al. Electric field reduced charging energies and two-electron bound excited states of single donors in silicon. Phys. Rev. B 84, 115428 (2011).
Acknowledgements
This research was conducted by the Australian Research Council Centre of Excellence for Quantum Computation and Communication Technology (project No. CE110001027), the US National Security Agency and the US Army Research Office under contract No. W911NF-08-1-0527. Computational resources on nanoHUB.org, funded by the NSF grant EEC-0228390, were used. MYS acknowledges a Laureate Fellowship. YW thanks Charles D Hill for useful discussion. This research is part of the Blue Waters sustained-petascale computing project, which is supported by the National Science Foundation (award number ACI 1238993) and the state of Illinois. Blue Waters is a joint effort of the University of Illinois at Urbana-Champaign and its National Center for Supercomputing Applications. This work is also part of the Accelerating Nano-scale Transistor Innovation with NEMO5 on Blue Waters PRAC allocation support by the National Science Foundation (award number OCI-0832623).
FUNDING
This study was funded by the Army Research Office (ARO)—W911NF-08-1-0527, the Australian Research Council (ARC)—CE110001027 and the National Science Foundation (NSF) grant EEC-0228390, NSF ACI 1238993 and NSF OCI-0832623.
Author information
Authors and Affiliations
Contributions
YW and RR conceived the design; YW and AT conducted the simulations; YW, AT, MYS and RR analysed the results; all authors contributed to discussion and reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no conflict of interest.
Additional information
Supplementary Information accompanies the paper on the npj Quantum Information website (http://www.nature.com/npjqi)
Supplementary information
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Wang, Y., Tankasala, A., Hollenberg, L. et al. Highly tunable exchange in donor qubits in silicon. npj Quantum Inf 2, 16008 (2016). https://doi.org/10.1038/npjqi.2016.8
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/npjqi.2016.8
This article is cited by
-
A solid-state quantum microscope for wavefunction control of an atom-based quantum dot device in silicon
Nature Electronics (2023)
-
Optimisation of electron spin qubits in electrically driven multi-donor quantum dots
npj Quantum Information (2022)
-
Impact of charge noise on electron exchange interactions in semiconductors
npj Quantum Information (2022)
-
Coherent control of a donor-molecule electron spin qubit in silicon
Nature Communications (2021)
-
Valley interference and spin exchange at the atomic scale in silicon
Nature Communications (2020)