Abstract
The first generation of quantum computers are on the horizon, fabricated from quantum hardware platforms that may soon be able to tackle certain tasks that cannot be performed or modelled with conventional computers. These quantum devices will not likely be universal or fully programmable, but special-purpose processors whose hardware will be tightly co-designed with particular target applications. Trapped atomic ions are a leading platform for first-generation quantum computers, but they are also fundamentally scalable to more powerful general purpose devices in future generations. This is because trapped ion qubits are atomic clock standards that can be made identical to a part in 1015, and their quantum circuit connectivity can be reconfigured through the use of external fields, without modifying the arrangement or architecture of the qubits themselves. In this forward-looking overview, we show how a modular quantum computer with thousands or more qubits can be engineered from ion crystals, and how the linkage between ion trap qubits might be tailored to a variety of applications and quantum-computing protocols.
Similar content being viewed by others
Quantum information processors have the potential to perform computational tasks that are difficult or impossible using conventional modes of computing.1–3 In a radical departure from classical information, the qubits of a quantum computer can simultaneously store bit values 0 and 1, and when measured they probabilistically assume definite states. Many interacting qubits, isolated from their environment, can represent huge amounts of information: there are exponentially many binary numbers that can co-exist, with entangled qubit correlations that can behave as invisible wires between the qubits. Even in the face of Moore’s Law, or the doubling in conventional computer power every year or two, the complexity of massively entangled quantum states of just a few hundred qubits can easily eclipse the capacity of classical information processing.4 There are but a few known applications that exploit this quantum advantage, such as Shor’s factoring algorithm,5 and future quantum information processors will likely be applied to special-purpose applications. On the other hand, a quantum computer has not yet been built; therefore, new quantum applications and algorithms will likely follow from the evolution and capability of quantum hardware.
In the 20 years since the advent of Shor’s algorithm5 and the discovery of quantum error correction,6–8 there has been remarkable progress in demonstrations of entangling quantum gates on <10 qubits in certain physical systems. Current efforts aim to scale to hundreds, thousands or even millions of interacting qubits. Unlike the classical scaling of bits and logic gates, however, large quantum systems are not comparable to the behaviour of just a few qubits. Just because 2 or 4 qubits can be completely controlled with negligible errors does not mean that this system can readily scale to >100 qubits.
In the last few years, two particular quantum hardware platforms have emerged as the leading candidates for scaling to interesting numbers of qubits: trapped atomic ions9,10 and superconducting circuits.11–13 These technologies will likely both be built out in coming years, and may find complementary uses. Superconducting circuitry exploits the significant advantages of modern lithography and fabrication technologies: it can be integrated on a solid-state platform, and many qubits can simply be printed on a chip. However, they suffer from inhomogeneities and decoherence, as no two superconducting qubits are the same, and their connectivity cannot be easily reconfigured without replacing the chip or modifying the wires connecting them within a very low-temperature environment. Trapped atomic ions, on the other hand, feature virtually identical qubits, and their linkage can be reconfigured by modifying externally applied electromagnetic fields. However, atomic qubit switching speeds (1–100 μs) are generally much slower than that of solid-state devices (1–100 ns), and the development of engineering infrastructure for trapped ion quantum computers and the mitigation of noise and decoherence from the applied control fields is just beginning.
In this paper, we anticipate the upcoming engineering efforts on trapped atomic ions for quantum computing, and highlight their reconfigurable quantum circuit connectivity as a flexible platform to be applied to a wide range of potential quantum applications. This path to scaling to thousands or more qubits will almost certainly involve the concept of architectural co-design,14 where algorithms and applications are invented alongside the development of trapped ion hardware, and the laboratory engineers fabricate an ion trap system that is well-adapted to certain types of quantum circuit applications.
Ion trap qubits and wires
Atomic ions can be confined in free space with electromagnetic fields supplied by nearby electrodes. The linear radio frequency (r.f.) trap is the typical choice for quantum information applications.9,10 When the ions are laser-cooled to bottom of the trapping potential, they form a linear crystal of qubits, with the Coulomb repulsion balancing the external confinement force, as shown in Figure 1a. Ions are typically loaded into traps by generating neutral atoms of the desired element and ionising the atoms once in the trapping volume. Ion trap depths are usually much larger than room temperature, so rare collisions with background gas do not necessarily eject the ion from the trap, but they can temporarily break up the crystal and scramble the qubits. Under typical ultrahigh vacuum conditions, these qubit interruptions occur roughly once per hour per ion, but cryogenic vacuum chambers can reduce the collision rate by orders of magnitude, where qubits may last months or longer. An alternative ion trap geometry is the Penning trap, which can confine large two-dimensional (2D) crystals for quantum information applications.15,16 However, the addressing and control of individual qubits and the binding strength of internal modes of motion may pose difficulties, and this platform is thus not considered here.
(a) Schematic of silicon chip-trap mounted on a ceramic pin grid array carrier with raised interposer, confining atomic ions that hover ~75 μm above the surface. The inset is an image of 7 atomic ytterbium (171Yb+) ions arranged in a linear crystal and laser-cooled to be nearly at rest. The few-micrometre separation between ions is determined by a balance between the external confinement force and Coulomb repulsion. (b,c) Reduced energy level diagram of a single 171Yb+ atomic ion, showing the atomic hyperfine levels and that represent a qubit. The electronic excited states and are separated from the ground states by an energy corresponding to an optical wavelength of 369.53 nm, and applied laser radiation (blue arrows) drives these transitions for (b) initialisation to state , and (c) fluorescence detection of the qubit state (, fluorescence, , no fluorescence).
Qubits stored in trapped atomic ions are represented by two stable electronic levels within each ion, often represented as an effective spin with the two states and , corresponding to bit values 0 and 1, respectively. The qubits can be initialised and detected with nearly perfect accuracy using conventional optical pumping and state-dependent fluorescence techniques.17 This restricts the atomic species of trapped ion qubits to those with simple electronic structure (e.g., those with a single valence electron: Be+, Mg+, Ca+, Sr+, Ba+, Zn+, Hg+, Cd+ and Yb+).
Figure 1b,c show the reduced energy level diagram of 171Yb+, where the qubit levels and are represented by the stable hyperfine levels of electron/nuclear spin in the ground electronic state, separated by frequency vHF=12.642812 GHz. Such states form an excellent frequency standard, and coherence times >1,000 s have been observed.18,19 The optically excited electronic states and are themselves split by a hyperfine coupling and separated from the ground states by an optical interval. Laser radiation tuned just below resonance in these optical transitions allows Doppler laser cooling to confine ions near the bottom of the trap. Other more sophisticated forms of laser cooling can bring the ions to nearly at rest in the trap.17 When laser beams resonant with both and transitions are applied, the ion rapidly falls into the state and no longer interacts with the light field (Figure 1b). This optical pumping technique allows the initialisation of a qubit with essentially fidelity. When a single laser resonant with the transition is applied, the closed cycling optical transition causes an ion in the state to fluoresce strongly at a rate scaled by the excited state radiative linewidth γ~2π×10 MHz, whereas an ion in the state stays dark, because the laser is far from its resonance (Figure 1c). The collection of even a small fraction of this fluorescence thus allows for the detection of the atomic qubit state with near-perfect efficiency, with integration times as low as ~20 μs.20 Other atomic species have similar initialisation/detection schemes.
Linking atomic qubits with the Coulomb interaction
The motion of many trapped ions is coupled through their mutual Coulomb repulsion, so the qubits can therefore be linked by relating the internal qubit states to the external motion of the ions, as depicted in Figure 2a. This can be accomplished by applying qubit state-dependent optical or microwave dipole forces to the ion(s).9,17,21–23 To see how this type of motional data bus works, we assume that a given ion responds to an external field by experiencing an equal and opposite energy shift with effective dipole moment μ that depends upon the qubit state through selection rules. When the field varies with position x, there is a qubit-state-dependent force of the form , where is the field gradient and is the Pauli matrix corresponding to the angular momentum of the qubit effective spin. Here we neglect higher order field gradients, which is justified when the ion is laser-cooled to much less than the characteristic length scale (or wavelength) of the applied field. For plane-wave radiation coupled with wavevector k and amplitude , , where ħ is Planck’s constant, and the Rabi frequency parametrises the field-qubit coupling. (For two-photon optical Raman couplings, the effective wavevector k is given by the wavevector difference between the two beams.17 The use of such Raman couplings between ground states also gives the practical advantage of being insensitive to the absolute optical phase at the position of the ion, instead depending upon the microwave or r.f. phase difference between the beams.24)
(a) Qubit-state-dependent forces on individual ions in a chain provide a coupling mechanism between qubits for the operation of entangling quantum logic gates. Optical dipole forces (indicated in red) displace two ions depending upon their qubit states, and the resulting modulation of the Coulomb interaction allows the implementation of entangling quantum gates between these two ions. This type of link can be generalised to operations involving any number of qubits or even the entire chain for applications in quantum simulations. (b) Concept of a QCCD ion trap,32 where ions can be shuttled between various zones for multiplexing (courtesy, NIST). (c) Energy levels of trapped ion excited with a fast laser pulse (blue upward arrow) that produces a single photon whose frequency, represented by the state or , is entangled with the resultant qubit state or , respectively. Alternative configurations allow the encoding of polarisation or time-bin photonic qubits. (d) Two ‘communication’ ions, immersed in a separate crystals of other ions, each produce single photons when driven by laser pulses (blue) as in c. With some probability, the photons arrive at the 50/50 beamsplitter and then interfere. This ‘Bell-state detection’ of the photons heralds the entanglement of the trapped ion qubits. (e) Modular distributed quantum computer. Several ELU modules, each with full control of 50–100 trapped ions through Coulomb gates, are connected through a photonic network utilising an optical crossconnect switch, inline fiber beamsplitters and a photon-counting imager.44
As this force acts differently on the two qubit states, it couples the qubit state to the collective motion of N ions, with characteristic speed , where is the recoil frequency of the ion crystal associated with field momentum ħk, Nm is the total mass of the ions and ω the frequency of harmonic oscillation of collective motion along the x direction. When this mapping affects multiple ions, entangling gates can be operated between separated ions, mediated through the motion. There are many protocols for the creation of controlled-NOT and other gates using this coupling to the collective motion of the ions.9 Current experiments with a few ions have realised entangled state fidelities of greater than 99.9%25,26 and operate in the range Rgate/2π~10–100 kHz, although with ultrafast high-intensity optical fields it may be possible to operate gates in the GHz range.27
As the number of ions N in the crystal grows, the gate speed slows down as . For large crystals, there will also be crosstalk between the many modes of collective motion. Background errors such as the decoherence (heating) of the motional modes28 or fluctuating fields that add random phases to the qubits will become important at longer times, thus there will be practical limits on the size of a single crystal for the performance of faithful quantum gates. Through the use of individual optical addressing of ions29,30 and pulse-shaping techniques,31 these errors should not be debilitating for the full control of single crystals ranging from N=10–100 qubits.
In order to scale beyond ~50 trapped ion qubits, we can shuttle trapped ions through space in order to couple spatially separated chains of ions, in a multiplexed architecture called the quantum charge-coupled device (QCCD)23,32,33 and depicted in Figure 2b. The QCCD architecture requires exquisite control of the atomic ion positions during shuttling and may require additional atomic ion species to act as ‘refrigerator’ ions to quench the excess motion from shuttling operations.34 Rudimentary versions of the QCCD idea have been employed in many quantum information applications such as teleportation and small quantum algorithms,9 and recent experiments have shown the reliable, repeatable and coherent shuttling of ion qubits over millimetre distances in microsecond timescales35,36 and through complex 2D junctions.37–40 The QCCD approach will help usher the development of trapped ion quantum computers with perhaps 50–1,000 qubits. However, scaling to many thousands or more qubits in the QCCD may be challenging because of the complexity of interconnects, diffraction of optical beams and the extensive hardware required for qubit control. In addition, as the number of qubits grows sufficiently large, the QCCD architecture will suffer from the complexity of moving quantum information arbitrarily through the entire system. Regardless of the speed of nearest-neighbour elementary shuttling operations, the QCCD shuttling complexity over large distances may eventually limit the quantum processing speed. More generally, it is likely that a large-scale quantum computer will require connections between distant qubits and a method for producing entanglement that is independent of distance.41
Linking atomic qubits with photons
To scale beyond the QCCD in a modular architecture, it will likely become necessary to link separate registers of trapped ion chains with photonic interfaces.42,43 This allows quantum gates to be performed between any qubits in the processor, regardless of their relative location,41,44,45 while supporting fault-tolerant error correction even in the face of photonic interconnects that succeed with small probability per attempt.44–46
A pair of trapped ion qubit modules (elementary logic units or ELUs) can be entangled with each other using propagating photons emitted by a subset of ions from each register, designated to be ‘communication qubits’. As shown in Figure 2c, the communication qubit is driven to an excited state with fast laser pulses (typically ~ps) so that at most one photon emerges from each qubit. Following appropriate radiative selection rules, there are multiple decay paths, resulting in entanglement between a photonic qubit (e.g., polarization, frequency) and the atomic qubit. When photons collected from two separate communication qubits are mode-matched and interfered on a 50/50 beamsplitter (Figure 2d), coincident detection of single photons on the output modes of the beamsplitter herald a Bell-state of the photons and thus the creation of entanglement between the memory qubits through entanglement swapping.47,48 For hyperfine atomic qubits, the optical path length of this interferometer need only be stabilised to well within the wavelength corresponding to the qubit frequency difference (~mm). The mean connection rate of this photonic interface is , where F is the fraction of light collection from each ion emitter, ηD is the single-photon detector efficiency and R is the repetition rate of the initialisation/excitation process limited by the emission rate γ (an alternative single-photon approach involving the weak excitation of the ions49,50 suffers from optical path length instabilities, and, as the light collection improves, the performance of this alternative protocol is inferior to the two-photon scheme discussed in the text.). For typical atomic transitions into free space with γ/2π~10 MHz, light collection fraction F~1–10% and detector efficiency ηD~20%, we find typical connection rates of ~100 Hz,51 but this could be markedly improved with integrated photonics, as discussed below. Although this ion–ion entanglement source utilising photonic channels is probabilistic, the detected photons announce when it does succeed, and thus the heralded entanglement of the trapped ions can be subsequently used for deterministic quantum information applications.52 Moreover, by performing such operations in parallel on many pairs, a FIFO (first in, first out) buffer can provide a synchronous stream of entangled ion pairs between the trapped ion modules that can be used as needed, thus eliminating the probabilistic nature of the connection.
In practice, the communication qubit must be well-isolated from the memory qubits so that scattered light from the excitation laser as well as the emitted photons themselves do not disturb the spectator qubit memories. It may be necessary to physically separate (shuttle) the communication qubit away from the others, invoking techniques from the QCCD approach, but ultimately using two different atomic species can eliminate this crosstalk,53–55 such as 171Yb+ for memory qubits and 138Ba+ for communication qubits. Here the communication qubits are connected through the photonic channel, and then mapped to neighbouring memory qubits through Coulomb gates as described above.
In Figure 2e, we show a concept of a large-scale modular trapped ion quantum-computing architecture, involving individual ELU modules that host Coulomb-based quantum links within the module and can be wired to other ELU modules through photonic connections as described above. By using a non-blocking optical cross-connect switch,56,57 the connectivity between the entire sample of qubits can be extended in order to scale up to very large numbers of ELU modules, potentially to thousands or millions of qubits.
Integration technologies for trapped ion quantum computers
Unlike classical solid-state circuits where large-scale integration of complex information processors is readily available, practical implementation of a trapped-ion quantum processor will require development of new integration technologies and system engineering approaches. In this section, we will describe the current efforts towards such technology development.
Chip traps and optical control of qubits
Reliable and reproducible fabrication of many identical ELU modules starts with the ion trap itself. Ion trap electrode structures can be fabricated by lithographically etching semiconductor platforms such as Si/SiO2 wafers and metallising the electrodes, with positions defined to sub-micrometer precision. The electrodes must hold high static and r.f. electrical potentials, with excellent insulating barriers between the electrodes, all in an ultrahigh vacuum (UHV) environment. The trap structure must also be optically open, and allow high-power laser beams to cross near the electrode surfaces to affect Coulomb gates or photonic couplings, without causing excessive light scattering. Finally, the ions must be spatially separated from other qubit memories during initialisation and measurement processes, requiring precise control over the electrical potentials over space and time in order to shuttle ions throughout the trapping regions.
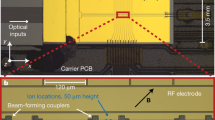
An approach to create the necessary electromagnetic potential to trap an ion above the surface of a chip was first suggested in 200458,59 and demonstrated in 2006,60 along with the first monolithic semiconductor ion trap.61 The design and fabrication of complex surface traps using silicon microfabrication processes has now matured, with examples of the Sandia high-optical access (HOA) trap62 and the GTRI/Honeywell ball-grid array (BGA) trap63 shown in Figure 3. Recent experiments have demonstrated high-performance qubit measurement20 and single-qubit quantum gates64–66 in such microfabricated surface traps that outperform conventional manually assembled macroscopic traps. The ability to design and simulate the electromagnetic trapping parameters prior to fabrication provides an attractive path to developing complex trap structures that are both repeatable and produced with high yield.
Once atomic ion qubits are produced and confined to standard semiconductor trap structures, interactions between arbitrary subsets of the qubits in a single ELU or reduced sets of ions between ELUs must be gated and controlled in order to perform the desired calculations, simulations or quantum circuit. For local Coulomb gates as described above, we require a fixed-frequency off-resonant laser to provide dipole forces and a laser beam distribution technology that drives the desired interactions to operate a programmable and reconfigurable quantum computer. Moreover, in order to accommodate shuttling of ions, the laser sources may require synchronisation with the shuttling protocol and in some cases the trap r.f. fields. In the 171Yb+ system, lasers at 355 nm are ideal for gate operations, with reliability owing to their widespread use in conventional UV lithography. For optical beam delivery, recent developments in micromirror technology67 and multi-channel acousto-optic modulator (AOM) technology developed for the optical communication and semiconductor fabrication industries68 are attractive solutions, and in the coming years these devices will be tightly integrated with trapped ion systems.
Compact lasers and vacuum system technology
A large-scale ion trap quantum computer requires several tunable laser systems to match electronic resonances in the atomic ion, with optical frequencies stable and accurate to better than 10 kHz, a fractional precision of ~10−10. Traditionally, a significant effort is dedicated to laser stabilisation, with individual optical components on an optical table utilising long optical path lengths. Such a large footprint invariably drifts because of environmental changes (temperature, humidity, air pressure and so on), and requires constant adjustments to keep the system operational. Compact and stable tunable semiconductor lasers have recently been developed that provide the narrow linewidths necessary for initialising and reading out trapped ion qubits.69–71 The complete optical system including the frequency stabilisation can be assembled on a compact optical breadboard or a microfabricated optical bench.72 Following the footsteps of laser integration in modern dense wavelength-division multiplexed optical communication systems,73 it is feasible to design and assemble a stabilised laser system where all lasers necessary for running an ion-trapping experiment are packaged in a compact box that fits on an instrument rack, with fibre optic delivery to the ion trap chip.
Trapped atomic ions are suspended in a UHV environment, where collisions with background molecules should be minimised for sustained operation. Although careful assembly of clean UHV chamber can help create such an environment, ultimate vacuum environment might require low-temperature operation (<10 K).74 Closed-cycle cryogenic technology will markedly reduce the volume and operational burden of a UHV environment, while improving the vacuum conditions for operating the trapped ion quantum computer. Figure 4 shows an example of a compact vacuum environment created on a ceramic package that holds the surface trap. After the trap is die-attached and wirebonded to the ceramic package, a sealed cover is assembled in a UHV environment (Figure 4a). The cover provides all optical access necessary to operate an ion trap, an ion source that utilises laser ablation technique to load the trap, and getter material that will efficiently pump any residual gas molecules at low temperatures. This compact ceramic package can be installed in a closed-cycle cryostat (Figure 4b) and cooled down to cryogenic temperatures (~5 K) to provide the operating environment for the ion trap quantum processor. Figure 4c shows an example of a compact optical layout sufficient to trap a chain of ions in the cryogenic environment, onto which further qubit control optics could be assembled. This approach is compatible with recent development in surface treatment techniques for ion traps that are shown to substantially reduce anomalous heating, which may be necessary for high-fidelity operation of multi-qubit gates.75,76
Compact cryogenic UHV enclosure for trapped ions. (a) On-package vacuum enclosure, sealed in a UHV environment, that contains the ion trap, getter pumps and the atomic source. (b) Upon installation and cooling in a compact cryostat, the UHV environment is established. (c) The optical components can be arranged in a compact volume around the cryostat to support the ion trap operation.
Photonic technology
Integrated optical technology will be critical for a large-scale trapped ion quantum computer. Although efficient light collection and detector arrays will be necessary for the measurement of many trapped ion qubits through state-dependent fluorescence, it will be crucial for the single-photon linking of ELU modules as discussed above. With high numerical-aperture collection optics, ~10% of the emitted photons can be collected,51 and more could be extracted through an optical cavity77,78 integrated with the ion trap.79 Highly efficient photonic Bell-state detectors with near-ideal mode-matching can be realised in fibre or waveguide beamsplitters80 and near-unit efficiency photon detectors.81,82 Taken together, these advances may allow the linking of two ELUs to approach the speed of local Coulomb-based gates (~10 kHz).
For large numbers of optically networked trapped ions with many optical communication qubits, multiplexed photonic circuit elements will be necessary. Non-blocking and transparent optical cross-connect switches with many input/output ports, developed for conventional optical communication networks and data centres,56,57 are well-suited for this task. Transparent optical switches establish an optical path between select input and output ports by using passive optical elements such as tilting mirrors83 and can guide single photons that are entangled with the trapped ion qubits to form quantum links. These devices can also be reconfigured in real time to make parallel connections between multiple ELUs.
The extension of the above integrated photonics technology, including detectors and waveguides to optical cross-connect switches, to the visible and blue portions of the spectrum where atomic ions respond will be highly valuable to the trapped ion quantum optical network. Alternatively, noiseless photonic conversion technology from visible/blue to infrared and telecom bands will have an important role, especially for long-distance quantum communication network applications.
Hardware and software for scalable controllers
Although these integration technologies have a crucial role in developing compact, stand-alone ion trap quantum hardware, a scalable controller system is needed to run such a system. The controller system consists of hardware needed to (1) maintain the operation of frequency-stabilised laser systems, (2) manage the ion position by control of r.f. and static voltages, (3) measure- and process-emitted photons with photon detectors and associated readout circuits, and (4) apply laser pulses that are generated by a digital system to prepare, measure and manipulate qubits. These controller systems must be designed to precisely track the amplitude and phase of the qubits used in the information-processing task. It must be accompanied by control software that the user can program to instruct the quantum hardware to carry out the desired task. Both the hardware and the software for the controller should be designed for modularity and expandability, consistent with a fully coherent control of all qubits in the system. The practical scalability of the ion trap processor may ultimately be limited by the scalability of the interface between such a classical controller and the ion qubits, or how many ion qubits the controller can manage. A careful design of such controller system amounts to the ‘operating system’ for the ion trap quantum processor.
Applications and opportunities for the trapped ion quantum processor
Quantum algorithms, applications and error-correcting codes are usually designed independently of the underlying hardware, and therefore do not respect the underlying geometry of the physical system. The modular ion trap architecture has a flexible and reconfigurable connectivity that allows for the realisation of arbitrary geometries with a minimal number of swaps and/or teleportation steps. In this section, we examine the opportunities that such a hardware affords, beyond conventional gate-model quantum applications such as Shor’s factoring algorithm.
Topology of interactions
Although the spatial geometry of a crystal of laser-cooled trapped ions is typically one-dimensional, the interaction graph between qubits within a single ELU module can be fully connected and have high or undefined dimensionality. Owing to the strong long-range Coulomb interaction between the ions, quantum gates can be realised directly between distant pairs of qubits in the chain.84 Furthermore, multiple two-qubit gates can be performed in parallel on the chain, and multi-qubit or even global entangling gates can be performed by carefully controlling the intensity and spectrum of the lasers on all ions.85,86 Such multi-qubit operations are useful for the generation of certain entangled states9,22, and for the simulation of long-range global Ising interactions between the spins.87,88 In the context of such multi-qubit operations, additional single-qubit gates can be used to remove links in the graph89 and generate arbitrary circuits.
In the larger ion trap quantum computer, such highly connected ELU modules are linked to other modules through photonic channels, as discussed above.44 This higher level graph is determined by the density of photon-coupled ions (Figure 5) and is itself dynamic and reconfigurable, leading to great advantages in the use of this type of hierarchical architecture for a host of quantum applications, and may even suggest algorithm structures that have not yet been discovered.
Each ELU holds a chain of ions. The ions for remote entanglement (purple circles) are located at the ends of the chains. The interaction of the ions via the normal modes of the crystal forms a complete graph as shown by the red and blue lines when the ions are arranged in a circle. The red lines show connections up to the fourth-nearest neighbour. The physical geometry can be observed in the break of the red connections between the communication ions at the end of the chain. Entangled pair generation between ELUs requires photonic connections (purple lines) between the ELUs and the optical networking switchyard (grey box). The remote entanglement is reconfigurable and renewable throughout the computation. The picture shows chains of 20 ions, with ions reserved for communication.
Quantum simulation
Quantum simulators exploit a standard well-controlled quantum system to emulate model Hamiltonians that cannot easily be understood or solved numerically.1 The global entangling operations between trapped atomic ions are naturally suited to simulate hard quantum problems, some that may not necessarily correspond to a physical system (such as graphs that have nonlocal structures), and others with local interactions such as quantum magnetic Ising models and many body spin physics. For instance, when executing state-dependent forces as discussed above, the applied field can be adjusted to simulate variable-range Ising models with interaction strength falling off with a power law 1/rα as the physical distance r increases, where the exponent can be tuned between α=0 (infinite-range) and α=3 (dipole-dipole).15,87,90 In addition, digital quantum simulation techniques, which apply a series of distinct control Hamiltonians in discrete time steps, can be applied to generate arbitrary spin models91 and to control the underlying graph structure.89 Ion-trap quantum simulations could assist our understanding of models of exotic materials (such as high-temperature superconductors), or even stimulate the search for new material properties that have not yet been observed.
Determining the equilibrium behaviour (ground state) of spins subject to an arbitrary Ising coupling graph and local field terms is an NP-hard problem.92 The quantum adiabatic algorithm attempts to find the ground state by starting in a strong transverse field and then adiabatically switching it off.93,94 As the minimum energy gap to the excited states is not known for the most difficult problems, ‘adiabatic’ in this case means slow enough to avoid excitations. The quantum-annealing algorithm is similar in style, but interaction with a thermal bath complicates the dynamics.95,96 Although a sufficiently cold bath could improve the possibility of finding the ground state, this is not always the case. Large-scale superconducting systems fabricated by D-Wave have generated significant controversy,97 and the results to date are consistent with simulations of an open-system quantum annealer having limited use.95 The main limitations are insufficient precision and stability in the coupling parameters, two-qubit couplings of fixed type, a simple 2D static network structure and a temperature that is much larger than the characteristic energy scales in the system. As the gaps are expected to shrink polynomially with the system size for good problems, the D-Wave system thus relies on thermal effects. Although trapped ion qubit couplings are roughly 1,000 times smaller than superconducting systems in absolute terms, ion trap architectures promise significant advantages: higher coupling precision, two-qubit couplings of different forms, arbitrary and reconfigurable network structure and an effective zero temperature environment.9 Although key challenges remain in such an ion trap quantum adiabatic processor, such as stable laser delivery and the engineering challenges of fabricating large-scale ion trap chips as discussed above, trapped atomic ions are well-suited to the generic problem of quantum adiabatic algorithms.
Machine learning and the Boltzmann machine
Many models of artificial intelligence or machine learning are inspired by natural neural networks. In a model where the communication between neurons is bi-directional, the problem of determining the state of output neurons can be mapped to calculate the thermal distribution of an Ising model.98 The process of learning is the strengthening and weakening of connections between neurons, so that the output neurons optimally classify the signal received by the input neurons. In the model, learning is achieved by tuning the Ising model parameters to optimise the classification. This model of learning, known as a ‘Boltzmann machine’,99 can be simulated using an adiabatic/annealing quantum protocol well-suited to the ion trap architecture.
The Boltzmann machine is borrowed from the field of machine learning and uses the thermal distribution of an Ising model to make classifications.99 These methods have had a recent renaissance because of increased computational power and large data sets making deep learning both practical and useful. The optimisation procedure involves inputting training data and observing the classifier labels. The Ising couplings between the spins are adjusted until the machine generates an optimal classification. Quantum annealing or the quantum adiabatic method can be used to determine the classification of the data. This may result in a different set of optimal coupling values that can also be tested on classical machines. Classical algorithms tend to use layers of spins where each layer can have arbitrary connections with the next layer: two layers is a reduced Boltzmann machine and many layers is a deep reduced Boltzmann machine. A full Boltzmann machine allows for connections between any spin. Quantum algorithms are predicted to speed up the tuning of the machine and have already provided insight into new classical algorithms.100,101 Both full and reduced Boltzmann machines can be implemented with our modular system. The natural connectivity suggests a different class of Boltzmann machines where the outputs of one full Boltzmann machine can be teleported to the inputs of a second full Boltzmann machine.
Quantum error correction
A truly scalable quantum computer requires that the computational failure rate does not depend on the system size. Fault-tolerant quantum error correction provides a method for generating arbitrarily small logical errors when the physical gate errors are below an accuracy threshold.102 The accuracy threshold is defined over a family of codes and a pseudothreshold for a specific code is the error rate per physical gate below which the logical error rate is smaller than the physical error rate. A full discussion of quantum error correction is outside the scope of this article, and we refer the reader to reviews by Gottesman103 and Terhal104 for more information. Given the importance of quantum error correction as the system size increases, we would like to make a few remarks on performing quantum error correction methods in ion-trap hardware.
The basic elements of quantum error correction have already been demonstrated in ion trap systems. Redundancy codes have been shown to reduce the damage caused by bit-flip105 or phase-flip errors.106 The seven qubit Steane code8 corrects both bit-flip and phase-flip errors and is the smallest example of a colour code.107 Ions have been encoded into the seven-qubit code108, but errror correction has not yet been performed. The current challenge in the field is to implement a fault-tolerant logical qubit memory.
In the near term, two promising implementations for quantum memories in single ELUs are small surface codes109 and the Steane logical qubit with Steane ancilla.8,110 These small error-correcting procedures only require 17–25 total ions per logical qubit to generate fault-tolerant circuits that can have error thresholds near 10−3. This error rate is compatible with the best current ion trap gates and measurements20,25,26,64–66, and the whole procedure can easily fit within a single ELU. These small codes are only guaranteed to correct single errors, so the total number of reliable, but non-universal, operations on many logical qubits will scale as the error threshold divided by the square of the physical error per operation. Fault tolerance requires repeated measurement of error syndromes and ion shuttling or a second-ion species will need to be used to reduce unwanted excitation of the data. This constraint is similar but less challenging than protecting the quantum data during generation of entanglement between communication qubits.
In the future, the architecture could support fault-tolerant quantum computation. Proposals already exist for implementing the surface code46 and the concatenated Steane code44 in a modular architecture. There is currently great interest in the surface code due to its high computational threshold around 1%111,112 in 2D architectures. Early papers on the surface code emphasised computation near the threshold resulting in large overheads. For a target logical error rate of 10−10, the surface code requires millions of physical qubits per logical qubit when the physical error is 95% of the threshold and a few hundred physical qubits per logical qubit when the error rate is 1% of threshold.112 The key feature of our architecture is that there are two length scales where nonlocal interactions are possible: within the ELU and between ELUs. This enables the testing of codes that cannot be easily implemented in a 2D geometry. The increased connectivity allows for a possible reduction in qubit resources by allowing universal gates through gauge fixing in a 3D colour code,113 which reduces the overhead due to magic state distillation114,115 and allows for the implementation of finite rate codes,116,117 which yield more logical qubits per physical qubit as the logical error decreases. We expect that future developments in quantum error correction will also benefit from a non-planar geometry.
Outlook
Quantum computers will look very different than the semiconductor-based computers of today, just as current solid-state semiconductor devices look nothing like the vacuum tubes, relays and mechanical gears of an earlier era. Athough trapped atomic ion qubits may be seen as exotic today, their exquisite quantum coherence, high-performance quantum logic gates and unmatched connectivity and reconfigurability makes the trapped ion platform a leading candidate for large-scale quantum computing. The continued progress in ion trap integration strategies and supporting technologies have the potential to enable practical quantum-computing machines in a matter of years. We expect this device development to be driven by applications that harness the connectivity and reconfigurability of trapped ion qubits, where quantum computer scientists work closely with physicists and engineers in the co-design of tomorrow’s quantum computer.
References
Feynman, R. Simulating physics with computers. Int. J. Theor. Phys. 21, 467 (1982).
Nielsen, M. A. & Chuang, I. L. Quantum Computation and Quantum Information (Cambridge Univ. Press, 2000).
Ladd, T. D. et al. Quantum computers. Nature 464, 45 (2010).
Van Meter, R. & Oskin, M. Architectural implications of quantum computing technologies. J. Emerg. Technol. Comput. Syst. 2, 31 (2006).
Shor, P. W. in 1994 Proceedings of the 35th Annual Symposium on Foundations of Computer Science. 124–134 (Washington DC, USA, 1994).
Shor, P. W. Scheme for reducing decoherence in quantum computer memory. Phys. Rev. A 52, R2493–R2496 (1995).
Calderbank, A. R. & Shor, P. W. Good quantum error-correcting codes exist. Phys. Rev. A 54, 1098–1105 (1996).
Steane, A. M. Error correcting codes in quantum theory. Phys. Rev. Lett. 77, 793 (1996).
Wineland, D. & Blatt, R. Entangled states of trapped atomic ions. Nature 453, 1008–1014 (2008).
Monroe, C. & Kim, J. Scaling the ion trap quantum processor. Science 339, 1164 (2013).
Devoret, M. H. & Schoelkopf, R. J. Superconducting circuits for quantum information: An outlook. Science 339, 1169 (2013).
Barends, R. et al. Coherent Josephson qubit suitable for scalable quantum integrated circuits. Phys. Rev. Lett. 111, 080502 (2013).
Corcoles, A. D. et al. Demonstration of a quantum error detection code using a square lattice of four superconducting qubits. Nat. Commun. 6, 6979 (2015).
Daydé, M., Marques, O . & Nakajima, K. (eds.). Lecture Notes in Computer Science Vol. 7851 (Springer, 2013).
Britton, J. W. et al. Engineered two-dimensional ising interactions in a trapped-ion quantum simulator with hundreds of spins. Nature 484, 489 (2012).
Bohnet, J. G. et al. Quantum spin dynamics and entanglement generation with hundreds of trapped ions. Science 352, 1297–1301 (2016).
Leibfried, D., Blatt, R., Monroe, C. & Wineland, D. Quantum dynamics of single trapped ions. Rev. Mod. Phys. 75, 281–324 (2003).
Bollinger, J. J., Heinzen, D. J., Itano, W. M., Gilbert, S. L. & Wineland, D. J. A 303-mhz frequency standard based on trapped Be+ ions. IEEE Trans. Instrum. Meas. 40, 126 (1991).
Fisk, P. T. H., Sellars, M. J., Lawn, M. A. & Coles, C. Coherent Josephson qubit suitable for scalable quantum integrated circuits. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 44, 344 (1997).
Noek, R. et al. High speed, high fidelity detection of an atomic hyperfine qubit. Opt. Lett. 38, 4735–4738 (2013).
Cirac, J. I. & Zoller, P. Quantum computation with cold trapped ions. Phys. Rev. Lett. 74, 4091–4094 (1995).
Sørensen, A. & Mølmer, K. Quantum computation with ions in thermal motion. Phys. Rev. Lett. 82, 1971–1974 (1999).
Wineland, D. J. et al. Experimental issues in coherent quantum-state manipulation of trapped atomic ions. J. Res. Nat. Inst. Stand. Tech 103, 259–328 (1998).
Lee, P. J. et al. Phase control of trapped ion quantum gates. J. Opt. B 7, S371 (2005).
Ballance, C. J., Harty, T. P., Linke, N. M., Sepiol, M. A. & Lucas, D. M. High-fidelity quantum logic gates using trapped-Ion hyperfine qubits. Phys. Rev. Lett. 117, 060504 (2016).
Gaebler, J. P. et al. High-fidelity universal gate set for 9Be+ ion qubits. Phys. Rev. Lett. 117, 060505 (2016).
Garcia-Ripoll, J. J., Zoller, P. & Cirac, J. I. Speed optimized two-qubit gates with laser coherent control techniques for ion trap quantum computing. Phys. Rev. Lett. 91, 157901 (2003).
Turchette, Q. A. et al. Heating of trapped ions from the quantum ground state. Phys. Rev. A 61, 063418 (2000).
Häffner, H., Roos, C. & Blatt, R. Quantum computing with trapped ions. Phys. Rep. 469, 155 (2008).
Choi, T. et al. Optimal quantum control of multimode couplings between trapped ion qubits for scalable entanglement. Phys. Rev. Lett. 112, 190502 (2014).
Zhu, S.-L., Monroe, C. & Duan, L.-M. Arbitrary-speed quantum gates within large ion crystals through minimum control of laser beams. Europhys. Lett. 73, 485–491 (2006).
Kielpinski, D., Monroe, C. & Wineland, D. Architecture for a large-scale ion-trap quantum computer. Nature 417, 709–711 (2002).
Lekitsch, B. et al. Blueprint for a microwave trapped-ion quantum computer. Preprint at arXiv:1508.00420 (2015).
Barrett, M. D. et al. Sympathetic cooling of 9Be+ and 24Mg+ for quantum logic. Phys. Rev. A 68, 042302 (2003).
Walther, A. et al. Controlling fast transport of cold trapped ions. Phys. Rev. Lett. 109, 080501 (2012).
Bowler, R. et al. Coherent diabatic ion transport and separation in a multizone trap array. Phys. Rev. Lett. 109, 080502 (2012).
Blakestad, R. B. et al. High-fidelity transport of trapped-ion qubits through an X-junction trap array. Phys. Rev. Lett. 102, 153002 (2009).
Moehring, D. L. et al. Design, fabrication and experimental demonstration of junction surface ion traps. New J. Phys. 13, 075018 (2011).
Wright, K. et al. Reliable transport through a microfabricated X-junction surface-electrode ion trap. New J. Phys. 15, 033004 (2013).
Shu, G. et al. Heating rates and ion-motion control in a Y-junction surface-electrode trap. Phys. Rev. A 89, 062308 (2014).
Metodi, T. S., Thaker, D. D., Cross, A. W., Chong, F. T. & Chuang, I. L. in 38th Annual IEEE/ACM International Symposium on Microarchitecture (MICRO’05), 305–316 (Barcelona, Spain, 2005).
DeVoe, R. G. Elliptical ion traps and trap arrays for quantum computation. Phys. Rev. A 58, 910 (1998).
Steane, A. M. & Lucas, D. M. Quantum computing with trapped ions, atoms and light. Fortsch. Phys. 48, 839 (2000).
Monroe, C. et al. Large scale modular quantum computer architecture with atomic memory and photonic interconnects. Phys. Rev. A 89, 022317 (2014).
Duan, L.-M. & Monroe, C. Colloquium : Quantum networks with trapped ions. Rev. Mod. Phys. 82, 1209–1224 (2010).
Nickerson, N., Li, Y. & Benjamin, S. C. Topological quantum computing with a very noisy network and local error rates approaching one percent. Nat. Commun. 4, 1756 (2013).
Simon, C. & Irvine, W. T. M. Robust long-distance entanglement and a loophole-free bell test with ions and photons. Phys. Rev. Lett. 91, 110405 (2003).
Moehring, D. L. et al. Entanglement of single-atom quantum bits at a distance. Nature 449, 68 (2007).
Cabrillo, C., Cirac, J. I., Garcia-Fernandez, P. & Zoller, P. Creation of entangled states of distant atoms by interference. Phys. Rev. A 59, 1025 (1999).
Slodička, L. et al. Atom-atom entanglement by single-photon detection. Phys. Rev. Lett. 110, 083603 (2013).
Hucul, D. et al. Modular entanglement of atomic qubits using photons and phonons. Nat. Phys. 11, 37–42 (2015).
Kok, P. et al. Linear optical quantum computing with photonic qubits. Rev. Mod. Phys. 79, 135–174 (2007).
Schmidt, P. O. et al. Spectroscopy using quantum logic. Science 309, 749 (2005).
Tan, T. R. et al. Multi-element logic gates for trapped-ion qubits. Nature 528, 380 (2015).
Ballance, C. J. et al. Hybrid quantum logic and a test of bell’s inequality using two different atomic species. Nature 528, 384 (2015).
Kim, J. et al. 1,100×1,100 port mems-based optical crossconnect with 4-db maximum loss. IEEE Photon. Technol. Lett. 15, 1537–1539 (2003).
Zheng, X. et al. Three-dimensional mems photonic cross-connect switch design and performance. IEEE J. Select. Top. Quant. Electron. 9, 571–578 (2003).
Chiaverini, J. et al. Surface-electrode architecture for ion-trap quantum information processing. Quant. Inf. Comput. 5, 419 (2005).
Kim, J. et al. System design for large-scale ion trap quantum information processor. Quant. Inf. Comput. 5, 515 (2005).
Seidelin, S. et al. Microfabricated surface-electrode ion trap for scalable quantum information processing. Phys. Rev. Lett. 96, 253003 (2006).
Stick, D. et al. Ion trap in a semiconductor chip. Nat. Phys. 2, 36–39 (2006).
Maunz, P. L. W. et al. Characterization of a High-Optical-Access Surface Trap Optimized for Quantum Information Processing. Technical Report, SAND2015-1045C 566993 (Sandia National Laboratories (SNL-NM), 2015).
Guise, N. D. et al. Ball-grid array architecture for microfabricated ion traps. J Appl Phys 117, 174901 (2015).
Wang, S. X., Labaziewicz, J., Ge, Y., Shewmon, R. & Chuang, I. L. Demonstration of a quantum logic gate in a cryogenic surface-electrode ion trap. Phys. Rev. A 81, 062332 (2010).
Mount, E. et al. Error compensation of single-qubit gates in a surface electrode ion trap using composite pulses. Phys. Rev. A 92 (2015).
Harty, T. P. et al. High-fidelity preparation, gates, memory, and readout of a trapped-ion quantum bit. Phys. Rev. Lett. 113, 220501 (2014).
Crain, S., Mount, E., Baek, S. & Kim, J. Individual addressing of trapped 171Yb+ ion qubits using a microelectromechanical systems-based beam steering system. Appl. Phys. Lett. 105, 181115 (2014).
Pape, D. R. Multichannel Bragg cells: design, performance, applications. Opt. Eng. 31, 2148–2158 (1992).
Ball, H., Lee, M. W., Gensemer, S. D. & Biercuk, M. J. A high-power 626 nm diode laser system for beryllium ion trapping. Rev. Sci. Instrum. 84, 063107 (2013).
Mount, E. et al. Scalable digital hardware for a trapped ion quantum computer. Preprint at arXiv:quant-ph/1504.00035 (2015).
Schäfer, V. M., Ballance, C. J., Tock, C. J. & Lucas, D. M. Optical injection and spectral filtering of high-power ultraviolet laser diodes. Opt. Lett. 40, 4265–4268 (2015).
Gates, J. V. II et al. Uncooled laser packaging based on silicon optical bench technology. Proc. SPIE 2610, 127–137 (1996).
Ramaswami, R., Sivarajan, K. N. & Sasaki, G. H. Optical Networks: A Practical Perspective 3rd edn (Morgan Kaufmann, 2010).
Labaziewicz, J. et al. Suppression of heating rates in cryogenic surface-electrode ion traps. Phys. Rev. Lett. 100, 013001 (2008).
Hite, D. A. et al. 100-fold reduction of electric-field noise in an ion trap cleaned with In situ argon-ion-beam bombardment. Phys. Rev. Lett. 109, 103001 (2012).
Daniilidis, N. et al. Surface noise analysis using a single-ion sensor. Phys. Rev. B 89, 245435 (2014).
Keller, M., Lange, B., Hayasaka, K., Lange, W. & Walther, H. Continuous generation of single photons with controlled waveform in an ion-trap cavity system. Nature 431, 1075 (2004).
Casabone, B. et al. Heralded entanglement of two ions in an optical cavity. Phys. Rev. Lett. 111, 100505 (2013).
Kim, T., Maunz, P. & Kim, J. Efficient collection of single photons emitted from a trapped ion into a single-mode fiber for scalable quantum-information processing. Phys. Rev. A 84, 063423 (2011).
Jenkins, R. M., Devereux, R. W. J. & Heaton, J. M. Waveguide beam splitters and recombiners based on multimode propagation phenomena. Opt. Lett. 17, 991–993 (1992).
Natarajan, C. M., Tanner, M. G. & Hadfield, R. H. Superconducting nanowire single-photon detectors: physics and applications. Superconductor Science and Technology 25, 063001 (2012).
Marsili, F. et al. Detecting single infrared photons with 93% system efficiency. Nat. Photon. 7, 210–214 (2013).
Aksyuk, V. et al. Beam-steering micromirrors for large optical cross-connects. J. Lightw. Technol. 21, 634–642 (2003).
Korenblit, S. et al. Quantum simulation of spin models on an arbitrary lattice with trapped ions. New J. Phys. 14, 095024 (2012).
Schindler, P. et al. A quantum information processor with trapped ions. New J. Phys. 15, 123012 (2013).
Debnath, S. et al. Demonstration of a programmable quantum computer module. Nature 536, 63–66 (2016).
Porras, D. & Cirac, J. I. Effective quantum spin systems with trapped ions. Phys. Rev. Lett. 92, 207901 (2004).
Monroe, C. et al. in Proceedings of the International School of Physics ‘Enrico Fermi,’ (eds Knoop, M., Marzoli, I., & Morigi, G. ) Vol. 189, Varenna, Italy, 2013 (2014).
Hayes, D., Flammia, S. T. & Biercuk, M. J. Programmable quantum simulation by dynamic Hamiltonian engineering. New J. Phys. 16, 083027 (2014).
Kim, K. et al. Entanglement and tunable spin-spin couplings between trapped ions using multiple transverse modes. Phys. Rev. Lett. 103, 120502 (2009).
Lanyon, B. P. et al. Universal digital quantum simulation with trapped ions. Science 334, 57–61 (2011).
Istrail, S. in Proceedings of the Thirty-second Annual ACM Symposium on Theory of Computing, STOC 2000, 87–96 (ACM, 2000).
Farhi, E. et al. A quantum adiabatic evolution algorithm applied to random instances of an np-complete problem. Science 292, 472–476 (2001).
Friedenauer, A., Schmitz, H., Glueckert, J. T., Porras, D. & Schaetz, T. Simulating a quantum magnet with trapped ions. Nat. Phys. 4, 757–761 (2008).
Boixo, S. et al. Evidence for quantum annealing with more than one hundred qubits. Nat. Phys. 10, 218 (2014).
Albash, T., Ronnow, T. F., Troyer, M. & Lidar, D. Reexamining classical and quantum models for the D-Wave precessor. E. Phys. J. Special Top. 224, 111–129 (2015).
Shin, S., Smith, G., Smolin, J. & Vazirani, U. How ‘Quantum’ is the D-wave machine? Preprint at arXiv:1401.7087 (2014).
Hopfield, J. J. Neural networks and physical systems with emergent collective computational abilities. Proc. Natl Acad. Sci. USA 79, 2554–2558 (1982).
Bengio, Y., Courville, A. & Vincent, P. Representation learning: A review and new perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 35, 1798–1828 (2013).
Wiebe, N., Kapoor, A. & Svore, K. Quantum deep learning. Preprint at arXiv:1412.3489 (2014).
Wiebe, N., Kapoor, A., Granade, C. & Svore, K. Quantum inspired training for Boltzmann machines. Preprint at arXiv:1507.02642 (2015).
Preskill, J. Reliable quantum computers. Proc. R. Soc. Lond. 454, 385–410 (1998).
Gottesman, D. in Proceedings of the Symposia in Applied Mathematics, Vol. 68, 13–58 (American Mathematical Society, 2010).
Terhal, B. M. Quantum error correction for quantum memories. Rev. Mod. Phys. 87, 307–346 (2015).
Chiaverini, J. et al. Realization of quantum error correction. Nature 432, 602–605 (2004).
Schindler, P. et al. Experimental repetitive quantum error correction. Science 332, 1059–1061 (2011).
Bombin, H. & Martin-Delgado, M. A. Topological quantum distillation. Phys. Rev. Lett. 97, 180501 (2006).
Nigg, D. et al. Quantum computations on a topologically encoded qubit. Science 345, 302–305 (2014).
Tomita, Y. & Svore, K. M. Low-distance surface codes under realistic quantum noise. Phys. Rev. A 90, 062320 (2014).
Abu-Nada, A., Fortescue, B. & Byrd, M. Relative performance of ancilla verification and decoding in the [[7,1,3]] Steane code. Phys. Rev. A 89, 062304 (2014).
Raussendorf, R. & Harrington, J. Fault-tolerant quantum computation with high threshold in two dimensions. Phys. Rev. Lett. 98, 190504 (2007).
Fowler, A. G., Mariantoni, M., Martinis, J. M. & Cleland, A. N. Surface codes: Towards practical large-scale quantum computation. Phys. Rev. A 86, 032324 (2012).
Bombin, H. Gauge color codes: optimal transversal gates and gauge fixing in topological stabilizer codes. New J. Phys. 17, 083002 (2015).
Bravyi, S. & Kitaev, A. Universal quantum computation with ideal clifford gates and noisy ancillas. Phys. Rev. A 71, 022316 (2005).
Trout, C. J. & Brown, K. R. Magic state distillation and gate compilation in quantum algorithms for quantum chemistry. Int. J. Quantum Chem. 115, 1296 (2015).
Tillich, J.-P. & Zemor, L. in Proceedings of the 2009 IEEE International Symposium on Information Theory (ISIT) 799–803 (Seoul, Korea, 2009).
Kovalev, A. A. & Pryadko, L. P. Quantum kronecker sum-product low-density parity-check codes with finite rate. Phys. Rev. A 88, 012311 (2013).
Acknowledgements
This work is supported by the US Army Research Office (ARO) with funds from the IARPA MQCO and LogiQ Programs and the ARO Atomic and Molecular Physics Program, the AFOSR MURI on Quantum Measurement and Verification, the DARPA Quiness Program, the Army Research Laboratory Center for Distributed Quantum Information, the NSF Physics Frontier Center at JQI and the NSF Physics at the Information Frontier program.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
JK and CM are founding scientists of ionQ. The remaining author declares no conflict of interest.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Brown, K., Kim, J. & Monroe, C. Co-designing a scalable quantum computer with trapped atomic ions. npj Quantum Inf 2, 16034 (2016). https://doi.org/10.1038/npjqi.2016.34
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/npjqi.2016.34
This article is cited by
-
Fault-tolerant connection of error-corrected qubits with noisy links
npj Quantum Information (2024)
-
A high-fidelity quantum matter-link between ion-trap microchip modules
Nature Communications (2023)
-
Programmable photonic integrated meshes for modular generation of optical entanglement links
npj Quantum Information (2023)
-
Noisy intermediate-scale quantum computers
Frontiers of Physics (2023)
-
Temperature estimation of a pair of trapped ions
Scientific Reports (2022)