Abstract
Quantum key distribution (QKD) promises unconditional security in data communication and is currently being deployed in commercial applications. Nonetheless, before QKD can be widely adopted, it faces a number of important challenges such as secret key rate, distance, size, cost and practical security. Here, we survey those key challenges and the approaches that are currently being taken to address them.
Similar content being viewed by others
Introduction
Why quantum key distribution?
For thousands of years, human beings have been using codes to keep secrets. With the rise of the Internet and recent trends to the Internet of Things, our sensitive personal financial and health data as well as commercial and national secrets are routinely being transmitted through the Internet. In this context, communication security is of utmost importance. In conventional symmetric cryptographic algorithms, communication security relies solely on the secrecy of an encryption key. If two users, Alice and Bob, share a long random string of secret bits—the key—then they can achieve unconditional security by encrypting their message using the standard one-time-pad encryption scheme. The central question then is: how do Alice and Bob share a secure key in the first place? This is called the key distribution problem. Unfortunately, all classical methods to distribute a secure key are fundamentally insecure because in classical physics there is nothing preventing an eavesdropper, Eve, from copying the key during its transit from Alice to Bob. On the other hand, standard asymmetric or public-key cryptography solves the key distribution problem by relying on computational assumptions such as the hardness of factoring. Therefore, such schemes do not provide information-theoretic security because they are vulnerable to future advances in hardware and algorithms, including the construction of a large-scale quantum computer.1
We remark that some secrets, for instance, census data, need to be kept secret for decades (e.g. 92 years in Canada (Statistical Canada webpage. Release of personal data after 92 years, URL: http://www12.statcan.gc.ca/census-recensement/2011/ref/about-apropos/personal-personnels-eng.cfm)). Currently, however, data transmitted in 2016 is vulnerable to technological advances made in the future as Eve might simply save the transcripts of communication in her memory and wait for the construction, for example, of a quantum computer some time before 2,108 (92 years from 2016). This is highly probable. Recall that ENIAC, the first general purpose electronics computer,2 which was largely inferior to modern computers, was invented only 70 years ago. The US National Security Agency is taking the threat of quantum computing seriously and has recently announced transition plans to quantum-resistant classical algorithms3 (These algorithms are typically based on hard computational problems involving for instance the structure of some specific lattices. Despite important progress in the development of such algorithms, it is still an open question whether they are secure against a quantum computer).
Quantum cryptography, or more specifically, quantum key distribution (QKD),4–7 promises in principle unconditional security—the Holy Grail of communication security—based on the laws of physics only.8–10 QKD has the advantage of being future-proof:11 unlike classical key distribution, it is not possible for an eavesdropper to keep a transcript of quantum signals sent in a QKD process, owing to the quantum non-cloning theorem.12,13 For this reason, QKD is an essential element of the future quantum-safe infrastructure, which will include both quantum-resistant classical algorithms and quantum cryptographic solutions. In the bigger context of quantum information, there has been tremendous scientific and engineering effort towards the long-term vision of a global quantum internet.14 Imagine a world where only a few large-scale quantum computers are available (just like the early days of classical computing when only a few classical computers were available and in line with the current trend towards cloud computing); users will have to access those powerful quantum computers at long distances via a quantum internet. QKD will have a central role in securing data communication links in such a quantum internet.
The potential applications of QKD include securing critical infrastructures (for instance, the Smart Grid), financial institutions and national defense. Experimental QKD has been performed over distances on the order of 100 km in standard telecom fibres as well as in free space, while the secure key rate has now reached a few Mbits per second. QKD has leaped out of the lab.15 In China, the deployment of a 2,000 km QKD network between Shanghai and Beijing is underway; in Europe, after the SECOQC network demonstration in 2008,16 the UK is now creating a quantum network facilitating device and system trials, and the integration of quantum and conventional communications; in Japan, QKD technologies will be put into test to secure transmission of sensitive genome data; and the US has also started installing its own QKD network.
Why practical challenges in QKD?
In this review, we will focus on practical issues in QKD. We remark that, historically, practical considerations in QKD have led to ground-breaking inventions. For example, the need to counter the photon-number-splitting attack17 triggered the invention of the decoy-state protocol,18–20 which allows efficient distillation of secure keys using weak coherent pulse based QKD systems that once were vulnerable. As another example, the need to counter detector side-channel attacks has led to the discovery of measurement device independent (MDI) QKD.21 New theory that is due to practical advances in QKD also includes, for instance, the quantum de Finetti theorem,22 while security loopholes in QKD are closely related to loopholes in Bell inequality tests23—a key subject in the foundations of quantum mechanics. These issues are therefore of great interest to mathematicians and theoretical physicists.
QKD is clearly of interest to engineers too. For instance, practical QKD is closely linked to the development of new single-photon detection technologies such as superconducting nanowire single-photon detectors (SNSPDs),24 superconducting transition-edge sensors (TES),25 frequency up-conversion single photon detectors,26,27 and self-differencing InGaAs avalanche photodiodes,28 as well as of high-performance homodyne detection techniques.29 It is also the motivation for high-speed quantum random number generators30 and broadband entangled photon sources.31
Practical QKD has steered innovation and is a precursor in the field of Quantum Information Processing.
Outline of the review
Despite the important theoretical and experimental achievements, a number of key challenges remain for QKD to be widely used for securing everyday interactions. For instance, much effort is being put into increasing the communication rate and range of QKD and making QKD systems low cost, compact and robust. New hardware such as chip-based QKD and new software such as novel protocols are being studied and developed. The security of practical QKD systems is another important challenge. In order to foil quantum hackers, protocols such as MDI-QKD and loss-tolerant QKD32 have been developed and are currently being experimentally implemented. Yet, a comprehensive theory of the model of a QKD source remains to be constructed. To further extend the reach of QKD, two different approaches—quantum repeaters and ground-to-satellite QKD—are being pursued. In view of the proliferation of mobile computing devices including smart phones, mobile QKD applications have also attracted recent attention. Furthermore, the standardisation of QKD components is currently being pursued in European Telecommunications Standards Institute.33 In what follows, we will highlight some of the above challenges and the various approaches that are being taken to tackle them.
Main protocols and implementations
We begin our discussion with a brief overview of the main QKD protocols currently studied and the state-of-the-art in their practical implementations. As our main focus here is the current challenges in the field, we refer the reader to a recent review7 for the necessary background on the rigorous information-theoretic (or, unconditional) security definition of QKD in the composable framework, secure communication schemes including the one-time pad, the standard BB84 QKD protocol, and basic QKD components.
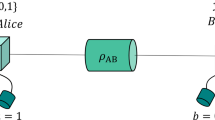
QKD protocols can be in essence divided with respect to the detection technique required to recover the key information encoded in the properties of light (Figure 1a). In discrete-variable (DV) protocols information is typically encoded in the polarisation or phase of weak coherent pulses simulating true single-photon states; hence the corresponding implementations employ single-photon detection techniques. The previously mentioned BB84 and decoy-state protocols are prominent examples in this category. Single-photon detection techniques are also necessary for the so-called distributed-phase-reference protocols, such as the coherent-one-way34 and differential-phase-shift (DPS)35 protocols, where the key information is encoded in photon arrival times or in the phase between adjacent weak coherent pulses. On the other hand, in continuous-variable (CV) QKD protocols information is encoded in the quadratures of the quantised electromagnetic field, such as those of coherent states,36,37 and homodyne or heterodyne detection techniques are used in this case. Such detectors are routinely deployed in classical optical communications, hence the CV approach offers the possibility for implementations based only on mature telecom components. All these protocols are prepare-and-measure in the sense that the transmitter, Alice, sends the encoded pulses to the receiver, Bob, who decodes as required by the specific protocol. On the contrary, in entanglement-based protocols,5 both parties receive parts of an entangled state and perform suitable measurements. More details on all protocols can be found in refs 6,7,38,39.
(a) Quantum key distribution systems use discrete-variable (DV) single-photon state encoding and single-photon detection techniques or continuous-variable (CV) quadrature field amplitude encoding and homodyne (or heterodyne) detection techniques. (b) State-of-the-art experimental setup for the implementation of the decoy-state BB84 QKD protocol.40 (c) State-of-the-art experimental setup for the implementation of the coherent state CV-QKD protocol.42 (d) Secret key generation rates demonstrated in some representative recent QKD experiments. Note that this figure is not meant to provide an exhaustive list of QKD implementations. Furthermore, protocol performance cannot be directly compared as different security assumptions are considered; for instance, decoy-state BB84 is secure against general coherent attacks while coherent-one-way (COW) and CV-QKD are secure against collective attacks. QKD is a subject of active ongoing research and so further developments are likely to occur in the near future. The loss coefficient of 0.2 dB/km in standard single-mode fibres at telecom wavelengths is assumed in this figure. Figures adapted with permission from: (a), ref. 180 © 2013 NPG, courtesy of Ping Koy Lam; (b), ref. 40 © 2013 OSA; (c) ref. 42 © 2013 NPG.
When it comes to practical demonstrations, performance of point-to-point links is assessed by the distance over which secret keys can be distributed and the rate of their distribution for a given security level. The security level is determined by the type of attacks considered in the corresponding security proof; demonstrating security against the so-called collective attacks6 is an important challenge for an implementation; however, information-theoretic security is achieved only when security against the most general (or coherent) attacks is proven. Hence, the ultimate goal is to provide this level of security at a speed and a distance that are compatible with practical applications. Some recent implementations have provided high levels of security: several QKD protocols have been demonstrated to provide composable security against collective attacks using reasonable data block sizes and practical setups, including decoy-state BB84,40 coherent-one-way,41 and CV-QKD.42,43 Among those protocols, the security of decoy-state BB84 QKD has been extended to cover coherent attacks, for realistic block sizes and with a minimal sacrifice in the secret key rate.44,45 Unfortunately, for coherent-one-way, the best security proof against coherent attacks currently gives a secret key rate that only scales quadratically with the loss.46 For CV-QKD with coherent states and heterodyne detection, a composable security proof against the most general attacks has recently been provided,47 but the current proof techniques do not allow a positive key rate for realistic block sizes in this case. Extending the security proofs for the latter protocols is therefore a pressing task in the theoretical study of QKD.
Figure 1b,c shows examples of advanced fibre-optic QKD systems allowing for real-time secret key generation over distances of 50 km with Mbit/s rates. In Figure 1d we summarise some important experimental achievements from both established and emerging QKD protocols (discussed in the following sections). Although the security assumptions and technological maturity vary in these implementations, these results illustrate the diversity of protocols and experimental solutions that the research community has invented to push the performance of QKD technology. Indeed, tremendous progress has been achieved in recent years, and avenues for further progress will be discussed in the next section. We remark, however, that there are fundamental limitations on what can be ultimately achieved. Over optical fibre networks, the attenuation of light in standard fibres at the telecom wavelength of 1,550 nm is 0.2 dB/km (or 0.16 dB/km in newly developed ultralow loss fibres). This unavoidable loss will not allow the range of point-to-point QKD links to exceed a few hundreds of kilometres as with overly excessive channel loss it would take several years to generate just one bit even using perfect light sources and detectors. Furthermore, with a practical lossy channel, the ultimate key rate is upper bounded by the so-called TGW bound48 (see also ref. 49 for a more recent result, quoted as the PLOB bound). These bounds provide a useful benchmark for the performance of all QKD protocol implementations.
Major challenges in performance and cost
In the quest for high performance and low-cost QKD systems, both hardware and software solutions are currently being pursued.
Hardware development
Key rate
Encryption keys generated by QKD can be used in a symmetric cipher scheme, such as Advanced Encryption Standard, which is quantum resistant, for enhanced security, or they can be combined with the one-time-pad encryption scheme for unconditional security. In both cases, the secure key rate achieved by the underlying QKD layer in a typical application scenario is crucial. Higher secure rates allow for a more frequent update of encryption keys in symmetric ciphers, and for a proportional increase in the one-time-pad communication bandwidth as this scheme requires the key to be as long as the message.
Presently, strong disparity exists between the classical and QKD communication rates. Classical optical communications delivering speeds of 100 Gbit/s per wavelength channel are currently being deployed,50 and a field trial featuring 54.2 Tbit/s aggregated data rate has recently been performed.51 On the other hand, the Mbit/s rates achieved by QKD systems today are sufficient, for instance, for video transmission; however, it is clear that if we want in the longer term to encrypt high volumes of classical network traffic using the one-time-pad, major developments on the secure key rate generated by QKD will be required.
The obtained key rate depends crucially on the performance of the detectors used. For QKD systems employing single-photon detection techniques, high efficiency and short dead time of the detectors are essential for reaching a high bit rate. The latest developments on high efficiency detectors52–54 are extremely promising; quantum efficiencies as high as 93% at telecom wavelengths have been reported for SNSPDs,53 and devices based on this technology with short dead time, low dark count, low time jitter and high detection efficiency are commercially available55 (Figure 2a,b). These results may allow for as much as a fourfold increase in the secret key rate, which currently stands at 1 Mbit/s over a 50 km fibre (or 10 dB loss) achieved using self-differencing InGaAs avalanche photodiodes with an ultrashort dead time40 (Figure 2c). Further key rate increase is possible using wavelength or spatial mode multiplexing technologies that have been routinely used for increasing the bandwidth in data communications.50,56,57 For CV-QKD systems, increasing the bandwidth of the homodyne or heterodyne detectors, while keeping at the same time the electronic noise low, is a necessary step for increasing the key rate beyond the 1 Mbit/s over 25 km that has been achieved.43 Further progress continues to be pursued, targeting also higher efficiency, which is currently around 60% for fibre-coupled detectors at telecom wavelengths.42 Furthermore, as shown in Figure 1c, a practical issue in these systems is that the strong phase reference pulse (or local oscillator) needs to be transmitted together with the signal at high clock rates; recent proposals that avoid this and use instead a local oscillator generated at Bob’s site58–60 are promising and will lead to more practical, high performance implementations.
(a) Superconducting nanowire chips. (b) Commercial SNSPDs with high detection efficiency. (c) Characterisation circuit for self-differencing InGaAs avalanche photodiodes.69 Figures adapted with permission from: (a) http://www.photonspot.com/, courtesy of Vikas Anant; (b) http://www.singlequantum.com/products, courtesy of Jessie Qin-Dregely.
Distance
Extending the communication range of QKD systems is a major driving factor for technological developments in view of future network applications. QKD systems based on single-photon detection champion the point-to-point communication distance (or channel loss). Here the low noise of single-photon detectors is the key enabling factor; in particular, the attainable range depends on the type and operation temperature of the detectors. InGaAs avalanche photodiodes can tolerate losses of 30 and 52 dB when cooled to −30 and −120 °C,41,61 respectively, whereas SNSPDs cooled to cryogenic temperatures have been demonstrated to withstand a record loss of 72 dB.62 This loss is equivalent to 360 km of standard single mode fibre or about 450 km of ultralow loss fibre. Although technologically possible, further extending the point-to-point distance is increasingly unappealing because the channel loss will inevitably reduce the key rate to a level of little practical relevance. This is also true for CV-QKD systems, which are in general more sensitive to losses. Here it is crucial to keep the excess noise—the noise exceeding the fundamental shot noise of coherent states—low and especially to be able to estimate the noise value precisely, which becomes increasingly difficult with the distance.38,42
We remark that advances towards high-performance QKD systems in terms of key rate and distance are coupled with the security guarantees offered by these systems. For instance, achieving composable security against general attacks requires in practice being able to perform efficient post-processing, including parameter estimation, over large data blocks with stable setups. Particularly for CV-QKD, performing efficient error correction and precise parameter estimation is of utmost importance.38,63
Cost and robustness
For QKD systems to be used in real world applications, low cost and robustness are indispensable features alongside high performance. Several avenues are currently being pursued. First, QKD systems have been shown to coexist with intense data traffic in the same fibre,64–67 thus eliminating the need for dark fibres that are not only expensive but also often unavailable. Access network architecture allows simultaneous access by a multitude of QKD users, and importantly they are compatible with full power Gigabit Passive Optical Network traffic in the same network.61,68 Room-temperature single-photon detectors have been shown to be suitable for DV-QKD over up to 100 km fibre, thus removing cooling requirements for the entire QKD system;44,69 for CV-QKD cooling is unnecessary. All these developments help reduce deployment cost as well as system complexity, footprint and power consumption.
Another important avenue to address the issue of cost and robustness is photonic integration.70 Chip-scale integration will bring high level of miniaturisation, leading to compact and light-weight QKD modules that can be mass-manufactured at low cost. Two main integration platforms are currently being explored, namely silicon (Si)71 and indium phosphide (InP),72 whereas alternative techniques include lithium niobate (LiNbO3) integration and glass waveguide technologies. For QKD protocols employing single-photon detection, the main difficulty comes from the receiver side so initial experiments have focused on transmitter integration. A LiNbO3 integrated polarisation controller was used for state preparation in a QKD implementation,73 whereas several techniques were combined to construct a handheld QKD sender module in ref. 74. More recently, a QKD transmitter chip that is reconfigurable to accommodate the state preparation for several QKD protocols, including decoy-state BB84, coherent-one-way and DPS, has been developed on InP75 (Figure 3), and Si transmitters have also been demonstrated independently by the U. of Toronto76 and also by Bristol group. (C. Erven and M. Thompson, private communication.)
Chip architecture combining several integrated photonic devices for the implementation of DV-QKD. (a) A monolithically integrated In-dium phosphide (InP) transmitter for GHz clock rate, reconfigurable, multi-protocol QKD. (b) A silicon oxynitride (Triplex) photonic receiver circuit for reconfigurable, multi-protocol QKD that passively decodes the quantum information with on-chip single-photon detectors. (c) The InP technology platform waveguide cross-section. (d) Wavelength tunable continuous-wave laser, formed from two tuneable distributed Bragg reflectors (T-DBR) and a semiconductor optical amplifier (SOA). (e) Microscopic image of electro-optic phase modulators in Mach-Zehnder interferometer. (f) The SiOxNy Triplex waveguide cross-section, with metalisation for heating elements. (g) Microscopic image of the receiver delay lines. Caption and Figure adapted with permission from ref. 75, courtesy of Philip Sibson, Chris Erven and Mark Thompson.
Chip-scale QKD receivers are also progressing. Low-loss planar-lightwave-circuits based on silica-on-silicon technology have been routinely used to replace fibre-based asymmetric Mach–Zehnder interferometres,75,77,78 a key enabling component for phase-based QKD protocols. Research efforts are currently focused on the integration of single-photon detectors using the aforementioned techniques, which will be essential for developing complete integrated systems. CV-QKD systems are particularly well suited for this objective because they only require the use of standard components. Indeed, Si photonic chips integrating many functionalities of a CV-QKD setup, including active elements such as amplitude and phase modulators and homodyne/heterodyne detectors based on germanium (Ge) photodiodes, have been developed.79
Development of chip-scale QKD is still at its early stages. Further research in this direction will help bring the QKD technology closer to its wide adoption.
New QKD protocols
In parallel to hardware development, much effort has also been devoted to novel QKD protocols aiming to outperform the established ones. Encouragingly, this line of research has led to protocols that may exhibit advantages when certain technical constraints are in place. Below, we discuss two protocols featuring high photon information capacity or noise tolerance.
High dimension-QKD
High dimension-QKD allows retrieval of more than 1 bit from each detected photon, thus offering an advantage in the photon information capacity when the photon rate is restrained.80–82 The choice for encoding is to use the arrival times of time-energy entangled photon pairs,83 whose continuous nature permits encoding of extremely large alphabets. A security proof against collective attacks has been developed,84 which was followed by a laboratory experiment demonstrating a photon information capacity of up to 6.9 bits per coincidence and a key rate of 2.7 Mbit/s over a 20 km fibre.85 Although this development has narrowed the key rate gap between entanglement based and prepare-and-measure QKD systems, its viability in a field environment will face a challenge to maintain the near unity interference visibility which was key to the obtained information capacity. High dimension-QKD without entanglement is also possible by exploiting the spatial degree of freedom, but its potential is restricted by the availability of high speed modulators.86,87
RR-DPS-QKD
The Round-Robin (RR) DPS protocol, which was proposed in 2014,88 removes the need for monitoring the channel disturbance to establish security, in stark contrast with conventional QKD protocols (see Figure 4a for the principle). Instead, Eve’s information can be tightly set, even to an arbitrarily low level, by just choosing experimental parameters. In theory, a positive key rate is possible for any quantum bit error rate (QBER) <50%. This extraordinary QBER tolerance makes it attractive for deployment when large systematic errors cannot be avoided. Shortly after its introduction the protocol has stimulated a number of experimental demonstrations.89–92 The RR-DPS-QKD protocol uses a transmitter identical to that found in a conventional DPS system,35 but requires a receiver that is capable of measuring the differential phase between any two pulses within a pulse group sent by Alice. Two different approaches are adopted. In the first, direct approach, a combination of optical switches and delay lines is used to bring the intended pulses into temporal overlap and then let them interfere90–92 (see for example Figure 4b). A more ingenious approach is to let a common phase reference interfere with all pulses sent by Alice, and then determine the differential phase between those pulses whose interference with the common reference produces a photon click.89 This latter approach avoids many problems associated with the direct one, such as loss and phase instability caused by optical delay lines and switches, but it will require remote optical phase locking for optimal performance. As it currently stands, the best key rate for RR-DPS-QKD is around 10 kbit/s for a 50 km distance in fibre91 and cannot compete with the more mature decoy-state BB84 protocol. RR-DPS-QKD has the advantage of being robust against encoding errors,93 but it is vulnerable to attacks on detectors, which will be discussed in the next section.
Major challenges in practical security
Although the security of a QKD protocol can be proven rigorously, its real-life implementation often contains imperfections that may be overlooked in the corresponding security proof. By exploiting such imperfections, various attacks, targeting either the source or the detectors, have been proposed; some of them have even been demonstrated to be effective against commercial systems.94–96 We refer the reader to a recent review7 for more details on quantum hacking and also countermeasures. To regain security in practical QKD, several solutions, including QKD based on testable assumptions,7 device independent (DI) QKD97,98 (see also ref. 99) and MDI-QKD,21 have been proposed. In the following, we discuss some important recent developments in this direction.
MDI-QKD
One promising long-term solution to side-channel attacks is DI-QKD, where the security relies on the violation of a Bell inequality and can be proven without knowing the implementation details. While recent loophole-free Bell experiments23,100,101 imply that DI-QKD could be implemented, the expected secure key rate is nevertheless impractically low even at short distances. A more practical solution is MDI-QKD, which is inherently immune to all side-channel attacks targeting the measurement device, usually the most vulnerable part in a QKD system. In fact, the measurement device in MDI-QKD can be treated as a ‘black box’ which could even be manufactured and operated by Eve. Building upon refs 102,103; ref. 21 proposed a practical scheme with weak coherent pulses and decoy states (Figure 5a), whose security against the most general coherent attacks, taking into account the finite data size effect, has been proved in ref. 104 (see also ref. 99, which studied an entanglement-based representation with general finite-dimensional systems, and ref. 105, which proposed a DI-QKD protocol with local Bell test).
(a) The schematic diagram of DV MDI-QKD proposed in ref. 21. (b) Simulation results of MDI-QKD and the TGW and PLOB bounds. DV MDI-QKD has a high key rate and is suitable for metropolitan networks. The achievable key rate is about 0.01 bit per pulse at a channel loss of 5 dB (which corresponds to 25 km telecom fibre). The key rate of DV MDI-QKD is only about 2 orders of magnitude away from the TGW bound at a practical distance. The simulation corresponds to the symmetric MDI-QKD case where the channels between Alice and Charlie and Charlie and Bob have the same amount of losses. It assumes high-efficiency SNSPDs with detection efficiency of 93% and dark count probability of 10−6 (per pulse),53 and an intrinsic error rate of 0.1%.106 The efficiency of error correction is assumed to be 1.16. Note that if the detection efficiency is reduced, for instance, to 50%, this induces a drop of the key rate of about a factor of 4. This means that for the metropolitan applications of DV MDI-QKD, the requirement on detector efficiency is not stringent. (c) MDI-QKD metropolitan area network experimental field test with untrusted relays.110 Figures adapted with permission from: (a) ref. 21, © 2012 APS; (b) ref. 112 courtesy of Feihu Xu; (c) ref. 110 courtesy of Qiang Zhang.
MDI-QKD21 is a natural building block for multi-user QKD networks, since the most expensive and complicated measurement device can be placed in an untrusted relay and shared among many QKD users.68 Several groups have demonstrated its feasibility. In particular, DV MDI-QKD was demonstrated over 200 km telecom fibre106 and 404 km of ultralow loss fibre107 in lab conditions, and over 30 km of deployed fibre.108 With highly efficient single-photon detectors, the tolerable channel loss can be as high as 60 dB, which corresponds to 300 km of standard telecom fibre.109 A real-life fibre based multi-user MDI-QKD network was also implemented recently110 (Figure 5c). Moreover, a 1 Mbit/s proof-of-principle MDI-QKD experiment was performed,111 thus illustrating the high key rate potential of DV MDI-QKD. This was also studied in ref. 112 for MDI-QKD employing state-of-the-art SNSPDs; in Figure 5b, simulation results of the secret key rate in this case show an achievable key rate of 0.01 bit per pulse over 25 km. With a transmission rate of 1 GHz, this corresponds to a secret key rate of 10 Mbit/s, which is sufficient for many cryptographic applications. As a comparison, we also present in Figure 5b the previously mentioned fundamental upper bounds per optical mode.48,49 We see that the key rate of DV MDI-QKD is only about 2 orders of magnitude away from the TGW bound at a practical distance, hence this protocol is suitable for high speed communications in metropolitan area networks.
It is important to emphasise that one fundamental assumption in MDI-QKD is that Eve cannot interfere with Alice and Bob’s state preparation processes. To prevent Eve from having access to quantum signals entering Alice’s or Bob’s labs and interfering with the state preparation process, MDI-QKD is commonly implemented using independent laser sources for Alice and Bob. Recently, gigahertz-clocked, phase-randomised pulses from independent gain-switched lasers have been demonstrated to interfere with high visibility, by control of the frequency chirp and/or emission jitter.111,113
DDI-QKD
One drawback of MDI-QKD is that its key rate scales quadratically with the detector efficiency. This is because in most of existing MDI-QKD protocols (except for ref. 114), secure keys are distilled from two-fold coincidence detection events (In MDI-QKD, the secure key rate R scales as TA×η×TB×η, where TA is the channel transmission from Alice to the measurement device, TB is the channel transmission from Bob to the measurement device, and η is the single-photon detection efficiency (assuming that all detectors have the same efficiency). The overall transmission of the whole channel (from Alice to Bob) is T=TA×TB, hence the key rate R of MDI-QKD scales as T×η2. This means that the key rate of MDI-QKD scales linearly with the whole channel transmittance (same as the case of conventional QKD and DDI-QKD), but quadratically with the detector efficiency.). Recently, the detector-device-independent (DDI) QKD protocol, designed to bridge the strong security of MDI-QKD with the high efficiency of conventional QKD, was proposed.115–117 In this protocol, the legitimate receiver employs a trusted linear optics network to decode information on photons received from an insecure quantum channel, and then performs a Bell state measurement (BSM) using uncharacterised detectors. One important advantage of this approach is that its key rate scales linearly with the detector efficiency. This is achieved by replacing the two-photon BSM scheme in the original MDI-QKD protocol (Figure 5a) by a single-photon BSM scheme.118 However, its ability to completely remove detector side-channel attacks has yet to be proven. Either countermeasures to Trojan horse attacks119 or some trustworthiness to the BSM device is still required to establish the security of DDI-QKD.120 In fact, mathematically the standard BB84 QKD protocol based on a four-state modulation scheme can be formulated into a DDI-QKD protocol.121 This highlights the underlying connection between DDI-QKD and the BB84 protocol. Finally, we remark that the advantage of DDI-QKD compared with MDI-QKD becomes insignificant if high detection efficiency detectors are used in both schemes.
CV MDI-QKD
The MDI-QKD scheme has been extended recently to the CV framework122 (see also refs 123,124 for a more restricted security analysis). In the CV framework, both Alice and Bob prepare Gaussian-modulated coherent states and send them to an untrusted third party, Charlie, who measures the correlation between the incoming quantum states. The CV MDI-QKD system requires high efficiency (>85%) homodyne detectors for a positive key rate.112 This efficiency requirement has been met in recent proof-of-principle laboratory free-space experiments.122,125 However, achieving the required efficiencies in a fibre-based optical network setting is more challenging, owing to the detector coupling loss and losses by fibre network interconnects and components110 (see also ref. 126 for a different perspective). When high efficiency detectors are in place, CV MDI-QKD would require an asymmetric configuration, where Charlie needs to be located close to one of the users. Even in this case, the expected key rate of the state-of-the-art CV MDI-QKD system drops to zero when the channel loss is above 6 dB (corresponding to 30 km standard telecom fibre).112,122 Therefore, for long distance (>30 km) applications, DV MDI-QKD is currently the only option available for MDI-QKD. A reliable phase reference between Alice and Bob also needs to be established in CV MDI-QKD, and may be possible to realise using recently proposed techniques for standard CV-QKD.58–60 Despite these challenges, CV MDI-QKD has the potential for very high key rates, within one order of magnitude from the TGW and PLOB bounds, at relatively short communication distances.
QKD with imperfect sources
Given that the security loopholes associated with the measurement device can be closed by MDI-QKD, an important remaining question is how to justify the assumption of trustable quantum state preparation, including single-mode operation, perfect global phase randomisation, no side channels, etc. On one hand, the imperfections in quantum state preparation need to be carefully quantified and taken into account in the security proof; on the other hand, practical countermeasures are required to prevent Trojan horse attacks119 on the source.
To address imperfections in quantum state preparation in QKD, a loss-tolerant protocol was proposed in ref. 32, which makes QKD tolerable to channel loss in the presence of source flaws (see also studies in refs 127,128). On the basis of the assumption that the single-photon components of the states prepared by Alice remain inside a two-dimensional Hilbert space, it was shown that Eve cannot enhance state preparation flaws by exploiting the channel loss and Eve’s information can be bounded by the rejected data analysis.129 The intuition for the security of loss-tolerant QKD protocol can be understood in the following manner. By assuming that the state prepared by Alice is a qubit, it becomes impossible for Eve to perform an unambiguous state discrimination (USD) attack.130 Indeed, in order for Eve to perform a USD attack, the states prepared by Alice must be linearly independent; but by having three or more states in a two-dimensional space, in general the set of states prepared by Alice is linearly dependent, thus making USD impossible.
The above loss-tolerant protocol has been further developed and demonstrated experimentally in ref. 131, where the authors implemented decoy-state QKD with imperfect state preparation and employed tight finite-key security bounds with composable security against coherent attacks. The work in ref. 32 has also been extended to the finite-key regime in ref. 132, where a wide range of imperfections in the laser source, such as the intensity fluctuations, have been taken into account. In ref. 133, a rigorous security proof of QKD systems using discrete-phase-randomised coherent states was given, thus removing the requirement for perfect phase randomisation. With respect to this, we note that gain-switched laser diodes are presently the de facto QKD light source, capable of naturally providing phase-randomised coherent pulses at a clock rate of up to 2.5 GHz.134,135
Progress has also been made on enhancing the security of QKD by carefully examining source imperfections in implementations. Refs 136,137 studied the risk of Trojan horse attacks due to back reflections from commonly used optical components in QKD. Similar research was also conducted for CV-QKD.138 In ref. 139, by using laser-induced damage threshold of single-mode optical fibre to bound the photon numbers in Eve’s Trojan horse pulses, the authors provided quantitative security bounds and a purely passive solution against a general Trojan horse attack.
All the above advances strongly suggest the feasibility of long-distance secure quantum communication with imperfect sources. A promising research direction is to apply the above techniques for QKD with imperfect sources to MDI-QKD leading to practical side-channel-free QKD. To achieve this goal, it is necessary to establish a comprehensive list of assumptions on the sources, and verify them one by one. In a recent experimental demonstration,140 the loss-tolerant protocol is applied to a MDI-QKD setting. Such an experiment thus addresses source and detector flaws at the same time.
We end our discussion on practical security by noting that in both classical and quantum cryptography, it is also important to carefully address the risks of side-channel attacks on the electronics and post-processing layers. Various side-channel attacks discovered in classical cryptography, such as the timing attack,141 the power-monitoring attack,142 and acoustic cryptanalysis,143 can also pose threats to quantum cryptography. Closing these side channels requires substantial future efforts.
Network QKD
So far, our discussion has been largely limited to point-to-point QKD links. Although these links are useful for some applications, QKD network structures must be considered in order to enable access by a greater many users and also to extend the reach and geographical coverage. In addition, the incorporation of mobile QKD nodes for key transports will add to network connection flexibility and allow even greater geographical coverage. In the following, we discuss approaches for building a QKD network and possibilities for future mobile QKD deployment.
Building QKD networks
An important issue in a network setting is the topology that allows for multiple users to access the network. A star topology is suitable for this purpose for relatively short distance (up to 400 km). Imagine a star network where there is at most one intermediate node between any two users, allowing for secure quantum communication among all users without the need for the relay to be trusted. In fact, this approach has already been demonstrated based on the MDI-QKD protocol.110 The long-term vision is for each user to use a simple and cheap transmitter and outsource all the complicated devices for network control and measurement to an untrusted network operator. As only one set of measurement devices will be needed for such a network that is shared by many users, the cost per user could be kept relatively low. The network provider would then be in a favourable position to deploy state-of-the-art technologies including high detection efficiency SNSPDs to enhance the performance of the network and to perform all network management tasks. The important advantage is that the network operator can be completely untrusted without compromising security. Experimental demonstrations of network MDI-QKD, either in optical fibres110 or in free space, are a major step towards such QKD networks with untrusted relays.
Nonetheless, MDI-QKD is limited in distance, hence in order to address the great challenge of extending the distance of secure QKD, three further approaches are possible. The first and the simplest approach is to use trusted relays. This is already feasible with current technology and indeed has been used as the standard in existing QKD networks.16,144 By setting up trusted nodes, for instance, every 50 km, to relay secrets, it is possible to achieve secure communication over arbitrarily long distances. The QKD network currently under development between Shanghai and Beijing is based on this approach.
The second approach is quantum repeaters, which remove the need for the users to trust the relay nodes. Quantum repeaters are beyond current technology, but have been a subject of intense research efforts in recent years. The long-term vision here is to construct a global quantum internet as described, for example, in ref. 14. Research efforts on quantum repeaters have focused on matter quantum memories and their interface with photonic flying qubits.145,146 However, new recent approaches manage to reduce the need for a quantum memory147 or to completely remove it by using all-photonic quantum repeaters.148
Finally, the third approach is ground-to-satellite QKD. By using one or a few trusted satellites as relay stations, it is possible to extend the distance of secure QKD to the global scale. To this end, several free-space studies, including experiments with low earth orbit (LEO) satellites, have been conducted.149–155 China, the EU and Canada are all currently exploring experimental ground-to-satellite QKD in ambitious long-term projects involving LEO satellites.
Mobile QKD
The studies in free-space QKD may also open the door to mobile QKD networks, which can be useful in many applications, such as ship-to-ship communication, airport traffic control, communication between autonomous vehicles, etc. In such a network, the mobility of QKD platforms requires the network to be highly reconfigurable—the QKD users should be able to automatically determine the optimal QKD route in real time based on their locations. Fast-beam tracking systems are indispensable. Furthermore, due to the strong ambient light, an effective filtering scheme is required to selectively detect quantum signals. Recent studies analyze the effect of fading and of atmospheric turbulence to CV-QKD156 and show that CV-QKD with coherent detection could be robust against ambient noise photons due to the intrinsic filtering function of the local oscillator.157 We also note that preliminary studies suggest that QKD at microwave wavelengths, which are widely used in wireless communications, might be feasible over short distances.158–160 Driven by various potential applications, we expect that mobile QKD will become an active research topic in the coming years.
Conclusion
In this review, we have discussed important challenges in practical QKD. These range from extending security proofs to the most general attacks allowed by quantum mechanics to developing photonic chips as well as side-channel-free systems and global-scale QKD networks. Addressing these challenges using some of the approaches that we have presented will open the way to the use of QKD technology for securing everyday interactions.
As the lead application of the field of Quantum Information Processing, advances in QKD will have important implications in many other applications too. For example, a great range of quantum communication protocols beyond QKD have been studied in recent years161 and their development has directly benefited from research in QKD. These include, for instance, quantum bit commitment,162–164 quantum secret sharing,165–167 quantum coin flipping,168,169 quantum fingerprinting,170,171 quantum digital signatures,172,173 blind quantum computing174,175 and position-based quantum cryptography.176–178 It is known that some of those protocols, such as quantum bit commitment and position-based quantum cryptography, cannot be perfectly achieved with unconditional security. However, other security models exist, such as, for instance, those based on relativistic constraints or on noisy storage assumptions,179 where by assuming that it is impossible for an eavesdropper to store quantum information for a long time, one can retrieve security for such protocols.
Determining the exact power and limitations of quantum communication is the subject of intense research efforts worldwide. The formidable developments that can be expected in the next few years will mark important milestones towards the quantum internet of the future.
Notes added in proof
After a completion of a preliminary version of this paper, a recent preprint181 has been posted on the arXiv that demonstrates the insecurity of DDI-QKD protocol. In addition, it has come to our attention that DI-QKD remains vulnerable to covert channels such as memory attack.182
References
Shor, P. W. Proceedings of the 35th Annual Symposium on Foundations of Computer Science (ed. Goldwasser, S.) 124–134 (IEEE Computer Society Press, 1994).
Encyclopedia Britannica. ENIAC. https://www.britannica.com/technology/ENIAC.
Cesare, C. Encryption faces quantum foe. Nature 525, 167–168 (2015).
Bennett, C. H. & Brassard, G. Proceedings of the IEEE International Conference on Computers, Systems, and Signal Processing (ed. Goldwasser, S.) 175–179 (IEEE Press, 1984).
Ekert, A. K. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 67, 661–663 (1991).
Scarani, V. et al. The security of practical quantum key distribution. Rev. Mod. Phys. 81, 1301 (2009).
Lo, H.-K., Curty, M. & Tamaki, K. Secure quantum key distribution. Nat. Photon. 8, 595–604 (2014).
Mayers, D. Unconditional security in quantum cryptography. J. ACM 48, 351–406 (2001).
Lo, H.-K. & Chau, H. F. Unconditional security of quantum key distribution over arbitrarily long distances. Science 283, 2050–2056 (1999).
Shor, P. W. & Preskill, J. Simple proof of security of the BB84 quantum key distribution protocol. Phys. Rev. Lett. 85, 441–444 (2000).
Unruh, D. Advances in Cryptology—Crypto 2013. Vol. 8043, 380–397 (Springer, 2013).
Wootters, W. K. & Zurek., W. H. A single quantum cannot be cloned. Nature 299, 802–803 (1982).
Dieks, D. Communication by EPR devices. Phys. Lett. 92A, 271–272 (1982).
Kimble., H. J. The quantum internet. Nature 453, 1023–1030 (2008).
Qiu, J. Quantum communications leap out of the lab. Nature 508, 441–442 (2014).
Peev, M. et al. The SECOQC quantum key distribution in vienna. New J. Phys. 11, 075001 (2009).
Huttner, B., Imoto, N., Gisin, N. & Mor, T. Quantum cryptography with coherent states. Phys. Rev. A 51, 1863–1869 (1995).
Hwang, W.-Y. Quantum key distribution with high loss: toward global secure communication. Phys. Rev. Lett. 91, 057901 (2003).
Lo, H.-K., Ma, X. & Chen, K. Decoy state quantum key distribution. Phys. Rev. Lett. 94, 230504 (2005).
Wang, X.-B. Beating photon-number-splitting attack in practical quantum cryptography. Phys. Rev. Lett. 94, 230503 (2005).
Lo, H.-K., Curty, M. & Qi, B. Measurement-device-independent quantum key distribution. Phys. Rev. Lett. 108, 130503 (2012).
Christandl, M., Koenig, R., Mitchison, G. & Renner, R. One-and-a-half quantum de Finetti theorems. Commun. Math. Phys 273, 473–498 (2007).
Hensen, B. et al. Experimental loophole-free violation of a Bell inequality using entangled electron spins separated by 1.3 km. Nature 526, 682 (2015).
Gol’Tsman, G. N. et al. Picosecond superconducting single-photon optical detector. Appl. Phys. Lett. 79, 705–707 (2001).
Lita, A. E., Miller, A. J. & Nam., S. W. Counting near-infrared single-photons with 95% efficiency. Opt. Express 16, 3032–3040 (2008).
Albota, M. A. & Wong, F. N. C. Efficient single-photon counting at 1.55 μm by means of frequency upconversion. Opt. Lett. 29, 1449–1451 (2004).
Langrock, C. et al. Highly efficient single-photon detection at communication wavelengths by use of upconversion in reverse-proton-exchanged periodically poled LiNbO3 waveguides. Opt. Lett. 30, 1725–1727 (2005).
Yuan, Z. L., Kardynal, B. E., Sharpe, A. W. & Shields, A. J. High speed single photon detection in the near infrared. Appl. Phys. Lett. 91, 041114 (2007).
Hansen, H. et al. Ultrasensitive pulsed, balanced homodyne detector: application to time-domain quantum measurements. Opt. Lett. 26, 1714–1716 (2001).
Jennewein, T., Achleitner, U., Weihs, G., Weinfurter, H. & Zeilinger, A. A fast and compact quantum random number generator. Rev. Sci. Instrum. 71, 1675–1680 (2000).
Zhu, E. Y. et al. Poled-fiber source of broadband polarization-entangled photon pairs. Opt. Lett. 38, 4397–4400 (2013).
Tamaki, K., Curty, M., Kato, G., Lo, H.-K. & Azuma, K. Loss-tolerant quantum cryptography with imperfect sources. Phys. Rev. A 90, 052314 (2014).
Alléaume, R. et al. Worldwide standardization activity for quantum key distribution. In Proceedings of the IEEE Globecom Workshops (GC Wkshps), 656–551 (2014).
Stucki, D., Brunner, N., Gisin, N., Scarani, V. & Zbinden, H. Fast and simple one-way quantum key distribution. Appl. Phys. Lett. 87, 194108 (2005).
Inoue, K., Waks, E. & Yamamoto, Y. Differential phase shift quantum key distribution. Phys. Rev. Lett. 89, 037902 (2002).
Grosshans, F. & Grangier, P. Continuous variable quantum cryptography using coherent states. Phys. Rev. Lett. 88, 057902 (2002).
Grosshans, F. et al. Quantum key distribution using gaussian-modulated coherent states. Nature 421, 238 (2003).
Diamanti, E. & Leverrier, A. Distributing secret keys with quantum continuous variables: principle, security and implementations. Entropy 17, 6072–6092 (2015).
Ma, X., Fung, C.-H. F. & Lo, H.-K. Quantum key distribution with entangled photon sources. Phys. Rev. A 76, 012307 (2007).
Lucamarini, M. et al. Efficient decoy-state quantum key distribution with quantified security. Opt. Express 21, 24550–24565 (2013).
Korzh, B. et al. Provably secure and practical quantum key distribution over 307 km of optical fibre. Nat. Photon. 9, 163–168 (2015).
Jouguet, P., Kunz-Jacques, S., Leverrier, A., Grangier, P. & Diamanti, E. Experimental demonstration of long-distance continuous-variable quantum key distribution. Nat. Photon. 7, 378 (2013).
Huang, D. et al. Continuous-variable quantum key distribution with 1 Mbit/s secure key rate. Opt. Express 23, 17511–17519 (2015).
Lim, C. C. W., Curty, M., Walenta, N., Xu, F. & Zbinden, H. Concise security bounds for practical decoy-state quantum key distribution. Phys. Rev. A 89, 022307 (2014).
Lucamarini, M., Dynes, J. F., Fröhlich, B., Yuan, Z. & Shields, A. J. Security bounds for efficient decoy-state quantum key distribution. IEEE J. Sel. Topics Quantum Electron 21, 6601408 (2015).
Moroder, T. et al. Security of distributed-phase-reference quantum key distribution. Phys. Rev. Lett. 109, 260501 (2012).
Leverrier, A. Composable security proof for continuous-variable quantum key distribution with coherent states. Phys. Rev. Lett. 114, 070501 (2015).
Takeoka, M., Guha, S. & Wilde, M. M. Fundamental rate-loss tradeoff for optical quantum key distribution. Nat. Commun. 5, 5235 (2014).
Pirandola, S., Laurenza, R., Ottaviani, C. & Banchi., L. The ultimate rate of quantum cryptography. Preprint at arXiv:1510.08863 (2015).
Winzer, P. J. Scaling optical fiber networks: Challenges and solutions. Opt. Photon. News 26, 28–35 (2015).
Huang, M. F. et al. Terabit/s Nyquist superchannels in high capacity fiber field trials using DP-16QAM and DP-8QAM modulation formats. J. Lightw. Technol. 32, 776–782 (2014).
Pernice, W. H. P. et al. High-speed and high-efficiency travelling wave single-photon detectors embedded in nanophotonic circuits. Nat. Commun. 3, 1325 (2012).
Marsili, F. et al. Detecting single infrared photons with 93% system efficiency. Nat. Photon. 7, 210–214 (2013).
Comandar, L. C. et al. Gigahertz-gated InGaAs/InP single-photon detector with detection efficiency exceeding 55% at 1550 nm. J. Appl. Phys. 117, 083109 (2015).
Scontel Superconducting nanotechnology. http://www.scontel.ru/; Single Quantum. http://www.singlequantum.com/; ID Quantique. http://www.idquantique.com/; Photon Spt. http://www.photonspot.com/ Accessed 19 October, 2016.
Bahrani, S., Razavi, M. & Salehi, J. A. Orthogonal frequency-division multiplexed quantum key distribution. J. Lightw. Technol. 33, 4687–4698 (2015).
Dynes, J. F. et al. Quantum key distribution over multicore fiber. Opt. Express 24, 8081–8087 (2016).
Qi, B., Lougovski, P., Pooser, R., Grice, W. & Bobrek, M. Generating the local oscillator ‘locally’ in continuous-variable quantum key distribution based on coherent detection. Phys. Rev. X 5, 041009 (2015).
Soh, D. B. S. et al. Self-referenced continuous-variable quantum key distribution. Phys. Rev. X 5, 041010 (2015).
Huang, D., Huang, P., Lin, D., Wang, C. & Zeng., G. High-speed continuous-variable quantum key distribution without sending a local oscillator. Opt. Lett. 40, 3695–3698 (2015).
Fröhlich, B. et al. Quantum secured gigabit optical access networks. Sci. Rep. 5, 18121 (2015).
Shibaba, H., Honjo, T. & Shimizu, K. Quantum key distribution over a 72 dB channel loss using ultralow dark count superconducting single-photon detectors. Opt. Lett. 39, 5078–5081 (2014).
Jouguet, P., Elkouss, D. & Kunz-Jacques, S. High bit rate continuous-variable quantum key distribution. Phys. Rev. A 90, 042329 (2014).
Patel, K. A. et al. Quantum key distribution for 10 Gb/s dense wavelength division multiplexing networks. Appl. Phys. Lett. 104, 051123 (2014).
Choi, I. et al. Field trial of a quantum secured 10 Gb/s DWDM transmission system over a single installed fiber. Opt. Express 22, 23121–23128 (2014).
Qi, B., Zhu, W., Qian, L. & Lo, H.-K. Feasibility of quantum key distribution through a dense wavelength division multiplexing network. New J. Phys. 12, 103042 (2010).
Kumar, R., Qin, H. & Alléaume, R. Coexistence of continuous variable QKD with intense DWDM classical channels. New J. Phys. 17, 043027 (2015).
Fröhlich, B. et al. A quantum access network. Nature 501, 69–72 (2013).
Comandar, L. C. et al. Room temperature single-photon detectors for high bit rate quantum key distribution. Appl. Phys. Lett. 104, 021101 (2014).
Hughes, R. J. et al. Network-centric quantum communications with applications to critical infrastructure protection. Preprint at arXiv:1305.0305 (2013).
Lim, A. E.-J. et al. Review of silicon photonics foundry efforts. IEEE J. Sel. Topics Quantum Electron 20, 405–416 (2014).
Smit, M. et al. An introduction to InP-based generic integration technology. Semicond. Sci. Technol. 29, 083001 (2014).
Zhang, P. et al. Reference-frame-independent quantum-key-distribution server with a telecom tether for an on-chip client. Phys. Rev. Lett. 112, 130501 (2014).
Vest, G. et al. Design and evaluadtion of a handheld quantum key distribution sender module. IEEE J. Sel. Topics Quantum Electron 21, 6600607 (2014).
Sibson, P. et al. Chip-based quantum key distribution. Preprint at arXiv:1509.00768 (2015).
Ma, C. et al. Integrated silicon photonic transmitter for polarization-encoded quantum key distribution. Optica (in press). Preprint on-line available at https://arxiv.org/abs/1606.04407.
Takesue, H. et al. Differential phase shift quantum key distribution experiment over 105 km fibre. New J. Phys. 7, 232 (2005).
Nambu, Y., Yoshino, K. & Tomita, A. Quantum encoder and decoder for practical quantum key distribution using a planar lightwave circuit. J. Mod. Opt. 55, 1953–1970 (2008).
Ziebell, M. et al. CLEO/Europe (EQEC, Munich, Germany, 2015).
Bechmann-Pasquinucci, H. & Tittel, W. Quantum cryptography using larger alphabets. Phys. Rev. A 61, 062308 (2000).
Bourennane, M., Karlsson, A. & Björk, G. Quantum key distribution using multilevel encoding. Phys. Rev. A 64, 012306 (2001).
Cerf, N. J., Bourennane, M., Karlsson, A. & Gisin, N. Security of quantum key distribution using d-level systems. Phys. Rev. Lett. 88, 127902 (2002).
Zhang, L., Silberhorn, C. & Walmsley, I. A. Secure quantum key distribution using continuous variables of single photons. Phys. Rev. Lett. 100, 110504 (2008).
Zhang, Z., Mower, J., Englund, D., Wong, F. N. C. & Shapiro, J. H. Unconditional security of time-energy entanglement quantum key distribution using dual-basis interferometry. Phys. Rev. Lett. 112, 120506 (2014).
Zhong, T. et al. Photon-efficient quantum key distribution using time-energy entanglement with high-dimensional encoding. New J. Phys. 17, 022002 (2015).
Mirhosseini, M. et al. High-dimensional quantum cryptography with twisted light. New J. Phys. 17, 033033 (2015).
Etcheverry, S. et al. Quantum key distribution session with 16-dimensional photonic states. Sci. Rep. 3, 2316 (2013).
Sasaki, T., Yamamoto, Y. & Koashi, M. Practical quantum key distribution protocol without monitoring signal disturbance. Nature 509, 475–478 (2014).
Guan, J. Y. et al. Experimental passive round-robin differential phase-shift quantum key distribution. Phys. Rev. Lett. 114, 180502 (2015).
Takesue, H., Sasaki, H., Tamaki, K. & Koashi, M. Experimental quantum key distribution without monitoring signal disturbance. Nat. Photon. 9, 827—831 (2015).
Wang, S. et al. Experimental demonstration of quantum key distribution without signal disturbance monitoring. Nat. Photon. 9, 832–836 (2015).
Li, Y. H. et al. Experimental round-robin differential phase-shift quantum key distribution. Phys. Rev. A 93, 030302(R) (2016).
Mizutani, A., Imoto, N. & Tamaki, K. Robustness of round-robin differential phase-shift quantum key distribution protocol against source flaws. Phys. Rev. A 92, 060303 (2015).
Zhao, Y., Fung, C.-H. F., Qi, B., Chen, C. & Lo, H.-K. Quantum hacking: experimental demonstration of time-shift attack against practical quantum-key-distribution systems. Phys. Rev. A 78, 042333 (2008).
Lydersen, L. et al. Hacking commercial quantum cryptography systems by tailored bright illumination. Nat. Photon. 4, 686–689 (2010).
Xu, F., Qi, B. & Lo, H.-K. Experimental demonstration of phase-remapping attack in a practical quantum key distribution system. New J. Phys. 12, 113026 (2010).
Mayers, D. & Yao, A. Quantum cryptography with imperfect apparatus. in Proceedingsof the 39th Annual Symposium on Foundations of Computer Science, 1998. 503–509 (IEEE, 1998).
Can, A. et al. Device-independent security of quantum cryptography against collective attacks. Phys. Rev. Lett. 98, 230501 (2007).
Braunstein, S. L. & Pirandola, S. Side-channel-free quantum key distribution. Phys. Rev. Lett. 108, 130502 (2012).
Shalm, L. K. et al. A strong loophole-free test of local realism. Phys. Rev. Lett. 115, 250402 (2015).
Giustina, M. et al. A significant-loophole-free test of Bell’s theorem with entangled photons. Phys. Rev. Lett. 115, 250401 (2015).
Biham, E., Huttner, B. & Mor, T. Quantum cryptographic network based on quantum memories. Phys. Rev. A 54, 2651 (1996).
Inamori, H. Security of practical time-reversed EPR quantum key distribution. Algorithmica 34, 340 (2002).
Curty, M. et al. Finite-key analysis for measurement-device-independent quantum key distribution. Nat. Commun. 5, 3732 (2014).
Lim, C. C. W., Portmann, C., Tomamichel, M., Renner, R. & Gisin, N. Device-independent quantum key distribution with local Bell test. Phys. Rev. X 3, 031006 (2013).
Tang, Y.-L. et al. Measurement-device-independent quantum key distribution over 200 km. Phys. Rev. Lett. 113, 190501 (2014).
Yin, H.-L. et al. Measurement device independent quantum key distribution over 404 km optical fibre. Preprint at arXiv:1606.06821 (2016).
Tang, Y.-L. et al. Field test of measurement-device-independent quantum key distribution. IEEE J. Sel. T. Quantum Electron. 21, 6600407 (2014).
Valivarthi, R. et al. Measurement-device-independent quantum key distribution: from idea towards application. J. Mod. Opt. 62, 1141–1150 (2015).
Tang, Y.-L. et al. Measurement-device-independent quantum key distribution over untrustful metropolitan network. Phys. Rev. X 6, 011024 (2015).
Comandar, L. C. et al. Quantum cryptography without detector vulnerabilities using optically-seeded lasers. Nat. Photon. 10, 312–315 (2016).
Xu, F., Curty, M., Qi, B., Qian, L. & Lo, H.-K. Discrete and continuous variables for measurement-device-independent quantum cryptography. Nat. Photon. 9, 772 (2015).
Yuan, Z.-L. et al. Interference of short optical pulses from independent gain-switched laser diodes for quantum secure communications. Phys. Rev. Applied 2, 064006 (2014).
Tamaki, K., Lo, H.-K., Fung, C.-H. F. & Qi, B. Phase encoding schemes for measurement-device-independent quantum key distribution with basis-dependent flaw. Phys. Rev. A 85, 042307 (2012).
González, P. et al. Quantum key distribution with untrusted detectors. Phys. Rev. A 92, 022337 (2015).
Lim, C. C. W. et al. Detector-device-independent quantum key distribution. Appl. Phys. Lett. 105, 221112 (2014).
Cao, W.-F. et al. Highly efficient quantum key distribution immune to all detector attacks. Preprint at arXiv:1410.2928v1 (2014).
Kim, Y.-H. Single-photon two-qubit entangled states: Preparation and measurement. Phys. Rev. A 67, 040301(R) (2003).
Gisin, N., Fasel, S., Kraus, B., Zbinden, H. & Ribordy, G. Trojan-horse attacks on quantum-key-distribution systems. Phys. Rev. A 73, 022320 (2006).
Qi, B. Trustworthiness of detectors in quantum key distribution with untrusted detectors. Phys. Rev. A 91, 020303(R) (2015).
Liang, W.-Y. et al. Simple implementation of quantum key distribution based on single-photon bell state measurement. Phys. Rev. A 92, 012319 (2015).
Pirandola, S. et al. High-rate measurement-device-independent quantum cryptography. Nat. Photon. 9, 397–402 (2015).
Li, Z., Zhang, Y.-C., Xu, F., Peng, X. & Guo, H. Continuous-variable measurement-device-independent quantum key distribution. Phys. Rev. A 89, 052301 (2014).
Ma, X.-C., Sun, S.-H., Jiang, M.-S., Gui, M. & Liang, L.-M. Gaussian-modulated coherent-state measurement-device-independent quantum key distribution. Phys. Rev. A 89, 042335 (2014).
Gehring, T. et al. Implementation of continuous-variable quantum key distribution with composable and one-sided-device-independent security against coherent attacks. Nat. Commun. 6, 8795 (2015).
Pirandola, S. et al. Reply to 'Discrete and continuous variables for measurement-device-independent quantum cryptography'. Nat. Photon. 9, 773 (2015).
Yin, Z.-Q. et al. Measurement-device-independent quantum key distribution with uncharacterized qubit sources. Phys. Rev. A 88, 062322 (2013).
Yin, Z.-Q. et al. Mismatched-basis statistics enable quantum key distribution with uncharacterized qubit sources. Phys. Rev. A 90, 052319 (2014).
Barnett, S. M., Huttner, B. & Phoenix, S. Eavesdropping strategies and rejected-data protocols in quantum cryptography. J. Mod. Opt. 40, 2501 (1993).
Dušek, M., Jahma, M. & Lütkenhaus, N. Unambiguous state discrimination in quantum cryptography with weak coherent states. Phys. Rev. A 62, 022306 (2000).
Xu, F. et al. Experimental quantum key distribution with source flaws. Phys. Rev. A 92, 032305 (2015).
Mizutani, A., Curty, M., Lim, C. C. W., Imoto, N. & Tamaki, K. Finite-key security analysis of quantum key distribution with imperfect light sources. New J. Phys. 17, 093011 (2015).
Cao, Z., Zhang, Z., Lo, H.-K. & Ma, X. Discrete-phase-randomized coherent state source and its application in quantum key distribution. New J. Phys. 17, 053014 (2015).
Yuan, Z. L. et al. Robust random number generation using steady-state emission of gain-switched laser diodes. Appl. Phys. Lett. 104, 261112 (2014).
Yuan, Z. L. et al. A directly phase-modulated light source. Phys. Rev. X 6, 031044 (2016).
Jain, N. et al. Trojan-horse attacks threaten the security of practical quantum cryptography. New J. Phys. 16, 123030 (2014).
Jain, N. et al. Risk analysis of trojan-horse attacks on practical quantum key distribution systems. IEEE J. Sel. Topics Quantum Electron 21, 6600710 (2015).
Stiller, B. et al. in 2015 Conference on Lasers and Electro-Optics (CLEO) (ed. Goldwasser, S.) (Optical Society of America, 2015).
Lucamarini, M. et al. Practical security bounds against the Trojan-horse attack in quantum key distribution. Phys. Rev. X 5, 031030 (2015).
Tang, Z., Wei, K., Bedroya, O., Qian, L. & Lo, H.-K. Experimental measurement-device-independent quantum key distribution with imperfect sources. Phys. Rev. A 93, 042308 (2016).
Paul, C. K. in Advances in Cryptology—CRYPTO 1996 104–113 (Springer, 1996).
Kocher, P., Jaffe, J. & Jun, B. in Advances in Cryptology—CRYPTO 1999 388–397 (Springer, 1999).
Genkin, D., Shamir, A. & Tromer, E. in Advances in Cryptology—CRYPTO 2014 444–461 (Springer, 2014).
Sasaki, M. et al. Field test of quantum key distribution in the Tokyo QKD network. Opt. Express 19, 10387 (2011).
Northup, T. E. & Blatt, R. Quantum information transfer using photons. Nat. Photon. 8, 356 (2014).
Bussières, F. et al. Quantum teleportation from a telecom-wavelength photon to a solid-state quantum memory. Nat. Photon. 8, 775 (2014).
Munro, W. J., Stephens, A. M., Devitt, S. J., Harrison, K. A. & Nemoto, K. Quantum communication without the necessity of quantum memories. Nat. Photon. 6, 777–781 (2012).
Azuma, K., Tamaki, K. & Lo, H.-K. All-photonic quantum repeaters. Nat. Commun. 6, 6787 (2015).
Buttler, W. T. et al. Daylight quantum key distribution over 1.6 km. Phys. Rev. Lett. 84, 5652 (2000).
Nauerth, S. et al. Air-to-ground quantum communication. Nat. Photon. 7, 382–386 (2013).
Wang, J.-Y. et al. Direct and full-scale experimental verifications towards ground-satellite quantum key distribution. Nat. Photon. 7, 387–393 (2013).
Vallone, G. et al. Experimental satellite quantum communications. Phys. Rev. Lett. 115, 040502 (2015).
Meyers, R. E. in Advanced Free Space Optics (FSO) 343–387 (Springer, 2015).
Elser, D. et al. in IEEE ICSOS 2015, (New Orleans, USA, 2015).
Bourgoin, J. P. et al. Free-space quantum key distribution to a moving receiver. Opt. Express 23, 33437–33447 (2015).
Usenko, V. C. et al. Entanglement of Gaussian states and the applicability to quantum key distribution over fading channels. New J. Phys. 14, 093048 (2012).
Heim, B. et al. Atmospheric continuous-variable quantum communication. New J. Phys. 16, 113018 (2014).
Usenko, V. C. & Filip, R. Feasibility of continuous-variable quantum key distribution with noisy coherent states. Phys. Rev. A 81, 022318 (2010).
Weedbrook, C., Pirandola, S., Lloyd, S. & Ralph, T. C. Quantum cryptography approaching the classical limit. Phys. Rev. Lett. 105, 110501 (2010).
Weedbrook, C., Pirandola, S. & Ralph, T. C. Continuous-variable quantum key distribution using thermal states. Phys. Rev. A 86, 022318 (2012).
Broadbent, A. & Schaffner, C. Quantum cryptography beyond quantum key distribution. Des. Codes Cryptogr. 78, 351–382 (2016).
Mayers, D. Unconditionally secure quantum bit commitment is impossible. Phys. Rev. Lett. 78, 3414–3417 (1997).
Lo, H.-K. & Chau, H. F. Is quantum bit commitment really possible? Phys. Rev. Lett. 78, 3410–3413 (1997).
Lunghi, T. et al. Practical relativistic bit commitment. Phys. Rev. Lett. 115, 030502 (2015).
Cleve, R., Gottesman, D. & Lo, H.-K. How to share a quantum secret. Phys. Rev. Lett. 83, 648–651 (1999).
Hillery, M., Bužek, V. & Berthiaume, A. Quantum secret sharing. Phys. Rev. A 59, 1829–1834 (1999).
Bell, B. A. et al. Experimental demonstration of graph-state quantum secret sharing. Nat. Commun. 5, 5480 (2014).
Berlin, G. et al. Flipping quantum coins. Nat. Commun. 2, 561 (2011).
Pappa, A. et al. Experimental plug and play quantum coin flipping. Nat. Commun. 5, 3717 (2014).
Buhrman, H., Cleve, R., Watrous, J. & Wolf, R. D. Quantum fingerprinting. Phys. Rev. Lett. 87, 167902 (2001).
Xu, F. et al. Experimental quantum fingerprinting. Nat. Commun. 6, 8735 (2015).
Gottesman, D. & Chuang, I. Quantum digital signatures. Preprint at quant-ph/0105032 (2001).
Donaldson, R. J. et al. Experimental demonstration of kilometer-range quantum digital signatures. Phys. Rev. A 93, 012329 (2016).
Broadbent, A., Fitzsimons, J. & Kashefi, E. in Proceedings of the 50th Annual Symposium on Foundations of Computer Science 517–526 (IEEE, 2009).
Barz, S. et al. Experimental demonstration of blind quantum computing. Science 335, 303 (2012).
Lau, H.-K. & Lo, H.-K. Insecurity of position-based quantum-cryptography protocols against entanglement attacks. Phys. Rev. A 83, 012322 (2011).
Buhrman, H. et al. Position-based quantum cryptography: Impossibility and constructions. SIAM J. Comput. 43, 150–178 (2014).
Chakraborty, K. & Leverrier, A. Practical position-based quantum cryptography. Phys. Rev. A 92, 052304 (2015).
Wehner, S., Curty, M., Schaffner, C. & Lo, H.-K. Implementation of two-party protocols in the noisy-storage model. Phys. Rev. A 81, 052336 (2010).
Lam, P.-K. & Ralph, T. Quantum cryptography: Continuous improvement. Nat. Photon. 7, 350 (2013).
Sajeed, S, Huang, A, Sun, S, Xu, F, Makarov, V & Curty, M. Insecurity of detector-device-independent quantum key distribution. https://arxiv.org/abs/1607.05814 (2016).
Barrett, J., Colbeck, R. & Kent, A. Memory attacks on device-independent quantum cryptography. Phys. Rev. Lett. 110, 010503 (2013).
Acknowledgements
We acknowledge helpful comments from many colleagues including Romain Alléaume, Hoi-Fung Chau, Marcos Curty, Philippe Grangier, Anthony Leverrier, Charles Ci Wen Lim, Marco Lucamarini, Xiongfeng Ma, Joyce Poon, Li Qian, Kiyoshi Tamaki and Feihu Xu. We thank our colleagues including Ping Koy Lam, Vikas Anant, Jessie Qin-Dregely, Chris Erven, Masato Koashi, Philip Sibson, Mark Thompson and Qiang Zhang for allowing us to reproduce some of their figures. We thank Warren Raye of Nature Partner Journals for securing the permission for reproductions of figures from various publishers. We acknowledge financial support from NSERC, CFI, ORF, the US Office of Naval Research (ONR), the Laboratory Directed Research and Development (LDRD) Program of Oak Ridge National Laboratory (managed by UT-Battelle LLC for the US Department of Energy), the City of Paris, the French National Research Agency, the Ile-de-France Region, the France-USA Partner University Fund, and the Commissioned Research of National Institute of Information and Communications Technology (NICT), Japan.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
Owing to the employments and consulting activities of some of the authors, they have financial interests in the commercial applications of quantum key distribution.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Diamanti, E., Lo, HK., Qi, B. et al. Practical challenges in quantum key distribution. npj Quantum Inf 2, 16025 (2016). https://doi.org/10.1038/npjqi.2016.25
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/npjqi.2016.25
This article is cited by
-
Improved security bounds against the Trojan-horse attack in decoy-state quantum key distribution
Quantum Information Processing (2024)
-
Controlling the helicity of light by electrical magnetization switching
Nature (2024)
-
Measurement device-independent quantum key distribution with vector vortex modes under diverse weather conditions
Scientific Reports (2023)
-
Recent progress in quantum photonic chips for quantum communication and internet
Light: Science & Applications (2023)
-
Combating errors in quantum communication: an integrated approach
Scientific Reports (2023)