Abstract
We introduce a new framework for constructing topological quantum memories, by recasting error recovery as a dynamical process on a field generating cellular automaton. We envisage quantum systems controlled by a classical hardware composed of small local memories, communicating with neighbours and repeatedly performing identical simple update rules. This approach does not require any global operations or complex decoding algorithms. Our cellular automata draw inspiration from classical field theories, with a Coulomb-like potential naturally emerging from the local dynamics. For a 3D automaton coupled to a 2D toric code, we present evidence of an error correction threshold above 6.1% for uncorrelated noise. A 2D automaton equipped with a more complex update rule yields a threshold above 8.2%. Our framework provides decisive new tools in the quest for realising a passive dissipative quantum memory.
Similar content being viewed by others
Introduction
Prolonging the lifetime of quantum information stored in a quantum device is a monumental challenge. Yet, it is the necessary first step in the effort to scale up quantum computing and quantum communication to a commercially viable level. As quantum coherence is intrinsically fragile, it is clear that increased robustness of the encoded information needs to rely heavily on quantum error correction.1,2 Topological codes in particular have emerged as the most promising quantum error correcting codes,3 where the toric code4,5 is a paradigmatic example. However, in three or fewer dimensions, excitations propagate at little energy cost under thermal dynamics, rapidly corrupting the encoded information.6 Schemes based on sequential measurements of the system’s error syndromes, and subsequent elimination of errors have been suggested to preserve the logical subspace.
When performing active error correction, it is essential for the decoding process to be much quicker than the decoherence time. Prior proposals have focused on the development of efficient decoding algorithms,7–9 or decoders with high error thresholds.10,11 Some of them offer the possibility of parallelization enabling a runtime logarithmic in the system size.8,12 This improves prospects, but still requires a computer with communication between many spatially separated cores. By incorporating a message routing system into a lattice of cores, such long-range communication can be achieved with only nearest-neighbour connections. However, the complexity, time lag, and communications traffic of such a system is not fully understood and has not been simulated. Hence, key obstacles remain.
In this work, we propose an entirely new approach towards designing topological quantum memories that naturally incorporates parallelization. Our design can be implemented via classical hardware composed of small local memories and a small set of local operations only depending on neighbouring memories and neighbouring physical qubits, without constituting universal local processors13,14 or demanding an explicit message routing system. That is, we develop simple cellular automata that efficiently perform active error correction on the toric code. The operational principles of our automata are based on the mediation of attractive long-range interactions between excitations. That way, excitations will tend to collapse together rather than to extend out and create logical errors in the code. Inspired by classical electrostatics and gravitational fields, we identify local update rules that induce such error correcting long-range fields.
We provide extensive numerical analysis of three specific decoders, two of which use a 2D automaton and the third using a 3D automaton. Two of our decoders have comparable threshold values to more conventional decoders that require more sophisticated hardware. We also provide detailed analysis of the equilibration and propagation characteristics of the fields generated by the automata, which justifies the choice of tunable parameters in our decoders. Finally, we study a class of long-range fields and their decoding capabilities, and observe that certain fields are too long-range to reliably identify excitation pairs.
Our schemes share some features with other proposals which add an auxiliary system in order to enforce suppression of error creation.15–22 Prior proposals typically use quantum auxiliary systems instead of classical auxiliary systems for studies of self-correcting memories, where full numerical investigations are prohibitively difficult. Our class of models in some sense combines the benefits of active and of passive memories. Indeed, provided that the cellular automaton update rules do not change in time, the decoding process can be interpolated down to continuous time. In this setting error correction acts simultaneously with error creation, effectively preventing the creating of long error strings. This would amount to a dissipative self-correcting memory.23,24 In this work, we focus on decoding devices but it should be clear that our design incentives promise a generalisation to new schemes of dissipative self-correction.
Materials and methods
The main purpose of this work is to present a fundamentally new class of decoders for the 2D toric code. The toric code has the important feature that it can be considered as a physical model with purely local interactions. In this model, the physical spins reside on the edges of a periodic L×L lattice, which we henceforth denote , and the stabiliser operators act on the four neighbouring spins in the star or plaquette formation (see Supplementary Material for a brief review of the toric code). Errors in the toric code appear as strings, where only the end points of the strings are revealed in the error syndrome measurements. We will refer to these endpoints as anyons, and they have the role of excitations in a classical statistical model.3,25 An error configuration is successfully decoded if all anyons are paired, such that all anyon paths are contractible loops on the torus. Throughout, we assume independent single site Pauli-spin X and Z errors at a rate p. In this way both error sectors decouple, and we can treat them independently. Here we consider only X errors, the Z errors can be treated identically.
The decoders we propose were conceived with the following goal in mind: To arrive at purely local update rules that are as simple as possible. By this we mean that the decoding can be implemented with simple local units of computation that depend only on nearest neighbours. The most natural model for this type of computation is a cellular automaton, which is indeed the nature of our class of decoders. In particular, we will consider an auxiliary cellular automaton, whose purpose is to communicate long-range information between anyons, that enables local decisions to correct errors in the toric code (see Figure 1).
Schematic presentation of the cellular automaton decoders. (a) The toric code on a periodic lattice controlled by a classical cellular automaton decoder on a 2D lattice. Blue spheres represent the physical qubits and the green boxes represent the elementary cells of the automaton. The communication between cells and with the syndrome measurements (anyons) is nearest neighbour, indicated via connecting tubes. (b) A 3D cellular automaton decoder with the central layer hosting the toric code. (c) The field, encoded in the cellular automaton, generated by the anyons of the toric code. Regions with a larger density of anyons have a larger field value. The profile of the field will depend on the specific characteristics of the automaton dynamics. The cellular automaton performs two tasks: (i) it updates the field in order to propagate information between distant anyons; and (ii) it moves the anyons in the direction of largest field gradient. (d) Logical information associated with one decoding run. The red diamonds are the ends of error strings, the orange lines are the actual physical error lines, and the blue dotted lines are the recovery paths dictated by the decoder.
The automaton extracts anyon information from the physical qubits via local stabiliser measurements at each cell of the toric code lattice , the resulting outcome is stored in some local registry, which we label qE(v). The automaton also uses an auxiliary classical system on another lattice Λ, and at each cell x∈Λ and at each time t it stores a real number ϕt(x). We will refer to the auxiliary system as the field generated by the ϕ-automaton. The simplest auxiliary lattice has cells coinciding with the toric code cell (so ), but we also consider larger dimensional auxiliary systems provided they include the toric code as a sub-lattice . Every auxiliary lattice considered herein is either a 2D torus, so , or a 3D torus with the x3=0 plane coinciding with the toric code lattice. To simplify later expressions, we extend the domain of qE to the whole auxiliary lattice with the understanding that anyons never leave the toric plane, so qE(x)=0 whenever x3≠0.
The system’s configuration at any given time is the triple {E, qE, ϕ}, where E is the actual error configuration. Assuming ideal measurements, qE is redundant as it is determined by the error configuration. The dynamics of the system are divided into update sequences, labelled by , in which {E, qE, ϕ} evolve. Each update sequence is subdivided into c+1 elementary steps, first there are c repetitions of a ϕ-update (in which only ϕ changes), followed by a single anyon update (a partial error correction where E and hence also qE change). As lattice cells only interact with their nearest neighbours, these elementary update rules must be local. In a single ϕ-update from time t to t+1, the field ϕt+1(x) can only depend on ϕt(x), qE(x) and values ϕt(y) where y is a neighbour of x. For each excited cell (where qE(x)=1) the anyon update rule decides whether the anyon hops to an adjacent site, and being similarly local, this rule depends only on ϕ values at adjacent sites. With good design of update rules, the ϕ values will meditate information between anyons about the location of their closest potential partners. Later, we derive suitable updates rules, which can be roughly be characterised as: take the average of your neighbours and add the charge. This corresponds to a local discretisation of Gauss’ law.
To fuse nearby anyons we desire that each anyon moves towards regions of higher field intensity. A natural way to achieve this is with the anyon update rule: find the adjacent cell with (unique) largest field value, then move there with probability 1/2. We also considered alternative anyon updates, but none yielded higher thresholds than this simple and intuitive strategy. Physically, an anyon hopping from x to y is implemented by a Pauli X applied to the qubit on the lattice edge separating cells x and y. All anyon hops occur in parallel resulting in partial correction of the error string E, to a new string and the anyon distribution similarly updates to . This process only removes anyons, with two anyons on the same site cancelling, eventually removing all anyons and so completing a whole error correction cycle. The ratio between the number of ϕ-updates per anyon update is labelled c, and can be understood as the speed of propagation of the field. We will call c the field velocity. A pseudocode of our algorithm is provided in the Supplementary Material.
Results
Numerical results
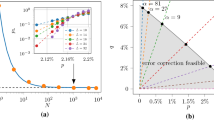
We numerically benchmarked our decoders using uncorrelated X and Z flip noise with error probability p. We say that a decoder is asymptotically working if it exhibits an error correction threshold pth. That is to say, if p<pth then increasing the lattice size linearly exponentially suppresses the probability of the decoder creating a logical error by mismatching anyons. Numerically, the threshold appears as a crossing for various lattice sizes, such as in Figures 2a,b. Further numerical results showing details of error suppression are provided in the Supplementary Material.
Performance of ϕ-automaton decoders. (a) Threshold plot for the 2D* and (b) the 3D ϕ-automaton decoder. The decoder fail rate decreases with system size below threshold and increases above threshold. The number of samples in a ranges from 2,800 samples per point for larger system sizes to 21,000 samples for smaller system sizes. In b the sample size per point is at least 20,000. The points were fitted using a universal scaling law.37 (c) 2D decoder fail rate as a function of lattice size L and field velocity c for P=6%. For very small c the decoder has a large fail rates due to self-interaction (see corresponding paragraph for details). At large c, the decoder also fails because of a stationary field with excessively long range. There exists a sweet spot around c∈[5,15] and L∈[20,80]. (d) Average number of sequences required for a 2D* and 3D ϕ-automaton decoder to remove all anyons with P=1%. The lines represent best fits using a logβ(L) function for the 2D* decoder and log(L) for the 3D decoder. The optimal fit yields β≈2.5.
Our results are summarised in Table 1. We present three decoders called the 2D, 2D* and 3D automata. The 2D* and 3D cases yield asymptotically working decoders, whereas the simple 2D decoder only suppresses errors up to a finite size lattice (e.g., L~60, Figure 2c). Although the 2D decoder is expected to be most suitable for modest storage needs, no strict asymptotic threshold exists. We consider two more decoders using precisely the same update rules, but different only either in how these updates are composed or in the lattice they are implemented on. The 2D* ϕ-automaton keeps the 2D lattice, but alters how updates are composed by letting c increase with each sequence , which increases the ratio of field updates to anyon updates as time increases. We find the 2D* ϕ-automaton has a threshold of ~8.2% (Figure 2a). Our second variant is the 3D ϕ-automaton, which keeps c constant in time, but implements the field updates on a 3D lattice. The toric code remains 2D, but is embedded in a plane of the 3D ϕ-automaton (Figure 1b). The 3D ϕ-automaton exhibits a noise threshold at ~6.1% (see Figure 2b). Although c is constant in time, it must scale logarithmically with L. These thresholds are only a few percent below the best thresholds using a centralized computing architecture. Further numerical data on performance below threshold is presented in the Supplementary Material.
Ideally, we would like all update rules to be completely independent of the system size L, and not to change throughout sequences. Yet, we find that this is not possible within the framework of ϕ automaton decoders. Indeed, simulations show that in order for the decoder to converge in a time, which is sub exponential in L, the field has to have propagated a distance of order log(L), which corresponds to a lower bound on the field velocity c≥cmin~log2(L). The dependence on log(L) can be understood by the fact that maximal clusters of errors below the error threshold are of order log(L) (see refs 26,27 and Supplementary Material), and the decoder must collapse these maximal clusters in a time proportional to their size. If c were to be taken independent of L, then beyond a critical cluster size, the field contribution due to an anyon’s self-interaction would dominate the contribution from the anyons at the other end of the cluster. Self-interaction prevents constant c decoders from converging in a time polylogarithmic in L, and the phenomena is discussed in detail later. Thus, in any field-based model, the field velocity must scale with the system size. Later in the article, we give an explicit lower bound on c, which is derived from the equilibration properties of the ϕ-automaton.
Given that we want our class of decoders to be adaptable to a setting where measurement data are regularly refreshed, it is desirable to have update rules that are invariant throughout sequences. However, this appears not to be possible when the fields are restricted to two spatial dimensions (Figure 2c). The ϕ-automaton decoder works asymptotically in three or higher dimensions because of the steady state profile of the field. Indeed, the steady state poisson field of a single charge scales as log(r) in two dimensions and as r2–D in higher dimension, where r is the distance from the source charge. From numerical simulations, we are lead to conclude that the 2D equilibrium field is too long range, and tends to break the cluster structure of the anyons by extending error strings rather than shrinking them. In higher dimensions the field profile decays steeply enough so that this is not the case. We also later address whether there is a proper threshold between the log(r) and the 1/r decaying fields.
Should we not be concerned with the field velocity changing across sequences, the 2D* ϕ-automaton decoder is preferable as it exhibits a higher threshold and can more easily be implemented in an integrated circuit type architecture.28,29 With c increasing linearly at each update sequence, this allows elements within the clusters to pair up, while simultaneously preventing the field from extending across clusters. The main mechanism responsible for the success of the 2D* decoder is analogous to the ‘Expanding Diamonds’ decoder from refs 30,31.
Finally, in Figure 2d we summarise the runtime estimates of our two working ϕ-automaton decoders. The 3D decoder completes an error correction cycle, pairing all anyons, in the order of log(L) update sequences, while the 2D* decoder terminates after ~log2.5(L) sequences. This can be seen as very strong evidence that the typical maximal error cluster is indeed of size ~log(L), and that our decoders collapse these clusters in optimal time. The 2D* decoder has a runtime ~log2.5(L) sequences as the value of c needs to exceed ~log2(L) before the ϕ-automaton can transmit information across a maximal cluster to collapse it. It should be noted that our estimate of the exponent of 2.5 is based on fitting a polylogarithmic function using 11 data points, and could be slightly off. Finally, each sequence is composed of c field updates and one anyon update, and so we can also quantify runtime in units of updates. For the 3D decoder, log(L) sequences with c=10·log2(L) gives a runtime of order log3(L) updates. For the 2D decoder log2.5(L) sequences with , we sum over to get a runtime of order log5(L) updates. Note that for the 3D decoder the runtime implies that asymptotically the vast majority of cells in the third dimension is not reached by any field information. Therefore the size of the third dimension has to scale as log3(L) only.
The ϕ-automaton
In this section we explore in detail the local update rules of the ϕ-automaton from physically motivated considerations. The key idea is to emulate a long-range field, such as from Newton’s law of gravitation or Coulomb’s law, which mediates an attractive force between the excitations of the toric code. In nature such long-range forces emerge from simple local dynamics in the field. Here we achieve the same effect on a discrete lattice governed by a cellular automaton. The notion of mutually attracting particles with equal charge rather corresponds to gravitational fields, but we will stick to a language that is mainly inspired by electrodynamics.
To elaborate on this analogy, we detour into electrostatics, where the electric field is the gradient of a scalar potential . Gauss’ law simplifies to Poisson’s equation
where D is the spatial dimension and q is the charge distribution. The only isotropic solution of Poisson’s equation with a single charge at the origin is
where r=dist(x, 0) denotes the distance of some lattice site x from the source charge at the origin. The minus in front of the logarithm is chosen to ensure that is convex for all D. The variety of long-range behaviour motivates the use of as an information mediator. Our goal is now to approximate via a cellular automaton.
A convenient discretization of the derivative is d: ϕ(x)→ϕ(x+1/2)−ϕ(x−1/2). Applying this prescription twice yields the double derivative d2: ϕ(x)→ϕ(x+1)+ϕ(x−1)−2ϕ(x). On a D-dimensional square lattice Λ, this generalises to the discrete Laplacian operator
where the sum 〈y, x〉 is over all cells y neighbouring cell x; so all y for which dist(x, y)=1.
We proceed by specifying a set of dynamical equations, or ϕ-automata update rules, whose stationary distribution satisfy the discrete Poisson equation ∇2ϕ(x)=Cq(x). Here the role of the charge is replaced by anyonic excitations, and we identify q with qE. Note that only gradients of ϕ will be considered meaningful for anyon movement, and so fields differing by an additive constant are deemed equivalent. Invoking the Jacobi method,32 we consider the following ϕ-automaton update rule
where 0<η<1/2 is a smoothing parameter we can freely choose and for convenience the unit charge is set to C=−2D/(1−η). These update rules are manifestly local. We can cast equation (4) as a matrix equation ϕt+1=Gϕt+qE, which should be read as
where G is a doubly stochastic block circulant matrix encoding the ϕ-automaton update steps. This reformulation allows us to leverage the machinery of matrix analysis.33
Stationary states and equilibration
Assume for now that the anyon configuration is fixed. By recursively iterating equation (5), we get
It is easy to see that in general the ϕ-automaton satisfying equation (4) does not converge, since the total field values build up steadily due to the charges. Indeed, when denotes the total charge present in the lattice, the total field increases by Q with each field update. However, it is important that the gradient of the field equilibrates towards a fixed value. With this in mind, we define to be the rescaled version of ϕt such that , where the constant K is chosen such that .
The matrix G can be diagonalized by Fourier transform (Supplementary Material), allowing us to obtain a unique solution. We find that the stationary field produced by a single anyon at the origin is
where the sum is over all Fourier components except the zero vector and are the eigenvalues of the matrix G,
The k=0 term is excluded from the sum in equation (7), which would provide an additive constant to the field. By omitting this term we fix the normalisation so that . It is also easy to see that the stationary distribution of a charge at cell y is given by . By linearity, the ϕ-automaton satisfies the superposition principle of fields, and hence the stationary distribution of a collection of charges is just the sum of the distributions of each individual charge. That is, .
The distance between and (as measured by Euclidean distance) can be shown by using matrix inequalities to decrease exponentially fast, so that (details in Supplementary Material)
where the distance is measured in the vector 2-norm . This would suggest a relaxation time of the ϕ-automaton of the order of L2, which can be understood as diffusive spreading of information. In the following section we will argue that the relevant contribution of the field converges in a time much faster for our decoders, because we are only interested in information propagating on distance scales of the order log(L), the maximal error cluster size.
Self-interaction
The ϕ-automaton carries information about distant anyons through local update rules. As has already been hinted at in the previous section, information takes time to propagate through the field, and the most relevant manifestation is in the pernicious phenomenon that we refer to as self-interaction. The field around an anyon is generated both by distant, potential partner anyons, but also by itself. This is a feature shared by all field theories. We can understand this self-interaction by considering two close-by anyons A and B, as in Figure 3. Our story begins with anyon A moving in the direction of largest local field gradient, towards anyons B. After anyon A has moved, it leaves behind its own field, which will typically be a local maximum of the ϕ-automaton. In order for anyon A at the end of the following sequence to again move in the direction of anyon B, the field gradient generated by anyon B has to be larger than the residual self field gradient around the cell of anyon A. We call this phenomenon self-interaction, and next derive conditions on the field velocity to prevent this from occurring.
Self-interaction. A setup with two isolated anyons A and B, and their fields in a self-interaction cycle. Suppose that the fields from each anyon starts in its stationary configuration (a). After one anyon update move, anyon A moves in the direction of largest field gradient towards anyon B. (b) Immediately after anyon A moves, the field which it leaves behind is much larger that the field from anyon B. (c) After a certain number of field updates, the residual self field from anyon A decreases, but might still tell the anyon to move in the wrong direction (d).
Suppose anyon A starts at the origin and anyon B is at cell y. Assuming the initial configuration is at equilibrium, . After anyon A moves, the field begins to relax towards , where e is a unit vector in the direction of anyon B. We want to estimate the time required before the field gradient generated by anyon B is larger than the self-interaction of anyon A. In other words, assuming , after what time do we have
where gl is the gradient at the origin due to a charge at a distance l=dist(0, y). It is not difficult to see that the left hand side of equation (10) does not depend on the field from anyon B.
A straightforward, but lengthy, calculation (in the Supplementary Material) shows that for all ϵ>0
whenever
where is a function of position, but is independent of t (see Supplementary Material for the exact form). Considering the second anyon at point y=e, it creates a field gradient near the first anyon (at the origin)
where {ej} is an orthonormal basis of unit vectors. Therefore, we must require that
By percolation arguments, the maximum cluster size of anyons can be argued to typically be order l~log(L). Given that the gradient is of the order ll–D, require ϵ~logl–D(L),
where the dependence on D has now cancelled.
The field profile
We already discussed in detail that when the field velocity c is kept invariant throughout sequences, the 2D and 3D decoders exhibit fundamentally different behaviour. Here we supplement these results by investigating another decoder model, not a cellular automata, to investigate the large c regime when fields are always close to stationary solutions. In order to address this question, we consider a class of power law potentials
for α>0.
We simulate anyon movements in these perfect fields, by inserting the sum of all anyon fields by hand, instead of simulating it locally by a cellular automaton. We alternate between these instantaneous field updates and the anyon update rule as defined before. For α=1 we expect a behaviour similar to the decoder with 3D ϕ-automaton. The benchmark presented in Figure 4b indeed shows a threshold at pth~6.3%, which is very close to the threshold of ~6.1% seen for the 3D ϕ-automaton. This independently confirms that our choice of finite c is sufficiently large for equilibration between distinct anyon moves.
(a) The failure rate pfail when the initial error rate is p=5%, for a range of lattice sizes L and a range of idealised decoders parameterised by α. These decoders are based on an auxiliary system consisting of explicit non-local computation using Coulomb potentials of 1/rα. At small α, α⩽1, the decoder is improper with large lattice sizes yielding large failure rates. Whereas, at larger α error correction is observed with increasing lattice size. (b) Threshold plot for the idealised decoder with a parameter value α=1, which is very close to the behaviour observed with the 3D ϕ-automaton.
Seeking to understand the transition between the 2D and the 3D stationary field behaviour, we consider various values of α and lattice sizes for fixed p=5% in Figure 4a. In general the decoder fail rate reduces with increasing α. This supports our claim that fields with a shorter range are more suited for efficient shrinking of errors. However, our main observation is that for α<0.5 the decoders fail rate increases drastically with the system size L. This means that the decoder does not exhibit a threshold above p=5% for α<0.5. Although it is difficult to certify numerically, for 0.5≤α≤0.7 we did not either find an indication of a threshold at any p up to lattice size L=400.
From these observations we infer that there has to exist a critical αT such that provides a asymptotically working decoder. For values of α below the transition, the increased contribution from far away anyons leads to the misidentification of error strings. Recall that anyons move according to the maximal field gradient of r−α, which is proportional to r−(α+1). The total field at a point is the sum of the contributions from all of the anyons, hence for an infinite lattice the gradient is only guaranteed to be finite for 1/rβ, when β>2. Only for α>1 does the gradient have a well-defined value asymptotically. Hence we expect αT=1 for the 2D toric code. This intuition is further supported by a simple simulation of the 1D toric code (i.e., the repetition code), where we observe a clear transition at α=0, which corresponds to a gradient of 1/r. Here we have allowed for values of α≤0 by setting for α<0 and for α=0.
We highlight that very high values of α are not favourable in general, as they require increased precision in the field resolution. Meanwhile, we expect that the 3D ϕ-automaton always gives rise to a field with slightly shorter range than 1/r (i.e., α>1). Therefore, the 3D ϕ-automaton seems to be sitting exactly at the sweet spot, providing a functioning long-range ϕ-field decoder with a maximally robust field.
Discussion
In this work, we have introduced a new class of decoders that pair anyonic excitations by mediating long-range information through an auxiliary field. The field, and the anyon movement, is generated by a cellular automaton, in such a way that the decoder has an intrinsically parallelised architecture. We have observed that the attractive interactions mediated by the cellular automaton can stabilise topological states. Further we have found indications that the stability exhibits a phase transition in the long-range parameter of the attractive field. We have identified two particular decoders within this class that exhibit an error threshold, one requiring a 3D auxiliary system with homogeneous update rules, with an error threshold above 6.1%, and another with a 2D auxiliary system and time dependent update rules with an error threshold above 8.2%. When below threshold both decoders also show noise suppression reducing exponentially with lattice size. Our schemes have two main conceptual limitations in their present formulation. First, the processing cost is determined by the field velocity c that must scale polylogarithmically with the system size L. Second, the field needs a precision sufficient to distinguish the presence of an anyon distance ~log(L) away. Encoding the field digitally, this is achieved by a local field register of log2(L) bits at every field site. At the same time, it is important to emphasise once again that the communication requirements are minimal, relying on nearest-neighbour communication only, requiring no wiring or long-distance communication. Next we discuss in detail how these costs compare with other approaches, and we will see that such logarithmic costs are generic.
The first, and most common approach to decoding errors is primarily designed for a serial computing architecture. Compared with these proposals our threshold values are only modestly smaller than the best decoders using Monte Carlo techniques10,11 or the minimum weight perfect matching algorithm,34 but are comparable to recent popular proposals based on real-space renormalization techniques8,9 or so-called expanding diamonds.30,31 However, our cellular automata decoders have a strict locality neighbourhood, and are hence potentially very attractive for implementations of topological quantum memories in integrated circuit type architectures, as were recently proposed in refs 28,29. Serially designed decoders allow for some parallelisation, and in some instances can even be adapted to run on a network of communicating cores.12 On the face of it these parallelised variants are similar to our proposal, but such schemes still need long-range communication between cores and this is achieved locally by routing communications across a network of cores. Such messages must be communicated over roughly log(L) distances and consequently also incurring order log(L) time lag. The advantage of our proposal is twofold. First, we require no explicit message routing system and so our decoder could be implemented using considerably simpler cores, allowing for greater miniaturisation. Second, we have numerically benchmarked the runtime of our proposal, whereas prior proposals for parallelisations have not been simulated and so the roughly logarithmic runtime has not yet been confirmed. These merits occur because we take a bottom–up approach which is parallel from the start, rather than attempting an ad hoc modification of existing serial decoders.
The second class of ideas is also based on cellular automata. It is commonly believed, that quantum error correction in two dimensions is related to the positive rates conjecture for classical systems in 1D. In analogy to the seminal work of Gacs13,35 on the resolution of the positive rates conjecture, one could expect that there exists a local cellular automaton decoder with update rules that are strictly system size independent. Harrington sketches such a programme for toric code decoders,14 but only gives explicit details for a scheme with logarithmic overhead. Unfortunately, in Gacs’ original work, the proven noise threshold is prohibitively small (~2−1,000), although the actual threshold might be considerably larger.35 Hence, the requirements might render the proposal practically infeasible. Furthermore, Gacs’ or Harrington’s update rules are more complicated than ours, again requiring more sophisticated computing hardware. Our proposals are based on physically motivated rules, have high thresholds with only logarithmic system size dependences for local parameters, and are therefore fully adequate for realistic implementations.
Our proposed 3D decoder and the analysis of the field profile is based on a working principle that is fundamentally different from all previous classes of approach. It is the only proposal that could be implemented on a simple multi-core architecture with cores storing a single variable and mundane I/O protocols (no message routing). The surprising result of our work is, that all the information that is required for local decoding decisions can be encoded in a physically motivated, attractive scalar field. The propagation of information using a field also implies intrinsic robustness against small deviations in field values and updates. Indeed, preliminary results indicate that our scheme also works if the local rules are applied asynchronously, relaxing the requirement for perfect synchronous operation of the decoding unit.
We have focused on some specific instances of cellular automata decoders working against a particular noise model, but the research project opens up many new possibilities within the same paradigm. The space of potential cellular automata is vast, small variations such as to anyon movement rules or lattice geometry could have substantial consequences on performance. Gauss’ law has proved an invaluable tool to our intuition, but it was just a guide, and departures from an electrostatic mindset could prove rewarding. We expect our models to be naturally robust to certain types of more invasive errors, because the field encodes global information in a smooth and local manner. Nevertheless, a more detailed study of correlated noise and errors in the measurements and in the field would be a valuable extension of the present study. The latter two points are especially interesting as stepping stones towards extending our proposal to a passive dissipative quantum memory. Exploring this wealth of decoder models will surely reveal many technological opportunities and a rich world of varied automata behaviours.36
References
Aharonov D, Ben-Or M . Fault-tolerant quantum computation with constant error rate. SIAM J Comput 2008; 38: 1207.
Gottesman D . Theory of fault-tolerant quantum computation. Phys Rev A 1998; 57: 127–137.
Dennis E, Kitaev A, Landahl A, Preskill J . Topological quantum memory. J Math Phys 2002; 43: 4452.
Kitaev A . Anyons in an exactly solved model and beyond. Ann Phys 2006; 321: 2–111.
Kitaev A . Fault-tolerant quantum computation by anyons. Ann Phys 2003; 303: 2–30.
Yoshida B . Feasibility of self-correcting quantum memory and thermal stability of topological order. Ann Phys 2011; 326: 2566–2633. 1103.1885.
Fowler AG, Whiteside AC, Hollenberg LCL . Towards practical classical processing for the surface code. Phys Rev Lett 2012; 108: 180501. 1110.5133.
Duclos-Cianci G, Poulin D . Fast decoders for topological quantum codes. Phys Rev Lett 2010; 104: 050504. 0911.0581.
Bravyi S, Haah J . Quantum self-correction in the 3d cubic code model. Phys Rev Lett 2013; 111: 200501. 1112.3252.
Wootton JR, Loss D . High threshold error correction for the surface code. Phys Rev Lett 2012; 109: 160503. 1202.4316.
Hutter A, Wootton JR, Loss D . Efficient markov chain monte carlo algorithm for the surface code. Phys Rev A 2014; 89: 022326. 1302.2669.
Fowler AG . Minimum weight perfect matching of fault-tolerant topological quantum error correction in average o(1) parallel time. Quant Inf Comp 2015; 15: 0145–0158. 1307.1740.
Gács P . Reliable cellular automata with self-organization. J Stat Phys 2001; 103: 45–267.
Harrington JW . Analysis of quantum error-correcting codes: symplectic lattice codes and toric codes. Thesis, California Institute of Technology, 2004.
Hamma A, Castelnovo C, Chamon C . Toric-boson model: Toward a topological quantum memory at finite temperature. Phys Rev B 2009; 79: 245122. 0812.4622.
Chesi S, Röthlisberger B, Loss D . Self-correcting quantum memory in a thermal environment. Phys Rev A 2010; 82: 022305. 0908.4264.
Pedrocchi FL, Chesi S, Loss D . Quantum memory coupled to cavity modes. Phys Rev B 2011; 83: 115415. 1011.3762.
Pedrocchi F, Hutter A, Wootton J, Loss D . Enhanced thermal stability of the toric code through coupling to a bosonic bath. Phys Rev A 2013; 88: 062313. 1309.0621.
Fujii K, Negoro M, Imoto N, Kitagawa M . Measurement-free topological protection using dissipative feedback. Phys Rev X 2014; 4: 041039. 1401.6350.
Hutter A, Wootton JR, Röthlisberger B, Loss D . Self-correcting quantum memory with a boundary. Phys Rev A 2012; 86: 052340. 1206.0991.
Hutter A, Pedrocchi FL, Wootton JR, Loss D . Effective quantum-memory hamiltonian from local two-body interactions. Phys Rev A 2014; 90: 012321. 1209.5289.
Becker D, Tanamoto T, Hutter A, Pedrocchi FL, Loss D . Dynamic generation of topologically protected self-correcting quantum memory. Phys Rev A 2013; 87: 042340. 1302.3998.
Pastawski F, Clemente L, Cirac JI . Quantum memories based on engineered dissipation. Phys Rev A 2011; 83: 012304. 1010.2901.
Kastoryano M, Wolf M, Eisert J . Precisely timing dissipative quantum information processing. Phys Rev Lett 2013; 110: 110501. 1205.0985.
Bombin H, Andrist RS, Ohzeki M, Katzgraber HG, Martin-Delgado MA . Strong resilience of topological codes to depolarization. Phys Rev X 2012; 2: 021004. 1202.1852.
Kovalev A, Pryadko L . Fault tolerance of quantum low-density parity check codes with sublinear distance scaling. Phys Rev A 2013; 87: 020304. 1208.2317.
Gottesman D . Fault-tolerant quantum computation with constant overhead. Quant Info Comp 2013; 14: 1338–1371.
Fowler AG, Mariantoni M, Martinis JM, Cleland AN . Surface codes: Towards practical large-scale quantum computation. Phys Rev A 2012; 86: 032324. 1310.2984v3.
Barends R, Kelly J, Megrant A, Veitia A, Sank D, Jeffrey E et al. Superconducting quantum circuits at the surface code threshold for fault tolerance. Nature 2014; 508: 500–503. 1402.4848.
Dennis E . Purifying Quantum States: Quantum And Classical Algorithms. Thesis, UCSB, 2003.
Wootton JR, Lahtinen V, Doucot B, Pachos JK . Engineering complex topological memories from simple abelian models. Ann Phys 2011; 326: 2307–2314. 0908.0708.
Saad Y . Iterative Methods for Sparse Linear Systems. SIAM, Philadelphia, 2003.
Bhatia R . Matrix Analysis. Springer: Heidelberg, 1997.
Wang DS, Fowler AG, Stephens AM, Hollenberg LCL . Threshold error rates for the toric and planar codes. Quant Info Comp 2010; 10: 456. 0905.0531v1.
Gray LF . A reader’s guide to gacs’s positive rates paper. J Stat Phys 2001; 103: 1–44.
Poulin D . Private communication.
Watson FHE, Barrett SD . Logical error rate scaling of the toric code. New J Phys 2014, 16: 093045. 1312.5213.
Acknowledgements
MJK thanks K Michnicki for very valuable insight and motivation in the buildup to the present work. We also thank D Poulin for - upon completion of the present work-making us aware of the existence of unpublished results by D Poulin and G Duclos-Cianci, who have previously considered cellular automata based decoders in the same spirit as us. A set of slides from 2011 alluding to their work are available online (http://www.physique.usherbrooke.ca/poulin/utilisateur/files/seminaires/2011Simon.pdf). We acknowledge support from the EU (SIQS, RAQUEL, COST, AQuS), the Alexander-von-Humboldt Foundation, the FQXi, the BMBF, and the ERC (TAQ). The DFG and the EPSRC (grant EP/M024261/1).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no conflict of interest.
Additional information
Supplementary Information accompanies the paper on the npj Quantum Information website (http://www.nature.com/npjqi)
Supplementary information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/4.0/
About this article
Cite this article
Herold, M., Campbell, E., Eisert, J. et al. Cellular-automaton decoders for topological quantum memories. npj Quantum Inf 1, 15010 (2015). https://doi.org/10.1038/npjqi.2015.10
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/npjqi.2015.10
This article is cited by
-
Convolutional neural network based decoders for surface codes
Quantum Information Processing (2023)
-
Cellular automaton decoders for topological quantum codes with noisy measurements and beyond
Scientific Reports (2021)
-
Electron Cloud Density Generated by Microring-Embedded Nano-grating System
Plasmonics (2020)
-
Decoding surface code with a distributed neural network–based decoder
Quantum Machine Intelligence (2020)
-
Fault-Tolerant Quantum Error Correction for non-Abelian Anyons
Communications in Mathematical Physics (2017)