Abstract
The quantum nature of the electromagnetic field imposes a fundamental limit on the sensitivity of optical precision measurements such as spectroscopy, microscopy and interferometry1. The so-called quantum limit is set by the zero-point fluctuations of the electromagnetic field, which constrain the precision with which optical signals can be measured2,3,4. In the world of precision measurement, laser-interferometric gravitational-wave detectors4,5,6 are the most sensitive position meters ever operated, capable of measuring distance changes of the order of 10−18 m r.m.s. over kilometre separations caused by gravitational waves from astronomical sources7. The sensitivity of currently operational and future gravitational-wave detectors is limited by quantum optical noise6. Here, we demonstrate a 44% improvement in displacement sensitivity of a prototype gravitational-wave detector with suspended quasi-free mirrors at frequencies where the sensitivity is shot-noise-limited, by injecting a squeezed state of light1,2,3. This demonstration is a critical step towards implementation of squeezing-enhancement in large-scale gravitational-wave detectors.
Similar content being viewed by others
Main
Laser-interferometric gravitational-wave detectors, such as those of the Laser Interferometer Gravitational-Wave Observatory5 (LIGO), are designed to measure distance changes of the order of 10−18 m, or one-thousandth of the diameter of the proton, caused by gravitational waves from astronomical sources such as neutron star or black hole binaries, supernovae and the Big Bang7. Their goals are to further verify Einstein’s theory of general relativity and open an entirely new window onto the universe5,7. The sensitivity of currently operational gravitational-wave detectors is largely limited by quantum optical noise. Next-generation gravitational-wave detectors, such as Advanced LIGO6, planned to be operational in the next few years, are anticipated to be limited in sensitivity by quantum optical noise at almost all frequencies in the gravitational-wave detection band (10 Hz–10 kHz). The mirrors used in these interferometric gravitational-wave detectors are suspended as pendulums, serving as quasi-free test masses in the gravitational-wave detection band5. The quantum noise arises from uncertainty products associated with the commutation relations between conjugate field operators.
The quantum limit can be circumvented by use of non-classical or squeezed states of light1,2,3, where fluctuations are reduced below the symmetric quantum limit in one quadrature at the expense of increased fluctuations in the canonically conjugate quadrature. Squeezed states comprise a phase-dependent distribution of zero-point fluctuations such that the fluctuations in one quadrature are smaller than those of a coherent state, at the expense of increased fluctuations in the canonically conjugate quadrature, while preserving the Heisenberg limit on the uncertainty product. Since squeezed states were first observed by Slusher et al. 8 in 1985, a number of experimental efforts have realized the proof-of-principle of quantum noise reduction or squeezing-enhancement in various high-precision applications, such as spectroscopic measurement9, lateral displacement measurement and imaging10,11, polarization measurement12 and interferometric phase measurement13. Incorporating the technique of squeezing-enhancement into practical devices has remained a great challenge, either because the quantum limit is not reached owing to excess classical noise, or because it is less onerous to enhance sensitivity by optimizing other parameters classically. Squeezed states are a useful ingredient for quantum teleportation14, quantum cryptography15 and quantum lithography16, but these applications are yet to reach the stage of practical implementation, in part owing to the complexity and technical challenges of working with squeezed states.
Laser-interferometric gravitational-wave detectors such as LIGO5, VIRGO17, GEO60018 and TAMA30020 are so sensitive (they measure distance changes of 10−18 m over kilometre separations) that they have already confronted the quantum limit19. In next-generation detectors, such as Advanced LIGO6, optimization of classical parameters will reach the limits of conventional technology. Any further improvement in sensitivity must rely on quantum techniques such as squeezing-enhancement, making gravitational-wave detectors an important practical application of squeezed states of light.
The quantum nature of light reveals itself in two effects that limit the precision of an optical measurement of mirror position in laser-interferometric gravitational-wave detectors: (1) photon shot noise, typically dominant at frequencies above 100 Hz, which arises from quantum uncertainty in the number of photons at the interferometer output; and (2) quantum radiation pressure noise, typically dominant at frequencies below 100 Hz, which arises from mirror displacements induced by quantum radiation pressure fluctuations6,21. The shot noise is caused by quantum fluctuations of a vacuum electromagnetic field that enters the antisymmetric port of the interferometer4. The displacement noise associated with the shot noise of a simple Michelson interferometer on a dark fringe in the frequency domain is given by5

where ℏ is the reduced Planck constant, c is the speed of light in vacuum, λ is the laser wavelength and P is the optical power incident on the beamsplitter.
The quantum limit in the laser-interferometric gravitational-wave detector can be overcome by the injection of squeezed states of light into the antisymmetric port of the interferometer4. Following the 1981 proposal of Caves4 to improve the sensitivity of quantum-noise-limited laser interferometers by squeezed-state injection, a handful of experimental efforts have realized the proof-of-principle on the table-top scale at megahertz frequencies13,22,23. Our demonstration of squeezing-enhancement shows improved sensitivity in a suspended-mirror prototype gravitational-wave detector by injecting a squeezed vacuum field with an inferred level of 9.3±0.1 dB relative to shot noise into the antisymmetric port (see the Methods section). An important distinction between our experiment and previous efforts is that it is the first implementation of squeezing-enhancement in a prototype gravitational-wave detector with suspended optics and a control and readout scheme similar to those used in the currently operational LIGO detectors, making it necessary to confront dynamical effects introduced by suspended mirrors such as optical springs24. It is, therefore, a critical step towards implementation of squeezing-enhancement in large-scale gravitational-wave detectors. In all of these experiments, including the one reported here, quantum radiation pressure noise was buried under other technical noise sources such as seismic noise and mirror thermal noise, and only the shot-noise limit was accessible (not buried under technical noise) for showing squeezing-enhancement. So far, quantum radiation pressure noise has not been observed in any experimental setting.
Terrestrial gravitational-wave detectors typically comprise a Michelson interferometer with a Fabry–Perot cavity in each arm, to increase the phase sensitivity of the detector. The Michelson interferometer is operated on or near a dark fringe. As most of the incident light returns towards the laser source, the gravitational-wave-induced signal can be increased by recycling the laser power back towards the beamsplitter. This is achieved by placing a partially transmitting mirror—the ‘power recycling’ mirror—between the laser source and the beamsplitter. Typical power-recycling gains of 30 to 70 have been realized in currently operational gravitational-wave detectors. Similarly, a partially transmissive mirror can also be placed at the antisymmetric port of the beamsplitter to further enhance the gravitational-wave-induced signal at the interferometer output. This ‘signal recycling’ mirror forms a complex optical cavity with the rest of the interferometer. The frequency-dependent optical response of the detector to incident gravitational waves can be tuned by operating the signal-recycling cavity at various detunings from resonance. Signal recycling is used in the GEO600 detector18, and is planned for the Advanced LIGO detector6.
The experiment reported here used a subconfiguration of the complete Advanced LIGO interferometer—a signal-recycled Michelson interferometer (SRMI), chosen in part because it is an important new feature of the optical configuration predicted for Advanced LIGO6,24. The shot-noise-limited displacement sensitivity of the SRMI is given in the frequency domain by25

where G is the signal-recycling gain, given by G=[ts/(1−rsrme−2iφ)]2, η is the power transmission efficiency from the signal-recycling mirror to the photodetector (including the quantum efficiency of the photodetector) and R is the squeeze factor3. Here, rs and ts are the amplitude reflectivity and transmissivity of the signal-recycling mirror, rm is the amplitude reflectivity of the Michelson interferometer and φ is the signal-recycling cavity detuning. We note that setting G=1, η=1 and R=0 in equation (2) leads to the familiar expression for the shot-noise limit in a Michelson interferometer, given in equation (1). In the experiment described below, η,rs and rm are measured to be 0.825,  and
and  respectively, and P and φ are obtained from fits to be 57 mW and 0, respectively.
respectively, and P and φ are obtained from fits to be 57 mW and 0, respectively.
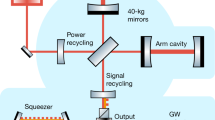
This experiment was carried out in a prototype gravitational-wave detector with suspended mirrors24, designed to closely mimic the kilometre-scale LIGO detectors. A schematic diagram of the experiment is shown in Fig. 1. Its major components are (1) an intensity- and frequency-stabilized Nd:YAG Master Oscillator Power Amplifier laser with a throughput of 5 W at 1,064 nm that serves as the light source for both the interferometer and the squeezed vacuum generator; (2) a triangular optical cavity—or mode cleaner—which consists of three free-hanging mirrors with a linewidth of 4 kHz to further stabilize the intensity, frequency and mode of the laser; (3) a test interferometer configured as a SRMI, comprising a 50/50 beamsplitter, two high-reflectivity end mirrors and a signal-recycling mirror, all suspended as single-loop pendulums (causing the optics to behave as inertial free masses); (4) a squeezed vacuum generator—or squeezer—that consists of a second-harmonic generator (SHG), a subthreshold vacuum-seeded optical parametric oscillator (OPO) pumped by a second-harmonic field, a monitor homodyne detector and an optical circulator to inject the generated squeezed vacuum field to the interferometer; and (5) a high-quantum-efficiency photodetector to sense differential motion of the interferometer mirrors. The Michelson interferometer is locked on a dark fringe using a static differential offset such that a small amount of the carrier light exits the signal-recycling cavity, whereas the signal-recycling cavity is locked on a carrier resonance. This d.c. component of the carrier light at the antisymmetric port acts as a local oscillator field for a gravitational-wave-induced signal to beat against, forming a homodyne detection or ‘d.c. readout’ scheme6.
BS: 50/50 beamsplitter; PD1 and PD2: photodetectors; PO: pickoff beamsplitter; DB: dichroic beamsplitter; SRM: signal-recycling mirror; EMX/EMY: end mirrors along the x/y axis, respectively; SHG: second-harmonic generator; OPO: optical parametric oscillator; GW: gravitational wave. The SHG, OPO, reference cavity, pre-mode cleaner, mode-cleaner and signal-recycling cavity are all locked by adaptations of Pound–Drever–Hall locking27. PD1 and PD2 are used for the laser intensity and frequency stabilization, whereas two photodetectors in the interferometer (not shown) and the length-sensing detector are used to control the interferometer. All of the mode-cleaner and interferometer optics are suspended by single-loop pendulums.
The noise performance of the interferometer is shown in Fig. 2. The comparison between the measured noise floor without squeezing and the theoretically predicted noise floor based on the measured optical power of 100 μW indicates that the interferometer is shot-noise-limited at frequencies above 42 kHz. In addition, the interferometer output power is changed by adjusting the Michelson offset to verify the  scaling of the shot-noise spectral density. At frequencies below 42 kHz, the noise is dominated by laser intensity noise and uncontrolled length fluctuations of the interferometer. The peaks at frequencies above 42 kHz are also due to the interferometer length fluctuations. In the shot-noise-limited frequency band, the detector sensitivity is (6.9±0.1)×10−17 m Hz−1/2. Systematic uncertainty in the displacement calibration is estimated to be 10%, but does not affect the relative improvement achieved by squeeze injection that was observed.
scaling of the shot-noise spectral density. At frequencies below 42 kHz, the noise is dominated by laser intensity noise and uncontrolled length fluctuations of the interferometer. The peaks at frequencies above 42 kHz are also due to the interferometer length fluctuations. In the shot-noise-limited frequency band, the detector sensitivity is (6.9±0.1)×10−17 m Hz−1/2. Systematic uncertainty in the displacement calibration is estimated to be 10%, but does not affect the relative improvement achieved by squeeze injection that was observed.
The result of the squeezing-enhancement in the interferometer is also shown in Fig. 2. The comparison between the two spectra shows that the noise floor of the interferometer was reduced by the injection of the squeezed vacuum field in the shot-noise-limited frequency band. Figure 3 shows the noise floor with a simulated gravitational-wave signal at 50 kHz, with and without injected squeezing. The broadband quantum noise floor was reduced from (6.9±0.1)×10−17 m Hz−1/2 to (4.8±0.1)×10−17 m Hz−1/2, whereas the strength of the simulated gravitational-wave signal was retained. This corresponds to a 44% increase in signal-to-noise ratio or detector sensitivity. In kilometre-scale gravitational-wave detectors, this would correspond to a factor of 1.443=3.0 increase in detection rate for isotropically distributed gravitational-wave sources. The squeeze factor is found to be R=0.36±0.03 where the error comes from the variance in each noise floor. Other peaks in the squeezing spectrum are due to optical crosstalk between the interferometer and the OPO, arising from inadequate isolation of the OPO from the interferometer output. It can be completely resolved by improved Faraday isolation, or use of an OPO in a bow-tie cavity configuration that geometrically separates the two fields26, and is not expected to be a problem in operational gravitational-wave detectors.
The simulated gravitational wave was generated by exciting the beamsplitter of the interferometer. The broadband shot-noise floor was reduced from (6.9±0.1)×10−17 m Hz−1/2 to (4.8±0.1)×10−17 m Hz−1/2 by the injection of squeezing, whereas the strength of the simulated gravitational-wave signal was retained, resulting in a 44% increase in signal-to-noise ratio or detector sensitivity.
The measurable squeezing effect was limited to frequencies above 42 kHz in this experiment, because the quantum noise is masked by classical noise at lower frequencies. Many of the factors that led to this limit in the experiment presented here are not expected to effect squeezing-enhancement in the LIGO interferometers. One of the greatest challenges of using suspended mirrors—a crucial feature of this work—is the coupling of seismic noise to the detector output, owing to large fluctuations in the positions and angles of the mirrors. In addition to the seismic noise coupling, laser frequency and intensity fluctuations also degrade the low-frequency performance of the detector. Unlike the urban campus siting of the prototype detector used here, the LIGO detectors are located in remote sites with much quieter seismic and acoustic environments, and are equipped with better vibration isolation and mirror control systems. Moreover, in the kilometre-scale detectors, the long Fabry–Perot cavities in their arms act as optical filters to mitigate laser noise in the gravitational-wave band19. Other challenges associated with suspended-mirror interferometry that had to be overcome in the present experiment include control of the mode overlap between the (relatively static) squeezed input and (dynamically fluctuating) interferometer output fields, interfacing of the in-vacuum parts of the experiment (the interferometer) with external optical systems (the squeezer) and optical isolation to mitigate optical feedback. Consequently, we expect the squeezing-enhancement to be effective at lower frequencies within the gravitational-wave detection band when implemented on the long-baseline LIGO detectors. This implementation of squeezing-enhancement in a gravitational-wave detector prototype with the suspended optics and the readout and control scheme similar to those used in the currently operational LIGO detectors firmly establishes the practical feasibility of squeezing injection for future improvements to existing gravitational-wave detectors worldwide.
Methods
Each optic of the interferometer is suspended as a single-loop pendulum mounted on a passive vibration isolation system within a single vacuum volume with a pressure of 10−6 torr. At frequencies above the pendulum resonant frequency (∼1 Hz), the suspensions attenuate seismic noise, causing the optics to behave as inertial free masses. The mirrors are held in place by feedback control designed to suppress low-frequency seismically driven motion. Magnets affixed to each optic are surrounded by current-carrying coils that actuate on the mirror positions and angles. Adaptations of the Pound–Drever–Hall locking27 are used to keep the mirrors of the interferometer at the desired operating point. More details can be found in refs 24, 28.
The OPO, operated below threshold, is used to produce a squeezed state by correlating the upper and lower quantum sidebands centred around the carrier frequency, in the presence of an energetic pump field. As all gravitational-wave detectors currently use high-power Nd:YAG laser sources at 1,064 nm, generating squeezed states at 1,064 nm is essential. The OPO is a cavity composed of a 10-mm-long quasi-phase-matched periodically poled KTiOPO4 crystal with anti-reflection-coated flat surfaces and two external coupling mirrors29. To generate a low-frequency squeezed state, the OPO is vacuum-seeded and pumped by 320 mW of a second-harmonic field which is generated by the SHG from the same laser source that is incident on the interferometer. An auxiliary laser that is frequency-shifted by 642 MHz relative to the carrier frequency is used to lock the OPO cavity by using a piezoelectric transducer on one of the coupling mirrors. This frequency-shifted light is orthogonally polarized to the vacuum field that seeds the OPO cavity and to the pump field, and therefore, does not enter the interferometer. This type of OPO locking scheme is necessary to generate a squeezed state of vacuum which is squeezed at all frequencies, not a squeezed state of light which is typically squeezed only at megahertz frequencies owing to laser excess noise at frequencies below 1 MHz (refs 23, 25).
The balanced homodyne detector is used to monitor the generated squeezed vacuum field before injection to the interferometer. It is composed of a 50/50 beamsplitter and a pair of photodiodes with matched quantum efficiencies of 93%. With a mode-cleaned coherent local oscillator field, the homodyne efficiency of this readout is 99.2%. The squeezing level measured by this detector is 7.4±0.1 dB (ref. 29). On the basis of this value and the composite detection efficiency, the squeezing level at the output of the OPO is inferred to be 9.3±0.1 dB (refs 25, 29).
The squeezed vacuum field is injected into the antisymmetric port of the interferometer via an optical circulator, a mode-matching telescope and steering mirrors. To ensure a high coupling efficiency of the squeezed vacuum field to the interferometer field, the transmission of the interferometer output through the OPO cavity in a transverse electromagnetic mode with the interferometer locked on a bright fringe is optimized by using the steering mirrors and mode-matching telescope. With the OPO cavity length scanned, the mode structure of the OPO transmission indicates the coupling efficiency of the interferometer mode to the OPO cavity mode or equivalently the optical loss due to the mode-mismatch between the interferometer and squeezed vacuum fields.
The interferometer output is detected by the length-sensing photodetector with a quantum efficiency of 93%. To show the validity of squeezing, it is critical to calibrate the shot-noise level correctly. As the Michelson interferometer and signal-recycling cavity are locked by using radiofrequency sidebands (as well as the d.c. carrier light at the length-sensing detector), it is important to verify that the carrier-to-sideband power ratio is sufficiently high so that the contribution of the sideband shot noise to the overall shot noise is small. Once the Michelson interferometer and signal-recycling cavity are locked, the Michelson offset feedback control system is turned on and the offset is optimized such that the interferometer output power is 100 μW. It is also important to optimize the control gain to stabilize the power so that drift of the shot-noise level is sufficiently lower than the effective squeezing level. The electronic noise of the readout is 6 dB below the shot noise. The combination of the detection efficiency (93%), the squeezing injection efficiency associated with the injection and round-trip loss (77.5%), the mode-overlap efficiency between the squeezed vacuum and interferometer field (96.0%), and the interferometer response determined by the reflectivity of the end test masses (99.5%), the reflectivity of the signal-recycling mirror (92.5%) and the Michelson offset (π/238) attenuates the injected squeezing level of 9.3±0.1 dB down to about 3 dB (ref. 25). This corresponds to the observed non-classical sensitivity improvement of 44%.
The squeezing phase is locked to the amplitude quadrature of the interferometer field by the noise-locking technique30 using a piezoelectric-transducer-actuated mirror. It is critical to stably control the squeezing phase relative to the interferometer field because the anti-squeezing would, otherwise, degrade the shot-noise level.
References
Scully, M. O. & Zubairy, M. S. Quantum Optics (Cambridge Univ. Press, Cambridge, 1997).
Breitenbach, G., Schiller, S. & Mlynek, J. Measurement of the quantum states of squeezed light. Nature 387, 471–475 (1997).
Walls, D. F. Squeezed states of light. Nature 306, 141–146 (1983).
Caves, C. M. Quantum-mechanical noise in an interferometer. Phys. Rev. D 23, 1693–1708 (1981).
Abramovici, A. et al. LIGO: The Laser Interferometer Gravitational-Wave Observatory. Science 256, 325–333 (1992).
<http://www.ligo.caltech.edu/advLIGO> (2001).
Thorne, K. S. In 300 Years of Gravitation (Cambridge Univ. Press, Cambridge, 1987).
Slusher, R. E., Hollberg, L. W., Yurke, B., Mertz, J. C. & Valley, J. F. Observation of squeezed states generated by four-wave mixing in an optical cavity. Phys. Rev. Lett. 55, 2409–2412 (1985).
Polzik, E. S., Carri, J. & Kimble, H. J. Spectroscopy with squeezed light. Phys. Rev. Lett. 68, 3020–3023 (1992).
Treps, N. et al. Surpassing the standard quantum limit for optical imaging using nonclassical multimode light. Phys. Rev. Lett. 88, 203601 (2002).
Treps, N. et al. A quantum laser pointer. Science 301, 940–943 (2003).
Grangier, P., Slusher, R. E., Yurke, B. & LaPorta, A. Squeezed-light-enhanced polarization interferometer. Phys. Rev. Lett. 59, 2153–2156 (1987).
Xiao, M., Wu, L.-A. & Kimble, H. J. Precision measurement beyond the shot-noise limit. Phys. Rev. Lett. 59, 278–281 (1987).
Furusawa, A. et al. Unconditional quantum teleportation. Science 282, 706–709 (1998).
Grosshans, F. & Grangier, P. Continuous variable quantum cryptography using coherent states. Phys. Rev. Lett. 88, 057902 (2002).
Boto, A. N. et al. Quantum interferometric optical lithography: Exploiting entanglement to beat the diffraction limit. Phys. Rev. Lett. 85, 2733–2736 (2000).
Fiore, L. D. & the VIRGO Collaboration, The present status of the VIRGO central interferometer. Class. Quant. Grav. 19, 1421–1428 (2002).
Willke, B. & the GEO Collaboration, The GEO600 gravitational wave detector. Class. Quant. Gravity 19, 1377–1387 (2002).
Abbott, B. et al. LIGO: The laser interferometer gravitational-wave observatory. Preprint at <http://arxiv.org/abs/0711.3041> (2007).
Ando, M. & the TAMA Collaboration, Stable operation of a 300-m laser interferometer with sufficient sensitivity to detect gravitational-wave events within our Galaxy. Phys. Rev. Lett. 86, 3950–3954 (2001).
Kimble, H. J., Levin, Y., Matsko, A. B., Thorne, K. S. & Vyatchanin, S. P. Conversion of conventional gravitational-wave interferometers into quantum nondemolition interferometers by modifying their input and/or output optics. Phys. Rev. D 65, 022002 (2002).
McKenzie, K., Shaddock, D. A., McClelland, D. E., Buchler, B. C. & Lam, P. K. Experimental demonstration of a squeezing-enhanced power-recycled Michelson interferometer for gravitational wave detection. Phys. Rev. Lett. 88, 231102 (2002).
Vahlbruch, H. et al. Demonstration of a squeezed-light-enhanced power- and signal-recycled Michelson interferometer. Phys. Rev. Lett. 95, 211102 (2005).
Miyakawa, O. et al. Measurement of optical response of a detuned resonant sideband extraction gravitational wave detector. Phys. Rev. D 74, 022001 (2006).
Goda, K. Development of Techniques for Quantum-Enhanced Laser-Interferometric Gravitational-Wave Detectors Thesis, Massachusetts Institute of Technology (2007).
Grosse, N. B., Bowen, W. P., McKenzie, K. & Lam, P. K. Harmonic entanglement with second-order nonlinearity. Phys. Rev. Lett. 96, 063601 (2006).
Drever, R. W. P. et al. Laser phase and frequency stabilization using an optical resonator. Appl. Phys. B 31, 97–105 (1983).
Abbott, B. et al. Conceptual design of the 40 meter laboratory upgrade for prototyping an Advanced LIGO interferometer. LIGO Technical Note, LIGO-T010115-R (2001).
Goda, K. et al. Generation of a stable low-frequency squeezed vacuum field with periodically poled KTiOPO4 at 1064 nm. Opt. Lett. 33, 92–94 (2008).
McKenzie, K. et al. Quantum noise locking. J. Opt. B 7, S421–S428 (2005).
Acknowledgements
We thank our colleagues at the LIGO Laboratory, especially the Quantum Measurement Group at MIT and the 40m Lab at Caltech, and also our colleagues at the Australian National University. This work was supported by National Science Foundation grants PHY-0107417 and PHY-0457264.
Author information
Authors and Affiliations
Contributions
K.G. played the leading role in carrying out the experiment reported here, which was part of his doctoral thesis. O.M., R.A., K.M., R.W., S.V. and A.J.W. maintained the best possible classical performance for the interferometer, whereas K.G., O.M., E.E.M., S.S. and N.M. were responsible for squeezed-state preparation, injection and squeeze-enhancement measurements. A.W. and N.M. are leaders of the Caltech 40m Lab and the MIT Quantum Measurement group, respectively.
Corresponding author
Rights and permissions
About this article
Cite this article
Goda, K., Miyakawa, O., Mikhailov, E. et al. A quantum-enhanced prototype gravitational-wave detector. Nature Phys 4, 472–476 (2008). https://doi.org/10.1038/nphys920
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys920
This article is cited by
-
Integrated quantum optical phase sensor in thin film lithium niobate
Nature Communications (2023)
-
Adaptive optical phase estimation for real-time sensing of fast-varying signals
Scientific Reports (2022)
-
Enhancing the precision limits of interferometric satellite geodesy missions
npj Microgravity (2022)
-
Multiphonon-resonance quantum Rabi model and adiabatic passage in a cavity-optomechanical system
Frontiers of Physics (2022)
-
Robust mechanical entanglement in an atom-assisted hybrid optomechanical system
Quantum Information Processing (2022)