Abstract
When a pure material is tuned to the point where a continuous phase-transition line is crossed at zero temperature, known as a quantum critical point (QCP), completely new correlated quantum ordered states can form1,2,3,4,5,6,7. These phases include exotic forms of superconductivity. However, as superconductivity is generally suppressed by a magnetic field, the formation of superconductivity ought not to be possible at extremely high field8. Here, we report that as we tune the ferromagnet, URhGe, towards a QCP by applying a component of magnetic field in the material’s easy magnetic plane, superconductivity survives in progressively higher fields applied simultaneously along the material’s magnetic hard axis. Thus, although superconductivity never occurs above a temperature of 0.5 K, we find that it can survive in extremely high magnetic fields, exceeding 28 T.
Similar content being viewed by others
Main
The formation of superconducting states close to magnetic quantum critical points (QCPs) first came to prominence in studies of the antiferromagnets CeCu2Ge2 (ref. 1), CeIn3 and CePd2Si2 (ref. 2) and more recently CeRhIn5 (refs 5,6). Theoretically, on tuning a material towards a QCP by application of pressure or magnetic field, the strength of the magnetic fluctuations that potentially bring about superconductivity increases. On approaching a ferromagnetic QCP, longitudinal magnetic fluctuations promote the formation of unconventional spin-triplet superconductivity9,10,11. Theories predict d-wave superconductivity close to QCPs involving antiferromagnetic states. The evolution of the superconductivity as a material is tuned more closely to the field or pressure of the underlying QCP depends on the balance between the weights of fluctuations that are pair forming and pair breaking12. The critical temperature for superconductivity, Ts, is predicted to saturate9 or may even decrease10. Experimentally, superconducting states in antiferromagnetic systems have been more extensively studied than in ferromagnets and measurements show Ts to have a dome-shaped pressure dependence crossing the underlying QCP2,5. However, recent work indicates that the pressure–temperature phase diagrams of antiferromagnetic systems might be more complex than previously thought5,6,13. As it is difficult to vary pressure continuously at low temperature, other properties of the superconducting state, such as the critical field to suppress superconductivity in CePd2Si2 (ref. 14), lack measurements at a sufficient number of pressures to discern how they vary approaching a QCP. For URhGe, the QCP is ferromagnetic rather than antiferromagnetic and can be approached by applying a magnetic field, which can be swept continuously.
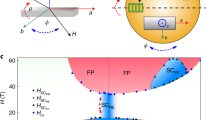
In zero magnetic field, URhGe undergoes a ferromagnetic transition at TCurie=9.5 K. Below this temperature, the ordered magnetic moment is aligned parallel or antiparallel to the crystallographic c axis15. Magnetic fields that correspond to opposite directions of the c-axis moment are separated in low magnetic field by a plane of first-order transitions that is crossed when the c-axis component of the magnetic field changes sign. The temperature above which this first-order transition plane ceases defines a line along which the phase transition is continuous. The schematic temperature–field phase diagram for fields throughout the b c plane is shown in Fig. 1. Close to a field of 12 T, the plane of first-order transitions bifurcates into two spurs. There is a corresponding tricritical point (TCP) at low, but non-zero temperature, where the continuous-transition line splits. The points where the continuous-transition line falls to zero temperature are QCPs4. URhGe is also close to a quantum TCP; such a point would occur if the TCP could be suppressed to zero temperature by varying some further tuning parameter. The phase diagram in Fig. 1 resembles that predicted theoretically for a ferromagnet driven towards a QCP (ref. 16) with the magnetic field applied along the b axis in the present case replacing pressure in the theoretical diagram.
The magnetization changes discontinuously on crossing the first-order transition surface shaded green that ends at finite temperature along a continuous-transition line. The continuous-transition line bifurcates at a TCP and falls to zero temperature at QCPs shown as blue points. The low-temperature resistivity (of the sample studied) at 50 mK for fields in the b c plane is shown by the colour shading on the lower face of the axis frame: yellow corresponding to a resistivity of approximately 5 μΩ cm and red to superconductivity (zero resistivity).
A consequence of the low-temperature TCP is that fluctuations develop with a similar strength at very low temperature at all points along the length of the first-order spurs. Experimentally, this is manifested by the peaks in the temperature-dependent part of the resistivity having comparable amplitudes crossing the weak first-order transition at different points4. Closer than 0.25 T to the spurs, there is an additional sharp peak in the normal-state resistivity, which is independent of temperature (up to 800 mK). We have attributed this effect to extra scattering of charge carriers from magnetic domains that form close to the first-order transition4. As the temperature is reduced to 50 mK, superconductivity occurs both in low applied magnetic fields below 2 T and at high applied fields engulfing the QCPs and the regions where the first-order transition is weak (Fig. 1). The magnitude of the fields at which superconductivity occurs relative to the superconducting transition temperature in both the low-field and high-field pockets implies that equal spins must be paired in contrast to opposite spin pairing in conventional superconductivity4,17.
Figure 2 shows our measurements with magnetic fields applied at different angles, γ, from the b axis towards the a-axis direction. The persistence of the sharp peak in the resistivity at 500 mK shows that the magnetic transition remains weakly first order as γ is increased. The field at which the peak occurs, HR(γ), is well modelled by the relation HR(γ)=HR(0)/cos(γ). For fields in the a b plane, the transition field is therefore crossed when the component of the field along the b axis is equal to HR(0) (henceforth abbreviated to HR) irrespective of the a-axis field. Application of a magnetic-field component parallel to the a axis for a constant b-axis field therefore enables us to determine the critical field for superconductivity at a constant offset from the QCP.
a, The measured resistance plotted against magnetic field for fields applied at γ=10∘ at 45 and 500 mK and also at 45 mK for γ=66∘, which is the measurement with the highest onset field for superconductivity. The geometric inset defines the angle, γ, of the field direction relative to the directions of the a and b crystal axes. b, The critical fields for superconductivity at 45 mK (at which the resistance has fallen to half its normal-state value) measured at different γ. Superconductivity occurs below Hsc1 and between Hsc2 and Hsc3. HR denotes the field at which the magnetic transition occurs, determined from the position of a sharp peak in the resistance at 500 mK. c, The same critical fields plotted in the Ha–Hb plane.
Within our experimental resolution, the angular dependence of the critical field for the low-field pocket of superconductivity at low temperature (denoted as Hsc1) follows the standard form for an anisotropic superconductor (with an orbitally limited critical field),

Hsc1a=φ0/2πξcξb=2.53 T, Hsc1b=φ0/2πξcξa=2.07 T and Hsc1c=φ0/2πξbξa=0.69 T are the critical fields along each of the crystal axes for the sample studied, determined in separate more accurate measurements (ξa,ξb and ξc are the coherence lengths along the different crystal axes and φ0 is the flux quantum). An equation of the same form as equation (1) is derived from the Ginzburg–Landau theory and is applicable in general close to the zero-field superconducting transition temperature, Ts. For URhGe, we can specialize to the case of no Pauli limiting17. In the absence of Pauli limiting, although the coherence lengths depend on temperature, for simple ellipsoidal Fermi surfaces (which can account for an anisotropic electronic effective mass) and isotropic s-wave superconductivity, the anisotropy of the coherence lengths and the angular dependence of the critical field is unchanged at low temperature from that close to Ts (ref. 18). Different factors can cause the anisotropy to be temperature dependent or modify the angular dependence of the critical field at low temperature19. (1) Strong coupling gives only minor modifications in case studies where detailed calculations have been made20. (2) Anisotropy of the superconducting order parameter can give changes of anisotropy with temperature of the order of 20% (refs 17,21). However, numerical calculations for different non-conventional superconductors18 suggest that equation (1) continues to provide a good phenomenological description of the angular dependence of the critical field at low temperature. (3) Special choices of Fermi-surface geometry can lead to major modifications of the form of the angular dependence at low temperature19. As the angular dependence we have measured is standard, the Fermi surface in URhGe cannot have such a special geometry in low magnetic field.
The present sample has a residual resistance ratio, RRR=50. RRR is the ratio of the electrical resistance at room temperature divided by the normal-state resistance at low temperature and is proportional to the defect-limited electronic mean-free-path. The critical field, Hsc1, of the present sample is larger than that for a previously studied lower quality sample with RRR=20(ref. 17). The ratio Hsc1c(RRR=50)/Hsc1c(RRR=20)≈Hsc1a(RRR=50)/Hsc1a(RRR=20)=1.34 is approximately equal to the ratio of the square of the superconducting transition temperatures of the two samples in zero magnetic induction (Ts(RRR=50)/Ts(RRR=20))2=(0.278 K/0.237 K)2=1.37 (ref. 17). This result is the theoretical expectation for a non-conventional superconducting state. The ratio Hsc1b(RRR=50)/Hsc1b(RRR=20)=1.70 is 30% larger than the above ratio; this is discussed further below in the light of our study of the high-field superconductivity.
The angular dependence of the critical fields, Hsc2 and Hsc3, bounding the pocket of superconductivity at high magnetic field is quite different from the angular dependence of the critical field for the low-field superconducting pocket. The field window over which the high-field superconductivity occurs extends to either side of HR(γ) up to the highest applied field of 28 T (Fig. 2b). The main result of our study is that the component of the critical field parallel to the a axis plotted as a function of Hb (that serves to tune the material through the underlying magnetic transition) shows a strong upward curvature as Hb approaches HR (Fig. 2c).
The measured angular dependence of Hsc1 shows that the Fermi-surface geometry does not give rise to a stronger anisotropy of the critical field than that which can be accounted for with an anisotropic effective mass. Assuming that the Fermi-surface geometry does not change radically with field, the strong field dependence of the critical fields Hsc2 and Hsc3 visible in Fig. 2 indicates that the magnitude of the coherence length changes as Hb is tuned through HR. The geometric average of the coherence length, ξ=(ξaξbξc)1/3, deduced from the measured Hsc1,Hsc2 and Hsc3, assuming a fixed coherence length anisotropy, is shown in Fig. 3 (see the Methods section). Remarkably, the low-field and high-field superconducting regions seem to lie on the same smoothly varying curve. Furthermore, the stronger than Ts2 increase of Hsc1b with sample quality can now be understood to result from an increase of φ0/2πξ2 as the low-field pocket of superconductivity extends to cover higher b-axis magnetic fields in better samples, reinforced by a reduction in the effectiveness of pair breaking by impurities owing to a shortening of the coherence length.
The quantity plotted is proportional to the inverse-square coherence length, φ0/2πξ2, given in units of magnetic field where ξ=(ξaξbξc)1/3 is the geometric mean of the coherence lengths along the different axes, calculated assuming a constant anisotropy. The vertical line marks the magnetic field at which the rotation transition occurs. The other straight line gives the value of φ0/2πξ2 below which the critical field for superconductivity for H∥b is less than the applied field along the b axis; superconductivity cannot occur when φ0/2πξ2 falls below this line. The coherence length, ξ, changes from 143 Å for the data point closest to the origin to 44 Å for the data point with the highest value of φ0/2πξ2. The line through the data points is to guide the eye.
Theoretically, 1/ξ≈kBTs/ℏvf, where Ts is the hypothetical superconducting temperature in the absence of magnetic field and vf is the Fermi velocity, inversely proportional to the effective electron quasi-particle mass for a fixed Fermi surface (ℏ is the Planck constant divided by 2π and kB is the Boltzmann constant). The increase of 1/ξ as the b-axis field approaches HR requires that the effective mass and/or Ts increase strongly. For field applied along the b axis, the measured critical temperature for superconductivity has an upward curvature when plotted against field approaching HR (ref. 4). Furthermore, the measured critical temperature reaches a higher value in the high-field superconducting pocket than found at zero field4. These measurements suggest that most of the increase of 1/ξ approaching HR over the field range measured can be accounted for by an increase of Ts. Theoretically, Ts depends exponentially on different contributions to the effective mass12, so this is not inconsistent with more modest changes of the effective mass. At a QCP driven by local physics, the effective quasi-particle mass diverges, as observed in YbRh2Si2 (refs 22,23). An increase of the effective mass is also predicted for a QCP in an itinerant ferromagnet24 and observed approaching magnetic-field-induced transitions in several materials25,26.
In other materials where QCPs have been studied experimentally under high magnetic field, including URu2Si2 (ref. 3) and Sr3Ru2O7 (refs 7,27), new states that are not superconducting have been found. Our work on URhGe shows that superconductivity can, however, survive to much higher magnetic fields close to a QCP than previously thought likely8.
Methods
The measurements were made with the M9 resistive magnet at the Grenoble High Magnetic Field Laboratory (GHMFL) in a top-loading dilution refrigerator equipped with a low-temperature rotator. The sample studied is the same as that used for resistivity measurements for fields in the b c plane4 and is a small bar aligned with its c axis parallel to the axis of rotation (within 1∘). Current was passed along the length of the sample (b axis). The position of 90∘ rotation with the field parallel to the a axis was determined so that HR(γ) changed symmetrically for positive and negative rotations of γ away from this direction.
The fixed value for the coherence length anisotropy used to estimate the geometrically averaged coherence length from the measured values of the critical fields Hsc1,Hsc2 and Hsc3 was chosen to give the measured critical field anisotropy of Hsc1 of the sample with RRR=20 with a constant value of φ0/2πξ2. Symmetry imposes that the leading field dependence of φ0/2πξ2 is quadratic around zero field. The lower quality sample has a lower value of Hscb1 than the higher quality sample and the change of φ0/2πξ2 from its zero-field value at Hscb1 is small enough to be neglected.
References
Jaccard, D., Behnia, K. & Sierro, J. Pressure induced heavy fermion superconductivity of CeCu2Ge2 . Phys. Lett. A 163, 475–480 (1992).
Mathur, N. D. et al. Magnetically mediated superconductivity in heavy fermion compounds. Nature 394, 39–43 (1998).
Harrison, N., Jaime, M. & Mydosh, J. A. Re-entrant hidden order at a metamagnetic quantum critical end point. Phys. Rev. Lett. 90, 96402 (2003).
Lévy, F., Sheikin, I., Grenier, B. & Huxley, A. D. Magnetic field-induced superconductivity in the ferromagnet URhGe. Science 309, 1343–1346 (2005).
Park, T. et al. Hidden magnetism and quantum criticality in the heavy fermion superconductor CeRhIn5 . Nature 440, 65–68 (2006).
Knebel, G., Aoki, D., Braithwaite, D., Salce, B. & Flouquet, J. Coexistence of antiferromagnetism and superconductivity in CeRhIn5 under high pressure and magnetic field. Phys. Rev. B 74, 020501R (2006).
Borzi, R. A. et al. Formation of a nematic fluid at high fields in Sr3Ru2O7. Science 315, 214–217 (2007)
Coleman, P. & Schofield, A. J. Quantum criticality. Nature 433, 226–299 (2005).
Roussev, R. & Millis, A. J. Quantum critical effects on transition temperature of magnetically mediated p-wave superconductivity. Phys. Rev. B 63, 140504 (2001).
Fay, D. & Appel, J. Coexistence of p-state superconductivity and itinerant ferromagnetism. Phys. Rev. B 22, 3173–3182 (1980).
Monthoux, P. & Lonzarich, G. G. p and d-wave superconductivity in quasi-two-dimensional metals. Phys. Rev. B 59, 14598–14605 (2001).
Millis, A. J., Sachdev, S. & Varma, C. M. Inelastic scattering and pair breaking in anisotropic and isotropic superconductors. Phys. Rev. B 37, 4975–4986 (1988).
Kawasaki, S. et al. New superconducting and magnetic phases emerge on the magnetic criticality in CeIn3 . J. Phys. Soc. Japan 73, 1647–1650 (2004).
Sheikin, I. et al. Superconductivity, upper critical field and anomalous normal state in CePd2Si2 near the quantum critical point. J. Low Temp. Phys. 122, 591–604 (2001).
Aoki, D. et al. Coexistence of superconductivity and ferromagnetism in URhGe. Nature 413, 613–616 (2001).
Belitz, D., Kirkpatrick, T. R. & Rollbühler, J. Tricritical behavior in itinerant quantum ferromagnets. Phys. Rev. Lett. 94, 24706 (2005).
Hardy, F. & Huxley, A. D. p-wave superconductivity in the ferromagnetic superconductor URhGe. Phys. Rev. Lett. 94, 247006 (2005).
Prohammer, M. & Carbotte, J. P. Upper critical field of s- and d-wave superconductors with anisotropic effective mass. Phys. Rev. B 42, 2032–2040 (1990).
Kita, T. & Arai, M. Ab initio calculations of Hc2 in type-II superconductors: Basic formalism and model calculations. Phys. Rev. B 70, 224522 (2004).
Werthamer, N. R. & McMillan, W. L. Temperature and purity dependence of the superconducting critical field, Hc2. IV. Strong coupling effects. Phys. Rev. 158, 415–417 (1967).
Scharnberg, K. & Klemm, R. A. Upper critical field in p-wave superconductors with broken symmetry. Phys. Rev. Lett. 54, 2445–2448 (1985).
Gegenwart, P. et al. Magnetic-field induced quantum critical point in YbRh2Si2 . Phys. Rev. Lett. 89, 056402 (2002).
Custers, J. et al. The break-up of heavy electrons at a quantum critical point. Nature 424, 524–527 (2003).
Lonzarich, G. G. in Electron, a Centenary Volume (ed. Springford, M.) 109–147 (Cambridge Univ. Press, Cambridge, 1997).
Paulsen, C. et al. Low temperature properties of the heavy-fermion compound CeRu2Si2 at the metamagnetic transition. J. Low Temp. Phys. 81, 317–339 (1990).
Borzi, R. A. et al. de Haas-van Alphen effect across the metamagnetic transition in Sr3Ru2O7 . Phys. Rev. Lett. 92, 216403 (2004).
Grigera, S. A. et al. Disorder-sensitive phase formation linked to metamagnetic quantum criticality. Science 306, 1154–1157 (2004).
Acknowledgements
Financial support was provided for work at the GHMFL from the European Commission. A.H. gratefully acknowledges support from the Royal Society, UK.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
About this article
Cite this article
Lévy, F., Sheikin, I. & Huxley, A. Acute enhancement of the upper critical field for superconductivity approaching a quantum critical point in URhGe. Nature Phys 3, 460–463 (2007). https://doi.org/10.1038/nphys608
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys608
This article is cited by
-
Dirac lines and loop at the Fermi level in the time-reversal symmetry breaking superconductor LaNiGa2
Communications Physics (2022)
-
Extreme magnetic field-boosted superconductivity
Nature Physics (2019)
-
High-field superconductivity at an electronic topological transition in URhGe
Nature Physics (2011)
-
Superconductivity and spin fluctuations
Frontiers of Physics (2011)
-
The Superconducting Ferromagnet UCoGe
Journal of Low Temperature Physics (2010)