Abstract
Gyrotrons are a high-power source of coherent microwave radiation1. Their oscillation mechanism is a cyclotron-resonance maser effect, in which a fraction of the rotational kinetic energy of a mildly relativistic magnetized electron beam is converted into electromagnetic energy. The most active area of gyrotron development is their potential use for heating magnetically confined fusion plasmas to the point of thermonuclear ignition. A major obstacle to this endeavour is that during high-power millimetre-wave operation2,3,4,5,6,7,8,9 competing modes and mode shifts seriously degrade a gyrotron’s stability and efficiency10,11,12,13. Here, we show that these problems can be overcome by active control of the electron-beam parameters during the oscillation. In doing so, we successfully demonstrate the robust steady-state operation of a 170 GHz gyrotron producing a continuous 1 MW output power with an unprecedented efficiency of over 55% in a hard-self-excitation region. Moreover, we find that an adjacent resonant mode previously expected to compete with and adversely affect the principal operating mode does not in fact jeopardize but rather helps this mode as a result of nonlinear effects. The result improves the outlook for using these devices for heating and instability control in future experimental fusion reactors, such as ITER14,15,16,17,18,19.
Similar content being viewed by others
Main
A basic configuration of the high-power gyrotron oscillator used in the experiment7 is shown in Supplementary Information, Figs S1,S2. The nominal operation mode is TE31,8, in a cylindrical open resonator, whose radius is 17.9 mm. An annular electron beam of 9.13 mm in radius is injected into the resonator along the axial magnetic field to excite TE31,8. The oscillation millimetre-wave power Posci is converted to a gaussian-like beam using a quasi-optical launcher20,21 attached to the resonator, and transmitted through an edge-cooled diamond window as Pout. Here, Pout∼0.92Posci due to the ohmic loss and the diffraction loss Ploss. The collector of the gyrotron is earthed. By applying a positive voltage Vd.c. to the resonator section against the collector, the energy recovery of the spent electron beam is available to enhance the overall efficiency22.
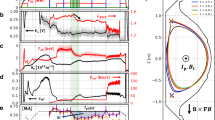
After a demonstration of 1 h oscillation at Pout=0.6 MW with fixed parameters, the operation parameters are actively controlled with a slow timescale to investigate the oscillation characteristics in the continuous-wave state. Figure 1a shows the dependence of the output power on the magnetic field in the resonator, Bc. Here, Vb∼−72.5 kV and Vd.c.∼25.5 kV. After the electron-beam Ib had stabilized at ∼30 A completely, which takes ∼1 min, the Bc scan started from 6.72 T. The frequency is ∼170 GHz. The power increases as the Bc decreases, that is, the cyclotron resonance mismatch factor Δ′=(1−(fce/γ f)) increases. Here, f and fce are oscillation and non-relativistic cyclotron frequencies, respectively, and γ is a relativistic factor of the initial electrons. The maximum power of 0.8 MW is obtained at Bc=6.63 T. The oscillation mode shifts from TE31,8 to TE30,8 (167 GHz) at Bc=6.625 T. Then, the scan direction of Bc is reversed. The TE30,8 continues up to Bc=6.66 T, and the oscillation returns to TE31,8. A clear hysteresis effect23,24 on the generated RF power was observed, which is the first demonstration of the high power gyrotron by Bc scanning with continuous-wave operation. Dangerous reverse rotational modes TE−28,9 TE−27,9, which cannot be transmitted to the output window, and other competing modes are not observed. Figure 1b is a corresponding numerical analysis, where self-consistent, single-mode equations are used25. The Bc range in which two branches exist, 6.625 T<Bc<6.68 T, corresponds to the hard-self-excitation region. In the area enclosed between the solid and dashed lines (hatched region), TE31,8 has a positive growth rate and the power increases up to saturation at the solid line. TE31,8 ceases at Bc∼6.625 T because Δ′ is too large to keep the oscillation, where the oscillation mode changes to TE30,8. The numerically predicted radio-frequency (RF) power behaviour of the TE31,8 mode agrees very well with the experiment. The result indicates that maximum power is obtained in the hard-excitation region, and the power limit is not determined by the interruption from other modes but by its own oscillation limit. In addition, the result suggests that the voltage depression by the space charge of the electron beam is ∼4.0 kV. A particle simulation predicts an average pitch factor α value of 〈α〉=1.4 ( ,
,  and v∥ being respectively the perpendicular and parallel electron velocity with respect to the magnetic field) and a voltage depression of ∼4.5 kV, which implies that the charge neutralization effect by ions was relatively small in this case. On the other hand, the single-mode simulation indicates that excitation of TE31,8 is possible at Bc>6.68 T, whereas TE31,8 was re-excited at Bc=6.66 T. There is a 0.02 T gap between them. In addition, the power of TE31,8 obtained for |Bc| values during the increasing phase of magnetic field (d|Bc|/dt>0) is higher than obtained for |Bc| values during the decreasing phase. This discrepancy can be explained by the increase of the ions in the resonator in the d|Bc|/dt>0 phase, which brings about the increase of the electron-beam energy. This acts, however, to enlarge the gap further from 0.02 to 0.03 T in the case of identical beam energy.
and v∥ being respectively the perpendicular and parallel electron velocity with respect to the magnetic field) and a voltage depression of ∼4.5 kV, which implies that the charge neutralization effect by ions was relatively small in this case. On the other hand, the single-mode simulation indicates that excitation of TE31,8 is possible at Bc>6.68 T, whereas TE31,8 was re-excited at Bc=6.66 T. There is a 0.02 T gap between them. In addition, the power of TE31,8 obtained for |Bc| values during the increasing phase of magnetic field (d|Bc|/dt>0) is higher than obtained for |Bc| values during the decreasing phase. This discrepancy can be explained by the increase of the ions in the resonator in the d|Bc|/dt>0 phase, which brings about the increase of the electron-beam energy. This acts, however, to enlarge the gap further from 0.02 to 0.03 T in the case of identical beam energy.
a, Experimental result at beam voltage Vb∼−72.5 kV and beam current Ib∼30 A. The TE31,8 mode is initially excited at Bc=6.72 T, and Bc is scanned along the direction of the arrows. Just after the oscillation shift to the TE30,8 mode, the Bc returned to higher field. Scan speed is 0.027 T min−1. b, Single-mode simulation results at the parameter of the experiment for TE31,8 and TE30,8 modes. Arrows indicate the directions of mode shifts. The double-headed arrow shows the gap between the expected and measured magnetic fields of the mode shift. The hatched area shows the region where the TE31,8 mode has a positive growth rate. Vb=−68.5 kV, Ib=30 A, 〈α〉=1.35, and its deviation Δα/α=5% are assumed.
This gap is explained by a nonlinear excitation on a two-mode interaction10. Figure 2a is the simulation result of time behaviour of two modes26, which are observed in the experiment, at Bc=6.67 T. Here, as initial powers, 1 kW and 1 mW are set for TE31,8 and TE30,8 modes, respectively, to close up the feature. TE30,8 grows to saturation in ∼10 ns. TE31,8 damps exponentially because the oscillation condition is not fulfilled. However, when TE30,8 exceeds ∼10 kW, TE31,8 begin to grow as a parasitic mode of the TE30,8, because the electron phase bunching by TE30,8 is also favourable for TE31,8. As shown in Fig. 2b, TE31,8 increases its power exponentially owing to TE30,8. When the power exceeds the threshold (dashed line in Fig. 1b), TE31,8 can grow by itself. TE31,8 forces the electron phase bunching as favourable for TE31,8 itself, and then begins to suppress TE30,8. Finally, the system is dominated by TE31,8, as observed in the experiment. These results imply that the adjacent TE30,8 is not a competing mode for TE31,8, but rather supports TE31,8. As a result, the substantial soft-self-excitation region of the dominant mode is expanded.
The Bc scan was also performed at different values of α. The results are shown as power contours of objective TE31,8 mode in Fig. 3. The vertical axis is the applied voltage between the anode and cathode terminals of the triode-type electron gun Vak, which determines α. Generally, as Vak is raised α increases, although it is not easy to identify the precise value of α. As a reference, the particle simulation indicates 〈α〉=1.6, 1.4 and 1.25 at Vak=44 kV, 42 kV (Fig. 1) and 40 kV, respectively. The solid line indicates the boundary between the TE31,8 and TE30,8 modes when Bc is scanned from the higher side, and the dashed line is that obtained for the inverse Bc scan. The region between the solid and dashed lines is the substantial hard-self-excitation region. Since the beam energy and current are stable, one can easily and precisely access the optimum without the mode shift and the electron trapping. The maximum power of 0.82 MW is obtained at the point denoted by a star symbol, then the efficiencies are ηRF (≡Pout/VbIb)=36.2% and ηTotal (≡(Pout/(Vb−Vd.c.)Ib))=56%. The optimum point can be accessed through any pass in the TE31,8 area. When Bc is decreased or Vak increased, the leak current to the anode Ia appears at the hatched area in the figure. The cause of Ia is the electrons reflected by the depressed collector potential. If Vd.c.=21.5 kV, Ia disappears because the minimum energy of the electron beam after the interaction is greater than 21.5 kV, and Vak up to 44.0 kV is available. Here, the high-pitch-factor electron beam 〈α〉∼1.6 is probably realized. Then, Pout∼0.85 MW and ηRF=39.1% is obtained. The oscillation efficiency in the resonator is the highest value observed at 170 GHz gyrotrons; ηosci (≡Posci/VbIb) is 42.5%. These facts indicate that the perpendicular efficiency, which is defined as the conversion efficiency from the perpendicular energy of the electron to the RF energy, is close to ∼60%. Once the nominal operating mode is excited, the oscillation is robust and the operation parameters can be selected freely in the TE31,8 region, including the hard-self-excitation region. However, when the parameters pass across the border and the adjacent TE30,8 mode is excited, one should go back to the TE31,8 region in the soft-self-excitation region to re-excite the nominal operating mode.
By increasing Ib to 38 A, the output power of 1.01 MW was obtained. Figure 4 shows an example of long-pulse oscillation. The total pulse duration is 1,100 s. After Vak increases to 42 kV, Bc decreases slowly from 6.70 to 6.625 T. Then, the oscillation enters the hard-self-excitation region and the power increases to 1.0 MW. At the same time, the power deposition to the collector decreases with the same amount of power. For 800 s, the power exceeds 1.0 MW. No limit was seen for pulse extension. Here, ηRF=36.5% and the overall efficiency with a 24.5 kV depressed collector is ηTotal=55%. At deeper depressed collector, VCD=26.5 kV, ηTotal=57% is obtained at 1.0 MW, whereas a small amount of trapped electron Ia∼5 mA appears. The achieved results exceed the requirement on the gyrotron for ITER (International Thermonuclear Experimental Reactor), that is, 1 MW output power at 170 GHz, 50% efficiency, 500 s pulse duration (burning time of plasma), for a plasma heating and current drive to perform an experiment of self-ignition and plasma sustain14,15 (see Supplementary Information, Fig. S3). Furthermore, the achieved parameters in terms of RF power and global efficiency are consistent with the requirement for an electron cyclotron resonance heating–electron cyclotron current drive system to be installed on a future commercial reactor27.
It should be noted that the high-efficiency state was difficult to attain without the active parameter control. In a conventional start-up scenario, the beam energy γ, that is, Δ′, and α are raised simultaneously, with a short timescale, which is usually less than 10 ms. However, important parameters such as Ib, α and f change significantly with a timescale of 0.1 s∼1 min. Then, negative effects such as large electron trapping or mode shift occurred during the oscillation when the optimum operation parameters were initially fixed. To avoid these effects, the initial parameters were set such as to reach the maximum efficiency in the soft-self-excitation region, which brings about the efficiency decrease. For example, efficiencies of long-pulse gyrotrons were 36–43% with the depressed collector (∼40% in the case of 170 GHz)2,4,5,6,7,8,9. In this paper it is proved that the accessibility to the maximum theoretical efficiency, in the hard-self-excitation region, is possible via the active parameter control, which allows a precise optimization of the relevant parameters such as 〈α〉 and Δ′. Furthermore, by a combination of an active beam-position control that determines the coupling coefficient with each mode, more flexible operation will be available. The results give a possibility of high-efficiency oscillation at higher frequency28, for example submillimetre to terahertz range, using further higher modes and higher-harmonic oscillation.
Methods
Power measurement
The output power Pout was measured calorimetrically. In Supplementary Information, Fig. S4, the configuration of the gyrotron and transmission line of the output power is shown. The output power Pout couples with the HE11 mode of the corrugated waveguide using two mirrors in a matching optics unit, and the RF power is transmitted to a dummy load composed of pre- and main-dummy loads (1.25 MW waterload model 1250, Calabazas Creek Research). All components are cooled by water; therefore, the deposition powers are identified from the temperature increases of the cooling water. The Pout of 1.01 MW is the summation of the dummy-load power (0.96 MW), transmission loss (∼0.01 MW) and coupling loss dissipated in the matching optics unit (0.04 MW). As for Figs 1a and 2, Pout was measured from the temperature increase of the output window of the gyrotron made of a synthetic diamond disc using an infrared camera (TVS-8500, Nippon Avionics). The time constant of the window temperature is ∼1.7 s, which is short enough compared with the scanning speed of Bc. The relationship between the window-temperature increase and Pout was obtained in advance.
On Bc scanning
In Fig. 1a, Bc is scanned using a main magnet of the gyrotron. Generally, the change of Bc causes a shift of the beam radius rb and the pitch factor α of the electron beam. However, in Fig. 1a, the scanning range is small (6.62 T–6.7 T). This gives small shifts of both rb and α, that is, Δrb∼0.01 mm and Δα∼0.01, respectively, which have a small influence on the gyrotron oscillation. Therefore, no additional effort has been made to keep rb and α constant in the experiment.
References
Thumm, M. High power gyro-devices for plasma heating and other applications. Int. J. Infrared Millim. Waves 26, 483–503 (2005).
Felch, K. et al. Recent ITER-relevant gyrotron tests. J. Phys. Conf. Ser. 25, 13–23 (2005).
Choi, E. et al. Megawatt power level 120 GHz gyrotrons for ITER start-up. J. Phys. Conf. Ser. 25, 1–7 (2005).
Dammertz, G. et al. High-power gyrotron development at Forschungzentrum Karlsruhe for fusion applications. IEEE Trans. Plasma Sci. 34, 173–186 (2006).
Piosczyk, B. et al. A 2 MW, 170 GHz, coaxial cavity gyrotron-experimental verification of the design of main components. J. Phys. Conf. Ser. 25, 24–32 (2005).
Agapova, M. V. et al. Proc. Joint 31th Int. Conf. on Infrared and Millimeter Waves and 14th Int. Conf. on Terahertz Electronics (Conference Digest), September 19–23, 2006, Shanghai, China 516 (IEEE, New Jersey, 2006).
Sakamoto, K. et al. Development of 170 GHz and 110 GHz gyrotrons for fusion devices. Nucl. Fusion 43, 729–737 (2003).
Sakamoto, K. et al. Development of long pulse and high power 170 GHz gyrotron. J. Phys. Conf. Ser. 25, 8–12 (2005).
Kasugai, A. et al. Long pulse operation of 170 GHz ITER gyrotron by beam current control. Fusion Eng. Des. 81, 2791–2796 (2006).
Nusinovich, G. S. Review of the theory of mode interaction in gyrodevices. IEEE Trans. Plasma Sci. 27, 313–326 (1999).
Whaley, D. R. et al. Startup methods for single-mode gyrotron operation. Phys. Rev. Lett. 75, 1304–1307 (1995).
Nusinovich, G. S. et al. Startup scenarios in high-power gyrotrons. IEEE Trans. Plasma Sci. 32, 841–851 (2004).
Nusinovich, G. S. et al. Slow processes in startup scenarios of long pulse gyrotrons. Phys. Plasmas 13, 083106 (2006).
Technical Basis for the ITER Final Design Report (FDR), 2001. http://www.iter.org.
Imai, T. et al. ITER R&D: Auxiliary Systems: Electron cyclotron heating and current drive system. Fusion Eng. Des. 55, 281–289 (2001).
Isayama, A. et al. Complete stabilization of a tearing mode in steady state high βp H-mode discharges by the first harmonic electron cyclotron heating/current drive on JT-60U. Plasma Phys. Control. Fusion 42, L37–L45 (2000).
Gantenbein, G. et al. Complete suppression of neoclassical tearing modes with current drive at the electron-cyclotron-resonance frequency in ASDEX Upgrade tokamak. Phys. Rev. Lett. 85, 1242–1245 (2000).
Luce, T. C. Development of burning plasma and advanced scenarios in the DIII-D tokamak. Nuclear Fusion 45, S86–S97 (2005).
Prater, R. Application of electron cyclotron current drive on ITER. J. Phys. Conf. Ser. 25, 257–265 (2005).
Neilson, J. Optimal synthesis of quasi-optical launchers for high power gyrotrons. Science 34, 635–641 (2006).
Minami, R. et al. The designs of high efficiency launcher of quasi-optical mode converter for high power gyrotrons. J. Infrared Millim. Waves 27, 13–24 (2006).
Sakamoto, K. et al. Major improvement of gyrotron efficiency with beam energy recovery. Phys. Rev. Lett. 73, 3532–3535 (1994).
Kisel, D. V. et al. An experimental study of gyrotron, operating at the second harmonic of the cyclotron frequency, with optimized distribution of the high-frequency field. Radio Eng. Electron Phys. 19, 95 (1974).
Dumbrajs, O. et al. Hysteresis-like effects in gyrotron oscillators. Phys. Plasmas 10, 1183 (2003).
Fliflet, A. W. et al. A self-consistent field theory for gyrotron oscillators: Application to a low Q gyromonotron. Int. J. Electron. 53, 505–522 (1982).
Fliflet, A. W. et al. Time-dependent multimode simulation of gyrotron oscillators. Phys. Rev. A 45, 6166–6176 (1991).
Maisonnier, D. et al. A conceptual study of commercial fusion power plants, EFDA(05)-27/4.10 (2005), http://www.efda.org/eu_fusion_programme/ scientific_and_technical_publications.htm (PPCS overall report final-with annexes.pdf).
Idehara, T. et al. in Conf. Digest of the 2006 Joint 31th Int. Conf. on Infrared and Millimeter Waves and 14th Int. Conf. on Terahertz Electronics, Shanghai, China (eds Shen, X. C., Lu, W., Zhang, J. & Dou, W. B.) 509 (IEEE, New Jersey, 2006).
Acknowledgements
The authors would like to thank T. Kariya, K. Hayashi and Y. Mitsunaka of Toshiba Electron Tubes and Devices for the gyrotron fabrication, and Yu. Ikeda and S. Komori of JAEA for their support of the experiment. We would like to thank T. Yamamoto, R. Yoshino, H. Takatsu and T. Tsunematsu for their encouragement.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Rights and permissions
About this article
Cite this article
Sakamoto, K., Kasugai, A., Takahashi, K. et al. Achievement of robust high-efficiency 1 MW oscillation in the hard-self-excitation region by a 170 GHz continuous-wave gyrotron. Nature Phys 3, 411–414 (2007). https://doi.org/10.1038/nphys599
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys599
This article is cited by
-
The Progress in the Studies of Mode Interaction in Gyrotrons
Journal of Infrared, Millimeter, and Terahertz Waves (2022)
-
State-of-the-Art of High-Power Gyro-Devices and Free Electron Masers
Journal of Infrared, Millimeter, and Terahertz Waves (2020)
-
Observation of a comb-shaped filamentary plasma array under subcritical condition in 303-GHz millimetre-wave air discharge
Scientific Reports (2019)
-
Broadband terahertz-power extracting by using electron cyclotron maser
Scientific Reports (2017)
-
Design of a Millimeter-Wave Concentrator for Beam Reception in High-Power Wireless Power Transfer
Journal of Infrared, Millimeter, and Terahertz Waves (2017)