Abstract
Periodic structures have a large influence on propagating waves. This holds for various types of waves over a large range of length scales: from electrons in atomic crystals1 and light in photonic crystals2,3,4 to acoustic waves in sonic crystals5. The eigenstates of these waves are best described with a band structure, which represents the relation between the energy and the wavevector (k). This relation is usually not straightforward: owing to the imposed periodicity, bands are folded into every Brillouin zone, inducing splitting of bands and the appearance of bandgaps. As a result, exciting phenomena such as negative refraction6,7, auto-collimation of waves8,9 and low group velocities10,11,12 arise. k-space investigations of electronic eigenstates have already yielded new insights into the behaviour of electrons at surfaces and in novel materials13,14,15,16. However, for a complete characterization of a structure, an understanding of the mutual coupling of eigenstates is also essential. Here, we investigate the propagation of light pulses through a photonic crystal structure using a near-field microscope17,18. Tracking the evolution of the photonic eigenstates in both k-space and time allows us to identify individual eigenstates and to uncover their dynamics and coupling to other eigenstates on femtosecond timescales even when co-localized in real space and time.
Similar content being viewed by others
Main
The structure under investigation is a two-dimensional photonic crystal structure, in which we fabricated a so-called directional coupler with two input waveguides and two output waveguides (Fig. 1a), by leaving single rows of holes unperforated. The waveguides were chosen as they support only a single eigenstate at the frequencies used in the experiment, which simplifies the k-space analysis. In the directional coupler, two waveguides run parallel, allowing the light to couple from the upper to the lower waveguide and vice versa. Although seemingly a simple photonic structure, the propagation of light through it already involves many photonic eigenstates and coupling between these states. Different orientations of the waveguides are present in the device resulting in eigenstates represented in k-space by different wavevectors. At the coupling section, the waveguides interact resulting in new symmetric and anti-symmetric eigenstates. Figure 1b shows the experimentally determined (time-averaged) transmission of both the upper and lower output waveguides obtained from ‘white-light’ transmission measurements. This input–output analysis reveals a frequency-specific response due to particular eigenstates. By tracking these eigenstates in time, we will quantitatively recover both the individual eigenstates as well as their coupling dynamics on a femtosecond timescale.
a, Scanning electron microscope image of the sample, with two input waveguides (left) and two output waveguides (right). The directional coupler (centre) is 45 lattice periods long. The inset shows a close-up of the membrane facet. b, Transmission spectra of the device for both output ports. The device transmits light in the wavelength range between 1,250 and 1,290 nm. Most light is transmitted to the upper output waveguide, but at larger optical wavelengths the coupling to the lower output waveguide increases.
We investigated the propagation of light in the photonic crystal structure with a phase-sensitive and time-resolved near-field microscope19, which is schematically shown in Fig. 2. Figure 3a shows the result of a near-field measurement at 1,260 nm, where the transmission efficiency through the structure is high (see Fig. 1b). The optical signal is shown in red and blue, representing positive and negative electric fields. The inset shows a section of the input waveguide, where the phase evolution of the propagating light is clearly resolved. At the delay time defined as 0 ps, the pulse is found to be located in the input waveguide. When we map the optical field at increased delay times (Fig. 3b–f), we observe the pulse dynamics in the structure: after entering the directional coupler, the pulse propagates into the upper and lower output waveguides. In the last two images recorded at 1.6 and 2.0 ps, the pulse exits the structure, with most of the light exiting through the upper output waveguide.
The aluminium-coated near-field probe (inset) is scanned over the surface and collects a minute fraction of the propagating light. The collected light is mixed interferometrically with a reference beam. Only the resulting interference signal is recorded. The delay time in the experiment is controlled by the optical delay line.
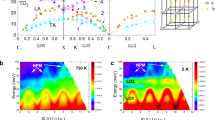
a–f, Raw data obtained from an interferometric near-field measurement with delay times increasing from 0 to 2.0 ps. The background (of 0.40±0.02 μW) is represented in black and the positive and negative interference values in red and blue, respectively. The consecutive images show an optical pulse entering the structure through the upper input waveguide and exiting the structure through both output waveguides. The inset in a shows a close-up of the measurement at 0 ps. g–l, k-space maps corresponding to a to f. In each k-space map, the eigenstates are visible as bright features. As time progresses, light couples sequentially to multiple eigenstates, because new features appear in k-space. The first Brillouin zone of the lattice is given by the dashed hexagon in g. The image orientation (kx,ky) corresponds to (x,y) in a–f. Line traces of the data are shown in green in c and i, corresponding to the data under the dashed green lines. (Both a–f and g–l are available with a higher time resolution as Supplementary Information.)
The consecutive measurements in Fig. 3a–f show the real-time dynamics of a femtosecond pulse travelling through a photonic crystal device. Although the images demonstrate the basic dynamics of the light propagating in such a structure, a detailed understanding of the propagating light remains hidden, as to that end the interplay between the eigenstates needs to be uncovered. When the propagation of a specific eigenstate in a waveguide (also called a waveguide mode) is to be investigated, there are a number of challenges. The first difficulty is to determine how many eigenstates are excited, as these states are usually excited simultaneously and propagate along the same path: they are co-localized in real space and time. Second, when multiple states are excited, separating them to investigate each individual state is impossible. However, in a k-space analysis, we recover the wavevectors present. When the eigenstates have different wavevectors, the states can be separated in k-space, even when co-localized in real space. By evaluating the eigenstates in both k-space and in time, we recover both the characteristic of each state and the coupling dynamics between them. In our experiment, the spatial frequencies (the wavevectors) contained in the real-space images are recovered through a two-dimensional Fourier transform. In this way, we obtain the wavevectors, direction and the amplitude of the corresponding eigenstates. (For a more detailed description, see the Supplementary Information.) Recently, this method has been applied to the investigation of phononic crystals20. By recovering the wavevectors as a function of time, we can investigate the dynamics of the individual eigenstates.
The k-space image of the measurement at 0 ps is shown in Fig. 3g. Two stripes are visible in this figure: these are the most prominent spatial frequencies contained in the light field in the input waveguide. The confinement of the light in a narrow structure, that is, the waveguide in real space, results in the elongated features (stripes) in k-space, as a small feature in real space is built up by a large number of spatial frequencies. In effect, the shape of the stripe is directly related to the lateral mode profile by a Fourier relation. The elongation of the stripe in k-space is therefore perpendicular to the direction of the waveguide. Owing to the long-range periodicity of the optical field along the waveguide, we obtain well-defined wavevectors in the direction of the waveguide. In this way, we have probed the eigenfunction of the light in the structure and have recovered the wavevectors corresponding to this optical field.
Note that we find two stripes in Fig. 3g, but only a single eigenstate is excited. This observation is a direct consequence of the Bloch wave nature of the guided light. The eigenfunction obeys Bloch’s theorem, which means that a single eigenfunction is composed of multiple wavevectors21 in such a way that the eigenfunction conforms to the imposed periodicity of the lattice. Therefore, the individual wavevectors, the Bloch harmonics, are spaced one reciprocal lattice vector apart in k-space. This can also be observed in Fig. 3g, as the wavevectors are spaced one Brillouin zone (dashed hexagon) apart. There are also harmonics with larger wavevectors but these could not be resolved in our k-space maps owing to their low amplitude. Interestingly, each Bloch harmonic has a different amplitude profile: the two k-space features have a different structure perpendicular to the propagation direction. This can be understood by realizing that in general the spatial mode pattern is more complicated close to the holes than in the centre of the waveguide. A complicated pattern requires the mixing of more harmonics22, with amplitudes such that together they form the pattern.
As the delay time is increased to 0.40 ps (Fig. 3h), we observe two new features, now with an elongation in the vertical direction. These vertical stripes correspond to the eigenstates of the directional coupler. We find both a positive and a negative wavevector at kx=1.43π/a and kx=−0.57π/a, respectively, where a is the period of the lattice. The coupling in the directional coupler occurs owing to a coherent superposition of a symmetric and anti-symmetric eigenstate (see the Supplementary Information), which have slightly different wavevectors. At the frequency used, the difference in the k-vector is too small to be resolved in our k-space maps.
Two new stripes appear in Fig. 3i, corresponding to the Bloch mode in the upper output waveguide. Note that the light in the lower output waveguide does not give rise to new features in k-space, because the waveguide geometry and direction are identical to the input waveguide. The k-space features therefore overlap with the wavevectors of the input waveguide.
Above, we discussed the evolution of the three most prominent eigenstates found in k-space during a time interval of 2.0 ps. In addition, other less pronounced eigenstates are present, for example those that show up as a circle of radius 0.54π/a around the origin. The circular shape indicates equally long wavevectors in every direction. In fact, the wavevectors correspond to light skimming over the surface in every direction, originating from scattering at the intersections. We also find evidence for reflections at the intersections: a reflected wave with an initial wavevector k will have a reflected wavevector −k, an equally large wavevector in the opposite direction. Indeed, in Fig. 3k two vertical features are found at kx=−1.43 and 0.57π/a.
As we have recovered the wavevectors of the device eigenstates, we can now investigate the individual states by selecting their wavevectors in k-space. To demonstrate this approach, we studied the amplitude of the light in the input waveguide, the two output waveguides and the reflected light into the upper input waveguide. As the eigenstate in one of the output waveguides has the same signature in k-space as the input waveguide, we carried out a selection in real space to separate the two.
The results are shown in Fig. 4. At each delay time, the real-space image is split into three sections: the upper input waveguide and the lower and upper output waveguides. A Fourier transform of each of these real-space images gives three k-space images, corresponding to the three waveguides. The E-field amplitude of the eigenstates in each of the waveguides is recovered by summation of the amplitude of the two Bloch harmonics k=1.43π/a and −0.57π/a. The amplitude pattern of the harmonics does not play a role, as we sum over the full width of the k-space pattern perpendicular to the waveguide direction. For the amplitude of the mode in the input waveguide, the maximum amplitude is found around 0.5 ps: as soon as the mode couples to the modes of the directional coupler its amplitude decreases. From the amplitude of the light in the lower and upper output waveguide, we obtain a splitting ratio of 1:5 (in intensity, or amplitude squared) in favour of the upper output waveguide.
Evolution of the amplitude in each of the most pronounced eigenstates as time progresses, determined from the k-space images. The blue line represents the amplitude in the input waveguide. The light travelling backwards in the input waveguide is shown by the dashed blue line (magnified five times), where the error bars are proportional to the noise of the Fourier transform. The red and green arrows show the exit time of the corresponding output pulses, determined by the centre-of-mass of the time versus intensity curves (amplitude squared). The time difference between the output pulses is 70±20 fs. The inset shows a schematic diagram of the position and propagation direction of the eigenstates.
Interestingly, the two output pulses do not exit the directional coupler at the same time. The characteristic exiting time is indicated by the arrows. These times are calculated by evaluating the centre-of-mass of the curves. Despite the identical path length for the two routes, the pulse in the lower output waveguide exits the directional coupler 70±20 fs later than the pulse in the upper output waveguide. This difference can be understood by noting the spectral characteristics of the device in combination with pulse dispersion. From the transmission spectra in Fig. 1b, we know that the low-frequency components couple more efficiently to the lower output waveguide. Owing to anomalous dispersion23, these low-frequency components arrive at a later time at the directional coupler, and therefore the output appears at a later time. The error of ±20 fs has two main contributions: the error in determining the centre-of-mass of the curves and a correction for the slightly different length of the measured output waveguides.
We have also analysed the light reflected back into the upper input waveguide, owing to reflections at the intersections, both at the right and the left side of the directional coupler. The reflected amplitude in the measured stretch of the input waveguide has two main peaks, at 1.1 ps and 1.8 ps, respectively. The first peak corresponds to the reflections at the left intersection and the second peak is caused by the reflected light at the right intersection in the directional coupler. The peaks between 0 and 0.8 ps do not exceed the noise level in the k-space maps, which is shown by the error bars in Fig. 4. The area under the curve of intensity versus delay time is proportional to the total energy reflected back into the upper input waveguide: in this case 2% of the input energy is reflected back.
Our measurement approach can be adopted to investigate and understand the behaviour of any complex optical system where electromagnetic waves are present at the surface, to probe its eigenstates, their relative amplitudes and their coupling in time. Care has to be taken in determining the relative amplitudes of eigenstates or of their Bloch harmonics, as these may be detected with a different efficiency, which depends, for example, on the wavevector. In addition, a number of oscillations of the optical field must be measured to assign a wavevector with a useful accuracy. Correspondingly, the concept of assigning wavevectors may not be very useful in small structures, for example in small-volume cavities. Nevertheless, the method is suited for the investigation of the majority of photonic crystal devices.
Moreover, it should be particularly exciting to implement the approach to probe novel classes of optical metamaterials where, for example, negative phase velocities and negative group velocities have been reported24. Our ability to observe the time-resolved interplay between the eigenstates underlying the counter-intuitive properties of metamaterials will spark exciting new avenues of research. Ultrafast, time-resolved studies on atomic systems in k-space have been limited to structural rearrangements of the crystal lattice itself25,26,27. The k-space representation of electronic eigenstates in time-averaged experiments has elucidated the properties of very diverse systems ranging from surfaces13 and carbon nanotubes15 to high-Tc superconductors14. Both of the techniques used, scanning tunnelling microscopy28 and angle-resolved photoemission29,30, can be modified to enable time-resolved measurements. Thus, tracking eigenstates in k-space as described here is, in principle, possible for electronic eigenstates. Such a development offers the exciting perspective of unravelling the dynamics and coupling of the electronic states on a femtosecond timescale.
Methods
The structure under investigation is a two-dimensional photonic crystal structure, consisting of air holes (period a=339 nm, radius 102 nm) in a GaAs membrane (thickness 250 nm), that has a two-dimensional photonic bandgap between vacuum wavelengths 1,220 nm and 1,350 nm. Femtosecond laser pulses (centre wavelength 1,260 nm, spectral width 12 nm) are launched into the structure, see also Fig. 2. The evanescent field of the propagating light is probed locally by a metal-coated tapered optical fibre (Fig. 2, inset). The spatial resolution is better than the so-called diffraction limit and is to first approximation determined by the size of the aperture (250 nm). The choice of the aperture diameter is a trade-off between higher resolution at smaller diameter and a strong decrease of the throughput as the diameter is decreased. The collected light is interferometrically mixed with a reference pulse from the same pulsed laser source. When the probe is scanned over the surface of the sample, the optical path length of the sample branch changes. Therefore, interference maxima and minima are obtained, depending on the phase of the light in the sample relative to the phase of the reference pulse. Owing to the duration of the laser pulses, interference will only be detected if there is sufficient time overlap between the pulses in the reference and sample branch. In this way, the scan will result in a spatial map of the interference, which generally appears like a ‘snapshot’ of the propagating pulse19. The instant at which such a ‘snapshot’ is recorded is determined by the arrival time of the reference pulse, also called the ‘delay time’.
References
Bloch, F. Über die quantenmechanik der elektronen in kristallgittern. Z. Physik 52, 555–600 (1928).
Soukoulis, C. M. (ed.) Photonic Crystals and Light Localization in the 21st Century (NATO Science Series, Kluwer Academic, Dordrecht, 2001).
Fujita, M., Takahashi, S., Tanaka, Y., Asano, T. & Noda, S. Simultaneous inhibition and redistribution of spontaneous light emission in photonic crystals. Science 308, 1296–1298 (2005).
Koenderink, A. F., Kafesaki, M., Soukoulis, C. M. & Sandoghdar, V. Spontaneous emission in the near field of two-dimensional photonic crystals. Opt. Lett. 30, 3210–3212 (2005).
Cervera, F. et al. Refractive acoustic devices for airborne sound. Phys. Rev. Lett. 88, 023902 (2002).
Hu, X. H. et al. Superlensing effect in liquid surface waves. Phys. Rev. E 69, 030201 (2004).
Feng, L. et al. Acoustic backward-wave negative refractions in the second band of a sonic crystal. Phys. Rev. Lett. 96, 014301 (2006).
Mahieu, G. et al. Direct evidence for shallow acceptor states with nonspherical symmetry in GaAs. Phys. Rev. Lett. 94, 026407 (2005).
Lu, Z. L. et al. Experimental demonstration of self-collimation inside a three-dimensional photonic crystal. Phys. Rev. Lett. 96, 173902 (2006).
Feynman, R. P. et al. Mobility of slow electrons in a polar crystal. Phys. Rev. 127, 1004–1017 (1962).
Gersen, H. et al. Real-space observation of ultraslow light in photonic crystal waveguides. Phys. Rev. Lett. 94, 073903 (2005).
Vlasov, Y. A., O’Boyle, M., Hamann, H. F. & McNab, S. J. Active control of slow light on a chip with photonic crystal waveguides. Nature 438, 65–69 (2005).
Crommie, M. F., Lutz, C. P. & Eigler, D. M. Imaging standing waves in a 2-dimensional electron gas. Nature 363, 524–527 (1993).
Shen, Z. X., Spicer, W. E., King, D. M., Dessau, D. S. & Wells, B. O. Photoemission-studies of high-Tc superconductors—the superconducting gap. Science 267, 343–350 (1995).
Lemay, S. G. et al. Two-dimensional imaging of electronic wavefunctions in carbon nanotubes. Nature 412, 617–620 (2001).
McElroy, K. et al. Relating atomic-scale electronic phenomena to wave-like quasiparticle states in superconducting Bi2Sr2CaCu2O8+δ . Nature 422, 592–596 (2003).
Betzig, E. & Trautman, J. K. Near-field optics—microscopy, spectroscopy, and surface modification beyond the diffraction limit. Science 257, 189–195 (1992).
Bozhevolnyi, S. I., Volkov, V. S., Devaux, E., Laluet, J. Y. & Ebbesen, T. W. Channel plasmon subwavelength waveguide components including interferometers and ring resonators. Nature 440, 508–511 (2006).
Balistreri, M. L. M., Gersen, H., Korterik, J. P., Kuipers, L. & van Hulst, N. F. Tracking femtosecond laser pulses in space and time. Science 294, 1080–1082 (2001).
Profunser, D. M., Wright, O. B. & Matsuda, O. Imaging ripples on phononic crystals reveals acoustic band structure and Bloch harmonics. Phys. Rev. Lett. 97, 055502 (2006).
Russell, P. St. J. Optics of Floquet–Bloch waves in dielectric gratings. Appl. Phys. B 39, 231–246 (1986).
Gersen, H. et al. Direct observation of Bloch harmonics and negative phase velocity in photonic crystal waveguides. Phys. Rev. Lett. 94, 123901 (2005).
Engelen, R. J. P. et al. Local probing of Bloch mode dispersion in a photonic crystal waveguide. Opt. Express 13, 4457–4464 (2005).
Dolling, G., Enkrich, C., Wegener, M., Soukoulis, C. M. & Linden, S. Simultaneous negative phase and group velocity of light in a metamaterial. Science 312, 892–894 (2006).
Rousse, A. et al. Non-thermal melting in semiconductors measured at femtosecond resolution. Nature 410, 65–68 (2001).
Greiner, M., Mandel, O., Esslinger, T., Hansch, T. W. & Bloch, I. Quantum phase transition from a superfluid to a Mott insulator in a gas of ultracold atoms. Nature 415, 39–44 (2002).
Siwick, B. J., Dwyer, J. R., Jordan, R. E. & Miller, R. J. D. An atomic-level view of melting using femtosecond electron diffraction. Science 302, 1382–1385 (2003).
Shigekawa, H., Takeuchi, O. & Aoyama, M. Development of femtosecond time-resolved scanning tunneling microscopy for nanoscale science and technology. Sci. Technol. Adv. Mater. 6, 582–588 (2005).
Damascelli, A. et al. Fermi surface, surface states, and surface reconstruction in Sr2RuO4 . Phys. Rev. Lett. 85, 5194–5197 (2000).
Szymanski, P., Garrett-Roe, S. & Harris, C. B. Time- and angle-resolved two-photon photoemission studies of electron localization and solvation at interfaces. Prog. Surf. Sci. 78, 1–39 (2005).
Acknowledgements
We thank M. Bonn for helpful discussions.
This work is part of the research program of the ‘Stichting voor Fundamenteel Onderzoek der Materie (FOM)’, which is financially supported by the ‘Nederlandse organisatie voor Wetenschappelijk Onderzoek (NWO)’.
Author information
Authors and Affiliations
Contributions
Y.S., N.I. and K.A. provided the sample. R.J.P.E. carried out the near-field measurements. R.J.P.E., H.G. and L.K. carried our the k-space analysis. R.J.P.E., Y.S., K.A. and L.K. planned the project. All authors contributed in discussions.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
About this article
Cite this article
Engelen, R., Sugimoto, Y., Gersen, H. et al. Ultrafast evolution of photonic eigenstates in k-space. Nature Phys 3, 401–405 (2007). https://doi.org/10.1038/nphys576
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys576
This article is cited by
-
Direct quantification of topological protection in symmetry-protected photonic edge states at telecom wavelengths
Light: Science & Applications (2021)
-
Imaging gigahertz zero-group-velocity Lamb waves
Nature Communications (2019)
-
Strong beaming of microwave surface waves with complementary split-ring-resonator arrays
Scientific Reports (2018)
-
Direct observation of negative-index microwave surface waves
Scientific Reports (2016)
-
A phased antenna array for surface plasmons
Scientific Reports (2016)