Abstract
The transformation of liquid water to solid ice is typically a slow process. To cool a sample below the melting point requires some time, as does nucleation from the metastable liquid1, so freezing usually occurs over many seconds2. Freezing conditions can be created much more quickly using isentropic compression techniques, which provide insight into the limiting timescales of the phase transition. Here, we show that water rapidly freezes without a nucleator under sufficient compression, establishing a practical limit for the metastable liquid phase. Above 7 GPa, compressed water completely transforms to a high-pressure phase within a few nanoseconds. The consistent observation of freezing with different samples and container materials suggests that the transition nucleates homogeneously. The observation of complete freezing on these timescales further implies that the liquid reaches a hypercooled state3.
Similar content being viewed by others
Main
Computational studies suggest that freezing can occur on 0.1–1 ns timescales, although for water such simulations require a highly confined geometry4 and/or strong electric fields5,6. Unconfined simulations of supercooled water7 indicate that freezing is possible on 100 ns timescales, many times faster than experimental observations. Simply cooling a liquid on that timescale is challenging: 107–1010 K s−1 cooling rates can be achieved by spraying droplets into a cryogen8, but it is difficult to carry out real-time measurements. The fastest real-time observation of freezing in expansion-cooled water clusters occurred on 10–30 μs timescales9, leaving a 2–3 decade gap between the experimental and computational studies of freezing.
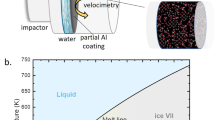
Adiabatic compression is an alternative route to solidification, even though liquids become hotter in the process. Temperature increase can be mitigated by using isentropic (rather than single shock wave) compression techniques, yielding the coldest possible adiabatic state. As shown in Fig. 1, isentropic compression of liquid water crosses the melt line between 2 and 3 GPa (T≈400 K). Although compression freezing involves a different portion of the phase diagram than cooling (ice VII (ref. 10) rather than ice Ih), freezing conditions are created very quickly, providing insight into the limiting phase-transition timescales. When liquid water is isentropically compressed above 2 GPa in the presence of a quartz or fused-silica window, freezing will be observed over 10–100 ns timescales11,12. The phase transition quickens with increasing pressure, but only in the presence of a silica window. Even at 5 GPa, where the liquid is nearly 70 K below the equilibrium melt line, no freezing is observed during compression within sapphire windows (≈800 ns experiment duration).
Solidification is characterized by two basic events: the onset and the completion of freezing. The onset of freezing is defined by the time needed to create freezing conditions (whether by cooling or compression), the nucleation time and a short growth period to permit detection; complete freezing occurs when the entire sample is transformed and depends on the growth dynamics of the solid phase. In classical nucleation theory13, the nucleation time is given by:

where Δg is the Gibb’s free-energy difference between liquid and solid phases, V is the sample volume and J0 and B are parameters specific to the nucleation process (for example, embryo shape). For systems lacking heterogeneous nucleation sites, a relevant issue is whether thermodynamic conditions approach the minimum nucleation time. In highly metastable states (large Δg), the limiting transition time is governed by homogeneous nucleation. Numerical simulations7 show ultrafast homogeneous nucleation in cooled water—can a similar phenomenon be observed experimentally in compressed water? A secondary question is whether such freezing reaches completion in the short duration (<1,000 ns) of an isentropic compression. These questions are addressed through multiple-shock and ramp-wave compression experiments, which mimic the isentrope shown in Fig. 1 and lead to freezing conditions in less than 100 ns.
Multiple-shock compression experiments use the plate-impact configuration shown in Fig. 2a. After impact, a right-going shock wave in the front window travels to the water sample (backed by an identical rear window), leading to a series of wave reflections. Results from three multiple shock-compression experiments are shown in Fig. 2b. The lowest stress experiment, SWS4 (5.2 GPa peak), shows an ideal stepwise compression of the water sample, indicating that no transition occurred (as in previous work11,12). Higher stress experiments, SWS3 and SWS1 (8.2 and 12.6 GPa peak, respectively), show a stress release during multiple-shock compression. Unlike heterogeneously nucleated freezing12, the final stress measured in the high-pressure experiments equals the impact stress. Reaching this state, where the interface moves at half the impact velocity, indicates that the phase-transition dynamics are complete. Note that the transition occurs on shocks that take water beyond 7 GPa, regardless of the peak state.
a, The impact of a sapphire impactor (IM) on the front window (FW) generates an initial shock wave. This wave travels to the water sample (S) and rear window (RW), compressing the sample (initially 0.1–0.3 mm thick) in stages. b, Stress history at the water–window interface. The dashed line indicates the prompt transition threshold near 7 GPa, whereas the dot–dash line indicates where liquid water becomes metastable.
Ramp-wave compression experiments use a continuous magnetic drive generated by an intense current pulse (10 MA, 500 ns duration) from the Sandia Z machine14. The complete experiment involves a rectangular coaxial transmission line containing multiple liquid samples; Fig. 3a illustrates a sample along one cardinal direction. Four interface stress histories from experiment Z1580 are shown in Fig. 3b. The north panel of this experiment contained hexane as a control liquid, as this material is known to remain a liquid under large compressions (evident from the smooth wave profile). The remaining panels contained water, each showing a stress release near 7 GPa. As described in the Methods section, this release indicates the transformation to a denser solid, such as ice VII (the thermodynamically favourable phase). The west and south panels used single-crystal sapphire windows, whereas the east panel contained single-crystal cubic zirconia windows. As the transition is nearly identical in both cases, the transformation apparently does not require a specific window surface for heterogeneous nucleation.
a, Current from the Sandia Z machine generates continuous stress waves in a thin liquid sample (≈0.02 mm) confined between transparent windows (FW and RW). b, Interface stress histories for isentropically compressed water and hexane (experiment Z1580). The abbreviations indicate the sample (water, W, or hexane, H) and window (sapphire, S, or cubic zirconia, CZ) materials. The dashed line indicates the prompt transition threshold near 7 GPa, whereas the dash–dot line indicates the pressure at which liquid water becomes metastable. The plots have been time shifted by 50 ns for visual clarity; actual compressions are nearly coincident.
In both multiple-shock and ramp-wave compression experiments, there is no detectable incubation period in the transformation beyond 7 GPa, that is, the metastable period is shorter than the diagnostic time resolution (0.2–0.5 ns in ramp-wave experiments). The rapid transition onset is not surprising given the nonlinear nucleation rate (equation (1)), and suggests the homogeneous nucleation limit has been reached. Homogeneous nucleation occurs 30–40 K (ref. 15) below the ice Ih melt line at ambient pressure and 70 K (ref. 16) below the ice III melt line at modest pressures. In comparison, isentropic compression to 7 GPa brings liquid water nearly 120 K below the ice VII boundary. This compression is applied over 100–200 ns, which is conceptually equivalent to an isobaric cooling rate of 108–109 K s−1 at 7 GPa. Such a cooling rate would be comparable to high-pressure jet freezing studies8. Our experiments reveal the nucleation of a high-pressure ice phase (most likely ice VII) in a first-order phase transition, rather than vitrification of the compressed liquid (see the Methods section).
As liquid water and ice have different refractive indices, the coexistence of the two phases leads to optical scattering and a loss of transparency. Figure 4 shows a double-pass transmission measurement along with the interface stress on the same panel (Z1580 west). During that experiment, the water sample experienced a transient opacity: over the course of approximately 4 ns, transmission dropped by nearly 11% before returning to its original value. This timescale closely matches the peak–trough time in the VISAR (velocity interferometer system for any reflector) measurement, indicating that the two phenomena are linked. Transient opacity was never observed in heterogeneously nucleated freezing11, but was found in high-pressure single-pass transmission measurements using sapphire windows17. No direct stress measurements were made in the previous work, but wave propagation simulations suggested that opacity loss corresponded to compression beyond 8 GPa. A 20% single-pass transmission drop was observed for an initially 0.100-mm-thick water sample, whereas an 11% double-pass drop (Fig. 4) was observed for a 0.025-mm-thick sample in this study. If optical scatterers span the entire sample during the point of minimum transmission, then sample thickness must scale directly with the measured extinction ratio:

where the factor of two accounts for the extra sample transit in a double-pass transmission measurement. This scaling holds between the two measurements, indicating that scattering spans the sample in both cases. The subsequent return of transparency indicates that these scattering sites disappear shortly after peak opacity, a sign that the material has left the mixed phase and become a pure solid.
Optical imaging studies11 of heterogeneously nucleated compression freezing indicate that large portions of a water sample may remain liquid while adjacent regions solidify. Once freezing begins, latent heat dissipation brings adjacent liquid regions to the melting temperature, which leads to decreasing solidification-front velocities in one dimension18 and growth instabilities in higher dimensions19. From a continuum viewpoint17, complete freezing along an isentrope is difficult (and in some cases, impossible) because the compression has a non-zero slope in pressure–volume space. However, the return of optical transparency observed in this work, along with the fact that multiple shock experiments reach the impact stress, indicates that complete freezing takes place above 7 GPa. The apparent contradiction can be explained if isentropic states beyond 7 GPa are hypercooled3. Hypercooling describes metastable states where latent heat emission is insufficient to bring the liquid phase to the melting temperature, so solidification is not substantially limited by latent heat dissipation. As such, it is possible for a single nucleation event to rapidly span the liquid sample, or for multiple nucleation events to coalesce without competition (unlike Ostwald ripening20, where large crystals grow at the expense of smaller ones). Certain equations of state for water may not yield hypercooling in this or any other domain (the model in ref. 12 does not), so the observation of complete freezing provides an important constraint in continuum modelling.
In summary, there is direct experimental evidence of ultra-rapid freezing in water. Under isentropic compression to 7 GPa (starting from ambient conditions), water undergoes a first-order phase transition within a few nanoseconds. Unlike previous reports of compression freezing, no obvious nucleation agent is required for this transition, although trace impurities not removed by standard purification techniques cannot be ruled out entirely (see the Methods section). The fast dynamics of the transition are compatible with the timescales of molecular dynamics simulations, and may serve as a benchmark for future computational studies of freezing in compressed liquids. Once initiated, the transition reaches complete solidification very quickly. The formation of a pure solid has important thermodynamic implications, and may be an indication of a hypercooled growth process. The observation of freezing on such short timescales is important in the emerging study of dynamic compression freezing, where solidification has been reported in numerical studies21 but experimental verification is lacking. The high-pressure phase diagram of water can be simulated with the TIP4P potential22, but it remains to be seen whether molecular dynamics simulations indicate ultrafast compression freezing.
Methods
The isentrope shown in Fig. 1 is calculated from an equation of state developed in ref. 12. Briefly, the model defines the Helmholtz free energy, f(T,v), for the liquid state from a constant specific heat, a high-pressure isotherm and the Hugoniot curve. Wave-propagation calculations using this model verify that multiple-shock compression of liquid water closely approximates isentropic compression.
The interface stresses shown in Figs 2 and 3 are calculated from the apparent velocity obtained by VISAR23 measurements. The actual velocity is determined by applying a window-specific correction to the measurements. For sapphire (HEMEX grade, c orientation), the correction is well known24; the correction for cubic zirconia (〈100〉 optical grade) was determined in separate experiments to be 1.84, and will be described in a future publication. The interface velocity was calculated from the Hugoniot curves of sapphire25 and cubic zirconia26.
Stress release (as shown in Figs 2 and 3) indicates that the water samples undergo a first-order phase transition. This statement follows from the fact that first-order transitions are accompanied by a discontinuous density change, which leads to a velocity (and hence stress) decrease on the rear surface. The argument can be formalized via mass and momentum conservation12, but may also be understood through an intuitive comparison of contraction and expansion. During the experiment, rear surface stress increases owing to the drive (multiple shock or ramp wave). If the sample undergoes an expansive phase transition during this time, an additional rear surface stress is applied in the same direction as the drive, causing the measured stress to increase. By the same logic, a contracting phase transition will decrease measured stress at the rear window interface. The observation of stress release is an indication of volume decrease (in addition to the overall compression), and the sample must therefore be undergoing a first-order phase transition.
Strictly speaking, the results of this work represent the experimental limit for metastable water, which could be due to heterogeneous nucleation in the sample bulk rather than homogeneous nucleation. To minimize the probability of heterogeneous nucleation, all experiments used environmental grade water (Fisher Scientific), which has a high electrical resistivity (≥20 MΩ cm at the time of bottling) and a low organic content (≤20 p.p.b.). The consistency of this work with earlier studies17 using freshly deionized/filtered/distilled water suggests that heterogeneous nucleators, if present, are not removed by standard water purification techniques. No purification technique can completely remove all bulk contamination27, so focus must be placed on the impurities known to induce freezing. However, predicting whether a material is a good ice nucleator is not a trivial matter, despite many decades of research28. Certain organics are known to enhance the formation of high-pressure ice phases29, but the effect of trace impurities is unknown.
References
Debenedetti, P. Metastable Liquids (Princeton Univ. Press, Princeton, 1996).
Heneghan, A. & Haymet, A. Liquid-to-crystal nucleation: a new generation lag-time apparatus. J. Chem. Phys. 117, 5319–5327 (2002).
Alexiades, V. & Solomon, A. Mathematical Modeling of Melting and Freezing Processes (Hemisphere Publishing, Washington, 1993).
Koga, K., Zeng, X. & Tanaka, H. Freezing of confined water: A bilayer ice phase in hydrophobic nanopores. Phys. Rev. Lett. 79, 5262–5265 (1997).
Svishchev, I. & Kusalik, P. Crystallization in liquid water in a molecular dynamics simulation. Phys. Rev. Lett. 73, 975–978 (1994).
Xia, X. & Berkowitz, M. Electric-field induced restructuring of water at a platinum-water interface: A molecular dynamics computer simulation. Phys. Rev. Lett. 74, 3193–3196 (1995).
Matsumoto, M., Saito, S. & Ohmine, I. Molecular dynamics simulation of the ice nucleation and growth processes leading to water freezing. Nature 416, 409–413 (2002).
Mayer, E. & Bruggeller, P. Vitrification of pure liquid water by high pressure jet freezing. Nature 298, 715–718 (1982).
Bartell, L. Nucleation rates in freezing and solid-state transitions. Molecular clusters as model systems. J. Phys. Chem. 99, 1080–1089 (1995).
Bridgman, P. Phase diagram of water to 45,000 kg/cm2. J. Chem. Phys. 5, 964–966 (1937).
Dolan, D. & Gupta, Y. Nanosecond freezing of water under multiple shock wave compression: Optical transmission and imaging measurements. J. Chem. Phys. 121, 9050–9057 (2004).
Dolan, D., Johnson, J. & Gupta, Y. Nanosecond freezing of water under multiple shock wave compression: Continuum modeling and wave profile measurements. J. Chem. Phys. 123, 64702 (2005).
Walton, A. in Nucleation (ed. Zettlemoyer, A.) (Marcel Dekker, New York, 1969).
Reisman, D. B. et al. Magnetically driven isentropic compression experiments on the Z accelerator. J. Appl. Phys. 89, 1625–1633 (2001).
Hare, D. & Sorensen, C. The density of supercooled water. II. Bulk samples cooled to the homogeneous nucleation limit. J. Chem. Phys. 87, 4840–4845 (1987).
Kanno, H., Speedy, R. & Angell, C. Supercooling of water to −92 ∘C under pressure. Science 189, 880–881 (1975).
Dolan, D. Time Dependent Freezing of Water Under Multiple Shock Compression. Thesis, Washington State Univ. (2003).
Carslaw, H. & Jaeger, J. Conduction of Heat in Solids 2nd edn (Oxford Univ. Press, Oxford, 1959).
Langer, J. Instabilities and pattern formation in crystal growth. Rev. Mod. Phys. 52, 1–28 (1980).
Boistelle, B. & Astier, J. Crystallization mechanisms in solution. J. Cryst. Growth 90, 14–30 (1988).
Streitz, F., Glosli, J. & Patel, M. Beyond finite-size scaling in solidification simulations. Phys. Rev. Lett. 96, 225701 (2006).
Sanz, E., Vega, C., Abascal, J. F. & MacDowell, L. Phase diagram of water from computer simulation. Phys. Rev. Lett. 92, 255701 (2004).
Barker, L. & Hollenbach, R. Laser interferometer for measuring high velocities of any reflecting surface. J. Appl. Phys. 43, 4669–4675 (1972).
Jones, S., Robinson, M. & Gupta, Y. Ordinary refractive index of sapphire in uniaxial tension and compression along the c axis. J. Appl. Phys. 93, 1023–1031 (2003).
Barker, L. & Hollenbach, R. Shock-wave studies of PMMA, fused silica, and sapphire. J. Appl. Phys. 41, 4208–4226 (1970).
Mashimo, T., Nakamura, A. & Kodama, M. Yielding and phase transition under shock compression of yttria-doped cubic zirconia single crystal and polycrystal. J. Appl. Phys. 77, 5060–5068 (1995).
Smith, V. in Ultrapurity: Methods and Techniques (eds Zief, M. & Speights, R.) (Marcel Dekker, New York, 1972).
Conrad, P., Ewing, G., Karlinsey, R. & Sadtchenko, V. Ice nucleation on BaF2(111). J. Chem. Phys. 122, 64709 (2005).
Evans, L. Selective nucleation of the high-pressure ices. J. Appl. Phys. 38, 4930–4932 (1967).
Pistorius, C., Rapoport, E. & Clark, J. Phase diagrams of H2O and D2O at high pressures. J. Chem. Phys. 48, 5509–5514 (1968).
Acknowledgements
The authors would like to thank the crew of the Sandia STAR and Z facilities for their contributions in the design, fabrication and assembly of the experiments, as well as the fielding of the VISAR and optical transmission diagnostics. P. G. Debenedetti is also acknowledged for his helpful discussions. Sandia is a multiprogram laboratory operated by Sandia Corporation, a Lockheed Martin Company, for the United States Department of Energy’s National Nuclear Security Administration under contract DE-AC04-94AL85000.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
About this article
Cite this article
Dolan, D., Knudson, M., Hall, C. et al. A metastable limit for compressed liquid water. Nature Phys 3, 339–342 (2007). https://doi.org/10.1038/nphys562
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys562
This article is cited by
-
Melting domain size and recrystallization dynamics of ice revealed by time-resolved x-ray scattering
Nature Communications (2023)
-
Real-time latent heat emission during dynamic-compression freezing of water
Communications Physics (2023)
-
Fast crystal growth of ice VII owing to the decoupling of translational and rotational ordering
Communications Physics (2023)
-
X-ray free electron laser heating of water and gold at high static pressure
Communications Materials (2021)
-
Anelasticity and Phase Transition During Ramp-Release in Tin
Journal of Dynamic Behavior of Materials (2021)