Abstract
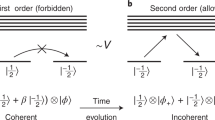
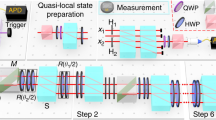
The modern concept of phases of matter has undergone tremendous developments since the first observation of topologically ordered states in fractional quantum Hall systems in the 1980s. In this paper, we explore the following question: in principle, how much detail of the physics of topological orders can be observed using state of the art technologies? We find that using surprisingly little data, namely the toric code Hamiltonian in the presence of generic disorders and detuning from its exactly solvable point, the modular matrices—characterizing anyonic statistics that are some of the most fundamental fingerprints of topological orders—can be reconstructed with very good accuracy solely by experimental means. This is an experimental realization of these fundamental signatures of a topological order, a test of their robustness against perturbations, and a proof of principle—that current technologies have attained the precision to identify phases of matter and, as such, probe an extended region of phase space around the soluble point before its breakdown. Given the special role of anyonic statistics in quantum computation, our work promises myriad applications both in probing and realistically harnessing these exotic phases of matter.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
References
Landau, L. D. Theory of phase transformations. Phys. Zs. Sowjet. 11, 26 (1937).
Ginzburg, V. L. & Landau, L. D. On the theory of superconductivity. J. Exp. Eheor. Phys. 20, 1064–1082 (1950).
Wen, X. G. Topological orders in rigid states. Int. J. Mod. Phys. B. 4, 239–271 (1990).
Wen, X. G. Quantum Field Theory of Many-Body Systems (Oxford Univ. Press, 2004).
Wen, X. G. & Niu, Q. Ground-state degeneracy of the fractional quantum Hall states in the presence of a random potential and on high-genus Riemann surfaces. Phys. Rev. B 41, 9377–9396 (1990).
Chen, X., Gu, Z. C. & Wen, X. G. Local unitary transformation, long-range quantum entanglement, wave function renormalization, and topological order. Phys. Rev. B. 82, 155138 (2010).
Tsui, D. C., Stormer, H. L. & Gossard, A. C. Two-dimensional magnetotransport in the extreme quantum limit. Phys. Rev. Lett. 48, 1559–1562 (1982).
Kitaev, A. & Preskill, J. Topological entanglement entropy. Phys. Rev. Lett. 96, 110404 (2006).
Jiang, H. C., Wang, Z. H. & Balents, L. Identifying topological order by entanglement entropy. Nat. Phys. 8, 902–905 (2012).
Keski-Vakkuri, E. & Wen, X. G. Ground state structure of hierarchical QH states on torus and modular transformation. Int. J. Mod. Phys. B. 07, 4227–4259 (1993).
Wen, X. G. Modular transformation and bosonic/fermionic topological orders in Abelian fractional quantum Hall states. Preprint at http://arXiv.org/abs/1212.5121 (2012).
Zhang, Y., Grover, T., Turner, A., Oshikawa, M. & Vishwanath, A. Quasiparticle statistics and braiding from ground-state entanglement. Phys. Rev. B. 85, 235151 (2012).
Zaletel, M. P., Mong, R. S. K. & Pollmann, F. Topological characterization of fractional quantum Hall ground states from microscopic hamiltonians. Phys. Rev. Lett. 110, 236801 (2013).
Bonderson, P., Shtengel, K. & Slingerland, J. K. Probing non-Abelian statistics with quasiparticle interferometry. Phys. Rev. Lett. 97, 016401 (2006).
Cincio, L. & Vidal, G. Characterizing topological order by studying the ground states on an infinite cylinder. Phys. Rev. Lett. 110, 067208 (2013).
Mei, J. W. & Wen, X. G. Modular matrices from universal wave-function overlaps in Gutzwiller-projected parton wave functions. Phys. Rev. B 91, 125123 (2015).
Moridi, H. & Wen, X. G. Universal wave-function overlap and universal topological data from generic gapped ground states. Phys. Rev. Lett 115, 036802 (2015).
Liu, F. Z., Wang, Z. H., You, Y. Z. & Wen, X. G. Modular transformations and topological orders in two dimensions. Preprint at http://arXiv.org/abs/1303.0829v2 (2014).
Li, K. et al. Experimental identification of non-Abelian topological orders on a quantum simulator. Phys. Rev. Lett. 118, 080502 (2017).
Jiang, S. H., Mesaros, A. & Ran, Y. Generalized modular transformations in (3+1)D topologically ordered phases and triple linking invariant of loop braiding. Phys. Rev. X. 4, 031048 (2014).
He, H., Moradi, H. & Wen, X. G. Modular matrices as topological order parameter by gauge symmetry preserved tensor renormalization approach. Phys. Rev. B 90, 205114 (2014).
Mei, J. W., Chen, J. Y., He, H. & Wen, X. G. SU(2) spin-rotation symmetric tensor network state for spin-1/2 Heisenberg model on kagome lattice and its modular matrices. Phys. Rev. B 95, 235107 (2017).
Bridgeman, J. C., Flammia, S. T. & Poulin, D. Detecting topological order with ribbon operators. Phys. Rev. B. 94, 205123 (2016).
Kitaev, A. Fault-tolerant quantum computation by anyons. Ann. Phys. (N. Y.) 303, 2–30 (2003).
Trebst, S., Werner, P., Troyer, M., Shtengel, K. & Nayak, C. Breakdown of a topological phase: quantum phase transition in a loop gas model with tension. Phys.Rev. Lett. 98, 070602 (2007).
Dusuel, S., Kamfor, M., Orus, R., Schmidt, K. P. & Vidal, J. Robustness of a perturbed topological phase. Phys. Rev. Lett. 106, 107203 (2011).
Wen, X. G. Quantum orders in an exact soluble model. Phys. Rev. Lett. 90, 016803 (2003).
Ryan, C. A., Negrevergne, C., Laforest, M., Knill, E. & Laflamme, R. Liquid-state nuclear magnetic resonance as a testbed for developing quantum control methods. Phys. Rev. A. 78, 012328 (2008).
Feynman, R. P. Simulating physics with computers. Int. J. Theor. Phys. 21, 467–488 (1982).
Shankar, R., Hegde, S. S. & Mahesh, T. S. Quantum simulation of a particle in one-dimensional potentials using NMR. Phys. Lett. A. 378, 10–15 (2014).
Dong, R. Y. Nuclear Magnetic Resonance of Liquid Crystals (Springer, 1997).
Luo, Z. H. et al. Experimental preparation of topologically ordered states via adiabatic evolution. Preprint at http://arXiv.org/abs/1608.06963v1 (2016).
Peng, X. H. et al. Preparation of pseudo-pure states by line-selective pulses in nuclear magnetic resonance. Chem. Phys. Lett. 340, 509–516 (2001).
Messiah, A. Quantum Mechanics (Wiley, 1976).
Hamma, A. & Lidar, D. A. Adiabatic preparation of topological order. Phys. Rev. Lett. 100, 030502 (2008).
Rowell, E., Stong, R. & Wang, Z. H. On classification of modular tensor categories. Comm. Math. Phys. 292, 343–389 (2009).
Vandersypen, L. M. et al. Experimental realization of Shor’s quantum factoring algorithm using nuclear magnetic resonance. Nature 414, 883–887 (2001).
Acknowledgements
We thank X. Wen and B. Zeng for helpful discussions. This work is supported National Key Basic Research Program of China (Grant No. 2013CB921800 and No. 2014CB848700), the National Science Fund for Distinguished Young Scholars (Grant No. 11425523), the National Natural Science Foundation of China (Grants No. 11375167, No. 11227901, No. 11575173, and No. 91021005), the Strategic Priority Research Program (B) of the CAS (Grant No. XDB01030400) and Key Research Program of Frontier Sciences of the CAS (Grant No. QYZDY-SSW-SLH004). Y.W. acknowledges support from the John Templeton foundation No. 39901. This research was supported in part by Perimeter Institute for Theoretical Physics. Research at Perimeter Institute is supported by the Government of Canada through the Department of Innovation, Science and Economic Development Canada and by the Province of Ontario through the Ministry of Research, Innovation and Science. Y.W. is also supported by the Shanghai Pujiang Program Grant No. KBH 1512328. L.-Y.H. would like to acknowledge support by the Thousand Young Talents Program, and Fudan University.
Author information
Authors and Affiliations
Contributions
X.P. initiated the project. L.-Y.H. and Y.W. formulated the theory. X.P. and Z.L. designed the experiment. Z.L. and L.-Y.H. performed the calculation. Z.L. carried out the experiment and analysed the data. X.P. and J.D. supervised the experiment. Z.L. and L.-Y.H. wrote the draft. All authors contributed to discussing the results and writing the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 2050 kb)
Rights and permissions
About this article
Cite this article
Luo, Z., Li, J., Li, Z. et al. Experimentally probing topological order and its breakdown through modular matrices. Nat. Phys. 14, 160–165 (2018). https://doi.org/10.1038/nphys4281
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys4281
This article is cited by
-
Symmetry fractionalized (irrationalized) fusion rules and two domain-wall Verlinde formulae
Journal of High Energy Physics (2024)
-
Noisy intermediate-scale quantum computers
Frontiers of Physics (2023)
-
Experimental quantum simulation of superradiant phase transition beyond no-go theorem via antisqueezing
Nature Communications (2021)
-
Circuit-based digital adiabatic quantum simulation and pseudoquantum simulation as new approaches to lattice gauge theory
Journal of High Energy Physics (2020)
-
Quantum simulation of the non-fermi-liquid state of Sachdev-Ye-Kitaev model
npj Quantum Information (2019)