Abstract
Quantum mechanics and Coulomb interaction dictate the behaviour of small circuits. The thermal implications cover fundamental topics from quantum control of heat to quantum thermodynamics, with prospects of novel thermal machines and an ineluctably growing influence on nanocircuit engineering1,2. Experimentally, the rare observations thus far include the universal thermal conductance quantum3,4,5,6,7 and heat interferometry8. However, evidence for many-body thermal effects paving the way to markedly different heat and electrical behaviours in quantum circuits remains wanting. Here we report on the observation of the Coulomb blockade of electronic heat flow from a small metallic circuit node, beyond the widespread Wiedemann–Franz law paradigm. We demonstrate this thermal many-body phenomenon for perfect (ballistic) conduction channels to the node, where it amounts to the universal suppression of precisely one quantum of conductance for the transport of heat, but none for electricity9. The inter-channel correlations that give rise to such selective heat current reduction emerge from local charge conservation, in the floating node over the full thermal frequency range (≲temperature × kB/h). This observation establishes the different nature of the quantum laws for thermal transport in nanocircuits.
Similar content being viewed by others
Main
The non-interacting ‘scattering’ approach to quantum transport describes coherent conductors as a set of independent channels10,11. However, in circuits with small floating nodes, the Coulomb interaction induces inter-channel correlations, including among distinct conductors connected to the same node. Consequences are wide-ranging, from the emblematic ‘Coulomb blockade’ suppression of electrical conduction at low voltages and temperatures12,13,14,15 to exotic ‘charge’ Kondo physics16,17. Remarkably, Coulomb effects can be profoundly different in the charge and heat sectors, in violation of the standard Wiedemann–Franz ratio between electronic conductances of heat and electricity (π2kB2T/3e2 with e the elementary electron charge, kB the Boltzmann constant, T the temperature). For ballistic conductors, along which electrons are never reflected backward, the electrical conductance Gelec is predicted18,19,20 and found21,22,23 immune against Coulomb blockade, essentially because charge flow is noiseless (Gelec = N × GQe, with N the number of channels, GQe = e2/h the electrical conductance quantum and h the Planck constant). Nonetheless, theory predicts9 a universal suppression of the heat conductance Gheat across ballistic conductors connected to a small, floating circuit node by precisely one quantum of thermal conductance GQh = π2kB2T/3h (Gheat = (N − 1) × GQh), as presently observed experimentally.
This violation of the Wiedemann–Franz relation does not result from an energy-dependent electronic density of states, or from the high-pass energy filtering across single electron transistors24,25. We describe the underlying mechanism in the spirit of ref. 9, specifically focusing on a metallic node connected to large voltage-biased electrodes through a total of N ballistic channels (Fig. 1a, b). Electronic heat currents can be viewed as the propagation of electrical current fluctuations within a broad frequency bandwidth, extending up to the thermal cutoff ∼kBT/h. For voltage-biased electrodes, the emitted fluctuations result from the thermal broadening of the electron Fermi distribution. For a floating circuit node, charge conservation imposes that the thermal emission of a net charge through a current pulse is accompanied by an opposite charge accumulation in the node. Since the node charge relaxes in the characteristic RC time (with R = 1/NGQe here, and C the node geometrical capacitance), the overall (net) charge fluctuations emitted from the node (thermal plus subsequent relaxation) are suppressed at frequencies below ∼1/RC. At low temperature kBT ≪ h/RC (kBT ≪ NEC here, with EC ≡ e2/2C the node charging energy), where this suppression covers the full thermal frequency range, it can result in an important reduction of the total heat current. Note that the electrical fluctuations emitted from such a floating node were previously explored in the context of using a ‘voltage probe’ to emulate inelastic mechanisms within the scattering theory of quantum transport (see, for example, ref. 26 and references within). An intuitive way to understand why, for ballistic conductors this reduction amounts universally to one heat transport channel, is to note9 that N ballistic electronic channels can be mapped onto a single charge mode (for example, identical current fluctuations on all electronic channels) and N − 1 independent neutral modes (for example, opposite current fluctuations on each of N − 1 pairs of electronic channels), as schematically illustrated Fig. 1b. The N − 1 ballistic neutral modes are completely decoupled from the global charge of the island, and therefore contribute each by one (universal) quantum of thermal conductance GQh. In contrast, the electrical current fluctuations propagating along the single charge mode are directly connected with fluctuations of the node’s charge. Negligible charge accumulation in the node for frequencies ≲kBT/h therefore completely blocks the charge mode and suppresses its contribution to heat transport, resulting in Gheat = (N − 1) × GQh.
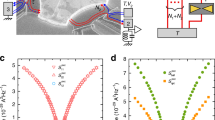
a, Device micrograph. A small metallic island (brighter) is in galvanic contact with three distinct branches of a 2DEG (darker grey; etched trenches visible underneath the island). The connection to large electrodes further away (represented by rectangles for branches 1 and 2) is controlled by the field effect using capacitively coupled gates (grey with a bright delimitation). The sample is set in the integer quantum Hall regime at filling factor ν = 2, where the current propagates along two chiral edge channels (lines with arrows). In the displayed configuration, electrodes 1, 2 and 3 are connected by, respectively, one, two and zero fully transmitted channels (N1 = 1, N2 = 2, N3 = 0). Applying a d.c. bias voltage V to electrode 1 dissipates the Joule power PJ into the island. The resulting temperature rise TΩ − T is determined from the measured increase of electrical fluctuations on electrode D. b, Heat flow schematic. Injected power and net outgoing heat current exactly compensate each other (PJ = Jheatel + Jheatph). The N ballistic electronic channels (here N = 3 shown as black lines) can be mapped onto one channel-symmetric charge mode suppressed by the heat Coulomb blockade (crossed symmetric charge pulses), and N − 1 independent dipole modes decoupled from the island’s charge (antisymmetric charge pulses).
The experiment expands on an approach introduced to measure the thermal conductance quantum across electronic channels5. In contrast to previous works5,6, the present implementation down to electronic temperatures of 8 mK (Methods) allows for the direct observation of the heat Coulomb blockade, which requires that energy transfers between electrons and phonons in the node remain negligible with respect to those through one ballistic channel. The device consists of a central metallic island (the circuit node, see Fig. 1a) separately connected to three large electrodes indexed by i ∈ {1,2,3} through, respectively, Ni ballistic quantum channels (N = N1 + N2 + N3). A Joule power PJ = V2GP/2 controlled by the d.c. voltage V applied to electrode 1 dissipates into the electronic fluid within the island (the remaining voltage generator power going into the large electrodes, see Methods), with electrodes 2 and 3 being grounded and GP the corresponding conductance across the device (here, GP = GQe/[N1−1 + (N2 + N3)−1]). As a result, the metallic island heats up to a steady-state electronic temperature TΩ > T (with T the base electronic temperature), such that PJ and net outgoing heat flow Jheat exactly compensate (PJ = Jheat). The determination of TΩ through thermal noise measurements therefore directly provides the Jheat–(TΩ − T) characteristics. In general, Jheat is the sum of different contributions, including mainly the electronic heat current Jheatel(N, TΩ, T) and thermal transfers to the substrate phonons Jheatph(TΩ, T): Jheat ≃ Jheatel + Jheatph. However, at TΩ < 20 mK, the rapidly decreasing energy transfers toward phonons are found to become negligible such that PJ = Jheat ≃ Jheatel.
The ballistic electronic channels are realized in a high-mobility Al(Ga)As two-dimensional electron gas (2DEG), tuned in the integer quantum Hall regime to the filling factor ν = 2 with an applied perpendicular magnetic field B ≃ 4.1 T. Without loss of generality, we benefit from the topologically protected ballistic character of the chiral quantum Hall channels (lines with arrows in Fig. 1a). With ν channels propagating along each edge, it is possible to adjust separately Ni ∈ {0,1,2} using the field effect. The device was tuned to N ∈ {2,3,4,5} with at least one ballistic channel connecting the central island to both the large electrodes 1 and 2 (N1 = 1, N2 ∈ {1,2} and N3 ∈ {0,1,2}, except for tests in Methods). The micrometre-scale metallic island, mainly composed of gold, is associated with a continuous electronic density of states and a charging energy EC ≃ kB × 0.3 K (Methods). By thermal annealing, we achieve negligible levels of electron reflection probability at the 2DEG/island interface, as detailed per channel in Methods. This is essential not only to reach the ballistic limit, but also because residual reflections would impede the noise thermometry through additional quantum shot noise. The electron temperature is obtained from electrical current fluctuations, resolved down to a statistical uncertainty of ±5 × 10−32 A2 Hz−1 at frequencies near 1 MHz, using a homemade preamplifier27 cooled to 3.9 K. Quantum shot-noise measurements provide the in situ calibrations of the noise amplification chain gain (±0.1%, all uncertainties and displayed error bars are statistical standard errors), and of the base electronic temperature T ≃ 8 mK (±1%, further confirmed by dynamical Coulomb blockade thermometry28, see Methods). At non-zero Joule power, the temperature increase (TΩ − T) of the metallic island electrons is directly connected to a rise in emitted current noise. In the spirit of the robust Johnson–Nyquist thermometry, the excess noise Sexc measured on the floating electrode D (Fig. 1a) with respect to the noise at V = 0 reads5,26,29: Sexc = 2GSkB(TΩ − T), with GS the electrical conductance across the device from electrode 2 to electrodes 1 and 3 (in absence of electrical Coulomb blockade, GS = GQe/[N2−1 + (N1 + N3)−1]). Note that further tests made to eliminate possible experimental artefacts are described in Methods.
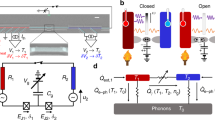
In Fig. 2a we show measurements of the excess noise spectral density Sexc (bottom-right inset) and of the conductances GS (left side of top-left inset) and GP (right side of top-left inset), all as a function of the d.c. voltage V applied to electrode 1. Each colour corresponds to one device configuration N [N1, N2, N3] ∈ {2 [1,1,0], 3 [1,1,1], 4 [1,1,2], 5 [1,2,2]}, with a colour code fixed from now on. The island heating is manifested in the increase of Sexc at finite V. In contrast, both GS and GP remain indistinguishable from their maximum quantum limit (respectively GQe/[N2−1 + (N1 + N3)−1] and GQe/[N1−1 + (N2 + N3)−1], displayed as thick ticks), independently of V. This demonstrates the absence of Coulomb blockade reduction of the electrical conductance across ballistic channels, at an experimental accuracy better than 0.1% (see also refs 21,22,23). Lines in the main panel of Fig. 2a represent, in a log–log scale, the electron temperature in the metallic island, TΩ, versus the injected Joule power PJ, with TΩ obtained from Sexc and the separately calibrated base temperature T ≃ 8.1 mK. As generally expected, TΩ is higher when there are fewer electronic channels to evacuate the dissipated PJ. Figure 2b displays as symbols the same data, as well as a subsequent run at T ≃ 8.0 mK, but now as the net heat flow Jheat = PJ versus TΩ2 − T2, and focusing on low temperatures (TΩ < 25 mK) where the phonon contribution Jheatph is reduced and where a full suppression of one electronic thermal channel is predicted9 (Methods). The straight dashed line closest to the data for N ballistic channels is (N − 1) × JQel, with JQel = π2kB2(TΩ2 − T2)/6h the quantum limit of heat flow per electronic channel. The mere observation that Jheat is well below predictions for N independent ballistic channels (N × JQel) directly demonstrates the specific suppression of heat transport from small circuit nodes, whereas electrical transport remains at the maximum quantum limit. Moreover, we find at such low temperatures a high-precision agreement with heat Coulomb blockade predictions for electronic heat flow, both in the quantitative prediction of a universal suppression of exactly one electronic channel whatever N and in the temperature power law ∝(TΩ2 − T2). This direct demonstration of heat Coulomb blockade in the absence of electrical Coulomb blockade constitutes the central result of the present work (see Methods for additional tests establishing the robustness of this observation).
a, The island electron temperature TΩ is plotted versus dissipated Joule power PJ, for different numbers N of connected ballistic channels. It is obtained from the excess noise spectral density Sexc measured electrode D, shown in the bottom-right inset versus the d.c. voltage V applied to electrode 1: TΩ = T + Sexc/(2kBGS), PJ = V2GP/2. Top-left inset: the device electrical conductances GS, P (lines, see text) match their expected quantum limited values (superimposed thick ticks on side axis) independently of V ; they are not reduced by Coulomb blockade. b, Symbols (statistical uncertainties shown when distinctly larger) represent the overall heat flow (Jheat = PJ) displayed versus TΩ2 − T2, at low temperatures where electron–phonon interactions are reduced (TΩ < 25 mK). The nearby straight dashed lines show (N − 1) × JQel, corresponding to a systematic heat current suppression of 1 × JQel.
Theory9 further predicts quantitatively a crossover of the electronic heat flow from (N − 1) × JQel to N × JQel, which extends mostly over one temperature decade around NEC/πkB (Methods). However, the relatively important and rapidly increasing thermal transfers between electrons and phonons at these higher temperatures prevent a direct observation from Jheat(TΩ). Following ref. 5, we separately consider the electronic heat current by focusing on the difference at the same value of TΩ between two numbers of connected ballistic channels (N ∈ {2,3,5} and Nref = 4). Indeed, any mechanism that does not depend on N cancels out in Jheat(N, T, TΩ) − Jheat(Nref, T, TΩ), including the electron–phonon contribution and the universal low-temperature suppression of one ballistic channel. However, signatures of the (N − 1) × JQel to N × JQel crossover can be observed since the temperature at which it takes place increases with N (Methods). Measurements of Jheat(N ∈ {2,3,5}, T, TΩ) − Jheat(Nref = 4, T, TΩ), normalized by the quantum limit of heat flow per channel JQel(T, TΩ), are shown as symbols versus TΩ in Fig. 3a. In this representation, deviations from N − Nref (N − 4, horizontal dashed lines) are specific signatures of the heat Coulomb blockade crossover. The quantitative prediction, without any fitting parameter, of the full heat Coulomb blockade theory (continuous lines, Methods) closely matches the data. For N − Nref = ±1 (N ∈ {3,5}, Nref = 4) the crossover signal is small, barely discernible at experimental accuracy, although in sign and magnitude agreement with predictions. For N − Nref = − 2 (N = 2, Nref = 4), the larger crossover signal precisely follows the theoretical prediction up to TΩ ≃ 60 mK, while at higher TΩ ≳ 60 mK the scatter of the data points rapidly increases due to the overwhelming (subtracted) electron–phonon contribution Jheatph. These observations further establish experimentally the full heat Coulomb blockade theory for ballistic channels at arbitrary temperatures, beyond the universal low-temperature suppression of one quantum channel.
a, Symbols (continuous lines) show the measured (predicted) heat current variation when changing N from Nref = 4 at fixed TΩ, renormalized by the quantum limit per channel JQel. The crossover toward the low-temperature heat Coulomb blockade of one ballistic channel specifically shows as a difference with respect to the nearby horizontal dashed line, whereas electron–phonon thermal transfers are cancelled out. b, Subtracting heat Coulomb blockade predictions, the displayed remaining part of the heat current (symbols; displayed error bars are statistical standard errors) collapses onto a single curve for all N ∈ {2,3,4,5}, fitted by a TΩ5.85 functional (line, Jheatph). Inset: direct comparison between Jthyel + Jheatph (black continuous lines) and measured total heat current Jheat (superimposed coloured dashed lines).
We now investigate the additional heat transfer mechanisms at work in our device. The main panel of Fig. 3b shows as symbols, in a log–log scale versus TΩ, the measured Jheat(N) reduced by the heat Coulomb blockade prediction for N ballistic electronic channels. We observe that the reduced data collapse for all N onto a single curve, which is closely reproduced by the functional 3.9 × 10−8(TΩ5.85 − T5.85) W (continuous line). This compares well with theoretical expectations for the electron–phonon contribution Jheatph in disordered conductors, where a temperature exponent of 4 or 6 is predicted depending on the nature of disorder30. In the inset of Fig. 3b, we directly confront the measured Jheat(N ∈ {2,3,4,5}, TΩ) (coloured dashed lines) with the essentially indistinguishable calculations (black continuous lines) obtained by adding up the full heat Coulomb blockade prediction and the above TΩ5.85 functional attributed to electron–phonon interactions.
Finally, we point out that the presently observed heat Coulomb blockade of one ballistic channel should be considered when exploiting the total outgoing heat flow from a floating node to investigate elusive exotic states6.
Methods
Sample.
The sample nanostructure is produced by standard e-beam lithography in a Ga(Al)As 2DEG buried 105 nm below the surface, of density 2.5 × 1011 cm−2 and of mobility 106 cm2 V −1 s−1. The central micrometre-sized island is composed of a metallic multilayer of nickel (30 nm), gold (120 nm) and germanium (60 nm). Its galvanic, Ohmic contact with the 2DEG is realized by thermal annealing (440 °C for 50 s).
The interface quality between the metallic island and the 2DEG is fully characterized, through the individual determination of the electron reflection probability at the interface for each connected quantum Hall channel, with the self-calibrated experimental procedure detailed in the Methods of ref. 17. We find a reflection probability below ≲0.001% (the statistical uncertainty) for the three channels closest to the edge (the outer edge channel of each of the three 2DEG branches), 0.08% for the inner edge channel toward electrode 3 used only for N ∈ {4,5}, and 0.5% for the inner edge channel toward electrode 2 used only for N = 5.
The typical electronic level spacing in the metallic island is estimated to be negligibly small (δ ≍ kB × 0.2 μK), based on the electronic density of states of gold (νF ≍ 1.14 × 1047 J−1 m−3) and the metallic island volume (≍3 μm3).
Finally, an important device parameter is the charging energy EC ≡ e2/2C. The value EC ≃ kB × 0.3 K is obtained by standard Coulomb diamond characterization, from the d.c. voltage height Vdiam of the observed diamonds (EC = eVdiam/2). These measurements are performed in the same cooldown, at the same magnetic field (data not shown, see, for example, Figure 1c of ref. 28 for a similar characterization of this sample at a higher quantum Hall filling factor).
Experimental set-up.
The device is fixed to the mixing chamber plate of a cryofree dilution refrigerator. Electrical measurement lines connected to the sample include several filters and thermalization stages. Two shields at base temperature screen spurious high-frequency radiations. Conductances are measured by standard low-frequency lock-in techniques, below 200 Hz. Further details, including on the noise measurement set-up used for the electronic thermometry, are provided in the Supplementary Information of ref. 28.
Electronic temperature.
The electronic temperature in the device is extracted from on-chip quantum shot-noise measurements28. For this purpose, we effectively short-circuit the central metallic island (equivalent circuit schematic shown bottom-left of Supplementary Fig. 1a) using the lateral continuous gate in the 2DEG branch #2 (gate closest to the bottom in Fig. 1a). The quantum point contact used to set N2 (bottom-right split gate in Fig. 1a) is here tuned to transmit a single channel with a transmission probability τ ≃ 0.5. Supplementary Fig. 1a shows as symbols the measured excess noise versus d.c. bias voltage V, and as a red continuous line the theoretical prediction at T = 7.97 mK for the simultaneously measured value τ ≃ 0.515 (variations of τ with V remain below 0.003 and are ignored). The very low statistical uncertainty of the data shown in the main panel (±5 × 10−32 A2 Hz−1, below one tenth of the symbols size) is obtained by averaging 153 sweeps. In practice, we fit each of the individual sweeps separately and extract from the statistical analysis of this ensemble of distinct measurements (shown as symbols in inset) the mean value of the temperature and the standard error (here T = 7.97 ± 0.06 mK). The same shot-noise thermometry is performed both just before and just after each run of the full experiment (two runs shown in the manuscript, the first one at T ≃ 8.1 mK and the second at T ≃ 8.0 mK).
In addition, we consolidate the device electronic temperature T with a different on-chip thermometry method based on dynamical Coulomb blockade, following ref. 28. For this purpose, the same quantum point contact (2DEG branch #2) is set to the tunnel regime τ ≍ 0.1 (in the absence of dynamical Coulomb blockade renormalization), and the device is tuned to N1 = 0 and N3 = 2, effectively implementing the schematic circuit shown in the bottom-left of Supplementary Fig. 1b with a series resistance h/2e2. The temperature is obtained by fitting the conductance data displayed as symbols in the main panel of Supplementary Fig. 1b, using the known values of the series resistance and of EC. We find T = 8 mK (corresponding calculation shown as a red line), in agreement with quantum shot-noise thermometry within the larger uncertainty of dynamical Coulomb blockade thermometry, which we estimate to ±1 mK (grey area).
Gain calibration of noise amplification chain.
The gain Gamp of the noise amplification chain is calibrated with the quantum shot-noise thermometry described in the section ‘Electronic temperature’, from the linear slope of the measured shot noise at e|V| ≫ kBT (see ref. 28 for a detailed discussion). As for the determination of T, we extract a different value of Gamp from each individual sweep of noise versus d.c. voltage. From an ensemble of 409 values, Gamp is extracted with a statistical uncertainty of ±0.1%. Note that the transmission probability τ enters as a factor τ(1 − τ) in the determination of Gamp. Here the value of τ is precisely measured simultaneously. Although τ exhibits a weak dependence with V (below 0.003), it is sufficiently small to have a negligible impact on Gamp at the approximately 0.1% level (note the particularly low impact in the vicinity of τ = 0.5) and was not taken into account.
The Gamp calibration was consolidated at an uncertainty level of approximately 1%, by additional quantum shot-noise measurements at τ ≃ 0.16 (for T ≃ 8 mK) and also at the higher electronic temperature T ≃ 16 mK (for τ ≃ 0.5). The comparison between the different quantum shot-noise and dynamical Coulomb thermometry described in the section ‘Electronic temperature’ further establishes the absolute calibration of Gamp, although at a less precise level of approximately 10%. Finally, we point out that the low-temperature heat Coulomb blockade reduction of heat current by precisely one JQel was also observed at the different integer quantum Hall filling factors ν = 3 and 4, using specific quantum shot-noise calibrations for the modified gain of the noise amplification chain (with our on-chip current to voltage conversion based on the quantum Hall resistance 1/νGQe, a larger ν therefore results in a lower Gamp).
Dissipated Joule power.
The expression PJ = V2GP/2 is used to calculate the Joule power dissipated in the electronic fluid of the floating metallic node, due to the applied d.c. bias voltage V (see Fig. 1a). It corresponds to one half of the standard two-terminal total power V2GP provided by the voltage generator. This expression can be straightforwardly derived for non-interacting electrons, within the Landauer–Büttiker scattering formalism. Essentially, it amounts to sharing equally the dissipation between cold electrodes, on the one hand, and central island, on the other hand, as expected in symmetric configurations. In the presence of interactions, one might wonder if the floating character of the central metallic node could possibly break this symmetry. However, the d.c. voltage of the central island as well as the d.c. current across it remain unchanged compared to their free-electron values, at experimental accuracy (with the island d.c. voltage deduced from the measured emitted current through the quantum limited electrical conductance of the connected ballistic channels, see top-left inset of Fig. 2a) and in agreement with theory for the present case of ballistic channels. This provides further evidence that the resulting Joule power dissipated into the central metallic island retains here its standard, non-interacting expression PJ = V2GP/2. We also point out that the same non-interacting expression for PJ is specifically expected, on qualitative grounds (a direct quantitative derivation is yet to be done), within the theoretical heat Coulomb blockade framework for the ballistic channels of ref. 9 (Eugene Sukhorukov, private communication).
Heat Coulomb blockade predictions.
We provide the theoretical expression Jthyel derived from ref. 9 for the net outgoing heat current Jheatel through N ballistic electronic channels connecting a floating metallic node of charging energy EC and at the temperature TΩ, to large electrodes at temperature T, for arbitrary values of TΩ and T:

with the function I given by

where ψ(z) is the digamma function. All the displayed theoretical predictions of the full heat Coulomb blockade theory (continuous lines in Fig. 3a, inset of Fig. 3b, Supplementary Figs 2 and 3a, inset of Supplementary Figs 3b and 4) were calculated using equation (1), without any fitting parameter. Note that these predictions assume a hot Fermi function characterized by the temperature TΩ for the distribution probability of the electrons in the metallic island. This is expected since the average dwell time of the electrons in the metallic island τD = h/δN ≃ 200/N μs (see, for example, ref. 31) is estimated to be much larger, by about four orders of magnitude, than the typical timescale of ∼10 ns for electron–electron inelastic collisions in similar metals (see, for example, ref. 32 for the connected measurement of the electron coherence time in gold).
Asymptotic limits of predictions.
The function I in equations (1) and (2) has the asymptotic forms

with a crossover centred on x ≍ 1.
At T, TΩ ≪ NEC/πkB, equation (1) therefore reduces to

with precisely one electronic channel effectively suppressed for heat conduction.
At NEC/πkB ≪ T, TΩ, equation (1) reads

which corresponds to a net reduction of the heat conductance (|T − TΩ| → 0) per ballistic electronic channel by the fixed amount ΔGheatel = ECkB/2h (always small with respect to GQh in the considered high-temperature limit).
At T ≪ NEC/πkB ≪ TΩ, equation (1) becomes

where the relative reduction due to heat Coulomb blockade progressively vanishes as TΩ increases.
Control experiment at T ≃ 16 mK.
We here demonstrate the robustness of our result with respect to base temperature T. The experiment is performed at a temperature twice as large as before, T ≃ 15.9 ± 0.1 mK, for the setting N = 2. As seen from the Jheat versus TΩ2 − T2 data shown as symbols in Supplementary Fig. 3a, this is still sufficiently low to directly and quantitatively establish the heat Coulomb blockade suppression of one ballistic channel. Note that this robustness also further validates the specific tests performed to rule out possible experimental artefacts (additional power injection by the measurement lines, voltage-dependent noise offset, calibration and thermometry issues).
We also find that exactly the same functional 3.9 × 10−8(TΩ5.85 − T5.85), attributed to electron–phonon (black continuous line in main panel of Supplementary Fig. 3b), matches the present T ≃ 16 mK data reduced by the predicted electronic heat flow (symbols in main panel of Supplementary Fig. 3b). Note that the observed independence of the electron–phonon coupling with temperature is a commonly used criterion to show that cold electrons and phonons are at the same temperature T (see, for example, ref. 33).
Supplementary experimental tests.
We also performed the following tests. (Test i) At N = 0, the measured noise is found to be independent of d.c. bias (applied either within the same 2DEG branch or in a disconnected branch, with the current flowing toward cold grounds not shown in Fig. 1), at experimental accuracy. In the language of ref. 6, the ‘source noise’ is negligible. (Test ii) At V = 0, the absolute measured noise does not change when tuning N to different values or by connecting the amplification noise chain to an edge channel emitted from a cold ground. This directly shows that the temperature T is homogeneous (the same T for all large electrodes and the metallic island, whatever N), and also that the power injected into the central island is negligible at V = 0 (in the presence of, for example, significant heating from the measurement lines, the central island temperature and consequently the noise measured would depend on N1,2,3; note that such an heating takes place in one of the test configurations discussed in Test iii). (Test iii) We checked that the observed heat Coulomb blockade is independent of the specific channel realization, by comparing three different device configurations all corresponding to N = 2 (see Supplementary Fig. 4): (N1 = 1, N2 = 1, N3 = 0) (main manuscript, red squares in Supplementary Fig. 4), (N1 = 0, N2 = 1, N3 = 1) (violet squares in Supplementary Fig. 4) and (N1 = 1, N2 = 0, N3 = 1) (black squares in Supplementary Fig. 4). The first two configurations give exactly the same result at experimental accuracy. The third configuration has the additional complication that, to perform the noise thermometry of the central island, we had to make use of an otherwise disconnected measurement line within the 2DEG branch 3, through which a non-negligible power was dissipated into the island even at V = 0 (as seen with measurements as discussed in Test ii, and also with other tests including quantum shot-noise and dynamical Coulomb blockade measurements). Nonetheless, heat Coulomb blockade predictions (and a full agreement with the first two device configurations) are verified when taking into account the separately calibrated temperature offset TΩ(V = 0) − T ≃ 5 mK (obtained through the approach of Test ii) and the additional dissipated power of 0.06 fW at V = 0. (Test iv) Finally, we verified the robustness of our results with respect to the integer quantum Hall filling factor ν at which the experiment is performed. The heat Coulomb blockade suppression of one ballistic channel was quantitatively observed experimentally not only at ν = 2 (main manuscript), but also at ν = 3 and ν = 4.
Comparison with previous experiments.
In the previous works refs 5,6, besides the robust ΔJheat approach to extract the quantum limit of electronic heat flow JQel, it was also attempted to determine the full electronic heat flow despite the non-negligible electron–phonon contribution at T ≳ 25 mK. For this purpose, a TΩ5 − T5 power law was assumed to model the transfer of energy from electrons at TΩ toward phonons at T. With this model, no heat Coulomb blockade was detected5,6. However, we here point out the sensitive influence of the electron–phonon power law exponent in the analysis of these previous experiments. Together with the higher T, it essentially impeded the observation of the heat Coulomb blockade. We illustrate this with the most accurate data of ref. 5, obtained at integer quantum Hall filling factor ν = 3. As pointed out in the supplementary methods of ref. 5, fitting the data for reference channel number Nref = 4 of this previous experiment with the electron–phonon temperature exponent as a free parameter (instead of assuming an exponent of 5) leads to a reduced overall electronic heat flow of approximately 3.5 × JQel, a factor in between Nref and Nref − 1, predicted respectively in the absence and in the presence of a heat Coulomb blockade. Reanalysing these previous data with the electron–phonon power law left as a free parameter, we find that they are indeed compatible at experimental accuracy with the present observation of the heat Coulomb blockade of one ballistic channel.
Data availability.
The data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.
Additional Information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Pekola, J. Towards quantum thermodynamics in electronic circuits. Nat. Phys. 11, 118–123 (2015).
Vinjanampathy, S. & Anders, J. Quantum thermodynamics. Contemp. Phys. 57, 545–579 (2016).
Schwab, K., Henriksen, E., Worlock, J. & Roukes, M. Measurement of the quantum of thermal conductance. Nature 404, 974–977 (2000).
Meschke, M., Guichard, W. & Pekola, J. P. Single-mode heat conduction by photons. Nature 444, 187–190 (2006).
Jezouin, S. et al. Quantum limit of heat flow across a single electronic channel. Science 342, 601–604 (2013).
Banerjee, M. et al. Observed quantization of anyonic heat flow. Nature 545, 75–79 (2017).
Cui, L. et al. Quantized thermal transport in single-atom junctions. Science 355, 1192–1195 (2017).
Giazotto, F. & Martínez-Pérez, M. J. The Josephson heat interferometer. Nature 492, 401–405 (2012).
Slobodeniuk, A., Levkivskyi, I. & Sukhorukov, E. Equilibration of quantum Hall edge states by an Ohmic contact. Phys. Rev. B 88, 165307 (2013).
Landauer, R. Residual resistivity dipoles. Z. Phys. B 21, 247–254 (1975).
Büttiker, M. Four-terminal phase-coherent conductance. Phys. Rev. Lett. 57, 1761–1764 (1986).
Kulik, I. & Shekhter, R. Kinetic phenomena and charge discreteness effects in granulated media. Sov. Phys. JETP 41, 308–316 (1975).
Averin, D. & Likharev, K. Coulomb blockade of single-electron tunneling, and coherent oscillations in small tunnel junctions. J. Low Temp. Phys. 62, 345–373 (1986).
Nazarov, Y. Anomalous current-voltage characteristics of tunnel junctions. Sov. Phys. JETP 68, 561–566 (1989).
Single Charge Tunneling (eds Grabert, H. & Devoret, M. H.) (Plenum, 1992).
Matveev, K. A. Quantum fluctuations of the charge of a metal particle under the Coulomb blockade conditions. Sov. Phys. JETP 72, 892–899 (1991).
Iftikhar, Z. et al. Two-channel Kondo effect and renormalization flow with macroscopic quantum charge states. Nature 526, 233–236 (2015).
Flensberg, K. Capacitance and conductance of mesoscopic systems connected by quantum point contacts. Phys. Rev. B 48, 11156–11166 (1993).
Yeyati, A. L., Martin-Rodero, A., Esteve, D. & Urbina, C. Direct link between Coulomb blockade and shot noise in a quantum-coherent structure. Phys. Rev. Lett. 87, 046802 (2001).
Kindermann, M. & Nazarov, Y. V. Interaction effects on counting statistics and the transmission distribution. Phys. Rev. Lett. 91, 136802 (2003).
Altimiras, C., Gennser, U., Cavanna, A., Mailly, D. & Pierre, F. Experimental test of the dynamical coulomb blockade theory for short coherent conductors. Phys. Rev. Lett. 99, 256805 (2007).
Parmentier, F. D. et al. Strong back-action of a linear circuit on a single electronic quantum channel. Nat. Phys. 7, 935–938 (2011).
Jezouin, S. et al. Tomonaga-Luttinger physics in electronic quantum circuits. Nat. Commun. 4, 1802 (2013).
Altimiras, C. et al. Chargeless heat transport in the fractional quantum Hall regime. Phys. Rev. Lett. 109, 026803 (2012).
Dutta, B. et al. Thermal conductance of a single-electron transistor. Phys. Rev. Lett. 119, 077701 (2017).
Blanter, Y. M. & Büttiker, M. Shot noise in mesoscopic conductors. Phys. Rep. 336, 1–166 (2000).
Liang, Y., Dong, Q., Gennser, U., Cavanna, A. & Jin, Y. Input noise voltage below 1 nV/Hz1/2 at 1 kHz in the HEMTs at 4.2 K. J. Low Temp. Phys. 167, 632–637 (2012).
Iftikhar, Z. et al. Primary thermometry triad at 6 mK in mesoscopic circuits. Nat. Commun. 7, 12908 (2016).
Blanter, Y. M. & Sukhorukov, E. V. Semiclassical theory of conductance and noise in open chaotic cavities. Phys. Rev. Lett. 84, 1280–1283 (2000).
Sergeev, A. & Mitin, V. Electron–phonon interaction in disordered conductors: static and vibrating scattering potentials. Phys. Rev. B 61, 6041–6047 (2000).
Brouwer, P. W. & Büttiker, M. Charge-relaxation and dwell time in the fluctuating admittance of a chaotic cavity. Europhys. Lett. 37, 441–446 (1997).
Pierre, F. et al. Dephasing of electrons in mesoscopic metal wires. Phys. Rev. B 68, 085413 (2003).
Rajauria, S. et al. Electron and phonon cooling in a superconductor-normal metal-superconductor tunnel junction. Phys. Rev. Lett. 99, 047004 (2007).
Acknowledgements
This work was supported by the French RENATECH network, the national French program ‘Investissements d’Avenir’ (Labex NanoSaclay, ANR-10-LABX-0035) and the French National Research Agency (project QuTherm, ANR-16-CE30-0010-01). We thank E. Sukhorukov for discussions.
Author information
Authors and Affiliations
Contributions
E.S. and F.P. performed the experiment with inputs from A.A.; A.A., E.S. and F.P. analysed the data; F.D.P. fabricated the sample with inputs from A.A.; A.C., A.O. and U.G. grew the 2DEG; Y.J. fabricated the high-electron-mobility transistor (HEMT) used for noise measurements; F.P. led the project and wrote the manuscript with inputs from A.A., E.S. and U.G.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 363 kb)
Rights and permissions
About this article
Cite this article
Sivre, E., Anthore, A., Parmentier, F. et al. Heat Coulomb blockade of one ballistic channel. Nat. Phys. 14, 145–148 (2018). https://doi.org/10.1038/nphys4280
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys4280
This article is cited by
-
Heat conductance of the quantum Hall bulk
Nature (2024)
-
Observing the universal screening of a Kondo impurity
Nature Communications (2023)
-
Direct determination of the topological thermal conductance via local power measurement
Nature Physics (2023)
-
Bolometric detection of Josephson inductance in a highly resistive environment
Nature Communications (2023)
-
Quantized charge fractionalization at quantum Hall Y junctions in the disorder dominated regime
Nature Communications (2021)