Abstract
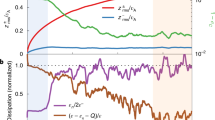
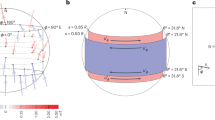
Jupiter’s turbulent weather layer contains phenomena of many different sizes, from local storms up to the Great Red Spot and banded jets. The global circulation is driven by complex interactions with (as yet uncertain) small-scale processes. We have calculated structure functions and kinetic energy spectral fluxes from Cassini observations over a wide range of length scales in Jupiter’s atmosphere. We found evidence for an inverse cascade of kinetic energy from length scales comparable to the first baroclinic Rossby deformation radius up to the global jet scale, but also a forward cascade of kinetic energy from the deformation radius to smaller scales. This second result disagrees with the traditional picture of Jupiter’s atmospheric dynamics, but has some similarities with mesoscale phenomena in the Earth’s atmosphere and oceans. We conclude that the inverse cascade driving Jupiter’s jets may have a dominant energy source at scales close to the deformation radius, such as baroclinic instability.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
References
Porco, C. C. et al. Cassini imaging of Jupiter’s atmosphere, satellites, and rings. Science 299, 1541–1547 (2003).
Ingersoll, A. P. et al. in Jupiter: The Planet, Satellites and Magnetosphere (eds Bagenal, F., Dowling, T. E. & McKinnon, W. B.) Ch. 6, 105–128 (Cambridge Univ. Press, 2004).
Vasavada, A. R. & Showman, A. P. Jovian atmospheric dynamics: an update after Galileo and Cassini. Rep. Prog. Phys. 68, 1935–1996 (2005).
Kolmogorov, A. N. The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers (English Translation 1991). Proc. R. Soc. Lond. A 434, 9–13 (1941).
Fjørtoft, R. On the changes in the spectral distribution of kinetic energy for twodimensional, nondivergent flow. Tellus 5, 225–230 (1953).
Kraichnan, R. Inertial ranges in two-dimensional turbulence. Phys. Fluids 10, 1417–1423 (1967).
Charney, J. G. Geostrophic turbulence. J. Atmos. Sci. 28, 1087–1095 (1971).
Salmon, R. Baroclinic instability and geostrophic turbulence. Geophys. Astrophys. Fluid Dyn. 15, 167–211 (1980).
Nastrom, G. D., Gage, K. S. & Jasperson, W. H. Kinetic energy spectrum of large- and mesoscale atmospheric processes. Nature 310, 36–38 (1984).
Boer, G. J. & Shepherd, T. G. Large-scale two-dimensional turbulence in the atmosphere. J. Atmos. Sci. 40, 164–184 (1983).
Burgess, B. H., Erler, A. R. & Shepherd, T. G. The troposphere-to-stratosphere transition in kinetic energy spectra and nonlinear spectral fluxes as seen in ECMWF analyses. J. Atmos. Sci. 70, 669–687 (2013).
Augier, P. & Lindborg, E. A new formulation of the spectral energy budget of the atmosphere, with application to two high-resolution general circulation models. J. Atmos. Sci. 70, 2293–2308 (2013).
Dewan, E. M. Stratospheric wave spectra resembling turbulence. Science 204, 832–835 (1979).
Lilly, D. K. Stratified turbulence and the mesoscale variability of the atmosphere. J. Atmos. Sci. 40, 749–761 (1983).
Tung, K. K. & Orlando, W. W. The k−3 and k−5/3 energy spectrum of atmospheric turbulence: quasigeostrophic two-level model simulation. J. Atmos. Sci. 60, 824–835 (2003).
Tulloch, R. & Smith, K. S. A theory for the atmospheric energy spectrum: depth-limited temperature anomalies at the tropopause. Proc. Natl Acad. Sci. USA 103, 14690–14694 (2006).
Lindborg, E. Horizontal wavenumber spectra of vertical vorticity and horizontal divergence in the upper troposphere and lower stratosphere. J. Atmos. Sci. 64, 1017–1025 (2007).
Vallgren, A., Deusebio, E. & Lindborg, E. Possible explanation of the atmospheric kinetic and potential energy spectra. Phys. Rev. Lett. 107, 268501 (2011).
Lindborg, E. Can the atmospheric kinetic energy spectrum be explained by two-dimensional turbulence? J. Fluid Mech. 388, 259–288 (1999).
Cho, J. Y. N. & Lindborg, E. Horizontal velocity structure functions in the upper troposphere and lower stratosphere: 1. Observations. J. Geophys. Res. 106, 10223–10232 (2001).
King, G. P., Vogelzang, J. & Stoffelen, A. Upscale and downscale energy transfer over the tropical Pacific revealed by scatterometer winds. J. Geophys. Res. 120, 346–361 (2015).
King, G. P., Vogelzang, J. & Stoffelen, A. Second-order structure function analysis of scatterometer winds over the tropical Pacific. J. Geophys. Res. 120, 362–383 (2015).
Scott, R. B. & Wang, F. Direct evidence of an oceanic inverse kinetic energy cascade from satellite altimetry. J. Phys. Oceanogr. 35, 1650–1666 (2005).
Tulloch, R., Marshall, J., Hill, C. & Smith, K. S. Scales, growth rates, and spectral fluxes of baroclinic instability in the ocean. J. Phys. Oceanogr. 41, 1057–1076 (2011).
Ingersoll, A. P. et al. Interaction of eddies and mean zonal flow on Jupiter as inferred from Voyager 1 and 2 images. J. Geophys. Res. 86, 8733–8743 (1981).
Salyk, C., Ingersoll, A. P., Lorre, J., Vasavada, A. & Del Genio, A. D. Interaction between eddies and mean flow in Jupiter’s atmosphere: analysis of Cassini imaging data. Icarus 185, 430–442 (2006).
Galperin, B. et al. Cassini observations reveal a regime of zonostrophic macroturbulence on Jupiter. Icarus 229, 295–320 (2014).
Choi, D. S. & Showman, A. P. Power spectral analysis of Jupiter’s clouds and kinetic energy from Cassini. Icarus 216, 597–609 (2011).
Maltrud, M. E. & Vallis, G. K. Energy and enstrophy transfer in numerical simulations of two-dimensional turbulence. Phys. Fluids A 5, 1760–1775 (1993).
Huang, H.-P., Galperin, B. & Sukoriansky, S. Anisotropic spectra in two-dimensional turbulence on the surface of a rotating sphere. Phys. Fluids 13, 225–240 (2001).
Scott, R. K. & Polvani, L. M. Forced-dissipative shallow-water turbulence on the sphere and the atmospheric circulation of the giant planets. J. Atmos. Sci. 64, 3158–3176 (2007).
Porco, C. C. et al. Cassini imaging science: instrument characteristics and anticipated scientific investigations at Saturn. Space Sci. Rev. 115, 363–497 (2004).
Vasavada, A. R., Porco, C. C. & The Cassini Imaging Science Team. Cassini Cylindrical-Projection Maps near Jupiter Closest Approach (NASA Planetary Data System, 2008); http://pds-atmospheres.nmsu.edu/Jupiter/CassiniMaps.txt
Kolmogorov, A. N. Dissipation of energy in the locally isotropic turbulence (English translation 1991). Proc. R. Soc. Lond. A 434, 15–17 (1941).
Davidson, P. A. Turbulence: An Introduction for Scientists and Engineers 2nd edn (Oxford Univ. Press, 2015).
Blažica, V., Žagar, N., Strajnar, B. & Cedilnik, J. Rotational and divergent kinetic energy in the mesoscale model ALADIN. Tellus A 65, 18918 (2013).
Gierasch, P. J. et al. Observation of moist convection in Jupiter’s atmosphere. Nature 403, 628–630 (2000).
Ingersoll, A. P., Gierasch, P. J., Banfield, D., Vasavada, A. R. & The Galileo Imaging Team. Moist convection as an energy source for the large-scale motions in Jupiter’s atmosphere. Nature 403, 630–632 (2000).
Blumen, W. Uniform potential vorticity flow: Part I. Theory of wave interactions and two-dimensional turbulence. J. Atmos. Sci. 35, 774–783 (1978).
Held, I. M., Pierrehumbert, R. T., Garner, S. T. & Swanson, K. L. Surface quasi-geostrophic dynamics. J. Fluid Mech. 282, 1–20 (1995).
Tulloch, R. & Smith, K. S. Quasigeostrophic turbulence with explicit surface dynamics: application to the atmospheric energy spectrum. J. Atmos. Sci. 66, 450–467 (2009).
Fincham, A. M. & Spedding, G. R. Low cost, high resolution DPIV for measurement of turbulent fluid flow. Exp. Fluids 23, 449–462 (1997).
Fincham, A. & Delerce, G. Advanced optimization of correlation imaging velocimetry algorithms. Exp. Fluids 29, S13–S22 (2000).
Young, R. M. B., Read, P. L., Armstrong, D. & Lancaster, A. J. Jupiter Horizontal Wind Velocities at Cloud Level from Cassini [data-set] (Oxford University Research Archive, 2017); http://dx.doi.org/10.5287/bodleian:D5oVPJVRv
Williams, E. Aviation Formulary v1.46 (2011); http://www.edwilliams.org/avform.htm
Seidelmann, P. K. et al. Report of the IAU/IAG working group on cartographic coordinates and rotational elements: 2006. Celest. Mech. Dyn. Astron. 98, 155–180 (2007).
Adams, J. C. & Swarztrauber, P. N. SPHEREPACK 3.0: a model development facility. Mon. Weath. Rev. 127, 1872–1878 (1999).
Adams, J. C. & Swarztrauber, P. N. SPHEREPACK 2.0: A Model Development Facility (Technical Report NCAR/TN-436+STR, NCAR, 1997).
Shepherd, T. G. A spectral view of nonlinear fluxes and stationary-transient interaction in the atmosphere. J. Atmos. Sci. 44, 1166–1178 (1987).
Acknowledgements
Support for R.M.B.Y. was provided by UK STFC Grant ST/K00106X/1. This work was supported in part by the US National Science Foundation under Grant No. NSF PHY11-25915. We are grateful to the Leverhulme Trust for their support of the International Network on Waves and Turbulence. Raw images were made available by the Cassini Imaging Science Team via the NASA PDS Atmospheres Node. Data sets C11 and S06 were kindly provided by D. Choi and C. Salyk. We wish to thank P. Davidson, B. Galperin, G. King, B. Marston, M. McIntyre, H. Scolan, F. Tabataba-Vakili, S. Thomson and A. Valeanu for useful discussions.
Author information
Authors and Affiliations
Contributions
R.M.B.Y. wrote the code to calculate the structure functions and spectral fluxes, and performed the calculations. R.M.B.Y. wrote the bulk of the paper with sections on background and interpretation written by P.L.R. Both authors designed the research, decided on the methods used, and discussed the results.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 1437 kb)
Rights and permissions
About this article
Cite this article
Young, R., Read, P. Forward and inverse kinetic energy cascades in Jupiter’s turbulent weather layer. Nature Phys 13, 1135–1140 (2017). https://doi.org/10.1038/nphys4227
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys4227
This article is cited by
-
Frontogenesis at Jovian high latitudes
Nature Physics (2024)
-
Quasi-two-dimensional turbulence
Reviews of Modern Plasma Physics (2023)
-
Moist convection drives an upscale energy transfer at Jovian high latitudes
Nature Physics (2022)
-
Phase separation of rotor mixtures without domain coarsening driven by two-dimensional turbulence
Communications Physics (2022)
-
Vorticity and divergence at scales down to 200 km within and around the polar cyclones of Jupiter
Nature Astronomy (2022)