Abstract
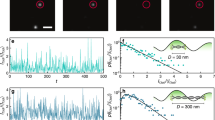
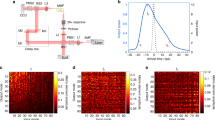
A fundamental challenge in physics is controlling the propagation of waves in disordered media despite strong scattering from inhomogeneities. Spatial light modulators enable one to synthesize (shape) the incident wavefront, optimizing the multipath interference to achieve a specific behaviour such as focusing light to a target region. However, the extent of achievable control is not known when the target region is much larger than the wavelength and contains many speckles. Here we show that for targets containing more than g speckles, where g is the dimensionless conductance, the extent of transmission control is substantially enhanced by the long-range mesoscopic correlations among the speckles. Using a filtered random matrix ensemble appropriate for coherent diffusion in open geometries, we predict the full distributions of transmission eigenvalues as well as universal scaling laws for statistical properties, in excellent agreement with our experiment. This work provides a general framework for describing wavefront-shaping experiments in disordered systems.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Akkermans, E. & Montambaux, G. Mesoscopic Physics of Electrons and Photons (Cambridge Univ. Press, 2007).
Sheng, P. Introduction to Wave Scattering, Localization and Mesoscopic Phenomena 2nd edn (Springer, 2006).
Mosk, A. P., Lagendijk, A., Lerosey, G. & Fink, M. Controlling waves in space and time for imaging and focusing in complex media. Nat. Photon. 6, 283–292 (2012).
Vellekoop, I. M. & Mosk, A. P. Focusing coherent light through opaque strongly scattering media. Opt. Lett. 32, 2309–2311 (2007).
Yaqoob, Z., Psaltis, D., Feld, M. S. & Yang, C. Optical phase conjugation for turbidity suppression in biological samples. Nat. Photon. 2, 110–115 (2008).
Hsieh, C.-L., Pu, Y., Grange, R. & Psaltis, D. Digital phase conjugation of second harmonic radiation emitted by nanoparticles in turbid media. Opt. Express 18, 12283–12290 (2010).
Conkey, D. B. & Piestun, R. Color image projection through a strongly scattering wall. Opt. Express 20, 27312–27318 (2012).
Horstmeyer, R., Ruan, H. & Yang, C. Guidestar-assisted wavefront-shaping methods for focusing light into biological tissue. Nat. Photon. 9, 563–571 (2015).
Sprik, R., Tourin, A., de Rosny, J. & Fink, M. Eigenvalue distributions of correlated multichannel transfer matrices in strongly scattering systems. Phys. Rev. B 78, 012202 (2008).
Aubry, A. & Derode, A. Random matrix theory applied to acoustic backscattering and imaging in complex media. Phys. Rev. Lett. 102, 084301 (2009).
Popoff, S. M. et al. Measuring the transmission matrix in optics: an approach to the study and control of light propagation in disordered media. Phys. Rev. Lett. 104, 100601 (2010).
Popoff, S. M., Lerosey, G., Fink, M., Boccara, A. C. & Gigan, S. Controlling light through optical disordered media: transmission matrix approach. New J. Phys. 13, 123021 (2011).
Drémeau, A. et al. Reference-less measurement of the transmission matrix of a highly scattering material using a DMD and phase retrieval techniques. Opt. Express 23, 11898–11911 (2015).
Stephen, M. J. & Cwilich, G. Intensity correlation functions and fluctuations in light scattered from a random medium. Phys. Rev. Lett. 59, 285–287 (1987).
Feng, S., Kane, C., Lee, P. A. & Stone, A. D. Correlations and fluctuations of coherent wave transmission through disordered media. Phys. Rev. Lett. 61, 834–837 (1988).
Mello, P. A., Akkermans, E. & Shapiro, B. Macroscopic approach to correlations in the electronic transmission and reflection from disordered conductors. Phys. Rev. Lett. 61, 459–462 (1988).
Sebbah, P., Hu, B., Genack, A. Z., Pnini, R. & Shapiro, B. Spatial-field correlation: the building block of mesoscopic fluctuations. Phys. Rev. Lett. 88, 123901 (2002).
Lee, P. A., Stone, A. D. & Fukuyama, H. Universal conductance fluctuations in metals: effects of finite temperature, interactions, and magnetic field. Phys. Rev. B 35, 1039–1070 (1987).
Dorokhov, O. N. On the coexistence of localized and extended electronic states in the metallic phase. Solid State Commun. 51, 381–384 (1984).
Imry, Y. Active transmission channels and universal conductance fluctuations. Europhys. Lett. 1, 249–256 (1986).
Mello, P. A., Pereyra, P. & Kumar, N. Macroscopic approach to multichannel disordered conductors. Ann. Phys. 181, 290–317 (1988).
Nazarov, Y. V. Limits of universality in disordered conductors. Phys. Rev. Lett. 73, 134–137 (1994).
Gérardin, B., Laurent, J., Derode, A., Prada, C. & Aubry, A. Full transmission and reflection of waves propagating through a maze of disorder. Phys. Rev. Lett. 113, 173901 (2014).
Sarma, R., Yamilov, A. G., Petrenko, S., Bromberg, Y. & Cao, H. Control of energy density inside a disordered medium by coupling to open or closed channels. Phys. Rev. Lett. 117, 086803 (2016).
de Boer, J. F., van Albada, M. P. & Lagendijk, A. Transmission and intensity correlations in wave propagation through random media. Phys. Rev. B 45, 658–666 (1992).
Stoytchev, M. & Genack, A. Z. Measurement of the probability distribution of total transmission in random waveguides. Phys. Rev. Lett. 79, 309–312 (1997).
Scheffold, F., Härtl, W., Maret, G. & Matijević, E. Observation of long-range correlations in temporal intensity fluctuations of light. Phys. Rev. B 56, 10942–10952 (1997).
Strudley, T., Zehender, T., Blejean, C., Bakkers, E. P. A. M. & Muskens, O. L. Mesoscopic light transport by very strong collective multiple scattering in nanowire mats. Nat. Photon. 7, 413–418 (2013).
Vellekoop, I. M. & Mosk, A. P. Universal optimal transmission of light through disordered materials. Phys. Rev. Lett. 101, 120601 (2008).
Davy, M., Shi, Z. & Genack, A. Z. Focusing through random media: eigenchannel participation number and intensity correlation. Phys. Rev. B 85, 035105 (2012).
Davy, M., Shi, Z., Wang, J. & Genack, A. Z. Transmission statistics and focusing in single disordered samples. Opt. Express 21, 10367–10375 (2013).
Ojambati, O. S., Hosmer-Quint, J. T., Gorter, K.-J., Mosk, A. P. & Vos, W. L. Controlling the intensity of light in large areas at the interfaces of a scattering medium. Phys. Rev. A 94, 043834 (2016).
Shi, Z. & Genack, A. Z. Transmission eigenvalues and the bare conductance in the crossover to Anderson localization. Phys. Rev. Lett. 108, 043901 (2012).
Yu, H. et al. Measuring large optical transmission matrices of disordered media. Phys. Rev. Lett. 111, 153902 (2013).
Yu, H., Lee, K. & Park, Y. Energy leakage in partially measured scattering matrices of disordered media. Phys. Rev. B 93, 104202 (2016).
Akbulut, D. et al. Optical transmission matrix as a probe of the photonic strength. Phys. Rev. A 94, 043817 (2016).
Goetschy, A. & Stone, A. D. Filtering random matrices: the effect of incomplete channel control in multiple scattering. Phys. Rev. Lett. 111, 063901 (2013).
Popoff, S. M., Goetschy, A., Liew, S. F., Stone, A. D. & Cao, H. Coherent control of total transmission of light through disordered media. Phys. Rev. Lett. 112, 133903 (2014).
Marčenko, V. A. & Pastur, L. A. Distribution of eigenvalues for some sets of random matrices. Math. USSR Sb. 1, 457–483 (1967).
Yamilov, A., Petrenko, S., Sarma, R. & Cao, H. Shape dependence of transmission, reflection, and absorption eigenvalue densities in disordered waveguides with dissipation. Phys. Rev. B 93, 100201 (2016).
Verrier, N., Depraeter, L., Felbacq, D. & Gross, M. Measuring enhanced optical correlations induced by transmission open channels in a slab geometry. Phys. Rev. B 93, 161114 (2016).
Pnini, R. & Shapiro, B. Fluctuations in transmission of waves through disordered slabs. Phys. Rev. B 39, 6986–6994 (1989).
García-Martín, A., Scheffold, F., Nieto-Vesperinas, M. & Sáenz, J. J. Finite-size effects on intensity correlations in random media. Phys. Rev. Lett. 88, 143901 (2002).
Liutkus, A. et al. Imaging with nature: compressive imaging using a multiply scattering medium. Sci. Rep. 4, 5552 (2014).
Hildebrand, W. K., Strybulevych, A., Skipetrov, S. E., van Tiggelen, B. A. & Page, J. H. Observation of infinite-range intensity correlations above, at, and below the mobility edges of the 3D Anderson localization transition. Phys. Rev. Lett. 112, 073902 (2014).
Peña, A., Girschik, A., Libisch, F., Rotter, S. & Chabanov, A. A. The single-channel regime of transport through random media. Nat. Commun. 5, 3488 (2014).
Hsu, C. W., Goetschy, A., Bromberg, Y., Stone, A. D. & Cao, H. Broadband coherent enhancement of transmission and absorption in disordered media. Phys. Rev. Lett. 115, 223901 (2015).
Aulbach, J., Gjonaj, B., Johnson, P. M., Mosk, A. P. & Lagendijk, A. Control of light transmission through opaque scattering media in space and time. Phys. Rev. Lett. 106, 103901 (2011).
Mounaix, M. et al. Spatiotemporal coherent control of light through a multiple scattering medium with the multispectral transmission matrix. Phys. Rev. Lett. 116, 253901 (2016).
Liew, S. F. et al. Coherent control of photocurrent in a strongly scattering photoelectrochemical system. ACS Photon. 3, 449–455 (2016).
Tripathi, S. & Toussaint, K. C. Quantitative control over the intensity and phase of light transmitted through highly scattering media. Opt. Express 21, 25890–25900 (2013).
Nocedal, J. Updating quasi-Newton matrices with limited storage. Math. Comput. 35, 773–782 (1980).
Liu, D. C. & Nocedal, J. On the limited memory BFGS method for large scale optimization. Math. Program. 45, 503–528 (1989).
Johnson, S. G. The NLopt Nonlinear-Optimization Package (2014); http://ab-initio.mit.edu/nlopt
Acknowledgements
We thank S. Popoff, Y. Bromberg, S. Knitter, R. Sarma, W. Xiong, F. Scheffold, E. Akkermans and I. M. Vellekoop for helpful discussions. This work is supported by the National Science Foundation under grant No. DMR-1307632 and ECCS-1068642, the US Office of Naval Research under grant No. N00014-13-1-0649, and the US–Israel Binational Science Foundation (BSF) under grant no. 2015509. A.G. acknowledges the support of LABEX WIFI (Laboratory of Excellence ANR-10-LABX-24) within the French Program ‘Investments for the Future’ under reference ANR-10-IDEX-0001-02 PSL.
Author information
Authors and Affiliations
Contributions
C.W.H. and S.F.L. performed the experiment. C.W.H. analysed the data. C.W.H. developed the theory descriptions. A.G. proposed the effective MP model. H.C. and A.D.S. supervised the project. All authors discussed and interpreted the results. C.W.H. and A.D.S. wrote the manuscript with input from all authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 445 kb)
Rights and permissions
About this article
Cite this article
Hsu, C., Liew, S., Goetschy, A. et al. Correlation-enhanced control of wave focusing in disordered media. Nature Phys 13, 497–502 (2017). https://doi.org/10.1038/nphys4036
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys4036
This article is cited by
-
Depth-targeted energy delivery deep inside scattering media
Nature Physics (2022)
-
3D printable diffractive optical elements by liquid immersion
Nature Communications (2021)
-
Scattering invariant modes of light in complex media
Nature Photonics (2021)
-
Demonstration and application of diffusive and ballistic wave propagation for drone-to-ground and drone-to-drone wireless communications
Scientific Reports (2020)
-
Engineered disorder in photonics
Nature Reviews Materials (2020)