Abstract
Differences in the behaviour of matter and antimatter have been observed in K and B meson decays, but not yet in any baryon decay. Such differences are associated with the non-invariance of fundamental interactions under the combined charge-conjugation and parity transformations, known as CP violation. Here, using data from the LHCb experiment at the Large Hadron Collider, we search for CP-violating asymmetries in the decay angle distributions of Λb0 baryons decaying to pπ−π+π− and pπ−K+K− final states. These four-body hadronic decays are a promising place to search for sources of CP violation both within and beyond the standard model of particle physics. We find evidence for CP violation in Λb0 to pπ−π+π− decays with a statistical significance corresponding to 3.3 standard deviations including systematic uncertainties. This represents the first evidence for CP violation in the baryon sector.
Similar content being viewed by others
Main
The asymmetry between matter and antimatter is related to the violation of the CP symmetry (CPV), where C and P are the charge-conjugation and parity operators. CP violation is accommodated in the standard model (SM) of particle physics by the Cabibbo–Kobayashi–Maskawa (CKM) mechanism that describes the transitions between up- and down-type quarks1,2, in which quark decays proceed by the emission of a virtual W boson and where the phases of the couplings change sign between quarks and antiquarks. However, the amount of CPV predicted by the CKM mechanism is not sufficient to explain our matter-dominated Universe3,4 and other sources of CPV are expected to exist. The initial discovery of CPV was in neutral K meson decays5, and more recently it has been observed in B0 (refs 6,7), B+(refs 8,9,10,11), and Bs0 (ref. 12) meson decays, but it has never been observed in the decays of any baryon. Decays of the Λb0 (bud) baryon to final states consisting of hadrons with no charm quarks are predicted to have non-negligible CP asymmetries in the SM, as large as 20% for certain three-body decay modes13. It is important to measure the size and nature of these CP asymmetries in as many decay modes as possible, to determine whether they are consistent with the CKM mechanism or, if not, what extensions to the SM would be required to explain them14,15,16.
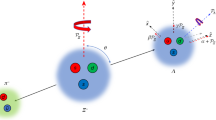
The decay processes studied in this article, Λb0 → pπ−π+π− and Λb0 → pπ−K+K−, are mediated by the weak interaction and governed mainly by two amplitudes, expected to be of similar magnitude, from different diagrams describing quark-level  transitions, as shown in Fig. 1. Throughout this paper the inclusion of charge-conjugate reactions is implied, unless otherwise indicated. CPV could arise from the interference of two amplitudes with relative phases that differ between particle and antiparticle decays, leading to differences in the Λb0 and
transitions, as shown in Fig. 1. Throughout this paper the inclusion of charge-conjugate reactions is implied, unless otherwise indicated. CPV could arise from the interference of two amplitudes with relative phases that differ between particle and antiparticle decays, leading to differences in the Λb0 and  decay rates. The main source of this effect in the SM would be the large relative phase (referred to as α in the literature) between the product of the CKM matrix elements VubVud∗ and VtbVtd∗, which are present in the different diagrams depicted in Fig. 1. Parity violation (PV) is also expected in weak interactions, but has never been observed in Λb0 decays.
decay rates. The main source of this effect in the SM would be the large relative phase (referred to as α in the literature) between the product of the CKM matrix elements VubVud∗ and VtbVtd∗, which are present in the different diagrams depicted in Fig. 1. Parity violation (PV) is also expected in weak interactions, but has never been observed in Λb0 decays.
The two diagrams show the transitions that contribute most strongly to Λb0 → pπ− π+ π− and Λb0 → pπ− K+ K− decays. In both cases, a pair of π+ π− (K+K−) is produced by gluon emission from the light quarks (u,d). The difference is in the b quark decay that happens on the left through a virtual W− boson emission (‘tree diagram’) and on the right as a virtual W− boson emission and absorption together with a gluon emission (‘loop diagram’). The magnitudes of the two amplitudes are expected to be comparable, and each is proportional to the product of the CKM matrix elements involved, which are shown in the figure.
To search for CP-violating effects one needs to measure CP-odd observables, which can be done by studying asymmetries in the  operator. This is a unitary operator that reverses both the momentum and spin three-vectors17,18, and is different from the antiunitary time-reversal operator T19,20 that also exchanges initial and final states. A non-zero CP-odd observable implies CP violation, and similar considerations apply to P-odd observables and parity violation21. Furthermore, different values of P-odd observables for a decay and its charge conjugate would imply CPV. In this paper, scalar triple products of final-state particle momenta in the Λb0 centre-of-mass frame are studied to search for P- and CP-violating effects in four-body decays. These are defined as
operator. This is a unitary operator that reverses both the momentum and spin three-vectors17,18, and is different from the antiunitary time-reversal operator T19,20 that also exchanges initial and final states. A non-zero CP-odd observable implies CP violation, and similar considerations apply to P-odd observables and parity violation21. Furthermore, different values of P-odd observables for a decay and its charge conjugate would imply CPV. In this paper, scalar triple products of final-state particle momenta in the Λb0 centre-of-mass frame are studied to search for P- and CP-violating effects in four-body decays. These are defined as  = pp ⋅ (ph1− × ph2+) for Λb0 and
= pp ⋅ (ph1− × ph2+) for Λb0 and 
 for
for  , where h1 and h2 are final-state hadrons: h1 = π and h2 = K for Λb0 → pπ−K+K− and h1 = h2 = π for Λb0 → pπ−π+π−. In the latter case there is an inherent ambiguity in the choice of the pion for h1 that is resolved by taking that with the larger momentum in the Λb0 rest frame, referred to as πfast. The following asymmetries may then be defined22,23:
, where h1 and h2 are final-state hadrons: h1 = π and h2 = K for Λb0 → pπ−K+K− and h1 = h2 = π for Λb0 → pπ−π+π−. In the latter case there is an inherent ambiguity in the choice of the pion for h1 that is resolved by taking that with the larger momentum in the Λb0 rest frame, referred to as πfast. The following asymmetries may then be defined22,23:


where N and  are the numbers of Λb0 and
are the numbers of Λb0 and  decays. These asymmetries are P-odd and
decays. These asymmetries are P-odd and  -odd and so change sign under P or
-odd and so change sign under P or  transformations, that is,
transformations, that is,  (
( )
)  (−
(− ) or
) or  (
( ) = −
) = − (−
(− ). The P- and CP-violating observables are defined as
). The P- and CP-violating observables are defined as

and a significant deviation from zero would signal PV or CPV, respectively.
Searches for CPV with triple-product asymmetries are particularly suited to Λb0 four-body decays to hadrons with no charm quark24 thanks to the rich resonant substructure, dominated by Δ(1232)++ → pπ+ and ρ(770)0 → π+π− resonances in the Λb0 → pπ−π+π− final state. The observable  is sensitive to the interference of
is sensitive to the interference of  -even and
-even and  -odd amplitudes with different CP-odd (‘weak’) phases. Unlike the overall asymmetry in the decay rate that is sensitive to the interference of
-odd amplitudes with different CP-odd (‘weak’) phases. Unlike the overall asymmetry in the decay rate that is sensitive to the interference of  -even amplitudes,
-even amplitudes,  does not require a non-vanishing difference in the CP-invariant (‘strong’) phase between the contributing amplitudes19,25. The observables
does not require a non-vanishing difference in the CP-invariant (‘strong’) phase between the contributing amplitudes19,25. The observables  ,
,  ,
,  and
and  are, by construction, largely insensitive to particle–antiparticle production asymmetries and detector-induced charge asymmetries26.
are, by construction, largely insensitive to particle–antiparticle production asymmetries and detector-induced charge asymmetries26.
This article describes measurements of the CP- and P-violating asymmetries introduced in equation (3) in Λb0 → pπ−π+π− and Λb0 → pπ−K+K− decays. The asymmetries are measured first for the entire phase space of the decay, integrating over all possible final-state configurations, and then in different regions of phase space so as to enhance sensitivity to localized CPV. The analysis is performed using proton–proton collision data collected by the LHCb detector, corresponding to 3.0 fb−1 of integrated luminosity at centre-of-mass energies of 7 and 8 TeV, and exploits the copious production of Λb0 baryons at the LHC, which constitutes around 20% of all b hadrons produced27. Control samples of Λb0 → pK−π+π− and Λb0 → Λc+π− decays, with Λc+ decaying to pK−π+, pπ−π+, and pK−K+ final states, are used to optimize the event selection and study systematic effects; the most abundant control sample consists of Λb0 → Λc+(pK−π+)π− decays mediated by b → c quark transitions in which no CPV is expected28. To avoid introducing biases in the results, all aspects of the analysis, including the selection, phase space regions, and procedure used to determine the statistical significance of the results, were fixed before the data were examined.
The LHCb detector29,30 is designed to collect data of b-hadron decays produced from proton–proton collisions at the Large Hadron Collider. It instruments a region around the proton beam axis, covering the polar angles between 10 and 250 mrad, where approximately 24% of the b-hadron decays occur31. The detector includes a high-precision tracking system with a dipole magnet, providing measurements of the momentum and decay vertex position of particle decays. Different types of charged particles are distinguished using information from two ring-imaging Cherenkov detectors, a calorimeter and a muon system. Simulated samples of Λb0 signal modes and control samples are used in this analysis to verify the experimental method and to study certain systematic effects. These simulated events model the experimental conditions in detail, including the proton–proton collision, the decays of the particles, and the response of the detector. The software used is described in refs 32,33,34,35,36,37,38. The online event selection is performed by a trigger system that takes fast decisions about which events to record. It consists of a hardware stage, based on information from the calorimeter and muon systems, followed by a software stage, which applies a full event reconstruction. The software trigger requires Λb0 candidates to be consistent with a b-hadron decay topology, with tracks originating from a secondary vertex detached from the primary pp collision point. The mean Λb0 lifetime is 1.5 ps (ref. 39), which corresponds to a typical flight distance of a few millimetres in the LHCb.
The Λb0 → pπ−h+h− candidates are formed by combining tracks identified as protons, pions, or kaons that originate from a common vertex. The proton or antiproton identifies the candidate as a Λb0 or  . There are backgrounds from b-hadron decays to charm hadrons that are suppressed by reconstructing the appropriate two- or three-body invariant masses, and requiring them to differ from the known charm hadron masses by at least three times the experimental resolution. For the Λb0 → Λc+π− control mode, only the Λb0 → ph+h−π− events with reconstructed ph+h− invariant mass between 2.23 and 2.31 GeV/c2are retained.
. There are backgrounds from b-hadron decays to charm hadrons that are suppressed by reconstructing the appropriate two- or three-body invariant masses, and requiring them to differ from the known charm hadron masses by at least three times the experimental resolution. For the Λb0 → Λc+π− control mode, only the Λb0 → ph+h−π− events with reconstructed ph+h− invariant mass between 2.23 and 2.31 GeV/c2are retained.
A boosted decision tree (BDT) classifier40 is constructed from a set of kinematic variables that discriminate between signal and background. The signal and background training samples used for the BDT are derived from the Λb0 → pK−π+π− control sample, since its kinematics and topology are similar to the decays under study; background in this sample is subtracted with the sPlot technique41, a statistical technique to disentangle signal and background contributions. The background training sample consists of candidates that lie far from the signal mass peak, between 5.85 and 6.40 GeV/c2. The control modes Λb0 → Λc+(pπ+π−)π− and Λb0 → Λc+(pK−K+)π− are used to optimize the particle identification criteria for the signal mode with the same final state. For events in which multiple candidates pass all selection criteria for a given mode, one candidate is retained at random and the rest discarded.
Unbinned extended maximum likelihood fits to the pπ−π+π− and the pπ−K+K− invariant mass distributions are shown in Fig. 2. The invariant mass distribution of the Λb0 signal is modelled by a Gaussian core with power-law tails42, with the mean and the width of the Gaussian determined from the fit to data. The combinatorial background is modelled by an exponential distribution with the rate parameter extracted from data. All other parameters of the fit model are taken from simulations except the yields. Partially reconstructed Λb0 decays are described by an empirical function43 convolved with a Gaussian function to account for resolution effects. The shapes of backgrounds from other b-hadron decays due to incorrectly identified particles, for example, kaons identified as pions or protons identified as kaons, are modelled using simulated events. These consist mainly of Λb0 → pK−π+π− and B0 → K+π−π−π+ decays for the Λb0 → pπ−π+π− sample and of similar final states for the Λb0 → pπ−K+K− sample, as shown in Fig. 2. The yields of these contributions are obtained from fits to data reconstructed under the appropriate mass hypotheses for the final-state particles. The signal yields of Λb0 → pπ−π+π− and Λb0 → pπ−K+K− are 6,646 ± 105 and 1,030 ± 56, respectively. This is the first observation of these decay modes.
The invariant mass distributions for (a) Λb0 → pπ−π+π− and (b) Λb0 → pπ−K+K− decays are shown. A fit is overlaid on top of the data points, with solid and dotted lines describing the projections of the fit results for each of the components described in the text and listed in the legend. Uncertainties on the data points are statistical only and represent one standard deviations, calculated assuming Poisson-distributed entries.
Signal candidates are split into four categories according to Λb0 or  flavour and the sign of
flavour and the sign of  or
or  to calculate the asymmetries defined in equations (1) and (2). The reconstruction efficiency for signal candidates with
to calculate the asymmetries defined in equations (1) and (2). The reconstruction efficiency for signal candidates with  > 0 is identical to that with
> 0 is identical to that with  < 0 within the statistical uncertainties of the control sample, and likewise for
< 0 within the statistical uncertainties of the control sample, and likewise for  , which indicates that the detector and the reconstruction program do not bias this measurement. This check is performed both on the Λb0 → Λc+(pK−π+)π− data control sample and on large samples of simulated events, using yields about 30 times those found in data, which are generated with no CP asymmetry. The CP asymmetry measured in the control sample is
, which indicates that the detector and the reconstruction program do not bias this measurement. This check is performed both on the Λb0 → Λc+(pK−π+)π− data control sample and on large samples of simulated events, using yields about 30 times those found in data, which are generated with no CP asymmetry. The CP asymmetry measured in the control sample is  %, compatible with CP symmetry. The asymmetries
%, compatible with CP symmetry. The asymmetries  and
and  in the signal samples are measured with a simultaneous unbinned maximum likelihood fit to the invariant mass distributions of the different signal categories, and are found to be uncorrelated. Corresponding asymmetries for each of the background components are also measured in the fit; they are found to be consistent with zero, and do not lead to significant systematic uncertainties in the signal asymmetries. The values of
in the signal samples are measured with a simultaneous unbinned maximum likelihood fit to the invariant mass distributions of the different signal categories, and are found to be uncorrelated. Corresponding asymmetries for each of the background components are also measured in the fit; they are found to be consistent with zero, and do not lead to significant systematic uncertainties in the signal asymmetries. The values of  and
and  are then calculated from
are then calculated from  and
and  .
.
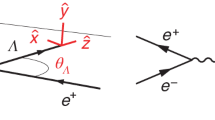
In four-body particle decays, the CP asymmetries may vary over the phase space due to resonant contributions or their interference effects, possibly cancelling when integrated over the whole phase space. Therefore, the asymmetries are measured in different regions of phase space for the Λb0 → pπ−π+π− decay using two binning schemes, defined before examining the data. Scheme A, defined in Table 1, is designed to isolate regions of phase space according to their dominant resonant contributions. Scheme B exploits in more detail the interference of contributions which could be visible as a function of the angle Φ between the decay planes formed by the pπfast− and the πslow−π+ systems, as illustrated in Fig. 3. Scheme B has ten non-overlapping bins of width π/10 in | Φ | . For every bin in each of the schemes, the Λb0 efficiencies for  > 0 and
> 0 and  < 0 are compared and found to be equal within uncertainties, and likewise the
< 0 are compared and found to be equal within uncertainties, and likewise the  efficiencies for
efficiencies for  > 0 and
> 0 and  < 0. The analysis technique is validated on the Λb0 → Λc+(pK−π+)π− control sample, for which the angle Φ is defined by the decay planes of the pK− and π+π− pairs, and on simulated signal events.
< 0. The analysis technique is validated on the Λb0 → Λc+(pK−π+)π− control sample, for which the angle Φ is defined by the decay planes of the pK− and π+π− pairs, and on simulated signal events.
The decay planes formed by the pπfast− (blue) and the πslow−π+ (red) systems in the Λb0 rest frame. The momenta of the particles, represented by vectors, determine the two decay planes and the angle Φ ∈ [−π, π] (ref. 19) measures their relative orientation.
The asymmetries measured in Λb0 → pπ−π+π− decays with these two binning schemes are shown in Fig. 4 and reported in Table 2, together with the integrated measurements. For each scheme individually, the compatibility with the CP-symmetry hypothesis is evaluated by means of a χ2 test, with χ2 = RTV−1R, where R is the array of  measurements and V is the covariance matrix, which is the sum of the statistical and systematic covariance matrices. An average systematic uncertainty, whose evaluation is discussed below, is assigned for all bins. The systematic uncertainties are assumed to be fully correlated; their contribution is small compared to the statistical uncertainties. The p-values of the CP-symmetry hypothesis are 4.9 × 10−2 and 7.1 × 10−4 for schemes A and B, respectively, corresponding to statistical significances of 2.0 and 3.4 Gaussian standard deviations (σ). A similar χ2 test is performed on
measurements and V is the covariance matrix, which is the sum of the statistical and systematic covariance matrices. An average systematic uncertainty, whose evaluation is discussed below, is assigned for all bins. The systematic uncertainties are assumed to be fully correlated; their contribution is small compared to the statistical uncertainties. The p-values of the CP-symmetry hypothesis are 4.9 × 10−2 and 7.1 × 10−4 for schemes A and B, respectively, corresponding to statistical significances of 2.0 and 3.4 Gaussian standard deviations (σ). A similar χ2 test is performed on  measurements with p-values for the P-symmetry hypothesis of 5.8 × 10−3 (2.8σ) and 2.4 × 10−2 (2.3σ), for scheme A and B, respectively. The overall significance for CPV in Λb0 → pπ−π+π− decays from the results of schemes A and B is determined by means of a permutation test44, taking into account correlations among the results. A sample of 40,000 pseudoexperiments is generated from the data by assigning each event a random
measurements with p-values for the P-symmetry hypothesis of 5.8 × 10−3 (2.8σ) and 2.4 × 10−2 (2.3σ), for scheme A and B, respectively. The overall significance for CPV in Λb0 → pπ−π+π− decays from the results of schemes A and B is determined by means of a permutation test44, taking into account correlations among the results. A sample of 40,000 pseudoexperiments is generated from the data by assigning each event a random  flavour such that CP symmetry is enforced. The sign of
flavour such that CP symmetry is enforced. The sign of  is unchanged if a Λb0 candidate stays Λb0 and reversed if the Λb0 candidate becomes
is unchanged if a Λb0 candidate stays Λb0 and reversed if the Λb0 candidate becomes  . The p-value of the CP-symmetry hypothesis is determined as the fraction of pseudoexperiments with χ2 larger than that measured in data. Applying this method to the χ2 values from schemes A and B individually, the p-values obtained agree with those from the χ2 test within the uncertainty due to the limited number of pseudoexperiments. To assess a combined significance from the two schemes, the product of the two p-values measured in data is compared with the distribution of the product of the p-values of the two binning schemes from the pseudoexperiments. The fraction of pseudoexperiments whose p-value product is smaller than that seen in data determines the overall p-value of the combination of the two schemes45. An overall p-value of 9.8 × 10−4 (3.3σ) is obtained for the CP-symmetry hypothesis, including systematic uncertainties.
. The p-value of the CP-symmetry hypothesis is determined as the fraction of pseudoexperiments with χ2 larger than that measured in data. Applying this method to the χ2 values from schemes A and B individually, the p-values obtained agree with those from the χ2 test within the uncertainty due to the limited number of pseudoexperiments. To assess a combined significance from the two schemes, the product of the two p-values measured in data is compared with the distribution of the product of the p-values of the two binning schemes from the pseudoexperiments. The fraction of pseudoexperiments whose p-value product is smaller than that seen in data determines the overall p-value of the combination of the two schemes45. An overall p-value of 9.8 × 10−4 (3.3σ) is obtained for the CP-symmetry hypothesis, including systematic uncertainties.
The results of the fit in each region of binning schemes A and B are shown. The asymmetries  and
and  for Λb0 → pπ−π+π− decays are represented by open boxes and filled circles, respectively. The error bars represent one standard deviation, calculated as the sum in quadrature of the statistical uncertainty resulting from the fit to the invariant mass distribution and the systematic uncertainties estimated as described in the main text. The values of the χ2/ndf are quoted for the P- and CP-conserving hypotheses for each binning scheme, where ndf indicates the number of degrees of freedom.
for Λb0 → pπ−π+π− decays are represented by open boxes and filled circles, respectively. The error bars represent one standard deviation, calculated as the sum in quadrature of the statistical uncertainty resulting from the fit to the invariant mass distribution and the systematic uncertainties estimated as described in the main text. The values of the χ2/ndf are quoted for the P- and CP-conserving hypotheses for each binning scheme, where ndf indicates the number of degrees of freedom.
For the Λb0 → pπ−K+K− decays, the smaller purity and signal yield of the sample do not permit PV and CPV to be probed with the same precision as for Λb0 → pπ−π+π−, and therefore only two regions of phase space are considered. One spans 1.43 < m(pK−) < 2.00 GeV/c2(bin 1) and is dominated by excited Λ resonances decaying to pK and the other covers the remaining phase space, 2.00 < m(pK−) < 4.99 GeV/c2(bin 2). The observables measured in these regions are given in Table 2 and are consistent with CP and P symmetry.
The main sources of systematic uncertainties for both pπ−π+π− and pπ−K+K− decays are experimental effects that could introduce biases in the measured asymmetries. This is tested by measuring the asymmetry  , integrated over phase space and in various phase space regions, using the control sample Λb0 → Λc+(pK−π+)π−, which is expected to exhibit negligible CPV. The results are in agreement with the CP-symmetry hypothesis; an uncertainty of 0.31% is assigned as a systematic uncertainty for the
, integrated over phase space and in various phase space regions, using the control sample Λb0 → Λc+(pK−π+)π−, which is expected to exhibit negligible CPV. The results are in agreement with the CP-symmetry hypothesis; an uncertainty of 0.31% is assigned as a systematic uncertainty for the  and
and  integrated measurements; an uncertainty of 0.60%, the largest asymmetry from a fit to scheme B measurements using a range of efficiency and fit models, is assigned for the corresponding phase space measurements. The systematic uncertainty arising from the experimental resolution in the measurement of the triple products
integrated measurements; an uncertainty of 0.60%, the largest asymmetry from a fit to scheme B measurements using a range of efficiency and fit models, is assigned for the corresponding phase space measurements. The systematic uncertainty arising from the experimental resolution in the measurement of the triple products  and
and  , which could introduce a migration of events between the bins, is estimated from simulated samples of Λb0 → pπ−π+π− and Λb0 → pπ−K+K− decays where neither P- nor CP-violating effects are present. The difference between the reconstructed and generated asymmetry is taken as a systematic uncertainty due to this effect, and is less than 0.06% in all cases. To assess the uncertainty associated with the fit models, alternative functions are used; these tests lead only to small changes in the asymmetries, the largest being 0.05%. For Λb0 → pπ−K+K− decays, this contribution is larger, about 0.28% for the
, which could introduce a migration of events between the bins, is estimated from simulated samples of Λb0 → pπ−π+π− and Λb0 → pπ−K+K− decays where neither P- nor CP-violating effects are present. The difference between the reconstructed and generated asymmetry is taken as a systematic uncertainty due to this effect, and is less than 0.06% in all cases. To assess the uncertainty associated with the fit models, alternative functions are used; these tests lead only to small changes in the asymmetries, the largest being 0.05%. For Λb0 → pπ−K+K− decays, this contribution is larger, about 0.28% for the  and
and  asymmetries.
asymmetries.
Further cross-checks are made to investigate the stability of the results with respect to different periods of recording data, different polarities of the spectrometer magnet, the choice made in the selection of multiple candidates, and the effect of the trigger and selection criteria. Alternative binning schemes are studied as a cross-check, such as using 8 or 12 bins in | Φ | for Λb0 → pπ−π+π− decays. For these alternative binning schemes, the significance of the CPV measurement of the modified scheme B is reduced to below 3σ. Nonetheless, the overall significance of the combination of these two additional binnings with schemes A and B remains above three standard deviations, with a p-value of 1.8 × 10−3 (3.1σ), consistent with the 3.3σ result seen in the baseline analysis. An independent analysis of the data based on alternative selection criteria confirmed the results. It used a similar number of events, of which 73.4% are in common with the baseline analysis, and gave p-values for CP symmetry of 3.4 × 10−3 (2.9σ) for scheme A and 1.4 × 10−4 (3.8σ) for scheme B.
In conclusion, a search for P and CP violation in Λb0 → pπ−π+π− and Λb0 → pπ−K+K− decays is performed on signal yields of 6,646 ± 105 and 1,030 ± 56 events. This is the first observation of these decay modes. Measurements of asymmetries in the entire phase space do not show any evidence of P or CP violation. Searches for localized P or CP violation are performed by measuring asymmetries in different regions of the phase space. The results are consistent with CP symmetry for Λb0 → pπ−K+K− decays, but evidence for CP violation at the 3.3σ level is found in Λb0 → pπ−π+π− decays. No significant P violation is found. This represents the first evidence of CP violation in the baryon sector, and indicates an asymmetry between baryonic matter and antimatter.
Data availability.
All data shown in histograms and plots are publicly available from HEPdata (https://hepdata.net).
References
Cabibbo, N. Unitary symmetry and leptonic decays. Phys. Rev. Lett. 10, 531–533 (1963).
Kobayashi, M. & Maskawa, T. CP violation in the renormalizable theory of weak interaction. Prog. Theor. Phys. 49, 652–657 (1973).
Sakharov, A. D. Violation of CP invariance, C asymmetry, and baryon asymmetry of the universe. JETP Lett. 5, 24–27 (1967); Sov. Phys. Usp. 34, 392–393 (1991).
Riotto, A. Theories of Baryogenesis. In Proc. Summer School in High-energy Physics and Cosmology (eds Gava, E. et al.) 326–436 (World Scientific, 1998).
Christenson, J. H., Cronin, J. W., Fitch, V. L. & Turlay, R. Evidence for the 2π decay of the K 2 0 Meson. Phys. Rev. Lett. 13, 138–140 (1964).
Aubert, B. et al. Observation of CP violation in the B0 meson system. Phys. Rev. Lett. 87, 091801 (2001).
Abe, K. et al. Observation of large CP violation in the neutral B meson system. Phys. Rev. Lett. 87, 091802 (2001).
Aubert, B. et al. Improved measurement of the CKM angle γ in B∓ → D(∗)K(∗)∓ decays with a Dalitz plot analysis of D decays to K S0π+π− and K S0K+K− . Phys. Rev. D 78, 034023 (2008).
Poluektov, A. et al. Evidence for direct CP violation in the decay B+ → D(∗)K+, D → K+π+π− and measurement of the CKM phase φ 3 . Phys. Rev. D 81, 112002 (2010).
Aaij, R. et al. Observation of CP violation in B± → DK± decays. Phys. Lett. B 712, 203–212 (2012); erratum 713, 351 (2012).
Aaij, R. et al. Measurement of CP violation in the phase space of B± → K±π+π− and B± → K±K+K− decays. Phys. Rev. Lett. 111, 101801 (2013).
Aaij, R. et al. First observation of CP violation in the decays of B s0 mesons. Phys. Rev. Lett. 110, 221601 (2013).
Hsiao, Y. K. & Geng, C. Q. Direct CP violation in Λ b0 decays. Phys. Rev. D 91, 116007 (2015).
Bensalem, W. & London, D. T-odd triple-product correlations in hadronic b decays. Phys. Rev. D 64, 116003 (2001).
Bensalem, W., Datta, A. & London, D. New physics effects on triple-product correlations in Λ b0 decays. Phys. Rev. D 66, 094004 (2002).
Bensalem, W., Datta, A. & London, D. T-violating triple-product correlations in charmless Λ b0 decays. Phys. Lett. B 538, 309–320 (2002).
Sachs, R. G. The Physics of Time Reversal (Univ. Chicago Press, 1987).
Branco, G. C., Lavoura, L. & Silva, J. P. CP Violation (Oxford Univ. Press, 1999).
Durieux, G. & Grossman, Y. Probing CP violation systematically in differential distributions. Phys. Rev. D 92, 076013 (2015).
Durieux, G. CP violation in multibody decays of beauty baryons. JHEP 10, 005 (2016).
Gasiorowicz, S. Elementary particle physics (Wiley, 1966).
Bigi, I. I. Y. Charm Physics: Like Botticelli in the Sistine Chapel. Preprint at https://arxiv.org/abs/hep-ph/0107102 (2001).
Gronau, M. & Rosner, J. L. Triple product asymmetries in K, D (s) and B (s) decays. Phys. Rev. D 84, 096013 (2011).
Gronau, M. & Rosner, J. L. Triple product asymmmetries in Λ b0 and Ξ b0 decays. Phys. Lett. B 749, 104–107 (2015).
Valencia, G. Angular correlations in the decay B → VV and CP violation. Phys. Rev. D 39, 3339–3345 (1989).
Aaij, R. et al. Search for CP violation using T-odd correlations in D0 → K+K−π+π− decays. JHEP 10, 005 (2014).
Aaij, R. et al. Measurement of b-hadron production fractions in 7 TeV pp collisions. Phys. Rev. D 85, 032008 (2012).
Aaij, R. et al. Study of the kinematic dependences of Λ b0 production in pp collisions and a measurement of the Λ b0 → Λ c+π− branching fraction. JHEP 08, 143 (2014).
Alves, A. A. Jr et al. The LHCb detector at the LHC. JINST 3, S08005 (2008).
Aaij, R. et al. LHCb detector performance. Int. J. Mod. Phys. A 30, 1530022 (2015).
LHCb collaboration. LHC-B: A Dedicated LHC Collider Beauty Experiment for Precision Measurements of CP Violation Letter of intent (CERN-LHCC-95-05, 1995); http://cds.cern.ch/record/290868
Sjöstrand, T., Mrenna, S. & Skands, P. PYTHIA 6.4 physics and manual. JHEP 05, 026 (2006).
Sjöstrand, T., Mrenna, S. & Skands, P. A brief introduction to PYTHIA 8.1. Comput. Phys. Commun. 178, 852–867 (2008).
Belyaev, I. et al. Handling of the generation of primary events in Gauss, the LHCb simulation framework. J. Phys. Conf. Ser. 331, 032047 (2011).
Lange, D. J. The EvtGen particle decay simulation package. Nucl. Instrum. Meth. A 462, 152–155 (2001).
Allison, J. et al. Geant4 developments and applications. IEEE Trans. Nucl. Sci. 53, 270–278 (2006).
Agostinelli, S. et al. Geant4: A simulation toolkit. Nucl. Instrum. Meth. A 506, 250–303 (2003).
Clemencic, M. et al. The LHCb simulation application, Gauss: design, evolution and experience. J. Phys. Conf. Ser. 331, 032023 (2011).
Olive, K. A. et al. Review of particle physics. Chin. Phys. C 38, 090001 (2014).
Breiman, L., Friedman, J. H., Olshen, R. A. & Stone, C. J. Classification and Regression Trees (Wadsworth International Group, 1984).
Pivk, M. & Le Diberder, F. R. sPlot: a statistical tool to unfold data distributions. Nucl. Instrum. Meth. A 555, 356–369 (2005).
Skwarnicki, T. A study of the radiative CASCADE transitions between the Upsilon-Prime and Upsilon resonances (Ph.D. thesis, 1986); https://inspirehep.net/record/230779
Albrecht, H. et al. Search for hadronic b → u decays. Phys. Lett. B 241, 278–282 (1990).
Fisher, R. A. The design of experiments (Oliver and Boyd Ltd., 1935).
Data analysis in high energy physics (eds Behnke, O., Kröninger, K., Schörner-Sadenius, T. & Schott, G.) (Wiley, 2013).
Acknowledgements
We express our gratitude to our colleagues in the CERN accelerator departments for the excellent performance of the LHC. We thank the technical and administrative staff at the LHCb institutes. We acknowledge support from CERN and from the national agencies: CAPES, CNPq, FAPERJ and FINEP (Brazil); NSFC (China); CNRS/IN2P3 (France); BMBF, DFG and MPG (Germany); INFN (Italy); FOM and NWO (The Netherlands); MNiSW and NCN (Poland); MEN/IFA (Romania); MinES and FASO (Russia); MinECo (Spain); SNSF and SER (Switzerland); NASU (Ukraine); STFC (United Kingdom); NSF (USA). We acknowledge the computing resources that are provided by CERN, IN2P3 (France), KIT and DESY (Germany), INFN (Italy), SURF (The Netherlands), PIC (Spain), GridPP (United Kingdom), RRCKI and Yandex LLC (Russia), CSCS (Switzerland), IFIN-HH (Romania), CBPF (Brazil), PL-GRID (Poland) and OSC (USA). We are indebted to the communities behind the multiple open source software packages on which we depend. Individual groups or members have received support from AvH Foundation (Germany), EPLANET, Marie Skłodowska-Curie Actions and ERC (European Union), Conseil Général de Haute-Savoie, Labex ENIGMASS and OCEVU, Région Auvergne (France), RFBR and Yandex LLC (Russia), GVA, XuntaGal and GENCAT (Spain), Herchel Smith Fund, The Royal Society, Royal Commission for the Exhibition of 1851 and the Leverhulme Trust (United Kingdom).
Author information
Authors and Affiliations
Consortia
Contributions
All authors have contributed to the publication, being variously involved in the design and the construction of the detectors, in writing software, calibrating sub-systems, operating the detectors and acquiring data, and finally analysing the processed data.
Corresponding author
Ethics declarations
Competing interests
The author declare no competing financial interests.
Rights and permissions
This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the articles Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the articles Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
The LHCb collaboration. Measurement of matter–antimatter differences in beauty baryon decays. Nature Phys 13, 391–396 (2017). https://doi.org/10.1038/nphys4021
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys4021
This article is cited by
-
A novel strategy for searching for CP violations in the baryon sector
Journal of High Energy Physics (2021)
-
SU(3)F analysis for beauty baryon decays
Journal of High Energy Physics (2020)
-
Baryon decays to purely baryonic final states
Scientific Reports (2019)
-
K0 S − K0 L asymmetries and CP violation in charmed baryon decays into neutral kaons
Journal of High Energy Physics (2018)
-
Characterization of the 1S–2S transition in antihydrogen
Nature (2018)